1 Introduction

Nonlinear ordinary differential equations (ODEs) and nonlinear partial differential equations (PDEs) play a very important role in describing some complex physical phenomena arising in various fields of science and engineering such as condensed matter, plasma physics, nonlinear quantum, nonlinear optics, biophysics, fluid mechanics, theory of turbulence and phase transitions. Many scientists pay attention to the research into the exact solution of these PDEs but, in general, it is difficult to obtain the exact solution of some partial differential equations. Nonetheless, with the development of the soliton theory, many powerful methods, such as inverse scattering theory [1], Hirota bilinear form [2, 3], Bäclund transformation [4], Darboux trasformation [5], homotopy perturbation method [6], a generalized Jacobi elliptic function expansion method [7], Lie symmetry [8–10] and so on, have been presented to obtain the exact solution of nonlinear PDEs. When these methods fail or are difficult to apply, numerical studies are essential to understand the behaviour of the solution of the nonlinear PDE. Numerical solutions of PDEs began in the early 1950s by finite difference approximation. They were followed by the finite element solution in 1960s and spectral methods in 1970s. Almost all of these standard schemes require a restriction on the step size for convergence to the exact solution. Mickens [11] gave a novel approach for developing new finite difference schemes for ODEs. According to Mickens’s approach, denominator functions for the discrete derivatives, in general, should be expressed in terms of more complicated functions of the step sizes than those conventionally used. In addition to normalising the denominator function, nonlinear terms must, in general, be modelled non-locally. The orders of the discrete derivatives must be exactly equal to the orders of the corresponding derivatives of the differential equations. If the orders of the discrete derivatives are larger than those occurring in the differential equations, then numerical instabilities, in general, occur. This approach may avoid the numerical instabilities by incorporating dynamics of the system into the scheme.

Recently, many scientist have paid attention to nonstandard finite difference (NSFD) solution of PDEs. Appadu [12] studied numerical solution of the 1D advection-diffusion equation using standard and NSFD schemes. Also, in [13] the author constructed three numerical methods to solve a 1-D KdVB equation. Appadu et al. [14] used three numerical methods to solve two test problems. Aydin et al. [15] proposed a linearly implicit nonstandard finite difference method for the numerical solution of modified Korteweg–de Vries equation. Koroglu et al. [16] studied the numerical solution of the modified Korteweg–de Vries (MKdV) equation by using an NSFD scheme with theta method which includes the implicit Euler and a Crank–Nicolson type discretization. Zhang et al. [17] developed an explicit NSFD scheme for the numerical solution of a coupled Burgers equation. In [18] Cui et al. proposed an NSFD scheme for an SIR epidemic model of childhood disease with constant strategy. In [19] Khalsaraei et al. introduced positivity preserving explicit finite difference schemes based on the nonstandard discretization method to approximate solution of the cross-diffusion system from bioscience. In [20] Chapwanya et al. designed several dynamically consistent NSFD schemes for some reaction-diffusion equations, advection-reaction equations and advection-reaction-diffusion equations by using the exact scheme of the Michaelis–Menten ordinary differential equation. Agbavon et al. [21] proposed four schemes, namely FTCS-ϵ, NSFD-ϵ, FTCS with artificial viscosity and NSFD with artificial viscosity. In [22] the authors presented numerical solutions of the FitzHugh–Naguma system of equations. The authors constructed four numerical methods to solve the Burgers–Huxley equation in [23].

The exact finite difference scheme is also an important issue for the construction of new numerical algorithms in ODE and PDE, and it plays a key role in determining the appropriate denominator function. It is a special NSFD scheme which is available if the solution of the ODE exists [24]. It is proposed to annihilate the weakness of a finite difference scheme such as numerical instability. Numerical instability is removed when a convenient denominator function is used instead of the standard step length Δt. In [25, 26] Rogers et al. constructed exact finite difference schemes for one- and two-dimensional linear systems with constant coefficients. Exact finite difference schemes for first order differential equations having three distinct fixed-points are studied in [27]. In [28] Jiang et al. constructed exact finite difference schemes for linear stochastic differential equations with constant coefficients.

The generalized KdV–Burger equation [29] is dispersive dissipative nonlinear PDE

$$ u_{t}+a\bigl(u^{p}\bigr)_{x}-b \bigl(u^{m}\bigr)_{xxx}+c\bigl(u^{q} \bigr)_{xx}=0, $$
(1)

where \(p,m,n\) are nonzero integers and \(a,b,c\) are nonzero real numbers. Equations of this type with values of \(p,m,q\) will be denoted by \(\operatorname{KdVB}(p,m,q)\). Equation (1) is a model equation incorporating the effects of dispersion \(u_{xxx}\), dissipation \(u_{xx}\) and nonlinearities \((u^{p}),(u^{m}),(u^{q})\). The \(\operatorname{KdVB}(p,m,q)\) equation (1) is a generalized equation in the following sense:

  1. 1

    If \(p=2,b=0\) and \(q=1\), equation (1) leads to the well-known Burgers equation [30–32]

    $$ u_{t}+2auu_{x}+cu_{xx}=0 $$
    (2)

    with the kink wave solution

    $$ u(x,t)=\frac{k}{a}+\frac{ck}{a}\tanh (\bigl(k(x-2kt)\bigr). $$
    (3)
  2. 2

    If \(p=2,c=0\) and \(m=1\), equation (1) leads to the well-known Korteweg–de Vries (KdV) equation [33]

    $$ u_{t}+2auu_{x}+bu_{xxx}=0 $$
    (4)

    with the soliton solution

    $$ u(x,t)=\frac{6ck^{2}}{a}\sec h^{2}\bigl(k\bigl(x-4ck^{2}t \bigr)\bigr). $$
    (5)
  3. 3

    If \(p=2,m=1\) and \(q=1\), equation (1) leads to the KdV–Burger equation [34, 35]

    $$ u_{t}+2auu_{x}+bu_{xxx}+cu_{xx}=0 $$
    (6)

    with the exact solution

    $$ u(x,t)=-\frac{3c^{2}}{25ab}\bigl(-\sec h^{2}\bigl(k(x-x_{0})- \alpha t\bigr)+2\tanh \bigl(k(x-x_{0})- \alpha t\bigr)+2\bigr). $$
    (7)
  4. 4

    If \(b=0\) and \(p=q=n\), then equation (1) leads to the generalized Burger \(B(n,n)\) equation [29]

    $$ u_{t}+a\bigl(u^{n}\bigr)_{x}+c \bigl(u^{q}\bigr)_{xx}=0. $$
    (8)
  5. 5

    If \(c=0\) and \(p=m=n\), then equation (1) leads to the generalized KdV \(K(n,n)\) equation [36]

    $$ u_{t}+a\bigl(u^{n}\bigr)_{x}+b \bigl(u^{n}\bigr)_{xxx}=0, $$
    (9)

    which has compact and noncompact structures [37].

In this study, we consider the \(\operatorname{KdVB}(2,1,2)\) equation

$$ u_{t}+\bigl(u^{2}\bigr)_{x}-0.1u_{xxx}+ \bigl(u^{2}\bigr)_{xx}=0 $$
(10)

and construct some exact finite difference and NSFD schemes which have never been proposed and studied in the literature before. The rest of the paper is organised as follows. In Sect. 2 three explicit and three fully implicit exact finite difference schemes are presented. In Sect. 3 a consistent linearly implicit NSFD scheme is constructed by extending the rules of NSFD schemes given in [38]. Local truncation error is also studied. We investigate the linear stability analysis for the NSFD and SFD schemes by using von Neumann stability analysis in Sect. 4. To illustrate the efficiency of the NSFD scheme, some numerical results are given in Sect. 5. Numerical solutions obtained by the NSFD scheme are compared with the standard finite difference (SFD) scheme. Finally, Sect. 6 gives a summary of the results obtained in this paper.

2 Exact finite difference schemes for \(\operatorname{KdVB}(2,1,2)\) equation

An exact finite difference scheme is a finite difference model for which the solution to the difference equation has the same general solution as the associated differential equation [38]. Recently, there has been an increasing interest in exact finite difference models for particular ODEs and PDEs, because they let a better construction of finite difference schemes (see [39, 40] and the references therein). These finite difference models do not exhibit numerical instabilities. However, not every ODE and PDE has an exact finite difference model. In this section we construct six exact finite difference schemes for the \(\operatorname{KdVB}(2,1,2)\) equation (10).

We start with the kink-wave solution

$$\begin{aligned} u(x,t)&=-\frac{1}{20} \biggl(1+\tanh \biggl[\frac{t}{20}+ \frac{x}{2} \biggr] \biggr) \\ &= -\frac{0.1}{1+e^{-(x+0.1t)}}. \end{aligned}$$
(11)

If \(\Delta t=10h\), then it can be shown that \(u(x+h,t)=u(x,t+\Delta t)\) and \(u(x-h,t)=u(x,t-\Delta t)\). The relations

$$ \begin{aligned} &\frac{1}{u(x,t)}=-10 \bigl(1+e^{-(x+0.1t)} \bigr), \\ &\frac{1}{u(x+h,t)}=-10 \bigl(1+e^{-(x+h+0.1t)} \bigr), \\ &\frac{1}{u(x-h,t)}=-10 \bigl(1+e^{-(x-h+0.1t)} \bigr) \end{aligned} $$
(12)

can be easily obtained from (11). Using these relations, we can write

$$ \begin{aligned} &\frac{1}{u(x,t)}-\frac{1}{u(x+h,t)}= \biggl(10+\frac{1}{u(x,t)} \biggr) \bigl(1-e^{-h} \bigr), \\ &\frac{1}{u(x,t)}-\frac{1}{u(x-h,t)}= \biggl(10+\frac{1}{u(x,t)} \biggr) \bigl(1-e^{h} \bigr). \end{aligned} $$
(13)

Let the step functions be \(\varPsi _{1}=e^{h}-1\), \(\varPsi _{2}=1-e^{-h}\), \(\varPhi _{1}=\frac{1-e^{-0.1\Delta t}}{0.1}\) and \(\varPhi _{2}=\frac{e^{0.1\Delta t}-1}{0.1}\). Then \(\varPhi _{1}=10\varPsi _{2}\) and \(\varPhi _{2}=10\varPsi _{1}\). Using relations (13), we can obtain the following forward and backward difference quotients:

$$ \begin{aligned}& \partial _{x}u= \frac{u(x+h,t)-u(x,t)}{\varPsi _{2}}=u(x+h,t) \bigl(1+10u(x,t)\bigr), \\ &\overline{\partial _{x}}u= \frac{u(x,t)-u(x-h,t)}{\varPsi _{1}}=u(x-h,t) \bigl(1+10u(x,t)\bigr) \end{aligned} $$
(14)

for first order spatial derivatives.

For the second and third derivatives, we have some possibilities. For the second derivative \(u_{xx}\), we consider the four possibilities \(u_{xx}=\partial _{x}\overline{\partial _{x}}u\), \(u_{xx}=\overline{\partial _{x}}\partial _{x}u\), \(u_{xx}=\partial _{x}\partial _{x}u\) or \(u_{xx}=\overline{\partial _{x}}\overline{\partial _{x}}u\), and for the third derivative \(u_{xxx}\), we consider the six possibilities \(u_{xxx}=\partial _{x}\partial _{x}\overline{\partial _{x}}u\), \(u_{xxx}=\partial _{x}\overline{\partial _{x}}\partial _{x}u\), \(u_{xxx}=\overline{\partial _{x}}\partial _{x}\partial _{x}u\), \(u_{xxx}=\partial _{x}\overline{\partial _{x}} \overline{\partial _{x}}u\), \(u_{xxx}=\overline{\partial _{x}}\overline{\partial _{x}}\partial _{x}u\) or \(u_{xxx}=\overline{\partial _{x}}\partial _{x} \overline{\partial _{x}}u\).

2.1 Implicit exact finite differences for \(\operatorname{KdVB}(2,1,2)\) equation

In this section three implicit exact finite difference model are constructed for the \(\operatorname{KdVB}(2,1,2)\) equation (10). If we select \(u_{xx}=\partial _{x}\overline{\partial _{x}}u\), with the help of (14), we can get

$$ \partial _{x}\overline{\partial _{x}}u= \frac{u(x+h,t)-u(x,t)}{\varPsi _{1}}+10u(x,t) \frac{u(x+h,t)-u(x-h,t)}{\varPsi _{1}}. $$
(15)

If we select \(u_{xxx}=\partial _{x}\partial _{x}\overline{\partial _{x}}u\), using equations (14) and (15), we can get

$$\begin{aligned} \partial _{x}\partial _{x}\overline{ \partial _{x}}u={}& 10\frac{u(x,t+\Delta t)-u(x,t)}{\varPhi _{1}} \\ &{}+10u(x+h,t) \frac{u(x+2h,t)-u(x+h,t)}{\varPsi _{2}} \\ & {}+10u(x+h,t)\frac{u(x+h,t)-u(x,t)}{\varPsi _{2}} \\ &{} +10u(x,t) \frac{u(x+2h,t)-2u(x+h,t)+u(x,t)}{\varPsi _{1}\varPsi _{2}} \\ &{} +10u(x,t) \frac{u(x+h,t)-2u(x,t)+u(x-h,t)}{\varPsi _{1}\varPsi _{2}} \\ &{} +20\frac{u(x+h,t)-u(x,t)}{\varPsi _{2}} \frac{u(x+h,t)-u(x-h,t)}{2\varPsi _{1}}. \end{aligned}$$
(16)

Now we consider solution (11) at the discrete point \((x_{j},t_{n})\):

$$ U_{j}^{n}=u(x_{j},t_{n})= - \frac{0.1}{1+e^{-(x_{j}+0.1t_{n})}}. $$
(17)

Then we can write an implicit exact finite difference scheme (IMPEXFDI) by means of (16):

$$\begin{aligned} &\frac{U_{j+2}^{n+1}-3U_{j+1}^{n+1}+3U_{j}^{n+1}-U_{j-1}^{n+1}}{\varPsi _{1}\varPsi _{2}^{2}} \\ &\quad = 10\frac{U_{j}^{n+1}-U_{j}^{n}}{\varPhi _{1}}+10U_{j+1}^{n+1} \biggl(\frac{U_{j+2}^{n+1}-U_{j+1}^{n+1}}{\varPsi _{2}} \biggr) \\ &\qquad{} +10U_{j+1}^{n+1} \biggl( \frac{U_{j+1}^{n+1}-U_{j}^{n+1}}{\varPsi _{2}} \biggr)+10U_{j}^{n+1} \biggl( \frac{U_{j+2}^{n+1}-2U_{j+1}^{n+1}+U_{j}^{n+1}}{\varPsi _{1}\varPsi _{2}} \biggr) \\ &\qquad{} +10U_{j}^{n+1} \biggl( \frac{U_{j+1}^{n+1}-2U_{j}^{n+1}+U_{j-1}^{n+1}}{\varPsi _{1}\varPsi _{2}} \biggr) \\ &\qquad{} +20 \biggl(\frac{U_{j+1}^{n+1}-U_{j}^{n+1}}{\varPsi _{2}} \biggr) \biggl(\frac{U_{j+1}^{n+1}-U_{j-1}^{n+1}}{2\varPsi _{1}} \biggr). \end{aligned}$$
(18)

Now we select \(u_{xx}=\overline{\partial _{x}}\partial _{x} u\). Using the first order derivative approximation (14), we get

$$ \overline{\partial _{x}}\partial _{x} u= \frac{u(x,t)-u(x-h,t)}{\varPsi _{2}}+10u(x,t) \frac{u(x+h,t)-u(x-h,t)}{\varPsi _{2}}. $$
(19)

We select \(u_{xxx}=\partial _{x}\overline{\partial _{x}}\partial _{x}u\), using (19), we have

$$\begin{aligned} \partial _{x}\overline{\partial _{x}} \partial _{x}u={}& 10\frac{u(x,t+\Delta t)-u(x,t)}{\varPhi _{1}}+20u(x,t) \frac{u(x+h,t)-u(x-h,t)}{2\varPsi _{2}} \\ &{} +20\frac{u(x+h,t)-u(x,t)}{\varPsi _{2}} \frac{u(x+h,t)-u(x-h,t)}{2\varPsi _{2}} \\ &{} +10u(x,t) \frac{u(x+2h,t)-2u(x+h,t)+u(x,t)}{\varPsi _{2}^{2}} \\ &{} +10u(x,t) \frac{u(x+h,t)-2u(x,t)+u(x-h,t)}{\varPsi _{2}^{2}}. \end{aligned}$$
(20)

Using (17), we can write the second implicit exact finite difference scheme (IMPEXFDII) by means of (20)

$$\begin{aligned} & \frac{U_{j+2}^{n+1}-3U_{j+1}^{n+1}+3U_{j}^{n+1}-U_{j-1}^{n+1}}{\varPsi _{1}\varPsi _{2}^{2}} \\ &\quad =10\frac{U_{j}^{n+1}-U_{j}^{n}}{\varPhi _{1}}+20U_{j}^{n+1} \frac{U_{j+1}^{n+1}-U_{j-1}^{n+1}}{2\varPsi _{2}} \\ &\qquad{} +20\frac{U_{j+1}^{n+1}-U_{j}^{n+1}}{\varPsi _{2}} \frac{U_{j+1}^{n+1}-U_{j-1}^{n+1}}{2\varPsi _{2}} \\ &\qquad{} +10U_{j}^{n+1} \frac{U_{j+2}^{n+1}-2U_{j+1}^{n+1}+U_{j}^{n+1}}{\varPsi _{2}^{2}} \\ &\qquad{} +10U_{j}^{n+1} \frac{U_{j+1}^{n+1}-2U_{j}^{n+1}+U_{j-1}^{n+1}}{\varPsi _{2}^{2}}. \end{aligned}$$
(21)

If we select \(u_{xx}=\partial _{x}\partial _{x} u\). Using the first order derivative approximation (14), we can obtain

$$ \partial _{x}\partial _{x} u= \frac{u(x+2h,t)-u(x+h,t)}{\varPsi _{2}}+10u(x+h,t) \frac{u(x+2h,t)-u(x,t)}{\varPsi _{2}}. $$
(22)

Now, we select \(u_{xxx}=\overline{\partial _{x}}\partial _{x}\partial _{x}u\), using (22) we have

$$\begin{aligned} \overline{\partial _{x}}\partial _{x} \partial _{x}u={}& 10\frac{u(x,t+\Delta t)-u(x,t)}{\varPhi _{1}}+10u(x+h,t) \frac{u(x+2h,t)-u(x+h,t)}{\varPsi _{2}} \\ &{} +10u(x+h,t)\frac{u(x+h,t)-u(x,t)}{\varPsi _{2}} \\ &{} +20\frac{u(x+h,t)-u(x,t)}{\varPsi _{1}} \frac{u(x+2h,t)-u(x,t)}{2\varPsi _{2}} \\ &{} +10u(x+h,t) \frac{u(x+2h,t)-2u(x+h,t)+u(x,t)}{\varPsi _{1}\varPsi _{2}} \\ &{} +10u(x+h,t) \frac{u(x+h,t)-2u(x,t)+u(x-h,t)}{\varPsi _{1}\varPsi _{2}}. \end{aligned}$$
(23)

Using (17), we can write the third implicit exact finite difference scheme (IMPEXFDIII) by means of (23):

$$\begin{aligned} & \frac{U_{j+2}^{n+1}-3U_{j+1}^{n+1}+3U_{j}^{n+1}-U_{j-1}^{n+1}}{\varPsi _{1}\varPsi _{2}^{2}} \\ &\quad = 10\frac{U_{j}^{n+1}-U_{j}^{n}}{\varPhi _{1} }+10U_{j+1}^{n+1} \frac{U_{j+2}^{n+1}-U_{j+1}^{n+1}}{\varPsi _{2}} \\ &\qquad{} +10U_{j+1}^{n+1} \frac{U_{j+1}^{n+1}-U_{j}^{n+1}}{\varPsi _{2}} \\ & \qquad{}+20\frac{U_{j+1}^{n+1}-U_{j}^{n+1}}{\varPsi _{1}} \frac{U_{j+2}^{n+1}-U_{j}^{n+1}}{2\varPsi _{2}} \\ & \qquad{}+10U_{j+1}^{n+1} \frac{U_{j+2}^{n+1}-2U_{j+1}^{n+1}+U_{j}^{n+1}}{\varPsi _{1}\varPsi _{2}} \\ &\qquad{} +10U_{j+1}^{n+1} \frac{U_{j+1}^{n+1}-2U_{j}^{n+1}+U_{j-1}^{n+1}}{\varPsi _{1}\varPsi _{2}}. \end{aligned}$$
(24)

2.2 Explicit exact finite differences for \(\operatorname{KdVB}(2,1,2)\) equation

Now, we will derive three explicit exact finite difference schemes for the \(\operatorname{KdVB}(2,1,2)\) equation (10). First, we select \(u_{xx}=\overline{\partial _{x}}\overline{\partial _{x}} u\). Using the first order derivative approximation (14), we can obtain

$$ \overline{\partial _{x}}\overline{\partial _{x}} u= \frac{u(x-h,t)-u(x-2h,t)}{\varPsi _{1}}+10u(x-h,t) \frac{u(x,t)-u(x-2h,t)}{\varPsi _{1}}. $$
(25)

Now, we select \(u_{xxx}=\partial _{x}\overline{\partial _{x}} \overline{\partial _{x}}u\), using (25), we have

$$\begin{aligned} \partial _{x}\overline{\partial _{x}} \overline{\partial _{x}}u={}& 10 \frac{u(x,t)-u(x,t-\Delta t)}{\varPhi _{2}}+10u(x-h,t) \frac{u(x,t)-u(x-h,t)}{\varPsi _{1}} \\ &{} +10u(x-h,t)\frac{u(x-h,t)-u(x-2h,t)}{\varPsi _{1}} \\ &{} +20\frac{u(x,t)-u(x-h,t)}{\varPsi _{2}} \frac{u(x,t)-u(x-2h,t)}{2\varPsi _{1}} \\ &{} +10u(x-h,t) \frac{u(x+h,t)-2u(x,t)+u(x-h,t)}{\varPsi _{1}\varPsi _{2}} \\ &{} +10u(x-h,t) \frac{u(x,t)-2u(x-h,t)+u(x-2h,t)}{\varPsi _{1}\varPsi _{2}}. \end{aligned}$$
(26)

Using (17), we can write the first explicit exact finite difference scheme (EXPEXFDI) by means of (26):

$$\begin{aligned} &\frac{U_{j+1}^{n}-3U_{j}^{n}+3U_{j-1}^{n}-U_{j-2}^{n}}{\varPsi _{1}^{2}\varPsi _{2}} \\ &\quad = 10\frac{U_{j}^{n}-U_{j}^{n-1}}{\varPhi _{2}}+10U_{j-1}^{n} \frac{U_{j}^{n}-U_{j-1}^{n}}{\varPsi _{1}} +10U_{j-1}^{n} \frac{U_{j-1}^{n}-U_{j-2}^{n}}{\varPsi _{1}} \\ &\qquad{} +20\frac{U_{j}^{n}-U_{j-1}^{n}}{\varPsi _{2}} \frac{U_{j}^{n}-U_{j-2}^{n}}{2\varPsi _{1}} +10U_{j-1}^{n} \frac{U_{j+1}^{n}-2U_{j}^{n}+U_{j-1}^{n}}{\varPsi _{1}\varPsi _{2}} \\ &\qquad{} +10U_{j-1}^{n} \frac{U_{j}^{n}-2U_{j-1}^{n}+U_{j-2}^{n}}{\varPsi _{1}\varPsi _{2}}. \end{aligned}$$
(27)

We select \(u_{xx}=\overline{\partial _{x}}\partial _{x} u\). Using the first order derivative approximation (14), we can obtain

$$ \overline{\partial _{x}}\partial _{x} u= \frac{u(x,t)-u(x-h,t)}{\varPsi _{2}}+10u(x,t) \frac{u(x+h,t)-u(x-h,t)}{\varPsi _{2}}. $$
(28)

Now, we select \(u_{xxx}=\overline{\partial _{x}}\overline{\partial _{x}}\partial _{x}u\), using (28), we have

$$\begin{aligned} \overline{\partial _{x}}\overline{\partial _{x}} \partial _{x}u={}& 10 \frac{u(x,t)-u(x,t-\Delta t)}{\varPhi _{2}}+10u(x-h,t) \frac{u(x,t)-u(x-h,t)}{\varPsi _{1}} \\ &{} +10u(x-h,t)\frac{u(x-h,t)-u(x-2h,t)}{\varPsi _{1}} \\ & {}+20\frac{u(x,t)-u(x-h,t)}{\varPsi _{1}} \frac{u(x+h,t)-u(x-h,t)}{2\varPsi _{2}} \\ &{} +10u(x,t) \frac{u(x+h,t)-2u(x,t)+u(x-h,t)}{\varPsi _{1}\varPsi _{2}} \\ &{} +10u(x,t) \frac{u(x,t)-2u(x-h,t)+u(x-2h,t)}{\varPsi _{1}\varPsi _{2}}. \end{aligned}$$
(29)

Using (17), we can write the second explicit exact finite difference scheme (EXPEXFDII) by means of (29):

$$\begin{aligned} &\frac{U_{j+1}^{n}-3U_{j}^{n}+3U_{j-1}^{n}-U_{j-2}^{n}}{\varPsi _{1}^{2}\varPsi _{2}} \\ &\quad = 10\frac{U_{j}^{n}-U_{j}^{n-1}}{\varPhi _{2}}+10U_{j-1}^{n} \frac{U_{j}^{n}-U_{j-1}^{n}}{\varPsi _{1}} +10U_{j-1}^{n} \frac{U_{j-1}^{n}-U_{j-2}^{n}}{\varPsi _{1}} \\ &\qquad{} +20\frac{U_{j}^{n}-U_{j-1}^{n}}{\varPsi _{1}} \frac{U_{j+1}^{n}-U_{j-1}^{n}}{2\varPsi _{2}} +10U_{j}^{n} \frac{U_{j+1}^{n}-2U_{j}^{n}+U_{j-1}^{n}}{\varPsi _{1}\varPsi _{2}} \\ & \qquad{}+10U_{j}^{n} \frac{U_{j}^{n}-2U_{j-1}^{n}+U_{j-2}^{n}}{\varPsi _{1}\varPsi _{2}}. \end{aligned}$$
(30)

Finally, select \(u_{xx}=\partial _{x}\overline{\partial _{x}} u\). Using the first order derivative approximation (14), we can obtain

$$ \partial _{x} \overline{\partial _{x}}u= \frac{u(x+h,t)-u(x,t)}{\varPsi _{1}}+10u(x,t) \frac{u(x+h,t)-u(x-h,t)}{\varPsi _{1}}. $$
(31)

Now, we select \(u_{xxx}=\overline{\partial _{x}}\partial _{x} \overline{\partial _{x}}u\), using (31), we have

$$\begin{aligned} \overline{\partial _{x}}\partial _{x} \overline{\partial _{x}}u={}& 10 \frac{u(x,t)-u(x,t-\Delta t)}{\varPhi _{2}}+10u(x,t) \frac{u(x+h,t)-u(x,t)}{\varPsi _{1}} \\ &{} +10u(x,t)\frac{u(x,t)-u(x-h,t)}{\varPsi _{1}} \\ &{} +20\frac{u(x,t)-u(x-h,t)}{\varPsi _{1}} \frac{u(x+h,t)-u(x-h,t)}{2\varPsi _{1}} \\ &{} +10u(x,t) \frac{u(x+h,t)-2u(x,t)+u(x-h,t)}{\varPsi _{1}^{2}} \\ & {}+10u(x,t) \frac{u(x,t)-2u(x-h,t)+u(x-2h,t)}{\varPsi _{1}^{2}}. \end{aligned}$$
(32)

Using (17), we can write the third explicit exact finite difference scheme (EXPEXFDIII) by means of (32):

$$\begin{aligned} &\frac{U_{j+1}^{n}-3U_{j}^{n}+3U_{j-1}^{n}-U_{j-2}^{n}}{\varPsi _{1}^{2}\varPsi _{2}} \\ &\quad= 10\frac{U_{j}^{n}-U_{j}^{n-1}}{\varPhi _{2}}+10U_{j}^{n} \frac{U_{j+1}^{n}-U_{j}^{n}}{\varPsi _{1}} +10U_{j}^{n} \frac{U_{j}^{n}-U_{j-1}^{n}}{\varPsi _{1}} \\ &\qquad{} +20\frac{U_{j}^{n}-U_{j-1}^{n}}{\varPsi _{1}} \frac{U_{j+1}^{n}-U_{j-1}^{n}}{2\varPsi _{1}} +10U_{j}^{n} \frac{U_{j+1}^{n}-2U_{j}^{n}+U_{j-1}^{n}}{\varPsi _{1}^{2}} \\ &\qquad{} +10U_{j}^{n} \frac{U_{j}^{n}-2U_{j-1}^{n}+U_{j-2}^{n}}{\varPsi _{1}^{2}}. \end{aligned}$$
(33)

Thus we have proven the following theorem.

Theorem 1

For the generalized KdV–Burgers’\(\operatorname{KdVB}(2,1,2)\)equation

$$ u_{t}+\bigl(u^{2}\bigr)_{x}-0.1u_{xxx}+ \bigl(u^{2}\bigr)_{xx}=0, $$

the implicit exact finite difference schemes are given by (18), (21) and (24) and the explicit exact finite difference schemes are given by (27),(30) and (33). The temporal step size satisfies\(\Delta t=10h\)and the step size functions satisfy

$$ \varPsi _{1}=e^{h}-1, \qquad \varPsi _{2}=1-e^{-h},\qquad \varPhi _{1}= \frac{1-e^{-0.1\Delta t}}{0.1}, \qquad \varPhi _{2}= \frac{e^{0.1\Delta t}-1}{0.1}. $$

3 NSFD scheme for the \(\operatorname{KdVB}(2,1,2)\) equation

We set up six exact finite difference schemes in Sect. 2. Although numerical instabilities do not arise in an exact finite difference model, it is not possible to construct an exact finite difference model for an arbitrary differential equation. In recent years, NSFD models have been proven to be one of the efficient numerical algorithms for large step sizes. They are not exact models, but they do not possess numerical instabilities when they are compared with standard finite difference models (see [16] and the references therein). In the construction of an NSFD model, it is assumed that the orders of the derivatives must be exactly equal to the orders of the corresponding derivatives of the differential equations [38]. In this study, we extend this rule and discretize the third order derivative by a second order finite difference. In this section, we build an NSFD scheme for the numerical solution of the \(\operatorname{KdVB}(2,1,2)\) equation (10).

The exact travelling wave solution of (10) is given by [41]

$$\begin{aligned} u(x,t)&=-\frac{1}{20} \biggl(1+\tanh \biggl[\frac{t}{20}+ \frac{x}{2} \biggr] \biggr) \\ &= -\frac{0.1}{1+e^{-(x+0.1t)}}. \end{aligned}$$
(34)

In the classical sense, a discrete scheme for the \(\operatorname{KdVB}(2,1,2)\) equation (10) can be

$$\begin{aligned} & \frac{u_{j}^{n+1}-u_{j}^{n}}{\Delta t}+ \frac{(u^{2})_{j+1}^{n}-(u^{2})_{j}^{n}}{h}+ \frac{(u^{2})_{j-1}^{n}-2(u^{2})_{j}^{n}+(u^{2})_{j+1}^{n}}{h^{2}} \\ &\quad -0.1 \frac{-(u)_{j-2}^{n}+2(u)_{j-1}^{n}-2(u)_{j+1}^{n}+(u)_{j+2}^{n}}{2h^{3}}=0. \end{aligned}$$
(35)

We re-write the \(\operatorname{KdVB}(2,1,2)\) equation (10) as follows:

$$ \begin{aligned}& u_{t}+\bigl(u^{2} \bigr)_{x}-0.1u_{xxx}+\bigl(u^{2} \bigr)_{xx}=0, \\ &u_{t}+2uu_{x}-0.1u_{xxx}+2(u_{x})^{2}+2uu_{xx}=0 \end{aligned} $$
(36)

and propose the following nonstandard finite difference discretization:

$$\begin{aligned} &\frac{U_{j}^{n+1}-U_{j}^{n}}{\varPhi }+2U_{j}^{n+1} \frac{U_{j}^{n}-U_{j-1}^{n}}{\varGamma }+ 2U_{j}^{n+1} \frac{U_{j+1}^{n}-2U_{j}^{n}+U_{j-1}^{n}}{\varGamma ^{2}} \\ &\quad{} +2 \biggl(\frac{U_{j+1}^{n}-U_{j}^{n}}{\varGamma } \biggr) \biggl(\frac{U_{j}^{n}-U_{j-1}^{n}}{\varGamma } \biggr)-0.1 \biggl( \frac{-U_{j-2}^{n}+2U_{j-1}^{n}-2U_{j+1}^{n}+U_{j+2}^{n}}{2\varGamma ^{3} } \biggr)=0, \end{aligned}$$
(37)

where Φ and Γ are time-step and space-step functions, respectively.

We solve for Φ and define \(s_{j}^{n}=e^{-(x_{j}+0.1t_{n})}\). After tedious calculations, we get

$$ \varPhi =0.1s \bigl(e^{-0.1\Delta t}-1 \bigr)2\varGamma ^{4} \times \frac{A}{B}, $$
(38)

where

$$\begin{aligned} A={}&(1+s) \bigl(1+se^{2h}\bigr) \bigl(1+se^{h}\bigr) \bigl(1+se^{-h}\bigr) \bigl(1+se^{-2h}\bigr), \\ B={}&(0.1)^{2}\varGamma se^{-3h}\bigl(e^{h}-1 \bigr)^{3}\bigl(e^{h}+1\bigr) \bigl(1+se^{-0.1\Delta t} \bigr) (1+s)^{2} \\ &{}\times \bigl(s-e^{h}+2se^{h}+se^{2h}-s^{2}e^{h} \bigr) \\ &{}-4\varGamma ^{3}(0.1)^{2}s\bigl(e^{h}-1\bigr) (1+s) \bigl(1+se^{-h}\bigr) \bigl(1+se^{-2h}\bigr) \bigl(1+se^{2h}\bigr) \\ &{}-4\varGamma ^{2}(0.1)^{2}se^{-h} \bigl(e^{h}-1\bigr)^{2}(s-1) (1+s) \bigl(1+se^{2h} \bigr) \bigl(1+se^{-2h}\bigr) \\ &{}-4(0.1)^{2}s^{2}\varGamma ^{2} e^{-h} \bigl(1-e^{h}\bigr)^{2}\bigl(1+se^{-0.1\Delta t}\bigr) \bigl(1+se^{2h}\bigr) \bigl(1+se^{-2h}\bigr). \end{aligned}$$

If we select

$$ \varGamma =e^{h}-1=h+\mathcal{O}\bigl(h^{2}\bigr), $$

then Φ can be written in a simple form

$$ \varPhi = \frac{1-e^{-0.1\Delta t}}{0.1}=\Delta t+ \mathcal{O}\bigl(\Delta t^{2} \bigr). $$

Therefore, the NSFD scheme for the \(\operatorname{KdVB}(2,1,2)\) equation is

$$\begin{aligned} &\frac{U_{j}^{n+1}-U_{j}^{n}}{\varPhi }+2U_{j}^{n+1} \frac{U_{j}^{n}-U_{j-1}^{n}}{\varGamma }+ 2U_{j}^{n+1} \frac{U_{j+1}^{n}-2U_{j}^{n}+U_{j-1}^{n}}{\varGamma ^{2}} \\ &\quad{}+2 \biggl(\frac{U_{j+1}^{n}-U_{j}^{n}}{\varGamma } \biggr) \biggl(\frac{U_{j}^{n}-U_{j-1}^{n}}{\varGamma } \biggr)-0.1 \biggl( \frac{-U_{j-2}^{n}+2U_{j-1}^{n}-2U_{j+1}^{n}+U_{j+2}^{n}}{2\varGamma ^{3} } \biggr)=0, \end{aligned}$$
(39)

where \(\varPhi =\frac{1-e^{-0.1\Delta t}}{0.1}\) and \(\varGamma =e^{h}-1\).

To analyse the local truncation error of NSFD scheme (39), we introduce the difference quotients:

$$ \begin{aligned} &\frac{\partial u_{j}^{n}}{\partial t} = \frac{u_{j}^{n+1}-u_{j}^{n}}{\varPhi },\qquad \frac{\overline{\partial } u_{j}^{n}}{\partial x} = \frac{u_{j}^{n}-u_{j-1}^{n}}{\varGamma },\qquad \frac{\partial u_{j}^{n}}{\partial x} = \frac{u_{j+1}^{n}-u_{j}^{n}}{\varGamma }, \\ &\frac{\partial \overline{\partial } u_{j}^{n}}{\partial x^{2}} = \frac{u_{j+1}^{n}-2u_{j}^{n}+u_{j-1}^{n}}{\varGamma ^{2}},\qquad \frac{\partial ^{3}u_{j}^{n}}{\partial x^{3}} = \frac{-u_{j-2}^{n}+2u_{j-1}^{n}-2u_{j+1}^{n}+u_{j+2}^{n}}{2\varGamma ^{3}}. \end{aligned} $$
(40)

We define the residual

$$\begin{aligned} \tau _{j}^{n} ={}&\frac{\partial u_{j}^{n}}{\partial t}+2u_{j}^{n+1} \frac{\overline{\partial } u_{j}^{n}}{\partial x} + 2u_{j}^{n+1} \frac{\partial \overline{\partial } u_{j}^{n}}{\partial x^{2}}+2 \frac{\partial u_{j}^{n}}{\partial x} \frac{\overline{\partial } u_{j}^{n}}{\partial x} -0.1 \frac{\partial ^{3} u_{j}^{n}}{\partial x^{3}} \\ ={}& \biggl(\frac{\partial u_{j}^{n}}{\partial t}-u_{t}(x_{j},t_{n}) \biggr)+2 \biggl(u_{j}^{n+1} \frac{\overline{\partial } u_{j}^{n}}{\partial x} -u(x_{j},t_{n})u_{x}(x_{j},t_{n}) \biggr) -0.1 \biggl(\frac{\partial ^{3} u_{j}^{n}}{\partial x^{3}}-u_{xxx}(x_{j},t_{n}) \biggr) \\ & {}+2 \biggl( \frac{\partial u_{j}^{n}}{\partial x} \frac{\overline{\partial } u_{j}^{n}}{\partial x}-u_{x}(x_{j},t_{n})u_{x}(x_{j},t_{n}) \biggr)+ 2 \biggl(u_{j}^{n+1} \frac{\partial \overline{\partial } u_{j}^{n}}{\partial x^{2}}-u(x_{j},t_{n})u_{xx}(x_{j},t_{n}) \biggr). \end{aligned}$$

If we choose Δt and Δx small enough, we know that \(\varPhi \approx \Delta t \) and \(\varGamma \approx \Delta x\). Then using Taylor’s series expansion about \((x_{j},t_{n})\), after the tedious computations, we conclude that \(\tau _{j}^{n}=\mathcal{O}(\Delta t+\Delta x^{2})\), and hence NSFD scheme (39) has the order of accuracy \(\mathcal{O}(\Delta t+\Delta x^{2})\). It is consistent with the \(\operatorname{KdVB}(2,1,2)\) equation (10) when \((\Delta t,\Delta x)\longrightarrow (0,0)\).

4 Linear stability analysis

In this section, we investigate the linear stability analysis for NSFD (39) and SFD (35) schemes by using von Neumann stability analysis. Although an application of the linear stability analysis to nonlinear equations cannot be justified, it is found to be effective in practice [42–45]. Since the von Neumann method is applicable only for linear PDE, we linearised the \(\operatorname{KdVB}(2,1,2)\) equation (10) around the constant solution. Assume that \(v:R^{2} \rightarrow R\) is a three times continuously differentiable function such that \(|v(t,x)|\ll 1\), and let \(u=\overline{u}+v(t,x)\), where u and u̅ are solutions to (10). Substituting \(u=\overline{u}+v(t,x)\) into (10), we get

$$ (\overline{u}+v)_{t}+(\overline{u}+v)^{2}_{x}-0.1( \overline{u}+v)_{xxx}+( \overline{u}+v)^{2}_{xx}=0, $$
(41)

which yields

$$ \overline{u}_{t}+v_{t}+\bigl( \overline{u}^{2}+2\overline{u}v+v^{2}\bigr)_{x}-0.1( \overline{u}_{xxx}+v_{xxx})+ \bigl(\overline{u}^{2}+2 \overline{u}v+v^{2}\bigr)_{xx}=0. $$
(42)

Using the fact that u̅ is a solution of (10) and ignoring the higher order terms \(v^{2}\), we obtain

$$ v_{t}+(2\overline{u})v_{x}-0.1v_{xxx}+(2 \overline{u})v_{xx}=0. $$
(43)

Linearisation about the constant solution \(\overline{u}=c/2\) takes the form

$$ v_{t}+cv_{x}-0.1v_{xxx}+cv_{xx}=0. $$
(44)

Now we apply NSFD (39) and SFD (35) schemes to linearised equation (44). Application of NSFD scheme (39) to linearised equation (44) yields

$$\begin{aligned} & \frac{V_{j}^{n+1}-V_{j}^{n}}{\varPhi }+c \frac{V_{j}^{n}-V_{j-1}^{n}}{\varGamma }+ c \frac{V_{j+1}^{n}-2V_{j}^{n}+V_{j-1}^{n}}{\varGamma ^{2}} \\ &\quad{}-0.1 \frac{-V_{j-2}^{n}+2V_{j-1}^{n}-2V_{j+1}^{n}+V_{j+2}^{n}}{2\varGamma ^{3}}=0. \end{aligned}$$
(45)

We define the error \(\epsilon _{j}^{n}=v(x_{j},t_{n})-V_{j}^{n}\), where \(v(x_{j},t_{n})\) is the exact solution at the mesh point \((x_{j},t_{n})\) and \(V_{j}^{n}\) is the approximate solution. Substituting \(V_{j}^{n}=v(x_{j},t_{n})-\epsilon _{j}^{n}\) into difference equation (45), the error \(\epsilon _{j}^{n}\) satisfies the same discrete equation

$$ \frac{\epsilon _{j}^{n+1}-\epsilon _{j}^{n}}{\varPhi }+c \frac{\epsilon _{j}^{n}-\epsilon _{j-1}^{n}}{\varGamma }+ c \frac{\epsilon _{j+1}^{n}-2\epsilon _{j}^{n}+\epsilon _{j-1}^{n}}{\varGamma ^{2}} -0.1 \frac{-\epsilon _{j-2}^{n}+2\epsilon _{j-1}^{n}-2\epsilon _{j+1}^{n}+\epsilon _{j+2}^{n}}{2\varGamma ^{3}}=0. $$
(46)

The von Neumann stability analysis uses the fact that every linear constant coefficient difference equation has a solution of the form

$$ \epsilon _{j}^{n}=\bigl(e^{\alpha \Delta t} \bigr)^{n}e^{i\beta j \Delta x}=( \xi )^{n}e^{i \beta j \Delta x},\quad \alpha, \beta \in \mathbf{R}, i^{2}=-1. $$
(47)

The function ξ is determined from the difference equation by substituting the Fourier mode (47) into (46), and we obtain \(\xi =a+ib\), where \(a=1-2c\frac{\varPhi }{\varGamma }\sin ^{2} (\frac{\beta \Delta x}{2})+4c \frac{\varPhi }{\varGamma ^{2}} \sin ^{2} (\frac{\beta \Delta x}{2})\) and \(b=-c\frac{\varPhi }{\varGamma }\sin (\beta \Delta x)-0.4 \frac{\varPhi }{\varGamma ^{3}}\sin ^{2} (\frac{\beta \Delta x}{2})\sin ( \beta \Delta x)\). Taking \(r=\frac{\varPhi }{\varGamma ^{2}}\) and using \(|\xi |\leq 1\), we find

$$ r\leq \frac{c(\varGamma -2)}{[0.2c+4c^{2}+1.25c^{2}\varGamma ^{2}-4c^{2}\varGamma ]+\frac{0.04}{\varGamma ^{2}}}. $$

Similarly, we apply SFD scheme (35) to linear equation (44) and get

$$\begin{aligned} &\frac{V_{j}^{n+1}-V_{j}^{n}}{\Delta t}+c \frac{V_{j+1}^{n}-V_{j}^{n}}{h}+ c \frac{V_{j+1}^{n}-2V_{j}^{n}+V_{j-1}^{n}}{h^{2}} \\ &\quad{}-0.1 \frac{-V_{j-2}^{n}+2V_{j-1}^{n}-2V_{j+1}^{n}+V_{j+2}^{n}}{2h^{3}}=0. \end{aligned}$$
(48)

Following similar steps as before, we obtain

$$ r\leq \frac{c(h-2)}{[0.2c+c^{2}+1.25c^{2}h^{2}+c^{2}h]+\frac{0.01}{h^{2}}}. $$

5 Numerical results

In this section, we illustrate the accuracy and efficiency of NSFD scheme (39). For this purpose, we consider the \(\operatorname{KdVB}(2,1,2)\) equation (10)

$$ u_{t}+\bigl(u^{2}\bigr)_{x}-0.1u_{xxx}+ \bigl(u^{2}\bigr)_{xx}=0,\quad x_{L}< x < x_{R}, t>0 $$
(49)

with the initial condition

$$ u(x,0)= -\frac{1}{20} \biggl(1+\tanh \biggl( \frac{x}{2}\biggr) \biggr),\quad x_{L}\leq x \leq x_{R} $$
(50)

and the boundary conditions

$$\begin{aligned} \begin{aligned}& u(x_{L},t)= - \frac{1}{20} \biggl(1+\tanh \biggl( \frac{t}{20}+\frac{x_{L}}{2} \biggr) \biggr), \\ &u(x_{R},t)= -\frac{1}{20} \biggl(1+\tanh \biggl( \frac{t}{20}+\frac{x_{R}}{2}\biggr) \biggr),\quad t>0. \end{aligned} \end{aligned}$$
(51)

We choose the spatial domain \(x_{L}=-25\leq x\leq 25=x_{R}\) and the temporal domain \(0\leq t\leq T\) in all computations. We consider equally spaced mesh points \(x_{j}=x_{L}+jh\) and \(t_{n}=n\Delta t, j=1,2,\ldots, M+1, n=0,1,2,\ldots, N\), with the spatial mesh size \(h=\Delta x=(x_{R}-x_{L})/M\) and the temporal mesh size \(\Delta t=T/N\). The accuracy is measured by using the \(L_{\infty }\) and \(L_{2}\) errors

$$ L_{\infty }= \max_{0\le j\le M}\bigl\{ \bigl\vert u(x_{j},t_{n})-U_{j}^{n} \bigr\vert \bigr\} ,\qquad L_{2}= \Biggl(h\sum_{j=1}^{M} \bigl\vert u(x_{j},t_{n})-U_{j}^{n} \bigr\vert ^{2} \Biggr)^{1/2} $$

at \(t=T\), where \(u(x_{j},t_{n})\) is the exact solution obtained from (11) and \(U_{j}^{n}\) is the discrete solution obtained from NSFD scheme (39) or the standard finite difference (SFD) scheme (35). The absolute error at each mesh points is measured according to

$$ \operatorname{Abs}(\operatorname{err})= \bigl\vert u(x_{j},t_{n})-U_{j}^{n} \bigr\vert ,\quad j=1,2,\ldots,M+1, n=0,1, \ldots,N. $$

Table 1 shows the \(L_{\infty }\) and \(L_{2}\) errors of NSFD scheme (39) at \(T=10\). Table 2 shows the efficiency of NSFD scheme (39) for various times. From Tables 1 and 2 we see that there is a good agrement between NSFD scheme (39) and exact solution (11). Figure 1 represents the surface of the wave obtained from exact solution (11) with SFD scheme (35) and NSFD schemes (39) for the spatial mesh size \(h=0.5\) and temporal mesh size \(\Delta t=0.6\). Figure 2 represents the wave in the spatial domain \(-25\leq x\leq 25\) at \(T=20\). In Figs. 1–2, we see that while the NSFD scheme does not produce spurious oscillations, the SFD scheme produces instability for \(\Delta t=0.6\). Figure 3 shows the absolute errors for the NSFD and SFD schemes. Figure 4 depicts the \(L_{\infty }\) and \(L_{2}\) errors for the same set of parameters. From those figures, we see that the NSFD scheme has good efficiency even for large step sizes.

Figure 1
figure 1

(a) Exact, (b) NSFD, (c) SFD: Surface of the wave for \(h=0.5,\Delta t=0.6\)

Full size image
Figure 2
figure 2

Instability of SFD scheme for step size \(\Delta t =0.6\)

Full size image
Figure 3
figure 3

(a) NSFD, (b) SFD: Absolute errors

Full size image
Figure 4
figure 4

(a) \(L_{\infty }\) errors, (b) \(L_{2}\) errors

Full size image
Table 1 The errors at \(T=10\) of NSFD scheme (39) with \(h=0.5\)
Full size table
Table 2 The errors at various time of NSFD scheme (39) with \(\Delta t=h^{2}=0.25\)
Full size table

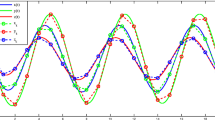
Figure 5 represents the long time integration of the NSFD scheme in the temporal domain \(0\leq t \leq 60\). We see that there is no difference between the exact solution and the numerical solution generated by the NSFD scheme. On the other hand, we know that the SFD scheme shows blow-up at \(T=20\) (see Fig. 1(c)). This blow-up phenomenon is corrected by choosing a small step size. Figure 6 depicts the exact solution together with numerical solutions generated by the SFD and the NSFD schemes for \(\Delta t=0.5\). In this case, we see that there are no big differences between the exact solution and the numerical solutions obtained by SFD and NSFD schemes. We know that \(\varGamma =e^{h}-1=h+\mathcal{O}(h^{2})\approx h\) for small h and \(\varPhi =(1-e^{-0.1\Delta t})/0.1=\Delta t+\mathcal{O}( \Delta t^{2})\approx \Delta t\) for small Δt. For this reason, we should note that the behaviour of the NSFD scheme will be similar to that of the SFD scheme for small h and Δt. To verify this fact, we choose \(h=0.5,\Delta t=0.005\) and depict the solution in Fig. 7. Figures 8–9 represent the absolute errors and the \(L_{\infty }\),\(L_{2}\) errors, respectively. From these figures, we see that the NSFD scheme is efficient as well as the SFD scheme.

Figure 5
figure 5

(a) Exact, (b) NSFD: Surface of the wave up to \(t=60\)

Full size image
Figure 6
figure 6

Solution generated by the SFD scheme at \(T=20\) with \(\Delta t=0.5\)

Full size image
Figure 7
figure 7

(a) Exact, (b) NSFD, (c) SFD: Surface of the wave for \(h=0.5,\Delta t=0.005\)

Full size image
Figure 8
figure 8

(a) NSFD, (b) SFD: Absolute errors

Full size image
Figure 9
figure 9

(a) \(L_{\infty }\) errors, (b) \(L_{2}\) errors

Full size image

Tables 3 and 4 represent the \(L_{\infty }\) and \(L_{2}\)-errors of the exact finite difference methods, IMPEXFDI (18), IMPEXFDII (21), IMPEXFDIII (24), EXPEXFDI (27), EXPEXFDII (30), EXPEXFDIII (33). If we select the step size \(h=0.5\) with different time steps Δt, the exact schemes are reduced to the NSFD scheme [39]. Figure 10 shows the \(L_{\infty }\) and \(L_{2}\)-errors of the exact schemes as \(h=0.5\) with different time steps Δt.

Figure 10
figure 10

(a) \(L_{\infty }\) and (b) \(L_{2}\) errors of exact finite difference

Full size image
Table 3 The errors of the implicit exact finite difference schemes with \(\Delta t=10h\)
Full size table
Table 4 The errors of the explicit exact finite difference schemes with \(\Delta t=10h\)
Full size table

6 Conclusion

In this work, we have constructed implicit and explicit exact finite difference schemes and a consistent linearly implicit NSFD scheme for the numerical solution of the generalized \(\operatorname{KdVB}(2,1,2)\) equation, which have never been proposed and studied in the literature before. Numerical solutions obtained from the NSFD scheme are compared with an SFD model. We show that the NSFD scheme well simulates the kink-wave solution of the \(\operatorname{KdVB}(2,1,2)\) equation even in the case of large step size, though the SFD scheme shows numerical instabilities. In addition, we see that there are no big differences between the exact solution and the NSFD scheme for small step sizes. Absolute errors, \(L_{\infty }\) and \(L_{2}\) errors show that the proposed NSFD model is very accurate, efficient and a powerful tool for the numerical solution of the \(\operatorname{KdVB}(2,1,2)\) equation. Following the process in this paper, exact and NSFD models for some other nonlinear PDEs can be obtained.