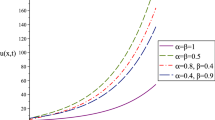
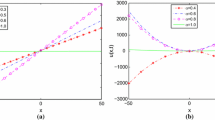
Abstract
In this paper, we show that the invariant subspace method can be successfully utilized to get exact solutions for nonlinear fractional partial differential equations with generalized fractional derivatives. Using the invariant subspace method, some exact solutions have been obtained for the time fractional Hunter–Saxton equation, a time fractional nonlinear diffusion equation, a time fractional thin-film equation, the fractional Whitman–Broer–Kaup-type equation, and a system of time fractional diffusion equations.
Similar content being viewed by others
1 Introduction
Fractional calculus has several applications in science and engineering [1, 2]. It is extensively used in modeling physical and engineering phenomena in the form of fractional partial differential equations [3–6]. Many definitions of the fractional derivative have been introduced in the literature, such as the Riemann–Liouville definition [2], the Caputo definition [2], the Riesz definition [2], the the Caputo–Fabrizio definition [7], and Atangana–Baleanu definition [8]. In recent years, a novel fractional derivative has appeared in the literature called the generalized fractional derivative [9, 10]
which generalizes the Riemann–Liouville fractional derivative. This generalized fractional derivative has attracted the interest of many researchers. Many properties and applications of this generalized fractional derivative can be found in [9–16]. Some basic properties of the generalized fractional derivative are given in the Appendix.
The invariant subspace method (ISM) is a very effective method that can be used for obtaining exact solutions of fractional partial differential equations. It is widely used in getting exact solutions of fractional differential equations with Riemann–Liouville and Caputo fractional derivatives [17–20]. It is also successfully utilized for getting exact solutions of fractional partial differential equations with conformable derivatives [21]. In this paper, we adapt the ISM to be utilized for obtaining exact solutions for some fractional partial differential equations with the generalized fractional Riemann–Liouville derivative. In the next section, we will introduce the ISM.
2 The invariant subspace method
The ISM can be used for solving the following fractional system of PDEs:
The ISM can be summarized in the following steps:
Step 1. Assume the solution of Eq. (1) in the form
where j and k depend upon the dimension of the invariant subspace.
Step 2. Determine the functions \(\boldsymbol{B}_{i} ( x ), \boldsymbol{D}_{i} ( x )\) as follows:
Solve the system of determining equations
$$\begin{aligned} &\biggl( \frac{d^{j}}{d x^{j}} + c_{j-1} ( x ) \frac{d ^{j-1}}{d x^{j-1}} +\cdots + c_{1} ( x ) \frac{d}{dx} + c _{0} ( x ) \biggr) F_{1} \bigl[ y_{1} ( x ), y_{2} (x) \bigr] =0,\\ &\biggl( \frac{d^{k}}{d x^{k}} + r_{k-1} ( x ) \frac{d^{k-1}}{d x^{k-1}} +\cdots + r_{1} ( x ) \frac{d}{dx} + r_{0} ( x ) \biggr) F_{2} \bigl[ y_{1} ( x ), y_{2} (x) \bigr] =0, \end{aligned} $$(3)to obtain the coefficients \(c_{0} ( x ), \dots, c_{j-1} ( x )\) and \(r_{0} ( x ), \dots, r_{k-1} ( x )\);
Solve the system of ordinary differential equations
$$\begin{aligned} &\biggl( \frac{d^{j}}{d x^{j}} + c_{j-1} ( x ) \frac{d ^{j-1}}{d x^{j-1}} +\cdots + c_{1} ( x ) \frac{d}{dx} + c _{0} ( x ) \biggr) y_{1} ( x ) =0,\\ & \biggl( \frac{d^{k}}{d x^{k}} + r_{k-1} ( x ) \frac{d^{k-1}}{d x ^{k-1}} +\cdots + r_{1} ( x ) \frac{d}{dx} + r_{0} ( x ) \biggr) y_{2} (x)=0, \end{aligned}$$(4)to obtain the solution
$$ y_{1} = \sum_{i=1}^{j} h_{i} \boldsymbol{B}_{i} ( x ),\qquad y _{2} = \sum _{i=1}^{k} s_{i} \boldsymbol{D}_{i} ( x ), $$(5)where \(h_{i}, i=1,\dots,j, s_{i}, i=1,\dots,k\) are arbitrary constants.
Step 3. Substitute Eq. (2) into Eq. (1) to obtain a system of fractional ordinary differential equations in \(A_{i} ( t )\) and \(C_{i} ( t )\).
In the following section, we solve some fractional differential equations using ISM.
3 Numerical examples
Example 3.1
Let us consider the time fractional Hunter–Saxton equation [19, 21]
Using the ISM, we have obtained the following:
Four-Dimensional Invariant Subspace Classification of Eq. (6). Here, Eq. (4) is given by
Also,
Substituting Eqs. (7) and (8) into Eq. (3) (with \(j=4\)), we obtain determining equations in \(a_{3}, a_{2}, a_{1}, a_{0}\). After solving them, we get
Substituting Eq. (9) into Eq. (7) and solving Eq. (7), we obtain
The solution of Eq. (6) can be written in the form
Substituting Eq. (11) into Eq. (6), we obtain
Assume
Using relation (A1) in the Appendix, system (12) becomes
Equation (12e) is satisfied when
Substituting Eq. (12f) into Eq. (12c), we obtain
Equation (12g) is satisfied when
Substituting Eq. (12f) and Eq. (12h) into Eq. (12d), we get
Equation (12i) is satisfied when
When substituting Eq. (12f), Eq. (12h) and Eq. (12j) into Eq. (12b), we can see that Eq. (12b) is satisfied identically. Hence, the solution of the system (12) is given by
where \(s_{3}\) is a constant. Finally, the solution of Eq. (6) is given by
Example 3.2
Let us consider the time fractional nonlinear diffusion equation [22]
Using the same technique used in Example 3.1, we obtain the following case for Eq. (15):
Three-Dimensional Invariant Subspace of Eq. (15). It is easy to show that Eq. (15) admits the invariant subspace [22] \(L\{1,x, x^{2} \}\). The solution of Eq. (15) can be formulated as
Substituting Eq. (16) into Eq. (15) and comparing both sides of Eq. (15), we get
We now solve system (17), to get
where \(b_{2}\) is a constant. Finally, the exact solution of Eq. (15) is given by
Example 3.3
Let us consider the time fractional thin-film equation [19, 21]
Using the same technique used in Example 3.1, we obtain the following cases for Eq. (19):
Case 1: Two-Dimensional Invariant Subspace Classification of Eq. (19). The two-dimensional invariant subspace admitted by Eq. (19) is {\(1, ( b_{3} +x)^{4}\)}, where \(b_{3} \) is a constant. Therefore, the solution of Eq. (19) can be written in the form
Substituting Eq. (20) into Eq. (19), we get
Upon solving Eq. (21), we get
where \(s_{1}\) satisfies the equation
and \(b_{4}\) is a constant.
The solution of Eq. (19), in this case, is given by
Case 2: Three-Dimensional Invariant Subspace Classification of Eq. (19). The first three-dimensional invariant subspace admitted by Eq. (19) is {\(1, \sin ( b_{5} x ), \cos ( b_{5} x )\)} with \(\beta =1-\gamma \) and \(b_{5}\) being a constant. Therefore, the solution of Eq. (19) can be written in the form
Substituting Eq. (25) into Eq. (19), we get
Upon solving Eq. (26), we get
where \(b_{6}\) is a constant.
The solution of Eq. (19), in this case, is given by
The second three-dimensional invariant subspace admitted by Eq. (19) is {\(1,x, ( b_{7} +x )^{4}\)} with \(\beta =1-\gamma \) and \(b_{7}\) being a constant. Therefore, the solution of Eq. (19) can be written in the form
Substituting Eq. (29) into Eq. (19), we get
Upon solving Eq. (30), we get
where \(b_{8}\) is a constant and \(s_{2}\) is the root of the equation
and \(\gamma \neq \{ 1,- \frac{3}{2} \}, \alpha \neq \frac{1}{2}, 1-\alpha + \frac{\mathrm{s}_{2}}{\rho } \neq 0, \frac{ \mathrm{s}_{2}}{\rho } \neq -1 \).
The solution of Eq. (19), in this case, is given by
Example 3.4
Let us consider the fractional Whitman–Broer–Kaup-type equation [19, 21]
For a two-dimensional invariant subspace, we can assume the solution of (33) in the form
Substituting (34) into (33), we obtain
Equating the coefficients of x with \(zero\), we obtain
The determining equations (36) have the solution
where \(b_{9}\) is a constant and \(s_{3}\) satisfies the equation
Substituting (37) into (34), we obtain
Example 3.5
Let us consider the following system of time fractional diffusion equations [20]:
It is easy to show that Eq. (39) admits the invariant subspace [20] \(L\{ \cos ( \sqrt{a_{0}} x ), \sin ( \sqrt{a _{0}} x ) \}\times L\{ e^{- b_{0} x} \}\). The solution of Eq. (39) can be formulated as
where \(\gamma =\beta a_{0}\) and \(\mu =-2 \rho _{1} b_{0}^{2}\). We now substitute Eq. (40) into Eq. (39) and compare both sides of Eq. (39) to get
The determining equations (41) have the solution [11]
where \(b_{10}, b_{11}\) and \(b_{12} \) are constants. In this case, the solution of Eq. (39) is given by
where \(E_{\alpha,\beta } ( t )\) is the Mittag-Leffler function defined by [2]
Also, Eq. (39) admits the invariant subspace [20] \(L\{1, e^{- b_{13} x}, e^{-2 b_{13} x} \}\times L\{1, e^{- b_{13} x} \}\). The solution of Eq. (39) can be formulated as
where \(\gamma =-4\beta b_{13}^{2}\). We now substitute Eq. (43) into Eq. (39) and compare both sides of Eq. (39) to get
The exact solution of the system (44) can’t be obtained, in general. A special solution of the system (44) when \(\mu =-2 \rho _{1} b_{13}^{2}\) is given by
In this case, the solution of Eq. (39) is given by
where, \(b_{13}, b_{14}, b_{15}, b_{16}\) are constants.
4 Conclusions
In this paper, we have utilized the ISM for getting exact solutions for some nonlinear fractional partial differential equations with generalized fractional derivatives. The obtained solutions in this paper are given in generalized forms which depend upon the parameter ρ. We can retrieve the obtained solutions in [19, 20, 22] by putting \(\rho =1\) in our obtained solutions. The ISM is a very powerful method that can be used to solve various fractional PDEs. In our future work, we will use the ISM for getting exact solutions of some fractional PDEs with Hilfer–Katugampola fractional derivatives [23].
References
Diethelm, K.: The Analysis of Fractional Differential Equations, an Application-Oriented Exposition Using Differential Operators of Caputo Type. Springer, Berlin (2010)
Kilbas, A., Srivastava, H., Trujillo, J.: Theory and Applications of Fractional Differential Equations. North-Holland, New York (2006)
Wu, G.C., Baleanu, D.: Variational iteration method for the Burgers’ flow with fractional derivatives—new Lagrange multipliers. Appl. Math. Model. 37(9), 6183–6190 (2013)
Sun, H., Zhang, Y., Baleanu, D., Chen, W., Chen, Y.: A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 64, 213–231 (2018)
Elsaid, A., Abdel Latif, M.S., Maneea, M.: Similarity solutions of fractional order heat equations with variable coefficients. Miskolc Math. Notes 17(1), 245–254 (2016)
Elsaid, A., Abdel Latif, M.S., Maneea, M.: Similarity solutions for multiterm time-fractional diffusion equation. Adv. Math. Phys. 2016 7304659 (2016)
Algahtani, O.J.J.: Comparing the Atangana–Baleanu and Caputo–Fabrizio derivative with fractional order: Allen Cahn model. Chaos Solitons Fractals 89, 552–559 (2016)
Atangana, A., Baleanu, D.: New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm. Sci. 20(2), 763–769 (2016)
Katugampola, U.N.: New approach to a generalized fractional integral. Appl. Math. Comput. 218, 860–865 (2011)
Katugampola, U.N.: A new approach to generalized fractional derivatives. Bull. Math. Anal. Appl. 6(4), 1–15 (2014)
Jarad, F., Abdeljawad, T.: A modified Laplace transform for certain generalized fractional operators. Results Nonlinear Anal. 1(2), 88–98 (2018)
Sene, N., Gómez-Aguilar, J.F.: Analytical solutions of electrical circuits considering certain generalized fractional derivatives. Eur. Phys. J. Plus 134(6), 260 (2019)
Jarad, F., Abdeljawad, T., Baleanu, D.: On the generalized fractional derivatives and their Caputo modification. J. Nonlinear Sci. Appl. 10(5), 2607–2619 (2017)
Gambo, Y.Y., Jarad, F., Abdeljawad, T.: Fractional vector calculus in the frame of a generalized Caputo fractional derivative. U.P.B. Sci. Bull., Ser. A 80(4), 219–228 (2018)
Gambo, Y.Y., Ameen, R., Jarad, F., Abdeljawad, T.: Existence and uniqueness of solutions to fractional differential equations in the frame of generalized Caputo fractional derivatives. Adv. Differ. Equ. 2018, 134 (2018)
Jarad, F., Abdeljawad, T.: Generalized fractional derivatives and Laplace transform. Discrete Contin. Dyn. Syst., Ser. S 13(3), 709–722 (2019)
Sahadevan, R., Bakkyaraj, T.: Invariant subspace method and exact solutions of certain nonlinear time fractional partial differential equations. Fract. Calc. Appl. Anal. 18(1), 146–162 (2015)
Sahadevan, R., Prakash, P.: Exact solution of certain time fractional nonlinear partial differential equations. Nonlinear Dyn. 85(1), 659–673 (2016)
Sahadevan, R., Prakash, P.: Exact solutions and maximal dimension of invariant subspaces of time fractional coupled nonlinear partial differential equations. Commun. Nonlinear Sci. Numer. Simul. 42, 158–177 (2017)
Sahadevan, R., Prakash, P.: On Lie symmetry analysis and invariant subspace methods of coupled time fractional partial differential equations. Chaos Solitons Fractals 104, 107–120 (2017)
Hashemi, M.S.: Invariant subspaces admitted by fractional differential equations with conformable derivatives. Chaos Solitons Fractals 107, 161–169 (2018)
Harris, P.A., Garra, R.: Analytic solution of nonlinear fractional Burgers-type equation by invariant subspace method. Nonlinear Stud. 20, 471–481 (2013)
Oliveira, D.S., Capelas de Oliveira, E.: Hilfer–Katugampola fractional derivatives. Comput. Appl. Math. 37(3), 3672–3690 (2018)
Acknowledgements
Not applicable.
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All three authors contributed equally to this work. They all read and approved the final version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Certain basic properties of the generalized fractional derivative
Appendix: Certain basic properties of the generalized fractional derivative
The definitions and properties of the generalized derivative used in this paper can be found in [9–16]. In this appendix, we give some basic properties of the generalized derivative.
Theorem A1
([10])
For\(0<\alpha <1\)and\(\rho\in\mathbb{ R}\), the generalized fractional derivative of\(f ( t ) = t ^{v}\)is given by
wherevis arbitrary constant.
Proof
Using the definition of the generalized fractional derivative [13–16], we get
Let
Assume \(\tau =t u^{\frac{1}{\rho }}\). So we get
where \(\beta ( m, n )\) is beta function defined as
So we obtain
Substituting Eq. (A3) into Eq. (A2), we obtain
Using the relation \(\varGamma ( \gamma +1 ) =\gamma \varGamma ( \gamma )\), we obtain
□
Remark
In [10], the generalized fractional derivative of \(f ( t ) = t^{v}\) is obtained as (see Eq. (5.7)) as
So we can see that there is a misprint in this relation. The correct relation is given by Eq. (A1).
Theorem A2
([11])
The Cauchy problem
has the solution
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Abdel Latif, M.S., Abdel Kader, A.H. & Baleanu, D. The invariant subspace method for solving nonlinear fractional partial differential equations with generalized fractional derivatives. Adv Differ Equ 2020, 119 (2020). https://doi.org/10.1186/s13662-020-02553-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02553-9