1 Introduction

The nonlinear partial differential equation (NLPDE) have been considered a fundamental icon in many research ideas. It has been used to formulate many natural, engineering, mechanical, and physical phenomena; this happens because it contains beforehand unknown multi-variable functions and its derivatives. During the last decade, many aspects have been formulated in NLPDE form. Study and investigation of the solitary wave for these models are considered as one of the basic interests of many researchers. The obtained solutions are used to motivate the semi-analytical and numerical schemes to be more accurate. Moreover, the solitary wave is a kind of wave which propagates without any time evolution in shape or size. Many analytical, semi-analytical and numerical schemes have been derived from investigating the physical dynamics of these models such as the Adomian decomposition method, the simplest equation method, modified tanh-function method, B-spline method, iterative method [1–14].

In this context, many nonlinear evolutions equations which represent many important phenomena have been studied and one investigated its properties and dynamical behavior such as by the Benjamin–Bona–Mahony equation, Bateman–Burgers equation, Benjamin–Ono equation, Boomeron equation, Calabi flow equation, Cauchy momentum equation, complex Monge–Ampère equation, Davey–Stewartson equation [15–30].

This research paper focuses on studying the Cahn–Allen equation which is considered as one of the essential models in the plasma physics, quantum mechanics, mathematical biology, and fluid dynamics and describes the dynamics of the phase separation in iron alloys. Moreover, it is also used in solidification and nucleation problems. The Allen–Cahn equation was derived to describe the process of phase separation in multicomponent alloy systems, including order–disorder transitions where it is a reaction–diffusion equation of mathematical physics. This model is given by

$$\begin{aligned} \textstyle\begin{cases} \varXi _{t}=\varUpsilon _{\varXi } [ \operatorname{\mathbf{div}} (\varepsilon _{n} ^{2} \bigtriangledown \varXi )-f'(\varXi ) ] & \text{on } \varOmega \times \varGamma , \\ \varXi =\varTheta & \text{on } \partial _{\varXi } \varOmega \times \varGamma , \\ -(\varepsilon _{n} ^{2} \bigtriangledown \varXi )\cdot m=q& \text{on } \partial _{q} \varOmega \times \varGamma , \\ \varXi =\varXi _{0}& \text{on } \varOmega \times \{0\}, \end{cases}\displaystyle \end{aligned}$$
(1)

where \(\varUpsilon _{\varXi }\), f, Θ, q, \(\varXi _{0}\), m represent the mobility, the free energy density, the control on the state variable at the portion of the boundary \(\partial _{\varXi } \varOmega \), the source control at \(\partial _{q} \varOmega \), the initial condition, and the outward normal to ∂Ω, respectively. This model is also the \(L^{2}\) gradient flow of the Ginzburg–Landau–Wilson free energy functional and close to the Cahn–Hilliard equation.

The Cahn–Allen equation (a.k.a. as Allen–Cahn equation or the Nagumo equation) is given by

$$\begin{aligned} \varXi _{t}=\Delta \varXi -f(\varXi ), \quad x\in R^{N}, t>0, \end{aligned}$$
(2)

where

$$\begin{aligned} f(\varXi )=\bigl(\varXi ^{2}-1\bigr) (\varXi -a). \end{aligned}$$
(3)

According to the interfaces that travel upwards in the vertical y direction with a constant speed c, we can rewrite Eq. (2) as

$$\begin{aligned} \varXi _{t}=\sum_{i=0}^{\infty } \partial _{x_{i}} ^{2} \varXi +\varXi _{y y}+a \varXi ^{2}+\varXi -\varXi ^{3}-a. \end{aligned}$$
(4)

According to the De Giorgi conjecture, the natural extension of Eq. (4) has the following form:

$$\begin{aligned} \varXi _{t}=\varXi _{y y}-\varXi -\varXi ^{3}+\Delta '\varXi . \end{aligned}$$
(5)

Thus, it is given in the simple form of

$$\begin{aligned} \varXi _{t}-\varXi _{xx}+\varXi ^{3}-\varXi =0. \end{aligned}$$
(6)

The strategy of this paper is summarized as follows: In Sect. 2, we apply the modified Khater method, Adomian decomposition method, and B-spline schemes [31–35] to the Cahn–Allen model [36–39]. In Sect. 3, we study our obtained solutions, showing a novel comparison between our solutions and the other existing results in the available literature. In Sect. 4, we draw a conclusion of all major results.

2 Application

In this section, the analytical, semi-analytical and numerical schemes are applied to our suggested model. Using the wave transformation \(\varXi =\varXi (x,t)=\varXi (\Im )\), \(\Im =k x+\omega t\) on Eq. (6) yields

$$\begin{aligned} \omega \varXi '-k^{2} \varXi ''+\varXi ^{3}-\varXi =0. \end{aligned}$$
(7)

Using the balance homogeneous rule between the highest order derivatives and nonlinear terms leads to \(n=1\).

2.1 Analytical solution

Applying the modified Khater method on Eq. (7) leads to formulating the general solution form of the Cahn–Allen equation,

$$\begin{aligned} \varXi (\Im )=\sum_{i=1}^{n} a_{i} K^{i f(\Im )}+\sum_{i=1}^{n} b_{i} K ^{-i f(\Im )}+a_{0}=a_{0}+a_{1} K^{f(\Im )}+\frac{b_{1}}{K^{ f( \Im )}}, \end{aligned}$$
(8)

where K is arbitrary constant and \(f(\Im )\) is a solution function of the following auxiliary equation:

$$\begin{aligned} f'(\Im )= \frac{\beta +\alpha k^{-f(\Im )}+\sigma k^{f(\Im )}}{\ln (K)}, \end{aligned}$$
(9)

where β, α, σ are arbitrary constants, which will be determined. Substituting Eq. (8) along with (9) into Eq. (7) and collecting all coefficients of the same power of \(k^{f(\Im )}\) gives an algebraic equation system. Solving the obtained system yields

$$\begin{aligned}& \textit{Family I}\quad \biggl[ a_{0}\to \frac{\sqrt{ (\beta ^{2}-4 \alpha \sigma ) ^{2}}-\beta \sqrt{\beta ^{2}-4 \alpha \sigma }}{2 (\beta ^{2}-4 \alpha \sigma )},a_{1} \to -\frac{\sigma }{\sqrt{\beta ^{2}-4 \alpha \sigma }},b_{1}\to 0, \\& \hphantom{\textit{Family I}\quad}{}\omega \to \frac{3 \sqrt{ (\beta ^{2}-4 \alpha \sigma ) ^{2}}}{2 (\beta ^{2}-4 \alpha \sigma )^{3/2}},k\to -\frac{1}{ \sqrt{2} \sqrt{\beta ^{2}-4 \alpha \sigma }} \biggr], \\& \textit{Family II}\quad \biggl[ a_{0}\to \frac{\sqrt{ (\beta ^{2}-4 \alpha \sigma ) ^{2}}-\beta \sqrt{\beta ^{2}-4 \alpha \sigma }}{2 (\beta ^{2}-4 \alpha \sigma )},a_{1} \to 0,b_{1}\to -\frac{\alpha }{\sqrt{ \beta ^{2}-4 \alpha \sigma }}, \\& \hphantom{\textit{Family II}\quad}{}\omega \to -\frac{3 \sqrt{ (\beta ^{2}-4 \alpha \sigma ) ^{2}}}{2 (\beta ^{2}-4 \alpha \sigma )^{3/2}},k\to -\frac{1}{ \sqrt{2} \sqrt{\beta ^{2}-4 \alpha \sigma }} \biggr]. \end{aligned}$$

Thus, the solitary wave solutions of the Cahn–Allen equation according to Family I are given as follows.

When \(\beta ^{2}-4 \alpha \sigma <0\) and \(\sigma \neq 0\)

$$\begin{aligned}& \varXi _{1}(x,t)=\frac{1}{2 (\beta ^{2}-4 \alpha \sigma ) ^{3/2}} \biggl[ \sqrt{\beta ^{2}-4 \alpha \sigma } \sqrt{ \bigl(\beta ^{2}-4 \alpha \sigma \bigr)^{2}}+ \bigl(4 \alpha \sigma -\beta ^{2} \bigr)^{3/2} \\& \hphantom{\varXi _{1}(x,t)=}{}\times \tan \biggl(\frac{\sqrt{4 \alpha \sigma -\beta ^{2}} (3 t \sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}-\sqrt{2} x (\beta ^{2}-4 \alpha \sigma ) )}{4 (\beta ^{2}-4 \alpha \sigma )^{3/2}} \biggr) \biggr], \end{aligned}$$
(10)
$$\begin{aligned}& \varXi _{2}(x,t)=\frac{1}{2 (\beta ^{2}-4 \alpha \sigma ) ^{3/2}} \biggl[ \sqrt{\beta ^{2}-4 \alpha \sigma } \sqrt{ \bigl(\beta ^{2}-4 \alpha \sigma \bigr)^{2}}+ \bigl(4 \alpha \sigma -\beta ^{2} \bigr)^{3/2} \\& \hphantom{\varXi _{2}(x,t)=}{}\times \cot \biggl(\frac{\sqrt{4 \alpha \sigma -\beta ^{2}} (3 t \sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}-\sqrt{2} x (\beta ^{2}-4 \alpha \sigma ) )}{4 (\beta ^{2}-4 \alpha \sigma )^{3/2}} \biggr) \biggr]. \end{aligned}$$
(11)

When \(\beta ^{2}-4 \alpha \sigma >0\) and \(\sigma \neq 0\)

$$\begin{aligned}& \varXi _{3}(x,t)=\frac{1}{2} \biggl( \frac{\beta ^{2}-4 \alpha \sigma }{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}}+\tanh \biggl(\frac{1}{4} \biggl( \frac{3 t (\beta ^{2}-4 \alpha \sigma )}{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}}-\sqrt{2} x \biggr) \biggr) \biggr), \end{aligned}$$
(12)
$$\begin{aligned}& \varXi _{4}(x,t)=\frac{1}{2} \biggl( \frac{\beta ^{2}-4 \alpha \sigma }{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}}+\coth \biggl(\frac{1}{4} \biggl( \frac{3 t (\beta ^{2}-4 \alpha \sigma )}{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}}-\sqrt{2} x \biggr) \biggr) \biggr). \end{aligned}$$
(13)

When \(\alpha \sigma <0\) and \(\sigma \neq 0\) and \(\alpha \neq 0\) and \(\beta =0\)

$$\begin{aligned}& \varXi _{5}(x,t)=-\frac{\sqrt{\alpha ^{2} \sigma ^{2}}+\alpha \sigma \tanh (\frac{1}{4} (\frac{3 \alpha \sigma t}{\sqrt{ \alpha ^{2} \sigma ^{2}}}+\sqrt{2} x ) )}{2 \alpha \sigma }, \end{aligned}$$
(14)
$$\begin{aligned}& \varXi _{6}(x,t)=-\frac{\sqrt{\alpha ^{2} \sigma ^{2}}+\alpha \sigma \coth (\frac{1}{4} (\frac{3 \alpha \sigma t}{\sqrt{ \alpha ^{2} \sigma ^{2}}}+\sqrt{2} x ) )}{2 \alpha \sigma }. \end{aligned}$$
(15)

When \(\alpha \sigma >0\) and \(\sigma \neq 0\) and \(\alpha \neq 0\) and \(\beta =0\)

$$\begin{aligned}& \varXi _{7}(x,t)=-\frac{\sqrt{\alpha ^{2} \sigma ^{2}}+\alpha \sigma \tanh (\frac{1}{4} (\frac{3 \alpha \sigma t}{\sqrt{ \alpha ^{2} \sigma ^{2}}}+\sqrt{2} x ) )}{2 \alpha \sigma }, \end{aligned}$$
(16)
$$\begin{aligned}& \varXi _{8}(x,t)=-\frac{\sqrt{\alpha ^{2} \sigma ^{2}}+\alpha \sigma \coth (\frac{1}{4} (\frac{3 \alpha \sigma t}{\sqrt{ \alpha ^{2} \sigma ^{2}}}+\sqrt{2} x ) )}{2 \alpha \sigma }. \end{aligned}$$
(17)

When \(\beta =0\) and \(\alpha =-\sigma \)

$$\begin{aligned} \varXi _{9}(x,t)=\frac{1}{2} \biggl(\coth \biggl( \frac{1}{4} \biggl(\frac{3 t}{\alpha ^{2}}-\sqrt{2} x \biggr) \biggr)+1 \biggr). \end{aligned}$$
(18)

When \(\alpha = 0\) and \(\beta \neq 0\) and \(\sigma \neq 0\)

$$\begin{aligned} \varXi _{10}(x,t)=\frac{1}{2} \beta \biggl(\frac{\beta }{\sqrt{\beta ^{4}}}+\frac{\frac{2 \sigma }{\sigma -2 e^{\frac{\beta (\sqrt{2} \beta ^{2} x-3 \sqrt{\beta ^{4}} t )}{2 (\beta ^{2} ) ^{3/2}}}}-1}{\sqrt{\beta ^{2}}} \biggr). \end{aligned}$$
(19)

When \(\beta =0\) and \(\alpha =\sigma \)

$$\begin{aligned} \varXi _{11}(x,t)=\frac{\alpha \sqrt{-\alpha ^{2}} \tan (C+\frac{ \alpha (3 \sqrt{\alpha ^{4}} t+\sqrt{2} \alpha ^{2} x )}{4 (-\alpha ^{2} )^{3/2}} )-\sqrt{\alpha ^{4}}}{2 \alpha ^{2}}. \end{aligned}$$
(20)

Meanwhile, the solitary wave solutions of the Cahn–Allen equation according to Family II are given as follows.

When \(\beta ^{2}-4 \alpha \sigma <0\) and \(\sigma \neq 0\)

$$\begin{aligned}& \varXi _{12}(x,t) \\& \quad =\frac{1}{2} \biggl[- \frac{\beta }{\sqrt{\beta ^{2}-4 \alpha \sigma }}+\frac{\beta ^{2}-4 \alpha \sigma }{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}} \\& \qquad {}+\frac{4 \alpha \sigma }{\sqrt{\beta ^{2}-4 \alpha \sigma } (\beta +\sqrt{4 \alpha \sigma -\beta ^{2}} \tan (\frac{\sqrt{4 \alpha \sigma -\beta ^{2}} (3 t \sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}+\sqrt{2} x (\beta ^{2}-4 \alpha \sigma ) )}{4 (\beta ^{2}-4 \alpha \sigma )^{3/2}} ) )} \biggr], \end{aligned}$$
(21)
$$\begin{aligned}& \varXi _{13}(x,t) \\& \quad =\frac{1}{2} \biggl[- \frac{\beta }{\sqrt{\beta ^{2}-4 \alpha \sigma }}+\frac{\beta ^{2}-4 \alpha \sigma }{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}} \\& \qquad {}+\frac{4 \alpha \sigma }{\sqrt{\beta ^{2}-4 \alpha \sigma } (\beta +\sqrt{4 \alpha \sigma -\beta ^{2}} \cot (\frac{\sqrt{4 \alpha \sigma -\beta ^{2}} (3 t \sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}+\sqrt{2} x (\beta ^{2}-4 \alpha \sigma ) )}{4 (\beta ^{2}-4 \alpha \sigma )^{3/2}} ) )} \biggr]. \end{aligned}$$
(22)

When \(\beta ^{2}-4 \alpha \sigma >0\) and \(\sigma \neq 0\)

$$\begin{aligned}& \varXi _{14}(x,t)=\frac{1}{2} \biggl[- \frac{\beta }{\sqrt{\beta ^{2}-4 \alpha \sigma }}+\frac{\beta ^{2}-4 \alpha \sigma }{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}} \\& \hphantom{\varXi _{14}(x,t)=}{}+\frac{4 \alpha \sigma }{\sqrt{\beta ^{2}-4 \alpha \sigma } (\beta -\sqrt{ \beta ^{2}-4 \alpha \sigma } \tanh (\frac{1}{4} (\frac{3 t (\beta ^{2}-4 \alpha \sigma )}{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}}+\sqrt{2} x ) ) )} \biggr], \end{aligned}$$
(23)
$$\begin{aligned}& \varXi _{15}(x,t)=\frac{1}{2} \biggl[- \frac{\beta }{\sqrt{\beta ^{2}-4 \alpha \sigma }}+\frac{\beta ^{2}-4 \alpha \sigma }{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}} \\& \hphantom{\varXi _{15}(x,t)=}{}+\frac{4 \alpha \sigma }{\sqrt{\beta ^{2}-4 \alpha \sigma } (\beta -\sqrt{ \beta ^{2}-4 \alpha \sigma } \coth (\frac{1}{4} (\frac{3 t (\beta ^{2}-4 \alpha \sigma )}{\sqrt{ (\beta ^{2}-4 \alpha \sigma )^{2}}}+\sqrt{2} x ) ) )} \biggr]. \end{aligned}$$
(24)

When \(\alpha \sigma <0\) and \(\sigma \neq 0\) and \(\alpha \neq 0\) and \(\beta =0\)

$$\begin{aligned}& \varXi _{16}(x,t)=\frac{1}{2} \biggl(\coth \biggl( \frac{1}{4} \biggl(\sqrt{2} x-\frac{3 \alpha \sigma t}{\sqrt{\alpha ^{2} \sigma ^{2}}} \biggr) \biggr)- \frac{\alpha \sigma }{\sqrt{\alpha ^{2} \sigma ^{2}}} \biggr), \end{aligned}$$
(25)
$$\begin{aligned}& \varXi _{17}(x,t)=\frac{1}{2} \biggl(\tanh \biggl( \frac{1}{4} \biggl(\sqrt{2} x-\frac{3 \alpha \sigma t}{\sqrt{\alpha ^{2} \sigma ^{2}}} \biggr) \biggr)- \frac{\alpha \sigma }{\sqrt{\alpha ^{2} \sigma ^{2}}} \biggr). \end{aligned}$$
(26)

When \(\beta =0\) and \(\alpha =-\sigma \)

$$\begin{aligned} \varXi _{18}(x,t)=\frac{1}{2} \biggl(\frac{\sqrt{\alpha ^{4}}}{\alpha ^{2}}+ \tanh \biggl(\frac{1}{4} \biggl(\frac{3 \sqrt{\alpha ^{4}} t}{ \alpha ^{2}}+\sqrt{2} x \biggr) \biggr) \biggr). \end{aligned}$$
(27)

When \(\beta =\frac{\alpha }{2}= \kappa \) and \(\sigma =0\)

$$\begin{aligned}& \varXi _{19}(x,t)=\frac{\sqrt{\kappa ^{4}}+\kappa \sqrt{\kappa ^{2}} (\frac{1}{e^{\frac{\kappa (3 \sqrt{\kappa ^{4}} t+ \sqrt{2} \kappa ^{2} x )}{2 (\kappa ^{2} )^{3/2}}}- \frac{1}{2}}+1 )}{2 \kappa ^{2}}. \end{aligned}$$
(28)

When \(\beta =0\) and \(\alpha =\sigma \)

$$\begin{aligned}& \varXi _{20}(x,t)=\frac{\alpha \sqrt{-\alpha ^{2}} \cot (C+\frac{ \alpha (\sqrt{2} \alpha ^{2} x-3 \sqrt{\alpha ^{4}} t )}{4 (-\alpha ^{2} )^{3/2}} )-\sqrt{\alpha ^{4}}}{2 \alpha ^{2}}. \end{aligned}$$
(29)

When \(\sigma =0\) and \(\beta \neq 0\) and \(\alpha \neq 0\)

$$\begin{aligned}& \varXi _{21}=\frac{1}{2} \beta \biggl( \frac{\beta }{\sqrt{\beta ^{4}}}+\frac{1-\frac{2 \beta }{\beta -\alpha e^{\frac{\beta (3 \sqrt{\beta ^{4}} t+ \sqrt{2} \beta ^{2} x )}{2 (\beta ^{2} )^{3/2}}}}}{\sqrt{ \beta ^{2}}} \biggr). \end{aligned}$$
(30)

2.2 Semi-analytical solution

Applying the Adomian decomposition method on Eq. (7) allows rewriting it as

$$\begin{aligned} L \varXi (\Im )+R \varXi (\Im )+N \varXi (\Im )=0, \end{aligned}$$
(31)

where L, R, N represent a differential operator, a linear operator and nonlinear term, respectively. Using the inverse operator \(L^{-1}\) on (31), yields

$$\begin{aligned} \sum_{i=0}^{\infty } \varXi _{i} (\Im ) =&\varXi (0)+\varXi '(0) \varXi + \frac{ \omega }{k^{2}} L^{-1} \Biggl( \sum _{i=0}^{\infty } (\varXi _{i})' \Biggr)-\frac{1}{k ^{2}} L^{-1} \Biggl( \sum _{i=0}^{\infty } \varXi _{i} \Biggr) \\ &{}+ \frac{1}{k^{2}} L^{-1} \Biggl( \sum _{i=0}^{\infty } A_{i} \Biggr). \end{aligned}$$
(32)

Under the condition \([ \alpha =-1, \beta =0, \sigma =4, \omega =-\frac{3}{8}, k=-\frac{1}{4 \sqrt{2}} ]\) on Eq. (14), we get

$$\begin{aligned}& \varXi _{\mathrm{exact}}=\frac{1}{2} \bigl( \tanh (2 \varXi )+1 \bigr) . \end{aligned}$$
(33)

So we obtain

$$\begin{aligned}& \varXi _{0}=\Im +\frac{1}{2}, \end{aligned}$$
(34)
$$\begin{aligned}& \varXi _{1} =\frac{8 \Im ^{5}}{5}+4 \Im ^{4}-\frac{4 \Im ^{3}}{3}-12 \Im ^{2}+ \frac{ \Im }{2}+\frac{1}{20}, \end{aligned}$$
(35)
$$\begin{aligned}& \varXi _{2} =\frac{128 \Im ^{10}}{75}+ \frac{128 \Im ^{9}}{15}+\frac{352 \Im ^{8}}{35}-\frac{544 \Im ^{7}}{21}- \frac{976 \Im ^{6}}{15}-\frac{3572 \Im ^{5}}{75}+\frac{138 \Im ^{4}}{5}+ \frac{704 \Im ^{3}}{15} \\& \hphantom{\varXi _{2} =}{}-\frac{7 \Im ^{2}}{2}. \end{aligned}$$
(36)

According to Eqs. (34)–(36), we get the semi-analytical solution of Eq. (6),

$$\begin{aligned} \varXi _{\text{Semi-Analytical}} =& \frac{1024 \Im ^{16}}{375}+ \frac{8192 \Im ^{15}}{375}+\frac{91{,}648 \Im ^{14}}{1575}-\frac{2048 \Im ^{13}}{225}- \frac{534{,}272 \Im ^{12}}{1575} \\ &{} -\frac{4{,}564{,}384 \Im ^{11}}{7875}+\frac{374{,}768 \Im ^{10}}{7875}+ \frac{85{,}928 \Im ^{9}}{75}+\frac{268{,}132 \Im ^{8}}{225} \\ &{}-\frac{146{,}998 \Im ^{7}}{1575}-\frac{860{,}104 \Im ^{6}}{1125} \\ &{}-\frac{155{,}033 \Im ^{5}}{750}+\frac{1701 \Im ^{4}}{50}+ \frac{37 \Im ^{3}}{300}- \frac{7 \Im ^{2}}{80}+\cdots. \end{aligned}$$
(37)

2.3 Numerical solution

This part discusses the numerical solution of the Cahn–Allen equation by using the quintic B-spline. Based on the quintic B-spline, the suggested solution of the ordinary differential of the Cahn–Allen equation is given as

$$\begin{aligned} \varphi (\Im )=\sum_{i=-1} ^{n+1} c_{i} B_{i}, \end{aligned}$$
(38)

where \(c_{i}\), \(B_{i}\) meet the conditions

$$\begin{aligned} L \varphi (\Im )=f\bigl(\Im _{i},\varphi (\Im _{i})\bigr) \quad \text{where } (i=0,1,\ldots,n) \end{aligned}$$
(39)

and

$$\begin{aligned} B_{i}(\Im )=\frac{1}{h^{5}}\textstyle\begin{cases} (\Im -\Im _{i-3})^{5},& \Im \in [\Im _{i-3},\Im _{i-2}], \\ (\Im -\Im _{i-3})^{5}-6 (\Im -\Im _{i-2})^{5},&\Im \in [\Im _{i-2},\Im _{i-1}], \\ (\Im -\Im _{i-3})^{5}-6 (\Im -\Im _{i-2})^{5}+15 (\Im -\Im _{i-1})^{5},& \Im \in [\Im _{i-1},\Im _{i}], \\ (\Im _{i+3}-\Im )^{5}-6 (\Im _{i+2}-\Im )^{5}+15 (\Im _{i+1}-\Im )^{5},& \Im \in [\Im _{i},\Im _{i+1}], \\ (\Im _{i+3}-\Im )^{5}-6 (\Im _{i+2}-\Im )^{5},&\Im \in [\Im _{i+1},\Im _{i+2}], \\ (\Im _{i+3}-\Im )^{5},&\Im \in [\Im _{i+2},\Im _{i+3}], \\ 0,&\text{otherwise}, \end{cases}\displaystyle \end{aligned}$$
(40)

where \(i \in [-2,n+2]\). Thus, the approximate solution is given as

$$\begin{aligned} \varXi _{i}(\Im )=c_{i-2}+26 c_{i-1}+66 c_{i}+26 c_{i+1}+c_{i+2}. \end{aligned}$$
(41)

Substituting Eq. (41) and its derivatives into Eq. (6) yields a system of equations. Solving this system gives the value of \(c_{i}\). Substituting the values of \(c_{i}\), \(B_{i}\) into Eq. (38), one obtains

3 Results and discussion

This section discusses and studies the solutions obtained in (2.1), (2.2), (2.3) to show the novel aspects of our obtained solutions. This study is organized as follows:

  1. 1.

    In Sect. 2.1, the modified Khater method is applied to the Cahn–Allen to get the analytical wave solutions of this equation to study the structure of the dynamics for phase separation in Fe–Cr–X (\(X=Mo, Cu\)) ternary alloys. We compare our obtained solutions with that obtained in [37].

    In that paper, Hosseini, Bekir, and Ansari have used the modified Kudryashov method to get the analytical wave solutions of the Cahn–Allen equation, and by focusing on their solutions, we find Eq. (30) is similar to \(u_{1,2}(x,t)\) when \([-\alpha =d, \beta =1, e=a ]\). On the other side, all other obtained solutions in our paper are considered as a different form of solutions of that obtained in [37]. Also, we can see that the modified Khater method gives many different forms of solutions, not like the modified Kudryashov method, and that is considered as a good advantage of the method itself. Moreover, we sketch some results in Figs. 1–6 of our solutions to show more physical properties of the phase separation in Fe–Cr–X (\(X=Mo, Cu\)) ternary alloys.

    Figure 1
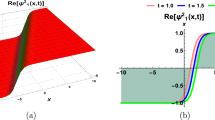
    figure 1

    Solitary wave of the Cahn–Allen equation by using Eq. (12) in three- (a), two- (c) dimensional and contour plot (b), when \([\sigma =1, \alpha =2, \beta =3 ]\), which shows the structure of the dynamics for phase separation in Fe–Cr–X (\(X=Mo, Cu\)) ternary alloys

    Full size image
    Figure 2
    figure 2

    Solitary wave of the Cahn–Allen equation by using Eq. (13) in three- (a), two- (c) dimensional and contour plot (b), when \([\sigma =1, \alpha =2, \beta =3 ]\), which shows the structure of the dynamics for phase separation in Fe–Cr–X (\(X=Mo, Cu\)) ternary alloys

    Full size image
    Figure 3
    figure 3

    Solitary wave of the Cahn–Allen equation by using Eq. (19) in three- (a), two- (c) dimensional and contour plot (b), when \([\sigma =1, \alpha =0, \beta =3 ]\), which shows the structure of the dynamics for phase separation in Fe–Cr–X (\(X=Mo, Cu\)) ternary alloys

    Full size image
    Figure 4
    figure 4

    Semi-analytical wave solution of the Cahn–Allen equation by using Eq. (37) in combined, separated, and radar plots

    Full size image
    Figure 5
    figure 5

    Semi-analytical wave solution of the Cahn–Allen equation by using Eq. (37) in three- (d), two- (f) dimensional, and contour (e) plots when \(x \in [-10,10]\), \(t \in [-10,10]\)

    Full size image
    Figure 6
    figure 6

    Numerical wave solution of the Cahn–Allen equation in combined, separated, and radar plots

    Full size image
  2. 2.

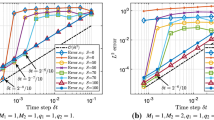
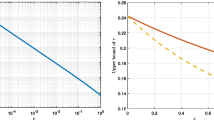
    In Sect. 2.2, the Adomian decomposition method is applied to get the semi-analytical solutions, and by using one of the obtained analytical solution we explain the comparison between these solutions in Table 1.

    Table 1 Comparison between analytical and semi-analytical solutions of the Cahn–Allen equation to calculate the values of absolute error, which explains the accuracy of both kinds of solutions
    Full size table
  3. 3.

    In Sect. 2.3, we apply the quintic B-spline to get the numerical solution of the Cahn–Allen equation. We explain the comparison between these solutions in Table 2.

    Table 2 Comparison between analytical and numerical solutions of the Cahn–Allen equation to discuss the absolute error between both of them that explains the convergence between these solutions
    Full size table
  4. 4.

    According to Tables 1 and 2, we can see the superiority of the Adomian decomposition method on the quintic B-spline where the absolute error between the analytical and semi-analytical solutions is smaller than that obtained between analytical and numerical solutions.

4 Conclusion

In this paper, the modified auxiliary equation, the Adomian decomposition method, and the B-spline scheme were successfully implemented on the Cahn–Allen equation to get the analytical, semi-analytical, and numerical solutions that show the structure of the dynamics for phase separation in Fe–Cr–X (\(X=Mo, Cu\)) ternary alloys. Some solutions are sketched to represent and explain the physical properties of them. Moreover, the comparison between these distinct solutions is given in the tables to show the absolute error between exact, semi-analytical, and numerical solutions. These tables show the superiority of the Adomian decomposition method on the quintic B-spline, since the absolute error obtained by the first method is smaller than that obtained by the second method. The solutions were represented, allowing a physical interpretation and better interpretation of their properties. In summary, this paper studied the Cahn–Allen equation and found relevant solutions that provide new explanations of real-world industrial phenomena. As we see in our paper, some numerical schemes can also be applied to this equation, such as in [23–25], and studying and using these methods to our model will be our future work.