1 Introduction

The construction and study of solutions for nonlinear partial differential equations (PDEs) are important, mainly because they are used as solutions of the models which explain complex physical phenomena in different fields of engineering and sciences, mainly in fluid mechanics, solid-state physics, plasma physics, plasma wave, and chemical physics. One such nonlinear PDE is the celebrated Korteweg–de Vries–Burgers equation [1,2,3]. The equation describes the mathematical modeling of liquid flow in a bubble and the liquid flow in an elastic pipeline [4]. It was derived in fluid mechanics to describe shallow water waves in a rectangular channel [5, 6] and plays an important role in plasma physics [7, 8].

Various methods [9,10,11,12] have been utilized to discover solutions of physical models described by PDEs. Among these methods, the Lie symmetry method, also called Lie group method, is one of the most dominant methods to establish exact solutions of nonlinear PDEs. It is based on the study of the invariance under one-parameter Lie group of point transformations [13,14,15,16]. A few but important contributions are in [17,18,19,20,21,22]. Thus, with the applications of Lie’s method, one can reduce nonlinear PDEs to the system of ordinary differential equations (ODEs) or at least reduce the number of independent variables. The obtained reduced ODEs are then used to find the invariant solution (exact solutions) of the nonlinear partial differential equations. Sometimes, in the procedure of reducing partial differential equations to ordinary differential equations, highly nonlinear equations, which are difficult to solve analytically, occurred. This is the main drawback in the traditional Lie group method. Therefore, in the quest of exact solutions of reduced nonlinear ODEs, various powerful methods are available in the literature such as the inverse scattering transform [23], truncated Painleve expansion [24], Jacobi elliptic function expansion [25], the F-expansion [26], the exp-function expansion method [27], \(( G'/G )\)-expansion method [28,29,30,31], and so on, but there is no unified method that can be used to deal with all types of nonlinear equations. The \(( G'/G )\)-expansion method has its own advantages: it is direct, concise, elementary, i.e., the general solutions of the second order linear ODE have been well known for the researchers, and effective, i.e.,it can be used for many other nonlinear PDEs, for instance the Burgers equation [32], KdV–Burgers equation [33]. Motivated by the reason above, we have used the modified \(( G'/G )\)-expansion method for soliton solutions of the reduced ODEs.

In this paper, we consider the variable coefficients version of the coupled KdV–Burgers equation [34,35,36]

$$ \begin{aligned} &u_{ t} + \tau _{ 1} ( t ) u u_{x} + \tau _{ 2} ( t ) w_{x x} + \tau _{ 3} ( t ) u_{x x x} = 0, \\ &w_{ t} + \kappa _{ 1} ( t ) w w_{x} + \kappa _{ 2} ( t ) w_{x x} + \kappa _{ 3} ( t ) u_{x x x} = 0, \end{aligned} $$
(1.1)

where \(\tau _{ i} ( t )\) and \(\kappa _{ i} ( t )\), \(i = 1, 2, 3\), are arbitrary time-dependent coefficients. We consider equation (1.1) for soliton solutions by using the Lie symmetry analysis and the modified \(( G'/G )\)-expansion method.

The paper is organized as follows. Section 2 is dedicated to some basics of Lie classical method for equation (1.1), and we fix the notations. Further in this section we derive the symmetries and admissible forms of the coefficients that admit the classical symmetry group corresponding to each member of the optimal system of subalgebras. Section 3 presents the reduced ODEs with the application of the modified \(( G'/G )\)-expansion method, and new soliton solutions of equation (1.1) are originated, which are expressed by hyperbolic functions, trigonometric functions, and rational functions. Some final remarks are specified in Sect. 4.

2 Lie symmetric reduction

Consider one-parameter Lie group of transformations for equation (1.1) as follows:

$$ \bigl( x^{*}, t^{*}, u^{*}, w^{*} \bigr) = \bigl( e^{\varepsilon \varGamma } x, e^{\varepsilon \varGamma } t, e^{\varepsilon \varGamma } u, e ^{\varepsilon \varGamma } w \bigr), $$
(2.1)

which is generated by a vector field of the form

$$ \varGamma = X ( x, t, u, w ) \frac{\partial }{\partial x} + T ( x, t, u, w ) \frac{\partial }{\partial t} + U ( x, t, u, w ) \frac{\partial }{\partial u} + W ( x, t, u, w ) \frac{\partial }{\partial w} $$
(2.2)

such that \(u^{ *} ( x^{ *}, t^{ *} )\) and \(w^{ *} ( x^{ *}, t^{ *} )\) are a solution of (1.1) whenever \(u ( x, t )\) and \(w ( x, t )\) are a solution of (1.1). Also \(e^{\varepsilon \varGamma } \) is denoted by the Lie series \(\sum_{k = 0} ^{\infty } \frac{\varepsilon ^{k}}{k !} \varGamma ^{k}\) with \(\varGamma ^{k} = \varGamma \varGamma ^{k - 1}\) and \(\varGamma ^{0} = 1\).

To discover the symmetries of equation (1.1), the infinitesimal invariance condition for the vector field (2.2) is given by the following relation:

$$\begin{aligned}& U_{ t} + \tau _{1}(t) U u_{x} + \tau _{1}(t) U_{x}u + \tau _{1}^{\prime } (t) T u u_{x} + \tau _{2}(t) W_{x x} + \tau _{2}^{\prime } (t) T w _{x x} \\& \quad {}+ \tau _{3}(t) U_{x x x}+ \tau _{3}^{\prime } (t) T u_{x x x} = 0, \\& W_{t} + \kappa _{1}(t) W w_{x} + \kappa _{1}(t) W_{x}w + \kappa _{1} ^{\prime } (t) T w w_{x} + \kappa _{2}(t) W_{x x} + \kappa _{2}^{\prime } (t) T w_{x x} \\& \quad {} + \kappa _{3}(t) U_{x x x} + \kappa _{3}^{\prime } (t) T u_{x x x} = 0. \end{aligned}$$
(2.3)

In the case of equation (1.1) we have to use the extended prolonged infinitesimals acting on an enlarged space (jet space), namely \(U_{t}\), \(U_{x}\), \(W_{x}\), \(W_{t}\), \(W_{x x}\), and \(U_{x x x}\) (for more details, see [13,14,15,16]) and decompose equations (2.3) to a large overdetermined system of linear PDEs for X, Y, U, and W known as determining equations:

$$ \begin{aligned} &U_{w} = U_{u u} = 0, \qquad W_{u} = W_{w w} = 0, \\ &X_{u} = X_{w} = X_{t} = X_{x x} = 0, \qquad T_{u} = T_{w} = T_{x} = 0, \\ &U_{t} + \tau _{1}(t) U_{x} u + \tau _{3}(t) U_{x x} = 0, \qquad W_{t} + \kappa _{1}(t) W_{x} w + \kappa _{3}(t) U_{x x} = 0, \\ &T_{t} - 3 X_{x} + \frac{\tau '_{3}(t)}{\tau _{3}(t)} T = 0, \qquad W_{w} - T_{t} - U_{u} + 3 X_{x} - \frac{\kappa '_{3}(t)}{\kappa _{3}(t)} T = 0, \\ &\tau _{1}(t) U + 2 \tau _{1}(t) X_{x} u - \tau '_{1}(t) T u - \tau _{1}(t) \frac{\tau '_{3}(t)}{\tau _{3}(t)} T u = 0, \\ &\tau _{2}(t) W_{w} + \tau _{2}(t) X_{x} - \tau '_{2}(t) T - \tau _{2}(t) U_{u} - \tau _{2}(t) \frac{\tau '_{3}(t)}{\tau _{3}(t)} T = 0, \\ &2 \kappa _{1}(t) W_{w} + 2 \kappa _{1}(t) X_{x} + \kappa '_{1}(t)T - \kappa _{1}(t) U_{u} - \kappa _{1}(t) \frac{\kappa '_{3}(t)}{\kappa _{3}(t)} T = 0, \\ &\kappa _{2}(t) W_{w} + \kappa _{2}(t) X_{x} + \kappa '_{2}(t) T - \kappa _{2}(t) U_{u} - \kappa _{2}(t) \frac{\tau '_{3}(t)}{\tau _{3}(t)} T = 0. \end{aligned} $$
(2.4)

The general solution of this large system (2.4), by setting the coefficients of different powers of u and w equal to zero, leads to the following expressions for infinitesimals:

$$ \begin{aligned} &X = a_{1} x + a_{5}, \\ &T = \frac{1}{\tau _{1}(t)} \biggl[ ( a_{1} - a_{2} ) \int \tau _{1}(t) \,dt + a_{4} \biggr], \\ &U = a_{2} u, \\ &W = a_{3} w. \end{aligned} $$
(2.5)

The time-dependent coefficients \(\tau _{i} ( t )\) and \(\kappa _{i} ( t )\), \(i = 1, 2, 3\), are associated as follows:

$$ \begin{aligned} &\tau _{2}^{\prime } ( t ) T + \tau _{2} ( t ) T_{t} + ( a_{3} - 2 a_{1} - a_{2} ) \tau _{2} ( t ) = 0, \\ &\tau _{3}^{\prime } ( t ) T + \tau _{3} ( t ) T_{t} - 3 a_{1} \tau _{3} ( t ) = 0, \\ &\kappa _{1}^{\prime } ( t ) T + \kappa _{1} ( t ) T_{t} + ( a_{3} - a_{1} ) \kappa _{1} ( t ) = 0, \\ &\kappa _{2}^{\prime } ( t ) T + \kappa _{2} ( t ) T_{t} - 2 a_{1} \kappa _{2} ( t ) = 0, \\ &\kappa _{3}^{\prime } ( t ) T + \kappa _{3} ( t ) T_{t} - ( a_{3} - a_{2} + 3a_{1} ) \kappa _{3} ( t ) = 0, \end{aligned} $$
(2.6)

where \(a_{1}\), \(a_{2}\), \(a_{3}\), \(a_{4}\), and \(a_{5}\) are arbitrary real constants. It follows that the Lie algebra of infinitesimal symmetries of the time-dependent coupled KdV–Burgers equation (1.1) is spanned by the following five linearly independent vector fields:

$$ \begin{aligned} &\varGamma _{1} = x \frac{\partial }{\partial x} + \frac{1}{\tau _{ 1} ( t )} \int \tau _{ 1} ( t ) \,dt\, \frac{\partial }{ \partial t}, \\ &\varGamma _{2} = u \frac{\partial }{\partial u} - \frac{1}{\tau _{ 1} ( t )} \int \tau _{ 1} ( t ) \,dt\, \frac{\partial }{ \partial t}, \\ &\varGamma _{3} = w \frac{\partial }{\partial w}, \\ &\varGamma _{4} = \frac{1}{\tau _{ 1} ( t )} \frac{\partial }{ \partial t}, \\ &\varGamma _{5} = \frac{\partial }{\partial x}. \end{aligned} $$
(2.7)

Further, in this section, we concentrate on the symmetry subalgebras, and we categorize their one-dimensional Lie subalgebras into equivalence classes under the action of the corresponding group. To categorize all the one-dimensional subalgebras of equation (1.1), we require considering the action of the adjoint representation of the symmetry group of equation (1.1). The adjoint representation of a Lie group to its algebra is a group action, and it is defined as follows:

$$ \operatorname{Ad } \bigl( \exp ( \varepsilon \varGamma _{i} ) \bigr) \varGamma _{j} = \varGamma _{j} - \varepsilon [ \varGamma _{i}, \varGamma _{j} ] + \frac{\varepsilon ^{2}}{2} \bigl[ \varGamma _{i}, [ \varGamma _{i}, \varGamma _{j} ] \bigr] - \cdots , $$
(2.8)

where \([ \varGamma _{i}, \varGamma _{j} ] = \varGamma _{i} \varGamma _{j} - \varGamma _{j} \varGamma _{i}\) is the commutator for the Lie algebra and ε is a parameter. More specifically, we start by considering a general element of the form \(\varGamma = a_{1} \varGamma _{1} + a_{2} \varGamma _{2} + a_{3} \varGamma _{3} + a_{4} \varGamma _{4} + a_{5} \varGamma _{5}\). Now we use all adjoint actions to simplify it as much as possible and classify all the different one-dimensional subalgebras of equation (1.1) as follows:

$$ \begin{aligned} (\mathrm{i})&\quad \varGamma _{1} + \lambda _{1} \varGamma _{2} + \lambda _{2} \varGamma _{3}, && ( \mathrm{ii})\quad \varGamma _{2} + \lambda _{3} \varGamma _{3}, \\ (\mathrm{iii})&\quad \varGamma _{3} + \lambda _{4} \varGamma _{4}, && (\mathrm{iv}) \quad \varGamma _{4} + \varGamma _{5}, \end{aligned} $$
(2.9)

where \(\lambda _{1}\), \(\lambda _{2}\), \(\lambda _{3}\), and \(\lambda _{4}\) are arbitrary constants.

3 Hyperbolic, trigonometric, and rational function solutions

In this section, we proceed to considering the symmetry variable for reduction of equation (1.1) to the systems of nonlinear ordinary differential equation (for details, see [37,38,39]) through the characteristic equation

$$ \frac{dx}{X ( x, t, u, w )} = \frac{dt}{T ( x, t, u, w )} = \frac{du}{U ( x, t, u, w )} = \frac{dw}{W ( x, t, u, w )} $$
(3.1)

for the different operators in the optimal system, and then we continue contracting soliton solutions of the main system (1.1) with the help of modified \(( G'/G )\)-expansion method.

3.1 Subalgebra \(\varGamma _{1} + \lambda _{1} \varGamma _{2} + \lambda _{2} \varGamma _{3}\)

The solutions of system (1.1) which are invariant under this subalgebra with the coefficient functions

$$\begin{aligned}& \tau _{2} ( t ) = \frac{K_{1}}{1 - \lambda _{ 1}} \tau _{1} ( t ) \biggl( \int \tau _{1} ( t ) \,dt \biggr) ^{ \frac{2 \lambda _{ 1} - \lambda _{ 2} + 1}{1 - \lambda _{ 1}}}, \qquad \tau _{3} ( t ) = \frac{K_{2}}{1 - \lambda _{ 1}} \tau _{1} ( t ) \biggl( \int \tau _{1} ( t ) \,dt \biggr) ^{\frac{\lambda _{ 1} + 2}{1 - \lambda _{ 1}}}, \\& \kappa _{1} ( t ) = \frac{K_{3}}{1 - \lambda _{ 1}} \tau _{1} ( t ) \biggl( \int \tau _{1} ( t ) \,dt \biggr) ^{ \frac{\lambda _{ 1} - \lambda _{ 2}}{1 - \lambda _{ 1}}}, \qquad \kappa _{2} ( t ) = \frac{K_{4}}{1 - \lambda _{ 1}} \tau _{1} ( t ) \biggl( \int \tau _{1} ( t ) \,dt \biggr) ^{ \frac{\lambda _{ 1} + 1}{ 1 - \lambda _{ 1}}}, \\& \kappa _{3} ( t ) = \frac{K_{5}}{1 - \lambda _{ 1}} \tau _{1} ( t ) \biggl( \int \kappa _{1} ( t ) \,dt \biggr) ^{ \frac{\lambda _{ 2} + 2}{1 - \lambda _{ 1}}} \end{aligned}$$
(3.2)

are given by the following relations:

$$ \begin{aligned} &u ( x, t ) = \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ \frac{\lambda _{ 1}}{1 - \lambda _{ 1}}} f ( \xi ), \\ &w ( x, t ) = \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ \frac{\lambda _{ 2}}{1 - \lambda _{ 1}}} g ( \xi ), \end{aligned} $$
(3.3)

where \(\xi = x ( \int \tau _{1} ( t ) )^{ \frac{ - 1}{1 - \lambda _{ 1}}}\) and \(f ( \xi )\), \(g ( \xi )\) are the solution of the system of nonlinear ordinary differential equations

$$ \begin{aligned} &\lambda _{ 1} f - f' \xi + (1 - \lambda _{ 1}) f f' + K_{1} g'' + K_{2} f''' = 0, \\ &\lambda _{ 2} g - g' \xi + K_{3} g g' + K_{4} g'' + K_{5} f''' = 0. \end{aligned} $$
(3.4)

Solving ODEs (3.4) for \(f ( \xi )\) and \(g ( \xi )\), substituting in equation (3.3) the main system (1.1) possesses the following solutions:

$$ \begin{aligned} &\begin{aligned} u ( x, t ) &= x \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - 1} + 12 K_{2} C_{2}^{2} - 4 C_{2}^{2} \sqrt{6} K_{2} \tanh \biggl( C_{1} + C_{2} x \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - 1} \biggr) \\ &\quad {}- 12 K_{2} C_{2}^{2} \tanh \biggl( C_{1} + C_{2} \biggl( x \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - 1} \biggr) \biggr) ^{2}, \end{aligned} \\ &\begin{aligned} w ( x, t ) &= \frac{x ( \int \tau _{1} ( t ) \,dt )^{ - 1}}{K_{3}} + \frac{20 \sqrt{6} K_{2}^{2} C _{3}^{2} \tanh ( C_{1} + C_{2} x ( \int \tau _{1} ( t ) \,dt )^{ - 1} )^{2}}{K_{1}} \\ &\quad {}- \frac{80 \sqrt{6} K_{2}^{2} C_{2}^{3} K_{3}}{6 K_{1} K_{3}}, \end{aligned} \end{aligned} $$
(3.5)

where \(K_{4} = - \frac{10 C_{2}^{2} K_{2}^{2} K_{3}}{3 K_{1}}\), \(K_{5} = - \frac{50 C_{2}^{2} K_{2}^{2} K_{3}}{3 K_{1}^{2}}\), \(\lambda _{1} = \lambda _{2} = 0\), and \(K_{1}\), \(K_{2}\), \(K_{3}\) are arbitrary constants.

3.2 Subalgebra \(\varGamma _{2} + \lambda _{3} \varGamma _{3}\)

The solutions of system (1.1) which are invariant under this subalgebra with the coefficient functions

$$\begin{aligned}& \tau _{2} ( t ) = K_{1} \tau _{1} ( t ) \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ \lambda _{3} - 1}, \qquad \tau _{3} ( t ) = K_{2} \tau _{1} ( t ) \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - 1}, \\& \kappa _{1} ( t ) = K_{3} \tau _{1} ( t ) \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ \lambda _{ 3} - 1}, \qquad \kappa _{2} ( t ) = K_{4} \tau _{1} ( t ) \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - 1}, \\& \kappa _{3} ( t ) = K_{5} \tau _{1} ( t ) \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - \lambda _{3}} \end{aligned}$$
(3.6)

are given by the following relations:

$$ \begin{aligned} &u ( x, t ) = \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - 1} f ( \xi ), \\ &w ( x, t ) = \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - \lambda _{ 3}} g ( \xi ), \end{aligned} $$
(3.7)

where \(\xi = x\) and \(f ( \xi )\), \(g ( \xi )\) are the solution of the system of nonlinear ordinary differential equations

$$ \begin{aligned} &{-} f + f f' + K_{1} g'' + K_{2} f''' = 0, \\ &{-} \lambda _{ 3} g + K_{3} g g' + K_{4} g'' + K_{5} f''' = 0. \end{aligned} $$
(3.8)

Now, under this subalgebra for arbitrary value of \(\lambda _{3}\), we are able to find out trivial solutions of nonlinear system (1.1). Therefore, to establish the nontrivial solution of system (1.1) by using equation (3.7), we have to solve equation (3.8) by the modified \(( G'/G )\)-expansion method [14, 15] with the restriction \(\lambda _{3} = 0\). Let us suppose that system (3.8) admits a solution in the modified \(( G'/G )\)-expansion method as follows:

$$ \begin{aligned} &f(\xi ) = a_{0} + \sum _{i = 1}^{P} \biggl\{ a_{i} \biggl( \frac{G'( \xi )}{G(\xi )} \biggr)^{i} + b_{i} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr)^{ - i} \biggr\} , \\ &g(\xi ) = c_{0} + \sum_{j = 1}^{q} \biggl\{ c_{j} \biggl( \frac{G'( \xi )}{G(\xi )} \biggr)^{j} + d_{j} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr)^{ - j} \biggr\} , \end{aligned} $$
(3.9)

where \(a_{0}\), \(a_{i}\), \(b_{i}\), \(c_{0}\), \(c_{j}\), \(d_{j}\), and μ are constants. The summation indexes p, q in equation (3.9) are positive integers, and function \(G(\xi )\) is the solution of the linear ODE

$$ G''(\xi ) + \mu G(\xi ) = 0. $$
(3.10)

The positive integers p, q may be decided in view of the homogeneous balance among the highest order derivative terms and nonlinear terms from equation (3.8). Therefore, equalizing the highest-order derivatives and nonlinear terms arriving in equation (3.8), we find \(p = 2\), \(q = 2\), and we set down

$$ \begin{aligned} &f(\xi ) = a_{0} + a_{1} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr) + a _{2} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr)^{2} + b_{1} \biggl( \frac{G'( \xi )}{G(\xi )} \biggr)^{ - 1} + b_{2} \biggl( \frac{G'(\xi )}{G( \xi )} \biggr)^{ - 2}, \\ &g(\xi ) = c_{0} + c_{1} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr) + c _{2} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr)^{2} + d_{1} \biggl( \frac{G'( \xi )}{G(\xi )} \biggr)^{ - 1} + d_{2} \biggl( \frac{G'(\xi )}{G( \xi )} \biggr)^{ - 2}. \end{aligned} $$
(3.11)

Further, substituting (3.11) into the system of ODEs (3.8), using linear ODE (3.10), and equating the coefficients of the same powers of \(( G'/G )\) to zero, we arrive at a set of simultaneous algebraic equations among \(a_{0}\), \(a_{1}\), \(a_{2}\), \(b_{1}\), \(b_{2}\), \(c_{0}\), \(c _{1}\), \(c_{2}\), \(d_{1}\), \(d_{2}\), and μ as follows:

$$\begin{aligned} (\mathrm{i})&\quad 24 b_{2} K_{2} \mu ^{3} + 2 b_{2}^{2} \mu = 0, \\ (\mathrm{ii})&\quad 6 d_{2} K_{1} \mu ^{2} + 6 b_{1} \mu ^{3} K_{2} + 3 \mu b_{1} b_{2} = 0, \\ (\mathrm{iii})&\quad 2 d_{1} K_{1} \mu ^{2} + 40 b_{2} \mu ^{2} K_{2} + 2 a _{0} \mu b_{2} + b_{1}^{2} \mu + 2 b_{2}^{2} = 0, \\ (\mathrm{iv})&\quad 8 d_{2} K_{1} \mu + 8 b_{1} \mu ^{2} K_{2} + a_{0} \mu b_{1} + b_{2} a_{1} \mu + 3 b_{1} b_{2} - b_{2} = 0, \\ (\mathrm{v})&\quad 2 d_{1} K_{1} \mu + 16 b_{2} \mu K_{2} + 2 a_{0} b_{2} - 2 b_{2} a_{2} \mu + b_{1}^{2} + 2 a_{2} b_{2} \mu - b_{1} = 0, \\ (\mathrm{vi})&\quad 2 d_{2}K_{2} - 2 a_{1}\mu ^{2}K_{2} + 2 b_{1} \mu K_{2} - a_{0} a_{1} \mu + a_{0} b_{1}+ a_{1}b_{2} - b_{1} a_{2} \mu \\ &\qquad {} + 2 c _{2} K_{1} \mu ^{2} - a_{0} = 0, \\ (\mathrm{vii})&\quad 2 c_{1} K_{1} \mu - 16 a_{2} \mu ^{2}K_{2} - 2 a_{0} a _{2} \mu - a_{1}^{2}\mu - a_{1} = 0, \\ (\mathrm{viii})&\quad 8 c_{2} K_{1} \mu - 8 a_{1} \mu K_{2} - 3 a_{1} a_{2} \mu - a_{0} a_{1} - a_{2} b_{1} - a_{2} = 0, \\ (\mathrm{ix})&\quad 2 c_{1} K_{1} - 40 a_{2} \mu K_{2} - 2 a_{0} a_{2} - a _{1}^{2} - 2 a_{2}^{2} \mu = 0, \\ (\mathrm{x})&\quad {-} 6 a_{1} K_{2} - 3 a_{1} a_{2} + 6 K_{1} c_{2} = 0, \\ (\mathrm{xi})&\quad {-} 24 a_{2} K_{2} - 2 a_{2}^{2} = 0. \end{aligned}$$
(3.12)

Also, when we put (3.11) into the second equation of (3.8), it brings the system of algebraic equations as follows:

$$\begin{aligned} (\mathrm{i})&\quad 24 b_{2} K_{5} \mu ^{3} + 2 K_{3} d_{2}^{2} \mu = 0, \\ (\mathrm{ii})&\quad 6 d_{2} K_{4} \mu ^{2} + 6 b_{1} \mu ^{3} K_{5} + 3 K_{3} \mu d_{1} d_{2} = 0, \\ (\mathrm{iii})&\quad 2 d_{1} K_{4} \mu ^{2} + 40 b_{2} \mu ^{2} K_{5} + 2 c _{0} \mu d_{2} K_{3} + K_{3} d_{1}^{2} \mu + 2 K_{3} d_{2}^{2} = 0, \\ (\mathrm{iv})&\quad 8 d_{2} K_{4} \mu + 8 b_{1} \mu ^{2} K_{5} + K_{3} c_{0} \mu d_{1} + K_{3} d_{2} c_{1} \mu + 3 K_{3} d_{1} d_{2} = 0, \\ (\mathrm{v})&\quad 2 d_{1} K_{4} \mu + 16 b_{2} \mu K_{5} + 2 K_{3} c_{0} d _{2} - 2 K_{3} d_{2} c_{2} \mu + K_{3} d_{1}^{2} + 2 K_{3} c_{2} d _{2} \mu = 0, \\ (\mathrm{vi})&\quad 2 d_{2}K_{4} - 2 a_{1}\mu ^{2}K_{5} + 2b_{1} \mu K_{5} - K_{3}c_{0} c _{1} \mu + K_{3}c_{0}d_{1} + K_{3}c_{1}d_{2} - K_{3}d_{1}c_{2}\mu \\ &\qquad + 2c_{2}K_{4}\mu ^{2} = 0, \\ (\mathrm{vii})&\quad 2 c_{1} K_{4} \mu - 16 a_{2} \mu ^{2}K_{5} - 2 K_{3} c _{0} c_{2} \mu - K_{3} c_{1}^{2}\mu = 0, \\ (\mathrm{viii})&\quad 8 c_{2} K_{4} \mu - 8 a_{1} \mu K_{5} - 3 K_{3} c_{1} c_{2} \mu - K_{3} c_{0} c_{1} - K_{3} c_{2} d_{1} = 0, \\ (\mathrm{ix})&\quad 2 c_{1} K_{4} - 40 a_{2} \mu K_{5} - 2 K_{3} c_{0} c _{2} - K_{3} c_{1}^{2} - 2 K_{3} c_{2}^{2} \mu = 0, \\ (\mathrm{x})&\quad {-} 6 a_{1} K_{5} - 3 K_{3} c_{1} c_{2} + 6 K_{4} c_{2} = 0, \\ (\mathrm{xi})&\quad {-} 24 a_{2} K_{5} - 2 K_{3} c_{2}^{2} = 0. \end{aligned}$$
(3.13)

On solving algebraic equations (3.12) and (3.13) for arbitrary values of \(K_{1}\) and \(K_{3}\), we get only the trivial solutions of the main system (1.1), which is not a physically interesting case. Therefore, we reach the following results:

Case 1:

$$ \begin{aligned} &a_{0} = a_{0}, \qquad b_{1} = 1, c_{0} = c_{0}, \qquad d_{1} = d_{1}\quad \mbox{and} \\ &a_{1} = a_{2} = b_{2} = c_{1} = c_{2} = d_{2} = K_{3} = \mu = 0; \end{aligned} $$
(3.14)

Case 2:

$$ \begin{aligned} &a_{0} = a_{0},\qquad b_{1} = 1,\qquad c_{1} = \frac{2 K_{4}}{K_{3}}\quad \mbox{and} \\ &a_{1} = a_{2} = b_{2} = c_{0} = c_{2} = d_{2} = d_{2} = K _{1} = \mu = 0. \end{aligned} $$
(3.15)

Now, when we substitute equations (3.14), (3.15) and the solution of linear equation (3.10) for \(\mu = 0\) into equation (3.11), we get the solution of nonlinear equation (3.8). Further, using the value of solution \(f ( \xi )\) and \(g ( \xi )\) into equation (3.7), we have rational solutions of equation (1.1) as follows.

Case 1 gives the rational solution of equation (1.1) by the following relation:

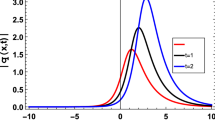
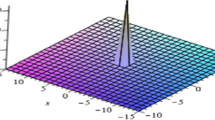
$$ \begin{aligned} &u ( x, t ) = \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - 1} \biggl[ a_{0} + \biggl( \frac{B}{A + B x} \biggr)^{ - 1} \biggr], \\ &w(x, t) = c_{0} + d_{1} \biggl( \frac{B}{A + B x} \biggr)^{ - 1}, \end{aligned} $$
(3.16)

where A and B are arbitrary constants (see Fig. 1).

Figure 1
figure 1

Oscillatory soliton solution (left) and dark soliton solution (right) given by equation (3.16) with \(A = 1\), \(B = 1\), \(a_{0} = c_{0} = d_{1} = 1\), and \(\tau _{1} ( t ) = \exp (t) + \sec (t) \tan (t) + t\)

Full size image

Similarly, Case 2 gives the rational solution by the following relation:

$$ \begin{aligned} &u ( x, t ) = \biggl( \int \tau _{1} ( t ) \,dt \biggr)^{ - 1} \biggl[ a_{0} + \biggl( \frac{B}{A + B x} \biggr)^{ - 1} \biggr], \\ &w(x, t) = \frac{2 K_{4}}{K_{3}} \biggl( \frac{B}{A + B x} \biggr) ^{2}, \end{aligned} $$
(3.17)

where A, B, \(K_{3}\), and \(K_{4}\) are arbitrary constants.

3.3 Subalgebra \(\varGamma _{3} + \lambda _{4} \varGamma _{4}\)

The solutions of system (1.1), which are invariant under this subalgebra with the coefficient functions

$$\begin{aligned}& \tau _{2} ( t ) = \frac{K_{1}}{\lambda _{4}} \tau _{1} ( t ) \exp \biggl( - \frac{1}{\lambda _{4}} \int \tau _{1} ( t ) \,dt \biggr), \qquad \tau _{3} ( t ) = \frac{K_{2}}{\lambda _{4}} \tau _{1} ( t ), \\& \kappa _{1} ( t ) = \frac{K_{3}}{\lambda _{4}} \tau _{1} ( t ) \exp \biggl( - \frac{1}{\lambda _{4}} \int \tau _{1} ( t ) \,dt \biggr), \qquad \kappa _{2} ( t ) = \frac{K_{4}}{\lambda _{4}} \tau _{1} ( t ), \\& \kappa _{3} ( t ) = \frac{K_{5}}{\lambda _{4}} \tau _{1} ( t ) \exp \biggl( \frac{1}{\lambda _{4}} \int \tau _{1} ( t ) \,dt \biggr), \end{aligned}$$
(3.18)

are given by the following relations:

$$ \begin{aligned} &u ( x, t ) = f ( \xi ), \\ &w ( x, t ) = \exp \biggl( \frac{1}{\lambda _{ 4}} \int \tau _{1} ( t ) \,dt \biggr) g ( \xi ), \end{aligned} $$
(3.19)

where \(\xi = x\) and \(f ( \xi )\), \(g ( \xi )\) are the solution of the system of nonlinear ordinary differential equations

$$ \begin{aligned} &\lambda _{4} f f' + K_{1} g'' + K_{2} f''' = 0, \\ &g + K_{3} g g' + K_{4} g'' + K_{5} f''' = 0. \end{aligned} $$
(3.20)

In this subalgebra, we also seek solutions of equation (3.20) by the modified \(( G'/G )\)-expansion method. Therefore, following the procedure adopted in subalgebra 3.2, we get \(p = 2\), \(q = 2\). So we can suppose that the solution of ODEs (3.20) is of the form

$$ \begin{aligned} &f(\xi ) = a_{0} + a_{1} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr) + a _{2} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr)^{2} + b_{1} \biggl( \frac{G'( \xi )}{G(\xi )} \biggr)^{ - 1} + b_{2} \biggl( \frac{G'(\xi )}{G( \xi )} \biggr)^{ - 2}, \\ &g(\xi ) = c_{0} + c_{1} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr) + c _{2} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr)^{2} + d_{1} \biggl( \frac{G'( \xi )}{G(\xi )} \biggr)^{ - 1} + d_{2} \biggl( \frac{G'(\xi )}{G( \xi )} \biggr)^{ - 2}. \end{aligned} $$
(3.21)

Substituting (3.21) into the system of ODEs (3.20), using linear ODE (3.10), and equating the coefficients of same powers of \(( G'/G )\) to zero, we obtain a set of simultaneous algebraic equations among \(a_{0}\), \(a_{1}\), \(a_{2}\), \(b_{1}\), \(b_{2}\), \(c_{0}\), \(c_{1}\), \(c_{2}\), \(d_{1}\), \(d _{2}\), and μ as follows:

$$\begin{aligned} (\mathrm{i}) &\quad 24 b_{2} K_{2} \mu ^{3} + 2 \lambda _{4} b_{2}^{2} \mu = 0, \\ (\mathrm{ii}) &\quad 6 d_{2} K_{1} \mu ^{2} + 6 b_{1} \mu ^{3} K_{2} + 3 \lambda _{4} \mu b_{1} b_{2} = 0, \\ (\mathrm{iii})&\quad 2 d_{1} K_{1} \mu ^{2} + 40 b_{2} \mu ^{2} K_{2} + 2 \lambda _{4} a_{0} \mu b_{2} + \lambda _{4} b_{1}^{2} \mu + 2 \lambda _{4} b_{2}^{2} = 0, \\ (\mathrm{iv})&\quad 8 d_{2} K_{1} \mu + 8 b_{1} \mu ^{2} K_{2} + a_{0} \lambda _{4} \mu b_{1} + b_{2} \lambda _{4} a_{1} \mu + 3 \lambda _{4} b _{1} b_{2} = 0, \\ (\mathrm{v})&\quad 2 d_{1} K_{1} \mu + 16 b_{2} \mu K_{2} + 2 \lambda _{4} a _{0} b_{2} - 2 \lambda _{4} b_{2} a_{2} \mu + \lambda _{4} b_{1}^{2} + 2 \lambda _{4} a_{2} b_{2} \mu = 0, \\ (\mathrm{vi})&\quad 2 d_{2}K_{2} - 2 a_{1}\mu ^{2}K_{2} + 2b_{1} \mu K_{2} - \lambda _{4}a_{0} a_{1}\mu + \lambda _{4}a_{0}b_{1}+ \lambda _{4} a_{1}b _{2} - \lambda _{4}b_{1}a_{2} \mu \\ &\qquad {} + 2 c_{2} K_{1} \mu ^{2} = 0, \\ (\mathrm{vii})&\quad 2 c_{1} K_{1} \mu - 16 a_{2} \mu ^{2}K_{2} - 2 \lambda _{4} a_{0} a_{2} \mu - a_{1}^{2} \lambda _{4} \mu = 0, \\ (\mathrm{viii})&\quad 8 c_{2} K_{1} \mu - 8 a_{1} \mu K_{2} - 3 \lambda _{4} a_{1} a_{2} \mu - \lambda _{4} a_{0} a_{1} - \lambda _{4} a_{2} b_{1} = 0, \\ (\mathrm{ix})&\quad 2 c_{1} K_{1} - 40 a_{2} \mu K_{2} - 2 \lambda _{4} a _{0} a_{2} - \lambda _{4} a_{1}^{2} - 2 \lambda _{4} a_{2}^{2} \mu = 0, \\ (\mathrm{x})&\quad {-} 6 a_{1} K_{2} - 3 \lambda _{4} a_{1} a_{2} + 6 K_{1} c _{2} = 0, \\ (\mathrm{xi})&\quad {-} 24 a_{2} K_{2} - 2 \lambda _{4} a_{2}^{2} = 0. \end{aligned}$$
(3.22)

Also, when we put (3.21) into the second equation of (3.20), it brings the system of algebraic equations as follows:

$$\begin{aligned} (\mathrm{i})&\quad 24 b_{2} K_{5} \mu ^{3} + 2 K_{3} d_{2}^{2} \mu = 0, \\ (\mathrm{ii})&\quad 6 d_{2} K_{4} \mu ^{2} + 6 b_{1} \mu ^{3} K_{5} + 3 K_{3} \mu d_{1} d_{2} = 0, \\ (\mathrm{iii})&\quad 2 d_{1} K_{4} \mu ^{2} + 40 b_{2} \mu ^{2} K_{5} + 2 c _{0} \mu d_{2} K_{3} + K_{3} d_{1}^{2} \mu + 2 K_{3} d_{2}^{2} = 0, \\ (\mathrm{iv})&\quad 8 d_{2} K_{4} \mu + 8 b_{1} \mu ^{2} K_{5} + K_{3} c_{0} \mu d_{1} + K_{3} d_{2} c_{1} \mu + 3 K_{3} d_{1} d_{2} + d_{2} = 0, \\ (\mathrm{v})&\quad 2 d_{1} K_{4} \mu + 16 b_{2} \mu K_{5} + 2 K_{3} c_{0} d _{2} - 2 K_{3} d_{2} c_{2} \mu + K_{3} d_{1}^{2} + 2 K_{3} c_{2} d _{2} \mu + d_{1} = 0, \\ (\mathrm{vi})&\quad 2 d_{2}K_{4} - 2 a_{1}\mu ^{2}K_{5} + 2b_{1} \mu K_{5} - K _{3}c_{0}c_{1}\mu + K_{3}c_{0}d_{1} + K_{3}c_{1}d_{2} - K_{3}d_{1}c _{2}\mu \\ &\qquad{} + 2c_{2}K_{4}\mu ^{2} + c_{0} = 0, \\ (\mathrm{vii})&\quad 2 c_{1} K_{4} \mu - 16 a_{2} \mu ^{2}K_{5} - 2 K_{3} c _{0} c_{2} \mu - K_{3} c_{1}^{2}\mu + c_{1} = 0, \\ (\mathrm{viii})&\quad 8 c_{2} K_{4} \mu - 8 a_{1} \mu K_{5} - 3 K_{3} c_{1} c_{2} \mu - K_{3} c_{0} c_{1} - K_{3} c_{2} d_{1} + c_{2} = 0, \\ (\mathrm{ix})&\quad 2 c_{1} K_{4} - 40 a_{2} \mu K_{5} - 2 K_{3} c_{0} c _{2} - K_{3} c_{1}^{2} - 2 K_{3} c_{2}^{2} \mu = 0, \\ (\mathrm{x})&\quad {-} 6 a_{1} K_{5} - 3 K_{3} c_{1} c_{2} + 6 K_{4} c_{2} = 0, \\ (\mathrm{xi})&\quad {-} 24 a_{2} K_{5} - 2 K_{3} c_{2}^{2} = 0. \end{aligned}$$
(3.23)

On solving algebraic equations (3.22) and (3.23) for arbitrary value of \(K_{5}\), we get only the trivial solutions of the main system (1.1), which is not a physically interesting case. Therefore, we reach the following results.

Case 1:

$$ \begin{aligned} &a_{2} = a_{2},\qquad c_{0} = c_{0},\qquad d_{1} = - \frac{1}{K_{3}}, \qquad K_{2} = - \frac{1}{12} \lambda _{4} a_{2}, \\ &a_{0} = a_{1} = b_{1} = b_{2} = c_{1} = c_{2} = d_{2} = K_{5} = \mu = 0; \end{aligned} $$
(3.24)

Case 2:

$$ \begin{aligned} &a_{2} = - \frac{12 K_{2}}{\lambda _{4}} , \qquad c_{0} = c_{0} , \qquad d_{1} = - \frac{1}{K _{3}} , \quad \mbox{and} \\ &a_{0} = a_{1} = b_{1} = b_{2} = c_{1} = c_{2} = d_{2} = K _{5} = \mu = 0 . \end{aligned} $$
(3.25)

Now when we substitute equations (3.24), (3.25) and the solution of linear equation (3.10) for \(\mu = 0\) into equation (3.21), we get the solution of nonlinear equation (3.20). Further, using the value of solution \(f ( \xi )\) and \(g ( \xi )\) into equation (3.19), we have rational solutions of equation (1.1) as follows.

Case 1 gives the rational solution of equation (1.1) by the following relation:

$$ \begin{aligned} &u(x, t) = a_{2} \biggl( \frac{B}{A + B x} \biggr)^{2}, \\ &w ( x, t ) = \exp \biggl( \frac{1}{\lambda _{ 4}} \int \tau _{1} ( t ) \,dt \biggr) \biggl[ c_{0} - \frac{1}{K_{3}} \biggl( \frac{B}{A + B x} \biggr)^{ - 1} \biggr], \end{aligned} $$
(3.26)

where A, B, \(K_{3}\), and \(\lambda _{4}\) are arbitrary constants (see Fig. 2).

Figure 2
figure 2

Smooth soliton solution (left) and breather soliton solution (right) given by equation (3.26) with \(K_{3} = - 1\), \(A = B = 1\), \(a_{2} = c_{0} = \lambda _{4} = 1\), and \(\tau _{1} ( t ) = \cos (t) + \sin (t)\)

Full size image

Similarly, Case 2 gives the rational solution of equation (1.1) by the following relation:

$$ \begin{aligned} &u(x, t) = - \frac{12 K_{2}}{\lambda _{4}} \biggl( \frac{A_{2}}{A_{1} + A_{2} x} \biggr)^{2}, \\ &w ( x, t ) = \exp \biggl( \frac{1}{\lambda _{ 4}} \int \tau _{1} ( t ) \,dt \biggr) \biggl[ c_{0} - \frac{1}{K_{3}} \biggl( \frac{A_{2}}{A_{1} + A_{2} x} \biggr)^{ - 1} \biggr], \end{aligned} $$
(3.27)

where A, B, \(K_{2}\), \(K_{3}\), and \(\lambda _{4}\) are arbitrary constants.

3.4 Subalgebra \(\varGamma _{4} + \varGamma _{5}\)

The solutions of system (1.1) which are invariant under this subalgebra with the coefficient functions

$$ \begin{aligned} &\tau _{2} ( t ) = K_{1} \tau _{1} ( t ), \qquad \tau _{3} ( t ) = K_{2} \tau _{1} ( t ), \qquad \kappa _{1} ( t ) = K_{3} \tau _{1} ( t ), \\ &\kappa _{2} ( t ) = K_{4} \tau _{1} ( t ), \qquad \kappa _{3} ( t ) = K_{5} \tau _{1} ( t ) \end{aligned} $$
(3.28)

are given by the following relations:

$$ \begin{aligned} &u ( x, t ) = f ( \xi ), \\ &w ( x, t ) = g ( \xi ), \end{aligned} $$
(3.29)

where \(\xi = x - \int \tau _{1}(t) \,dt\) and \(f ( \xi )\), \(g ( \xi )\) are the solution of the system of nonlinear ordinary differential equations

$$ \begin{aligned} &{-} f' + f f' + K_{1} g'' + K_{2} f''' = 0, \\ &{-} g' + K_{3} g g' + K_{4} g'' + K_{5} f''' = 0. \end{aligned} $$
(3.30)

In this subalgebra, follow the procedure in a manner similar to the preceding subalgebra to solve equations (3.30) by the modified \(( G'/G )\)-expansion method, we get the solution of ODEs (3.30) as follows:

$$ \begin{aligned} &f(\xi ) = a_{0} + a_{1} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr) + a _{2} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr)^{2} + b_{1} \biggl( \frac{G'( \xi )}{G(\xi )} \biggr)^{ - 1} + b_{2} \biggl( \frac{G'(\xi )}{G( \xi )} \biggr)^{ - 2}, \\ &g(\xi ) = c_{0} + c_{1} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr) + c _{2} \biggl( \frac{G'(\xi )}{G(\xi )} \biggr)^{2} + d_{1} \biggl( \frac{G'( \xi )}{G(\xi )} \biggr)^{ - 1} + d_{2} \biggl( \frac{G'(\xi )}{G( \xi )} \biggr)^{ - 2}. \end{aligned} $$
(3.31)

By substituting (3.31) into the system of ODEs (3.30), using linear ODE (3.10), and equating the coefficients of same powers of \(( G'/G )\) to zero we obtain a set of simultaneous algebraic equations among \(a_{0}\), \(a_{1}\), \(a_{2}\), \(b_{1}\), \(b_{2}\), \(c_{0}\), \(c_{1}\), \(c_{2}\), \(d_{1}\), \(d _{2}\), and μ as follows:

$$\begin{aligned} (\mathrm{i})&\quad 24 b_{2} K_{2} \mu ^{3} + 2 b_{2}^{2} \mu = 0, \\ (\mathrm{ii})&\quad 6 d_{2} K_{1} \mu ^{2} + 6 b_{1} \mu ^{3} K_{2} + 3 \mu b_{1} b_{2} = 0, \\ (\mathrm{iii})&\quad 2 d_{1} K_{1} \mu ^{2} + 40 b_{2} \mu ^{2} K_{2} + 2 a _{0} \mu b_{2} + b_{1}^{2} \mu + 2 b_{2}^{2} - 2 b_{2} \mu = 0, \\ (\mathrm{iv})&\quad 8 d_{2} K_{1} \mu + 8 b_{1} \mu ^{2} K_{2} + a_{0} \mu b_{1} + b_{2} a_{1} \mu + 3 b_{1} b_{2} - b_{1} \mu = 0, \\ (\mathrm{v})&\quad 2 d_{1} K_{1} \mu + 16 b_{2} \mu K_{2} + 2 a_{0} b_{2} - 2 b_{2} a_{2} \mu + b_{1}^{2} + 2 a_{2} b_{2} \mu - 2 b_{2} = 0, \\ (\mathrm{vi})&\quad 2 d_{2}K_{2} - 2a_{1} \mu ^{2}K_{2} + 2b_{1}\mu K_{2} - a _{0}a_{1}\mu + a_{0}b_{1} + a_{1}b_{2} - b_{1}a_{2}\mu \\ &\qquad {}+ 2 c_{2}K_{1} \mu ^{2} + a_{1} \mu - b_{1} = 0, \\ (\mathrm{vii})&\quad 2 c_{1} K_{1} \mu - 16 a_{2} \mu ^{2}K_{2} - 2 a_{0} a _{2} \mu - a_{1}^{2}\mu + 2 a_{2} \mu = 0, \\ (\mathrm{viii})&\quad 8 c_{2} K_{1} \mu - 8 a_{1} \mu K_{2} - 3 a_{1} a_{2} \mu - a_{0} a_{1} - a_{2} b_{1} + a_{1} = 0, \\ (\mathrm{ix})&\quad 2 c_{1} K_{1} - 40 a_{2} \mu K_{2} - 2 a_{0} a_{2} - a _{1}^{2} - 2 a_{2}^{2} \mu + 2 a_{2} = 0, \\ (\mathrm{x})&\quad {-} 6 a_{1} K_{2} - 3 a_{1} a_{2} + 6 K_{1} c_{2} = 0, \\ (\mathrm{xi})&\quad {-} 24 a_{2} K_{2} - 2 a_{2}^{2} = 0. \end{aligned}$$
(3.32)

Also, when we put (3.31) into the second equation of (3.30), it brings the system of algebraic equations as follows:

$$\begin{aligned} (\mathrm{i})&\quad 24 b_{2} K_{5} \mu ^{3} + 2 K_{3} d_{2}^{2} \mu = 0, \\ (\mathrm{ii})&\quad 6 d_{2} K_{4} \mu ^{2} + 6 b_{1} \mu ^{3} K_{5} + 3 K_{3} \mu d_{1} d_{2} = 0, \\ (\mathrm{iii})&\quad 2 d_{1} K_{4} \mu ^{2} + 40 b_{2} \mu ^{2} K_{5} + 2 c _{0} \mu d_{2} K_{3} + K_{3} d_{1}^{2} \mu + 2 K_{3} d_{2}^{2} - 2 d _{2} \mu = 0, \\ (\mathrm{iv})&\quad 8 d_{2} K_{4} \mu + 8 b_{1} \mu ^{2} K_{5} + K_{3} c_{0} \mu d_{1} + K_{3} d_{2} c_{1} \mu + 3 K_{3} d_{1} d_{2} - d_{1} \mu = 0, \\ (\mathrm{v})&\quad 2 d_{1} K_{4} \mu + 16 b_{2} \mu K_{5} + 2 K_{3} c_{0} d _{2} - 2 K_{3} d_{2} c_{2} \mu + K_{3} d_{1}^{2} + 2 K_{3} c_{2} d _{2} \mu - 2 d_{2} = 0, \\ (\mathrm{vi})&\quad 2 d_{2}K_{4} - 2 a_{1}\mu ^{2}K_{5} + 2 b_{1} \mu K_{5} - K_{3}c_{0}c_{1}\mu + K_{3}c_{0}d_{1} + K_{3}c_{1}d_{2} - K_{3}d_{1}c _{2}\mu \\ &\qquad {}+ 2 c_{2}K_{4}\mu ^{2} + c_{1}\mu - d_{1} = 0, \\ (\mathrm{vii})&\quad 2 c_{1} K_{4} \mu - 16 a_{2} \mu ^{2}K_{5} - 2 K_{3} c _{0} c_{2} \mu - K_{3} c_{1}^{2}\mu + 2 c_{2} \mu = 0, \\ (\mathrm{viii})&\quad 8 c_{2} K_{4} \mu - 8 a_{1} \mu K_{5} - 3 K_{3} c_{1} c_{2} \mu - K_{3} c_{0} c_{1} - K_{3} c_{2} d_{1} + c_{1} = 0, \\ (\mathrm{ix})&\quad 2 c_{1} K_{4} - 40 a_{2} \mu K_{5} - 2 K_{3} c_{0} c _{2} - K_{3} c_{1}^{2} - 2 K_{3} c_{2}^{2} \mu + 2 c_{2} = 0, \\ (\mathrm{x})&\quad {-} 6 a_{1} K_{5} - 3 K_{3} c_{1} c_{2} + 6 K_{4} c_{2} = 0, \\ (\mathrm{xi})&\quad {-} 24 a_{2} K_{5} - 2 K_{3} c_{2}^{2} = 0. \end{aligned}$$
(3.33)

Similarly solving these algebraic equations as under the above subalgebras yields the following.

Case 1:

$$ \begin{aligned} &a_{0} = - \frac{1}{8} \frac{a_{2} c_{1}^{2} - 8 c_{2}^{2}}{c_{2}^{2}}, \qquad a_{1} = \frac{c_{1} a_{2}}{c_{2}}, \qquad a_{2} = a_{2}, \\ &b_{1} = \frac{1}{16} \frac{a_{2} c_{1}^{3}}{c_{2}^{3}}, \qquad b_{2} = \frac{1}{256} \frac{a_{2} c_{1}^{4}}{c_{2}^{4}}, \qquad c_{0} = - \frac{1}{8} \frac{K_{3} c_{1}^{2} - 8 c_{2}}{K_{3} c_{2}}, \\ &c_{1} = c_{1}, \qquad c_{2} = c_{2}, \qquad d_{1} = \frac{1}{16} \frac{ c_{1}^{3}}{c_{2}^{2}}, \\ &d_{2} = \frac{1}{256} \frac{c_{1}^{4}}{c_{2}^{3}}, \qquad K_{1} = \frac{5}{12}\frac{c_{1} a_{2}^{2}}{c_{2}^{2}}, \qquad K_{2} = - \frac{1}{12}a_{2}, \\ &K_{3} = K_{3}, \qquad K_{4} = \frac{5}{12} c_{1} K_{3}, \qquad K_{5} = - \frac{1}{12} \frac{c_{2}^{2}}{a_{2}} K_{3}, \qquad \mu = - \frac{1}{16} \frac{c_{1}^{2}}{c_{2}^{2}}. \end{aligned} $$
(3.34)

Case 2:

$$ \begin{aligned} &a_{0} = 1, \qquad a_{1} = a_{1}, \qquad a_{2} = 0,\qquad b_{1} = b_{2} = 0, \qquad c_{0} = \frac{c_{1}}{2 K_{4}}, \\ & c_{1} = c_{1}, \qquad c_{2} = 0, \qquad d_{1} = d_{2} = 0, \qquad K_{1} = \frac{a_{1}^{2}}{2 c_{1}}, \\ &K_{2} = 0, \qquad K_{3} = \frac{ 2 K_{4}}{c_{1}}, \qquad K_{5} = 0, \\ &K_{4} = K_{4}, \qquad \mu = \mu . \end{aligned} $$
(3.35)

Now, when we substitute equations (3.34), (3.35) and the solution of linear equation (3.10) into equation (3.31), we get the solution of nonlinear equation (3.30). Further, using the value of solution \(f ( \xi )\) and \(g ( \xi )\) into equation (3.29), we have hyperbolic, trigonometric, and rational function solutions of equation (1.1) as follows.

Case 1:

Now, under Case 1 we have \(\mu = - \frac{1}{16} \frac{c_{1}^{2}}{c _{2}^{2}}\), i.e., (\(\mu < 0\)), then the hyperbolic function solution of the main system (1.1) is given as follows:

$$\begin{aligned}& \begin{aligned} u (x, t) &= - \frac{1}{8} \frac{a_{2} c_{1}^{2} - 8 c_{2}^{2}}{c_{2} ^{2}} \\ &\quad {}+ \frac{c_{1} a_{2}}{c_{2}} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr] \\ &\quad {}+ a_{2} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr]^{2} \\ &\quad {}+ \frac{1}{16} \frac{a_{2} c_{1}^{3}}{c_{2}^{3}} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr]^{ - 1} \\ &\quad {}+ \frac{1}{256}\frac{a_{2} c_{1}^{4}}{c_{2}^{4}} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr]^{ - 2}, \end{aligned} \\& \begin{aligned}[b] w(x, t) &= - \frac{1}{8} \frac{K_{3} c_{1}^{2} - 8 c_{2}}{K_{3} c_{2}} \\ &\quad {}+ c_{1} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr] \\ &\quad {}+ c_{2} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr]^{2} \\ &\quad {}+ \frac{1}{16}\frac{ c_{1}^{3}}{c_{2}^{2}} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr]^{ - 1} \\ &\quad {}+ \frac{1}{256} \frac{c_{1}^{4}}{c_{2}^{3}} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr]^{ - 2}, \end{aligned} \end{aligned}$$
(3.36)

where \(a_{2}\), \(c_{1}\), \(c_{2}\), \(K_{3}\), and A, B are arbitrary constants.

Again under Case 1, if we substitute \(\mu = 0\) in equation (3.34), then we have \(K_{1} = K_{4} = c_{1} = 0\). Therefore, for \(\mu = 0\), we obtained the rational function solutions of equation (1.1) as follows:

$$ \begin{aligned} &u (x, t) = 1 + a_{2} \biggl[ \frac{B}{A + B ( x - \int \tau _{1}(t)\,dt )} \biggr]^{2}, \\ & w(x, t) = \frac{1}{8 K_{3}} + c_{2} \biggl[ \frac{B}{A + B ( x - \int \tau _{1}(t)\,dt )} \biggr]^{2}, \end{aligned} $$
(3.37)

where A, B and \(a_{2}\), \(c_{2}\), \(K_{3}\) are arbitrary constants.

Case 2:

If \(\mu > 0\), the trigonometric function solution of the main equation (1.1) is given by the following relation:

$$ \begin{aligned} &u (x, t) = 1 + a_{1} \biggl[ \sqrt{ \mu } \frac{A \sin ( \sqrt{ \mu } ( x - \int \tau _{1}(t)\,dt ) ) - B \sin ( \sqrt{\mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sin ( \sqrt{\mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sin ( \sqrt{\mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr], \\ &w(x, t) = \frac{c_{1}}{2 K_{4}} + c_{1} \biggl[ \sqrt{\mu } \frac{A \sin ( \sqrt{\mu } ( x - \int \tau _{1}(t)\,dt ) ) - B \sin ( \sqrt{\mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sin ( \sqrt{\mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sin ( \sqrt{\mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr], \end{aligned} $$
(3.38)

where A, B, and \(K_{4}\) are arbitrary constants.

If \(\mu < 0\), then the hyperbolic function solution of the main system (1.1) is given as follows:

$$ \begin{aligned} &u (x, t) = 1 + a_{1} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sin ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sin ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr], \\ &w(x, t) = \frac{c_{1}}{2 K_{4}} + c_{1} \biggl[ \sqrt{ - \mu } \frac{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )}{A \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t) \,dt ) ) + B \sinh ( \sqrt{ - \mu } ( x - \int \tau _{1}(t)\,dt ) )} \biggr], \end{aligned} $$
(3.39)

where A, B, and \(K_{4}\) are arbitrary constants.

When \(\mu = 0\), we obtain the rational solution as follows:

$$ \begin{aligned} &u (x, t) = 1 + a_{1} \biggl[ \frac{B}{A + B ( x - \int \tau _{1}(t)\,dt )} \biggr], \\ &w (x, t) = \frac{c_{1}}{2 K_{4}} + c_{1} \biggl[ \frac{B}{A + B ( x - \int \tau _{1}(t)\,dt )} \biggr], \end{aligned} $$
(3.40)

where A, B, and \(K_{4}\) are arbitrary constants (see Fig. 3).

Figure 3
figure 3

Kink compacton soliton solutions given by equation (3.40) with \(a_{1} = 1\), \(c_{1} = - 1\), \(K_{4} = - 1\), \(A = B = 1\), and \(\tau _{1} ( t ) = \cos ech^{2} ( t )\)

Full size image

4 Concluding and discussion

In this paper, the authors have studied new soliton solutions of time-dependent coupled KdV–Burgers equation with the help of two methods: the Lie symmetry group method and the modified \(( G'/G )\)-expansion method. Thus, by the applications of Lie symmetry method, we have reduced nonlinear PDEs (1.1) to the system of nonlinear ODEs under different subalgebras. The reduced nonlinear ODEs are highly nonlinear, which is difficult to solve analytically. Therefore, in the quest of solutions for the reduced nonlinear ODEs, we take the help of a novel method called \(( G'/G )\)-expansion method. The physical behaviors of the obtained solutions are represented with the help of Fig. 1, Fig. 2, and Fig. 3.