Abstract
In this paper, we consider the local and global bifurcation of nonnegative nonconstant solutions of a general Brusselator model
where \(d_{1},d_{2},a>0\) are fixed parameters with \(d_{2}>d_{1}\), \(b>0\) is a bifurcation parameter; \(f\in C([0,\infty ) ,[0,\infty ))\) is a strictly increasing function and \(f'(f^{-1}(a))\in (0,\infty )\). Moreover, via the Rabinowitz bifurcation theorem, we obtain the global structure of nonconstant solutions under the condition that \(\frac{f(s)}{s^{2}}\) is nonincreasing in \((0,\infty )\).
Similar content being viewed by others
1 Introduction
In 1968, Prigogine and Lefever [15] introduced firstly the Brusselator model for a chemical reaction-diffusion of self-catalysis as follows:
where \(\varOmega \subset \mathbb{R}^{N}\) (\(N\geq 1\)) is a smooth and bounded domain, n denotes the outward unit normal vector on ∂Ω, u and v represent the concentration of two intermediary reactants having the diffusion rates \(d_{1},d_{2}\in (0,\infty )\) with \(d_{2}>d_{1}\), \(a,b>0\) are the fixed concentrations. Indeed, (1.1) has been extensively investigated in the last decades from both analytical and numerical point of view (see [1,2,3,4,5,6,7,8, 11,12,13,14, 17, 18]). Most of the authors are interested in finding spatially nonconstant solutions of the equilibrium problem
In [3, 4, 13, 14], they obtained the existence or nonexistence of the nonconstant solutions of (1.2) by a priori estimate and topological degree theory. Peng and Wang [13] considered the following problem:
and proved the nonexistence for nonconstant of (1.3) for either small λ, large θ, or small b. Note that [3, 4, 13, 14] only studied the existence and nonexistence of nonnegative nonconstant solutions of (1.2). They could not get the global structure of the nonconstant solutions due to the limitations of the tools used. Ma and Hu [11] applied the Rabinowitz bifurcation theorem to get the global structure of nonconstant solutions of (1.2). Inspired by [11], we will consider the new, more general form of the Brusselator model:
where \(d_{1},d_{2},a>0\) are fixed parameters and \(d_{2}>d_{1}\), \(b>0\) is a bifurcation parameter. Clearly, \(f(u)=\frac{f(u)}{u}\cdot u\), then (1.4) is seen to be equivalent to
Compared with problem (1.2), \(\frac{f(u)}{u}\) can be regarded as a variable coefficient. It is well known that the linear terms \((b+1)u\) and bu in (1.2) cannot withstand any small perturbation. In fact, (1.5) has been widely applied in chemical and biological fields. We will study the local and global behavior of nonnegative nonconstant solutions of (1.4) under the following assumptions:
- (H1):
\(f\in C([0,\infty ),[0,\infty ))\) is a strictly increasing function.
- (H2):
\(f'(f^{-1}(a))\in (0,\infty )\).
- (H3):
\(\frac{f(s)}{s^{2}}\) is nonincreasing in \((0,\infty )\).
Remark 1.1
If \(f(u)=u\), then (1.4) will reduce to (1.2). However, if \(f(u)=u+u^{2}\), a perturbation term is added to bu and \((b+1)u\) in (1.2). It is easy to see that this small perturbation leads to the results in [11] that are not available.
The rest of the paper is organized as follows: In Sect. 2, we give a priori estimate and some preliminary results. Section 3 is devoted to studying the local bifurcation of nonnegative nonconstant solutions of (1.4) with N = 1 under conditions (H1)–(H2). Finally, in Sect. 4, we add condition (H3) to obtain the global bifurcation of nonnegative nonconstant solutions of (1.4) with N = 1.
2 Preliminary results
At first, let us look for the constant solution of (1.4). To get it, it suffices to look for the constant solution of the following problem:
By (H1), problem (2.1) has a unique solution \((f^{-1}(a),\frac{ab}{[f ^{-1}(a)]^{2}})\). Obviously, this is the unique solution of (1.4).
Basic to a priori estimate of the solutions of (1.4) is the following result which is due to Lou and Ni (see [9, Proposition 2.2] or [10, Lemma 2.1]).
Lemma 2.1
Let \(g\in C^{1}(\bar{\varOmega }\times \mathbb{R})\).
- (1)
If \(w\in C^{2}(\varOmega )\cap C^{1}(\bar{\varOmega })\)satisfies
$$ \triangle w+g(x,w)\geq 0 \quad \textit{in }\varOmega , \qquad \frac{\partial w}{\partial n}\leq 0 \quad \textit{on }\partial \varOmega , $$and \(w(x_{0})=\max_{\bar{\varOmega }}w\), then \(g(x_{0},w(x_{0})) \geq 0\).
- (2)
If \(w\in C^{2}(\varOmega )\cap C^{1}(\bar{\varOmega })\)satisfies
$$ \triangle w+g(x,w)\leq 0 \quad \textit{in }\varOmega , \qquad \frac{\partial w}{\partial n}\geq 0 \quad \textit{on }\partial \varOmega , $$and \(w(x_{0})=\min_{\bar{\varOmega }}w\), then \(g(x_{0},w(x_{0})) \leq 0\).
Now, we will give a priori estimate of the nonnegative nonconstant solutions of (1.4).
Lemma 2.2
Let (H1), (H2), and (H3) hold. Then any nonnegative nonconstant solution \((u,v)\)of (1.4) satisfies
Proof
Let \(x_{0}\in \bar{\varOmega }\) be the minimum point of u. From (2) of Lemma 2.1, we have
Then \(u(x_{0})\geq f^{-1}(\frac{a}{b+1})\) by (H1), and so
Let \(x_{1}\in \bar{\varOmega }\) be the maximum point of v. Similarly, we can get that
Then
Combining this with (2.2), from (H3), we show
Let \(w=d_{1}u+d_{2}v\). Then it follows from (1.4) that
Now, let \(x_{2}\in \bar{\varOmega }\) be the maximum point of w. By (1) of Lemma 2.1, \(a-f(u(x_{2}))\geq 0\). Then, from (H1), it is easy to see \(u(x_{2})\leq f^{-1}(a)\). Combining this with (2.3), we know that, for any \(x\in \bar{\varOmega }\),
then
From (2) of Lemma 2.1, if \(x_{3}\in \bar{\varOmega }\) is the minimum point of v, then
and
Consequently, the proof is completed. □
For any fixed \(l>0\). It is well known that
has a sequence of simple eigenvalues
the corresponding eigenfunctions are
Let
X constitutes the Banach space in \(C^{2}\) norm and Y is a Hilbert space based on the inner product
where \(w_{1}=(u_{1},v_{1})\), \(w_{2}=(u_{2},v_{2})\in Y\).
3 Local bifurcation
For simplicity, let us consider (1.4) with \(N=1\) and \(\varOmega =(0,l)\),
Clearly, \(\bar{w}:=(f^{-1}(a),\frac{ab}{[f^{-1}(a)]^{2}})\) is the unique constant solution of (3.1).
Define the mapping \(P:(0,\infty )\times X\rightarrow Y\),
For the fixed \(b>0\), \(w=(u,v)\) is a solution of (3.1) if and only if \((b,w)\) is a zero-point of P. Note that for any \(b>0\), since w̄ is the constant solution of (3.1). Let
and
We also have to Taylor expand f at the point \(f^{-1}(a)\). The purpose of the rest of this section is to solve \(b_{0}\) and prove that \((b_{0},\bar{w})\) is the bifurcation point of . First of all, we substitute (3.2) and (3.3) into (3.1) and let the higher-order term of ε be equal to 0. Then we can get the problem
In (3.4), by using the undetermined coefficient method, it follows that
Moreover, it is not difficult to prove that (3.4) has a nontrivial solution \((u_{1},v_{1})\),
Next, we substitute (3.2) and (3.3) into (3.1) and let the higher-order term of \(\varepsilon ^{2}\) be equal to 0, then (3.1) becomes the following system:
where
In order to solve \(b_{1}\) from (3.5), let us consider the following adjoint system of the homogeneous system related to (3.5):
It is not difficult to verify that (3.6) has a solution \((y_{2},z_{2})\),
It is obvious that the vectors \((-F_{1},F_{1})\) and \((y_{2},z_{2})\) should be orthogonal in \(L^{2}(0,l)\) by virtue of the solvability condition for (3.5), i.e.,
In fact,
Let us substitute \(b_{0}\), \(u_{1}\), and \(v_{1}\) into (3.7), then \(b_{1}^{j}:=b_{1}=0\), and so \(F_{1}\) will reduce to
Therefore, a particular solution \((u_{2},v_{2})\) of (3.5) can be obtained as follows:
where
Since \(b_{1}=0\), we have to solve \(b_{2}\). We substitute (3.2) and (3.3) into (3.1) and let the higher-order term of \(\varepsilon ^{3}\) be equal to 0, then a problem similar to (3.5) is obtained:
where
Clearly, (3.6) is also the adjoint system of the homogeneous system related to (3.8), then
and, according to values of \(u_{1}\), \(u_{2}\), \(v_{1}\), and \(v_{2}\), we have
Thus,
From the above analysis, we obtain the main result of this section.
Theorem 3.1
Assume that (H1) and (H2) hold. Then, for any positive integerj, \((b_{0}^{j},\bar{w})\)is a bifurcation point of . Moreover, there is a nontrivial solution \({\phi (\varepsilon )}=(b(\varepsilon ),u(\varepsilon ),v(\varepsilon ))\)of (3.1) ifεis small enough, whereb, u, andvare continuous with respect toε, and
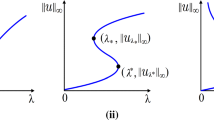
The set of zero-points ofPconstitutes two curves in a neighborhood of the bifurcation point \((b_{0}^{j},\bar{w})\).
Let \(\mathbb{C}\) be the closure of the nonconstant solution set of , \(\varGamma _{j}\) be a connected component of \(\mathbb{C} \cup \{(b_{0}^{j},\bar{w})\}\), and \((b_{0}^{j},\bar{w})\in \varGamma _{j}\). In a small neighborhood of bifurcation point \((b_{0}^{j},\bar{w})\), the curve \(\varGamma _{j}\) is determined by the eigenfunction \(\varphi _{j}\), where \(\varphi _{j}\) has j zeros in the interval \([0,l]\).
4 Global bifurcation
Theorem 4.1
Let (H1), (H2), and (H3) hold. If \(\mu _{j}\neq \frac{[f^{-1}(a)]^{2}}{d_{2}}\), \(j=1,2,\ldots \) , then the projection of continuum \(\varGamma _{j}\)is unbounded on theb-axis.
Proof
(3.1) can be written as follows:
where
Let \(\tilde{u}=u-f^{-1}(a)\), \(\tilde{v}=v-\frac{ab}{[f^{-1}(a)]^{2}}\). Then (4.1) is equivalent to the following problem:
where g̃ and h̃ are higher-order terms of ũ, ṽ, and
In this way, we convert the constant solution \(\bar{w}=(f^{-1}(a),\frac{ab}{[f ^{-1}(a)]^{2}})\) of (3.1) to the trivial solution \(\theta =(0,0)\) of (4.2).
Let \(H_{1}:Y\rightarrow X\) and \(H_{2}:Y\rightarrow X\) be the inverse of operators \(\frac{f'(f^{-1}(a))}{d_{1}}I-\frac{d^{2}}{dx^{2}}\) and \(\frac{[f^{-1}(a)]^{2}}{d_{2}}I-\frac{d^{2}}{dx^{2}}\) with Neumann boundary conditions, respectively. Set \(U=(\tilde{u},\tilde{v})\),
It can be verified that (4.2) is equivalent to
in X. For any fixed number \(b>0\), \(K(b)\) and \(W(U)\) are linear compact operators in X and \(W(U)=o(\|U\|)\). By the Rabinowitz global bifurcation theorem [16], we need to verify
- (i)
1 is an eigenvalue of \(K(b_{0}^{j})\) and its algebraic multiplicity is 1;
- (ii)
the index of \(I-K(b)-W\) changes when b crosses \(b_{0}^{j}\).
Now, we will prove (i). Suppose , \(\xi =\sum a_{j}\varphi _{j}\), \(\psi =\sum c_{j}\varphi _{j}\). Let
i.e.,
thus,
where
By computation, \(\det L_{j}=0\) if and only if \(b=b_{0}^{j}\), taking \(b=b_{0}^{j}\) leads to
and
Then \(\ker (K(b_{0}^{j})-I)=\operatorname{span}(\varPsi )\), . This implies that 1 is the eigenvalue of \(K=K(b^{j}_{0})\) and \(\dim \ker (K-I)=1\). The algebraic multiplicity of the eigenvalue 1 is the dimension of the generalized null space \(\bigcup^{\infty }_{i=1}\ker (K-I)^{i}\), therefore, \(\ker (K-I)\cap \operatorname{Im}(K-I)=\{\theta ^{T}\}\).
Let \(K^{T}\) be the transposed matrix of K,
and , \(\xi ^{*}=\sum a_{j}^{*}\varphi _{j}\), \(\psi ^{*}=\sum c_{j} ^{*}\varphi _{j}\). Suppose \(\varPsi ^{*}\in \ker (K^{T}-I)\). Then
From the definition of \(H_{1}\), \(H_{2}\), (4.4) can also be written as
That is to say,
where
Similarly, \(\det B_{j}=0\) if and only if \(b=b_{0}^{j}\), taking \(b=b_{0}^{j}\) leads to
and
Then . According to \(\mu _{j}\neq \frac{[f^{-1}(a)]^{2}}{d _{2}}\), we obtain
This suggests that \(\varPsi \notin (\ker (K^{*}-I))^{\perp }=\operatorname{Im}(K-I)\), and so (i) is proved. Now, we will prove (ii). From (i), for any \(b>0\), \(b\neq b_{0}^{j}\) and b belongs to a small neighborhood of \(b^{j}_{0}\), \(K(b)-I:X\rightarrow X\) is a bijection. Fix \(b>0\), then θ is a solution of (4.3) and θ is isolated. From the Leray–Schauder fixed point theory, we can get
where B is a sufficiently small ball centered at θ, γ is the sum of the algebraic multiplicity of the eigenvalues of \(K(b)\) and \(\gamma >1\). We are going to verify that, for \(\varepsilon >0\) is small enough,
If τ is an eigenvalue of \(K(b)\) and is the corresponding eigenfunction, then
i.e.,
By virtue of \(\xi =\sum a_{j}\varphi _{j}\) and \(\psi =\sum c_{j}\varphi _{j}\), we can get
Then the characteristic equation is
If \(\tau =1\), b can be solved from (4.6):
Therefore, by calculating the corresponding eigenvalues of (4.6), we can obtain that when b passes through \(b_{0}^{j}\), the number of eigenvalues of \(K(b)\), which is greater than 1, is the same and their algebraic multiplicities are equal. By plugging (4.7) into (4.6), we have
Then
and so (4.8) has two different roots \(\tau _{1}=1\), \(\tau _{2}=\frac{[f ^{-1}(a)]^{2}}{d_{2}\mu _{j}}\). Thus two things will happen:
- (a)
if \(\mu _{j}>\frac{[f^{-1}(a)]^{2}}{d_{2}}\), then \(\tau _{1}(b_{0} ^{j})=1\), \(\tau _{2}(b_{0}^{j})<1\);
- (b)
if \(\mu _{j}<\frac{[f^{-1}(a)]^{2}}{d_{2}}\), then \(\tau _{1}(b_{0} ^{j})=1\), \(\tau _{2}(b_{0}^{j})>1\).
When scenario (a) occurs, b passes through \(b_{0}^{j}\) and \(\tau _{2}(b)<1\). From (4.6), \(\tau _{1}(b_{0}^{j}+\varepsilon )>1\), \(\tau _{1}(b_{0}^{j}-\varepsilon )<1\). Therefore, the matrix \(K(b_{0}^{j}+ \varepsilon )\) has exactly one more eigenvalue, that is, >1, than \(K(b_{0}^{j}-\varepsilon )\) does, and its algebraic multiplicity is 1. Then (4.5) holds. That is to say, the index jumps as b goes through \(b_{0}^{j}\).
When scenario (b) occurs, b passes through \(b_{0}^{j}\) and \(\tau _{2}(b)>1\). From (4.6), \(\tau _{1}(b_{0}^{j}+\varepsilon )>1\), \(\tau _{1}(b_{0}^{j}-\varepsilon )<1\). Similarly, the index jumps as b goes through \(b_{0}^{j}\). Therefore, (ii) is true regardless of (a) or (b). Thus, by the index jump principle and [16, Theorem 1.3], it follows that there exists a connected component \(\hat{\varGamma }_{j}\) of nontrivial solutions of (4.3) and \(\hat{\varGamma }_{j}\) comes from the bifurcation point \((b_{0}^{j},\theta )\). We know that \(\hat{\varGamma }_{j}\) is also the connected component \(\varGamma _{j}\) of the nonconstant solution of (3.1) from \((b_{0}^{j},\bar{w})\). \(\hat{\varGamma }_{j}\) and \(\varGamma _{j}\) are both in \(\mathbb{R}\times X\). By the Rabinowitz global bifurcation theorem, the connected component \(\varGamma _{j}\) joins \((b_{0}^{j}, \bar{w})\) to either ∞ or \((b_{0}^{k},\bar{w})\) in \(\mathbb{R} \times X\), where \(k\neq j\). We first prove that the latter situation will not happen. According to Theorem 3.1, the solution on the connected component sent from \((b_{0}^{j},\bar{w})\) is related to \(\varphi _{j}\), and \(\varphi _{j}\) has j zeros in the interval \([0,l]\). In the same way, the solution on the connected component sent from \((b_{0}^{k},\bar{w})\) is related to \(\varphi _{k}\), and \(\varphi _{k}\) has k zeros in the interval \([0,l]\). If the connected component sent \(\varGamma _{j}\) joining \((b_{0}^{j},\bar{w})\) to \((b_{0}^{k},\bar{w})\), the solution \((b,w)\in \varGamma _{j}\) is related to both \(\varphi _{j}\) and \(\varphi _{k}\), which is impossible. On the other hand, Lemma 2.2 shows that, if \(b=b_{c}\in (0,\infty )\), then the solutions u and v of (3.1) are both bounded. So the connected component \(\varGamma _{j}\) will not join \((b_{0}^{j},\bar{w})\) to \((b_{c},\infty )\). Therefore, the connected component \(\varGamma _{j}\) can only join \((b_{0}^{j},\bar{w})\) to either \((\infty ,\infty )\) or \((\infty ,m)\), where \(m\in (0,\infty )\). But in any case, the projection of continuum \(\varGamma _{j}\) is unbounded on the b-axis. □
References
Brown, K.J., Davidson, F.A.: Global bifurcation in the Brusselator system. Nonlinear Anal. 24, 1713–1725 (1995)
Gao, C., Lv, L., Wang, Y.: Spectra of a discrete Sturm–Liouville problem with eigenparameter-dependent boundary conditions in Pontryagin space. Quaest. Math. 1, 1–26 (2019)
Ghergu, M.: Non-constant steady-state solutions for Brusselator type systems. Nonlinearity 21, 2331–2345 (2008)
Ghergu, M., Rǎdulescu, V.: Turing patterns in general reaction-diffusion systems of Brusselator type. Commun. Contemp. Math. 12, 661–679 (2010)
Guo, G., Wu, J., Ren, X.: Hopf bifurcation in general Brusselator system with diffusion. Appl. Math. Mech. 32, 1177–1186 (2011)
Li, B., Wang, M.: Diffusion-driven instability and Hopf bifurcation in Brusselator system. Appl. Math. Mech. 29, 825–832 (2008)
Li, Y.: Hopf bifurcations in general systems of Brusselator type. Nonlinear Anal., Real World Appl. 28, 32–47 (2016)
Liao, M., Wang, Q.: Stability and bifurcation analysis in a diffusive Brusselator-type system. Int. J. Bifurc. Chaos Appl. Sci. Eng. 26, 1–11 (2016)
Lou, Y., Ni, W.: Diffusion, self-diffusion and cross-diffusion. J. Differ. Equ. 131, 79–131 (1996)
Lou, Y., Ni, W.: Diffusion vs. cross-diffusion: an elliptic approach. J. Differ. Equ. 154, 157–190 (1999)
Ma, M., Hu, J.: Bifurcation and stability analysis of steady states to a Brusselator model. Appl. Math. Comput. 236, 580–592 (2014)
Ma, S.: The stochastic Hopf bifurcation analysis in Brusselator system with random parameter. Appl. Math. Comput. 219, 306–319 (2012)
Peng, R., Wang, M.: Pattern formation in the Brusselator system. J. Math. Anal. Appl. 309, 151–166 (2005)
Peng, R., Yang, M.: On steady-state solutions of the Brusselator-type system. Nonlinear Anal. 71, 1389–1394 (2009)
Prigogine, I., Lefever, R.: Symmetry breaking instabilities in dissipative systems II. J. Chem. Phys. 48, 1665–1700 (1968)
Rabinowitz, P.H.: Some global results for nonlinear eigenvalue problems. J. Funct. Anal. 7, 487–513 (1971)
Tzou, J.C., Ward, M.J.: The stability and slow dynamics of spot patterns in the 2D Brusselator modal: the effect of open systems and heterogeneities. Physica D 373, 13–37 (2018)
Zhou, J., Mu, C.: Pattern formation of a coupled two-cell Brusselator model. J. Math. Anal. Appl. 366, 679–693 (2010)
Acknowledgements
We are very grateful to the anonymous referees for their valuable suggestions.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated.
Funding
This work was supported by the National Natural Science Foundation of China (No. 11671322).
Author information
Authors and Affiliations
Contributions
The authors claim that the research was realized in collaboration with the same responsibility. All authors read and approved the last version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
All of the authors of this article claim that together they have no competing interests.
Additional information
Abbreviations
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhao, Z., Ma, R. Local and global bifurcation of steady states to a general Brusselator model. Adv Differ Equ 2019, 491 (2019). https://doi.org/10.1186/s13662-019-2426-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2426-4