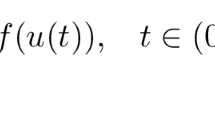Abstract
In this paper, we study the existence and multiplicity of solutions of the quasilinear problems with minimum and maximum
where \(\phi :(-a,a)\rightarrow \mathbb{R}\) (\(0< a<\infty \)) is an odd increasing homeomorphism, \(F:C^{1}[0,T]\rightarrow L^{1}[0,T]\) is an unbounded operator, \(T>1\) is a constant and \(A, B\in \mathbb{R}\) satisfy \(B>A\). By using the Leray–Schauder degree theory and the Brosuk theorem, we prove that the above problem has at least two different solutions.
Similar content being viewed by others
1 Introduction
In this paper we study the following quasilinear problem
subjected to nonlinear boundary conditions
where \(\phi :(-a,a)\rightarrow \mathbb{R}\) is an increasing homeomorphism, \(\phi (0)=0\), a is a positive constant, \(F:C^{1}[0,T] \rightarrow L^{1}[0,T]\) is an unbounded operator, \(T>1\) is a constant and \(A, B\in \mathbb{R}\) satisfy \(B>A\). A typical example should be
The differential operator we are considering, known as the mean curvature operator in Minkowski space, which is originated in the study in differential geometry or special relativity, has the property that the mean extrinsic curvature (trace of its second fundamental form) is, respectively, zero or constant; see [1, 10, 23] and [24].
A solution of the problem (1.1) and (1.2) is a function \(u\in C^{1}[0,T]\) such that \(\max_{t\in [0,T]}|u'(t)|< a\), \(\phi (u')\in AC[0,T]\), u satisfies (1.2) and (1.1) is satisfied for a.e. \(t\in [0,T]\).
It is well known that the singular ϕ-Laplacian problem (1.1) with Dirichlet boundary conditions have been introduced in [7, 10, 16], and a detailed study of homogeneous Dirichlet and Neumann problems has been given in [7]. The various boundary value problems above are reduced to the search of a fixed point for some operator defined on the space \(C^{1}[0,T]\). Those operators are completely continuous, and a novel feature linked to the nature of the function ϕ lies in the fact that those operators map \(C^{1}[0,T]\) into the cylinder of functions \(u\in C^{1}[0,T]\) such that \(\max_{[0,T]}|u'|< a\). This property plays a very important role in the search of the prior bound for the possible fixed point by using the Leray–Schauder approach.
Notice also that, according to [12], existence and multiplicity of positive solutions of the homogeneous Dirichlet problems for singular ϕ-Laplacian have been obtained by reduction to an equivalent nonsingular problem to which variational or topological methods apply in a classical fashion.
However, a very interesting result was showed in [8]: that the Dirichlet problem
is still solvable for any right-hand member F, like in the homogeneous case considered in [7], but under the restriction
For other nonhomogeneous cases, see [2,3,4] and [9].
When \(\phi =I\), (1.1) can be reduced to
Many authors considered (1.5) with functional boundary value problem; see [5, 6, 14, 15, 17, 19] and [20]. In particular, the problem (1.5) and (1.2) has been studied in [5, 19] and [20]. On the other hand, the existence and multiplicity of solutions for nonlinear second-order discrete problems with minimum and maximum also has been studied in [17]. Moreover, the boundary condition (1.2) originates in the description of pest density changes, which plays an important role in the study of pest quantities; see [5].
Note that \(\phi :\mathbb{R}\rightarrow \mathbb{R}\) is an odd increasing homeomorphism; the classical p-Laplacian cases, for which \(\phi (s)=|s|^{p-2}s\), the existence and multiplicity results of p-Laplacian problem with functional boundary conditions have been studied in [18, 20] and [22]; for the other cases, see [21]. Also, functional fractional boundary value problems with a singular ϕ-Laplacian were studied in [11].
To the best of our knowledge, there have been few discussions of the singular ϕ-Laplacian problem with minimum and maximum. Motivated by the above papers, the purpose of this paper is to give sufficient conditions imposed upon the nonlinearity F and the numbers A, B (\(B>A\)) so that there exist at least two different solutions of the problem (1.1) and (1.2).
Throughout this paper we shall make the following assumptions:
- (H1)
There exists a continuous nondecreasing function \(f:[0,\infty ) \rightarrow [0,\infty )\) such that
$$ \bigl\vert (Fu) (t) \bigr\vert \leq f \bigl( \bigl\vert u'(t) \bigr\vert \bigr), \quad \mbox{a.e. }t\in [0,T], u\in C^{1}[0,T]. $$ - (H2)
\(\int _{0}^{\infty } \frac{ds}{f(\phi ^{-1}(s))}\geq T\).
The remainder of this paper is arranged as follows. In Sect. 2, we give some notations and the prior estimate for the possible solutions of (1.1) and (1.2). Section 3 is devoted to proving the existence and multiplicity of solutions of (1.1) and (1.2), and we also give an application to illustrate our main results.
2 Preliminaries
In this section we collect some preliminary results that will be used below.
We denote the usual norm in \(L^{1}(0,T)\) by \(\|\cdot \|_{L^{1}}\). Let \(X:=C[0,T]\) be the Banach space endowed with the uniform norm \(\|\cdot \|_{\infty }\), \(Y:=C^{1}[0,T]\) be the Banach space equipped with the norm \(\|u\|_{C^{1}}=\|u\|_{\infty }+\|u'\|_{\infty }\), the corresponding open ball of center at 0 and radius r is denoted by \(B_{r}\).
Definition 2.1
Let \(\omega : X\rightarrow \mathbb{R}\) be a functional. ω is increasing if
For each \(\omega : X\rightarrow \mathbb{R}\), \(\operatorname{Im}(\omega )\) denotes the range of ω.
Set \(\mathcal{A}=\{\omega \mid \omega :X \rightarrow \mathbb{R} \text{ is continuous and increasing}\}\), \(\mathcal{A}_{0}=\{\omega \mid \omega \in \mathcal{A}, \omega (0)=0\}\).
Remark 2.2
Conspicuously, \(\min \{u(t) \mid t\in [0,T]\}\) and \(\max \{u(t)\mid t\in [0,T]\}\) belong to \(\mathcal{A}\). If we take
then the boundary condition (1.2) is equal to
So, in the rest part of the paper we only deal with (1.1) and (2.1).
Lemma 2.3
([20, Lemma 4])
Let \(\omega \in \mathcal{A}\), \(k \in [0,1]\)and \(u\in X\), the equality \(\omega (u)-k\omega (-u)=0\)is satisfied. Then there exists a \(\delta \in [0,T]\)such that \(u(\delta )=0\).
Lemma 2.4
([20, Lemma 5])
Let \(\omega \in \mathcal{A}\), \(h \in \operatorname{Im}(\omega )\). Then there exists a unique \(k\in X\)such that \(\omega (k)=h\).
Lemma 2.5
(Bihari lemma, [19, Lemma 2.1]; [20, Lemma 1])
Let \(p:[0,+\infty )\rightarrow (0,+\infty )\)be a nondecreasing continuous function, \(P:[0,+\infty )\rightarrow [0,+\infty )\)be defined by \(P(u)=\int _{0}^{u}\frac{dt}{p(t)}\)and let \(b\in [c,d]\subset \mathbb{R}\). If \(v\in X\)satisfies the inequality
then
provided \(\lim_{u\rightarrow \infty } P(u)>b-c\), and
provided \(\lim_{u\rightarrow \infty }P(u)>d-b\). Here \(P^{-1}\)denotes the inverse function toP.
As in [5], we define the function \(\psi : X\rightarrow \mathbb{R}\) by the formula
Lemma 2.6
([5])
For all \(u\in Y\), the functionalψis continuous and
Lemma 2.7
Suppose thatuis a solution of (1.1) on \([0,T]\). Then
where \(P^{-1}\)denotes the inverse function to
Proof
Set
Let \(\mu (C_{+})\) and \(\mu (C_{-})\) be the Lebesgue measure of \(C_{+}\), \(C_{-}\), respectively.
If \(C_{+}=\emptyset\) (resp. \(C_{-}=\emptyset \)), then \(\psi (u')=0\) (resp. \(\psi (-u')=0\)) and (2.3) is clearly established. Assume \(C_{+}\neq \emptyset \) and \(C_{-}\neq \emptyset \). \(u'\in X\), \(C_{+}\), \(C_{-}\) are open subsets of \([0,T]\) and therefore \(C_{+}\) (resp. \(C_{-}\)) is a union of at most countable set of disjoint open intervals \((a_{i},b_{i})\), \(i\in I_{+}\subset \mathbb{N}\) (resp. \((c _{j},d_{j})\), \(j\in I_{-}\subset \mathbb{N}\)) without common elements, i.e.
Of course, for any \(i\in I_{+}\), \(u'(a_{i})\neq 0\) or \(u'(b_{i}) \neq 0\) (resp. \(u'(c_{j})\neq 0\) or \(u'(d_{j})\neq 0\) for any \(j \in I_{-}\)) imply \(a_{i}=0\) or \(b_{i}=T\) (resp. \(c_{j}=0\) or \(d _{j}=T\)). Furthermore, \(C_{+}\neq (0,T)\), since in the opposite case \(C_{-}=\emptyset \), which makes a contradiction. Similarly, \(C_{-}\neq (0,T)\).
By the inequality \(\mu (C_{+})+\mu (C_{-})\leq T\), it is easy to see that
Next we prove the inequality
Fix \(i\in I_{+}\), let \(u'(\eta )=0\), \(\eta \in \{a_{i},b_{i}\}\). Combining (1.1) with \(\phi (0)=0\), we have
For \(t\in [a_{i},b_{i}]\), \(u'(t)\geq 0\). Since ϕ is an increasing homeomorphism and because of (H1), we get
From Lemma 2.5 with \(b=\eta \), \(c=a_{i}\), \(d=b_{i}\), \(v(s)=\phi (u'(s))\) and \(p(v)=f(\phi ^{-1}(v))\), it is not difficult to see that
Subsequently, \(0\leq u'(t)\leq \phi ^{-1} (P^{-1}(b_{i}-a_{i}) )\) for \(t\in [a_{i},b_{i}]\), \(i\in I_{+}\). Thus
Moreover,
As a consequence, (2.5) is satisfied.
Next, we will show that
Fix \(j\in I_{-}\), let \(u'(\zeta )=0\), \(\zeta \in \{c_{j},d_{j}\}\). Together (1.1) with \(\phi (0)=0\), which implies
We have \(u'(t)\leq 0\) on \([c_{j},d_{j}]\). Combining the fact that ϕ is an odd increasing homeomorphism and (H1), we obtain
Thus
From Lemma 2.5 with \(b=\zeta \), \(c=c_{j}\), \(d=d_{j}\), \(v(s)=\phi (|u'(s)|)\) and \(p(v)=f(\phi ^{-1}(v))\), it is easy to verify that
Hence, \(0\leq -u'(t)\leq \phi ^{-1} (P^{-1}(d_{j}-c_{j}) )\) for \(t\in [c_{j},d_{j}]\), \(j\in I_{-}\). So
Furthermore,
Therefore, (2.8) is satisfied.
The result follows now from (2.4), (2.5) and (2.8). □
Let us consider the homotopy problem
depending on the parameter λ.
The next lemma gives prior bounds for solutions of (2.12) and (1.2).
Lemma 2.8
Suppose thatuis a solution of (2.12) for any \(\lambda \in [0,1]\)and satisfies the boundary condition (1.2) with \(A=0\). Then the following conclusions are fulfilled:
Proof
From \(\omega (u)=A=0\) and Lemma 2.3, there exists a \(\delta \in [0,T]\) such that \(u(\delta )=0\). Thus
this together with (2.1) shows that we obtain (2.13).
Taking into account \(\phi :(-a,a)\) and (2.13), we deduce that
□
We now state the following important lemma.
Lemma 2.9
LetBbe a positive constant, \(\omega \in \mathcal{A}\)andψbe defined in (2.2). Set
where \(\rho =B+a\)and \(\rho < aT\).
Define \(\varPhi _{i}: \overline{\varOmega }\rightarrow Y\times \mathbb{R} ^{2}\) (\(i=1,2\)),
Then
whereD, Idenote the Leray–Schauer degree and the identity operator on \(Y\times \mathbb{R}^{2}\), respectively.
Proof
Obviously, Ω is a bounded open subset of the Banach space \(Y\times \mathbb{R}^{2}\) with usual norm, and it is symmetric with respect to \(\theta \in \varOmega \).
Define \(G_{i}:[0,1]\times \varOmega \rightarrow Y\times \mathbb{R}^{2}\) (\(i=1,2\)),
For all \((u,\alpha ,\beta )\in \overline{\varOmega }\), it is clear that \(G_{i}(1,u,\alpha ,\beta )=\varPhi _{i}(u,\alpha ,\beta )\) (\(i=1,2\)). Hence to prove \(D(I-\varPhi _{i},\varOmega ,0)\neq 0\), we only need to prove the following hypotheses holding by the Borsuk theorem [13, Theorem 8.3].
- (1)
\(G_{i}(0,\cdot ,\cdot ,\cdot )\) is an odd operator on Ω̅, that is,
$$ G_{i}(0,-u,-\alpha ,-\beta )=-G_{i}(0,u,\alpha ,\beta ) \quad (i=1,2), (u,\alpha ,\beta )\in \overline{\varOmega }; $$(2.18) - (2)
\(G_{i}\) is a completely continuous operator;
- (3)
\(G_{i}(\lambda ,u,\alpha ,\beta )\neq (u,\alpha ,\beta )\) for \((\lambda ,u,\alpha ,\beta )\in [0,1]\times \partial \varOmega \).
In fact, we take \((u,\alpha ,\beta )\in \overline{\varOmega }\), for \(i=1\),
Analogously \(G_{2}(0,-u,-\alpha ,-\beta )=-G_{2}(0,u,\alpha ,\beta )\). So (1) is asserted.
Next we show that (2) holds.
Let \(\{(\lambda _{n},u_{n},\alpha _{n},\beta _{n})\}\subset [0,1]\times \overline{\varOmega }\) be a sequence. Then, for each \(n\in \mathbb{Z} ^{+}\) and by the fact that \(t\in [0,T]\), \(0\leq \lambda _{n}\leq 1\), \(\|u _{n}\|_{C^{1}}<\rho \), \(|\alpha _{n}|\leq \rho \), \(|\beta _{n}|<\phi (a)\); meanwhile, \(\{\omega (u_{n})\}\), \(\{\omega (-u_{n})\}\), \(\{\psi (u_{n})\}\) and \(\{\psi (-u_{n})\}\) are bounded. By the Arzelà–Ascoli theorem, it is not difficult to verify they are relatively compact. Then \(G_{i}(\lambda ,u,\alpha ,\beta )\) is convergent in \(Y\times \mathbb{R}^{2}\). It follows from the continuity of \(\phi ^{-1}\), ω and ψ that \(G_{i}\) (\(i=1,2\)) is continuous. So \(G_{i}\) (\(i=1,2\)) are completely continuous.
Finally, we prove that (3) is valid. Assume on the contrary that
for some \((\lambda _{0},u_{0},\alpha _{0},\beta _{0})\in [0,1]\times \partial \varOmega \). Then
By Lemma 2.3 (take \(u=u_{0}\), \(k=1-\lambda _{0}\)) and (2.21), there exist \(\gamma \in [0,T]\) and, consequently, \(u_{0}(\gamma )=0\). Together with (2.20) this shows that we obtain
and
The rest of the proof is divided into three cases.
Case 1. If \(\beta _{0} =0\), it follows from (2.23), (2.24) that \(\alpha _{0} =0\), \(u_{0}=0\), then
which is a contradiction.
Case 2. If \(\beta _{0} >0\), one deduces from \(\phi ^{-1}(\beta _{0})-(1- \lambda _{0})\phi ^{-1}(-\beta _{0})>0\) and the definition of ψ in (2.2) that
Combining this with (2.22), we have
and
Hence, \(\beta _{0}\leq \phi (\frac{\lambda _{0}\rho }{T})< \phi (a)\).
On the other hand, according to (2.23)–(2.25), for each \(t\in [0,T]\), we conclude that
Thus \((u_{0},\alpha _{0},\beta _{0})\notin \partial \varOmega \), a contradiction.
Case 3. If \(\beta _{0} <0\), it follows that \(\phi (\beta '_{0})- \phi ((\lambda _{0}-1)\beta '_{0})<0\), and by the definition of ψ in (2.2), we obtain
Combining this with (2.22), we deduce that
If \(\lambda _{0}=0\), then (2.26) implies \(\phi ^{-1}(\beta _{0})- \phi ^{-1}(-\beta _{0})=0\), which contradicts \(\phi (\beta '_{0})-\phi (- \beta '_{0})<0\).
If \(\lambda _{0}=1\), then \(\lambda _{0}B=0\), i.e. \(B=0\), which is impossible.
If \(\lambda _{0}\in (0,1)\), then
This is a contradiction. The proof is completed. □
3 Existence and multiplicity results
Theorem 3.1
Assume that (H1), (H2) hold andPis defined by Lemma 2.5. Let \(A=0\). Then, for any \(B\in \mathbb{R}\)satisfying
problems (1.1) and (1.2) have at least two different solutions.
Proof
Fix \(B\in \mathbb{R}\) and let (3.1) be satisfied. Let \(A=0\). Let us consider the boundary conditions
and
where \(\psi :X\rightarrow \mathbb{R}\) is defined by (2.2).
Suppose u is a solution of (1.1), then, from Lemma 2.6,
Now, if (1.1) and (3.2) has a solution \(u_{1}\), then Lemma 2.7 and (3.2) show that \(\psi (-u'_{1})< B\) and
As a consequence, \(u_{1}\) is a solution of (1.1) and (3.2), such that \(u_{1}\) is also a solution of (1.1) and (1.2).
Similarly, if (1.1) and (3.3) have a solution \(u_{2}\), then \(\psi (u'_{2})< B\) and
Therefore, \(u_{2}\) is also a solution of (1.1) and (1.2).
Furthermore, it follows from \(\psi (u'_{1})=B\) and \(\psi (u'_{2})< B\) that \(u_{1}\neq u_{2}\). Next, we only need to prove (1.1) and (3.2), or that (1.1) and (3.2) have solutions, respectively.
Let \(\rho =B+a\). According to (3.1), \(\rho < aT\) is satisfied. Set
Define \(\varGamma _{1}:[0,1]\times \overline{\varOmega }\rightarrow Y\times \mathbb{R}^{2}\),
It is easy to check that
Let us consider the parameter equation
Obviously, when \(\lambda =1\), u is a solution of (1.1) and (3.2) if and only if \((u(t),u(0),\phi (u'(0)))\) is a solution of (3.9). By Lemma 2.9, to prove \(D(I-\varPhi _{i},\varOmega ,0)\neq 0\), we only need to show the following hypotheses:
- (h1)
\(\varGamma _{1}(\lambda ,u,\alpha ,\beta )\) is a completely operator;
- (h2)
\(\varGamma _{1}(\lambda ,u,\alpha ,\beta )\neq (u,\alpha ,\beta )\) for any \((\lambda ,u,\alpha ,\beta )\in [0,1]\times \partial \varOmega \).
According to the continuity of \(\phi ^{-1}\), F, ω and ψ, it is clear that \(\varGamma _{1}(\lambda ,u,\alpha ,\beta )\) is continuous. Suppose that \(\{(\lambda _{n},u_{n},\alpha _{n},\beta _{n})\}\subset [0,1] \times \overline{\varOmega }\) is a sequence. Set
We have
It follows from \(0\leq \lambda _{n}\leq 1\), \(\|u_{n}\|_{C^{1}}<\rho \), \(\|u'_{n}\|_{ \infty }< a\), \(|\alpha _{n}|<\rho \) and \(|\beta _{n}|<\phi (a)\) that
for \(n\in \mathbb{N}\), \(t_{1}, t_{2}\in [0,T]\).
Since ϕ is increasing, combining (3.13), (3.14) and (3.15) with the Arzelà–Ascoli theorem, there exists a sequence \(\{\eta _{n}\}\) such that \(\{v_{\eta _{n}}\}\) is convergent in Y. By \(\omega (u_{n})\leq \max \{\omega (a),\omega (-a)\}\), \(0\leq \psi (u'_{n}) \leq \rho \), it follows that \(\{\tau _{n}\}\) and \(\{\xi _{n}\}\) are bounded. Without loss of generality, we can assume that \(\{ \tau _{\eta _{n}}\}\) and \(\{\xi _{\eta _{n}}\}\) are convergent. Thus \(\{(u_{n},\alpha _{n},\beta _{n})\}\) is convergent in \(Y\times \mathbb{R}^{2}\), which implies \(\varGamma _{1}(\lambda ,u,\alpha ,\beta )\) is completely continuous.
To prove (h2), we assume on the contrary that
for some \((\lambda _{0},u_{0},\alpha _{0},\beta _{0})\in [0,1]\times \partial \varOmega \). Then
and
From (3.17), we have
Hence, \(u_{0}\) is a solution of (2.12) and (1.2). By Lemma 2.8,
Moreover, \(\alpha _{0}=u_{0}(0)\), \(\phi (u'_{0}(0))=\beta _{0}\), so
which contradicts with \((u_{0},\alpha _{0},\beta _{0})\in \partial \varOmega \).
Similarly, consider the operator \(\varGamma _{2}:[0,1]\times \overline{ \varOmega }\rightarrow Y\times \mathbb{R}^{2}\),
we can obtain a solution of (1.1) and (3.3). □
Theorem 3.2
Assume that (H1), (H2) hold andPis defined by Lemma 2.5. Then, for \(A, B\in \mathbb{R}\)satisfying \(A\in \operatorname{Im}( \omega )\)and
(1.1) and (1.2) have at least two different solutions.
Proof
Suppose \(A\in \operatorname{Im}(\omega )\). From Lemma 2.4, there exists a unique \(k\in \mathbb{R}\) such that \(\omega (k)=A\).
Define \(\widetilde{\omega }: X\rightarrow \mathbb{R}\),
then \(\widetilde{\omega }(u)=0\). Define the continuous operator \(\widetilde{F}: Y\rightarrow L^{1}[0,T]\),
Hence, by (H1),
Then it follows from Theorem 3.1 that
has at least two different solutions \(\tilde{u}_{1}\), \(\tilde{u}_{2}\). Notice that \(\tilde{u}(t)\) is a solution of (3.23) and (3.24) if and only if \(\tilde{u}(t)+A\) is a solution of (1.1) and (2.1). Then it is not difficult to see that
are two different solutions of (1.1) and (2.1), Therefore, \(u_{i}(t)\) are two different solutions of problem (1.1) and (1.2). □
Remark 3.3
Since \(\phi :(-a,a)\rightarrow \mathbb{R}\) (\(0< a< \infty \)) is an odd increasing homeomorphism, clearly, \(\|u'\|_{ \infty }< a\) and \(\phi ^{-1}\) is bounded. We do not need the assumption \(\int _{0}^{\infty } \frac{t}{f(t)}\,ds=\infty \), which plays a very important role in [5, 19] and [20] for the classical case \(\phi =I\).
Finally, we give an example to illustrate our main result.
Example 3.4
Let \(F_{i}: Y\rightarrow L^{1}[0,\pi ]\) (\(i=1,2\)) be the continuous operators such that \(|(F_{i}u)(t)|\leq 1\) for any \(u\in Y\) and \(g\in X\), \(|g(r)|\leq r^{2}\) for \(r\in \mathbb{R}\).
Consider the following singular ϕ-Laplacian:
submitted to the nonlinear boundary conditions
Set \(\phi (s)=\frac{s}{\sqrt{1-s^{2}}}\). Then \(\phi :(-1,1)\rightarrow \mathbb{R}\) is an increasing homeomorphism, \(\phi (0)=0\), \(\phi ^{-1}(s)=\frac{s}{\sqrt{1+s ^{2}}}\) and \(\phi ^{-1}:\mathbb{R}\rightarrow (-1,1)\). We take \(f(r)=1+r^{2}\) for \(r\in [0,\infty )\). It is not difficult to see that
Clearly,
As a consequence, (H1) and (H2) are satisfied. In addition,
Since \(P'(u)=\frac{1}{2}(1+\frac{1}{1+2u})>0\) for \(u\in [0,\infty )\), and P is strictly monotone increasing, of course, \(P^{-1}\) exists. By a simple computation, we have
It follows that \(\nu (u)=\min \{u(t) \mid t\in [0,\pi ]\}\), \(\omega (u)=\min \{u(t) \mid t\in [0,\pi ]\}\) and \(\nu ,\omega \in \mathcal{A}\), by Theorem 3.2, for \(A,B\in \mathbb{R}\) and A, B satisfy
Then the problem (3.26) and (3.27) has at least two different solutions.
References
Agarwal, P., O’Regan, D., Staněk, S.: Positive and dead core solutions of singular Dirichlet boundary value problems with ψ-Laplacian. Comput. Math. Appl. 54(2), 255–266 (2007)
Agarwal, P., O’Regan, D., Staněk, S.: Dead core problems for singular equations with ψ-Laplacian. Bound. Value Probl. 2007, Article ID 18961 (2007)
Agarwal, P., O’Regan, D., Staněk, S.: Dead cores of singular Dirichlet boundary value problems with ϕ-Laplacian. Appl. Math. 53(4), 381–399 (2008)
Alías, L.J., Palmer, B.: On the Gaussian curvature of maximal surfaces and the Calabi–Bernstein theorem. Bull. Lond. Math. Soc. 33(4), 454–458 (2001)
Bereanu, C., Jebelean, P., Mawhin, J.: Non-homogeneous boundary value problems for ordinary and partial differential equations involving singular ϕ-Laplacians. Mat. Contemp. 36, 51–65 (2009)
Bereanu, C., Jebelean, P., Torres, P.J.: Positive radial solutions for Dirichlet problems with mean curvature operators in Minkowski space. J. Funct. Anal. 264(1), 270–287 (2013)
Bereanu, C., Mawhin, J.: Existence and multiplicity results for some nonlinear problems with singular ϕ-Laplacian. J. Differ. Equ. 243(2), 536–557 (2007)
Bereanu, C., Mawhin, J.: Nonhomogeneous boundary value problems for some nonlinear equations with singular ϕ-Laplacian. J. Math. Anal. Appl. 352(1), 218–233 (2009)
Brykalov, S.A.: Solutions with given maximum and minimum. Differ. Uravn. 29(6), 938–942 (1993) (in Russian)
Brykalov, S.A.: A second-order nonlinear problem with two-point and integral boundary conditions. Proc. Georgian Acad. Sci., Math. 1(3), 273–279 (1993)
Cabada, A., Staněk, S.: Functional fractional boundary value problems with singular ϕ-Laplacian. Appl. Math. Comput. 219(4), 1383–1390 (2012)
Cheng, S.-Y., Yau, S.-T.: Maximal spacelike hypersurfaces in the Lorentz–Minkowski spaces. Ann. Math. 104, 407–419 (1976)
Coelho, I., Obersnel, F., Omari, P.: Positive solutions of the Dirichlet problem for the one-dimensional Minkowski-curvature equation. Adv. Nonlinear Stud. 12(3), 621–638 (2012)
Deimling, K.: Nonlinear Functional Analysis. Springer, Berlin (1985)
Goodrich, C.S.: On nonlocal BVPs with nonlinear boundary conditions with asymptotically sublinear or superlinear growth. Math. Nachr. 285(11–12), 1404–1421 (2012)
Goodrich, C.S.: On nonlinear boundary conditions satisfying certain asymptotic behavior. Nonlinear Anal. 76, 58–67 (2013)
Ma, R., Gao, C.: Existence and multiple solutions for nonlinear second-order discrete problems with minimum and maximum. Adv. Differ. Equ. 2008, Article ID 586020 (2008)
Manásevich, R., Mawhin, J.: Boundary value problems for nonlinear perturbations of vector p-Laplacian-like operators. J. Korean Math. Soc. 37(5), 665–685 (2000)
Rachunková, I., Staněk, S., Tvrdy, M.: Solvability of Nonlinear Singular Problems for Ordinary Differential Equations. Contemporary Mathematics and Its Applications. Hindawi Publishing Corporation, New York (2008)
Staněk, S.: Multiplicity results for second order nonlinear problems with maximum and minimum. Math. Nachr. 192, 225–237 (1998)
Staněk, S.: Multiple solutions for some functional boundary value problems. Nonlinear Anal. 32(3), 427–438 (1998)
Staněk, S.: Existence principles for higher order nonlocal boundary value problems and their applications to singular Sturm–Liouville problems. Ukr. Math. J. 60(2), 277–298 (2008)
Staněk, S.: Existence principles for singular vector nonlocal boundary value problems with ϕ-Laplacian and their applications. Acta Univ. Palacki. Olomuc., Fac. Rerum Nat., Math. 50(1), 99–118 (2011)
Treiberg, A.E.: Entire spacelike hypersurfaces of constant mean curvature in Minkowski space. Invent. Math. 66, 39–56 (1982)
Acknowledgements
Not applicable.
Availability of data and materials
Not applicable.
Funding
Supported by the National Science Foundation of China under Grant 11761044 and LZCU-ZDJSXK-201606. The two funds can partly support our research and the publishing of our research paper.
Author information
Authors and Affiliations
Contributions
The authors completed the main part of this paper by discussing together. YZ was a major contributor in writing the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhang, Y., Wang, S. Multiplicity of solutions for mean curvature operators with minimum and maximum in Minkowski space. Adv Differ Equ 2019, 506 (2019). https://doi.org/10.1186/s13662-019-2394-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2394-8