Abstract
A non-autonomous almost periodic prey–predator system with impulsive effects and multiple delays is proposed in this paper, Holling’s type-IV systems and ratio-dependent functional responses are also involved in the model. By applying absolute inequalities, integral inequalities, differential inequalities and the mean-value theorem and other mathematical analysis techniques, we obtain some sufficient conditions which guarantee the permanence of the system. Moreover, we obtain the existence and the uniqueness of the almost periodic solution which is uniformly asymptotically stable by constructing a series of Lyapunov functionals. Finally, we present several numerical examples to verify the theoretical results and present some discussions of pest management in the agricultural ecological system.
Similar content being viewed by others
1 Introduction
It is well known that there are two kinds of controlling strategies in the agricultural pest management: biological control and chemical control. The biological control is utilizing the predation of natural enemies to control the number of pests, while the chemical control is to achieve the rapid reduction of pests by artificial insecticides. Naturally, the enemies of the pests and the crops will also be affected and decrease in the process of artificial insecticides more or less; see [1].
As the dynamics in the agricultural ecological system is concerned, the specie of crops, the pests and the enemies constitute a food-chain system, and the artificial insecticides irregularly decreasing the number of species can be described by impulsive perturbations on the food-chain system; see [1,2,3,4] etc.
On the other hand, when we refer to a prey–predator system or a food-chain system, a functional response (that is, the preying effects of predators on the prey) is one of the most important factors which should be considered. As regards the functional response being considered, Holling originally proposed three types, called Holling type I, II and III, respectively; see [5]. All of these three functional responses are all bounded monotonic increasing functions. The inherent feature of these functions means that the more prey in the environment the better off the predator, which is true in many predator–prey interactions. However, several experiments showed that a non-monotonic response occurs at the microbial level. When the nutrient concentration reaches a high level an inhibitory effect on the specific growth rate may occur. To model such an inhibitory effect, Andrews suggested the function
which is called the Monod–Haldane function, and the biological meaning of the parameters can be found in [6, 7]. Mathematical analysis shows that the Monod–Haldane function has a jump and declines at a critical value, and it also can be called the Holling type IV response function.
In addition, it is reported that when the predators have to search, share or compete for food, a predator-dependent functional response is more reasonable in many situations. And there is much significant evidence in a laboratory and natural systems. It has been proved that models with a ratio-dependent functional response can exhibit much richer, more complicated and more reasonable or acceptable dynamics since Arditi and Ginzburg proposed the ratio-dependent predator–prey model in [8], which attracted the interest of many scholars; see [9,10,11,12,13].
Enlightened by the above literature, we will study an impulsive food-chain system with both Holling type IV and ratio-dependent functional responses, in which digest delays are also considered in the process of predation,
where \(x(t)\), \(y(t)\), \(z(t)\) represent the population density of the prey, and the lower and the higher predator at time t, respectively. \(r_{i}(t)\) and \(d_{i}(t)\) denote the intrinsic growth rate and the inner density resistance of them. \(a_{i}(t)\), \(b_{i}(t)\), \(m_{ij}(t)\) are the coefficients functions of the functional response. \(t_{k}\) is the impulsive controlling time, \(\tau _{1},\tau _{2}>0\) is the digest delay and \(q_{ik}>-1\) is the impulsive controlling constants, where \(q_{ik}>0\) means planting and \(q_{ik}<0\) means harvest. For an agricultural ecological control system, the absolute value of the \(q_{ik}\) is meant to acknowledge the poisonousness of the pesticide when \(q_{ik}<0\), \(i,j=1\), \(2,3; k\in N\).
It is supposed that:
-
(H1)
All the function mentioned above such as \(r_{i}(t)\), \(d _{i}(t)\), \(r_{i}(t)\), \(a_{i}(t)\), \(b_{i}(t)\), \(m_{ij}(t)\) (\(i,j=1,2,3\)) are all bounded and positive almost periodic functions;
-
(H2)
\(Q_{i}(t)= \prod_{0< t_{k}< t}(1+q_{ik})\) is almost period functions and there exist positive constants \(Q^{L}_{i}\) and \(Q^{M}_{i}\) such that \(Q^{L}_{i} \leq Q_{i}(t)\leq Q^{M}_{i}\), \(i=1,2,3\).
In the next section, we will give some useful lemmas and then prove our main results such as permanence of the system, and the existence and the uniqueness of an almost periodic solution which is uniformly asymptotically stable by constructing a series of Lyapunov functionals. In the last section, we give some numerical examples to support our theoretical results, then we provide a brief discussion and a summary of our main results.
2 Preliminaries
In the beginning of this section, we will give some notation. For a real continuous function \(f(t)\) we define
Denote \(K= \{{t_{k}}\in R |t_{k}< t_{k+1}, \lim_{k\rightarrow \pm \infty }t_{k}=\pm \infty , k\in N \}\), in which all the sets of all sequences are unbounded and increasing. Let \(\varOmega \subset R\), \(\varOmega \neq \varPhi \), \(\tau = \max_{1\leq i\leq 2}\{\tau _{i}\}\), \(\xi _{0}\in R\). Also, we denote by \(PC(\xi _{0})\) the space of all functions \(\phi :[\xi _{0}-\tau ,\xi _{0}]\rightarrow \varOmega \) having points of discontinuity at \(\mu _{1},\mu _{2},\ldots \in [\xi _{0}-\tau ,\xi _{0}]\) of the first kind and being left continuous at these points.
For \(J\subset R, PC(J,R)\) is the space of all piecewise continuous functions from J to R with points of discontinuity of the first kind \(t_{k}\), at which it is left continuous.
Let \(\phi _{1}, \phi _{2}, \phi _{3}\in PC(0)\), denote \(x(t)=x(t;0,\phi _{1})\), \(y(t)=y(t;0,\phi _{2})\), \(z(t)=z(t;0,\phi _{3})\), \(x,y,z \in \varOmega \), the solution of system (2) satisfying the following initial conditions:
The solution of system (2) with initial conditions (4) is a piecewise continuous function with points of discontinuity of the first kind \(t_{k}, k\in Z\), and for the set of the sequence \(\{t_{k}^{j}\}\), \(t ^{k}_{j}=t_{k+j}-t_{k}\), \((k,j\in N,{t_{k}}\in K)\), and for the function \(\varphi \in PC(R,R)\), the uniformly almost periodicity is defined in the same way as in [14].
For the non-impulsive system
with initial values
The expressions of the functions \(D_{i}(t)\) (\(i=1,2,3\)), \(B_{1}(t)\), \(B_{23}(t)\), \(M_{12}(t)\), \(M_{21}(t)\), \(M_{23}(t)\), \(M_{32}(t) \) are given as follows:
Then we have the following lemmas.
Lemma 2.1
Assume that \((u(t),v(t),w(t))^{T}\) is any solution of system (5) with initial conditions (6), then \(u(t)>0\), \(v(t)>0\), \(w(t)>0\) for all \(t\in R^{+}\).
Proof
Denote
Then, from system (5) we have
This completes the proof of this lemma. □
Lemma 2.2
For the impulsive system (2) and the non-impulsive system (5), we have the following results:
-
(1)
If \((u(t),v(t),w(t))^{T}\) is a solution of system (5), then
$$ \bigl(x(t),y(t),z(t)\bigr)^{T}= \bigl(Q_{1}(t)u(t),Q_{2}(t)v(t), Q_{3}(t)w(t) \bigr) ^{T} $$is a solution of system (2);
-
(2)
If \((x(t),y(t),z(t))^{T}\) is a solution of system (2), then
$$ \bigl(u(t),v(t),v(t)\bigr)^{T}= \bigl(Q^{-1}_{1}(t)x(t),Q^{-1}_{2}(t)y(t),Q^{-1} _{3}(t)z(t) \bigr)^{T} $$is a solution of system (5).
Proof
For \((u(t),v(t),w(t))^{T}\) being a solution of system (5), the conclusion follows.
That is, for any \(t\neq t_{k}\), \(k\in N\),
satisfies each equation of system (5), which yields
which can be easily simplified to
Note that \(u(t)\), \(v(t)\), \(w(t)\) are continuous on each interval \((t_{k}, t_{k+1}]\), in the following we only need to prove the continuity of them at the impulsive points \(t=t_{k}\).
In fact,
which yields
Similarly, \(v(t^{+}_{k})=v(t^{-}_{k})=v(t_{k})\), \(w(t^{+}_{k})=w(t^{-} _{k})=w(t_{k})\). These means \(u(t)\), \(v(t)\), \(w(t)\) are continuous at the impulsive points \(t=t_{k}\).
Therefore, \(u(t)\), \(v(t)\), \(w(t)\) are continuous on the whole interval \([0,\infty )\). Then we complete the proof of the first conclusion.
Similarly, we can easily prove that the second conclusion also holds by the previous definitions of the function \(D_{i}(t)\) (\(i=1,2,3\)), \(B_{1}(t)\), \(B_{23}(t)\), \(M_{12}(t)\), \(M_{21}(t)\), \(M_{23}(t)\), \(M_{32}(t) \). □
Let \(R^{3}\) be the plane Euclidean space with element \(X=(x,y,z)^{T}\) and norm \(|X|_{0}=|x|+|y|+|z|\), \(C=C([-\tau ,0],R^{3})\), \(B\in R^{+}\), and denote
with \(\|\varphi \|= \sup_{s\in [-\tau ,0]}|\varphi (s)|_{0}= \sup_{s\in [-\tau ,0]} (|\varphi _{1}(s)|+|\varphi _{2}(s)|+| \varphi _{3}(s)| )\).
Definition 2.1
(see [15])
Consider the following almost periodic system with delay:
where \(f(t,\varphi )\) is continuous in \((t,\varphi )\in R\times C_{B}\) and almost periodic in t uniformly for \(\varphi \in C_{B}\), \(\forall \rho >0\), \(\exists M(\rho )>0\) such that \(|f(t,\varphi )| \leq M(\rho )\) as \(t\in R\), \(\varphi \in C_{\rho }\), while \(x_{t}\in C _{B}\) is defined as \(x_{t}(s)=x(t+s)\) for \(s\in [-\tau ,0] \). Here
is called the associate product system of (13).
By the conclusions of [14, 15], we have Lemma 2.3.
Lemma 2.3
(see [15])
For \(\phi ,\psi \in C_{B}\), suppose that there exists a Lyapunov function \(V(t,\phi ,\psi )\) defined on \(R^{+}\times C_{B}\times C_{B}\) satisfying the following three conditions:
-
(1)
\(u (\|\phi -\psi \| ) \leq V(t,\phi ,\psi ) \leq v (\|\phi -\psi \| )\), where \(u,v\in \mathcal{P}\) = {\(u:R ^{+}\rightarrow R^{+}| u\) is continuous increasing function and \(u(s)\rightarrow 0\), as \(s\rightarrow 0\)};
-
(2)
there exists a positive constant \(L>0\), such that for any \(\bar{\phi },\bar{\psi }, \hat{\phi },\hat{\psi } \in C_{B}\)
$$ \bigl\vert V(t,\bar{\phi },\bar{\psi })-V(t,\hat{\phi }, \hat{\psi )} \bigr\vert \leq L \bigl( \Vert \bar{\phi }-\hat{\phi } \Vert + \Vert \bar{\psi }-\hat{\psi } \Vert \bigr); $$ -
(3)
\(D^{+}V(t,\phi ,\psi )|_{\text{(14)}}\leq -\gamma V(t,\phi ,\psi )\), where γ is a positive constant.
Further, assume that (13) has a solution \(x(t,v,\phi )\) such that \(|x(t,v,\phi )|\leq B_{1}\) for \(t\geq v \geq 0\), \(B>B_{1}>0\). Then system (13) has a unique almost periodic solution which is uniformly asymptotically stable.
Lemma 2.4
For \(a>0\), \(b>0\), \(u(0)=u _{0}>0\):
-
(1)
If the inequality \(u'(t) \leq u(t) (a-bu(t) )\) holds, then \(\limsup_{t\rightarrow +\infty } u(t) \leq \frac{a}{b}\).
-
(2)
If the inequality \(u'(t) \geq u(t) (a-bu(t) )\) holds, then \(\liminf_{t\rightarrow +\infty }u(t) \geq \frac{a}{b}\).
3 Main results
In this section, if we denote conditions (H3) and (H4) as follows:
-
(H3)
\(r^{L}_{1}a^{L}_{1}>m^{M}_{12}Q^{M}_{2}v^{*}\);
-
(H4)
\(r^{L}_{2}b^{L}_{2}>m^{M}_{23}\);
where
Then we have Theorem 3.1.
Theorem 3.1
Assume that the coefficients of system (5) satisfy the conditions (H1)–(H4), then any positive solution \((u(t),v(t),w(t))^{T}\) of system (5) satisfies
Proof
Let \((u(t),v(t),w(t))^{T}\) be any solution of the non-impulsive system (5), if we use inequalities to enlarge the right side of each equation of system (5), then we have
It follows from the first inequality of Lemma 2.3 that
On the other hand, if we use inequalities to decrease the right side of each equation of system (5), then we have
It follows from the second inequality of Lemma 2.3 that
Thus, combining (18) with (22), we complete the proof of this theorem. □
Theorem 3.2
Assume that (H1)–(H4) hold, then any positive solution \((x(t),y(t),z(t))^{T}\) of system (2) satisfies
Here \(M_{1}=Q^{M}_{1}u^{*}\), \(M_{2}=Q^{M}_{2}v^{*}\), \(M_{3}=Q^{M}_{3}w ^{*}; m_{1}=Q^{L}_{1}u_{*}\), \(m_{2}=Q^{L}_{2}v_{*}\), \(m_{3}=Q^{L}_{3}w_{*}\).
Proof
Since \((x(t),y(t),z(t))^{T}\) is a solution of system (5), then, by the second conclusion of Lemma 2.2,
is a solution of system (5).
Then it follows from Theorem 3.1 that
which implies that
This completes the proof of this theorem. □
Remark
System (2) is permanent under the conditions (H1)–(H4).
Considering the ecological meanings, one of the most important problems which one is usually concerned with is: does the system have an almost periodic solution? The we wonder: if there exists an almost periodic solution, is it uniformly asymptotically stable or not?
Thus, in the following section, we suppose all of the coefficient functions of system (2) are almost periodic, and system (2) is also called an almost periodic system for this case. It follows from Lemma 2.3 that, if the almost periodic system (2) satisfies all of three conditions in the lemma, then there exists a unique almost periodic solution which is uniformly asymptotically stable. Here
Theorem 3.3
Assume that (H1)–(H4) hold, furthermore assume that there exist three positive \(\lambda _{1}\), \(\lambda _{2}\) and \(\lambda _{3}\) satisfying:
-
(H5)
\(\lambda _{1}K_{1}>\lambda _{1}K_{2}+\lambda _{2}L_{4}\),
-
(H6)
\(\lambda _{1}K_{3}+\lambda _{2}L_{1}>\lambda _{2}L_{2}+ \lambda _{3}N_{2}\),
then there exists an unique almost periodic solution which is uniformly asymptotically stable for the almost periodic system (2).
Proof
First, we prove that system (5) has a unique uniformly asymptotically stable almost periodic solution.
In order to achieve this aim, we take a transformation
Then system (5) can be transformed into following system:
Suppose that \(U_{1}(t)= (x_{1}(t),y_{1}(t),z_{1}(t) )^{T}\) and \(U_{2}(t)= (x_{2}(t),y_{2}(t),z_{2}(t) )^{T}\) are any two solutions of system (31), then the product system of (31) reads
According to Theorem 3.2, for any \(t\in R^{+}\) we have
If we denote
then, for any \(\varPhi =(\phi _{1},\phi _{2},\phi _{3})^{T}=(x_{1t},y_{1t},z _{1t})^{T}\in S^{*}\), we can choose \(\varPsi =(\psi _{1},\psi _{2},\psi _{3})^{T}=(x_{2t},y_{2t},z_{2t})^{T}\in S^{*}\) such that
Consider a Lyapunov functional \(V(t)=V(t,\varPhi ,\varPsi )=V(t,(x_{1t},y _{1t},y_{1t})^{T},(x_{2t},y_{2t},z_{2t})^{T})\) defined on \(R^{+} \times S^{*}\times S^{*}\) as follows:
where
Obviously, \(V(t)\) is a positive-defined Lyapunov functional. Further, by the definitions of \(S^{*}\) and \(V(t)=V(t,\varPhi ,\varPsi )\), there is some positive constant M large enough such that
By the structure of \(V(t)\), it is easy to see that
where \(\underline{\lambda }=\min \{\lambda _{1},\lambda _{2},\lambda _{3}\}>0\).
Moreover, by the integrative inequality and the absolute-value inequality properties we have
where
Let \(u,v\in C(R^{+},R^{+})\), choose \(u=\underline{\lambda }s\), \(v=\bar{ \lambda }s\), then the first condition of Lemma 2.3 is satisfied.
For \(\forall \bar{\varPhi }=(x_{1t},y_{1t},z_{1t})^{T}\), \(\bar{\varPsi }=(x _{2t},y_{2t},z_{2t})^{T}\), \(\hat{\varPhi }=(x^{*}_{1t},y^{*}_{1t},z^{*}_{1t})^{T}\), \(\hat{\varPsi }=(x^{*}_{2t},y^{*}_{2t},z^{*}_{2t})^{T}\in S^{*}\), then it is easy to make the calculation
which yields
Thus,
This means the second condition of Lemma 2.3 is satisfied.
Now, we only need to check the last condition of Lemma 2.3.
Thus, we calculate the right derivative \(D^{+}V_{i}(t)\) of \(V_{i}(t)\) along the product system (32), respectively:
By applying the equations in the product system (30) we have
By reducing the fractions in the above formula to a common denominator and following the mean-value theorem, we can calculate several terms as follows:
where \(\xi _{i}(t)\) lies between \(x_{1}(t)\) and \(x_{2}(t)\), \(\eta _{j}(t)\) lies between \(y_{1}(t)\) and \(y_{2}(t)\), \(i=1, 2,3\); \(j=1,2\).
By applying (43)–(45) and utilizing the absolute inequality we have
Similarly, for another two Lyapunov functions \(V_{1}(t)\), \(V_{2}(t)\) we can get
On the other hand, utilizing the property of the integral upper limit function we have
By the definition of \(V(t)\) and combining with (46)–(49), we can easily give the following estimations for the right derivatives of \(V(t)\):
If we denote \(\delta =\min \{K_{1}-K_{2}-\frac{\lambda _{2}L_{4}}{ \lambda _{1}}, \frac{\lambda _{1}K_{3}}{\lambda _{2}}+L_{1}-L_{2}-\frac{ \lambda _{3}N_{2}}{\lambda _{2}}, \frac{\lambda _{2}L_{3}}{\lambda _{3}}+N _{1} \}\), then \(\delta >0\) by the inequalities (H5) and (H6) in this theorem.
Therefore, having combined the inequality (50) with (38) and (39) we have
Let \(\gamma = \frac{\underline{\lambda }|\varPhi (0)-\varPsi (0)|_{0}}{M}\delta \), then \(\gamma >0\) and
This means the last condition of Lemma 2.3 is satisfied. Thus, by the lemma, system (31) admits a unique uniformly asymptotically stable almost periodic solution \((x(t),y(t),z(t))^{T}\). \((u(t),v(t),w(t))^{T}=(e ^{x(t)},e^{y(t)},e^{z(t)})^{T}\).
Moreover, by the transformation (30), we can conclude that system (5) admits a unique uniformly asymptotically stable almost periodic solution.
Finally, we will explain that system (2) has a unique uniformly asymptotically stable almost periodic solution.
In fact, from Lemma 2.2, we know that
is a solution of system (2). Since condition (H2) holds, similar to the proofs of Lemma 31 and Theorem 79 in [18], we can also prove that \((x(t),y(t),z(t))^{T}\) is almost periodic.
Therefore, \((x(t),y(t),z(t))^{T}\) is the unique uniformly asymptotically stable almost periodic solution of system (2) because of the uniqueness and the uniformly asymptotical stability of \((u(t),v(t),w(t))^{T}\). This completes the proof of this theorem. □
4 Numerical simulations and discussions
In this section, we will give a numerical example to illustrate the feasibility of our analytical results, then some discussions of the effects of impulsive perturbations and time delays on the system are presented in the end of the paper.
Consider a non-autonomous prey–predator system (2) with impulsive effects and delays with the following periodic coefficient functions:
Obviously, they are all positive, bounded and almost periodic functions, which satisfy the condition (H1) in the paper.
If we set the chemical controlling intensity as \(q_{1k}=-0.05\), \(q_{2k}=-0.08\), \(q _{3k}=-0.04\), \(t_{k}=k\), \(t\in [0,15]\), then one can easily calculate that \(Q^{L}_{1}=0.4633\), \(Q^{L}_{2}=0.2863\), \(Q^{L}_{3}=0.5421\), \(Q^{M}_{1}=Q^{M} _{2}=Q^{M}_{3}=1\), and we have
which satisfies condition (H2) in the paper.
Furthermore, according to the notations in the previous section we can easily calculate
which yields
At the moment, it is easy to calculate
which means conditions (H3) and (H4) in Theorem 3.1 are satisfied. According to the result of this theorem, system (2) should be permanent. By the numerical simulation with the initial condition \(\phi _{1}(s)=x _{1}(0)=1.0\), \(\phi _{2}(s)=y_{1}(0)=2.5\), \(\phi _{3}(s)=z_{1}(0)=0.4\), \(s \in [-\tau ,0]\), one very clearly observes the persistence of all species in Fig. 1.
Similarly, we can check that conditions (H5) and (H6) in Theorem 3.3 are also satisfied for the above coefficients. By the conclusion of this theorem, system (2) admits a unique uniformly asymptotically stable almost periodic solution. In order to verify this point, we choose two different initial conditions as follows:
Case 1: \(\phi _{1}(s)=x_{1}(0)=1.05\), \(\phi _{2}(s)=y_{1}(0)=4.5\), \(\phi _{3}(s)=z_{1}(0)=1.4\), \(s \in [-\tau ,0]\);
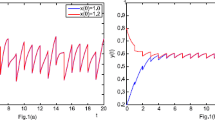
Case 2: \(\phi _{1}(s)=x_{2}(0)=1.2\), \(\phi _{2}(s)=y_{2}(0)=5.5\), \(\phi _{3}(s)=z_{2}(0)=1.6\), \(s \in [-\tau ,0]\), where the other coefficients are the same as above. And we solve system (2) numerically and plot the time-series of the each specie in these two cases in Fig. 2. On the one hand, we can observe the periodicity of the each population clearly by this figure. On the other hand, we can also conclude that, although the initial number of the three populations is different, the population density of each population becomes the same eventually over time. This means that there exists an almost periodic solution which is asymptotically stable.
Time-series of the species in system (2) with Case 1: \(x_{1}(0)=1.05\), \(y _{1}(0)=4.5\), \(z_{1}(0)=1.4\) and Case 2: \(x_{2}(0)=1.2\), \(y_{2}(0)=5.5\), \(z _{2}(0)=1.6\)
Finally, we will discuss the effect of chemical control; for example, people often use pesticide on pest control. And we choose the following three different chemical control strengths for system (2):
Case a: \(q_{1k}=-0.05\), \(q_{2k}=-0.08\), \(q_{3k}=-0.04\), \(t_{k}=k\), \(t \in [0,50]\),
Case b: \(q_{1k}=-0.10\), \(q_{2k}=-0.20\), \(q_{3k}=-0.08\), \(t_{k}=k\), \(t \in [0,50]\),
Case c: \(q_{1k}=-0.20\), \(q_{2k}=-0.30\), \(q_{3k}=-0.16\), \(t_{k}=k\), \(t \in [0,50]\). with the same initial condition \(\phi _{1}(s)=x_{1}(0)=1.05\), \(\phi _{2}(s)=y_{1}(0)=4.5\), \(\phi _{3}(s)=z_{1}(0)=1.4\), \(s \in [-\tau ,0]\).
We plot the time-series of the pest specie \(y(t)\) for the above three cases in Fig. 3. To our surprise, from the simulations, we find that even if we continuously increase the concentration of pesticides, the average number of pest populations will not decrease, but increase from 4.7438 (the green line) to 6.3744 (the blue line) and 7.7930 (the red line).
By the theoretical analysis and numerical simulations in this paper, we can conclude that appropriate chemical control and biological control strategies can guarantee the crops, pests and natural enemies in the agricultural ecological system to coexist in a certain range of quantities, and even control their quantity as a good cyclic behavior. On the contrary, excessive chemical control, such as only increasing the concentration of pesticides, may increase the resistance of pests and the pest population density will not decrease but increase, which leads to the ultimate failure of pest control.
References
Zhan, G., Wang, K., Chen, L.: Mathematical Theory and Calculation of the Pest Control. Science Press, Beijing (2014)
Jatav, K., Dhar, J.: Hybrid approach for pest control with impulsive releasing of natural enemies and chemical pesticides: a plant-pest-natural enemy model. Nonlinear Anal. Hybrid Syst. 12, 79–92 (2014)
Chakraborty, K., Das, K., Yu, H.: Modeling and analysis of a modified Leslie–Gower type three species food chain model with an impulsive control strategy. Nonlinear Anal. Hybrid Syst. 15, 171–184 (2015)
Tian, Y., Zhang, T., Sun, K.: Dynamics analysis of a pest management prey–predator model by means of interval state monitoring and control. Nonlinear Anal. Hybrid Syst. 23, 122–141 (2017)
Holling, C.S.: Some characteristics of simple types of predation and parasitism. Can. Entomol. 9, 385–398 (1966)
Andrews, J.: A mathematical model for the continuous culture of the microorganisms utilizing inhibitory substrates. Biotechnol. Bioeng. 10, 707–723 (1968)
Hwang, J., Xiao, D.: Analyses of bifurcations and stability in a predator–prey system with Holling type-IV functional response. Acta Math. Appl. Sin. 20, 167–178 (2004)
Arditi, R., Ginzburg, L.R., Akcakaya, H.R.: Variation in plankton densities among lakes: a case for ratio-dependent predation models. Am. Nat. 138, 1287–1296 (1991)
Hsu, S., Hwang, T., Kuang, Y.: Global analysis of the Michaelis–Menten type ratio-dependent predator–prey system. J. Math. Biol. 42, 489–506 (2001)
Sen, M., Banerjee, M., Morozov, M.: Bifurcation analysis of a ratio-dependent prey–predator model with the Allee effect. Ecol. Complex. 11, 12–27 (2012)
Ding, W., Huang, W.: Global dynamics of a ratio-dependent Holling–Tanner predator–prey system. J. Math. Anal. Appl. 460, 458–475 (2018)
Zeng, X., Gu, Y.: Existence and the dynamical behaviors of the positive solutions for a ratio-dependent predator–prey system with the crowing term and the weak growth. J. Differ. Equ. 264, 3559–3595 (2018)
Zhang, X., Liu, Z.: Periodic oscillations in age-structured ratio-dependent predator–prey model with Michaelis–Menten type functional response. Phys. D, Nonlinear Phenom. 389, 51–63 (2019)
He, C.: Almost Periodic Differential Equations. Higher Education Press, Beijing (1992)
Zheng, Z.: Theory of Functional Differential Equations. Anhui Education Press, Hefei (1994)
Chen, F., Li, Z., Chen, X.: Dynamic behaviors of a delay differential equation model of plankton allelopathy. J. Comput. Appl. Math. 206, 733–754 (2007)
Tian, B., Qiu, Y., Chen, N.: Periodic and almost periodic solution for a non-autonomous epidemic predator–prey system with time-delay. Appl. Math. Comput. 215, 779–790 (2009)
Samoilenko, A.M., Perestyuk, N.A.: Impulsive Differential Equations. World Scientific, Singapore (1995)
Acknowledgements
The authors would like to express their deep gratitude to the editor and the anonymous referee for his/her careful reading and valuable comments.
Availability of data and materials
The data set supporting the conclusions of this article is included within the article.
Funding
This work is supported by Sichuan Science and Technology Program under Grant 2017JY0336 and Hunan Science and Technology Program under Grant 2019JJ50399, Longshan Talent Research Fund of Southwest University of Science and Technology under Grant 17LZX670 and 18LZX622.
Author information
Authors and Affiliations
Contributions
All authors contributed equally and significantly in writing this paper. All authors have read and approved the final paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tian, B., Zhang, P., Li, J. et al. A non-autonomous impulsive food-chain model with delays. Adv Differ Equ 2019, 395 (2019). https://doi.org/10.1186/s13662-019-2300-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2300-4