Abstract
In this paper, a non-selective harvesting Lotka–Volterra amensalism discrete model incorporating partial closure for the populations is proposed and studied. By applying the relevant conclusions of difference inequality and some calculation technique, sufficient conditions are obtained to ensure the permanence and extinction of the system. By constructing a suitable Lyapunov function, sufficient conditions that ensure the global attractivity of the system are obtained. Finally, numerical simulations show the feasibility of our results.
Similar content being viewed by others
1 Introduction
During the last decade, the study of dynamic behaviors of the amensalism model has become one of the most important research topics, see [1,2,3,4,5,6,7,8,9,10,11,12]; here, amensalism means that a species inflicts harm on other species without any costs or benefits received by the other. Such topics as the stability of the equilibrium [1, 3,4,5, 8], the existence of the positive periodic solution [2, 9, 11], the extinction of the species [8, 10], the influence of the cover [8, 12], the influence of the functional response [10], etc. have been extensively studied. Recently, Xiong et al. [1] proposed the following amensalism model:
where u, \(r_{i}\), \(P_{i}\), \(i = 1, 2\), are all positive constants. They investigated the local stability property of the equilibria of system (1.1).
On the other hand, as was pointed out by Chakraborty et al. [13], the study of resource management, including fisheries, forestry, and wildlife management, is very important. They argued that it is necessary to harvest the population, but harvesting should be regulated so that both the ecological sustainability and conservation of the species can be implemented in a long run. Already, they proposed a non-selective harvesting predator-prey system incorporating partial closure for the populations, they investigated the local and global stability property of the system, and some interesting results related to the optimal harvesting were obtained. Recently, Chen [3] proposed the following non-selective harvesting Lotka–Volterra amensalism model incorporating partial closure for the populations:
They investigated the local and global stability of the boundary and interior equilibria. They proved that depending on the fraction of the stock available for harvesting, the system maybe extinction, partial survival, or two species may coexist in a stable state.
As we all know, though most dynamic behaviors of population models are based on the continuous models governed by differential equations, the discrete time models governed by difference equation are more appropriate than the continuous ones when the size of the population is rarely small or the population has non-overlapping generations. It has been found that the dynamic behaviors of the discrete system is rather complex and contains richer dynamics than the continuous ones [14]. Recently, more and more scholars pay attention to studying the discrete population models (see [14,15,16,17,18,19] and the references cited therein).
However, to the best of our knowledge, to this day, seldom did scholars propose and consider the influence of harvesting on the discrete amensalism model. This motivates us to propose and study the discrete system of (1.2). The aim of this paper is to investigate the permanence, extinction, and global attractivity of the following system:
where \(x_{1}(n)\), \(x_{2}(n)\) denote the population densities of the two species at any time n. \(r_{i}(p_{i})\) represents the intrinsic growth rate (environmental carrying capacity) of the ith species, \(q_{i}\) is the catchability co-efficient of the two species. E is the combined fishing effort used to harvest, and m (\(0 < m < 1\)) is the fraction of the stock available for harvesting. One could refer to [1, 13, 20] for more background and the adjustment of system (1.3). Throughout this paper, we assume that \(\{\mu (n) \}\), \(\{r_{i}(n) \}\), \(\{p_{i}(n) \}\), \(\{q_{i}(n) \}\) are bounded non-negative almost sequences such that
Here, for any bounded sequence \(\{a(n) \}\), \(a^{u}= \sup_{n\in N} \{a(n) \}\), \(a^{l}=\inf_{n\in N} \{a(n) \}\).
From the point of view of biology, we assumed that \(x_{i}(0)>0\), (\(i=1,2\)). Then it is easy to see that the solutions of (1.3) with the above initial condition remain positive for all \(n\in N^{+}= \{0,1,2,\ldots \}\).
The organization of this paper is as follows. In Sect. 2, we give some useful lemmas. Sufficient conditions for the permanence and extinction of (1.3) are given in Sect. 3 and Sect. 4. Then, in Sect. 5, we establish sufficient conditions for the global attractivity of (1.3). Some examples together with their numeric simulations are presented in Sect. 6. We end this paper with a brief discussion.
2 Preliminaries
In this section, we will introduce several useful lemmas.
Lemma 2.1
([21])
Assume that \(\{x(k) \}\) satisfies \(x(k)>0\) and
for \(k\in N\), where \(a(k)\) and \(b(k)\) are non-negative sequences bounded above and below by positive constants. Then
Lemma 2.2
([22])
Assume that \(\{x(k) \}\) satisfies
\(\limsup_{k\to +\infty }x(k)\leq x^{*}\) and \(x(N_{0})>0\), where \(a(k)\) and \(b(k)\) are non-negative sequences bounded above and below by positive constants and \(N_{0}\in N\). Then
3 Permanence
Theorem 3.1
Assume that
Then system (1.3) is permanent.
Proof
From the equations of system (1.3), it follows that
It follows from Lemma 2.1 that
So, for small enough \(\varepsilon >0\), there exists \(n_{1}>0\), for all \(n>n_{1}\), we have
Then, for \(n>n_{1}\), we have
From Lemma 2.2 and letting \(\varepsilon \to 0\), we have
where
From the second equation of system (1.3) it follows that
From Lemma 2.2 we have
where
So the proof of Theorem 3.1 is completed. □
4 Extinction
Theorem 4.1
Assume that
let \((x_{1}(n), x_{2}(n))^{T}\) be any positive solution of system (1.3), then
Proof
From (1.3) we have
By using (4.1), we get
That is,
For \(x_{i}(0)>0\), \(i=1,2\). So it is easy to get that \(x_{i}(n)>0\), \(i=1,2\). Since \((H_{2})\) holds, we have
The proof of Theorem 4.1 is completed. □
In this section, we will use the analysis technique of [14].
Theorem 4.2
Assume that
holds, let \((x_{1}(n),x_{2}(n))^{T}\) be any positive solution of system (1.3), then the species \(x_{2}\) is permanent, while \(x_{1}\) will be driven to extinction.
Proof
By (\(H_{3}\)) we can choose positive constants α and β such that
Thus
and there exists \(\delta >0\)
Let \((x_{1}(n),x_{2}(n))^{T}\) be any positive solution of system (1.3). For any \(k\in N\), we can get
Then, inequalities (4.3)–(4.6) lead to
Summating both sides of (4.7) from 0 to \(n-1\), we obtain
Then
Theorem 3.1 implies that \(x_{2}(n)\) is bounded eventually. Then the above inequality (4.9) shows that \(\lim_{n\to \infty }x_{1}(n)=0\). Since \(r_{2}^{l}-q_{2}^{u}Em>0\), then the species \(x_{2}\) is permanent.
The proof of Theorem 4.2 is completed. □
5 Globally attractive
Theorem 5.1
Assume that \(m> \frac{r_{2}^{u}}{q_{2}^{l}E}\) \((H_{4})\) holds and there exists a positive constant \(\eta >0\) such that
holds, then species \(x_{1}\) is globally attractive while \(x_{2}\) will be driven to extinction.
Proof
Suppose that \((x_{1}(n), x_{2}(n))^{T}\), \((x_{1}^{*}(n), x _{2}^{*}(n))^{T}\) are any two positive solutions of system (1.3). Under the assumption condition \((H_{4})\), it follows from Theorem 4.1 that \(\lim_{n\to +\infty }x_{2}(n)=0\). Since \(\limsup_{n\to \infty }x_{1}(n)< M_{1}\), then for small enough \(\varepsilon >0\), there exists \(N_{0}>0\), for all \(n>N_{0}\), we have
To end the proof of Theorem 5.1, it is enough to show that \(\lim_{n\to +\infty }(x_{1}(n)-x_{1}^{*}(n))=0\).
Let \(V(n)=|\ln x_{1}(n)-\ln x_{1}^{*}(n)|\). From (1.3) we have
Since \(\ln x_{1}(n)-\ln x_{1}^{*}(n)= \frac{1}{\xi _{1}(n)}(x_{1}(n)-x_{1}^{*}(n))\), where \(\min \{x _{1}(n), x_{1}^{*}(n) \}\leq \xi _{1}(n)\leq \max \{x_{1}(n), x _{1}^{*}(n) \}\leq M_{1}+\varepsilon \). So we can get
Letting \(\varepsilon \to 0\), it follows that
then
that is,
therefore
So it is easy to know that \(\lim_{n\to +\infty }(x_{1}(n)-x _{1}^{*}(n))=0\).
The proof of Theorem 5.1 is completed. □
Similarly, we can get the following theorem.
Theorem 5.2
Assume that there exists a positive constant \(\gamma >0\) such that
holds, then the species \(x_{2}\) is globally attractive.
6 Examples and numeric simulations
The following examples lend credence to the plausibility of the main results.
Example 6.1
Corresponding to system (1.3), we assume that
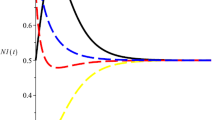
It is easy to see that \(\frac{r_{2}^{l}}{q_{2}^{u}E}=0.4\), \(M_{2}= \frac{p_{2}^{u}}{r_{2}^{l}}\exp (r_{2}^{u}-1)=0.5\), \(\frac{r_{1}^{l}p_{1}^{l}-r_{1}^{u}\mu ^{u}M_{2}}{q_{1}^{u}p_{1}^{l}E}=0.25\), \(m=0.1<\min \{0.4, 0.25 \}\). Then the conditions of Theorem 3.1 are satisfied (see Fig. 1).
Dynamic behaviors of system (6.1) with initial condition \((x_{1}(t),x_{2}(t))^{T}=(0.1, 0.45)^{T},(0.25, 0.25)^{T},(0.35, 0.1)^{T}\)
Example 6.2
Corresponding to system (1.3), we assume that
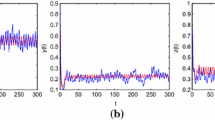
It is easy to see that \(\frac{r_{1}^{u}}{q_{1}^{l}E}=0.2\), \(\frac{r_{2}^{u}}{q_{2}^{l}E}=0.7\), \(m=0.8>\max \{0.2, 0.7 \}\). Then the conditions of Theorem 4.1 are satisfied (see Fig. 2).
Dynamic behaviors of system (6.2) with initial condition \((x_{1}(t),x_{2}(t))^{T}=(0.1, 0.3)^{T},(0.25, 0.6)^{T},(0.35, 0.1)^{T}\)
Example 6.3
Corresponding to system (1.3), we assume that
It is easy to see that \(r_{1}^{u}-q_{1}^{l}Em=0.09>0\), \(r_{2}^{l}-q _{2}^{u}Em=0.05>0\), \(\frac{r_{1}^{u}-q_{1}^{l}Em}{r_{2}^{l}-q_{2}^{u}Em}=1.8< \frac{r_{1}^{l}\mu ^{l}p_{2}^{l}}{r_{2}^{u}p_{1}^{u}}\approx 9.09\). Then the conditions of Theorem 4.2 are satisfied (see Fig. 3).
Dynamic behaviors of system (6.3) with initial condition \((x_{1}(t),x_{2}(t))^{T}=(0.1, 0.3)^{T},(0.25, 0.6)^{T},(0.35, 0.1)^{T}\)
Example 6.4
Corresponding to system (1.3), we assume that
It is easy to see that \(m=0.8> \frac{r_{2}^{u}}{q_{2}^{l}E}=0.7\), \(\min \{ \frac{r_{1}^{l}}{p_{1}^{u}}, \frac{2}{M_{1}}- \frac{r_{1}^{u}}{p_{1}^{l}}=\min \{1,1 \} \}>0\), \(M _{1}= \frac{p_{1}^{u}}{r_{1}^{l}}\exp (r_{1}^{u}-1)=1\). Then the conditions of Theorem 5.1 are satisfied (see Fig. 4).
Dynamic behaviors of system (6.4) with initial condition \((x_{1}(t),x_{2}(t))^{T}=(0.1, 0.8)^{T},(0.25, 0.6)^{T},(0.35, 0.3)^{T}\)
7 Discussion
With the aim of the ecological sustainability and conservation of the species to be implemented in a long run, in this paper, we have attempted to study the dynamic behaviors of a non-selective harvesting Lotka–Volterra discrete amensalism model. We have proved that if \((H_{1})\) holds, then the system is permanent, which means that if m, which is the fraction of the stock available for harvesting, is small enough, the system will coexist. Theorem 4.1 implies that if m is large enough, then the system will be driven to extinction. Theorem 4.2 gives some threshold on m, which ensures that the species \(x_{2}\) is permanent while \(x_{1}\) will be driven to extinction. In Sect. 5, sufficient conditions for the global attractivity of (1.3) are given, which means that if m is larger than a certain value and satisfies \((H_{5})\), then the species \(x_{1}\) is globally attractive while \(x_{2}\) will be driven to extinction. The results obtained in this paper maybe useful in designing the natural protection area.
References
Xiong, H.H., Wang, B.B., Zhang, H.L.: Stability analysis on the dynamic model of fish swarm amensalism. Adv. Appl. Math. 5(2), 255–261 (2016)
Han, R.Y., Xue, Y.L., Yang, L.Y., et al.: On the existence of positive periodic solution of a Lotka–Volterra amensalism model. J. Rongyang Univ. 33(2), 22–26 (2015)
Chen, B.G.: Dynamic behaviors of a non-selective harvesting Lotka–Volterra amensalism model incorporating partial closure for the populations. Adv. Differ. Equ. 2018, 111 (2018)
Sun, G.C.: Qualitative analysis on two populations amensalism model. J. Jiamusi Univ. (Nat. Sci. Ed.) 21(3), 283–286 (2003)
Zhang, Z.P.: Stability and bifurcation analysis for a amensalism system with delays. Math. Numer. Sin. 2, 213–224 (2008)
Sita Rambabu, B., Narayan, K.L., Bathul, S.: A mathematical study of two species amensalism model with a cover for the first species by homotopy analysis method. Adv. Appl. Sci. Res. 3(3), 1821–1826 (2012)
Chen, F.D., He, W.X., Han, R.Y.: On discrete amensalism model of Lotka–Volterra. J. Beihua Univ. Nat. Sci. 16(2), 141–144 (2015)
Xie, X.D., Chen, F.D., He, M.X.: Dynamic behaviors of two species amensalism model with a cover for the first species. J. Math. Comput. Sci. 16, 395–401 (2016)
Lin, Q.X., Zhou, X.Y.: On the existence of positive periodic solution of a amensalism model with Holling II functional response. Commun. Math. Biol. Neurosci. 2017, Article ID 3 (2017)
Chen, J.H., Wu, R.X.: A two species amensalism model with non-monotonic functional response. Commun. Math. Biol. Neurosci. 2016, Article ID 19 (2016)
Chen, F.D., Zhang, M.S., Han, R.Y.: Existence of positive periodic solution of a discrete Lotka–Volterra amensalism model. J. Shengyang Univ. (Nat. Sci.) 27(3), 251–254 (2015)
Wu, R.X., Zhao, L., Lin, Q.X.: Stability analysis of a two species amensalism model with Holling II functional response and a cover for the first species. J. Nonlinear Funct. Anal. 2016, Article ID 46 (2016)
Chakraborty, K., Das, S., Kar, T.K.: On non-selective harvesting of a multispecies fishery incorporating partial closure for the populations. Appl. Comput. Math. 221, 581–597 (2013)
Li, Z., Chen, F.D.: Extinction in two dimensional discrete Lotka–Volterra competitive system with the effect of toxic substances. Dyn. Contin. Discrete Impuls. Syst., Ser. B, Appl. Algorithms 15(2), 165–178 (2008)
Chen, X.Y., Shi, C.L.: Permanence and global attractivity of a discrete Nicholson’s blowflies model with delay. J. Math. Res. Appl. 37(2), 233–241 (2017)
Li, Y.K., Zhang, T.W.: Almost periodic solution for a discrete hematopoiesis model with time delay. Int. J. Biomath. 5(1), 1–9 (2012)
Li, Z., Han, M.A., Chen, F.D.: Almost periodic solutions of a discrete almost periodic logistic equation with delay. Appl. Math. Comput. 232(1), 743–751 (2014)
Zhou, T.J., Zhang, X.L., Xiang, M.H., Wu, Z.H.: Permanence and almost periodic solution of a predator–prey discrete system with Holling IV functional response. Int. J. Biomath. 2016(3), 39–64 (2016)
Li, Z., Chen, F.D.: Almost periodic solutions of a discrete almost periodic logistic equation. Math. Comput. Model. 50(1–2), 254–259 (2009)
Kar, T.K., Chaudhuri, K.S.: On non-selective harvesting of two competing fish species in the presence of toxicity. Ecol. Model. 161(1–2), 125–137 (2003)
Chen, F.D.: Permanence and global attractivity of a discrete multi-species Lotka–Volterra competition predator–prey systems. Appl. Math. Comput. 182(1), 3–12 (2006)
Chen, F.D.: Permanence for the discrete mutualism model with time delays. Math. Comput. Model. 47(3–4), 431–435 (2008)
Acknowledgements
Not applicable.
Availability of data and materials
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
Funding
This work is supported by the Natural Science Project of Fujian province (2015 J 01012, 2015 J 01019) and the Funding of the Young Key Teachers Training Program of Zhengzhou Chenggong University of Finance and Economics.
Author information
Authors and Affiliations
Contributions
QQS is a major contributor in writing the manuscript. FDC is responsible for numerical simulation and drawing. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
We agree to publish in your journal.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Su, Q., Chen, F. The influence of partial closure for the populations to a non-selective harvesting Lotka–Volterra discrete amensalism model. Adv Differ Equ 2019, 281 (2019). https://doi.org/10.1186/s13662-019-2209-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2209-y