1 Introduction

Difference equations describe the observed evolution of a phenomenon at discrete time steps. Thus, difference equations are used as discrete models of the workings of physical or artificial systems. The asymptotic behavior of the solutions of linear difference equations is a qualitative property having important applications in many areas, including control theory, mathematical biology, neural networks, and so forth. We cannot use numerical methods to study the asymptotic behavior of all solutions of a given equation due to the global nature of that behavior. Therefore, the analytical study of those qualitative properties has been attracting considerable interest from mathematicians and engineers, as the only method to gain insight into those properties.

This paper is concerned with the study of the asymptotic behavior of the solutions of a general class of difference equations

$$ x_{n+1}=ax_{n-l}+bx_{n-k}+f ( x_{n-l},x_{n-k} ), $$
(1.1)

where l and k are nonnegative integers, a and b are nonnegative real numbers, and \(f (u,v ): ( 0,\infty ) ^{2}\rightarrow ( 0,\infty ) \) is a continuous and homogeneous real function of degree zero. The construction of this new class of difference equations is complex and involves several cases. For example, one can assume \(a = 0\) or \(b = 0\) or both. That makes our analysis better suited for studying those equations. For studies on equations of a similar form, the reader is referred to [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. We begin our study with a review of the background on equations having a similar form to the one we consider in this paper.

Kalabušić and Kulenović [15] and Kulenović and Ladas [18] studied the difference equation

$$ x_{n+1}=\frac{a_{1}x_{n-l}+a_{2}x_{n-k}}{b_{1}x_{n-l}+b_{2}x_{n-k}}. $$

Elsayed [12] investigated the asymptotic behavior of the difference equation

$$ x_{n+1}=A+\frac{a_{1}x_{n-l}+a_{2}x_{n-k}}{b_{1}x_{n-l}+b_{2}x_{n-k}}. $$

Zayed and El-Moneam [26, 27, 29] studied the asymptotic behavior of the difference equation

$$ x_{n+1}=Ax_{n}+\frac{a_{1}x_{n}+a_{2}x_{n-k}}{b_{1}x_{n}+b_{2}x_{n-k}}, $$

whereas Zayed and El-Moneam [28] studied the global and asymptotic properties of the solutions of the difference equation

$$ x_{n+1}=Ax_{n}+Bx_{n-k}+\frac{a_{1}x_{n}+a_{2}x_{n-k}}{b_{1}x_{n}+b_{2}x_{n-k}}. $$

Notice that these equations as well as several other equations not listed above are special cases of equation (1.1).

The results in this paper make three main contributions to the study of linear difference equations. First, we formulate a general class of difference equations as a means of establishing general theorems for the asymptotic behavior of its solutions and the solutions of equations that are special cases of the studied equation. Second, we study the asymptotic behavior of the solutions of this more general class of difference equations using an efficient method introduced in [12] and modified in [19]. Theorem 3.2 establishes how this method can be applied to equation (1.1). In particular, this method is also valid and can be applied to several classes of difference equations for which the classical method fails to give results. Moreover, we consider difference equations with real coefficients and initial values which extend and slightly improve previous results. Third, we can use our analysis to check and verify the results obtained by other researchers.

For the basic definitions and auxiliary lemmas we use for establishing our results, namely equilibrium points, local stability, and periodicity of the solutions, we refer the reader to [1, 9, 17, 18]. For the convenience of the reader, we present below some related results.

Lemma 1.1

(see [17, Theorem 1.3.7])

Assume that \(p,q\in \mathbb{R} \) and \(k\in \{ 0,1,2,\ldots \} \). Then \(\vert p \vert + \vert q \vert <1\) is a sufficient condition for the asymptotic stability of the difference equation

$$ x_{n+1}+px_{n}+qx_{n-k}=0,\quad n=0,1,2, \ldots. $$

Lemma 1.2

(see [9, Corollary 4])

Let \(f:\mathbb{R} _{+}^{n}\rightarrow \mathbb{R} \) be continuous and differentiable on \(\mathbb{R} _{++}^{n}\). If f is homogeneous of degree k, then \(D_{j}f=\partial f/\partial x_{j}\) is homogeneous of degree \(k-1\).

The rest of the paper is organized as follows. In Sect. 2, we study the stability behavior and boundedness of the solutions of equation (1.1) and give an illustrative example in support of our analysis. In Sect. 3, we present a technique to investigate the periodic behavior of the solutions of equation (1.1). A distinguishing feature of our criteria is that the coefficients l and k of equation (1.1) can be odd or even. Two examples are provided to illustrate the new method for studying periodic solutions. In Sect. 4, the practicability, maneuverability, and efficiency of the results obtained are illustrated via two applications.

2 Dynamics of equation (1.1)

2.1 Local stability

Here, we investigate the local stability of the equilibrium point of equation (1.1), which is given by

$$ \overline{x}=a\overline{x}+b\overline{x}+f ( \overline {x},\overline{x} ). $$

Hence, the positive equilibrium point is

$$ \overline{x}=\frac{1}{1-a-b}f ( 1,1 ),\quad a+b< 1. $$

Now, we define the function \(\phi ( u,v ): ( 0,\infty ) ^{2}\rightarrow ( 0,\infty ) \) by

$$ \phi ( u,v ) =au+bv+f ( u,v ) $$

so that

$$\begin{aligned} &\frac{\partial\phi}{\partial u} ( u,v )= a+f_{u} ( u,v ), \\ &\frac{\partial\phi}{\partial v} ( u,v )= b+f_{v} ( u,v ). \end{aligned}$$

Theorem 2.1

The equilibrium point of equation (1.1) \(\overline {x}= ( 1-a-b ) ^{-1}f ( 1,1 ) \) is locally asymptotically stable if

$$ \vert \rho \vert -\rho< ( 1-a-b ) f ( 1,1 ), $$

where

$$ \rho= \textstyle\begin{cases} bf ( 1,1 ) - ( 1-a-b ) f_{u} ( 1,1 ) & \textit{if }f_{u}>0, \\ af ( 1,1 ) - ( 1-a-b ) f_{v} ( 1,1 ) & \textit{if }f_{u}< 0. \end{cases} $$

Proof

The linearized equation of equation (1.1) about x̅ is the linear difference equation

$$ y_{n+1}-\frac{\partial\phi}{\partial u} ( \overline {x},\overline{x} ) y_{n-l}-\frac{\partial\phi}{\partial v} ( \overline{x},\overline{x} )y_{n-k}=0. $$

Hence, by Lemma 1.1, equation (1.1) is locally stable if

$$ \biggl\vert \frac{\partial\phi}{\partial u} ( \overline {x},\overline{x} ) \biggr\vert + \biggl\vert \frac{\partial\phi}{\partial v} ( \overline{x},\overline{x} ) \biggr\vert < 1. $$

Therefore,

$$ \bigl\vert a+f_{u} ( \overline{x},\overline{x} ) \bigr\vert + \bigl\vert b+f_{v} ( \overline{x},\overline{x} ) \bigr\vert < 1. $$
(2.1)

From Euler’s homogeneous function theorem, we deduce that \(uf_{u}=-vf_{v}\) and thus \(f_{u}f_{v}<0\). If \(f_{u}>0\), then

$$ \bigl\vert b-f_{u} ( \overline{x},\overline{x} ) \bigr\vert < 1-a-f_{u} ( \overline{x},\overline{x} ). $$

Using Lemma 1.2, we get

$$ \biggl\vert b-\frac{1}{\overline{x}}f_{u} ( 1,1 ) \biggr\vert < 1-a-\frac{1}{\overline{x}}f_{u} ( 1,1 ), $$

which implies that inequality (2.1) is equivalent to

$$ \biggl\vert \frac{b}{1-a-b}f ( 1,1 ) -f_{u} ( 1,1 ) \biggr\vert < \frac{1-a}{1-a-b}f ( 1,1 ) -f_{u} ( 1,1 ), $$

and so

$$ \bigl\vert bf ( 1,1 ) - ( 1-a-b ) f_{u} ( 1,1 ) \bigr\vert < ( 1-a ) f ( 1,1 ) - ( 1-a-b ) f_{u} ( 1,1 ). $$

Next, if \(f_{u}<0\), then

$$ \bigl\vert a-f_{v} ( \overline{x},\overline{x} ) \bigr\vert < 1-b-f_{v} ( \overline{x},\overline{x} ). $$

Similarly, we find

$$ \bigl\vert af ( 1,1 ) - ( 1-a-b ) f_{v} ( 1,1 ) \bigr\vert < ( 1-b ) f ( 1,1 ) - ( 1-a-b ) f_{v} ( 1,1 ), $$

which completes the proof. □

Example 2.1

Consider the difference equation

$$ x_{n+1}=ax_{n-l}+bx_{n-k}+c\frac{x_{n-l}}{x_{n-k}}, $$
(2.2)

where c is a positive real number. Note that \(f ( u,v ) =c u/v\). By Theorem 2.1, the equilibrium point of equation (2.2) \(\overline{x}=c/(1-a-b)\) is locally asymptotically stable if

$$ \bigl\vert b- ( 1-a-b ) \bigr\vert < b. $$

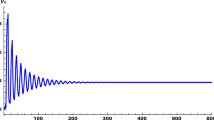
For example, for \(l=0\), \(k=1\), \(a=0.2\), \(b=0.3\), \(c=1\), \(x_{-1}=2.8\), and \(x_{0}=1.5\), the stable solution of (2.2) is shown in Fig. 1.

Figure 1
figure 1

Stable solution corresponding to difference equation (2.2)

Full size image

2.2 Boundedness

In this section, we study the boundedness of the solutions of equation (1.1).

Theorem 2.2

If \(a+b < 1\) and there exists a positive constant L such that \(f ( u,v ) < L\) for all \(u,v\in ( 0,\infty )\), then every solution of equation (1.1) is bounded.

Proof

From equation (1.1), we obtain

$$\begin{aligned} x_{n+1} &= ax_{n-l}+bx_{n-k}+f ( x_{n-l},x_{n-k} ) \\ &< ax_{n-l}+bx_{n-k}+L. \end{aligned}$$

Using a comparison, we can write the right-hand side as follows:

$$y_{n+1}=ay_{n-l}+by_{n-k}+L, $$

and this equation is locally stable if \(a+b<1\) and converges to the equilibrium point \(\overline{y}=L/ ( 1-a-b ) \). Then we have \(x_{n}< y_{n}\) and

$$\limsup_{n\rightarrow\infty}x_{n}\leq\frac{L}{1-a-b}. $$

Thus, every solution of (1.1) is bounded. □

Remark 2.3

As fairly noticed by the referees, the global asymptotic stability of equation (1.1) remains an open problem for further research.

3 Periodic solutions

Theorem 3.1

If l and k are either odd or even, then equation (1.1) has no solutions of prime period two.

Proof

Suppose that l and k are even and equation (1.1) has a prime period two solution

$$ \ldots,p,q,p,q,\ldots. $$

Then \(x_{n-l}=x_{n-k}=q\). From equation (1.1), we have

$$\begin{aligned} p &= ( a+b ) q+f ( q,q ), \\ q &= ( a+b ) p+f ( p,p ). \end{aligned}$$

Thus, we get

$$ p=q=\frac{1+a+b}{1- ( a+b ) ^{2}}f ( 1,1 ), $$

which is a contradiction. Another case can be shown similarly. This completes the proof. □

Theorem 3.2

Assume that l is odd and k is even. Then equation (1.1) has a prime period two solution

$$ \ldots,p,q,p,q,\ldots $$

if and only if

$$ \bigl[ ( 1-a ) -b\tau \bigr] f ( \tau,1 ) = \bigl[ ( 1-a ) \tau-b \bigr] f ( 1, \tau ), $$
(3.1)

where \(\tau=p/q\).

Proof

Without loss of generality, we can assume that \(l>k\). Now, let equation (1.1) have a prime period two solution

$$ \ldots,p,q,p,q,\ldots. $$

Since l is odd and k is even, we arrive at \(x_{n-l}=p\) and \(x_{n-k}=q\). From equation (1.1), we get

$$\begin{aligned} &p= ap+bq+f ( p,q ), \\ &q= aq+bp+f ( q,p ). \end{aligned}$$

This yields

$$\begin{aligned} &( 1-a ) p= bq+f ( \tau,1 ), \\ &( 1-a ) q= bp+f ( 1,\tau ), \end{aligned}$$

where \(\tau=p/q\). Then we obtain

$$\begin{aligned} &\bigl( ( 1-a ) ^{2}-b^{2} \bigr) p= bf ( 1,\tau ) + ( 1-a ) f ( \tau,1 ), \\ &\bigl( ( 1-a ) ^{2}-b^{2} \bigr) q= bf ( \tau ,1 ) + ( 1-a ) f ( 1,\tau ). \end{aligned}$$

Since \(p=\tau q\), we find

$$ \bigl[ ( 1-a ) -b\tau \bigr] f ( \tau,1 ) = \bigl[ ( 1-a ) \tau-b \bigr] f ( 1, \tau ). $$

On the other hand, suppose that (3.1) is satisfied. Now, we choose

$$\begin{aligned} &x_{-l+2r}=\lambda f ( 1,\tau ) +\mu f ( \tau,1 ) \quad\text{and}\\ & x_{-l+2r+1}=\lambda f ( \tau,1 ) +\mu f ( 1,\tau ),\quad r=0,1,2,\ldots, ( l-1 )/2, \end{aligned}$$

where

$$ \lambda=\frac{b}{ ( 1-a ) ^{2}-b^{2}}, \qquad \mu=\frac {1-a}{ ( 1-a ) ^{2}-b^{2}}, $$

and \(\tau\in \mathbb{R} ^{+}\). Hence, we see that

$$\begin{aligned} x_{1}={}& ax_{-l}+bx_{-k}+f ( x_{-l},x_{-k} ) \\ ={}& a \bigl[ \lambda f ( 1,\tau ) +\mu f ( \tau ,1 ) \bigr] +b \bigl[ \lambda f ( \tau,1 ) +\mu f ( 1,\tau ) \bigr] \\ &{}+f \bigl( \bigl[ \lambda f ( 1,\tau ) +\mu f ( \tau ,1 ) \bigr], \bigl[ \lambda f ( \tau,1 ) +\mu f ( 1,\tau ) \bigr] \bigr). \end{aligned}$$
(3.2)

From (3.1), we have

$$ [ \mu-\lambda\tau ] f ( \tau,1 ) = [ \mu\tau -\lambda ] f ( 1,\tau ), $$

and so

$$ \mu f ( \tau,1 ) +\lambda f ( 1,\tau ) =\tau \bigl[ \lambda f ( \tau,1 ) +\mu f ( 1,\tau ) \bigr], $$

which together with (3.2) implies that

$$\begin{aligned} x_{1} &= a\lambda f ( 1,\tau ) +a\mu f ( \tau,1 ) +b\lambda f ( \tau,1 ) +b\mu f ( 1,\tau ) +f ( \tau ,1 ) \\ &= ( a\mu+b\lambda+1 ) f ( \tau,1 ) + ( a\lambda +b\mu ) f ( 1,\tau ) \\ &= \mu f ( \tau,1 ) +\lambda f ( 1,\tau ). \end{aligned}$$

Similarly, we can show that \(x_{2}=\lambda f ( \tau,1 ) +\mu f ( 1,\tau ) \). Then, by induction, we conclude that

$$ x_{2n-1}=\mu f ( \tau,1 ) +\lambda f ( 1,\tau ) \quad\text{and}\quad x_{2n}=\lambda f ( \tau,1 ) +\mu f ( 1,\tau ) \quad\text{for all }n>0. $$

This completes the proof. □

Theorem 3.3

Assume that l is even and k is odd. Then equation (1.1) has a prime period two solution

$$ \ldots,p,q,p,q,\ldots $$

if and only if

$$ \bigl[ a- ( 1-b ) \tau \bigr] f ( \tau,1 ) = \bigl[ a\tau - ( 1-b ) \bigr] f ( 1,\tau ), $$
(3.3)

where \(\tau=p/q\).

Proof

The proof is similar to that of Theorem 3.2 and thus is omitted. □

Example 3.1

Consider equation (2.2) and assume that l is odd and k is even. By virtue of Theorem 3.2, equation (2.2) has a prime period two solution

$$ \ldots,p,q,p,q,\ldots $$

if and only if

$$ ( \tau-1 ) \bigl( b-\tau+a\tau+b\tau+b\tau^{2} \bigr) =0. $$

Since \(\tau\neq1\), we obtain

$$ \frac{1+\tau^{2}}{\tau}=\frac{1-a-b}{b}. $$

Letting

$$ H ( \tau ) =\frac{1+\tau^{2}}{\tau}>\min_{\tau\in \mathbf{\mathbb{R} }^{+}}H ( \tau ) =2 \quad\text{for }\tau\in\mathbf{\mathbb{R} }^{+}\backslash \{ 1 \}, $$

we get \(a+3b<1\). For a numerical example, we take \(l=1\), \(k=0\), \(a=0.3\), \(b=0.2\), \(c=1\), \(x_{-1}=3.3333\), and \(x_{0}=1.6667\); see Fig. 2.

Figure 2
figure 2

Prime period two solution of equation (2.2)

Full size image

Remark 3.4

Consider the equation

$$ x_{n+1}=ax_{n}+bx_{n-k}+\frac{px_{n}+x_{n-k}}{qx_{n}+x_{n-k}}, $$
(3.4)

which was studied by Zayed and El-Moneam [28]. Define the function

$$ f ( u,v ) =\frac{pu+v}{qu+v}. $$

Then f is homogeneous with degree zero and

$$ f_{u} ( u,v ) =\frac{ ( p-q ) v}{ ( qu+v ) ^{2}} \quad\text{and}\quad f_{v} ( u,v ) =\frac{ ( q-p ) u}{ ( qu+v ) ^{2}}. $$

From Theorem 2.1, the positive equilibrium point of equation (3.4) is

$$ \overline{x}=\frac{1}{1-a-b}\frac{p+1}{q+1}. $$

This point is asymptotically stable if \(p>q\) and

$$ \biggl\vert \frac{b}{1-a-b} ( p+1 ) -\frac{ p-q}{q+1} \biggr\vert < \frac{1-a}{1-a-b} ( p+1 ) -\frac{ p-q}{q+1}. $$

Since \(1-a-b>0\), we obtain the condition

$$ \frac{b}{1-a-b} ( p+1 ) >\frac{ p-q }{ q+1 }. $$

Also, if \(q>p\), then we have the condition

$$ \frac{a}{1-a-b} ( p+1 ) >\frac{ p-q }{ q+1 }. $$

(Results of Theorem 6 in [28]). From Theorem 3.1, if k is even, then equation (3.4) has no prime period two solutions. Furthermore, using Theorem 3.3, if k is odd, then equation (3.4) has a prime period two solution if and only if

$$ \bigl( a- ( 1-b ) \tau \bigr) ( p\tau+1 ) ( q+\tau ) = \bigl( a\tau- ( 1-b ) \bigr) ( p+\tau ) ( q\tau+1 ) $$

and so

$$ ( \tau-1 ) \bigl( ( p+aq-bp ) \bigl( 1+\tau ^{2} \bigr) + \bigl( ( p-1 ) ( q-1 ) ( a+1-b ) + ( 2p+2aq-2bp ) \bigr) \tau \bigr) =0. $$

Since \(\tau\neq1\), we have

$$ - \biggl( \frac{ ( p-1 ) ( q-1 ) ( a+1-b ) }{p+aq-bp }+2 \biggr) = \frac{1+\tau^{2}}{\tau} >\underset{\tau\in \mathbb{R} ^{+}}{ \min}\frac{1+\tau^{2}}{\tau}=2. $$

Thus,

$$ \frac{ ( 1-p ) ( q-1 ) ( a+1-b ) }{ p+aq-bp }>4. $$

We note that if \(p,q>1\) or \(p,q<1\), then equation (3.4) has no prime period two solutions.

Remark 3.5

Several equations that have been studied in [26, 27, 29] can be treated as special cases of (1.1).

4 Applications

Here, two test cases are given to validate the asymptotic behavior of the proposed new class of difference equations.

4.1 Application 1

Consider the difference equation

$$ x_{n+1}=ax_{n-l}+\sum_{i=0}^{\beta}c_{i} \biggl( \frac {x_{n-l}}{x_{n-k}} \biggr) ^{i}, $$
(4.1)

where \(\beta\geq2\) is a positive integer and \(c_{i}\) are positive real numbers for all \(i=0,1,\ldots,\beta\). Now, we define the functions

$$ \phi ( u,v ) =au+f ( u,v ) $$

and

$$ f ( u,v ) =\sum_{i=0}^{\beta}c_{i} \biggl( \frac {u}{v} \biggr) ^{i}, $$

where f is homogeneous with degree zero and

$$ f_{u} ( u,v ) =\sum_{i=1}^{\beta}ic_{i} \frac{u^{i-1}}{v^{i}}. $$

Note that \(f_{u}>0\). Then, by Theorem 2.1, the positive equilibrium point

$$ \overline{x}=\frac{1}{1-a}\sum_{i=0}^{\beta}c_{i} $$

of equation (4.1) is locally asymptotically stable if

$$ \sum_{i=1}^{\beta} ( 2i-1 ) c_{i}< c_{0}. $$

For a numerical example, we take \(l=0\), \(k=1\), \(\beta=3\), \(c_{0}=2\), \(c_{1}=0.2\), \(c_{2}=0.2\), \(c_{3}=0.1\), \(x_{-1}=5.5\), and \(x_{0}=4.5\); see Fig. 3.

Figure 3
figure 3

Stable solution of difference equation (4.1)

Full size image

Assume that l is odd and k is even. It follows from Theorem 3.2 that equation (4.1) has a prime period two solution \(\ldots,p,q,p,q,\ldots\) if and only if

$$ ( 1-a ) \sum_{i=0}^{\beta}c_{i} \tau^{i}= ( 1-a ) \tau \sum_{i=0}^{\beta}c_{i} \tau^{-i}. $$

If \(a\neq1\), then

$$ c_{0}=\sum_{i=1}^{\beta}c_{i} \frac{1-\tau^{2i-1}}{\tau^{i-1} ( 1-\tau ) }. $$

Now, we have

$$ H ( \tau ) = \frac{1-\tau^{2i-1}}{\tau^{i-1} ( 1-\tau ) } >2i-1 \quad\text{for }i\geq2 \text{ and }\tau\in\mathbf{\mathbb{R} }^{+}\backslash \{ 1 \}. $$

Then, we get \(\sum_{i=1}^{\beta} ( 2i-1 ) c_{i}< c_{0}\). For a numerical example, we take \(l=1\), \(k=0\), \(\beta=2\), \(a=0.1\), \(c_{0}=19/3\), \(c_{1}=2\), \(c_{2}=1\), \(x_{-1}=23.704\), and \(x_{0}=7.9012\); see Fig. 4.

Figure 4
figure 4

Prime period solution of equation (4.1)

Full size image

Conjecture 1

Note that, if \(\sum_{i=1}^{\beta} ( 2i-1 ) c_{i}< c_{0}\), then every solution of equation (4.1) converges either to the equilibrium point or to a periodic solution having period two.

4.2 Application 2

Consider the difference equation

$$ x_{n+1}=ax_{n-l}+bx_{n-k}+e^{-cx_{n-l}/x_{n-k}}, $$
(4.2)

where c is a real number. For \(c>0\), define the function

$$ f ( u,v ) =e^{-cu/v}, $$

which is homogeneous with degree zero and

$$\begin{aligned} &f_{u} ( u,v )= -\frac{c}{v}e^{-cu/v}< 0, \\ &f_{v} ( u,v )= \frac{cu}{v^{2}}e^{-cu/v}>0. \end{aligned}$$

By Theorem 2.1, the positive equilibrium point of equation (4.2)

$$ \overline{x}=\frac{e^{-c}}{1-a-b} $$

is locally asymptotically stable if

$$ \bigl\vert a- ( 1-a-b ) c \bigr\vert - \bigl( a- ( 1-a-b ) c \bigr) < 1-a-b. $$

Then

$$ a> ( 1-a-b ) c $$

or

$$ ( 1-a-b ) ( 2c-1 ) < 2a. $$

For a numerical example, we take \(l=0\), \(k=1\), \(a=0.8\), \(b=0.1\), \(c=1\), \(x_{-1}=5\), and \(x_{0}=5.9\); see Fig. 5. Taking into account that \(0< f ( u,v ) <1\), an application of Theorem 2.2 implies that every solution of equation (4.2) is bounded in this case.

Figure 5
figure 5

Stable solution of difference equation (4.2)

Full size image

Let l be odd and k be even. By Theorem 3.2, equation (4.2) has a prime period two solution \(\ldots,p,q,p,q,\ldots\) if and only if

$$ \bigl( ( 1-a ) -b\tau \bigr) e^{c ( 1/\tau-\tau ) }= ( 1-a ) \tau-b, $$

that is,

$$ c=\frac{\tau}{1-\tau^{2}} \ln\frac{ ( 1-a ) \tau-b}{ ( 1-a ) -b\tau}. $$

For a numerical example, we take \(l=1\), \(k=0\), \(a=0.2\), \(b=0.3\), \(c=-1.2479\), \(x_{-1}=18.663\), and \(x_{0}=9.3316\); see Fig. 6.

Figure 6
figure 6

Prime period solution of equation (4.2)

Full size image