A new two-level implicit scheme of order two in time and four in space based on half-step spline in compression approximations for unsteady 1D quasi-linear biharmonic equations

Abstract

In this article, we discuss a new two-level implicit scheme of order of accuracy two in time and four in space based on the spline in compression approximations for the numerical solution of 1D unsteady quasi-linear biharmonic equations. We use only two half-step points and a central point on a uniform mesh for spline approximations and derivation of the method. The proposed method is derived directly from the continuity condition of the first order derivative of the spline function. For model linear problem, the proposed scheme is shown to be unconditionally stable. The proposed method has successfully tested on the Kuramoto–Sivashinsky equation and extended the Fisher–Kolmogorov equation. From the computational experiment, we obtain better numerical results compared to the results obtained by other researchers.

1 Introduction

We consider the fourth order unsteady biharmonic equation with variable coefficient of the form

$$ A(x,t)u_{xxxx} + u_{t} = f(x,t,u,u_{x},u_{xx},u_{xxx}), \quad (x, t) \in \Omega, $$

(1.1)

where $\Omega \equiv \{ (x,t) \mid 0 < x < 1, t > 0 \}$ is the solution space.

The equation above may be written in a coupled manner as follows:

$$\begin{aligned}& u_{xx} = v,\quad (x,t) \in \Omega, \end{aligned}$$

(1.2)

$$\begin{aligned}& A(x,t)v_{xx} = - u_{t} + f(x,t,u,u_{x},v,v_{x}) \equiv g(x,t,u,v,u_{x},v_{x},u_{t}),\quad (x,t) \in \Omega. \end{aligned}$$

(1.3)

The initial and boundary values are given by

$$\begin{aligned}& u(x,0) = u_{0}(x), \quad 0 \le x \le 1, \end{aligned}$$

(1.4)

$$\begin{aligned}& u(0,t) = a_{0}(t), \quad\quad u(1,t) = a_{1}(t), \quad t > 0, \end{aligned}$$

(1.5)

$$\begin{aligned}& u_{xx}(0,t) = v(0,t) = b_{0}(t), \quad\quad u_{xx}(1,t) = v(1,t) = b_{1}(t),\quad t > 0, \end{aligned}$$

(1.6)

where $u_{0}$, $a_{0}$, $b_{0}$, $a_{1}$, and $b_{1}$ are smooth functions, and we assume that their required higher order derivatives exist in the solution region Ω.

Many physical problems in terms of linear or nonlinear biharmonic equations are of common occurrence in engineering and science. Famous nonlinear PDEs of type (1.1) are generalized Kuramoto–Sivashinsky (GKS) equation, extended Fisher–Kolmogorov (EFK) equation, etc. The physical appearance and behavior of these equations were discussed in [1–10]. During the last decade, several numerical methods have been discussed for the solution of GKS and EFK equations. Xu and Shu [11] proposed a local discontinuous Galerkin method for the Kuramoto–Sivashinsky (KS) equation. Khater and Temsah [12] used a Chebyshev spectral collocation method to solve the GKS equation. Lai and Ma [13] studied a lattice Boltzmann method, and Uddin et al. [14] discussed a mesh-free method for the numerical solution of GKS equation. Using a B-spline collocation method, Mittal and Arora [15] and Lakestani and Dehghan [16] solved the GKS equation. Using a cubic Hermite collocation method, Ganaiea et al. [17] obtained the numerical solution of KS equation. Most recently, Mohanty and Kaur [18] developed a Numerov type compact variable mesh method for the solution of KS equation. A polynomial scaling function technique was used by Rashidinia and Jokar [19] for solving the GKS equation. Danumjaya and Pani [20] constructed a numerical scheme based on an orthogonal cubic spline collocation method for the solution of EFK equation. Using a splitting technique, Doss and Nandini [21] proposed an $H^{1}$-Galerkin mixed finite element method for the solution of EFK equation.

It is quite challenging to obtain the numerical solution of 1D unsteady nonlinear biharmonic equations due to their highly complex mechanism of solitary wave interaction. Over the last few decades, there has been a good amount of research work carried out for the numerical solution of biharmonic equation. In 1984, Stephenson [22] derived single cell discretizations of order two and four for the solution of biharmonic problems of first and second kind. Using three uniform grid points, a two-level implicit method of order two in time and four in space for the solution of (1.1) was constructed by Mohanty [23]. Most recently, Mohanty and Kaur [18] proposed a class of two-level implicit finite difference methods on a variable grid. Spline techniques are widely used for second order parabolic and hyperbolic PDEs in the literature. Jain et al. [24] discussed a finite difference method based on the spline in compression technique for the numerical solution of conservations laws. Kadalbajoo and Patidar [25] proposed a variable mesh spline in compression method for singular perturbation problems. Using second order consistency condition, Mohanty et al. [26, 27] presented a spline in compression method for hyperbolic and parabolic PDEs. Recently, Mohanty and Sharma [28, 29] derived new algorithms based on spline in compression approximations for the system of quasi-linear parabolic PDEs. To the authors’ knowledge, no spline methods of order of accuracy two in time and four in space for the solution of nonlinear time-dependent biharmonic equation have been developed so far. In the present article, we propose a new two-level implicit numerical method of order of accuracy two in time and four in space, based on trigonometric spline approximations for the solution of PDE (1.1).

We use only two half-step points and one central point in x-direction at each time level, and no fictitious points are required for incorporating the boundary conditions. It is known that the difference methods for the biharmonic equation are based on five or more grid points in x-direction, and thus require fictitious points outside the solution region. These fictitious points are then eliminated by discretizing the given derivative boundary conditions. However, using the standard second order central differences for the boundary conditions, the accuracy of the overall numerical scheme is affected even if a higher order scheme is used at internal grid points. The algorithm presented in this paper reduces the fourth order PDE into coupled elliptic-parabolic equations, and we do not require to discretize the derivative boundary conditions. It attains order of accuracy two in time and four in space by using only three spatial grid points at each time level. The main attraction of this work is the application of the proposed high accuracy numerical method to the KS equation, GKS equation, and EFK equation.

The rest of this paper is organized as follows: In Sect. 2, we discuss the spline in compression function and its properties for the coupled equation. In Sect. 3, we present a new two-level implicit spline in compression method for 1D unsteady quasi-linear biharmonic problem of second kind, which is further derived in Sect. 4. In Sect. 5, the proposed spline in compression method is shown to be unconditionally stable for a linear biharmonic problem. In Sect. 6, we implement the proposed method on the KS equation, GKS equation, and EFK equation. We also compare our numerical results with the results of other researchers available in the literature. It is shown that the proposed numerical method yields better results as compared to the results given by other researchers. Concluding remarks are given in Sect. 7.

2 Spline in compression approximations and their properties

For the approximate solution of the proposed initial-boundary value problem, we discretize the space interval $[0,1]$ as $0 = x_{0} < x_{1} <\cdots < x_{L} < x_{L + 1} = 1$, where L is a positive integer. The proposed spline approximation consists of two half-step points $x_{l \pm 1/2}$ and a central point $x_{l}$, $l = 0,1,2,\ldots,L$ with two end points $x_{0}$ and $x_{L + 1}$. The neighboring half-step points are defined as $x_{l - 1/2} = x_{l} - \frac{h}{2}$ and $x_{l + 1/2} = x_{l} + \frac{h}{2}$, $l = 1(1)L$, where $h = x_{l + 1} - x_{l}$, $l = 0(1)L$ is the mesh size in x-direction and $k = t_{j + 1} - t_{j} > 0$, $j = 0,1,2,\ldots$ , is the mesh spacing in t-direction. Let $U_{l}^{j} = u(x_{l},t_{j})$ be the exact solution value of $u(x,t)$ approximated by $u_{l}^{j}$. Also let $V_{l}^{j} = v(x_{l},t_{j})$ be the exact solution value of $v(x,t)$ approximated by $v_{l}^{j}$. Now suppose $M = U_{xx}$ and $N = V_{xx}$.

A non-polynomial spline function which interpolates the value $U_{l}^{j}$ at jth time level is given by

$$\begin{aligned} P_{j}(x) ={}& a_{l}^{j} + b_{l}^{j}(x - x_{l}) + c_{l}^{j}\sin \bigl[\tau (x - x_{l})\bigr] + d_{l}^{j}\cos \bigl[\tau (x - x_{l})\bigr],\\ & x_{l - 1} \le x \le x_{l},l = 1(1)L + 1, j > 0, \end{aligned}$$

(2.1)

which satisfies the following properties at jth time level:

• (i) $P_{j}(x) \in C^{2}[0,1]$,

• (ii) $P_{j}(x_{l}) = U_{l}^{j}$, $P_{j}(x_{l - 1}) = U_{l - 1}^{j}$,

where τ is an arbitrary parameter and $P''_{j}(x_{l}) = M_{l}^{j}$, $P''_{j}(x_{l - 1}) = M_{l - 1}^{j}$, $P''_{j}(x_{l - 1/2}) = M_{l - 1/2}^{j}$.

Using these properties, we get the coefficients

$$\begin{aligned}& a_{l}^{j} = U_{l}^{j} + \frac{M_{l}^{j}}{\tau^{2}},\quad\quad b_{l}^{j} = \frac{U_{l}^{j} - U_{l - 1}^{j}}{h} + \frac{M_{l}^{j}}{\tau \mu} - \frac{M_{l - 1/2}^{j}}{\tau \mu} \cos \mu, \\& c_{l}^{j} = \frac{M_{l - 1/2}^{j} - M_{l}^{j}\cos \mu}{\tau^{2}\sin \mu}, \quad\quad d_{l}^{j} = \frac{ - M_{l}^{j}}{\tau^{2}}, \end{aligned}$$

where $\mu = (\tau h/2)$. Substituting the coefficients $a_{l}^{j}$, $b_{l}^{j}$, $c_{l}^{j}$, $d_{l}^{j}$ into Eq. (2.1), we obtain the spline in compression function $P_{j}(x)$ defined as

$$\begin{aligned}& \begin{aligned}[b] P_{j}(x) &= \biggl( U_{l}^{j} + \frac{M_{l}^{j}}{\tau^{2}} \biggr) + \biggl( \frac{U_{l}^{j} - U_{l - 1}^{j}}{h} + \frac{M_{l}^{j}}{\tau \mu} - \frac{M_{l - 1/2}^{j}}{\tau \mu} \cos \mu \biggr) ( x - x_{l} ) \\ &\quad{} + \biggl( \frac{M_{l - 1/2}^{j} - M_{l}^{j}\cos \mu}{\tau^{2}\sin \mu} \biggr)\sin \bigl[\tau (x - x_{l})\bigr] - \frac{M_{l}^{j}}{\tau^{2}}\cos \bigl[\tau (x - x_{l}) \bigr], \\ &\quad x \in [x_{l - 1},x_{l}], \end{aligned} \end{aligned}$$

(2.2)

$$\begin{aligned}& \begin{aligned}[b] P_{j}(x) &= \biggl( U_{l}^{j} + \frac{M_{l}^{j}}{\tau^{2}} \biggr) + \biggl( \frac{U_{l + 1}^{j} - U_{l}^{j}}{h} - \frac{M_{l}^{j}}{\tau \mu} + \frac{M_{l + 1/2}^{j}}{\tau \mu} \cos \mu \biggr) ( x - x_{l} ) \\ &\quad{} + \biggl( \frac{M_{l}^{j}\cos \mu - M_{l + 1/2}^{j}}{\tau^{2}\sin \mu} \biggr)\sin \bigl[\tau (x - x_{l})\bigr] - \frac{M_{l}^{j}}{\tau^{2}}\cos \bigl[\tau (x - x_{l}) \bigr], \\ &\quad x \in [x_{l},x_{l + 1}]. \end{aligned} \end{aligned}$$

(2.3)

Similarly, a non-polynomial spline function which interpolates the value $V_{l}^{j}$ at jth time level is given by

$$\begin{aligned}& \begin{aligned}[b] Q_{j}(x) &= \biggl( V_{l}^{j} + \frac{N_{l}^{j}}{\tau^{2}} \biggr) + \biggl( \frac{V_{l}^{j} - V_{l - 1}^{j}}{h} + \frac{N_{l}^{j}}{\tau \mu} - \frac{N_{l - 1/2}^{j}}{\tau \mu} \cos \mu \biggr) ( x - x_{l} ) \\ &\quad{} + \biggl( \frac{N_{l - 1/2}^{j} - N_{l}^{j}\cos \mu}{\tau^{2}\sin \mu} \biggr)\sin \bigl[\tau (x - x_{l})\bigr] - \frac{N_{l}^{j}}{\tau^{2}}\cos \bigl[\tau (x - x_{l})\bigr], \\&\quad x \in [x_{l - 1},x_{l}], \end{aligned} \end{aligned}$$

(2.4)

$$\begin{aligned}& \begin{aligned}[b] Q_{j}(x) &= \biggl( V_{l}^{j} + \frac{N_{l}^{j}}{\tau^{2}} \biggr) + \biggl( \frac{V_{l + 1}^{j} - V_{l}^{j}}{h} - \frac{N_{l}^{j}}{\tau \mu} + \frac{N_{l + 1/2}^{j}}{\tau \mu} \cos \mu \biggr) ( x - x_{l} ) \\ &\quad{} + \biggl( \frac{N_{l}^{j}\cos \mu - N_{l + 1/2}^{j}}{\tau^{2}\sin \mu} \biggr)\sin \bigl[\tau (x - x_{l})\bigr] - \frac{N_{l}^{j}}{\tau^{2}}\cos \bigl[\tau (x - x_{l})\bigr],\\&\quad x \in [x_{l},x_{l + 1}], \end{aligned} \end{aligned}$$

(2.5)

where $Q_{j}(x)$ satisfies the following properties at jth time level:

• (i) $Q_{j}(x) \in C^{2}[0,1]$,

• (ii) $Q_{j}(x_{l}) = V_{l}^{j}$, $Q_{j}(x_{l - 1}) = V_{l - 1}^{j}$, and $Q''_{j}(x_{l}) = N_{l}^{j}$, $Q''_{j}(x_{l - 1}) = N_{l - 1}^{j}$, $Q''_{j}(x_{l - 1/2}) = N_{l - 1/2}^{j}$.

Using the continuity of the first derivative of $P_{j}(x)$ and $Q_{j}(x)$, that is, $P'_{j}(x_{l} - ) = P'_{j}(x_{l} + )$ and $Q'_{j}(x_{l} - ) = Q'_{j}(x_{l} + )$, we obtain the following consistency conditions:

$$\begin{aligned}& \frac{U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j}}{h^{2}} = \alpha M_{l + 1/2}^{j} + 2\beta M_{l}^{j} + \alpha M_{l - 1/2}^{j} + O \bigl(h^{4}\bigr), \quad l = 1(1)L, \end{aligned}$$

(2.6)

$$\begin{aligned}& \frac{V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j}}{h^{2}} = \alpha N_{l + 1/2}^{j} + 2\beta N_{l}^{j} + \alpha N_{l - 1/2}^{j} + O \bigl(h^{4}\bigr), \quad l = 1(1)L, \end{aligned}$$

(2.7)

where

$$\begin{aligned}& \alpha = \frac{1}{2\mu^{2}} \biggl[ \frac{\mu}{\sin \mu} - \cos \mu \biggr] = \frac{1}{3} - \frac{\mu^{2}}{90} + O \bigl( \mu^{4} \bigr), \end{aligned}$$

(2.8)

$$\begin{aligned}& \beta = \frac{1}{2\mu^{2}} ( 1 - \mu \cot \mu ) = \frac{1}{6} + \frac{\mu^{2}}{90} + O \bigl( \mu^{4} \bigr). \end{aligned}$$

(2.9)

On equating the coefficients of $M_{l}^{j}$ and $N_{l}^{j}$ in (2.7)–(2.8), we obtain the condition

$$ \alpha + \beta = 1/2. $$

(2.10)

Substituting the values of α and β in (2.10) and neglecting $O(\mu^{4})$ terms, we get

$$ \tan (\mu /2) = \mu /2. $$

(2.11)

The above equation has an infinite number of roots, the smallest positive non-zero root being given by $\mu = 8.986818916$.

Further, from (2.2)–(2.5), we get

$$\begin{aligned}& P'_{j}(x_{l - 1/2}) = \frac{U_{l}^{j} - U_{l - 1}^{j}}{h} - \frac{h}{4} \bigl( 2\beta M_{l}^{j} - \alpha M_{l - 1/2}^{j} \bigr), \end{aligned}$$

(2.12)

$$\begin{aligned}& P'_{j}(x_{l + 1/2}) = \frac{U_{l + 1}^{j} - U_{l}^{j}}{h} + \frac{h}{4} \bigl( 2\beta M_{l}^{j} - \alpha M_{l + 1/2}^{j} \bigr), \end{aligned}$$

(2.13)

$$\begin{aligned}& Q'_{j}(x_{l - 1/2}) = \frac{V_{l}^{j} - V_{l - 1}^{j}}{h} - \frac{h}{4} \bigl( 2\beta N_{l}^{j} - \alpha N_{l - 1/2}^{j} \bigr), \end{aligned}$$

(2.14)

$$\begin{aligned}& Q'_{j}(x_{l + 1/2}) = \frac{V_{l + 1}^{j} - V_{l}^{j}}{h} + \frac{h}{4} \bigl( 2\beta N_{l}^{j} - \alpha N_{l + 1/2}^{j} \bigr). \end{aligned}$$

(2.15)

Relations (2.12)–(2.15) are important properties of spline functions.

3 Formulation of a spline in compression method

In order to derive the high accuracy numerical method based on a spline function and its properties for PDEs (1.2)–(1.3), we require the following three point approximations:

For $r = 0, \pm 1$, we denote

$$\begin{aligned}& \bar{t}_{j} = t_{j} + \theta k, \end{aligned}$$

(3.1)

$$\begin{aligned}& \bar{A}_{l}^{j} = A ( x_{l}, \bar{t}_{j} ), \end{aligned}$$

(3.2)

$$\begin{aligned}& \bar{A}_{xl}^{j} = A_{x} ( x_{l}, \bar{t}_{j} ), \end{aligned}$$

(3.3)

$$\begin{aligned}& \bar{A}_{xxl}^{j} = A_{xx} ( x_{l}, \bar{t}_{j} ), \end{aligned}$$

(3.4)

$$\begin{aligned}& \bar{U}_{l \pm r}^{j} = \theta U_{l \pm r}^{j + 1} + ( 1 - \theta )U_{l \pm r}^{j}, \end{aligned}$$

(3.5)

$$\begin{aligned}& \bar{U}_{l \pm 1/2}^{j} = \frac{1}{2} \bigl( \bar{U}_{l \pm 1}^{j} + \bar{U}_{l}^{j} \bigr), \end{aligned}$$

(3.6)

$$\begin{aligned}& \bar{V}_{l \pm r}^{j} = \theta V_{l \pm r}^{j + 1} + ( 1 - \theta )V_{l \pm r}^{j}, \end{aligned}$$

(3.7)

$$\begin{aligned}& \bar{V}_{l \pm 1/2}^{j} = \frac{1}{2} \bigl( \bar{V}_{l \pm 1}^{j} + \bar{V}_{l}^{j} \bigr), \end{aligned}$$

(3.8)

$$\begin{aligned}& \bar{U}_{tl \pm r}^{j} = \frac{1}{k} \bigl( U_{l \pm r}^{j + 1} - U_{l \pm r}^{j} \bigr), \end{aligned}$$

(3.9)

$$\begin{aligned}& \bar{U}_{tl \pm 1/2}^{j} = \frac{1}{2k} \bigl( U_{l \pm 1}^{j + 1} + U_{l}^{j + 1} - U_{l \pm 1}^{j} - U_{l}^{j} \bigr), \end{aligned}$$

(3.10)

$$\begin{aligned}& \bar{U}_{xl}^{j} = \frac{\bar{U}_{l + 1}^{j} - \bar{U}_{l - 1}^{j}}{2h}, \end{aligned}$$

(3.11)

$$\begin{aligned}& \bar{U}_{xl + 1/2}^{j} = \frac{\bar{U}_{l + 1}^{j} - \bar{U}_{l}^{j}}{h}, \end{aligned}$$

(3.12)

$$\begin{aligned}& \bar{U}_{xl - 1/2}^{j} = \frac{\bar{U}_{l}^{j} - \bar{U}_{l - 1}^{j}}{h}, \end{aligned}$$

(3.13)

$$\begin{aligned}& \bar{V}_{xl}^{j} = \frac{\bar{V}_{l + 1}^{j} - \bar{V}_{l - 1}^{j}}{2h}, \end{aligned}$$

(3.14)

$$\begin{aligned}& \bar{V}_{xl + 1/2}^{j} = \frac{\bar{V}_{l + 1}^{j} - \bar{V}_{l}^{j}}{h}, \end{aligned}$$

(3.15)

$$\begin{aligned}& \bar{V}_{xl - 1/2}^{j} = \frac{\bar{V}_{l}^{j} - \bar{V}_{l - 1}^{j}}{h}, \end{aligned}$$

(3.16)

$$\begin{aligned}& \bar{U}_{xxl}^{j} = \frac{\bar{U}_{l + 1}^{j} - 2\bar{U}_{l}^{j} + \bar{U}_{l - 1}^{j}}{h^{2}}, \end{aligned}$$

(3.17)

$$\begin{aligned}& \bar{V}_{xxl}^{j} = \frac{\bar{V}_{l + 1}^{j} - 2\bar{V}_{l}^{j} + \bar{V}_{l - 1}^{j}}{h^{2}}, \end{aligned}$$

(3.18)

where $\theta = \frac{1}{2}$.

Also define

$$\begin{aligned}& M_{l}^{j} = V_{l}^{j},\quad\quad M_{l \pm 1/2}^{j} = V_{l \pm 1/2}^{j}, \end{aligned}$$

and

$$N_{l}^{j} = \frac{1}{A_{l}^{j}} \bigl[ - U_{tl}^{j} + F_{l}^{j} \bigr],\quad\quad N_{l \pm 1/2}^{j} = \frac{1}{A_{l \pm 1/2}^{j}} \bigl[ - U_{tl \pm 1/2}^{j} + F_{l \pm 1/2}^{j} \bigr]. $$

Further, we define the following approximations:

$$\begin{aligned}& \bar{F}_{l}^{j} = f \bigl( x_{l}, \bar{t}_{j},\bar{U}_{l}^{j},\bar{V}_{l}^{j}, \bar{U}_{xl}^{j},\bar{V}_{xl}^{j} \bigr), \end{aligned}$$

(3.19)

$$\begin{aligned}& \bar{F}_{l + 1/2}^{j} = f \bigl( x_{l + 1/2}, \bar{t}_{j},\bar{U}_{l + 1/2}^{j},\bar{V}_{l + 1/2}^{j}, \bar{U}_{xl + 1/2}^{j},\bar{V}_{xl + 1/2}^{j} \bigr), \end{aligned}$$

(3.20)

$$\begin{aligned}& \bar{F}_{l - 1/2}^{j} = f \bigl( x_{l - 1/2}, \bar{t}_{j},\bar{U}_{l - 1/2}^{j},\bar{V}_{l - 1/2}^{j}, \bar{U}_{xl - 1/2}^{j},\bar{V}_{xl - 1/2}^{j} \bigr), \end{aligned}$$

(3.21)

$$\begin{aligned}& \bar{M}_{l}^{j} = \bar{V}_{l}^{j}, \end{aligned}$$

(3.22)

$$\begin{aligned}& \bar{M}_{l + 1/2}^{j} = \bar{V}_{l + 1/2}^{j}, \end{aligned}$$

(3.23)

$$\begin{aligned}& \bar{M}_{l - 1/2}^{j} = \bar{V}_{l - 1/2}^{j}, \end{aligned}$$

(3.24)

$$\begin{aligned}& \bar{N}_{l}^{j} = \frac{1}{\bar{A}_{l}^{j}} \bigl[ - \bar{U}_{tl}^{j} + \bar{F}_{l}^{j} \bigr], \end{aligned}$$

(3.25)

$$\begin{aligned}& \bar{N}_{l + 1/2}^{j} = \frac{1}{\bar{A}_{l + 1/2}^{j}} \bigl[ - \bar{U}_{tl + 1/2}^{j} + \bar{F}_{l + 1/2}^{j} \bigr], \end{aligned}$$

(3.26)

$$\begin{aligned}& \bar{N}_{l - 1/2}^{j} = \frac{1}{\bar{A}_{l - 1/2}^{j}} \bigl[ - \bar{U}_{tl - 1/2}^{j} + \bar{F}_{l - 1/2}^{j} \bigr]. \end{aligned}$$

(3.27)

From the properties of spline functions (2.12)–(2.15), we have the following approximations:

$$\begin{aligned}& \hat{U}_{xl - 1/2}^{j} = \frac{\bar{U}_{l}^{j} - \bar{U}_{l - 1}^{j}}{h} - \frac{h}{4} \bigl( 2\beta \bar{M}_{l}^{j} - \alpha \bar{M}_{l - 1/2}^{j} \bigr), \end{aligned}$$

(3.28)

$$\begin{aligned}& \hat{U}_{xl + 1/2}^{j} = \frac{\bar{U}_{l + 1}^{j} - \bar{U}_{l}^{j}}{h} + \frac{h}{4} \bigl( 2\beta \bar{M}_{l}^{j} - \alpha \bar{M}_{l + 1/2}^{j} \bigr), \end{aligned}$$

(3.29)

$$\begin{aligned}& \hat{V}_{xl - 1/2}^{j} = \frac{\bar{V}_{l}^{j} - \bar{V}_{l - 1}^{j}}{h} - \frac{h}{4} \bigl( 2\beta \bar{N}_{l}^{j} - \alpha \bar{N}_{l - 1/2}^{j} \bigr), \end{aligned}$$

(3.30)

$$\begin{aligned}& \hat{V}_{xl + 1/2}^{j} = \frac{\bar{V}_{l + 1}^{j} - \bar{V}_{l}^{j}}{h} + \frac{h}{4} \bigl( 2\beta \bar{N}_{l}^{j} - \alpha \bar{N}_{l + 1/2}^{j} \bigr). \end{aligned}$$

(3.31)

We consider the following linear combinations in order to increase the accuracy of the scheme:

$$\begin{aligned}& \hat{U}_{l}^{j} = \bar{U}_{l}^{j} + ah^{2}\bar{U}_{xxl}^{j}, \end{aligned}$$

(3.32)

$$\begin{aligned}& \hat{V}_{l}^{j} = \bar{V}_{l}^{j} + bh^{2}\bar{V}_{xxl}^{j}, \end{aligned}$$

(3.33)

$$\begin{aligned}& \hat{U}_{xl}^{j} = \bar{U}_{xl}^{j} + ch \bigl( \bar{M}_{l + 1/2}^{j} - \bar{M}_{l - 1/2}^{j} \bigr), \end{aligned}$$

(3.34)

$$\begin{aligned}& \hat{V}_{xl}^{j} = \bar{V}_{xl}^{j} + dh \bigl( \bar{N}_{l + 1/2}^{j} - \bar{N}_{l - 1/2}^{j} \bigr), \end{aligned}$$

(3.35)

where $a = b = \frac{ - 1}{4}$ and $c = d = \frac{ - 1}{6}$.

Further, we define

$$\begin{aligned}& \hat{F}_{l}^{j} = f \bigl( x_{l}, \bar{t}_{j},\hat{U}_{l}^{j},\hat{V}_{l}^{j}, \hat{U}_{xl}^{j},\hat{V}_{xl}^{j} \bigr), \end{aligned}$$

(3.36)

$$\begin{aligned}& \hat{F}_{l + 1/2}^{j} = f \bigl( x_{l + 1/2}, \bar{t}_{j},\bar{U}_{l + 1/2}^{j},\bar{V}_{l + 1/2}^{j}, \hat{U}_{xl + 1/2}^{j},\hat{V}_{xl + 1/2}^{j} \bigr), \end{aligned}$$

(3.37)

$$\begin{aligned}& \hat{F}_{l - 1/2}^{j} = f \bigl( x_{l - 1/2}, \bar{t}_{j},\bar{U}_{l - 1/2}^{j},\bar{V}_{l - 1/2}^{j}, \hat{U}_{xl - 1/2}^{j},\hat{V}_{xl - 1/2}^{j} \bigr). \end{aligned}$$

(3.38)

Then, at each grid point $( x_{l},t_{j} )$, the spline in compression method for the system of differential equations (1.2)–(1.3) is given by

$$\begin{aligned}& \bar{U}_{l + 1}^{j} - 2\bar{U}_{l}^{j} + \bar{U}_{l - 1}^{j} = \frac{h^{2}}{3} \bigl( \bar{V}_{l + 1/2}^{j} + \hat{V}_{l}^{j} + \bar{V}_{l - 1/2}^{j} \bigr) + \hat{T}_{1l}^{j}, \end{aligned}$$

(3.39)

$$\begin{aligned}& \begin{aligned}[b] & \biggl[ \bar{A}_{l}^{j} + \frac{h^{2}}{12} \biggl( \bar{A}_{xxl}^{j} - \frac{2 ( \bar{A}_{xl}^{j} )^{2}}{\bar{A}_{l}^{j}} \biggr) \biggr] \bigl[ \bar{V}_{l + 1}^{j} - 2 \bar{V}_{l}^{j} + \bar{V}_{l - 1}^{j} \bigr] \\ &\quad\quad{} + \frac{h^{2}}{12} \biggl[ 10\bar{U}_{tl}^{j} + \biggl( 1 - \frac{h\bar{A}_{xl}^{j}}{\bar{A}_{l}^{j}} \biggr)\bar{U}_{tl + 1}^{j} + \biggl( 1 + \frac{h\bar{A}_{xl}^{j}}{\bar{A}_{l}^{j}} \biggr)\bar{U}_{tl - 1}^{j} \biggr] \\ &\quad = \frac{h^{2}}{3} \biggl[ \biggl( 1 - \frac{h\bar{A}_{xl}^{j}}{2\bar{A}_{l}^{j}} \biggr) \hat{F}_{l + 1/2}^{j} + \biggl( 1 + \frac{h\bar{A}_{xl}^{j}}{2\bar{A}_{l}^{j}} \biggr) \hat{F}_{l - 1/2}^{j} + \hat{F}_{l}^{j} \biggr] + \hat{T}_{2l}^{j}, \end{aligned} \end{aligned}$$

(3.40)

where truncation errors $\hat{T}_{1l}^{j} = O ( k^{2}h^{2} + h^{6} )$ and $\hat{T}_{2l}^{j} = O ( k^{2}h^{2} + kh^{4} + h^{6} )$.

4 Derivation of the numerical algorithm

In this section, we derive the spline method from the consistency conditions given by (2.6)–(2.7).

Substituting the values

$$\begin{aligned}& M_{l}^{j} = V_{l}^{j},\qquad M_{l \pm \frac{1}{2}}^{j} = V_{l \pm \frac{1}{2}}^{j},\qquad N_{l}^{j} = \frac{1}{A_{l}^{j}} \bigl[ - U_{tl}^{j} + F_{l}^{j} \bigr], \\& N_{l \pm 1/2}^{j} = \frac{1}{A_{l \pm 1/2}^{j}} \bigl[ - U_{tl \pm 1/2}^{j} + F_{l \pm 1/2}^{j} \bigr] \quad \text{into (2.6)--(2.7)}, \end{aligned}$$

we get

$$\begin{aligned}& U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} = \frac{h^{2}}{3} \bigl( V_{l + 1/2}^{j} + V_{l}^{j} + V_{l - 1/2}^{j} \bigr) + O \bigl( h^{6} \bigr), \end{aligned}$$

(4.1)

$$\begin{aligned}& \begin{aligned}[b] V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j} ={}& \frac{h^{2}}{3}\biggl[ \frac{1}{A_{l + 1/2}^{j}} \bigl( - U_{tl + 1/2}^{j} + F_{l + 1/2}^{j} \bigr) + \frac{1}{A_{l - 1/2}^{j}} \bigl( - U_{tl - 1/2}^{j} + F_{l - 1/2}^{j} \bigr) \\ &{}+ \frac{1}{A_{l}^{j}} \bigl( - U_{tl}^{j} + F_{l}^{j} \bigr)\biggr] + O \bigl( h^{6} \bigr). \end{aligned} \end{aligned}$$

(4.2)

At the mesh point $(x_{l},t_{j})$, let us denote

$$\begin{aligned}& \frac{\partial^{p + q}U_{l}^{j}}{\partial x^{p}\partial t^{q}} = U_{pq},\qquad \frac{\partial^{p + q}V_{l}^{j}}{\partial x^{p}\partial t^{q}} = V_{pq},\qquad \frac{\partial^{p + q}A_{l}^{j}}{\partial x^{p}\partial t^{q}} = A_{pq},\quad \mbox{and} \\& \alpha_{l}^{(1)j} = \biggl( \frac{\partial f}{\partial U} \biggr)_{l}^{j},\quad\quad \alpha_{l}^{(2)j} = \biggl( \frac{\partial f}{\partial V} \biggr)_{l}^{j},\quad\quad \beta_{l}^{(1)j} = \biggl( \frac{\partial f}{\partial U_{x}} \biggr)_{l}^{j},\quad\quad \beta_{l}^{(2)j} = \biggl( \frac{\partial f}{\partial V_{x}} \biggr)_{l}^{j}, \\& \xi_{l}^{j} = \biggl( \frac{\partial f}{\partial t} \biggr)_{l}^{j}. \end{aligned}$$

To simplify (4.2), we need the following approximations:

$$\begin{aligned}& \frac{1}{A_{l \pm 1/2}^{j}} = \frac{1}{A_{00}} \biggl[ 1 \mp \frac{hA_{10}}{2A_{00}} - \frac{h^{2}}{8A_{00}} \biggl\{ A_{20} - 2\frac{ ( A_{10} )^{2}}{A_{00}} \biggr\} \pm O \bigl( h^{3} \bigr) \biggr], \end{aligned}$$

(4.3)

$$\begin{aligned}& U_{tl \pm 1/2}^{j} = U_{tl}^{j} \pm \frac{h}{2}U_{11} + \frac{h^{2}}{8}U_{21} \pm O \bigl( h^{3} \bigr), \end{aligned}$$

(4.4)

$$\begin{aligned}& 2hU_{11} = \bigl( U_{tl + 1}^{j} - U_{tl - 1}^{j} \bigr) + O \bigl( h^{3} \bigr), \end{aligned}$$

(4.5)

$$\begin{aligned}& h^{2}U_{21} = \bigl( U_{tl + 1}^{j} - 2U_{tl}^{j} + U_{tl - 1}^{j} \bigr) + O \bigl( h^{4} \bigr), \end{aligned}$$

(4.6)

$$\begin{aligned}& F_{l + 1/2}^{j} + F_{l - 1/2}^{j} = 2F_{l}^{j} + O \bigl( h^{2} \bigr) = 2 ( A_{00}V_{20} + U_{01} ) + O \bigl( h^{2} \bigr), \end{aligned}$$

(4.7)

$$\begin{aligned}& h^{2}V_{20} = V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j} + O \bigl( h^{4} \bigr). \end{aligned}$$

(4.8)

With the help of (4.3)–(4.8), the consistency conditions (4.1)–(4.2) may be re-written as follows:

$$\begin{aligned}& U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} = \frac{h^{2}}{3} \bigl( V_{l + 1/2}^{j} + V_{l}^{j} + V_{l - 1/2}^{j} \bigr) + O \bigl( h^{6} \bigr), \end{aligned}$$

(4.9)

$$\begin{aligned}& \biggl[ A_{00} + \frac{h^{2}}{12} \biggl( A_{20} - \frac{2 ( A_{10} )^{2}}{A_{00}} \biggr) \biggr] \bigl[ V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j} \bigr] \\ & \quad\quad{} + \frac{h^{2}}{12} \biggl[ 10U_{tl}^{j} + \biggl( 1 - \frac{hA_{10}}{A_{00}} \biggr)U_{tl + 1}^{j} + \biggl( 1 + \frac{hA_{10}}{A_{00}} \biggr)U_{tl - 1}^{j} \biggr] \\ & \quad = \frac{h^{2}}{3} \biggl[ \biggl( 1 - \frac{hA_{10}}{2A_{00}} \biggr)F_{l + 1/2}^{j} + \biggl( 1 + \frac{hA_{10}}{2A_{00}} \biggr)F_{l - 1/2}^{j} + F_{l}^{j} \biggr] + O \bigl( h^{6} \bigr). \end{aligned}$$

(4.10)

Simplifying approximations (3.5)–(3.18) using a Taylor series expansion, we obtain

$$\begin{aligned}& \bar{U}_{l}^{j} = U_{l}^{j} + \theta kU_{01} + O \bigl( k^{2} \bigr), \end{aligned}$$

(4.11)

$$\begin{aligned}& \bar{U}_{l \pm 1}^{j} = U_{l \pm 1}^{j} + \theta k ( U_{01} \pm hU_{11} ) + O \bigl( k^{2} \bigr), \end{aligned}$$

(4.12)

$$\begin{aligned}& \bar{U}_{l \pm 1/2}^{j} = U_{l \pm 1/2}^{j} + \theta kU_{01} + \frac{h^{2}}{8}U_{20} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.13)

$$\begin{aligned}& \bar{V}_{l}^{j} = V_{l}^{j} + \theta kV_{01} + O \bigl( k^{2} \bigr), \end{aligned}$$

(4.14)

$$\begin{aligned}& \bar{V}_{l \pm 1}^{j} = V_{l \pm 1}^{j} + \theta k ( V_{01} \pm hV_{11} ) + O \bigl( k^{2} \bigr), \end{aligned}$$

(4.15)

$$\begin{aligned}& \bar{V}_{l \pm 1/2}^{j} = V_{l \pm 1/2}^{j} + \theta kV_{01} + \frac{h^{2}}{8}V_{20} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.16)

$$\begin{aligned}& \bar{U}_{tl}^{j} = U_{01} + \frac{k}{2}U_{02} + O \bigl( k^{2} \bigr), \end{aligned}$$

(4.17)

$$\begin{aligned}& \bar{U}_{tl \pm 1}^{j} = U_{tl \pm 1}^{j} + \frac{k}{2}U_{02} + O \bigl( kh + k^{2} \bigr), \end{aligned}$$

(4.18)

$$\begin{aligned}& \bar{U}_{tl \pm 1/2}^{j} = U_{tl \pm 1/2}^{j} + \frac{k}{2}U_{02} + \frac{h^{2}}{8}U_{21} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.19)

$$\begin{aligned}& \bar{U}_{xl}^{j} = U_{10} + \frac{h^{2}}{6}U_{30} + \theta kU_{11} + O \bigl( k^{2} + h^{4} \bigr), \end{aligned}$$

(4.20)

$$\begin{aligned}& \bar{U}_{xl \pm 1/2}^{j} = U_{xl \pm 1/2}^{j} + \frac{h^{2}}{24}U_{30} + \theta kU_{11} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.21)

$$\begin{aligned}& \bar{V}_{xl}^{j} = V_{10} + \frac{h^{2}}{6}V_{30} + \theta kV_{11} + O \bigl( k^{2} + h^{4} \bigr), \end{aligned}$$

(4.22)

$$\begin{aligned}& \bar{V}_{xl \pm 1/2}^{j} = V_{xl \pm 1/2}^{j} + \frac{h^{2}}{24}V_{30} + \theta kV_{11} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.23)

$$\begin{aligned}& \bar{U}_{l + 1}^{j} - 2\bar{U}_{l}^{j} + \bar{U}_{l - 1}^{j} = \bigl( U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} \bigr) + \theta kU_{21} + O\bigl(k^{2}h^{2} + kh^{4} \bigr), \end{aligned}$$

(4.24)

$$\begin{aligned}& \bar{V}_{l + 1}^{j} - 2\bar{V}_{l}^{j} + \bar{V}_{l - 1}^{j} = \bigl( V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j} \bigr) + \theta kV_{21} + O\bigl(k^{2}h^{2} + kh^{4} \bigr), \end{aligned}$$

(4.25)

$$\begin{aligned}& \bar{U}_{xxl}^{j} = U_{xxl}^{j} + \theta kU_{21} + \frac{h^{2}}{12}U_{40} + O\bigl(k^{2} + kh^{2} + h^{4}\bigr), \end{aligned}$$

(4.26)

$$\begin{aligned}& \bar{V}_{xxl}^{j} = V_{xxl}^{j} + \theta kV_{21} + \frac{h^{2}}{12}V_{40} + O\bigl(k^{2} + kh^{2} + h^{4}\bigr). \end{aligned}$$

(4.27)

With the help of (4.11)–(4.23), from (3.19)–(3.21), we obtain

$$\begin{aligned}& \begin{aligned}[b] \bar{F}_{l}^{j} &= F_{l}^{j} + \theta k \bigl[ \xi_{l}^{j} + U_{01} \alpha_{l}^{(1)j} + V_{01}\alpha_{l}^{(2)j} + U_{11}\beta_{l}^{(1)j} + V_{11} \beta_{l}^{(2)j} \bigr] \\ &\quad{} + \frac{h^{2}}{6} \bigl[ U_{30}\beta_{l}^{(1)j} + V_{30}\beta_{l}^{(2)j} \bigr] + O \bigl( k^{2} + h^{4} \bigr), \end{aligned} \end{aligned}$$

(4.28)

$$\begin{aligned}& \begin{aligned}[b] \bar{F}_{l \pm 1/2}^{j} &= F_{l \pm 1/2}^{j} + \theta k \bigl[ \xi_{l}^{j} + U_{01} \alpha_{l}^{(1)j} + V_{01}\alpha_{l}^{(2)j} + U_{11}\beta_{l}^{(1)j} + V_{11} \beta_{l}^{(2)j} \bigr] \\ &\quad{} + \frac{h^{2}}{24} \bigl[ 3U_{20}\alpha_{l}^{(1)j} + 3V_{20}\alpha_{l}^{(2)j} + U_{30} \beta_{l}^{(1)j} + V_{30}\beta_{l}^{(2)j} \bigr] \\ &\quad{} + O \bigl( \pm kh \pm h^{3} + k^{2} + kh^{2} + h^{4} \bigr). \end{aligned} \end{aligned}$$

(4.29)

Further, we can write

$$\begin{aligned}& \frac{1}{\bar{A}_{l}^{j}} = \frac{1}{A ( x_{l},\bar{t}_{j} )} = \frac{1}{A ( x_{l},t_{j} + \theta k )} = \frac{1}{A_{l}^{j}} \biggl[ 1 - \theta k\frac{A_{tl}^{j}}{A_{l}^{j}} + O \bigl( k^{2} \bigr) \biggr], \end{aligned}$$

(4.30)

$$\begin{aligned}& \frac{1}{\bar{A}_{l \pm 1/2}^{j}} = \frac{1}{A_{l \pm 1/2}^{j}} \biggl[ 1 - \theta k\frac{A_{tl \pm 1/2}^{j}}{A_{l \pm 1/2}^{j}} + O \bigl( k^{2} \bigr) \biggr]. \end{aligned}$$

(4.31)

Using (4.28)–(4.31) and simplifying (3.22)–(3.27), we obtain

$$\begin{aligned}& \overline{M}_{l}^{j} = U_{xxl}^{j} + O \bigl( k + h^{2} \bigr), \end{aligned}$$

(4.32)

$$\begin{aligned}& \overline{M}_{l \pm 1/2}^{j} = U_{xxl \pm 1/2}^{j} + O \bigl( k + h^{2} \bigr), \end{aligned}$$

(4.33)

$$\begin{aligned}& \bar{N}_{l}^{j} = V_{xxl}^{j} + O \bigl( k + h^{2} \bigr), \end{aligned}$$

(4.34)

$$\begin{aligned}& \bar{N}_{l \pm 1/2}^{j} = V_{xxl \pm 1/2}^{j} + O \bigl( k + h^{2} \bigr). \end{aligned}$$

(4.35)

Using (4.32)–(4.35) in (3.28)–(3.31), we obtain

$$\begin{aligned}& \hat{U}_{xl \pm 1/2}^{j} = U_{xl \pm 1/2}^{j} + \theta kU_{11} + O \bigl( \pm kh \pm h^{3} + k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.36)

$$\begin{aligned}& \hat{V}_{xl \pm 1/2}^{j} = V_{xl \pm 1/2}^{j} + \theta kV_{11} + O \bigl( \pm kh \pm h^{3} + k^{2} + kh^{2} + h^{4} \bigr). \end{aligned}$$

(4.37)

Simplifying (3.37)–(3.38), we obtain

$$\begin{aligned} \hat{F}_{l \pm 1/2}^{j} &= F_{l \pm 1/2}^{j} + \theta k \bigl[ \xi_{l}^{j} + U_{01} \alpha_{l}^{(1)j} + V_{01}\alpha_{l}^{(2)j} + U_{11}\beta_{l}^{(1)j} + V_{11} \beta_{l}^{(2)j} \bigr] \\ &\quad{} + \frac{h^{2}}{8} \bigl[ U_{20}\alpha_{l}^{(1)j} + V_{20}\alpha_{l}^{(2)j} \bigr] + O \bigl( \pm kh \pm h^{3} + k^{2} + kh^{2} + h^{4} \bigr). \end{aligned}$$

(4.38)

Now, using the above approximations and simplifying (3.32)–(3.35), we obtain

$$\begin{aligned}& \hat{U}_{l}^{j} = U_{l}^{j} + \theta kU_{01} + ah^{2}U_{20} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.39)

$$\begin{aligned}& \hat{V}_{l}^{j} = V_{l}^{j} + \theta kV_{01} + bh^{2}V_{20} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.40)

$$\begin{aligned}& \hat{U}_{xl}^{j} = U_{xl}^{j} + \theta kU_{11} + \frac{h^{2}}{6} [ 1 + 6c ]U_{30} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.41)

$$\begin{aligned}& \hat{V}_{xl}^{j} = V_{xl}^{j} + \theta kV_{11} + \frac{h^{2}}{6} [ 1 + 6d ]V_{30} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr). \end{aligned}$$

(4.42)

Equating the coefficient of $h^{2}$ to zero in Eqs. (4.41) and (4.42), we obtain $c = d = \frac{ - 1}{6}$, and Eqs. (4.41) and (4.42) reduce to

$$\begin{aligned}& \hat{U}_{xl}^{j} = U_{xl}^{j} + \theta kU_{11} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr), \end{aligned}$$

(4.43)

$$\begin{aligned}& \hat{V}_{xl}^{j} = V_{xl}^{j} + \theta kV_{11} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr). \end{aligned}$$

(4.44)

With the help of (4.39)–(4.44), from (3.36), we obtain

$$\begin{aligned} \hat{F}_{l}^{j} &= F_{l}^{j} + \theta k \bigl[ \xi_{l}^{j} + U_{01} \alpha_{l}^{(1)j} + V_{01}\alpha_{l}^{(2)j} + U_{11}\beta_{l}^{(1)j} + V_{11} \beta_{l}^{(2)j} \bigr] \\ &\quad{} + h^{2} \bigl[ aU_{20}\beta_{l}^{(1)j} + bV_{20}\beta_{l}^{(2)j} \bigr] + O \bigl( k^{2} + kh^{2} + h^{4} \bigr). \end{aligned}$$

(4.45)

At the grid point $(x_{l},t_{j})$, differentiating (1.2)–(1.3) with respect to ‘t’, we obtain a relation

$$\begin{aligned}& U_{21} = V_{01}, \end{aligned}$$

(4.46)

$$\begin{aligned}& A_{00}V_{21} + A_{01}V_{20} = - U_{02} + \xi_{l}^{j} + U_{01} \alpha_{l}^{(1)j} + V_{01}\alpha_{l}^{(2)j} + U_{11}\beta_{l}^{(1)j} + V_{11} \beta_{l}^{(2)j}. \end{aligned}$$

(4.47)

Using (4.46)–(4.47), we may re-write (4.38) and (4.45) as

$$\begin{aligned}& \begin{aligned}[b] \hat{F}_{l \pm 1/2}^{j} &= F_{l \pm 1/2}^{j} + \theta k [ A_{00}V_{21} + A_{01}V_{20} + U_{02} ] + \frac{h^{2}}{8} \bigl[ U_{20} \alpha_{l}^{(1)j} + V_{20}\alpha_{l}^{(2)j} \bigr], \\ &\quad{} +O \bigl( \pm kh \pm h^{3} + k^{2} + kh^{2} + h^{4} \bigr), \end{aligned} \end{aligned}$$

(4.48)

$$\begin{aligned}& \begin{aligned}[b] \hat{F}_{l}^{j} &= F_{l}^{j} + \theta k [ A_{00}V_{21} + A_{01}V_{20} + U_{02} ] + \frac{h^{2}}{8} \bigl[ aU_{20} \alpha_{l}^{(1)j} + bV_{20}\alpha_{l}^{(2)j} \bigr] \\ &\quad{} + O\bigl(k^{2} + kh^{2} + h^{4}\bigr). \end{aligned} \end{aligned}$$

(4.49)

It is easy to verify that

$$\begin{aligned}& \bar{A}_{l}^{j} = A_{00} + \theta kA_{01} + O \bigl( k^{2} \bigr), \end{aligned}$$

(4.50)

$$\begin{aligned}& \bar{A}_{xl}^{j} = A_{10} + \theta kA_{11} + O \bigl( k^{2} \bigr), \end{aligned}$$

(4.51)

$$\begin{aligned}& \bar{A}_{xxl}^{j} = A_{20} + \theta kA_{21} + O \bigl( k^{2} \bigr). \end{aligned}$$

(4.52)

$$\begin{aligned}& \bar{U}_{l + 1}^{j} - 2\bar{U}_{l}^{j} + \bar{U}_{l - 1}^{j}= U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} + \theta kh^{2}U_{21} + O \bigl( k^{2}h^{2} + kh^{4} \bigr), \end{aligned}$$

(4.53)

$$\begin{aligned}& \bar{V}_{l + 1}^{j} - 2\bar{V}_{l}^{j} + \bar{V}_{l - 1}^{j}= V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j} + \theta kh^{2}V_{21} + O \bigl( k^{2}h^{2} + kh^{4} \bigr), \end{aligned}$$

(4.54)

$$\begin{aligned}& \biggl[ \bar{A}_{l}^{j} + \frac{h^{2}}{12} \biggl( \bar{A}_{xxl}^{j} - \frac{2 ( \bar{A}_{xl}^{j} )^{2}}{\bar{A}_{l}^{j}} \biggr) \biggr] \bigl[ \bar{V}_{l + 1}^{j} - 2\bar{V}_{l}^{j} + \bar{V}_{l - 1}^{j} \bigr] \\& \quad = \biggl[ A_{l}^{j} + \frac{h^{2}}{12} \biggl( A_{xxl}^{j} - \frac{2 ( A_{xl}^{j} )^{2}}{A_{l}^{j}} \biggr) \biggr] \bigl[ V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j} \bigr] + \theta kh^{2} [ A_{00}V_{21} + A_{01}V_{20} ] \\& \quad\quad{} + O \bigl( k^{2}h^{2} + kh^{4} + h^{6} \bigr), \end{aligned}$$

(4.55)

$$\begin{aligned}& \biggl( 1 - \frac{h\bar{A}_{xl}^{j}}{\bar{A}_{l}^{j}} \biggr)\bar{U}_{tl + 1}^{j} = \biggl( 1 - \frac{hA_{10}}{A_{00}} \biggr)U_{tl + 1}^{j} + \frac{k}{2}U_{20} + O \bigl( kh + k^{2} + kh^{2} \bigr), \end{aligned}$$

(4.56)

$$\begin{aligned}& \biggl( 1 + \frac{h\bar{A}_{xl}^{j}}{\bar{A}_{l}^{j}} \biggr)\bar{U}_{tl - 1}^{j} = \biggl( 1 + \frac{hA_{10}}{A_{00}} \biggr)U_{tl - 1}^{j} + \frac{k}{2}U_{20} + O \bigl( - kh + k^{2} + kh^{2} \bigr), \end{aligned}$$

(4.57)

$$\begin{aligned}& 10\bar{U}_{tl}^{j} + \biggl( 1 - \frac{h\bar{A}_{xl}^{j}}{\bar{A}_{l}^{j}} \biggr)\bar{U}_{tl + 1}^{j} + \biggl( 1 + \frac{h\bar{A}_{xl}^{j}}{\bar{A}_{l}^{j}} \biggr)\bar{U}_{tl - 1}^{j} \\& \quad = 10U_{tl}^{j} + \biggl( 1 - \frac{hA_{xl}^{j}}{A_{l}^{j}} \biggr)U_{tl + 1}^{j} + \biggl( 1 + \frac{hA_{xl}^{j}}{A_{l}^{j}} \biggr)U_{tl - 1}^{j} + 6kU_{02} \\& \quad\quad{} + O \bigl( k^{2} + kh^{2} + h^{4} \bigr). \end{aligned}$$

(4.58)

With the help of approximations (4.48)–(4.58), from (3.39)–(3.40), we obtain

$$\begin{aligned}& \bigl( U_{l + 1}^{j} - 2U_{l}^{j} + U_{l - 1}^{j} \bigr) = \frac{h^{2}}{3} \biggl[ V_{l + 1/2}^{j} + V_{l}^{j} + V_{l - 1/2}^{j} + h^{2} \biggl( \frac{1}{4} + b \biggr)V_{20} \biggr] + \hat{T}_{1l}^{j}, \end{aligned}$$

(4.59)

$$\begin{aligned}& \biggl[ A_{00} + \frac{h^{2}}{12} \biggl( A_{20} - \frac{2 ( A_{10} )^{2}}{A_{00}} \biggr) \biggr] \bigl[ V_{l + 1}^{j} - 2V_{l}^{j} + V_{l - 1}^{j} \bigr] \\& \quad\quad{} + \frac{h^{2}}{12} \biggl[ 10U_{tl}^{j} + \biggl( 1 - \frac{hA_{10}}{A_{00}} \biggr)U_{tl + 1}^{j} + \biggl( 1 + \frac{hA_{10}}{A_{00}} \biggr)U_{tl - 1}^{j} + 6kU_{02} \biggr] \\& \quad = \frac{h^{2}}{3}\biggl[ \biggl( 1 - \frac{hA_{10}}{2A_{00}} \biggr)F_{l + 1/2}^{j} + \biggl( 1 + \frac{hA_{10}}{2A_{00}} \biggr)F_{l - 1/2}^{j} + F_{l}^{j} + h^{2} \biggl( a + \frac{1}{4} \biggr)U_{20} \alpha_{l}^{(1)j} \\& \quad\quad{} + h^{2} \biggl( b + \frac{1}{4} \biggr)V_{20}\alpha_{l}^{(2)j} \biggr] + \hat{T}_{2l}^{j}. \end{aligned}$$

(4.60)

Comparing (4.59)–(4.60) with the consistency conditions (4.9)–(4.10), we obtain

$$\begin{aligned}& \hat{T}_{1l}^{j} = \frac{ - h^{4}}{3} \biggl( b + \frac{1}{4} \biggr)V_{20} + O \bigl( k^{2}h^{2} + kh^{4} + h^{6} \bigr), \end{aligned}$$

(4.61)

$$\begin{aligned}& \begin{aligned}[b] \hat{T}_{2l}^{j} &= kh^{2} \biggl( \frac{1}{2} - \theta \biggr)U_{02} - \frac{h^{4}}{3} \biggl[ \biggl( a + \frac{1}{4} \biggr)U_{20} \alpha_{l}^{(1)j} + \biggl( b + \frac{1}{4} \biggr)V_{20}\alpha_{l}^{(2)j} \biggr] \\ &\quad{} + O \bigl( k^{2}h^{2} + kh^{4} + h^{6} \bigr). \end{aligned} \end{aligned}$$

(4.62)

The proposed method (3.39)–(3.40) to be of $O ( k^{2} + kh^{2} + h^{4} )$, the coefficients of $kh^{2}$ and $h^{4}$ in (4.61)–(4.62) must be zero.

Thus

$$\begin{aligned}& \theta = \frac{1}{2}, \quad\quad a = b = \frac{ - 1}{4}. \end{aligned}$$

Whenever $A=A(x,t,u)$, the differential equation (1.1) becomes quasi-linear. In order to solve the quasi-linear differential equation when $A=A(x,t,u)$, we need to modify the method (3.39)–(3.40). The details of the technique to write numerical schemes for quasi-linear problems are discussed in [18, 23, 26, 28]. The same technique can be used here to write a numerical scheme for quasi-linear differential equation (1.1) when $A=A(x,t,u)$.

5 Stability analysis

For stability analysis of the proposed method, we consider the linearized KS equation without second order derivative term

$$ u_{t} + \gamma u_{x} + \delta u_{xxxx} = 0, $$

(5.1)

where $\gamma,\delta > 0$ are constants. Applying the proposed method (3.39)–(3.40) to the linearized KS equation (5.1) and neglecting local truncation errors, we obtain the following non-polynomial schemes in a coupled form:

$$\begin{aligned}& 12 \bigl( u_{l - 1}^{j + 1} - 2u_{l}^{j + 1} + u_{l + 1}^{j + 1} \bigr) - h^{2} \bigl( v_{l - 1}^{j + 1} + 10v_{l}^{j + 1} + v_{l + 1}^{j + 1} \bigr) \\& \quad = - 12 \bigl( u_{l - 1}^{j} - 2u_{l}^{j} + u_{l + 1}^{j} \bigr) + h^{2} \bigl( v_{l - 1}^{j} + 10v_{l}^{j} + v_{l + 1}^{j} \bigr), \end{aligned}$$

(5.2)

$$\begin{aligned}& ( 1 - 3\gamma \lambda h )u_{l - 1}^{j + 1} + 10u_{l}^{j + 1} + ( 1 + 3\gamma \lambda h )u_{l + 1}^{j + 1} \\& \quad\quad {}+ \lambda \biggl[ \biggl( 6\delta + \frac{\gamma \alpha h^{3}}{2} \biggr)v_{l - 1}^{j + 1} - 12\delta v_{l}^{j + 1} + \biggl( 6\delta + \frac{\gamma \alpha h^{3}}{2} \biggr)v_{l + 1}^{j + 1} \biggr] \\& \quad = ( 1 + 3\gamma \lambda h )u_{l - 1}^{j} + 10u_{l}^{j} + ( 1 - 3\gamma \lambda h )u_{l + 1}^{j} \\& \quad\quad{} - \lambda \biggl[ \biggl( 6\delta + \frac{\gamma \alpha h^{3}}{2} \biggr)v_{l - 1}^{j} - 12\delta v_{l}^{j} + \biggl( 6\delta - \frac{\gamma \alpha h^{3}}{2} \biggr)v_{l + 1}^{j} \biggr]. \end{aligned}$$

(5.3)

To apply the von Neumann linear stability method, we consider that the numerical solutions are given by $u_{l}^{j} = \rho^{j}e^{i\eta l}$ and $v_{l}^{j} = \sigma^{j}e^{i\eta l}$ for $i = \sqrt{ - 1}$, where ρ, σ are amplification factors and η is the phase angle. Substituting these in Schemes (5.2)–(5.3), we obtain the following matrix form:

$$ \boldsymbol{Ay}^{j + 1} = \boldsymbol{By}^{j}, $$

(5.4)

where

$$\begin{array}{c}\mathit{y}=\left[\begin{array}{c}\mathit{u}\\ \mathit{v}\end{array}\right],\mathit{A}=\left[\begin{array}{cc}p& q\\ r& s\end{array}\right],\mathit{B}=\left[\begin{array}{cc}p& q\\ r^{\ast }& s\end{array}\right],\hfill \\ p=-{sin}^2\frac{\eta }{2},q=-\frac{h^2}{4}(1-\frac{1}{3}{sin}^2\frac{\eta }{2}),\hfill \\ r=(1-\frac{1}{3}{sin}^2\frac{\eta }{2})+i\frac{\gamma \lambda h}{8}sin\eta ,r^{\ast }=(1-\frac{1}{3}{sin}^2\frac{\eta }{2})-i\frac{\gamma \lambda h}{8}sin\eta ,\hfill \\ d=-\frac{\delta \lambda }{2}{sin}^2\frac{\eta }{2}-\frac{i\gamma \alpha \lambda h^3}{48}sin\eta .\hfill \end{array}$$

Now, define the amplification matrix H as

$$ \boldsymbol{H} = \boldsymbol{A}^{ - 1}\boldsymbol{B}. $$

(5.5)

Let the eigenvalues of the amplification matrix H be $\omega = \omega_{1},\omega_{2}$. The von Neumann necessary condition for linear stability of system (5.2)–(5.3) is that $\max \vert \omega \vert \le 1$. By direct calculation, the eigenvalues of H are given by

$$\omega_{1} = - 1,\quad\quad \omega_{2} = \frac{C + iD}{C^{ *} - iD}, $$

where

$$\begin{aligned}& C = - \frac{h^{2}}{4} \biggl( 1 - \frac{1}{3}\sin^{2} \frac{\eta}{2} \biggr)^{2} + \frac{\delta \lambda}{2}\sin^{4} \frac{\eta}{2}, \\& C^{ *} = - \frac{h^{2}}{4} \biggl( 1 - \frac{1}{3} \sin^{2}\frac{\eta}{2} \biggr)^{2} - \frac{\delta \lambda}{2} \sin^{4}\frac{\eta}{2}, \\& D = \frac{\gamma \lambda h}{8} \biggl( 1 - \frac{1}{3}\sin^{2} \frac{\eta}{2} \biggr) + \frac{\gamma \alpha \lambda h^{3}}{48}\sin^{2} \frac{\eta}{2}\sin \eta. \end{aligned}$$

It is noticed that $\max \vert \omega_{1} \vert = 1$ and $\max \vert \omega_{2} \vert \le 1$ if

$$ \frac{\delta \lambda}{2}h^{2} \biggl( 1 - \frac{1}{3} \sin^{2}\frac{\eta}{2} \biggr)^{2}\sin^{4} \frac{\eta}{2} \ge 0. $$

(5.6)

Inequality (5.6) is true for all values of phase angle η. Hence system (5.3)–(5.4) is unconditionally stable.

6 Numerical results

In this section, we apply the proposed spline in compression method to the GKS equation, KS equation, and EFK equation with different parameters. The exact solutions are provided as a test procedure. The initial and boundary conditions can be obtained from the exact solutions. Whenever PDE (1.1) is quasi-linear or nonlinear, the proposed method builds a coupled nonlinear block system. In the following examples, we use Newton’s block Gauss–Seidel iteration method [30–33] for the solution of a coupled nonlinear block system. In each case iterations were stopped when the absolute error tolerance ≤10⁻¹⁰ is achieved.

Example 1

(Kuramoto–Sivashinsky equation)

$$\begin{aligned}& u_{t} + uu_{x} + u_{xx} + u_{xxxx} = 0, \quad - 30 < x < 30, t > 0. \end{aligned}$$

(6.1)

The exact solution [13, 34] is given by

$$u(x,t) = \beta_{0} + \frac{15}{19}\sqrt{\frac{11}{19}} \bigl\{ - 9\tanh \bigl( \kappa (x - \beta_{0}t - x_{0}) \bigr) + 11\tanh^{3} \bigl( \kappa (x - \beta_{0}t - x_{0}) \bigr) \bigr\} . $$

For computation, we choose the values $\beta_{0} = 5$, $\kappa = \frac{1}{2}\sqrt{\frac{11}{19}}$, $x_{0} = - 12$ in the solution domain $[-30, 30]$ with $h = 1/150$ and $k =1/100$. To check the accuracy of the proposed method, we compute the global relative errors (GRE) defined using the formula

$$\begin{aligned}& \mathrm{GRE}= \frac{\sum_{l = 1}^{L} \vert u_{l}^{j} - U_{l}^{j} \vert }{\sum_{l = 1}^{L} \vert U_{l}^{j} \vert } , \end{aligned}$$

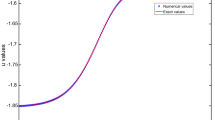
where $u_{l}^{j}$ and $U_{l}^{j}$ denote the numerical and exact solution values at the grid point $(x_{l},t_{j})$, respectively. We compare our numerical results with the results given in [13, 15, 18]. The GREs for the solutions of (6.1) are presented in Table 1a at different time levels. We show the comparison of exact and numerical solutions at various time levels in Fig. 1. In Table 1b, the GRE is compared with the results given in [15] to exhibit the effect of change in the number of grid points.

Figure 1

Example 1: Comparison between numerical and exact solutions at different time levels

Table 1 Example 1: The global relative errors

Example 2

(Kuramoto–Sivashinsky equation)

$$\begin{aligned}& u_{t} + uu_{x} - u_{xx} + u_{xxxx} = 0, \quad - 50 < x < 50, t > 0. \end{aligned}$$

(6.2)

The exact solution [13, 34] is given by

$$u(x,t) = \beta_{0} + \frac{15}{19\sqrt{19}} \bigl\{ - 3\tanh \bigl( \kappa (x - \beta_{0}t - x_{0}) \bigr) + \tanh^{3} \bigl( \kappa (x - \beta_{0}t - x_{0}) \bigr) \bigr\} . $$

For computation, we choose the values $\beta_{0} = 5$, $\kappa = \frac{1}{2\sqrt{19}}$, $x_{0} = - 25$ in the interval $[-50, 50]$ with $h= 1/200$ and $k=1/100$. In Table 2, the GRE is compared with the results given in [13, 15]. At various time levels, we present the graph between numerical and exact solutions in Fig. 2.

Figure 2

Example 2: Comparison between numerical and exact solutions at different time levels

Table 2 Example 2: The global relative errors

Example 3

(Generalized Kuramoto–Sivashinsky equation)

$$\begin{aligned}& u_{t} + uu_{x} + u_{xx} + 4u_{xxx} + u_{xxxx} = 0, \quad - 30 < x < 30,t > 0. \end{aligned}$$

(6.3)

The exact solution [13, 34] is given by

$$\begin{aligned} u(x,t) &= \beta_{0} + 9 - 15\bigl\{ \tanh \bigl( \kappa (x - \beta_{0}t - x_{0}) \bigr) + \tanh^{2} \bigl( \kappa (x - \beta_{0}t - x_{0}) \bigr) \\ &\quad{} - \tanh^{3} \bigl( \kappa (x - \beta_{0}t - x_{0}) \bigr) \bigr\} . \end{aligned}$$

For computation, we choose the values $\beta_{0} = 6$, $\kappa = 0.5$, $x_{0} = - 10$ in the solution domain $[-30, 30]$ with $h= 1/10$ and $k=1/10{,}000$. The GRE is reported in Table 3 and the results are compared with the results given in [13, 18]. In Fig. 3, we present the comparison of exact and numerical solutions at $t = 1$.

Figure 3

Example 3: Comparison between numerical and exact solutions at $t = 1$

Table 3 Example 3: The global relative errors

Example 4

(Extended Fisher–Kolmogorov equation)

$$\begin{aligned}& u_{t} - u_{xx} + \gamma u_{xxxx} + u^{3} - u = 0, \quad - 4 < x < 4,t > 0. \end{aligned}$$

(6.4)

The initial and boundary conditions [20] are given by

$$\begin{aligned}& u(x,0) = - \sin (\pi x),\quad - 4 \le x \le 4, \\& u(-4,t) = 0, \quad\quad u(4,t) = 0, \quad t> 0, \\& u_{xx}( - 4,t) = 0, \quad\quad u_{xx}(4,t) = 0. \end{aligned}$$

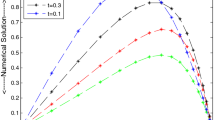
For the above conditions, we plotted graphs (Fig. 4a–4c) of the computed solution at different time levels. We observe that the behavior of the numerical solution at $\gamma = 0$ and $\gamma = 0.0001$ is almost similar. However, we notice that as time t increases, the solution curves fall to zero rapidly for $\gamma = 0.1$, which ensures the stabilizing character of the EFK equation.

Figure 4

Example 4: (a) The profiles of $u(x,t)$ versus x for $\gamma = 0$. (b) The profiles of $u(x,t)$ versus x for $\gamma = 0.0001$. (c) The profiles of $u(x,t)$ versus x for $\gamma = 0.1$

7 Final discussion

In this paper, we have discussed a new two-level implicit numerical method in a coupled form based on spline in compression approximations for the solution of time-dependent quasi-linear biharmonic equations. The proposed spline method uses only three spatial grid points $x_{l}$, $x_{l \pm 1/2}$, and no fictitious points for incorporating the boundary conditions are needed. The numerical solution of $u _{xx}$ is obtained as a by-product of the method. The numerical results clearly suggest that the scheme produces better results in comparison with the existing results given in [13, 15, 18]. It is noted from Tables 1, 2 and 3 that the accuracy of the solution for the KS equation decreases with time due to the time truncation errors of the time derivative term. The graphical illustration of numerical solution at various time levels establishes similar features as those existing in the literature. The proposed method is easily implemented and approximates the exact solution of highly nonlinear GKS equation and KS equation. The graphical results of EFK equation obtained by the proposed scheme exhibit the correct physical behavior for different values of γ. Similar patterns have been depicted in [20]. It is expected that the proposed method will be helpful in solving other nonlinear 1D time-dependent biharmonic problems in applied sciences and engineering.