Structure of solitary wave solutions of the nonlinear complex fractional generalized Zakharov dynamical system

Lu, Dianchen; Seadawy, Aly R.; Khater, Mostafa M. A.

doi:10.1186/s13662-018-1734-4

Structure of solitary wave solutions of the nonlinear complex fractional generalized Zakharov dynamical system

Research
Open access
Published: 03 August 2018

Volume 2018, article number 266, (2018)
Cite this article

Download PDF

You have full access to this open access article

Advances in Difference Equations Submit manuscript

Structure of solitary wave solutions of the nonlinear complex fractional generalized Zakharov dynamical system

Download PDF

1369 Accesses
24 Citations
Explore all metrics

Abstract

The analytical and solitary traveling solutions of the nonlinear complex fractional generalized Zakharov equations are investigated. The nonlinear complex fractional generalized Zakharov equations describe the interaction between dispersive and non-dispersive waves in one dimension. Analytical and solitary traveling wave solutions were obtained through applying a generalized Kudryashov and a novel $(\frac{G'}{G})$-expansion methods. Novel solutions were the results of our investigated model, which illustrated the effectiveness and the power of the obtained methods in regards to accuracy, power, and effectiveness compared to the previously used methods.

A novel approach for solitary wave solutions of the generalized fractional Zakharov-Kuznetsov equation

Article 11 July 2017

New Solitary Wave Solutions and Dynamical Behaviors of the Nonlinear Fractional Zakharov System

Article 05 February 2024

A novel analytical technique to obtain the solitary solutions for nonlinear evolution equation of fractional order

Article Open access 22 June 2020

1 Introduction

The nonlinear complex fractional generalized-Zakharov system characterizes the proliferation of Langmuir waves in the ionized plasma. This model was discovered by Irving Langmuir and Lewi Tonks in the 1920s. Langmuir waves are known as plasma oscillations, they represent the fast oscillation of the electron density in conducting media. This oscillation can describe the instability in the dielectric function of free electron gas. While the ionization is defined as an atom which could be positively or negatively charged through acquiring or losing an electron or more, and that is always synchronized with other chemical shifts.

The nonlinear model of nonlinear complex fractional generalized-Zakharov system is very important and has many applications related to this phenomenon. Long time ago, researchers were trying to discover new physical features of the nonlinear model. Vladimir Zakharov in 1972 was the first who introduced this system. Then, further research was done to continue this trend, and the results obtained were analytical and solitary traveling wave solutions. In 1996, Malfliet et al. used the tanh method [1]; in 2009, Borhanifar et al. used the Exp-function method [2]; in 2003, Li et al. used the improved tanh method and symbolic computation [3]; in 2004, Yong et al. used the Riccati equation method [4]; in 2012, Naher Hasibun et al. used the Exp-function method [5]; in 2007, Abdou used the extended tanh method [6]; in 2015, Tuluce Demiray et al. used the extended trial equation method [7]; in 2007, Zhang et al. used a direct algebraic method [8, 9]; in 2008 Wazwaz and Abdul-Majid used the extended tanh method [10]; in 2009, Zhang et al. used the new generalized algebraic method [11]; in 2005, Wazwaz and Abdul-Majid used the sine-cosine algorithm [12]; in 2011, Kabir et al. used the modified Kudryashov method [13]; in 2009, Layeni used the rational auxiliary equation method [14]; in 2010, Betchewe et al. used [15], and so on [16–20].

From the above discussed studies, lots of methods were derived to solve the nonlinear partial differential equation models as follows: the $( \frac{G'}{G} ) $-expansion method extended the $( \frac{G'}{G} ) $-expansion method, the tanh-function method extended a simple equation method, the modified simple equation method extended the Jacobian method, a novel $( \frac{G'}{G} ) $-expansion method, and so on [21–55].

This paper is regulated as follows: In Sect. 2, we apply a generalized Kudryashov method and a novel $( \frac{G'}{G} ) $-expansion method to get the exact and solitary traveling wave solutions of the nonlinear complex fractional generalized-Zakharov equations. In Sect. 3, conclusion is presented and discussed.

2 Formulation for the nonlinear complex fractional generalized-Zakharov equations

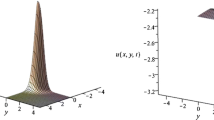
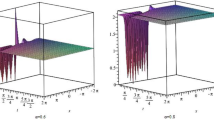
Consider the nonlinear complex fractional generalized-Zakharov equations in the form [21–23]:

$$ \textstyle\begin{cases} i \frac{D^{\alpha } P}{D t^{\alpha }}+ P_{x x}-2 \delta \vert P \vert ^{2} P+2 P Q=0, \\ \frac{D^{2 \alpha } Q}{D t^{2 \alpha }}-Q_{x x}+( \vert P \vert ^{2})_{x x}=0. \end{cases} $$

(1)

Using the following traveling wave transformation $[P(x,t)=Y(x,t) e ^{i \phi } , \phi =k x+\frac{c t^{\alpha }}{\alpha } , Y(x,t)=Y( \xi ) , Q(x,t)=Q(\xi ) , \xi =x-\frac{2 k t^{\alpha }}{\alpha } ]$ on system (1), we obtain

$$ \textstyle\begin{cases} Y''-(c+k^{2}) Y - 2 \delta Y^{3} + 2 Y Q=0, \\ (4 k^{2}-1) Q'' + (Y^{2})''=0. \end{cases} $$

(2)

Integrating twice the second equation in system (2), where the constant of integration equals zero, we get $[ Q(\xi )=\frac{Y ^{2}}{1-4 k^{2}} ] $. Substituting $Q(\xi )$ into the first equation of system (2), we obtain

$$ Y''-\bigl(c+k^{2}\bigr) Y+ \biggl(\frac{2}{1-4 k^{2}}-2 \delta \biggr) Y^{3}=0. $$

(3)

Balancing Eq. (3) by using the relation between the highest order derivative term and the nonlinear term, we get $Y'' \& Y^{3}\Rightarrow N+2=3N\Rightarrow N=1$.

2.1 Exact and solitary wave solution of the nonlinear complex fractional generalized-Zakharov equations by using a generalized Kudryashov method

We use a generalized Kudryashov method on the nonlinear complex fractional generalized-Zakharov equations that suppose the general solution of it in the following form:

$$ Y(\xi )={\frac{a_{{0}}+a_{{1}} E( \xi ) +a_{{2}} E^{2}( \xi ) }{b _{{0}}+b_{{1}} E(\xi ) }}. $$

(4)

Substituting Eq. (4) and its derivatives into Eq. (3) and equating the coefficient of different power of $E^{i}( \xi )$ to zero, we obtain a system of algebraic equations by solving it with any computer program like (Maple, Mathematica and so on). We get the following:

$$\begin{aligned}& k=\sqrt{1-c},\quad\quad a_{0}=0, \quad\quad a_{1}=-b_{1} \sqrt{ \frac{4 c-3}{4 c \delta -3 \delta -1}}, \quad\quad a_{2}=b_{1} \sqrt{\frac{4 c-3}{4 c \delta -3 \delta -1}},\\& b_{0}=-\frac{b_{1}}{2}, \end{aligned}$$

where $[ \frac{4 c-3}{4 c \delta -3 \delta -1}>0, c\neq 1 ] $. Consequently, the solitary wave solution for Eqs. (1) is as follows:

$$\begin{aligned}& P(x,t)=\frac{2 \sqrt{{\frac{4 c-3}{-1+ ( 4 c-3 ) \delta }}} \alpha {\mathrm{e}^{{\frac{x\alpha -2 k{t}^{\alpha }}{ \alpha }}}}}{{\alpha }^{2} {\mathrm{e}^{{\frac{-4 k{t}^{\alpha }+2 x \alpha }{\alpha }}}}-1} e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned}$$

(5)

$$\begin{aligned}& Q(x,t)=\frac{ ( -4 c+3 ) {\alpha }^{2}{\mathrm{e}^{{\frac{-4 k{t}^{\alpha }+2 x\alpha }{\alpha }}}}}{ ( 4 c\delta -3 \delta -1 ) ( {\mathrm{e}^{{\frac{-4 k{t}^{\alpha }+2 x \alpha }{\alpha }}}}{\alpha }^{2}-1 ) ^{2} ( -1+c ) }. \end{aligned}$$

(6)

2.2 Exact and solitary wave solution of the nonlinear complex fractional generalized-Zakharov equations by using novel $(\frac{G'}{G})$-expansion method

We use a novel $(\frac{G'}{G})$-expansion method on the nonlinear complex fractional generalized-Zakharov equations that suppose the general solution of it in the following form:

$$ Y(\xi )=\frac{a_{-1}}{(d+\frac{G'}{G})}+a_{0}+a_{1} \biggl(d+\frac{G'}{G}\biggr). $$

(7)

Substituting Eq. (7) and its derivatives into Eq. (3) and equating the coefficient of different power of $(d+\frac{G'}{G})^{i}$ to zero, we obtain a system of algebraic equations by solving it with any computer program like (Maple, Mathematica, Matlap and so on). We get the following:

Family 1

$$\begin{aligned}& \mu =\frac{1}{4} {\frac{2 {k}^{2}+{\lambda }^{2}+2 c}{v-1}}, \quad\quad a _{{-1}}=0, \\& a_{{0}}=\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{ { \frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}, \quad\quad a_{{1}}=- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} { \frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}. \end{aligned}$$

Consequently, the solitary wave solution for Eqs. (1) is as follows:

• When $(\Omega =\lambda^{2}-4 \lambda \mu +4 \mu >0)$ and $(\lambda (v-1)\neq 0)$ or $(\mu (v-1)\neq 0)$:

$$\begin{aligned}& \begin{aligned}[b] P_{11}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}- \delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}- \delta +1}{\frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}- \delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \tanh \biggl( \frac{\sqrt{\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{ \alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(8)

$$\begin{aligned}& \begin{aligned}[b] Q_{11}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \tanh \biggl( \frac{\sqrt{\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(9)

$$\begin{aligned}& \begin{aligned}[b] P_{12}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}- \delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}- \delta +1}{\frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}- \delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \coth \biggl( \frac{\sqrt{\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{ \alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(10)

$$\begin{aligned}& \begin{aligned}[b] Q_{12}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \coth \biggl( \frac{\sqrt{\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(11)

$$\begin{aligned}& \begin{aligned}[b] P_{13}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}- \delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}- \delta +1}{\frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}- \delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \biggl( \tanh \biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \\ & \quad {} \pm i \operatorname {sech}\biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr] e ^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(12)

$$\begin{aligned}& \begin{aligned}[b] Q_{13}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \biggl( \tanh \biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \\ & \quad {}\pm i \operatorname {sech}\biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(13)

$$\begin{aligned}& \begin{aligned}[b] P_{14}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}- \delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}- \delta +1}{\frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}- \delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \biggl( \coth \biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \\ & \quad {}\pm \operatorname {csch}\biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr] e ^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(14)

$$\begin{aligned}& \begin{aligned}[b] Q_{14}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \biggl( \coth \biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \\ & \quad {}\pm \operatorname {csch}\biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(15)

$$\begin{aligned}& \begin{aligned}[b] P_{15}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}- \delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}- \delta +1}{\frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}- \delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{1}{4(v-1)} \biggl( 2 \lambda +\sqrt{\Omega } \biggl( \tanh \biggl( \frac{\sqrt{\Omega }}{4} \biggl( c-\frac{2 k t ^{\alpha }}{\alpha } \biggr) \biggr) \\ & \quad {}\pm \coth \biggl( \frac{\sqrt{ \Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(16)

$$\begin{aligned}& \begin{aligned}[b] Q_{15}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{1}{4(v-1)} \biggl( 2 \lambda +\sqrt{\Omega } \biggl( \tanh \biggl( \frac{\sqrt{\Omega }}{4} \biggl( c-\frac{2 k t ^{\alpha }}{\alpha } \biggr) \biggr) \\ & \quad {}\pm \coth \biggl( \frac{\sqrt{ \Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(17)

$$\begin{aligned}& \begin{aligned}[b] P_{16}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}- \delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}- \delta +1}{\frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}- \delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda + \frac{\pm \sqrt{ \Omega ( A^{2}+B^{2} ) }-A \sqrt{\Omega } \cosh ( \sqrt{ \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sinh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +B} \biggr) \biggr) \biggr]\hspace{-20pt} \\ & \quad {}\times e^{i (k x+\frac{c t ^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(18)

$$\begin{aligned}& \begin{aligned}[b] Q_{16}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda \\ & \quad {}+ \frac{\pm \sqrt{ \Omega ( A^{2}+B^{2} ) }-A \sqrt{\Omega } \cosh ( \sqrt{ \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sinh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +B} \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(19)

$$\begin{aligned}& \begin{aligned}[b] P_{17}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}- \delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}- \delta +1}{\frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}- \delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda \\ & \quad {}+ \frac{\pm \sqrt{ \Omega ( A^{2}+B^{2} ) }+A \sqrt{\Omega } \cosh ( \sqrt{ \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sinh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +B} \biggr) \biggr) \biggr] e^{i (k x+\frac{c t ^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned}& \begin{aligned}[b] Q_{17}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda \\ & \quad {}+ \frac{\pm \sqrt{ \Omega ( A^{2}+B^{2} ) }+A \sqrt{\Omega } \cosh ( \sqrt{ \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sinh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +B} \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(21)

$$\begin{aligned}& \begin{aligned}[b] P_{18}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}- \delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}- \delta +1}{\frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}- \delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{2 \mu \cosh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{ \Omega } \sinh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) -\lambda \cosh ( \frac{\sqrt{ \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) } \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(22)

$$\begin{aligned}& \begin{aligned}[b] Q_{18}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{2 \mu \cosh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{ \Omega } \sinh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) -\lambda \cosh ( \frac{\sqrt{ \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(23)

$$\begin{aligned}& \begin{aligned}[b] P_{19}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}- \delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}- \delta +1}{\frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}- \delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{2 \mu \sinh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{ \Omega } \cosh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) -\lambda \sinh ( \frac{\sqrt{ \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) } \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(24)

$$\begin{aligned}& \begin{aligned}[b] Q_{19}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{2 \mu \sinh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{ \Omega } \cosh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) -\lambda \sinh ( \frac{\sqrt{ \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(25)

$$\begin{aligned}& \begin{aligned}[b] P_{110}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{2 \mu \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) -\lambda \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm i \sqrt{ \Omega }} \biggr) \biggr] \\ & \quad {} \times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(26)

$$\begin{aligned}& \begin{aligned}[b] Q_{110}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-30pt} \\ & \quad {} \times \biggl( d+\frac{2 \mu \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) -\lambda \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm i \sqrt{ \Omega }} \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(27)

$$\begin{aligned}& \begin{aligned}[b] P_{111}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{2 \mu \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) -\lambda \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm i \sqrt{ \Omega }} \biggr) \biggr] \\ & \quad {} \times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(28)

$$\begin{aligned}& \begin{aligned}[b] Q_{111}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{2 \mu \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) -\lambda \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm i \sqrt{ \Omega }} \biggr) \biggr]^{2}, \end{aligned} \end{aligned}$$

(29)

where A, B are arbitrary real constants and $A^{2}+B^{2}>0$.

• When $( \Omega =\lambda^{2}-4 \lambda \mu +4 \mu <0 ) $ and $( \lambda (v-1)\neq 0 ) $ or $( \mu (v-1) \neq 0 ) $:

$$\begin{aligned}& \begin{aligned}[b] P_{112}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda +\sqrt{-\Omega } \tan \biggl( \frac{\sqrt{-\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr] e^{i (k x+\frac{c t ^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(30)

$$\begin{aligned}& \begin{aligned}[b] Q_{112}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda +\sqrt{-\Omega } \tan \biggl( \frac{\sqrt{-\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(31)

$$\begin{aligned}& \begin{aligned}[b] P_{113}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{-\Omega } \cot \biggl( \frac{\sqrt{-\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{ \alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(32)

$$\begin{aligned}& \begin{aligned}[b] Q_{113}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{-\Omega } \cot \biggl( \frac{\sqrt{-\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(33)

$$\begin{aligned}& \begin{aligned}[b] P_{114}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda +\sqrt{-\Omega } \biggl( \tan \biggl( \sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \\ & \quad {} \pm \sec \biggl( \sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr] e ^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(34)

$$\begin{aligned}& \begin{aligned}[b] Q_{114}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda +\sqrt{-\Omega } \biggl( \tan \biggl( \sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \\ & \quad {} \pm \sec \biggl( \sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(35)

$$\begin{aligned}& \begin{aligned}[b] P_{115}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{-\Omega } \biggl( \cot \biggl( \sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \\ & \quad {} \pm \csc \biggl( \sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr] e ^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(36)

$$\begin{aligned}& \begin{aligned}[b] Q_{115}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{-\Omega } \biggl( \cot \biggl( \sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr) \\ & \quad {} \pm \csc \biggl( \sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(37)

$$\begin{aligned}& \begin{aligned}[b] P_{116}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{1}{4(v-1)} \biggl( -2 \lambda +\sqrt{- \Omega } \biggl( \tan \biggl( \frac{\sqrt{-\Omega }}{4} \biggl( c-\frac{2 k t ^{\alpha }}{\alpha } \biggr) \biggr) \\ & \quad {}- \cot \biggl( \frac{\sqrt{-\Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(38)

$$\begin{aligned}& \begin{aligned}[b] Q_{116}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{1}{4(v-1)} \biggl( -2 \lambda +\sqrt{- \Omega } \biggl( \tan \biggl( \frac{\sqrt{-\Omega }}{4} \biggl( c-\frac{2 k t ^{\alpha }}{\alpha } \biggr) \biggr) \\ & \quad {} - \cot \biggl( \frac{\sqrt{-\Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(39)

$$\begin{aligned}& \begin{aligned}[b] P_{117}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda \\ & \quad {} + \frac{\pm \sqrt{- \Omega ( A^{2}-B^{2} ) }-A \sqrt{-\Omega } \cos ( \sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sin ( \sqrt{-\Omega } ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +B} \biggr) \biggr) \biggr] e^{i (k x+\frac{c t ^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(40)

$$\begin{aligned}& \begin{aligned}[b] Q_{117}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda \\ & \quad {}+ \frac{\pm \sqrt{- \Omega ( A^{2}-B^{2} ) }-A \sqrt{-\Omega } \cos ( \sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sin ( \sqrt{-\Omega } ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +B} \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(41)

$$\begin{aligned}& \begin{aligned}[b] P_{118}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda \\ & \quad {}+ \frac{\pm \sqrt{- \Omega ( A^{2}-B^{2} ) }+A \sqrt{-\Omega } \cos ( \sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sin ( \sqrt{-\Omega } ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +B} \biggr) \biggr) \biggr] e^{i (k x+\frac{c t ^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(42)

$$\begin{aligned}& \begin{aligned}[b] Q_{118}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{1}{2(v-1)} \biggl( -\lambda \\ & \quad {}+ \frac{\pm \sqrt{- \Omega ( A^{2}-B^{2} ) }+A \sqrt{-\Omega } \cos ( \sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sin ( \sqrt{-\Omega } ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +B} \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(43)

$$\begin{aligned}& \begin{aligned}[b] P_{119}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{2 \mu \cos ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{- \Omega } \sin ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) +\lambda \cos ( \frac{\sqrt{- \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) } \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(44)

$$\begin{aligned}& \begin{aligned}[b] Q_{119}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{2 \mu \cos ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{- \Omega } \sin ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) +\lambda \cos ( \frac{\sqrt{- \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(45)

$$\begin{aligned}& \begin{aligned}[b] P_{120}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d+\frac{2 \mu \sin ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{- \Omega } \cos ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) -\lambda \sin ( \frac{\sqrt{- \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) } \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(46)

$$\begin{aligned}& \begin{aligned}[b] Q_{120}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{2 \mu \sin ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{- \Omega } \cos ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) -\lambda \sin ( \frac{\sqrt{- \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(47)

$$\begin{aligned}& \begin{aligned}[b] P_{121}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{2 \mu \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{-\Omega } \sin ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +\lambda \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm \sqrt{- \Omega }} \biggr) \biggr]\hspace{-20pt} \\ & \quad {} \times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(48)

$$\begin{aligned}& \begin{aligned}[b] Q_{121}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{2 \mu \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{-\Omega } \sin ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +\lambda \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm \sqrt{- \Omega }} \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(49)

$$\begin{aligned}& \begin{aligned}[b] P_{122}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{2 \mu \sin ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{-\Omega } \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) -\lambda \sin ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm \sqrt{- \Omega }} \biggr) \biggr]\hspace{-20pt} \\ & \quad {} \times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(50)

$$\begin{aligned}& \begin{aligned}[b] Q_{122}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d+\frac{2 \mu \sin ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{-\Omega } \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) -\lambda \sin ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm \sqrt{- \Omega }} \biggr) \biggr]\hspace{-20pt} \\ & \quad {} \times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(51)

where A, B are arbitrary real constants and $A^{2}-B^{2}>0$.

• When $\mu =0$ and $\lambda (v-1)\neq 0$, we have:

$$\begin{aligned}& \begin{aligned}[b] P_{123}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{\lambda k}{(v-1) ( k+\cosh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )-\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) } \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(52)

$$\begin{aligned}& \begin{aligned}[b] Q_{123}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{\lambda k}{(v-1) ( k+\cosh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )-\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(53)

$$\begin{aligned}& \begin{aligned}[b] P_{124}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{\lambda ( \cosh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )+\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) }{(v-1) ( k+\cosh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )+\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) } \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(54)

$$\begin{aligned}& \begin{aligned}[b] Q_{124}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{\lambda ( \cosh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )+\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) }{(v-1) ( k+\cosh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )+\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(55)

$$\begin{aligned}& \begin{aligned}[b] P_{125}(x,t) &=\biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}- {\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1} {\frac{1}{ \sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}} \\ & \quad {} \times \biggl( d-\frac{1}{(v-1) ( c-\frac{2 k t^{\alpha }}{ \alpha } ) + C} \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{ \alpha })}, \end{aligned} \end{aligned}$$

(56)

$$\begin{aligned}& \begin{aligned}[b] Q_{125}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[\frac{1}{2} \bigl( ( 2 v-2 ) d-\lambda \bigr) \sqrt{{\frac{4 {k}^{2}-1}{4 \delta {k}^{2}-\delta +1}}}-{\frac{4 {k}^{2}v-4 {k}^{2}-v+1}{4 \delta {k}^{2}-\delta +1}{ \frac{1}{\sqrt{{\frac{4 {k}^{2}+1}{4 \delta {k}^{2}-\delta +1}}}}}}\hspace{-20pt} \\ & \quad {} \times \biggl( d-\frac{1}{(v-1) ( c-\frac{2 k t^{\alpha }}{ \alpha } ) + C} \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(57)

Family 2

$$ k=\sqrt{\frac{\delta -1}{4 \delta }}, \quad\quad v=1, \quad\quad a_{-1}=0, \quad\quad a_{0}=- \frac{4 \delta \lambda a_{1} (d \lambda -\mu )}{4 c \delta +\delta -1}. $$

So, the solitary traveling wave solutions are as follows:

• When $(\Omega =\lambda^{2}-4 \lambda \mu +4 \mu >0)$ and $(\lambda (v-1)\neq 0)$ or $(\mu (v-1)\neq 0)$:

$$\begin{aligned}& \begin{aligned}[b] P_{21}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{} +a_{1} \biggl( d- \frac{1}{2(v-1)} \biggl( \lambda +\sqrt{ \Omega } \tanh \biggl( \frac{\sqrt{\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(58)

$$\begin{aligned}& \begin{aligned}[b] Q_{21}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[- \frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d- \frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \tanh \biggl( \frac{\sqrt{ \Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(59)

$$\begin{aligned}& \begin{aligned}[b] P_{22}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d- \frac{1}{2(v-1)} \biggl( \lambda +\sqrt{ \Omega } \coth \biggl( \frac{\sqrt{\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(60)

$$\begin{aligned}& \begin{aligned}[b] Q_{22}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d- \frac{1}{2(v-1)} \biggl( \lambda +\sqrt{\Omega } \coth \biggl( \frac{\sqrt{ \Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(61)

$$\begin{aligned}& \begin{aligned}[b] P_{23}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl(d- \frac{1}{2(v-1)}\biggl(\lambda +\sqrt{ \Omega } \biggl( \tanh \biggl(\sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha }\biggr) \biggr)\hspace{-20pt} \\ & \quad {} \pm i \operatorname {sech}\biggl(\sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr)\biggr)\biggr)\biggr)\biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(62)

$$\begin{aligned}& \begin{aligned}[b] Q_{23}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl(d- \frac{1}{2(v-1)} \biggl(\lambda +\sqrt{\Omega } \biggl( \tanh \biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr) \\ & \quad {} \pm i \operatorname {sech}\biggl(\sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr)\biggr)\biggr)\biggr)\biggr]^{2}. \end{aligned} \end{aligned}$$

(63)

$$\begin{aligned}& \begin{aligned}[b] P_{24}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl(d- \frac{1}{2(v-1)}\biggl(\lambda +\sqrt{ \Omega } \biggl( \coth \biggl(\sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{ \alpha }\biggr)\biggr)\hspace{-20pt} \\ & \quad {} \pm \operatorname {csch}\biggl(\sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr)\biggr)\biggr)\biggr)\biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(64)

$$\begin{aligned}& \begin{aligned}[b] Q_{24}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl(d- \frac{1}{2(v-1)} \biggl(\lambda +\sqrt{\Omega } \biggl( \coth \biggl( \sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr)\biggr)\hspace{-20pt} \\ & \quad {} \pm \operatorname {csch}\biggl(\sqrt{\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr)\biggr)\biggr)\biggr)\biggr]^{2}. \end{aligned} \end{aligned}$$

(65)

$$\begin{aligned}& \begin{aligned}[b] P_{25}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl(d- \frac{1}{4(v-1)} \biggl(2 \lambda +\sqrt{\Omega } \biggl( \tanh \biggl( \frac{\sqrt{\Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr)\hspace{-20pt} \\ & \quad {} \pm \coth \biggl(\frac{\sqrt{\Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr)\biggr)\biggr)\biggr)\biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(66)

$$\begin{aligned}& \begin{aligned}[b] Q_{25}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ & \quad {}+a_{1} \biggl(d- \frac{1}{4(v-1)} \biggl(2 \lambda +\sqrt{\Omega } \biggl( \tanh \biggl( \frac{\sqrt{ \Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr) \\ & \quad {} \pm \coth \biggl(\frac{\sqrt{\Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha } \biggr) \biggr)\biggr)\biggr)\biggr)\biggr]^{2}. \end{aligned} \end{aligned}$$

(67)

$$\begin{aligned}& \begin{aligned}[b] P_{26}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl( d+ \frac{1}{2(v-1)} \biggl( - \lambda \\ &\quad{} +\frac{\pm \sqrt{\Omega ( A^{2}+B^{2} ) }-A \sqrt{ \Omega } \cosh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sinh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) +B} \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(68)

$$\begin{aligned}& \begin{aligned}[b] Q_{26}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1}+a_{1} \biggl( d+ \frac{1}{2(v-1)} \biggl( -\lambda \\ &\quad{}+\frac{\pm \sqrt{\Omega ( A ^{2}+B^{2} ) }-A \sqrt{\Omega } \cosh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sinh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) +B} \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(69)

$$\begin{aligned}& \begin{aligned}[b] P_{27}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl( d+ \frac{1}{2(v-1)} \biggl( - \lambda \\ &\quad{}+\frac{\pm \sqrt{\Omega ( A^{2}+B^{2} ) }+A \sqrt{ \Omega } \cosh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sinh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) +B} \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(70)

$$\begin{aligned}& \begin{aligned}[b] Q_{27}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1}+a_{1} \biggl( d+ \frac{1}{2(v-1)} \biggl( -\lambda \\ &\quad{}+\frac{\pm \sqrt{\Omega ( A ^{2}+B^{2} ) }+A \sqrt{\Omega } \cosh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{A \sinh ( \sqrt{\Omega } ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) +B} \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(71)

$$\begin{aligned}& \begin{aligned}[b] P_{28}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+ \frac{2 \mu \cosh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) }{\sqrt{\Omega } \sinh ( \frac{\sqrt{ \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) - \lambda \cosh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) } \biggr) \biggr] e^{i (k x+\frac{c t ^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(72)

$$\begin{aligned}& \begin{aligned}[b] Q_{28}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+\frac{2 \mu \cosh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \sinh ( \frac{\sqrt{ \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) - \lambda \cosh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(73)

$$\begin{aligned}& \begin{aligned}[b] P_{29}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+ \frac{2 \mu \sinh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) }{\sqrt{\Omega } \cosh ( \frac{\sqrt{ \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) - \lambda \sinh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) } \biggr) \biggr] e^{i (k x+\frac{c t ^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(74)

$$\begin{aligned}& \begin{aligned}[b] Q_{19}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+\frac{2 \mu \sinh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \cosh ( \frac{\sqrt{ \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) - \lambda \sinh ( \frac{\sqrt{\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(75)

$$\begin{aligned}& \begin{aligned}[b] P_{210}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+ \frac{2 \mu \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) -\lambda \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm i \sqrt{ \Omega }} \biggr) \biggr] \\ &\quad{}\times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(76)

$$\begin{aligned}& \begin{aligned}[b] Q_{210}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1}+a_{1} \biggl( d \\ &\quad{}+\frac{2 \mu \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \sinh ( {\sqrt{ \Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) - \lambda \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{ \alpha }}{\alpha } ) ) \pm i \sqrt{\Omega }} \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(77)

$$\begin{aligned}& \begin{aligned}[b] P_{211}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+ \frac{2 \mu \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \cosh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) -\lambda \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm i \sqrt{ \Omega }} \biggr) \biggr] \\ &\quad{}\times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(78)

$$\begin{aligned}& \begin{aligned}[b] Q_{211}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1}+a_{1} \biggl( d \\ &\quad{}+\frac{2 \mu \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{\Omega } \cosh ( {\sqrt{ \Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) - \lambda \sinh ( {\sqrt{\Omega }} ( c-\frac{2 k t^{ \alpha }}{\alpha } ) ) \pm i \sqrt{\Omega }} \biggr) \biggr]^{2}, \end{aligned} \end{aligned}$$

(79)

where A, B are arbitrary real constants and $A^{2}+B^{2}>0$.

• When $( \Omega =\lambda^{2}-4 \lambda \mu +4 \mu <0 ) $ and $( \lambda (v-1)\neq 0 ) $ or $( \mu (v-1) \neq 0 ) $:

$$\begin{aligned}& \begin{aligned}[b] P_{212}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+ \frac{1}{2(v-1)} \biggl( - \lambda +\sqrt{-\Omega } \tan \biggl( \frac{\sqrt{-\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr] \\ &\quad{}\times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(80)

$$\begin{aligned}& \begin{aligned}[b] Q_{212}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[- \frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+ \frac{1}{2(v-1)} \biggl( -\lambda +\sqrt{-\Omega } \tan \biggl( \frac{\sqrt{- \Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(81)

$$\begin{aligned}& \begin{aligned}[b] P_{213}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d- \frac{1}{2(v-1)} \biggl( \lambda +\sqrt{- \Omega } \cot \biggl( \frac{\sqrt{-\Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(82)

$$\begin{aligned}& \begin{aligned}[b] Q_{213}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d-\frac{1}{2(v-1)} \biggl( \lambda +\sqrt{-\Omega } \cot \biggl( \frac{\sqrt{- \Omega }}{2} \biggl( c-\frac{2 k t^{\alpha }}{\alpha } \biggr) \biggr) \biggr) \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(83)

$$\begin{aligned}& \begin{aligned}[b] P_{214}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl(d+ \frac{1}{2(v-1)} \biggl(-\lambda +\sqrt{-\Omega } \biggl( \tan \biggl(\sqrt{- \Omega } \biggl( c-\frac{2 k t^{ \alpha }}{\alpha }\biggr)\biggr)\hspace{-30pt} \\ & \quad {} \pm \sec \biggl(\sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr)\biggr)\biggr)\biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(84)

$$\begin{aligned}& \begin{aligned}[b] Q_{214}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl(d+ \frac{1}{2(v-1)} \biggl(-\lambda +\sqrt{-\Omega } \biggl( \tan \biggl( \sqrt{- \Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr)\biggr) \\ & \quad {} \pm \sec \biggl(\sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr)\biggr)\biggr)\biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(85)

$$\begin{aligned}& \begin{aligned}[b] P_{215}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl(d- \frac{1}{2(v-1)} \biggl(\lambda +\sqrt{-\Omega } \biggl( \cot \biggl(\sqrt{-\Omega } \biggl( c-\frac{2 k t^{ \alpha }}{\alpha }\biggr) \biggr)\hspace{-20pt} \\ & \quad {} \pm \csc \biggl(\sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr)\biggr)\biggr)\biggr)\biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(86)

$$\begin{aligned}& \begin{aligned}[b] Q_{215}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl(d- \frac{1}{2(v-1)} \biggl(\lambda +\sqrt{-\Omega } \biggl( \cot \biggl( \sqrt{- \Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr)\biggr) \\ & \quad {} \pm \csc \biggl(\sqrt{-\Omega } \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr)\biggr)\biggr)\biggr)\biggr]^{2}. \end{aligned} \end{aligned}$$

(87)

$$\begin{aligned}& \begin{aligned}[b] P_{216}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl(d+ \frac{1}{4(v-1)} \biggl(-2 \lambda +\sqrt{-\Omega } \biggl( \tan \biggl( \frac{\sqrt{-\Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr)\biggr) \\ & \quad {} - \cot \biggl(\frac{\sqrt{-\Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha }\biggr) \biggr)\biggr)\biggr)\biggr)\biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(88)

$$\begin{aligned}& \begin{aligned}[b] Q_{216}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl(d+ \frac{1}{4(v-1)} \biggl(-2 \lambda +\sqrt{-\Omega } \biggl( \tan \biggl(\frac{\sqrt{- \Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{\alpha }\biggr) \biggr) \\ & \quad {} - \cot \biggl(\frac{\sqrt{-\Omega }}{4} \biggl( c-\frac{2 k t^{\alpha }}{ \alpha }\biggr) \biggr)\biggr)\biggr)\biggr)\biggr]^{2}. \end{aligned} \end{aligned}$$

(89)

$$\begin{aligned}& \begin{aligned}[b] P_{217}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl(d+ \frac{1}{2(v-1)} \biggl(-\lambda \\ &\quad{} +\frac{\pm \sqrt{-\Omega (A^{2}-B^{2})}-A \sqrt{-\Omega } \cos (\sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha }) )}{A \sin (\sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha }) )+B}\biggr)\biggr) \biggr] \\ & \quad {} \times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(90)

$$\begin{aligned}& \begin{aligned}[b] Q_{217}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1}+a_{1} \biggl(d+ \frac{1}{2(v-1)} \biggl(-\lambda \\ &\quad{}+\frac{\pm \sqrt{-\Omega (A^{2}-B^{2})}-A \sqrt{-\Omega } \cos (\sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha }) )}{A \sin (\sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha }) )+B}\biggr)\biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(91)

$$\begin{aligned}& \begin{aligned}[b] P_{218}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl(d+ \frac{1}{2(v-1)} \biggl(-\lambda \\ &\quad{}+\frac{\pm \sqrt{-\Omega (A^{2}-B^{2})}+A \sqrt{-\Omega } \cos (\sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha }) )}{A \sin (\sqrt{- \Omega } ( c-\frac{2 k t^{\alpha }}{\alpha }) )+B}\biggr)\biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(92)

$$\begin{aligned}& \begin{aligned}[b] Q_{218}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1}+a_{1} \biggl(d+ \frac{1}{2(v-1)}\biggl(-\lambda \\ &\quad{}+\frac{\pm \sqrt{-\Omega (A^{2}-B^{2})}+A \sqrt{-\Omega } \cos (\sqrt{-\Omega } ( c-\frac{2 k t^{ \alpha }}{\alpha }))}{A \sin (\sqrt{-\Omega } ( c-\frac{2 k t ^{\alpha }}{\alpha }) )+B}\biggr)\biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(93)

$$\begin{aligned}& \begin{aligned}[b] P_{219}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d- \frac{2 \mu \cos ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) }{\sqrt{-\Omega } \sin ( \frac{\sqrt{- \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) + \lambda \cos ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) } \biggr) \biggr] \\ &\quad{}\times e^{i (k x+\frac{c t ^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(94)

$$\begin{aligned}& \begin{aligned}[b] Q_{219}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d-\frac{2 \mu \cos ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) }{\sqrt{-\Omega } \sin ( \frac{\sqrt{- \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) + \lambda \cos ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(95)

$$\begin{aligned}& \begin{aligned}[b] P_{220}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+ \frac{2 \mu \sin ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) }{\sqrt{-\Omega } \cos ( \frac{\sqrt{- \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) - \lambda \sin ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) } \biggr) \biggr] \\ &\quad{}\times e^{i (k x+\frac{c t ^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(96)

$$\begin{aligned}& \begin{aligned}[b] Q_{220}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d+\frac{2 \mu \sin ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) }{\sqrt{-\Omega } \cos ( \frac{\sqrt{- \Omega }}{2} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) - \lambda \sin ( \frac{\sqrt{-\Omega }}{2} ( c-\frac{2 k t ^{\alpha }}{\alpha } ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(97)

$$\begin{aligned}& \begin{aligned}[b] P_{221}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d- \frac{2 \mu \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{-\Omega } \sin ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) +\lambda \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) \pm \sqrt{- \Omega }} \biggr) \biggr]\hspace{-20pt} \\ &\quad{}\times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(98)

$$\begin{aligned}& \begin{aligned}[b] Q_{221}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1}+a_{1} \biggl( d \\ &\quad{}-\frac{2 \mu \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) }{\sqrt{-\Omega } \sin ( {\sqrt{- \Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) + \lambda \cos ( {\sqrt{-\Omega }} ( c-\frac{2 k t^{ \alpha }}{\alpha } ) ) \pm \sqrt{-\Omega }} \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(99)

$$\begin{aligned}& \begin{aligned}[b] P_{222}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl(d+ \frac{2 \mu \sin ({\sqrt{- \Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha }) )}{\sqrt{-\Omega } \cos ({\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha }) )- \lambda \sin ({\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{ \alpha }) )\pm \sqrt{-\Omega }}\biggr)\biggr]\hspace{-20pt} \\ &\quad{}\times e^{i (k x+\frac{c t^{ \alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(100)

$$\begin{aligned}& \begin{aligned}[b] Q_{222}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl(d+\frac{2 \mu \sin ({\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha }) )}{\sqrt{-\Omega } \cos ({\sqrt{-\Omega }} ( c-\frac{2 k t ^{\alpha }}{\alpha }) )-\lambda \sin ({\sqrt{-\Omega }} ( c-\frac{2 k t^{\alpha }}{\alpha }) )\pm \sqrt{-\Omega }}\biggr)\biggr]\hspace{-20pt} \\ &\quad{}\times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(101)

where A, B are arbitrary real constants and $A^{2}-B^{2}>0$.

• When $\mu =0$ and $\lambda (v-1)\neq 0$, we have:

$$\begin{aligned}& \begin{aligned}[b] P_{223}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{} +a_{1} \biggl( d- \frac{\lambda k}{(v-1) ( k+\cosh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )-\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) } \biggr) \biggr] \\ &\quad{}\times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(102)

$$\begin{aligned}& \begin{aligned}[b] Q_{223}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d-\frac{ \lambda k}{(v-1) ( k+\cosh (\lambda ( c-\frac{2 k t^{ \alpha }}{\alpha } ) )-\sinh (\lambda ( c-\frac{2 k t^{ \alpha }}{\alpha } ) ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(103)

$$\begin{aligned}& \begin{aligned}[b] P_{224}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d- \frac{\lambda ( \cosh ( \lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )+\sinh ( \lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) }{(v-1) ( k+\cosh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )+\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) } \biggr) \biggr] \\ &\quad{}\times e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(104)

$$\begin{aligned}& \begin{aligned}[b] Q_{224}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1} \\ &\quad{}+a_{1} \biggl( d-\frac{ \lambda ( \cosh (\lambda ( c-\frac{2 k t^{\alpha }}{ \alpha } ) )+\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{ \alpha } ) ) ) }{(v-1) ( k+\cosh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) )+\sinh (\lambda ( c-\frac{2 k t^{\alpha }}{\alpha } ) ) ) } \biggr) \biggr]^{2}. \end{aligned} \end{aligned}$$

(105)

$$\begin{aligned}& \begin{aligned}[b] P_{225}(x,t) &=\biggl[-\frac{4 \delta \lambda a_{1} (d \lambda - \mu )}{4 c \delta +\delta -1}+a_{1} \biggl( d- \frac{1}{(v-1) ( c-\frac{2 k t^{\alpha }}{\alpha } ) + C} \biggr) \biggr] e^{i (k x+\frac{c t^{\alpha }}{\alpha })}, \end{aligned} \end{aligned}$$

(106)

$$\begin{aligned}& \begin{aligned}[b] Q_{225}(x,t) &=\frac{1}{1-4 k^{2}} \biggl[-\frac{4 \delta \lambda a _{1} (d \lambda -\mu )}{4 c \delta +\delta -1}+a_{1} \biggl( d-\frac{1}{(v-1) ( c-\frac{2 k t^{\alpha }}{\alpha } ) + C} \biggr) \biggr]^{2}, \end{aligned} \end{aligned}$$

(107)

where C, k are arbitrary constants.

3 Conclusion

We implement two recent methods called a generalized Kudryashov method and a novel $( \frac{G'}{G} ) $-expansion method. We obtain many forms of solutions that cover all previous solutions obtained by implementation of different methods [1–20]. We get new forms of analytical wave solutions for the nonlinear complex fractional generalized-Zakharov equations. Studying the physical properties of these kinds of models is very motivating and interesting. As we see, both of these methods are very direct, effective, and powerful, and we also showed the ability of these methods to be applied to different kinds of nonlinear partial differential equations whether they are of the fractional order or of the integer order.

References

Malfliet, W., Hereman, W.: The tanh method: I. Exact solutions of nonlinear evolution and wave equations. Phys. Scr. 54(6), 563 (1996)
Article MathSciNet MATH Google Scholar
Borhanifar, A., Kabir, M.M., Vahdat, L.M.: New periodic and soliton wave solutions for the generalized Zakharov system and $(2+1)$-dimensional Nizhnik–Novikov–Veselov system. Chaos Solitons Fractals 42(3), 1646–1654 (2009)
Article MathSciNet MATH Google Scholar
Li, B., Chen, Y., Zhang, H.: Exact travelling wave solutions for a generalized Zakharov–Kuznetsov equation. Appl. Math. Comput. 146(2), 653–666 (2003)
MathSciNet MATH Google Scholar
Yong, C., Biao, L.: New exact travelling wave solutions for generalized Zakharov–Kuznetsov equations using general projective Riccati equation method. Commun. Theor. Phys. 41, 1 (2004)
Article MATH Google Scholar
Naher, H., Abdullah, F.A., Akbar, M.A.: New traveling wave solutions of the higher dimensional nonlinear partial differential equation by the Exp-function method. J. Appl. Math. 2012, Article ID 575387 (2012)
MathSciNet MATH Google Scholar
Abdou, M.A.: The extended tanh method and its applications for solving nonlinear physical models. Appl. Math. Comput. 190(1), 988–996 (2007)
MathSciNet MATH Google Scholar
Tuluce Demiray, S., Bulut, H.: Some exact solutions of generalized Zakharov system. Waves Random Complex Media 25(1), 75–90 (2015)
Article MathSciNet MATH Google Scholar
Zhang, H.: New exact travelling wave solutions of the generalized Zakharov equations. Rep. Math. Phys. 60(1), 97–106 (2007)
Article MathSciNet MATH Google Scholar
Seadawy, A.: Modulation instability analysis for the generalized derivative higher order nonlinear Schrödinger equation and its the bright and dark soliton solutions. J. Electromagn. Waves Appl. 31(14), 1353–1362 (2017)
Article MathSciNet Google Scholar
Wazwaz, A.-M.: The extended tanh method for the Zakharov–Kuznetsov (ZK) equation, the modified ZK equation, and its generalized forms. Commun. Nonlinear Sci. Numer. Simul. 13(6), 1039–1047 (2008)
Article MathSciNet MATH Google Scholar
Zhang, L.-H.: Travelling wave solutions for the generalized Zakharov–Kuznetsov equation with higher-order nonlinear terms. Appl. Math. Comput. 208(1), 144–155 (2009)
Article MathSciNet MATH Google Scholar
Wazwaz, A.-M.: Exact solutions with solitons and periodic structures for the Zakharov–Kuznetsov (ZK) equation and its modified form. Commun. Nonlinear Sci. Numer. Simul. 10(6), 597–606 (2005)
Article MathSciNet MATH Google Scholar
Kabir, M.M., Khajeh, A., Abdi Aghdam, E., Yousefi Koma, A.: Modified Kudryashov method for finding exact solitary wave solutions of higher-order nonlinear equations. Math. Methods Appl. Sci. 34(2), 213–219 (2011)
Article MathSciNet MATH Google Scholar
Layeni, O.P.: A new rational auxiliary equation method and exact solutions of a generalized Zakharov system. Appl. Math. Comput. 215(8), 2901–2907 (2009)
MathSciNet MATH Google Scholar
Betchewe, G., Bouetou, T.B., Victor, K.K., Kofane, T.C.: Dynamical survey of a generalized-Zakharov equation and its exact travelling wave solutions. Appl. Math. Comput. 217(1), 203–211 (2010)
MathSciNet MATH Google Scholar
Shang, Y., Huang, Y., Yuan, W.: New exact traveling wave solutions for the Klein–Gordon–Zakharov equations. Comput. Math. Appl. 56(5), 1441–1450 (2008)
Article MathSciNet MATH Google Scholar
Jin, S., Markowich, P.A., Zheng, C.: Numerical simulation of a generalized Zakharov system. J. Comput. Phys. 201(1), 376–395 (2004)
Article MathSciNet MATH Google Scholar
Al-Muhiameed, Z.I.A., Abdel-Salam, E.A.-B.: Generalized Jacobi elliptic function solution to a class of nonlinear Schrödinger-type equations. Math. Probl. Eng. 2011, Article ID 575679 (2011)
Article MATH Google Scholar
El-Wakil, S.A., Degheidy, A.R., Abulwafa, E.M., Madkour, M.A., Attia, M.T., Abdou, M.A.: Exact travelling wave solutions of generalized Zakharov equations with arbitrary power nonlinearities. Int. J. Nonlinear Sci. 7(4), 455–461 (2009)
MathSciNet Google Scholar
Huang, D.-J., Zhang, H.-Q.: New exact travelling waves solutions to the combined KdV-MKdV and generalized Zakharov equations. Rep. Math. Phys. 57(2), 257–269 (2006)
Article MathSciNet MATH Google Scholar
Lu, D., Seadawy, A.R., Ali, A.: Applications of exact traveling wave solutions of modified Liouville and the symmetric regularized long wave equations via two new techniques. Results Phys. 9, 1403–1410 (2018)
Article Google Scholar
Khater, M., Seadawy, A.R., Lu, D.: New optical soliton solutions for nonlinear complex fractional Schrödinger equation via new auxiliary equation method and novel $G'/G$-expansion method. Pramana 90, 59 (2018)
Article Google Scholar
Seadawy, A.R., Lu, D., Khater, M.M.A.: New wave solutions for the fractional-order biological population model, time fractional burgers, Drinfel’d–Sokolov–Wilson and system of shallow water wave equations and their applications. Eur. J. Comput. Mech. 26, 508–524 (2017)
Article MathSciNet Google Scholar
Seadawy, A.R., Lu, D., Khater, M.M.A.: Bifurcations of traveling wave solutions for Dodd–Bullough–Mikhailov equation and coupled Higgs equation and their applications. Chin. J. Phys. 55(4), 1310–1318 (2017)
Article Google Scholar
Khater, M.M.A., Seadawy, A.R., Lu, D.: Elliptic and solitary wave solutions for Bogoyavlenskii equations system, couple Boiti–Leon–Pempinelli equations system and time-fractional Cahn–Allen equation. Results Phys. 7, 2325–2333 (2017)
Article Google Scholar
Lu, D., Seadawy, A.R., Khater, M.M.A.: Bifurcations of new multi soliton solutions of the van der Waals normal form for fluidized granular matter via six different methods. Results Phys. 7, 2028–2035 (2017)
Article Google Scholar
Hafez, M.G., Alam, M.N., Akbar, M.A.: Exact traveling wave solutions of the Klein–Gordon equation using the novel $(G'/G)$-expansion method. Results Phys. 4, 177–184 (2014)
Article Google Scholar
Alam, M.N., Akbar, M.A., Mohyud-Din, S.T.: General traveling wave solutions of the strain wave equation in microstructured solids via the new approach of generalized $(G'/G)$-expansion method. Alex. Eng. J. 53(1), 233–241 (2014)
Article Google Scholar
Alam, M.N., Akbar, M.A., Harun-Or-Roshid: Study of nonlinear evolution equations to construct traveling wave solutions via the new approach of the generalized $(G'/G)$-expansion method. Math. Stat. 1(3), 102–112 (2013)
Google Scholar
Islam, R., Alam, M.N., Hossain, A.K.M.K.S., Harun-Or-Roshid, Akbar, M.A.: Traveling wave solutions of nonlinear evolution equations via $\operatorname{Exp}(-\Phi(\eta))$-expansion method. Glob. J. Sci. Front. Res. 13(11), 63–71 (2013)
Google Scholar
Ravichandran, C., Jothimani, K., Baskonus, H.M., Valliammal, N.: New results on nondensely characterized integrodifferential equations with fractional order. Eur. Phys. J. Plus 133(109), 1–10 (2018)
Google Scholar
Baskonus, H.M., Hammouch, Z., Mekkaoui, T., Bulut, H.: Chaos in the fractional order logistic delay system: circuit realization and synchronization. AIP Conf. Proc. 1738, 290005 (2016)
Article Google Scholar
Baskonus, H.M., Mekkaoui, T., Hammouch, Z., Bulut, H.: Active control of a chaotic fractional order economic system. Entropy 17(8), 5771–5783 (2015)
Article Google Scholar
Baskonus, H.M., Bulut, H.: On the numerical solutions of some fractional ordinary differential equations by fractional Adams–Bashforth–Moulton method. Open Math. 13(1), 547–556 (2015)
Article MathSciNet MATH Google Scholar
Esen, A., Sulaiman, T.A., Bulutb, H., Baskonus, H.M.: Optical solitons to the space-time fractional $(1+1)$-dimensional coupled nonlinear Schrödinger equation. Optik, Int. J. Light Electron Opt. 167, 150–156 (2018)
Article Google Scholar
Zhang, Z.: New exact traveling wave solutions for the nonlinear Klein–Gordon equation. Turk. J. Phys. 32, 235–240 (2008)
Google Scholar
Zhang, Z., Liu, Z., Miao, X., Chen, Y.: New exact solutions to the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity. Appl. Math. Comput. 216, 3064–3072 (2010)
MathSciNet MATH Google Scholar
Zhang, Z., Li, Y., Liu, Z., Miao, X.: New exact solutions to the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity via modified trigonometric function series method. Commun. Nonlinear Sci. Numer. Simul. 16(8), 3097–3106 (2011)
Article MathSciNet MATH Google Scholar
Zhang, Z., Liu, Z., Miao, X., Chen, Y.: Qualitative analysis and traveling wave solutions for the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity. Phys. Lett. A 375, 1275–1280 (2011)
Article MathSciNet MATH Google Scholar
Zhang, Z., Xia, F.-L., Li, X.-P.: Bifurcation analysis and the travelling wave solutions of the Klein–Gordon–Zakharov equations. Pramana 80(1), 41–59 (2013)
Article Google Scholar
Zhang, Z.-Y., Gan, X.-Y., Yu, D.-M., Zhang, Y.-H., Li, X.-P.: A note on exact traveling wave solutions of the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity. Commun. Theor. Phys. 57, 764–770 (2012)
Article MathSciNet MATH Google Scholar
Miao, X., Zhang, Z.: The modified $(G/G')$-expansion method and traveling wave solutions of nonlinear the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity. Commun. Nonlinear Sci. Numer. Simul. 16(11), 4259–4267 (2011)
Article MathSciNet MATH Google Scholar
Khater, A.H., Callebaut, D.K., Seadawy, A.R.: General soliton solutions of an n-dimensional complex Ginzburg–Landau equation. Phys. Scr. 62, 353–357 (2000)
Article MathSciNet Google Scholar
Seadawy, A.: The generalized nonlinear higher order of KdV equations from the higher order nonlinear Schrödinger equation and its solutions. Optik, Int. J. Light Electron Opt. 139, 31–43 (2017)
Article Google Scholar
Seadawy, A.R.: Travelling wave solutions of a weakly nonlinear two-dimensional higher order Kadomtsev–Petviashvili dynamical equation for dispersive shallow water waves. Eur. Phys. J. Plus 132, 29 (2017)
Article Google Scholar
Khater, A.H., Callebaut, D.K., Seadawy, A.R.: Nonlinear dispersive Kelvin–Helmholtz instabilities in magnetohydrodynamic flows. Phys. Scr. 67, 340–349 (2003)
Article MATH Google Scholar
Seadawy, A.R.: Solitary wave solutions of two-dimensional nonlinear Kadomtsev–Petviashvili dynamic equation in a dust acoustic plasmas. Pramana 89(3), 49 (2017)
Article Google Scholar
Seadawy, A.R., El-Rashidy, K.: Rayleigh–Taylor instability of the cylindrical flow with mass and heat transfer. Pramana 87, 20 (2016)
Article Google Scholar
Kilic, B., Inc, M.: Soliton solutions for the Kundu–Eckhaus equation with the aid of unified algebraic and auxiliary equation expansion methods. J. Electromagn. Waves Appl. 30, 871–879 (2016)
Article Google Scholar
Inc, M., Ates, E., Tchier, F.: Optical solitons of the coupled nonlinear Schrödinger’s equation with spatiotemporal dispersion. Nonlinear Dyn. 85, 1319–1329 (2016)
Article MATH Google Scholar
Tchier, F., Inc, M., Kilic, B., Akgül, A.: On soliton structures of generalized resonance equation with time dependent coefficients. Optik 128, 218–223 (2017)
Article Google Scholar
Kilic, B., Inc, M.: Optical solitons for the Schrodinger–Hirota equation with power law nonlinearity by the Backlund transformation. Optik 138, 64–67 (2017)
Article Google Scholar
Al Qurashi, M., Baleanu, D., Inc, M.: Optical solitons of transmission equation of ultra-short optical pulse in parabolic law media with the aid of Backlund transformation. Optik 140, 114–122 (2017)
Article Google Scholar
Tchier, F., Aslan, E.C., Inc, M.: Optical solitons in parabolic law medium: Jacobi elliptic function solution. Nonlinear Dyn. 85, 2577–2582 (2016)
Article MathSciNet Google Scholar
Al Qurashi, M.M., Yusuf, A., Aliyu, A.I., Inc, M.: Optical and other solitons for the fourth-order dispersive nonlinear Schrödinger equation with dual-power law nonlinearity. Superlattices Microstruct. 105, 183–197 (2017)
Article Google Scholar

Download references

Acknowledgements

The authors thank the referees for their suggestions and comments.

Funding

Funding information is not applicable / No funding was received.

Author information

Authors and Affiliations

Department of Mathematics, Faculty of Science, Jiangsu University, Zhenjiang, China
Dianchen Lu & Mostafa M. A. Khater
Mathematics Department, Faculty of Science, Taibah University, Al-Madinah Al-Munawarah, Saudi Arabia
Aly R. Seadawy
Mathematics Department, Faculty of Science, Beni-Suef University, Beni-Suef, Egypt
Aly R. Seadawy

Authors

Dianchen Lu
View author publications
You can also search for this author in PubMed Google Scholar
Aly R. Seadawy
View author publications
You can also search for this author in PubMed Google Scholar
Mostafa M. A. Khater
View author publications
You can also search for this author in PubMed Google Scholar

Contributions

All parts contained in the research were carried out by the authors through hard work and review of the various references and contributions in the field of mathematics and applied physics. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Aly R. Seadawy.

Ethics declarations

Competing interests

This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors. The authors did not have any competing interests in this research.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Reprints and permissions

About this article

Cite this article

Lu, D., Seadawy, A.R. & Khater, M.M.A. Structure of solitary wave solutions of the nonlinear complex fractional generalized Zakharov dynamical system. Adv Differ Equ 2018, 266 (2018). https://doi.org/10.1186/s13662-018-1734-4

Download citation

Received: 11 April 2018
Accepted: 27 July 2018
Published: 03 August 2018
DOI: https://doi.org/10.1186/s13662-018-1734-4

Structure of solitary wave solutions of the nonlinear complex fractional generalized Zakharov dynamical system

Abstract

Similar content being viewed by others

A novel approach for solitary wave solutions of the generalized fractional Zakharov-Kuznetsov equation

New Solitary Wave Solutions and Dynamical Behaviors of the Nonlinear Fractional Zakharov System

A novel analytical technique to obtain the solitary solutions for nonlinear evolution equation of fractional order

1 Introduction

2 Formulation for the nonlinear complex fractional generalized-Zakharov equations

2.1 Exact and solitary wave solution of the nonlinear complex fractional generalized-Zakharov equations by using a generalized Kudryashov method

2.2 Exact and solitary wave solution of the nonlinear complex fractional generalized-Zakharov equations by using novel \((\frac{G'}{G})\)-expansion method

Family 1

Family 2

3 Conclusion

References

Acknowledgements

Funding

Author information

Authors and Affiliations

Contributions

Corresponding author

Ethics declarations

Competing interests

Additional information

Publisher’s Note

Rights and permissions

About this article

Cite this article

Keywords

Navigation

Structure of solitary wave solutions of the nonlinear complex fractional generalized Zakharov dynamical system

Abstract

Similar content being viewed by others

A novel approach for solitary wave solutions of the generalized fractional Zakharov-Kuznetsov equation

New Solitary Wave Solutions and Dynamical Behaviors of the Nonlinear Fractional Zakharov System

A novel analytical technique to obtain the solitary solutions for nonlinear evolution equation of fractional order

1 Introduction

2 Formulation for the nonlinear complex fractional generalized-Zakharov equations

2.1 Exact and solitary wave solution of the nonlinear complex fractional generalized-Zakharov equations by using a generalized Kudryashov method

2.2 Exact and solitary wave solution of the nonlinear complex fractional generalized-Zakharov equations by using novel \((\frac{G'}{G})\)-expansion method

Family 1

Family 2

3 Conclusion

References

Acknowledgements

Funding

Author information

Authors and Affiliations

Contributions

Corresponding author

Ethics declarations

Competing interests

Additional information

Publisher’s Note

Rights and permissions

About this article

Cite this article

Share this article

Keywords

Search

Navigation