1 Introduction

Fractional calculus is a branch of mathematical analysis. Fractional integral and differential models have attracted great interest due to their applications in many fields of science and engineering. Some interesting applications of fractional calculus can be found in viscoelasticity [1], electromagnetic waves [2], chaotic systems [3], physical systems [4], optimization [5], nonlinear dynamical systems [6], heat transfer modeling [7], and dynamics of interfaces between nanoparticles and substrates [8].

In addition, the application of fractional calculus in viscoelasticity has become an interesting field of study to be considered. For example, fractional derivatives without singular kernels have been proposed as mathematical tools to describe the mathematical models in viscoelasticity [9, 10]. New fractional-order Maxwell and Voigt models within the framework of general fractional derivatives are proposed and used to describe the complex behaviors of the general fractional-order viscoelasticity with memory effect [11]. In [12], a new model is given to illustrate the efficiency of fractional-order operators to the line viscoelasticity. Recently, the viscoelastic characteristics of real materials have been efficiently demonstrated and illustrated with the local fractional models [13] such as local fractional two-dimensional Burgers-type equations [14], the local fractional Klein-Gordon equation, the Helmholtz equation [15], and other types of equations.

Due to a wide range of applications of fractional calculus, the theoretical and numerical analysis of fractional differential equations has been receiving increasing attention by many researchers [16, 17]. Consequently, many methods have been developed to give numerical solutions for fractional equations, including fractional differential transform method [18], Adomian’s decomposition method [19, 20], homotopy analysis method [21, 22], wavelet method [23–26], mixed method [27], and other methods [28–30].

Recently, some fractional-order functions (polynomial or wavelet) have been proposed to solve fractional differential equations. Bhrawy et al. [31] proposed the fractional-order generalized Laguerre functions to find numerical solution of systems of fractional differential equations. Yuzbasi [32] presented a collocation method based on the fractional-order Bernstein polynomials for the fractional Riccati type differential equations. Kazem [33] used fractional-order Legendre functions to solve the fractional differential equations. In [34, 35], fractional-order Bernoulli wavelets were used to solve the fractional differential equations. However, according to the authors’ knowledge, these methods as mentioned above have not been used to solve fractional integro-differential equations. In the present paper, we are planning to generalize new functions based on Euler polynomials and to acquire numerical solution of the fractional integro-differential equations without discretizing. This method is accurate, advantageous, and easy to implement in solving the fractional integro-differential equations.

We organize the rest of the paper as follows. In Sect. 2, we introduce some basic definitions and mathematical preliminaries of fractional calculus theory. In Sect. 3, the fractional-order Euler functions and their properties are obtained. Section 4 is devoted to constructing the FEFs operational matrix of fractional integration. In Sect. 5, the numerical scheme for solving the fractional integro-differential equations is expressed. In Sect. 6, we discuss the convergence of the method presented in Sect. 5. Finally, we report our numerical results and demonstrate the accuracy of the proposed method by considering numerical examples.

2 Preliminaries and notations

There are several definitions for fractional derivatives such as the one in Riemann–Liouville’s sense and the one in Caputo’s sense [36].

Definition 2.1

The Riemann–Liouville fractional integral operator \(I^{v}\) of order v is given by

$$ I^{v} f(t)= \textstyle\begin{cases} \frac{1}{\Gamma (v)}\int^{t}_{0} (t-\tau)^{v-1}f(\tau)\,\mathrm{d}\tau,&\nu>0, t>0,\\ f(t),&\nu=0. \end{cases} $$
(1)

For the Riemann–Liouville fractional integral, we have

$$\begin{gathered} \mbox{(1)}\quad I^{v} \bigl( \lambda_{1}f(t)+\lambda_{2} g(t)\bigr) = \lambda_{1}I^{v} f(t)+\lambda_{2} I^{v}g(t),\qquad\mbox{(2)}\quad I^{v_{1}}I^{v_{2}} f(t) = I^{v_{1}+v_{2}} f(t), \\ \mbox{(3)}\quad I^{v_{2}}I^{v_{1}} f(t) = I^{v_{1}}I^{v_{2}} f(t),\qquad\mbox{(4)}\quad I^{v}t^{\beta}= \frac{\Gamma(\beta+1)}{\Gamma(\beta +v+1)}t^{v+\beta},\quad\beta>-1, \end{gathered} $$

where \(\lambda_{1}\), \(\lambda_{2}\) are constants.

Definition 2.2

The fractional derivative of \(f(t)\) in the Caputo sense is defined as

$$ \bigl(D^{\nu}f\bigr) (t)=\frac{1}{\Gamma(m-\nu)} \int^{t}_{0} \frac{f^{(m)}(\tau)}{(t-\tau)^{\nu+1-m}}\,\mathrm{d}\tau, \quad m-1< \alpha\leq m, m\in N, $$
(2)

where \(t>0\), \(f \in C^{m}_{-1}\). For the Caputo derivative, we have: if \(m-1<\nu\leq m\), \(m\in N\) and \(f\in C^{m}_{\upsilon}\), \(\upsilon\geq-1\), then

$$\bigl(D^{\nu}I^{\nu}\bigr) (t)=f(t), $$

and

$$ \bigl(I^{\alpha} D^{\alpha} f\bigr) (t)=f(t)-\sum _{k=0}^{m-1}f^{(k)}\bigl(0^{+}\bigr) \frac{t^{k}}{k!}, \quad t>0. $$
(3)

Definition 2.3

(Generalized Taylor’s formula, [33])

Suppose that \(D^{i\alpha} f(t) \in C(0, 1]\) for \(i = 0, 1, \ldots, m + 1\), then we have

$$ f(t)= \sum_{i=0}^{m} \frac{t^{i\alpha}}{\Gamma(i\alpha+1)}D^{i\alpha }f(0+)+ \frac{t^{(m+1)\alpha}}{\Gamma((m+1)\alpha+1)}D^{(m+1)\alpha}f(\xi), $$
(4)

with \(0<\xi\leq t\), for all \(t \in(0,1]\). Also, we have

$$ \Biggl\vert f(t)-\sum_{i=0}^{m} \frac{t^{i\alpha}}{\Gamma(i\alpha +1)}D^{i\alpha}f(0+) \Biggr\vert \leq M_{\alpha}\frac{t^{(m+1)\alpha }}{\Gamma((m+1)\alpha+1)}, $$
(5)

where \(M_{\alpha}\geq \sup_{\xi\in(0,1]} |D^{(m+1)\alpha}f(\xi)|\). In case of \(\alpha= 1\), the generalized Taylor’s formula (4) reduces to the classical Taylor’s formula.

3 Fractional-order Euler functions

3.1 Euler polynomials

The Euler basis polynomials \(E_{m}(t)\) of degree m are constructed from the following relation [37]:

$$ \sum_{k=0}^{m} \binom{m}{k}E_{k}(t)+E_{m}(t)=2t^{m}, $$
(6)

where \(\binom{m}{k}\) is a binomial coefficient. We define the Euler vector \(E(t)\) as follows: \(E(t) = [E_{0}(t), E_{1}(t),\ldots, E_{m}(t)]^{T}\) and

$$ E(t)=DX(t), $$
(7)

where \(X(t) = [1, t, \ldots, t^{m}]^{T}\) and D is an upper triangular matrix with non-zero diagonal elements, thus it is non-singular and hence \(D^{-1}\) exists.

Euler polynomials have the following properties:

$$\begin{gathered} \mbox{(1)}\quad E_{n}'=nE_{n-1}(t), \qquad\mbox{(2)}\quad E_{n+1}(t+1)+E_{n}(t)=2t^{n}, \\ \mbox{(3)}\quad E_{n}(t)=\frac{1}{n+1}\sum _{k=1}^{n+1}\bigl(2-2^{k+1}\bigr) \binom {n+1}{k}B_{k}(0)t^{n+1-k},\quad n=1,2,\ldots, \end{gathered} $$

where \(B_{k}(t)\), \(k = 0, 1, \ldots \) , are the Bernoulli polynomials of order k which are defined as follows:

$$ \sum_{k=0}^{n}\binom{n+1}{k}B_{k}(t)=(n+1)t^{n}. $$

Using property (3) of the Euler polynomials, the Euler polynomials can be represented in the following matrix form:

( E 0 ( t ) E 1 ( t ) ⋮ E m ( t ) ) = ( 2 − 2 2 1 ( 1 1 ) B 1 ( 0 ) 0 … 0 2 − 2 3 2 ( 2 2 ) B 2 ( 0 ) 2 − 2 2 2 ( 2 1 ) B 1 ( 0 ) … 0 ⋮ ⋮ ⋱ ⋮ 2 − 2 m + 2 m + 1 ( m + 1 m + 1 ) B m + 1 ( 0 ) 2 − 2 m + 1 m + 1 ( m + 1 m ) B m ( 0 ) … 2 − 2 2 m + 1 ( m + 1 1 ) B 1 ( 0 ) ) ( 1 t ⋮ t m ) .

Also, these polynomials satisfy the following formula:

$$ \int_{0}^{1} E_{m}(t)E_{n}(t) \,\mathrm{d}t = {(-1)}^{n-1}\frac {m!(n+1)!}{(m+n+1)!}E_{m+n+1}(0),\quad m,n \geq1. $$
(8)

Euler polynomials form a complete basis over the interval \([0, 1]\).

3.2 Fractional-order Euler functions

The fractional-order Euler functions (FEFs) are constructed by change of variable t to \(x^{\alpha}\) (\(\alpha> 0\)) on the Euler polynomials. Let the FEFs \(E_{m}(x^{\alpha})\) be denoted by \(E_{m}^{\alpha}(x)\). By using Eq. (6) the analytic form of \(E_{m}^{\alpha}(x)\) of order mα is given by

$$ \sum_{k=0}^{m} \binom{m}{k}E^{\alpha}_{k}(x)+E^{\alpha}_{m}(x)=2x^{m\alpha}. $$
(9)

The fractional-order Euler polynomials can be represented in the following matrix form:

( E 0 α ( x ) E 1 α ( x ) ⋮ E m α ( x ) ) ⏟ E α = ( 2 − 2 2 1 ( 1 1 ) B 1 ( 0 ) 0 … 0 2 − 2 3 2 ( 2 2 ) B 2 ( 0 ) 2 − 2 2 2 ( 2 1 ) B 1 ( 0 ) … 0 ⋮ ⋮ ⋱ ⋮ 2 − 2 m + 2 m + 1 ( m + 1 m + 1 ) B m + 1 ( 0 ) 2 − 2 m + 1 m + 1 ( m + 1 m ) B m ( 0 ) … 2 − 2 2 m + 1 ( m + 1 1 ) B 1 ( 0 ) ) ⏟ B α ( 1 x α ⋮ x m α ) ⏟ X α
(10)

and the first basic polynomials are expressed by

$$ \begin{aligned} &E_{0}^{\alpha}(x)=1, \qquad E_{1}^{\alpha}(x)=x^{\alpha}- \frac{1}{2}, \qquad E^{\alpha}_{2}(x)=x^{2\alpha}-x^{\alpha}, \\ &E_{3}(x)=x^{3\alpha}-\frac {2}{3}x^{2\alpha}+ \frac{1}{4},\qquad \ldots. \end{aligned} $$

Furthermore, these polynomials satisfy the following formula:

$$ \int_{0}^{1} E^{\alpha}_{m}(x)E^{\alpha}_{n}(x)x^{1-\alpha} \,\mathrm{d}x={(-1)}^{n-1}\frac{m!(n+1)!}{(m+n+1)!}E_{m+n+1}(0), \quad m,n \geq1. $$
(11)

Also, fractional-order Euler functions form a complete basis over the interval \([0, 1]\).

3.3 Function approximation

A function \(f(x)\), square integrable in \([0,1]\), can be expanded as the following formula:

$$ f(x)=\sum_{i=0}^{\infty}c_{i}E_{i}^{\alpha}(x). $$
(12)

In practice, only the first \(m+1\)-terms FEFs are considered, then we have

$$ f(x)\simeq \sum_{i=0}^{m}c_{i}E_{i}^{\alpha}(x)=C^{\mathrm{T}}E^{\alpha}(x), $$
(13)

where the coefficient vector C and the Euler function vector \(E^{\alpha}(x)\) are given by

$$\begin{aligned}& C=[c_{0},c_{1},\dots,c_{m}]^{\mathrm{T}}, \end{aligned}$$
(14)
$$\begin{aligned}& E^{\alpha}(x)=\bigl[E_{0}^{\alpha}(x),E_{1}^{\alpha}(x), \dots,E_{m}^{\alpha}(x)\bigr]^{\mathrm{T}}. \end{aligned}$$
(15)

To evaluate C, we let

$$ a_{j}= \int_{0}^{1}E^{\alpha}_{j}(x)f(x)x^{1-\alpha} \,\mathrm{d}x. $$

Using Eq. (13), we obtain

$$ a_{j}=\sum_{i=0}^{m}c_{i} \int_{0}^{1}E^{\alpha}_{i}(x)E^{\alpha}_{j}(x)x^{\alpha -1} \,\mathrm{d}x=\sum_{i=0}^{m}c_{i}d_{ij}^{\alpha}, $$

where \(d_{ij}^{\alpha}=\int_{0}^{1}E^{\alpha}_{i}(x)E^{\alpha}_{j}(x)x^{\alpha -1} \,\mathrm{d}x\) and \(i=j= 0,1,2,\ldots,m\).

Therefore,

$$ A^{\mathrm{T}}=C^{\mathrm{T}}D, $$

with

$$ A=[a_{0},a_{1},\dots,a_{m}]^{\mathrm{T}} \quad \text{and}\quad D = \bigl[d_{ij}^{\alpha}\bigr], $$

where D is a matrix of order \((m+1)\times(m+1)\) and is given by

$$ D = \int_{0}^{1}E^{\alpha}(x)E^{\alpha T}(x)x^{\alpha-1} \,\mathrm{d}x. $$
(16)

The matrix D in Eq. (16) can be calculated by using Eq. (11).

4 The FEFs operational matrix of the fractional integration

The Riemann–Liouville fractional integration of the vector \(E^{\alpha}(x)\) given in Eq. (15) can be expressed by

$$ I^{\nu}E^{\alpha}(x) = P^{(\nu,\alpha)}E^{\alpha}(x), $$
(17)

where \(P^{(\nu,\alpha)}\) is the \((m+1) \times(m+1)\) Riemann–Liouville fractional operational matrix of integration. By using Eq. (10) and the properties of the operator \(I^{\nu}\), for \(i=0,1,\ldots, m\), we have

$$\begin{aligned} I^{\nu}E^{\alpha}(x) = & I^{\nu}B^{\alpha}X^{\alpha}(x)= B^{\alpha}I^{\nu} X^{\alpha}(x) \\ =&B^{\alpha}\Phi^{(\nu,\alpha)} X^{\alpha}(x)= B^{\alpha}\Phi^{(\nu,\alpha )} \bigl(B^{\alpha}\bigr)^{-1} E^{\alpha}(x), \end{aligned}$$
(18)

where \(\Phi^{(\nu,\alpha)}\) is the Riemann–Liouville operation matrix of fractional integration of the vector \(X^{\alpha}(x)\). Using the properties of the operator \(I^{\nu}\), for \(r=0,1,\ldots, m\), we have

$$\begin{aligned} I^{\nu}X^{\alpha}_{r}(x) = & I^{\nu}x^{r\alpha} = \frac{\Gamma(\alpha r+1)}{\Gamma(\alpha r+1+\nu)}x^{r\alpha+\nu}. \end{aligned}$$

Assume that \(x^{r\alpha+\upsilon}\) can be expanded in terms of fractional-order functions as

$$ x^{r\alpha+\upsilon} \simeq\sum_{j=0}^{m} \theta_{r,j}^{(\nu, \alpha )}X^{\alpha}_{j}(x). $$
(19)

Therefore, we get

$$ \Phi^{(\nu,\alpha)}= \bigl[\theta_{r,j}^{(\nu, \alpha)}\bigr]. $$

So, combining Eq. (17) and Eq. (18), we can get

$$ P^{(\nu,\alpha)} = B^{\alpha}\Phi^{(\nu,\alpha)} \bigl(B^{\alpha}\bigr)^{-1}. $$
(20)

5 Application of the operation matrix of fractional integration

Consider the following fractional integro-differential equation with weakly singular kernel:

$$\begin{aligned}& D^{\nu}y(x)=\lambda \int_{0}^{x} \frac{y(s)}{(x-s)^{\beta}} \,\mathrm{d}s+p(x)y(x)+f(x), \quad\nu>0, 0\leq\beta< 1, x\in I, \end{aligned}$$
(21)
$$\begin{aligned}& y^{(i)}(0)=y_{0}^{(i)},\quad i=1,2,\ldots, n-1, \end{aligned}$$
(22)

where \(y(x)\) is an unknown function, \(f(x)\) and \(p(x)\) are known continuous functions on \(I := [0, X]\), \(y^{(i)}_{0}\) (\(i = 0, 1, \ldots, n-1\)) are given real numbers, \(n := \lceil\nu\rceil\) is the smallest integer which is bigger than the real number, ν, λ are real constants, and \(D^{\nu}\) denotes the Caputo fractional-order derivative of order ν.

Now we approximate \(D^{\nu}y(x)\), \(p(x)\), and \(f(x)\) in terms of FEFs as follows:

$$ D^{\nu}y(x)\approx C^{\mathrm{T}}E^{\alpha}(x), \qquad f(x) \approx F^{\mathrm{T}}E^{\alpha}(x),\qquad p(x)\approx P^{\mathrm{T}}E^{\alpha}(x), $$
(23)

where \(F = {[f_{0}, f_{1}, \ldots, f_{m}]}^{T}\), \(P = {[p_{0}, p_{1}, \ldots, p_{m}]}^{T}\). Using Eqs. (3) and (17), we have

$$ y(x)\approx C^{\mathrm{T}}P^{(\upsilon,\alpha)}E^{\alpha}(x)+\sum _{k=0}^{n-1}y^{(k)}\bigl(0^{+}\bigr) \frac{t^{k}}{k!}. $$
(24)

In the above summation, we substitute the supplementary conditions (22) and approximate them with the FEFs, we can get

$$ y(x)\approx\bigl(C^{\mathrm{T}}P^{(\upsilon,\alpha)}+\tilde{C}^{\mathrm{T}} \bigr)E^{\alpha}(x)=A^{\mathrm{T}}E^{\alpha}(x), $$
(25)

where A, C̃ are m̂-vectors.

By Eqs. (1), (17), and (25), there is

$$\begin{aligned} \int_{0}^{x}\frac{y(s)}{(x-s)^{\beta}}\,\mathrm{d}s=A^{\mathrm{T}} \int_{0}^{x}\frac {E^{\alpha}(x)}{(x-s)^{\beta}}\,\mathrm{d}s = \Gamma(1-\beta)A^{\mathrm{T}} P^{(1-\beta,\alpha)}E^{\alpha}(x). \end{aligned}$$
(26)

By substituting Eqs. (23), (25), and (26) into Eq. (21), we obtain

$$\begin{aligned} C^{\mathrm{T}}E^{\alpha}(x) =&\lambda\Gamma(1-\beta)A^{\mathrm{T}}P^{(1-\beta ,\alpha)}E^{\alpha}(x) \\ &{}+A^{\mathrm{T}}E^{\alpha}(x)\bigl[E^{\alpha}(x) \bigr]^{T} P+F^{\mathrm{T}}E^{\alpha}(x). \end{aligned}$$
(27)

Let \(E^{\alpha}(x)[E^{\alpha}(x)]^{T} P= \hat{P}E^{\alpha}(x)\), where P̂ is the product operational matrix of FEFs that can be computed easily. Therefore, we have

$$\begin{aligned} C^{\mathrm{T}}=\lambda\Gamma(1-\beta)A^{\mathrm{T}}P^{(1-\beta,\alpha)} +A^{\mathrm{T}}\hat{P}+F^{\mathrm{T}}, \end{aligned}$$
(28)

which is a system of linear algebraic equations in terms of the unknown elements of the vector C.

6 Error analysis

A function \(f(x) \in L^{2}[0, 1]\) can be expanded as

$$f(x) \approx\sum_{i=0}^{m}c_{i}E_{i}^{\alpha}(x) = C^{T}E^{\alpha}(x)=f_{m}(x). $$

The error analysis of the FEFs approximation is given by the following theorem.

Theorem 6.1

Suppose that \(D^{k\alpha}f(x) \in C(0,1]\) for \(k=1,2,\ldots, n\), and \(Y_{m}^{\alpha}= \operatorname{span}\{E_{0}^{\alpha}(x), E_{1}^{\alpha}(x), \ldots, E_{m}^{\alpha}(x)\} \) is a vector space. If \(f_{m}(x)\) is the best approximation of f out of \(Y_{m}^{\alpha}\), then the mean error bound is presented as follows:

$$ \Vert f-f_{m} \Vert _{2} \leq\frac{M_{\alpha}}{\Gamma((m+1)\alpha +1)\sqrt{(2m+2)\alpha+1}}, $$

where \(M_{\alpha}\geq\sup_{\xi\in(0,1]}|D^{(m+1)\alpha}f^{(}x)|\).

Proof

Considering the generalized Taylor’s formula \(y(x)= \sum_{i=0}^{m} \frac {x^{i\alpha}}{\Gamma(i\alpha+1)}D^{i\alpha}f(0^{+})\), from Definition 2.3, we have

$$ \bigl\vert f(x)-y(x) \bigr\vert \leq M_{\alpha}\frac{x^{(m+1)\alpha }}{\Gamma((m+1)\alpha+1)}. $$

Since \(f_{m}(x)\) is the best approximation to f from \(Y_{m}^{\alpha}\) and \(y \in Y_{m}^{\alpha}\), so we have

$$\begin{aligned} \Vert f-f_{m} \Vert ^{2}_{2} \leq& \Vert f-y \Vert ^{2}_{2}= \int^{1}_{0}\bigl[f(x)-y(x)\bigr]^{2} \,\mathrm{d}x \\ =& \int^{1}_{0} M_{\alpha}^{2} \frac{x^{(2m+2)\alpha}}{\Gamma((m+1)\alpha +1)^{2}}\,\mathrm{d}x \\ = &\frac{M_{\alpha}^{2}}{\Gamma((m+1)\alpha+1)^{2}} \int^{1}_{0}x^{(2m+2)\alpha }\,\mathrm{d}x \\ =&\frac{M_{\alpha}^{2}}{\Gamma((m+1)\alpha+1)^{2}((2m+2)\alpha+1)}. \end{aligned}$$

The theorem is proved by taking the square roots. Therefore, FEFs approximations of \(f(x)\) are convergent. □

7 Numerical examples

To show the efficiency and accuracy of the proposed method, we consider the following four examples. In order to demonstrate the error of the FEFs method, we introduce the absolute error and root-mean-square error:

$$ e_{m}(x)= \bigl\vert y(x)-y_{m}(x) \bigr\vert ,\qquad \xi_{m}= \biggl( \int_{0}^{1} e_{m}^{2}(x) \,\mathrm{d}x \biggr)^{\frac{1}{2}}, $$

where \(y(x)\) is the exact solution and \(y_{m}(x)\) is the numerical solution by the presented method.

Example 1

Consider the following fractional-order integro-differential equation:

$$ D^{\frac{1}{2}}y(x)= \int_{0}^{x} y(s)\,\mathrm{d}s+y(x)+ \frac{8}{3\Gamma (1/2)}-x^{2}-\frac{1}{3}x^{3}, \quad x \in[0,1], $$
(29)

with the condition \(y(0) = 0\). The exact solution of this equation is \(y(x) = x^{2}\). In this problem we apply the FEFs method to solve Eq. (29) with various values of m and α. Table 1 shows the absolute errors \(e_{m}(x)\) for various values of α. The comparisons show that the best case of α for this equation is \(\alpha=\frac{1}{2}\). Also, we can see the absolute error is the same or slightly smaller than that in [38] when \(\alpha=\frac{1}{2}\), \(m=4\).

Table 1 The absolute errors for different α, m of the FEFs and \(M = 6\) of the Legendre wavelet
Full size table

Example 2

Consider the following fractional-order integro-differential equation with weakly singular kernel [39, 40]:

$$ D^{\frac{1}{3}}y(x)= \int_{0}^{x} \frac{y(s)}{(x-s)^{1/2}} \,\mathrm{d}s+p(x)y(x)+f(x), \quad x\in[0,1], $$
(30)

where

$$f(x)=\frac{6x^{\frac{8}{3}}}{\Gamma(\frac{11}{3})}+\biggl(\frac{32}{35}-\frac {\Gamma(\frac{1}{2})\Gamma(\frac{7}{3})}{\Gamma(\frac{17}{6})} \biggr)x^{\frac {11}{6}}+\Gamma\biggl(\frac{17}{6}\biggr)x, \qquad p(x)=- \frac{32}{35}x^{\frac{1}{2}} $$

with the condition \(y(0) = 0\). The exact solution of this equation is \(y(x) = x^{\frac{4}{3}} + x^{3}\). In this problem we apply the FEFs method to solve Eq. (30) with various values of m. Table 2 shows the root-mean-square errors for the second kind Chebyshev polynomials method (SKCP) [40] and the FEFs method with \(\alpha=1, \frac{2}{3}\). From Table 2, we can see that both of them obtain good approximations with the exact solution and the FEFs method has smaller root-mean-square errors. In this experiment, we also check the convergence rates of the numerical solutions with respect to the value of m. From the numerical results in Table 3, one can see that the order of convergence is two for the FEFs method, which is consistent with our theoretical result.

Table 2 The root-mean-square errors \(\xi_{m}\) of the FEFs method and the SKCP method
Full size table
Table 3 Convergence rates of the FEFs method for Example 2 and Example 3
Full size table

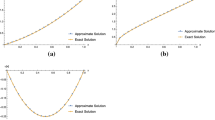
The comparisons between the numerical solutions and the exact solution for \(m = 4,5,6\) are given in Fig. 1.

Figure 1
figure 1

Comparisons of numerical solutions and exact solution of Example 2 for different m

Full size image

Example 3

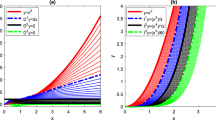
Consider this equation [40]

$$ D^{\nu}y(x)= \int_{0}^{x} \frac{y(s)}{(x-s)^{1/2}} \,\mathrm{d}s+p(x)y(x)+f(x), \quad x\in[0,1], $$
(31)

where \(f(x)=2x\), \(p(x)=-\frac{16}{15}x^{\frac{1}{2}} \) with the condition \(y(0) = 0\). The exact solution is \(y(x) = x^{2} \) when \(\nu= 1\). By setting \(m=5\), we obtain numerical solutions for various values of \(\alpha=\nu\). In Fig. 2, we show the numerical solutions obtained by the presented method and the exact solution for various values of \(\nu =\alpha\). It is obvious from Fig. 2 that, as ν is close to 1, the numerical solutions converge to the exact solution. Table 4 shows the root-mean-square errors for the second kind Chebyshev polynomials method (SKCP) [40] and the FEFs method for \(\alpha=1\) with different m. From Table 4, we can see that the errors decay as m increases and the FEFs method has smaller root-mean-square errors. The convergence rates of the numerical solutions with respect to the value of m are shown in Table 3.

Figure 2
figure 2

Numerical solutions and exact solution for \(m=5\), \(\alpha= \nu\), with \(\nu=0.7,0.8,0.9,1\)

Full size image
Table 4 The root-mean-square errors \(\xi_{m}\) of the FEFs method and the SKCP method for Example 3
Full size table

Example 4

Consider this equation

$$ D^{\frac{1}{4}}y(x)=- \int_{0}^{x} \frac{y(s)}{(x-s)^{1/2}} \,\mathrm{d}s+p(x)y(x)+f(x), \quad x\in[0,1], $$
(32)

where \(f(x)=\pi+\frac{\sqrt{\pi} x^{-\frac{3}{4}}}{\Gamma(\frac{1}{4})}-x\), \(p(x)=x^{\frac{3}{2}} \) with the condition \(y(0) = 0\). The exact solution is \(y(x) = \frac {1}{\sqrt{x}} \). In this case, there is a singularity at point \(x = 0\). The solution can be seen in Fig. 3 with \(\alpha=1.2\), \(m = 7,8,9\). As it is observed, our method provides a reasonable estimate even in this case with singular solution.

Figure 3
figure 3

Comparisons of numerical solutions and exact solution of Example 4 for different m

Full size image

8 Conclusion

In this paper, the fractional-order Euler functions (FEFs) based on Euler polynomials have been constructed to solve the fractional integro-differential equations with weakly singular kernel. The operational matrix of the fractional integration has been derived. By using the operational matrix of fractional integration and the fractional Euler function, we transform the initial problem into a linear algebraic system of equations. By solving the linear system, numerical solutions are obtained. Also, we have considered various types of solutions with smooth, non-smooth, and even singular behavior. In all the considered cases, the method provided reasonable estimates. The numerical results approved that the proposed method is accurate and relatively simple to implement and has very high accuracy.