1 Introduction

Partial differential equations with nonlocal boundary conditions have been widely used to build mathematical models in various fields of science and engineering such as thermoelasticity, physics, medical science, chemical engineering, and so on (see [1–6]).

This work is concerned with the following two-dimensional Poisson equation with two integral boundary conditions:

figure a

where \(f(x,y)\), \(\mu_{i}(y)\ (i=1,2)\), \(\mu_{j}(x)\ (j=3,4)\) are some given smooth functions, and \(\xi_{1}\), \(\xi_{2}\) are constants such that \(0<\xi_{1}<\xi_{2}<1\).

FDM is preferred by many researchers because of its simple format and easy programming. Recently, Sapagovas [7] presented a difference scheme of fourth-order approximation for Poisson equation with two integral boundary conditions. The author also studied its solvability and justified an iteration method for solving the corresponding difference system. Berikelashvili [8] constructed some difference schemes for Poisson problem with one integral condition and obtained its estimate of the convergence rate. For Poisson equation with Bitsadze–Samarskii nonlocal boundary, a new method was developed [9] which used the five-point difference scheme to discretize Laplace operator. There are also some literature works on nonlinear and high order elliptic problems with nonlocal boundary conditions. In [10, 11], the authors presented some iterative methods for the system of difference equations to solve nonlinear elliptic equation with integral condition. Pao and Wang [12, 13] used finite difference method to construct a coupled system of two second-order equations for fourth-order elliptic equations with nonlocal boundary conditions.

In recent years, the radial basis function (RBF) collocation method is very popular for PDEs to seek numerical solution, especially for elliptic equations with nonlocal boundary [14–16]. However, the numerical results of RBF collocation method often suffer from shape parameter and condition number of the collocation matrix. As for some other numerical methods for elliptic equations with nonlocal boundary conditions, e.g., FEM, we refer the reader to [17–19].

To our knowledge, few studies not only focus on building high accuracy difference schemes which are of optimal or asymptotic optimal order for error estimation and showing theoretical proofs, but also on displaying corresponding numerical tests for Poisson problem with nonlocal boundary conditions. Therefore, how to design a high accuracy scheme and prove that it is of optimal or asymptotic optimal order for error estimation is a great challenge for us. In this work, we consider a two-dimensional Poisson problem with two integral conditions. The first novel idea is that we build a high accuracy difference scheme by introducing the equivalent relations which are convenient to discretize two nonlocal conditions. The second one is that we ingeniously apply the discrete Fourier transformation (DFT) to transform the two-dimensional problem to a one-dimensional problem for error analysis. Besides, we prove that the difference scheme can reach the asymptotic optimal error estimate in the maximum norm. Numerical examples confirm the correctness of theoretical results.

This work is organized as follows. In Sect. 2, we present a finite difference scheme for Problem (1.1a)–(1.1e). In Sect. 3, the error equations of the scheme are analyzed with the DFT and the corresponding error estimates are presented. In Sect. 4, we show numerical results to support our conclusions. Finally, a summary of this article and future work in this field are discussed.

2 The finite difference discretization

For convenience of discretizing the integral boundary conditions, we can easily prove the equivalent relations as follows.

Lemma 2.1

Suppose that the solution \(u\in C^{2}(\bar{\Omega})\) in Problem (1.1a)–(1.1e), and \(\mu_{i}(y)\ (i=1,2)\) and \(\mu_{j}(x)\ (j=3,4)\) satisfy the following consistent properties:

$$\begin{aligned} &\int_{0}^{\xi_{1}}\mu_{1}(y)\,dy= \mu_{3}(0),\qquad \int_{0}^{\xi_{1}}\mu_{2}(y)\,dy=\mu _{3}(1), \end{aligned}$$
(2.1)
$$\begin{aligned} &\int^{1}_{\xi_{2}}\mu_{1}(y)\,dy= \mu_{4}(0),\qquad \int^{1}_{\xi_{2}}\mu_{2}(y)\,dy=\mu _{4}(1). \end{aligned}$$
(2.2)

Then the integral boundary conditions (1.1d) and (1.1e) are equivalent to the nonlocal boundary conditions

$$\begin{aligned} u_{y}|_{y=\xi_{1}}-u_{y}|_{y=0}&= \phi_{1}(x) \end{aligned}$$
(2.3)

and

$$\begin{aligned} u_{y}|_{y=1}-u_{y}|_{y=\xi_{2}}&= \phi_{2}(x), \end{aligned}$$
(2.4)

respectively, where

$$\begin{aligned} \phi_{1}(x)= \int^{\xi_{1}}_{0} f(x,y)\,dy-\mu''_{3}(x),\qquad \phi_{2}(x)= \int^{1}_{\xi_{2}} f(x,y)\,dy-\mu''_{4}(x). \end{aligned}$$

Proof

Integrating two sides of (1.1a) about the variable y over the interval \([0,\xi_{1}]\) and using (1.1d), we have

$$\begin{aligned} \mu''_{3}(x)+ \int^{\xi_{1}}_{0} u_{yy}\,dy = \int^{\xi_{1}}_{0} u_{xx}\,dy+ \int^{\xi _{1}}_{0} u_{yy}\,dy= \int^{\xi_{1}}_{0} f(x,y)\,dy, \end{aligned}$$

i.e.,

$$\begin{aligned} u_{y}|_{y=\xi_{1}}-u_{y}|_{y=0}= \int_{0}^{\xi_{1}} f(x,y)\,dy-\mu''_{3}(x), \end{aligned}$$

which yields (2.3).

In turn, when (2.3) holds, together with (1.1a), we can obtain

$$\begin{aligned} \int_{0}^{\xi_{1}} u_{xx}\,dy= \mu''_{3}(x). \end{aligned}$$

Integrating two sides of the above expression about the variable x twice, we have

$$\begin{aligned} \int_{0}^{\xi_{1}}u\,dy=\mu_{3}(x)+C_{1}x+C_{2}, \end{aligned}$$

where \(C_{1}\) and \(C_{2}\) are two constants.

Let \(x=0\) and \(x=1\) in the above equation respectively, and from (1.1b)–(1.1c) and (2.1), we get

$$\begin{aligned} C_{1}=C_{2}=0, \end{aligned}$$

which yields

$$\begin{aligned} \int_{0}^{\xi_{1}} u\,dy=\mu_{3}(x). \end{aligned}$$

Therefore, (1.1d) is equivalent to (2.3)

Similarly, from (1.1a)–(1.1c) and (2.2), we can also derive that (1.1e) is equivalent to (2.4). Thus, the proof of this lemma is completed. □

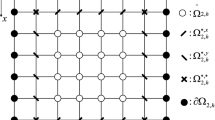
Based on Lemma 2.1, we are now in a position to present the finite difference scheme for Problem (1.1a)–(1.1e). Divide Ω into an \(N\times N\) mesh by

$$\begin{aligned} 0=x_{0}< x_{1}< \cdots< x_{N}=1,\qquad 0=y_{0}< y_{1}< \cdots< y_{N}=1, \end{aligned}$$

where \(x_{i}=i h, y_{j}=j h\), \(h=\frac{1}{N}\) is the stepsize in both x and y directions, and N is the corresponding partition number. For convenience, we only discuss Problem (1.1a)–(1.1e) under the assumption that \(\xi_{1}\) and \(\xi_{2}\) are two rational constants. Moreover, assume that \(\xi_{m}= N_{m} h\) \((m=1,2)\), where \(N_{1},N_{2}\) are integers and \(0< N_{1}< N_{2}< N\).

Let U be the finite difference approximation of u. Denote \(u_{i,j} = u(x_{i}, y_{j})\), \(U_{i,j}=U(x_{i},y_{j})\), \(f_{i,j}=f(x_{i},y_{j})\), \((\mu_{m})_{j}=\mu_{m}(y_{j})\), and \((\phi_{m})_{i}=\phi_{m}(x_{i})\) \((m=1,2)\). Then the governing equation (1.1a) and two local boundary conditions (1.1b) and (1.1c) can be discretized as follows:

$$ \textstyle\begin{cases} \frac{U_{i-1,j}-2U_{i,j}+U_{i+1,j}}{h^{2}}+\frac {U_{i,j-1}-2U_{i,j}+U_{i,j+1}}{h^{2}}=f_{i,j},\quad i,j=1,\ldots,N-1,\\ U_{0,j}=(\mu_{1})_{j}, \qquad U_{N,j}=(\mu_{2})_{j},\quad j=1,\ldots,N-1. \end{cases} $$
(2.5)

From Lemma 2.1, two nonlocal boundary conditions (1.1d) and (1.1e) can be discretized as follows:

$$ \textstyle\begin{cases} \frac{1}{h} (\frac{3}{2}U_{i,N_{1}}-2U_{i,N_{1}-1}+\frac {1}{2}U_{i,N_{1}-2} )-\frac{1}{h} (-\frac {3}{2}U_{i,0}+2U_{i,1}-\frac{1}{2}U_{i,2} ) =(\phi_{1})_{i}, \\ \frac{1}{h} (\frac{3}{2}U_{i,N}-2U_{i,N-1}+\frac {1}{2}U_{i,N-2} )-\frac{1}{h} (-\frac {3}{2}U_{i,N_{2}}+2U_{i,N_{2}+1}-\frac{1}{2}U_{i,N_{2}+2} ) =(\phi_{2})_{i}, \\ \quad i=1,\ldots,N-1. \end{cases} $$
(2.6)

3 Error estimate

Denote the error at point \((x_{i},y_{j})\) by \(e_{i,j}:=U_{i,j}-u_{i,j}\). Suppose that the exact solution \(u\in C^{4}(\bar{\Omega})\). Then, from (2.5) and (2.6), we have

$$ \textstyle\begin{cases} \frac{e_{i-1,j}-2e_{i,j}+e_{i+1,j}}{h^{2}}+\frac {e_{i,j-1}-2e_{i,j}+e_{i,j+1}}{h^{2}}=\alpha_{i,j}, \quad \text{$i,j=1,\ldots,N-1$,} \\ e_{0,j}=e_{N,j}=0, \quad \text{$j=1,\ldots,N-1$,} \end{cases} $$
(3.1)

and

$$\begin{aligned} \textstyle\begin{cases} \frac{1}{h} (\frac{3}{2}e_{i,N_{1}}-2e_{i,N_{1}-1}+\frac {1}{2}e_{i,N_{1}-2} ) -\frac{1}{h} (-\frac{3}{2}e_{i,0}+2e_{i,1}-\frac{1}{2}e_{i,2} )=(\beta_{1})_{i}, \\ \frac{1}{h} (\frac{3}{2}e_{i,N}-2e_{i,N-1}+\frac {1}{2}e_{i,N-2} ) -\frac{1}{h} (-\frac{3}{2}e_{i,N_{2}}+2e_{i,N_{2}+1}-\frac {1}{2}e_{i,N_{2}+2} )=(\beta_{2})_{i},\\ \quad i=1,\ldots,N-1, \end{cases}\displaystyle \end{aligned}$$
(3.2)

where \(\alpha_{i,j}\) and \((\beta_{m})_{i}\ (m=1,2)\) are the corresponding local truncation errors satisfying

$$\begin{aligned} \max_{i,j=1,\ldots, N-1}\bigl\{ \vert \alpha_{i,j} \vert , \bigl\vert (\beta_{1})_{i} \bigr\vert , \bigl\vert (\beta _{2})_{i} \bigr\vert \bigr\} \lesssim h^{2}. \end{aligned}$$
(3.3)

Aiming to present the estimation of the errors \(e_{i,j}\ (i,j=1,2,\ldots,N-1)\), we introduce the following DFT formula:

$$\begin{aligned} {e}_{i,j} = \sqrt{2h}\sum_{k=1}^{N-1} \widehat{e}_{k,j} \sin{k\pi x_{i}},\quad i,j=1,2,\ldots,N-1. \end{aligned}$$
(3.4)

Taking the DFT for \(\alpha_{i,j}\) and \((\beta_{m})_{i}\), respectively, we find

$$\begin{aligned} \textstyle\begin{cases} {\alpha}_{i,j} =\sqrt{2h}\sum_{k=1}^{N-1} \widehat{\alpha}_{k,j} \sin {k \pi x_{i}},\quad i,j=1,\ldots,N-1, \\ {(\beta_{m})}_{i}=\sqrt{2h}\sum_{k=1}^{N-1} (\widehat{\beta}_{m})_{k} \sin {k\pi x_{i}},\quad i=1,\ldots,N-1, m=1,2. \end{cases}\displaystyle \end{aligned}$$

Since \(\sqrt{2h} (\sin k\pi x_{i})_{(N-1)\times(N-1)}\) is an orthogonal matrix, the following inverse DFT formulas hold:

$$\begin{aligned} \textstyle\begin{cases} \widehat{\alpha}_{k,j} =\sqrt{2h}\sum_{i=1}^{N-1} {\alpha}_{i,j} \sin {i \pi x_{k}},\quad k,j=1,\ldots,N-1, \\ (\widehat{\beta}_{m})_{k}= \sqrt{2h}\sum_{i=1}^{N-1} {(\beta_{m})}_{i} \sin {i\pi x_{k}}, \quad k=1,\ldots,N-1, m=1,2. \end{cases}\displaystyle \end{aligned}$$
(3.5)

Thereby, from (3.3) and (3.5), we can derive

$$\begin{aligned} \max_{k,j=1,\ldots,N-1}\bigl\{ \vert \widehat{ \alpha}_{k,j} \vert , \bigl\vert (\widehat{\beta }_{1})_{k} \bigr\vert , \bigl\vert (\widehat{\beta}_{2})_{k} \bigr\vert \bigr\} \lesssim h^{\frac{3}{2}}. \end{aligned}$$
(3.6)

Substituting (3.4) into the first equation of (3.1) and (3.2), respectively, we have

$$\begin{aligned} \textstyle\begin{cases} \widehat{e}_{k,j-1}-\omega_{k}\widehat{e}_{k,j}+\widehat {e}_{k,j+1}=h^{2}\widehat{\alpha}_{k,j}\quad \text{$j=1,\ldots,N-1$,} \\ \frac{3}{2}\widehat{e}_{k,N_{1}}-2\widehat{e}_{k,N_{1}-1}+\frac {1}{2}\widehat{e}_{k,N_{1}-2} +\frac{3}{2}\widehat{e}_{k,0}-2\widehat{e}_{k,1}+\frac{1}{2}\widehat {e}_{k,2}=h(\widehat{\beta}_{1})_{k}, \\ \frac{3}{2}\widehat{e}_{k,N}-2\widehat{e}_{k,N-1}+\frac{1}{2}\widehat{e}_{k,N-2} +\frac{3}{2}\widehat{e}_{k,N_{2}}-2\widehat{e}_{k,N_{2}+1}+\frac {1}{2}\widehat{e}_{k,N_{2}+2}=h(\widehat{\beta}_{2})_{k}, \end{cases}\displaystyle \end{aligned}$$
(3.7)

where

$$\begin{aligned} \omega_{k}=2+4\sin^{2}{\theta_{k}},\qquad \theta_{k}=\frac{k \pi h}{2}. \end{aligned}$$
(3.8)

Let \(\varepsilon_{k,j}=\widehat{e}_{k,j}+h^{2}p_{k,j}\), where \(p_{k,j}\) satisfies

$$\begin{aligned} \textstyle\begin{cases} -p_{k,j-1}+\omega_{k}p_{k,j}-p_{k,j+1}=\widehat{\alpha}_{k,j},\quad \text{$j=1,\ldots,N-1$,} \\ p_{k,0}=p_{k,N}=0 . \end{cases}\displaystyle \end{aligned}$$
(3.9)

From (3.7) and (3.9), one can see that

$$\begin{aligned} \textstyle\begin{cases} \varepsilon_{k,j-1}-\omega_{k}\varepsilon_{k,j}+\varepsilon_{k,j+1}=0,\quad \text{$j=1,\ldots,N-1$,} \\ \frac{3}{2}\varepsilon_{k,N_{1}}-2\varepsilon_{k,N_{1}-1}+\frac {1}{2}\varepsilon_{k,N_{1}-2} +\frac{3}{2}\varepsilon_{k,0}-2\varepsilon_{k,1}+\frac{1}{2}\varepsilon _{k,2}=h(\widetilde{\beta}_{1})_{k}, \\ \frac{3}{2}\varepsilon_{k,N}-2\varepsilon_{k,N-1}+\frac {1}{2}\varepsilon_{k,N-2} +\frac{3}{2}\varepsilon_{k,N_{2}}-2\varepsilon_{k,N_{2}+1}+\frac {1}{2}\varepsilon_{k,N_{2}+2}=h(\widetilde{\beta}_{2})_{k}, \end{cases}\displaystyle \end{aligned}$$
(3.10)

where \((\widetilde{\beta}_{m})_{k}\) \((m=1,2)\) are defined by

$$\begin{aligned} &(\widetilde{\beta}_{1})_{k}=(\widehat{ \beta}_{1})_{k}+h\biggl(\frac {3}{2}p_{k,N_{1}}-2p_{k,N_{1}-1} +\frac{1}{2}p_{k,N_{1}-2}+\frac{3}{2}p_{k,0}-2p_{k,1}+ \frac{1}{2}p_{k,2}\biggr), \\ &(\widetilde{\beta}_{2})_{k}=(\widehat{ \beta}_{2})_{k}+h\biggl(\frac{3}{2}p_{k,N}-2p_{k,N-1} +\frac{1}{2}p_{k,N-2}+\frac{3}{2}p_{k,N_{2}}-2p_{k,N_{2}+1}+ \frac{1}{2}p_{k,N_{2}+2}\biggr). \end{aligned}$$

Let \(\Vert \widehat{\alpha}_{k}\Vert =\max_{j=1,\ldots,N-1} |\widehat{\alpha}_{k,j}| \). Now, we can obtain the following estimates.

Lemma 3.1

Suppose that \(p_{k,j}\) satisfies (3.9). Then we have

$$\begin{aligned} \max_{j=1,\ldots,N-1} \vert p_{k,j} \vert \lesssim\frac{h^{-2}}{k^{2}} \Vert \widehat {\alpha}_{k} \Vert \end{aligned}$$
(3.11)

and

$$\begin{aligned} \max_{j=0,\ldots,N-1} \vert p_{k,j+1}-p_{k,j} \vert \lesssim h^{-1} \Vert \widehat {\alpha}_{k} \Vert . \end{aligned}$$
(3.12)

Proof

Let \(|p_{k,\ell}|=\max_{j=1,\ldots,N-1} |p_{k,j}|\). Then, from (3.8) and (3.9), we have

$$\begin{aligned} \vert \widehat{\alpha}_{k,\ell} \vert = \vert {-}p_{k,\ell-1}+\omega_{k}p_{k,\ell}-p_{k,\ell+1} \vert \geq(\omega_{k}-2) \vert p_{k,\ell} \vert =4 \sin^{2}\theta_{k} \vert p_{k,\ell} \vert . \end{aligned}$$
(3.13)

Recalling that \(\theta_{k}=\frac{k\pi h}{2}\), \(h=\frac{1}{N}\), and \(1\leq k\leq N-1\), we can derive

$$\begin{aligned} \sin\theta_{k} \geq\frac{2}{\pi} \theta_{k} = k h. \end{aligned}$$
(3.14)

Therefore, one can easily infer (3.11).

Let \(\delta_{k,i}=\widehat{\alpha}_{k,i}-4\sin^{2}{\theta_{k}}p_{k,i}\), \(i=1,\ldots,N-1\). From (3.13), we have

$$\begin{aligned} \vert {\delta_{k,i}} \vert \leq2 \Vert {\widehat{ \alpha}_{k}} \Vert . \end{aligned}$$
(3.15)

From (3.9), we get

$$\begin{aligned} -p_{k,i-1}+2p_{k,i}-p_{k,i+1}=\delta_{k,i}. \end{aligned}$$

Then, summing the above equations over i from 1 to j (\(1\leq j\leq N-1\)), we obtain

$$\begin{aligned} p_{k,j+1}-p_{k,j} = p_{k, 1}-p_{k,0}- \sum^{j}_{i=1}\delta_{k,i}. \end{aligned}$$
(3.16)

Furthermore, summing (3.16) over j from 1 to \(N-1\) and noticing \(p_{k,N}=p_{k,0}=0\), we get

$$\begin{aligned} -(p_{k,1}-p_{k,0})=(N-1) (p_{k,1}-p_{k,0})- \sum^{N-1}_{j=1}\sum ^{j}_{i=1}\delta_{k,i}. \end{aligned}$$

From (3.15) and the above equation, we have

$$\begin{aligned} \vert {p_{k,1}-p_{k,0}} \vert \lesssim h^{-1} \Vert {\widehat{\alpha}_{k}} \Vert . \end{aligned}$$

Therefore, using (3.15) again together with (3.16), we finally obtain (3.12) which completes the proof. □

Now we present the convergence theorem for Problem (1.1a)–(1.1e).

Theorem 3.1

Suppose that \(u\in C^{4}(\overline{\Omega})\). Then, for \(i,j=1,\ldots,N-1\), we have

$$\begin{aligned} U_{i,j}=u_{i,j}+O \bigl({h^{2}|\ln h}| \bigr). \end{aligned}$$
(3.17)

Proof

Let \(\lambda_{k}=(\sqrt{1+\sin^{2}{\theta_{k}}}+\sin{\theta_{k}})^{2}, k=1,\ldots, N-1\). Obviously,

$$ \lambda_{k}+\lambda_{k}^{-1}= \omega_{k}, \qquad \sqrt{\lambda_{k}}-\frac{1}{\sqrt {\lambda_{k}}}=2\sin{ \theta_{k}}. $$
(3.18)

From (3.10), we have

$$ \varepsilon_{k,j}=C_{1}\bigl(\lambda_{k}^{j}- \lambda_{k}^{N_{1}-j}\bigr) + C_{2}\bigl(\lambda _{k}^{j}-\lambda_{k}^{N+N_{2}-j}\bigr), $$
(3.19)

where \(\eta= \frac{3}{2}-2\lambda_{k} +\frac{1}{2}\lambda^{2}_{k}, \overline{\eta} = \frac{3}{2}-2\lambda^{-1}_{k} +\frac{1}{2}\lambda^{-2}_{k}\),

\(C_{1} = \frac{h(\widetilde{\beta}_{2})_{k}}{(1-\lambda ^{N_{1}-N_{2}-N}_{k})(\lambda^{N}_{k}\overline{\eta}+\lambda^{N_{2}}_{k} \eta)}\) and \(C_{2} = \frac{h(\widetilde{\beta}_{1})_{k}}{(1-\lambda ^{N+N_{2}-N_{1}}_{k})(\lambda^{N_{1}}_{k}\overline{\eta}+\eta)}\).

From the definition of \((\widetilde{\beta}_{m})_{k}\) \((m=1,2)\), Lemma 3.1, and (3.6), we obtain

$$\begin{aligned} \bigl\vert {(\widetilde{\beta}_{m})_{k})} \bigr\vert & \leq \bigl\vert {(\widehat{\beta}_{m})_{k}} \bigr\vert + 4h^{-1} \Vert {\widehat{\alpha}_{k}} \Vert \lesssim h^{\frac{3}{2}},\quad m=1,2. \end{aligned}$$
(3.20)

Note the fact that

$$\begin{aligned} \lambda_{k}^{\frac{N}{2}} & \geq\biggl(1+\sin{ \frac{k\pi}{2N}}\biggr)^{N} \geq\biggl(1+\frac{k}{N} \biggr)^{N} \geq2. \end{aligned}$$
(3.21)

Then we have

$$\begin{aligned} 1-\lambda^{N_{1}-N_{2}-N}_{k} \geq1-\lambda^{-N}_{k} \geq\frac{1}{2}. \end{aligned}$$

From the above inequality, (3.19), (3.20), and (3.21), we get

$$\begin{aligned} \vert {\varepsilon_{k,j}} \vert & \leq \vert {C_{1}} \vert \max\bigl\{ \lambda_{k}^{j}, \lambda_{k}^{N_{1}-j} \bigr\} + \vert {C_{2}} \vert \max\bigl\{ \lambda_{k}^{j}, \lambda_{k}^{N+N_{2}-j}\bigr\} \\ & \leq \vert {C_{1}} \vert \lambda^{N-1}_{k} + \vert {C_{2}} \vert \lambda^{N+N_{2}-1}_{k} \\ & \lesssim\frac{h^{\frac{5}{2}}}{1-\lambda^{N_{1}-N_{2}-N}_{k} } \biggl( \frac{\lambda^{N-1}_{k}}{ \vert {\lambda^{N}_{k} \overline{\eta}+\lambda^{N_{2}}_{k} \eta} \vert } +\frac{\lambda^{N_{1}-1}_{k}}{ \vert {\lambda^{N_{1}}_{k} \overline{\eta}+\eta} \vert } \biggr) \\ & \lesssim h^{\frac{5}{2}} \biggl( \frac{\lambda^{N-1}_{k}}{ \vert {\lambda^{N}_{k} \overline{\eta}+\lambda^{N_{2}}_{k} \eta} \vert } +\frac{\lambda^{N_{1}-1}_{k}}{ \vert {\lambda^{N_{1}}_{k} \overline{\eta}+\eta} \vert } \biggr). \end{aligned}$$

From (3.18), (3.21), and (3.14), we have

$$\begin{aligned} \bigl\vert {\lambda^{N}_{k} \overline{\eta}+ \lambda^{N_{2}}_{k} \eta} \bigr\vert & = \frac{1}{2} \sqrt{\lambda_{k}} \biggl(\sqrt{\lambda_{k}}- \frac{1}{\sqrt {\lambda_{k}}} \biggr) \bigl(\lambda^{N-2}_{k}(3 \lambda_{k}-1)-\lambda ^{N_{2}}_{k}(3- \lambda_{k})\bigr) \\ & \gtrsim\lambda^{N-1}_{k} \bigl(1-\lambda^{N_{2}-N+1}_{k} \bigr)\sin{\theta_{k}} \gtrsim kh\lambda^{N-1}_{k} \bigl(1-\lambda^{\xi_{2} N-N+1}_{k}\bigr) \gtrsim kh \lambda^{N-1}_{k}. \end{aligned}$$

Similar to the above estimation, we can derive

$$\begin{aligned} \bigl\vert {\lambda^{N_{1}}_{k} \overline{\eta}+\eta} \bigr\vert \gtrsim kh\lambda^{N_{1}-1}_{k}. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \vert \varepsilon_{k,j} \vert \lesssim\frac{h^{\frac{3}{2}}}{k}. \end{aligned}$$

From the definition of \(\varepsilon_{k,j}\), Lemma 3.1, and (3.6), we have

$$\begin{aligned} \vert \widehat{e}_{k,j} \vert = \bigl\vert \varepsilon_{k,j}-h^{2} p_{k,j} \bigr\vert \leq \vert \varepsilon_{k,j} \vert +h^{2} \vert p_{k,j} \vert \lesssim\frac{h^{\frac{3}{2}}}{k} + \frac{ \Vert \widehat{\alpha}_{k} \Vert }{k^{2}} \lesssim\frac{h^{\frac{3}{2}}}{k}. \end{aligned}$$

Together with (3.4), we finally obtain (3.17), which completes the proof. □

4 Numerical experiments

In this section, we present two typical examples to demonstrate the theoretical results and compare the numerical results with the RBF collocation method [15].

Example 4.1

Consider Problem (1.1a)–(1.1e), and let

$$\begin{aligned} &f(x,y)=-2\pi^{2} \sin{\pi x}\sin{\pi y},\qquad \xi_{1} = \frac{1}{4}, \qquad \xi _{2}=\frac{1}{2},\qquad \mu_{1}(y)= \mu_{2}(y)=0, \\ &\mu_{3}(x)=-\frac{1}{\pi} \biggl(\frac{\sqrt{2}}{2}-1 \biggr) \sin{\pi x}, \qquad \mu_{4}(x)= \frac{1}{\pi}\sin{\pi x} . \end{aligned}$$

One can check that the exact solution is \(u(x,y)=\sin{\pi x}\sin{\pi y}\).

In this experiment, we take the uniform partition for Ω and employ the preconditioned conjugate gradient method to solve the corresponding difference equations (2.5) and (2.6). Numerical results are shown in Tables 1 and 2, where the norms \(\| u-U\|_{m}\ (m= 2, \infty)\) are defined by \(\| u-U\|_{2} = \frac{1}{N} (\sum_{i=1}^{N} \sum_{j=1}^{N} |{u_{i,j}-U_{i,j}}|^{2} )^{\frac{1}{2}}\), \(\|u-U\|_{\infty} = \max_{1\leq i,j \leq N} |{u_{i,j}-U_{i,j}}|\), respectively. To illustrate the pointwise error, we choose four typical points and show the corresponding errors in Table 2. From the results, one can see that the convergent order is close to two, which validates the correctness of the theoretical results.

Table 1 The errors for finite difference method in two norms
Full size table
Table 2 The errors for finite difference method in the sense of pointwise
Full size table

Now, we adopt the RBF collocation method to solve Example 4.1. Like [15], we examine efficiency of the method based on regular distribution and MQ RBF, i.e., let RBF

$$\begin{aligned} \phi(r) = \sqrt{1+\epsilon^{2} r^{2}}, \end{aligned}$$
(4.1)

where ϵ is the shape parameter. Take \(\epsilon=2\) and the results are shown in Tables 3 and 4, where \(\kappa(A)\) and \(U_{\mathrm{RBF}}\) denote the condition number of the discretize linear system and the corresponding approximation solution, respectively. By comparing Tables 3 and 4 with Tables 1 and 2, one can see that when h decreases gradually from \(1/16\) to \(1/128\), one fact is that the RBF collocation method has better approximation to the exact solution than our method. But the other fact is that the \(\kappa(A)\) becomes larger which would make the discretize linear system unsolvable. Meanwhile, the convergence rate of errors for RBF collocation method decreases rapidly near to zero. In turn, the convergence rate of errors for our method is always kept at about 4 whether h is large or small. Therefore, we can conclude that our method is far more stable than the RBF collocation method, and it can get better approximation numerical results to the exact solution with h becoming smaller.

Table 3 The errors for the RBF collocation method in two norms
Full size table
Table 4 The errors for the RBF collocation method in the sense of pointwise
Full size table

Example 4.2

Consider Problem (1.1a)–(1.1e), and let

$$\begin{aligned} &f(x,y)=\bigl(4+x+y^{2}\bigr)e^{x},\qquad \xi_{1} = \frac{1}{4},\qquad \xi_{2}=\frac{1}{2},\qquad \mu _{1}(y)=y^{2},\qquad \mu_{2}(y)=e\bigl(1+y^{2}\bigr), \\ &\mu_{3}(x)=\frac{1}{4}xe^{x}+\frac{1}{192}e^{x},\qquad \mu_{4}(x)= \frac{1}{2}xe^{x}+\frac{7}{24}e^{x}. \end{aligned}$$

One can verify that the exact solution is \(u(x,y)=e^{x}(x+y^{2})\).

In this example, take the same partitions as in Example 4.1 and let the shape parameter \(\epsilon=6\). The numerical results of our method are shown in Tables 5 and 6, while the results of the RBF collocation method are shown in Tables 7 and 8. From Tables 5 and 6, one can see that the convergent order is close to two, which confirms the correctness of theoretical results again. From Tables 7 and 8, the approximation solution obtained by the RBF collocation method is very close to the exact solution when \(h=1/16, 1/32\) and \(1/64\). However, the ratio of error norms drops sharply to zero when \(h=1/128\). By comparison with Tables 5 and 6, the fact that our approach is more stable than the RBF collocation method is demonstrated once again.

Table 5 The errors for finite difference solutions in two norms
Full size table
Table 6 The errors for finite difference solutions in the sense of pointwise
Full size table
Table 7 The errors for the RBF collocation method in two norms
Full size table
Table 8 The errors for the RBF collocation method in the sense of pointwise
Full size table

5 Summary and conclusions

In this paper, we construct a high accuracy difference scheme for Poisson equation with two integral boundary conditions and prove that the scheme can reach the asymptotic optimal error estimate. Numerical results verify the correctness of theoretical analysis. In the future, we will work on designing some other high order difference schemes (e.g., fourth-order nonstandard compact finite difference [20], or sixth-order implicit finite difference [21]) for Poisson problem with other nonlocal boundary conditions. Besides, we will also try to apply some other analytic methods for error estimation, e.g., homotopy analysis transform method [22, 23], or Lie symmetry analysis method [24, 25].