Abstract
In this work, we study the diabetes model and its complications with the Caputo–Fabrizio fractional derivative. A deterministic mathematical model pertaining to the fractional derivative of the diabetes mellitus is discussed. The analytical solution of the diabetes model is derived by exerting the homotopy analysis method, the Laplace transform and the Padé approximation. Moreover, existence and uniqueness of the solution are examined by making use of fixed point theory and the Picard–Lindelof approach. Ultimately, for illustrating the obtained results some numerical simulations are performed.
Similar content being viewed by others
1 Introduction
Nowadays, diabetes is world-wide a quiet epidemic heavily enlarging the charge of non-communicable diseases and generally stimulated by reducing the levels of activity and enhancing pervasiveness of obesity. Mainly, two types of diabetes are studied: Type 1 diabetes, too familiar as insulin dependent diabetes mellitus, attacking people below the age of 40 and representing 10 to 15 percent of the diabetic population. Then, Type II diabetes, previously recognized as non-insulin dependent diabetes mellitus, describing the majority (85 to 90 percent). Although in all age groups with the spreading epidemic of obesity, it is anticipated that in 10 year’s time, there will be additional children having Type II rather than having Type I; see [1–8]. In recent years many authors have studied different mathematical models to describe diabetes and related issues such as Boutayeb et al. [9], Mahataa et al. [10], Pandit et al. [11], Makroglou et al. [12] and others.
It has been demonstrated by many scientists and mathematicians that fractional extensions of mathematical models of integer order represent the natural fact in a very systematic way such as in the approaches of Caputo [13], Podlubny [14], Miller and Ross [15], Baleanu et al. [16], Singh et al. [17, 18], Kumar et al. [19] and others. Lately, Caputo and Fabrizio [20] suggested an innovative idea of non-integer order derivative possessing non-singular kernel, and the authors in [21] described the additional characteristics. In the present article, we employ a newly found arbitrary order derivative to the diabetes model. The principal aim of the present article is to use a novel non-integer order derivative to study the diabetes model and present the details of uniqueness and existence of the solution of the diabetes model with the help of a fixed point theorem and the Picard–Lindelof approach.
In this work, we study the fractional diabetes model by applying the homotopy analysis transform method (HATM). The HATM is a new and well organized mixture of the HAM [22–24] and standard Laplace transform technique [25–29].
The development of the present article is given in the following sequential manner: In Sect. 2, the CF derivative of arbitrary order is explored. In Sect. 3, the diabetes model and exact solution associated to the newly CF arbitrary order derivative is described. We also discuss special solutions of the model in this portion. By exerting the fixed point theorem and the Picard–Lindelof approach, uniqueness and existence of the solutions of the system are analyzed in Sect. 4. Section 5 contains a stability analysis of an iterative scheme. In Sect. 6, the numerical simulations are graphically shown. Lately in Sect. 7, the conclusions are discussed.
2 Preliminaries
Definition 2.1
Let \(l(\eta ) \in H^{1}(x,y),y > x,\sigma \in [0,1]\) then the CF arbitrary order derivative [20] is given as
In Eq. (1) \(M(\sigma )\) denotes a normalization of the function fulfilling the property \(M(0) = 1 = M(1)\) and its details can be found in a paper authored by Caputo and Fabrizio [20]. This derivative can be presented as follows, if \(l \notin H^{1}(a,b)\):
Note 1
If \(\beta = \frac{1 - \sigma}{\sigma} \in [0,\infty ),\sigma = \frac{1}{1 + \beta} \in [0,1]\), then Eq. (2) converts to the following form:
Furthermore,
The corresponding integral was described by [21].
Definition 2.2
Let \(0 < \sigma < 1\), then the non-integer order integral of \(l(\eta )\) is presented as
By making use of Eq. (5), we have
In view of the result (6), the authors of [21] introduced the modified CF derivative of order \(0 < \sigma < 1\) expressed as
3 HATM for fractional diabetes model and its complication
The classical diabetes model and its complications [1] are given by
where D indicates the no. of diabetics with no complications at time η. C denotes the no. of diabetics having complications. I represents the occurrence of diabetes mellitus.
μ denotes the rate of natural mortality, λ indicates the probability of a diabetic person spreading a complication, γ shows the rate of healing complications, ν stands for the rate at which diabetic patients having complication converts critically disabled and δ denotes the mortality rate because of complications. \(N(\eta) = C(\eta) +D(\eta)\) indicates the size of diabetics at the time η. Taking \(N (\eta) = C(\eta) +D(\eta)\), we get
In Eq. (9), \(\theta = \gamma + \mu + \nu + \delta\) with initial conditions
The model (9) is not able to contain the entire memory effect of the biological system and the spreading of diabetes. To involve these discussed effects into the mathematical representation of the diabetes model, we modify the equation by changing the first order time derivative to the novel propounded CF arbitrary order derivative [20] as represented by
with initial conditions given in Eq. (10).
Solution. By performing the Laplace transform to Eq. (11),
On simplifying, we get
The non-linear operator is defined as
and thus we have
and
The mth order deformation equation is presented as
and
On employing the inversion of the Laplace transform, we get
and
On solving the above equations, for \(k=1,2,3,\ldots\) , we get
i.e. \(C_{1}(\eta ) = -\hbar \alpha [1 + \sigma (\eta - 1)]\), where \(\alpha = - qC_{0} + \lambda N_{0}\).
i.e. \(N_{1}(\eta ) = - \hbar \beta [1 + \sigma (\eta - 1)]\), where \(\beta = I - mC_{0} - \mu N_{0}\), and so on.
Consequently, the solution of Eq. (11) is given as
or
and
or
where \(q = \lambda + \theta,m = \nu + \delta\) and \(\theta = \gamma + \mu + \nu + \delta\).
4 Existence and uniqueness analysis
The fractional diabetic model (11) can be reduced to an integral equation of Volterra type when the integral related to the CF derivative is employed. We recall that the Caputo–Fabrizio non-integer order integral of \(l(\eta )\) is the average of \(l(\eta )\) and its Riemann–Liouville integral of fractional order.
Now using the integral operator of fractional order introduced by Losada and Nieto [21] on the system (11), we get
A possibility of reducing Eq. (20) to the iterative approach is presented as follows:
Now, we get the subsequent iterative algorithm
Here we assume that we can get the exact solution by taking the limit as n tends to infinity.
4.1 Existence of the solution by Picard–Lindelof approach
Theorem 1
We discuss the existence of the solution by applying the Picard–Lindelof approach.
Proof
We express the operators as
where \(k_{1}(\eta,C)\) and \(k_{2}(\eta,N)\) are contractions with respect to C and N for the first and second functions, respectively.
Let
where
On consideration of the Picard operator, we have
given as follows:
where \(\xi (\eta ) = \{ C(\eta ),N(\eta ) \},\xi_{0}(\eta ) = \{ g_{1},g_{2} \}\text{ and }\Delta ( \eta,\xi (\eta ) ) = \{ k_{1}(\eta,C(\eta ),k_{2}(\eta,N(\eta ) \}\).
Next we suppose the solution of the fractional diabetic model are bounded within a time period,
where we demand that
By employing the fixed point theorem pertaining to Banach space along with the metric, we obtain
Now we have
with \(\beta < 1\). Since ξ is a contraction, we have \(\rho \beta < 1\), hence the defined operator ϕ is also a contraction. Therefore, the diabetic model involving CF derivative given in Eq. (11) has a unique set of solutions. □
5 Stability analysis of iterative scheme
Let \(( \wp, \Vert \cdot \Vert )\) indicate a Banach space and W represent a self-map of ℘. Let \(h_{n + 1} = \varphi (W,h_{n})\) be a specific iterative scheme. Let us consider \(\aleph (W)\) to be the fixed point set of W possessing at least one element and let \(h_{n}\) be convergent and converge to \(z \in \aleph (W)\). If \(\{ h_{n}\} \subseteq \wp\) and we define \(a_{n} = \Vert h_{n + 1} - \varphi (W,h_{n}) \Vert \), and if \(\operatorname{Lim} _{n \to \infty} a^{n} = 0\) yields the result \(\operatorname{Lim} _{n \to \infty} h^{n} = z\), then the iteration algorithm \(h_{n + 1} = \varphi (W,h_{n})\) is termed W-stable.
Theorem 2
([30])
Let \(( \wp, \Vert \cdot \Vert )\) be a Banach space and W be a self-map of the Banach space ℘ that leads to the result
\(\forall x,y \in \wp\), where H and h s.t. \(0 \le H, 0 \le h \le 1\). Furthermore, it is supposed that Wis Picard W-stable.
We assume that the fractional diabetes model (11) is connected with the subsequent iterative formula
In the above equation \(\frac{s + \sigma (1 - s)}{s}\) stands for the Lagrange multiplier.
Further, we develop the following result given as a theorem.
Theorem 3
Consider G to be a self-map expressed in the subsequent manner:
then the iterations are G-stable in \(L^{2}(a,b)\) if \(( 1 - (\lambda + \theta )\varpi_{1}(\eta ) + \lambda \varpi_{2}(\eta ) ) < 1\) and \(( 1 - (\nu + \delta )\varpi_{3}(\eta ) - \mu \varpi_{4}(\eta ) ) < 1\).
Proof
First of all it will be shown that G has a fixed point. To prove the above theorem, we derive the result given below for \((n,m) \in N \times N\).
and
We consider that the solutions play some role, i.e.,
Further, on using the result (37) in (35) and (36),
and
where \(\varpi_{1},\varpi_{2},\varpi_{3}\) and \(\varpi_{4}\) are functions occurring from \(L^{ - 1} [ \frac{s + \sigma (1 - s)}{s}L( \bullet ) ]\) with \(( 1 - (\lambda + \theta )\varpi_{1}(\eta ) + \lambda \varpi_{2}(\eta ) ) < 1\) and \(( 1 - (\nu + \delta )\varpi_{3}(\eta ) - \mu \varpi_{4}(\eta ) ) < 1\).
Consequently, the self-map G possesses a fixed point. Further, we will show that the conditions associated with Theorem 2 are satisfied by G. Let Eqs. (38) and (39) hold, thus on putting
Then from Eq. (40), we can notice that for the mapping G along with the condition associated with Theorem 2 holds. Consequently for the considered mapping G and the conditions pertaining to Theorem 2 are satisfied, hence G is Picard G-stable. Thus, the proof of Theorem 3 is finished. □
6 Numerical results and discussion
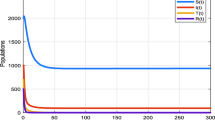
In the present portion, we compute the numerical results for \(C(\eta )\) and \(N(\eta )\) at \(\sigma = 0.70,\sigma = 0.85\) and \(\sigma = 1\). The special solution of the non-integer diabetes model is derived by applying HATM and the Padé approximation [31] with as distinct parameters the number of \(\nu = 0.05,\delta = 0.05,\mu = 0.02,\gamma = 0.08,\lambda = 0.02\) and \(I = 60\mbox{,}000\). Fig. 1 depicts the nature of the number of diabetics having complications corresponding to the time for distinct order of fractional derivative. Figure 2 represents the impact of order of CF derivative on the size of the diabetics corresponding to time. Figure 3 indicates the effect of the rate at which diabetic patients having complications converted into the number of critically disabled diabetics having complications with respect to time. Figure 4 depicts the effect of the rate at which diabetic patients having complications converted into the size of critically disabled diabetics with respect to time. Figure 5 shows the effect of the mortality rate because of complications on the number of diabetics having complications with respect to time. Figure 6 indicates the effect of the mortality rate because of complications on the size of diabetics with respect to time. Figure 7 presents the effect of the natural mortality rate on the number of diabetics having complications with respect to time. Figure 8 presents the effect of the natural mortality rate on the size of diabetics with respect to time. Graphical behavior reveals that the model is significantly dependent on the arbitrary order. Figures 1–8 demonstrate the clear difference at \(\sigma = 1\), \(\sigma = 0.85\) and \(\sigma = 0.70\). The model represents a new feature of \(\sigma = 0.85\) and \(\sigma = 0.70\), that was invisible when modeling with \(\sigma = 1\).
7 Conclusions
In this study, we have applied the novel introduced Caputo–Fabrizio arbitrary order derivative to the diabetes model and sloved the fractional problem via HATM and Padé approximation. The HATM is a pioneering and strong computational scheme to solve non-integer order differential equations. The HATM carries an auxiliary parameter ħ, which is very useful to modify and manage the convergence of the series solutions. Hence, it can be determined that HATM is manageable, straightforward to employ, and a stronger computational procedure for examining linear and non-linear problems. The uniqueness and existence of the solutions are explored by exerting fixed point theory and the Picard–Lindelof approach. Some numerical results are analyzed to describe the effect of the arbitrary order. The effects of various parameters on the number of diabetics having complications and the size of diabetics with respect to time are shown graphically. By numerical simulation we can observe that when \(\sigma \to 1\) the Caputo–Fabrizio non-integer order derivative reveals more absorbing characteristics. The results of this study are very helpful for medical practitioners dealing with diabetes and related issues. Thus, we have concluded that the CF derivative is useful in the description of physical, chemical, biological, medical, social, and engineering processes.
References
Boutayeb, A., Twizell, E.H., Achouayb, K., Chetouani, A.: A mathematical model for the burden of diabetes and its complications. Biomed. Eng. Online 3(1), 20 (2004) https://doi.org/10.1186/1475-925X-3-20
Zecchin, C., Facchinetti, A., Sparacino, G., De Nicolao, G., Cobelli, C.: A new neural network approach for short-term glucose prediction using continuous glucose monitoring time-series and meal information. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2011, 5653–5656 (2011)
Sharief, A.A., Sheta, A.: Developing a mathematical model to detect diabetes using multigene genetic programming. Int. J. Adv. Res. in Artif. Intell. (IJARAI) 3(10), 54 (2014)
Rosado, Y.C.: Mathematical model for detecting diabetes. In: Proceedings of the National Conference on Undergraduate Research (NCUR), University of Wisconsin La-Crosse, La-Crosse (2009)
Ackerman, E., Gatewood, I., Rosevear, J., Molnar, G.: Blood glucose regulation and diabetes. In: Heinmets, F. (ed.) Concepts and Models of Biomathematics, pp. 131–156. Decker, New York (1969)
De Gaetano, A., Hardy, T., Beck, B., Abu-Raddad, E., Palumbo, P., Bue-Valleskey, J., Pørksen, N.: Mathematical models of diabetes progression. Am. J. Physiol: Endocrinol. Metab. 295, E1462–E1479 (2008) First published September 9, 2008. https://doi.org/10.1152/ajpendo.90444.2008
Patil, B.M., Joshi, R.C., Toshniwal, D.: Hybrid prediction model for type-2 diabetic patients. Expert Syst. Appl. 379(12), 8102–8108 (2010)
Enagi, A.I., Bawa, M., Sani, A.M.: Mathematical study of diabetes and its complication using the homotopy perturbation method. Int. J. Math. Comput. Sci. 12(1), 43–63 (2017)
Boutayeb, A., Chetouani, A., Achouyab, A., Twizel, E.H.: A non-linear population model of diabetes mellitus. J. Appl. Math. Comput. 21, 127–139 (2016)
Mahataa, A., Mondal, S.P., Alam, S., Roy, B.: Mathematical model of glucose-insulin regulatory system on diabetes mellitus in fuzzy and crisp environment. Ecol. Genet. Gen. 2, 25–34 (2017)
Pandit, S.V., Giles, V.R., Damir, S.S.: A mathematical model of the electrophysiological alterations in rat ventricular myocytes in type-I diabetes. Biophys. J. 84(2), 832–841 (2013)
Makroglou, A., Li, J., Kuang, Y.: Mathematical models and software tools for the glucose-insulin regulatory system and diabetes: an overview. Appl. Numer. Math. 56(3–4), 559–573 (2006)
Caputo, M.: Elasticita e Dissipazione. Zani-Chelli, Bologna (1969)
Podlubny, I.: Fractional Differential Equations. Academic Press, New York (1999)
Miller, K.S., Ross, B.: An Introduction to the Fractional Calculus and Fractional Differential Equations. Wiley, New York (1993)
Baleanu, D., Guvenc, Z.B., Tenreiro Machado, J.A. (eds.): New Trends in Nanotechnology and Fractional Calculus Applications. Springer, Dordrecht (2010)
Singh, J., Kumar, D., Hammouch, Z., Atangana, A.: A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 316, 504–515 (2018)
Singh, J., Kumar, D., Baleanu, D.: On the analysis of chemical kinetics system pertaining to a fractional derivative with Mittag–Leffler type kernel. Chaos 27, 103113 (2017). https://doi.org/10.1063/1.4995032
Kumar, D., Singh, J., Baleanu, D., Sushila: Analysis of regularized long-wave equation associated with a new fractional operator with Mittag–Leffler type kernel. Physica A 492, 155–167 (2018)
Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1, 73–85 (2015)
Losada, J.J., Nieto, J.: Properties of the new fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1, 87–92 (2015)
Liao, S.J.: Beyond Perturbation: Introduction to Homotopy Analysis Method. Chapman and Hall/CRC Press, Boca Raton (2003)
Liao, S.J.: An approximate solution technique not depending on small parameters: a special example. Int. J. Non-Linear Mech. 30, 371–380 (1995)
Kumar, S., Kumar, D., Singh, J.: Numerical computation of fractional Black–Scholes equation arising in financial market. Egypt. J. Basic Appl. Sci. 1(3–4), 177–183 (2014)
Khuri, S.A.: A Laplace decomposition algorithm applied to a class of nonlinear differential equations. J. Appl. Math. 1, 141–155 (2001)
Kumar, D., Agarwal, R.P., Singh, J.: A modified numerical scheme and convergence analysis for fractional model of Lienard’s equation. J. Comput. Appl. Math. (2017). https://doi.org/10.1016/j.cam.2017.03.011
Kumar, D., Singh, J., Baleanu, D.: A fractional model of convective radial fins with temperature-dependent thermal conductivity. Rom. Rep. Phys. 69(1), 103 (2017)
Kumar, D., Singh, J., Baleanu, D.: Analytic study of Allen–Cahn equation of fractional order. Bull. Math. Anal. Appl. 1, 31–40 (2016)
Khan, M., Gondal, M.A., Hussain, I., Vanani, S.K.: A new comparative study between homotopy analysis transform method and homotopy perturbation transform method on semi infinite domain. Math. Comput. Model. 55, 1143–1150 (2012)
Qing, Y., Rhoades, B.E.: T-stability of Picard iteration in metric spaces. Fixed Point Theory Appl., 2008 Article ID 418971 (2008)
Boyd, J.P.: Padé approximants algorithm for solving nonlinear ordinary differential equation boundary value problems on an unbounded domain. Comput. Phys. 11, 299–303 (1997)
Acknowledgements
The authors would like to thank the anonymous reviewers for their valuable comments and suggestions to improve the final version of the article.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
JS, DK and DB designed the study, developed the methodology, collected the data, performed the analysis, and wrote the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Singh, J., Kumar, D. & Baleanu, D. On the analysis of fractional diabetes model with exponential law. Adv Differ Equ 2018, 231 (2018). https://doi.org/10.1186/s13662-018-1680-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1680-1