Download PDF

Advances in Difference Equations

, 2018:130 | Cite as

Exponentially practical stability of discrete time singular system with delay and disturbance

Open Access
Research
First Online:
Received:
Accepted:
  • 114 Downloads

Abstract

In this paper, we consider exponentially practical stability of a discrete time singular system with disturbance. By using Lyapunov–Krasovskii stability theory, some criteria for exponentially practical stability of such a system are derived. Moreover, by using a Razumikhin-type technique, the criteria for exponentially practical stability of a discrete time singular system with delay and disturbance are also obtained. Some numerical examples are given to show the success of our theoretical results.

Keywords

Discrete time system Singular system Delay Exponentially practical stability Disturbance 
Download article PDF

1 Introduction

Singular systems, which are also called descriptor systems, implicit systems, or generalized systems, have been investigated extensively in many areas [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21]. Generally, the systems can be described using algebraic and differential equations. Such systems are natural presentations of several dynamic systems which are better than regular systems, such as economical systems, chemical systems, robotic systems, etc. [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 20, 21, 22]. Moreover, singular systems are very complicated because we have to consider the stability of the systems as well as the regularity and also impulse free (in case of continuous singular systems) or causality (in case of discrete singular systems) [2, 11, 18]. In addition, a discrete time system is often represented in the real world systems such as population models and switched systems. There are several studies on the stability of a discrete time system [2, 3, 4, 8, 9, 10, 11, 12, 13, 14, 15, 17, 18, 22, 23, 24].

In real world systems, the variation of systems’ current status often depends not only on the current state but also on the past state of the systems; such systems are called time delay systems. Examples of time delay systems are population dynamic models, mechanical transmissions, and digital control systems [4, 7, 8, 9, 10, 12, 13, 14]. It is well known that time delay may cause instability, oscillation, and poor performance of systems. For the above-mentioned reasons, time delay systems have been extensively discussed in many literature works [2, 4, 6, 7, 8, 9, 10, 13, 14, 15, 16, 18, 19, 22, 23]. As is known, most common approaches to studying stability analysis of a time delay system are Lyapunov–Krasovskii functional approach and Razumikhin-type technique. In the case of Lyapunov–Krasovskii functional method, it requires that a candidate Lyapunov–Krasovskii functional is decreasing on the whole state space. Meanwhile, the Razumikhin-type technique has an advantage that the Lyapunov–Krasovskii functional is not required to be decreasing on the whole state space. In general, disturbance inputs often occur in modeling of phenomena and engineering systems which may be due to data transformation, unknown disturbances, or measurement errors [4, 10, 24, 25]. Therefore, it is important to study the stability of a discrete time singular system with delay and disturbance.

Considering asymptotic stability, it is more desirable to consider exponential stability criterion for dynamical systems [1, 6, 7, 8, 9, 10, 18, 19, 20, 21, 24, 25]. For exponential stability, it is required that all solutions starting near an equilibrium point not only stay nearby, but tend to the equilibrium point very fast with exponential decay rate. In practice, we may only need to stabilize a system into the region of a phase space where the system may oscillate near the state in which the implementation is still acceptable. This concept is called practical stability [18, 22, 26, 27, 28, 29] which is very useful for studying the asymptotic behavior of the system in which the origin is not necessarily an equilibrium point. In this case, practical stability is an important concept to analyze the asymptotic behavior of solutions with respect to a small neighborhood of the origin. Recently, there have been several studies on practical stability of continuous time systems with delay, see [26, 27, 28, 29]. However, there have been few studies on practical stability of discrete time systems with delay [22, 23]. In [3], the authors studied discrete time singular systems with disturbance and obtained some stability criteria by using Lyapunov stability theory. In [23], the authors used the Razumikhin-type technique to derive the exponentially practical stability condition for impulsive discrete time systems with delay. Motivated by the above discussions, we propose to study exponentially practical stability of a discrete time singular system with delay and disturbance. We shall derive a new criterion for exponentially practical stability of the system, namely the solutions tend to the origin state with exponential decay rate in the early stage (but eventually oscillate in a neighborhood of the origin), in which the performance is still acceptable.

This work is organized as follows. In Sect. 2, some notations and definitions are introduced. In Sect. 3, we present some criteria for exponentially practical stability of a discrete time system with disturbance, exponentially practical stability of a discrete time singular system with disturbance, exponentially practical stability of a discrete time system with delay and disturbance, and exponentially practical stability of a discrete time singular system with delay and disturbance; definitions and assumption will be used in the proof our result. Some numerical examples are given to show the effectiveness of our theoretical result in Sect. 4. The last section concludes the work.

2 Preliminaries

Consider the following discrete time singular system with delay and disturbance:
$$\begin{aligned} \textstyle\begin{cases}Ex(k+1)=Ax(k)+Bx(k-\tau)+Gw(k), \\ x(s)=\varphi(s),\quad s\in\mathbb{N}_{k_{0}-\tau}, \end{cases}\displaystyle \end{aligned}$$
(2.1)
where \(x(k)\in\mathbb{R}^{n}\) is the state vector, \(w(k)\in\Omega =\lbrace w(k)\in\mathbb{R}^{m}/ \Vert w(k) \Vert \leq\overline {w},\exists \overline{w}>0,\forall k\geq k_{0}\rbrace\) is the disturbance, \(A, B, G\), and E are constant matrices with appropriate dimensions where E is a singular matrix with \(\operatorname{rank}(E)=r< n\), τ is constant delay, \(\varphi\in \mathcal{C}_{\tau}:=\{f: \mathbb{N}_{-\tau } \longrightarrow \mathbb{R}^{n}, f \text{ is continuous}\}\) is the initial function with \(\Vert \varphi \Vert =\max_{\theta\in\mathbb {N}_{k_{0}-\tau}}\lbrace \Vert \varphi(\theta) \Vert \rbrace\), where \(\mathbb{N}_{k_{0}-\tau}=\{k_{0}-\tau,k_{0}-\tau+1,\ldots ,k_{0}-1,k_{0}\}\), and \(\mathbb{N}_{k_{0}}=\{k_{0},k_{0}+1,k_{0}+2,\ldots\}, k_{0} \geq0 \). A function \(\rho:\mathbb{R}^{+}_{0}\longrightarrow\mathbb {R}\), is called a K-function if it is a nonnegative continuous function where \(\mathbb{R}^{+}_{0}\) is the set of nonnegative real numbers. Let \(\mathrm{floor}(r):=\lfloor r \rfloor\) be the greatest integer that is less than or equal to r, and let \(\mathrm{ceil}(r):=\lceil r \rceil\) be the least integer that is greater than or equal to r.

Definition 2.1

([18])

System (2.1) is said to be regular if \(\det(zE-A)\neq0\) for some \(z \in\mathbb{C}\). System (2.1) is said to be causal if \(\deg(\det(zE-A))= \operatorname{rank}(E)\).

3 Main results

In this section, we consider exponentially practical stability problems for the following four cases: a discrete time system with disturbance, a discrete time singular system with disturbance, a discrete time system with delay and disturbance, and a discrete time singular system with delay and disturbance.

First, we consider the discrete time system with disturbance as follows:
$$\begin{aligned} \textstyle\begin{cases}x(k+1)=f(k,x(k),w(k)), \\ x(k_{0})=x_{0}, \end{cases}\displaystyle \end{aligned}$$
(3.1)
where disturbance \(w(k)\in\Omega\), where Ω is defined as in (2.1), \(f:\mathbb{R}\times\mathbb{R}^{n}\times\Omega\longrightarrow \mathbb{R}^{n}\) is continuous and locally Lipschitz in \((x,w)\), uniformly in k with Lipschitz constant L which satisfies \(f(k,0,0)=0\). Let \(x(k;k_{0},x_{0},w)\) denote the trajectory of system (3.1) with initial state \(x(k_{0})=x_{0}\) and disturbance signal \(w(k)\in\Omega\).

Definition 3.1

System (3.1) is exponentially practically stable in the pth-moment for some \(p>0\) if for all \(k\geq k_{0}\) there exist constants \(0<\lambda<1, \eta>0, r>0\) such that
$$\begin{aligned} \bigl\Vert x(k;k_{0},x_{0},w) \bigr\Vert ^{p} \leq\eta \Vert x_{0} \Vert ^{p}\lambda ^{k-k_{0}}+r, \quad\forall w(k)\in\Omega. \end{aligned}$$

Theorem 3.1

If there exist a Lyapunov function\(V(k,x(k))\), aK-functionρ, and positive constants\(c_{1},c_{2},c_{3},a,p; c_{3}< c_{2}\)such that the following conditions hold for all\(k\geq k_{0}, x(k)\in\mathbb{R}^{n}, w(k)\in\Omega\):
  1. (i)

    \(c_{1} \Vert x(k) \Vert ^{p}\leq V(k,x(k))\leq c_{2} \Vert x(k) \Vert ^{p}+a\),

     
  2. (ii)

    \(\Delta V(k,x(k))=V(k+1,x(k+1))-V(k,x(k))\leq-c_{3} \Vert x(k) \Vert ^{p}+ \rho( \Vert w(k) \Vert )\).

     

Then system (3.1) is exponentially practically stable in thepth-moment with\(\eta= \frac{c_{2}}{c_{1}}, \lambda=1-\frac{c_{3}}{c_{2}}\), and\(r=\frac{a}{c_{1}}+\frac{a_{1}}{c_{1} ( 1-\sigma ) }\), where\(a_{1}=\frac{c_{3}a}{c_{2}}+\rho_{1}\)and\(\rho_{1}=\sup_{w(k)\in\Omega }\lbrace\rho( \Vert w(k) \Vert ) \rbrace\).

Proof

From (i) and (ii), we obtain that
$$\begin{aligned} &V\bigl(k+1,x(k+1;k_{0},x_{0},w)\bigr)-V \bigl(k,x(k;k_{0},x_{0},w)\bigr)\\ &\quad\leq-c_{3} \bigl\Vert x(k;k_{0},x_{0},w) \bigr\Vert ^{p}+\rho \bigl( \bigl\Vert w(k) \bigr\Vert \bigr) \\ &\quad\leq-\frac{c_{3}}{c_{2}}V\bigl(k,x(k;k_{0},x_{0},w)\bigr)+ \frac{c_{3}a}{c_{2}}+\rho_{1} \\ &\quad =-\frac{c_{3}}{c_{2}}V\bigl(k,x(k;k_{0},x_{0},w) \bigr)+a_{1} \end{aligned}$$
for all \(k\geq k_{0}, w(k)\in\Omega\), where \(\rho_{1}=\sup_{w(k)\in \Omega}\lbrace\rho( \Vert w(k) \Vert ) \rbrace, a_{1}=\frac {c_{3}a}{c_{2}}+\rho_{1}\). Without loss of generality, we may assume that \(c_{3}< c_{2}\), and let \(\sigma=1-\frac{c_{3}}{c_{2}}\). Then \(0<\sigma<1\), and it follows that
$$\begin{aligned} &V\bigl(k+1,x(k+1;k_{0},x_{0},w)\bigr)\\ &\quad\leq\biggl(1- \frac{c_{3}}{c_{2}}\biggr) V\bigl(k,x(k;k_{0},x_{0},w) \bigr)+a_{1} \\ &\quad= \sigma V\bigl(k,x(k;k_{0},x_{0},w)\bigr)+a_{1} \\ &\quad\leq\sigma \bigl[ \sigma \bigl( V\bigl(k-1,x(k-1;k_{0},x_{0},w) \bigr)+a_{1} \bigr) \bigr] +a_{1} \\ &\quad\leq\sigma^{2} \bigl[ \sigma \bigl( V\bigl(k-2,x(k-2;k_{0},x_{0},w) \bigr)+a_{1} \bigr) \bigr]+\sigma a_{1} +a_{1} \\ &\quad\vdots \\ &\quad\leq\sigma^{k+1}V(k_{0},x_{0},w)+ \sigma^{k}a_{1}+\sigma^{k-1}a_{1}+\cdots +a_{1}. \end{aligned}$$
Thus,
$$\begin{aligned} V\bigl(k,x(k;k_{0},x_{0},w)\bigr)\leq\sigma^{k-k_{0}}V(k_{0},x_{0},w)+ \frac {a_{1}}{1-\sigma}. \end{aligned}$$
From (i), we can see that
$$\begin{aligned} c_{1} \bigl\Vert x(k;k_{0},x_{0},w) \bigr\Vert ^{p} &\leq V\bigl(k,x(k;k_{0},x_{0},w) \bigr)\leq \sigma ^{k-k_{0}}V(k_{0},x_{0},w)+ \frac{a_{1}}{1-\sigma} \\ &\leq \sigma^{k-k_{0}} \bigl( c_{2} \Vert x_{0} \Vert ^{p} +a \bigr)+\frac {a_{1}}{1-\sigma}. \end{aligned}$$
Thus,
$$\begin{aligned} \bigl\Vert x(k;k_{0},x_{0},w) \bigr\Vert ^{p} &\leq\frac{c_{2}}{c_{1}}\sigma ^{k-k_{0}} \Vert x_{0} \Vert ^{p}+\frac{\sigma^{k-k_{0}}a}{c_{1}}+\frac {a_{1}}{c_{1} ( 1-\sigma ) } \\ &\leq\frac{c_{2}}{c_{1}}\sigma^{k-k_{0}} \Vert x_{0} \Vert ^{p}+\frac {a}{c_{1}}+\frac{a_{1}}{c_{1} ( 1-\sigma ) } \\ &=c_{4}\sigma^{k-k_{0}} \Vert x_{0} \Vert ^{p}+a_{2}, \end{aligned}$$
where \(c_{4}=\frac{c_{2}}{c_{1}}\) and \(a_{2}=\frac{a}{c_{1}}+\frac{a_{1}}{c_{1} ( 1-\sigma ) }\). It follows that
$$\begin{aligned} \bigl\Vert x(k;k_{0},x_{0},w) \bigr\Vert ^{p} \leq c_{4}\sigma^{k-k_{0}} \Vert x_{0} \Vert ^{p}+a_{2} \quad\mbox{for all } k\geq k_{0},w(k) \in\Omega. \end{aligned}$$
Therefore, system (3.1) is exponentially practically stable in the pth-moment with \(\eta=c_{4}, \lambda=\sigma\), and \(r=a_{2}\). □
Then, we will consider system (2.1) without delay, namely a discrete time singular system with disturbance, as follows:
$$\begin{aligned} \textstyle\begin{cases}Ex(k+1)=Ax(k)+Gw(k), \\ x(k_{0})=x_{0}. \end{cases}\displaystyle \end{aligned}$$
(3.2)

Definition 3.2

The singular system (3.2) is said to be exponentially practically stable in the pth-moment for some \(p>0\) if, for all \(k\geq k_{0}\), there exist constants \(0<\lambda<1, \eta >0, r>0\) for each disturbance \(w(k)\in\Omega\) such that
$$\begin{aligned} \bigl\Vert Ex(k;k_{0},x_{0},w) \bigr\Vert ^{p} \leq\eta \Vert x_{0} \Vert ^{p} \lambda^{k-k_{0}}+r, \end{aligned}$$
where \(x(k,k_{0},x_{0},w)\) is the state trajectory of a system with initial state \(x_{0}\).

Theorem 3.2

Assume that the singular system (3.2) is regular and causal. Then the singular system (3.2) is exponentially practically stable in thepth-moment with respect to\(w(k)\), if there exists a Lyapunov function\(V(k,x(k))\)such that
  1. (i)

    \(c_{1} \Vert Ex(k) \Vert ^{p}\leq V(k,x(k))\leq c_{2} \Vert Ex(k) \Vert ^{p}+a\),

     
  2. (ii)

    \(\Delta V(k,x(k))=V(k+1,x(k+1))-V(k,x(k))\leq-c_{3} \Vert x(k) \Vert ^{p}+ \rho( \Vert w(k) \Vert )\)hold for some positive constants\(a, c_{1}, c_{2}, c_{3}, p; c_{3}< c_{2}\)and aK-functionρ.

     

Proof

Assume that system (3.2) is regular and causal. Then, from [30], there exist nonsingular matrices \(M, N\) with appropriate dimensions such that
$$ MEN= \begin{pmatrix}I_{r}& 0\\0&0_{n-r} \end{pmatrix} ,\qquad MAN= \begin{pmatrix}A_{1}& 0\\0&I_{n-r} \end{pmatrix} ,\qquad {MG}= \begin{pmatrix}G_{1}\\G_{2} \end{pmatrix} . $$
Let \(y(k)=N^{-1}x(k)= \bigl [{\scriptsize\begin{matrix}{}y_{1}(k)\cr y_{2}(k)\end{matrix}} \bigr ] \), then system (3.2) is transformed to the system
$$\begin{aligned} & y_{1}(k+1)=A_{1}y_{1}(k)+G_{1}w(k), \end{aligned}$$
(3.3)
$$\begin{aligned} & y_{2}(k)=-G_{2}w(k) \end{aligned}$$
(3.4)
with initial state \(y_{0}\) satisfying \(\bigl ({\scriptsize\begin{matrix}{} I_{r}& 0\cr 0&0\end{matrix}} \bigr ) y_{0}= \bigl ({\scriptsize\begin{matrix}{} y_{10}\cr 0\end{matrix}} \bigr ) \). From the Lyapunov function \(V(k,x(k))\) satisfying conditions (i) and (ii), we obtain the following estimations:
$$\begin{aligned} &c_{1} \bigl\Vert Ex(k) \bigr\Vert ^{p}\leq V \bigl(k,x(k)\bigr)\leq c_{2} \bigl\Vert Ex(k) \bigr\Vert ^{p}+a, \\ &c_{1} \bigl\Vert ENy(k) \bigr\Vert ^{p}\leq V \bigl(k,Ny(k)\bigr)\leq c_{2} \bigl\Vert ENy(k) \bigr\Vert ^{p}+a, \\ &c_{1} \bigl\Vert M^{-1}MEN y(k) \bigr\Vert ^{p}\leq V\bigl(k,Ny(k)\bigr)\leq c_{2} \bigl\Vert M^{-1}MEN y(k) \bigr\Vert ^{p}+a, \\ &c_{1}\left\Vert M^{-1} \begin{bmatrix}y_{1}(k)\\0 \end{bmatrix} \right\Vert ^{p}\leq V\bigl(k,Ny(k)\bigr)\leq c_{2} \left\Vert M^{-1} \begin{bmatrix}y_{1}(k)\\0 \end{bmatrix} \right\Vert ^{p}+a, \\ &c_{1}\left\Vert M^{-1}N^{-1}N \begin{bmatrix}y_{1}(k)\\0 \end{bmatrix} \right\Vert ^{p}\leq V\bigl(k,Ny(k) \bigr)\leq c_{2} \left\Vert M^{-1}N^{-1}N \begin{bmatrix}y_{1}(k)\\0 \end{bmatrix} \right\Vert ^{p}+a. \end{aligned}$$
Let \(\overline{y}(k)=Ny(k), \overline{y_{1}}(k)=N \bigl [{\scriptsize\begin{matrix}{} y_{1}(k)\cr 0\end{matrix}} \bigr ] \). Then we obtain
$$\begin{aligned} c_{1} \bigl\Vert M^{-1}N^{-1} \overline{y_{1}}(k) \bigr\Vert ^{p}\leq V\bigl(k,\overline {y}(k)\bigr)\leq c_{2} \bigl\Vert M^{-1}N^{-1} \overline{y_{1}}(k) \bigr\Vert ^{p}+a, \end{aligned}$$
which in turn gives
$$\begin{aligned} c_{1} \bigl\Vert M^{-1}N^{-1} \overline{y_{1}}(k) \bigr\Vert ^{p}\leq V\bigl(k,\overline {y_{1}}(k)\bigr)\leq c_{2} \bigl\Vert M^{-1}N^{-1} \overline{y_{1}}(k) \bigr\Vert ^{p}+a. \end{aligned}$$
From which it follows that
$$\begin{aligned} V\bigl(k,\overline{y_{1}}(k)\bigr)& \geq c_{1} \bigl( \bigl\Vert M^{-1}N^{-1}\overline {y_{1}}(k) \bigr\Vert ^{2} \bigr) ^{\frac{p}{2}} \\ &= c_{1} \bigl( \bigl\Vert \overline{y_{1}}^{T}(k) \bigl(M^{-1}N^{-1}\bigr)^{T} \bigl(M^{-1}N^{-1} \bigr)\overline{y_{1}}(k) \bigr\Vert \bigr) ^{\frac{p}{2}} \\ &\geq c_{1} \bigl( \lambda_{\mathrm{min}} \bigl( \bigl(M^{-1}N^{-1} \bigr)^{T} \bigl(M^{-1}N^{-1}\bigr) \bigr) \bigr) ^{\frac{p}{2}} \bigl\Vert \overline {y_{1}}(k) \bigr\Vert ^{p}. \end{aligned}$$
Similarly, we have
$$ V\bigl(k,\overline{y_{1}}(k)\bigr)\leq c_{2} \bigl\Vert M^{-1} \bigr\Vert ^{p} \bigl\Vert N^{-1} \bigr\Vert ^{p} \bigl\Vert \overline{y_{1}}(k) \bigr\Vert ^{p}+a. $$
Thus,
$$ \overline{c}_{1} \bigl\Vert \overline{y_{1}}(k) \bigr\Vert ^{p}\leq V\bigl(k,\overline {y_{1}}(k)\bigr)\leq \overline{c}_{2} \bigl\Vert \overline{y_{1}}(k) \bigr\Vert ^{p}+a, $$
where \(\overline{c}_{1} =c_{1} ( \lambda_{\mathrm{min}} ( (M^{-1}N^{-1})^{T} (M^{-1}N^{-1}) ) ) ^{\frac{p}{2}}\), and \(\overline{c}_{2} =c_{2} \Vert M^{-1} \Vert ^{p} \Vert N^{-1} \Vert ^{p}\).
Furthermore, we have the following estimations for \(\Delta V(k,x(k))\):
$$\begin{aligned} &\Delta V\bigl(k,x(k)\bigr)=V\bigl(k+1,x(k+1)\bigr)-V\bigl(k,x(k)\bigr) \leq-c_{3} \bigl\Vert x(k) \bigr\Vert ^{p}+ \rho\bigl( \bigl\Vert w(k) \bigr\Vert \bigr), \\ &\Delta V\bigl(k,Ny(k)\bigr)=V\bigl(k+1,Ny(k+1)\bigr)-V\bigl(k,Ny(k)\bigr) \leq-c_{3} \bigl\Vert Ny(k) \bigr\Vert ^{p}+ \rho\bigl( \bigl\Vert w(k) \bigr\Vert \bigr), \\ &\Delta V\bigl(k,\overline{y}(k)\bigr)=V\bigl(k+1,\overline{y}(k+1)\bigr)-V \bigl(k,\overline {y}(k)\bigr)\leq-c_{3} \bigl\Vert \overline{y}(k) \bigr\Vert ^{p}+ \rho\bigl( \bigl\Vert w(k) \bigr\Vert \bigr), \\ &\Delta V\bigl(k,\overline{y_{1}}(k)\bigr)=V\bigl(k+1, \overline{y_{1}}(k+1)\bigr)-V\bigl(k,\overline {y_{1}}(k) \bigr)\leq-c_{3} \bigl\Vert \overline{y_{1}}(k) \bigr\Vert ^{p}+ \rho\bigl( \bigl\Vert w(k) \bigr\Vert \bigr). \end{aligned}$$
From (3.3) with \(\overline{y_{1}}(k)=N \bigl[{\scriptsize\begin{matrix}{}y_{1}(k)\cr0\end{matrix}} \bigr] \), we have
$$\begin{aligned} \overline{y_{1}}(k+1)=\overline{A_{1}} \overline{y_{1}}(k)+\overline {G_{1}}\overline{w}(k), \end{aligned}$$
(3.5)
where \(\overline{A_{1}}=N \bigl[{\scriptsize\begin{matrix}{} A_{1} & 0 \cr 0 & 0 \end{matrix}}\bigr] N^{-1}, \overline{G_{1}}=N \bigl[{\scriptsize\begin{matrix}{} G_{1} & 0 \cr 0 & 0 \end{matrix}}\bigr] \), and \(\overline{w}(k)= \bigl[{\scriptsize\begin{matrix}{} w(k) \cr 0 \end{matrix}} \bigr] \). Therefore, we may conclude that there exists a Lyapunov function \(V(k,\overline{y_{1}}(k))\) for system (3.5) which satisfies the following conditions:
  1. (i)

    \(\overline{c}_{1} \Vert \overline{y_{1}}(k) \Vert ^{p}\leq V(k,\overline {y_{1}}(k))\leq\overline{c}_{2} \Vert \overline{y_{1}}(k) \Vert ^{p}+a\),

     
  2. (ii)

    \(\Delta V(k,\overline{y_{1}}(k))=V(k+1,\overline {y_{1}}(k+1))-V(k,\overline{y_{1}}(k))\leq-c_{3} \Vert \overline{y_{1}}(k) \Vert ^{p}+ \rho( \Vert w(k) \Vert )\).

     
Hence, from Theorem 3.1, there exist constants \(0<\lambda<1, \eta _{0}>0, r_{0}>0\) such that
$$\begin{aligned} \bigl\Vert \overline{y_{1}}(k) \bigr\Vert ^{p} \leq\eta_{0} \Vert \overline{y_{10}} \Vert ^{p}\lambda^{k-k_{0}}+r_{0},\quad \forall k\geq k_{0}, \end{aligned}$$
(3.6)
where \(\overline{y_{10}}=N \bigl[{\scriptsize\begin{matrix}{} y_{10} \cr 0\end{matrix}}\bigr] \). Thus, we have
$$\begin{aligned} \bigl\Vert y_{1}(k) \bigr\Vert ^{p} & \leq \eta_{0} \bigl\Vert N^{-1} \bigr\Vert ^{p} \Vert N \Vert ^{p} \Vert y_{10} \Vert ^{p}\lambda^{k-k_{0}}+ \bigl\Vert N^{-1} \bigr\Vert ^{p}r_{0} \\ &= \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{1},\quad \forall k\geq k_{0}, \end{aligned}$$
(3.7)
where \(\eta_{1}=\eta_{0} \Vert N^{-1} \Vert ^{p} \Vert N \Vert ^{p}, r_{1}= \Vert N^{-1} \Vert ^{p}r_{0}\). From (3.4), we have \(y_{2}(k)=-G_{2}w(k)\), which in turn gives
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert \leq \Vert G_{2} \Vert \bigl\Vert w(k) \bigr\Vert . \end{aligned}$$
(3.8)
Thus, it follows from (3.7) and (3.8) that
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert \leq \bigl\Vert y_{1}(k) \bigr\Vert + \bigl\Vert y_{2}(k) \bigr\Vert . \end{aligned}$$
Therefore,
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert \leq \bigl( \eta_{1} \Vert y_{10} \Vert ^{p}\lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}}+\overline{w} \Vert G_{2} \Vert . \end{aligned}$$
(3.9)
From (3.9), there are four cases to be considered according to the values of p and \(r_{1}\) as follows:
(Case I). \(0< p<1, 0<r_{1}<1\). Since \(0<\lambda<1\), we may assume without loss of generality that
$$ \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{1}< 1 $$
for all \(k\geq k_{0}\). Let \(\lfloor\frac{1}{p}\rfloor=n, n\in\mathbb {I}^{+}\). Then, by the binomial theorem, we obtain
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert \leq{}& \bigl( \eta_{1} \Vert y_{10} \Vert ^{p}\lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}}+\overline{w} \Vert G_{2} \Vert \\ \leq{}& \bigl( \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{1} \bigr) ^{\lfloor\frac{1}{p}\rfloor}+\overline{w} \Vert G_{2} \Vert \\ ={}& \bigl( \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{1} \bigr) ^{n}+\overline{w} \Vert G_{2} \Vert \\ ={} &\bigl( \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}} \bigr) ^{n}+ \begin{pmatrix} n\\1 \end{pmatrix} \bigl( \eta_{1} \Vert y_{10} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{n-1} r_{1}\\ &{}+ \begin{pmatrix} n\\2 \end{pmatrix} \bigl( \eta_{1} \Vert y_{10} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{n-2} r_{1}^{2}+\cdots+r_{1}^{n} +\overline{w} \Vert G_{2} \Vert \\ \leq{}& \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}} + \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}r_{1}\\ &{}+ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}r_{1}+\cdots + \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1} +\overline{w} \Vert G_{2} \Vert \\ = {}& \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}} + ( n-1 ) \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}r_{1} + \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1}+\overline{w} \Vert G_{2} \Vert \\ ={}&\left [ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} + ( n-1 ) \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1} \right ] \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}} +\left [ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1}+\overline{w} \Vert G_{2} \Vert \right ] \\ ={}&\eta_{2} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{2}, \end{aligned}$$
where \(\eta _{2} =\bigl[\bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) + ( n-1 ) \bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) r_{1} \bigr] \eta_{1} \) and \(r_{2}= \bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) r_{1}+\overline{w} \Vert G_{2} \Vert \).
(Case II) \(0< p<1, r_{1}\geq1\). Since \(0<\lambda<1\), we may assume without loss of generality that
$$ \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}< 1 $$
for all \(k\geq k_{0}\). Let \(\lceil\frac{1}{p} \rceil=n, n\in\mathbb {I}^{+}\). Then, by the binomial theorem, we obtain
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert \leq {}&\bigl( \eta_{1} \Vert y_{10} \Vert ^{p}\lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}}+\overline{w} \Vert G_{2} \Vert \\ \leq{}& \bigl( \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{1} \bigr) ^{n}+\overline{w} \Vert G_{2} \Vert \\ ={}& \bigl( \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}} \bigr) ^{n}+ \begin{pmatrix} n\\1 \end{pmatrix} \bigl( \eta_{1} \Vert y_{10} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{n-1} r_{1}\\ &{}+ \begin{pmatrix} n\\2 \end{pmatrix} \bigl( \eta_{1} \Vert y_{10} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{n-2} r_{1}^{2}+\cdots+r_{1}^{n} +\overline{w} \Vert G_{2} \Vert \\ \leq{}& \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}r_{1}^{n} + \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}r_{1}^{n}\\ &{}+ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}r_{1}^{n}+ \cdots + \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1}^{n} + \overline{w} \Vert G_{2} \Vert \\ ={}&n \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}r_{1}^{n}+ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1}^{n} + \overline{w} \Vert G_{2} \Vert \\ ={}&\eta_{3} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{3}, \end{aligned}$$
where \(\eta _{3} =n \bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) \eta_{1} r_{1}^{n}\), and \(r_{3}= \bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) r_{1}^{n} +\overline{w} \Vert G_{2} \Vert \).
(Case III) \(p\geq1, 0< r_{1}<1\). Since \(0<\lambda<1\), we may assume without loss of generality that
$$ \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{1}< 1 $$
for all \(k\geq k_{0}\). Let \(\lceil p \rceil=n, n\in\mathbb{I}^{+}\). Then, by the binomial theorem, we obtain
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert & \leq \bigl( \eta_{1} \Vert y_{10} \Vert ^{p}\lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}}+\overline{w} \Vert G_{2} \Vert \\ &\leq \bigl( \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{1} \bigr) ^{ \frac{1}{n} }+\overline{w} \Vert G_{2} \Vert \\ &\leq \bigl( \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}} \bigr) ^{ \frac{1}{n} } +r_{1}^{\frac{1}{n}}+ \overline{w} \Vert G_{2} \Vert \\ &\leq\eta_{1}^{\frac{1}{n}} \Vert y_{10} \Vert ^{\frac{p}{n}} \lambda ^{\frac{k-k_{0}}{n}}+r_{1}^{\frac{1}{n}}+ \overline{w} \Vert G_{2} \Vert \\ &\leq\eta_{1}^{\frac{1}{n}} \Vert y_{10} \Vert ^{\frac{p}{n}-p} \Vert y_{10} \Vert ^{p} \bigl( \lambda^{\frac{1}{n}}\bigr) ^{k-k_{0}} +r_{1}^{\frac {1}{n}}+ \overline{w} \Vert G_{2} \Vert \\ &=\eta_{4} \Vert y_{10} \Vert ^{p} \lambda_{1}^{k-k_{0}}+r_{4}, \end{aligned}$$
where \(\eta _{4}=\eta_{1}^{\frac{1}{n}} \Vert y_{10} \Vert ^{\frac{p}{n}-p}, r_{4}=r_{1}^{\frac{1}{n}}+\overline{w} \Vert G_{2} \Vert \), and \(0<\lambda _{1}=\lambda^{\frac{1}{n}} <1\).
(Case IV) \(p\geq1, r_{1}\geq1\). Let \(\lfloor p \rfloor=n, n\in\mathbb{I}^{+}\). Then, by the binomial theorem, we obtain
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert & \leq \bigl( \eta_{1} \Vert y_{10} \Vert ^{p}\lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}}+\overline{w} \Vert G_{2} \Vert \\ &\leq \bigl( \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}}+r_{1} \bigr) ^{ \frac{1}{n} }+\overline{w} \Vert G_{2} \Vert \\ &\leq \bigl( \eta_{1} \Vert y_{10} \Vert ^{p} \lambda^{k-k_{0}} \bigr) ^{ \frac{1}{n} } +r_{1}^{\frac{1}{n}}+ \overline{w} \Vert G_{2} \Vert \\ &\leq\eta_{1}^{\frac{1}{n}} \Vert y_{10} \Vert ^{\frac{p}{n}} \lambda ^{\frac{k-k_{0}}{n}}+r_{1}+\overline{w} \Vert G_{2} \Vert \\ &\leq\eta_{1}^{\frac{1}{n}} \Vert y_{10} \Vert ^{\frac{p}{n}-p} \Vert y_{10} \Vert ^{p} \bigl( \lambda^{\frac{1}{n}}\bigr) ^{k-k_{0}} +r_{1}+\overline {w} \Vert G_{2} \Vert \\ &=\eta_{4} \Vert y_{10} \Vert ^{p} \lambda_{1}^{k-k_{0}}+r_{5}, \end{aligned}$$
where \(\eta_{4}= \eta_{1}^{\frac{1}{n}} \Vert y_{10} \Vert ^{\frac{p}{n}-p}, r_{5}=r_{1}+\overline{w} \Vert G_{2} \Vert \), and \(0<\lambda_{1}=\lambda^{\frac {1}{n}} <1\). Therefore, from (Case I) to (Case IV), we obtain
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert \leq \eta_{5} \Vert y_{10} \Vert ^{p} \lambda _{2}^{k-k_{0}}+r_{6}, \end{aligned}$$
(3.10)
where \(\eta_{5}=\max\lbrace\eta_{2},\eta_{3},\eta_{4}\rbrace, r_{6}=\max \lbrace r_{2},r_{3},r_{4},r_{5} \rbrace\), and \(0<\lambda_{2}= \min\lbrace \lambda, \lambda_{1} \rbrace<1\).

From \({ME}x_{0}=MEN y_{0}= \bigl({\scriptsize\begin{matrix}{}I_{r}& 0\cr 0&0 \end{matrix}}\bigr) y_{0}\) and \(y_{0}= \bigl({\scriptsize\begin{matrix}{}y_{10}\cr 0 \end{matrix}}\bigr) \), it follows that \(\Vert y_{10} \Vert \leq \Vert M \Vert \Vert E \Vert \Vert x_{0} \Vert \).

Since \(x(k)=Ny(k)\), it follows from (3.10) that
$$\begin{aligned} \bigl\Vert Ex(k) \bigr\Vert &\leq \Vert E \Vert \Vert N \Vert \bigl\Vert y(k) \bigr\Vert \\ &\leq \Vert E \Vert \Vert N \Vert \bigl( \eta_{5} \Vert y_{10} \Vert ^{p} \lambda_{2}^{k-k_{0}}+r_{6} \bigr) \\ &\leq \eta_{5} \Vert E \Vert \Vert N \Vert \Vert M \Vert ^{p} \Vert E \Vert ^{p} \Vert x_{0} \Vert ^{p} \lambda_{2}^{k-k_{0}}+ \Vert E \Vert \Vert N \Vert r_{6} \\ &=\eta_{6} \Vert x_{0} \Vert \lambda_{2}^{k-k_{0}}+r_{7}, \end{aligned}$$
where \(\eta_{6}=\eta_{5} \Vert E \Vert ^{p+1} \Vert N \Vert \Vert M \Vert ^{p} \Vert x_{0} \Vert ^{p-1} \) and \(r_{7}= \Vert E \Vert \Vert N \Vert r_{6}\).

Therefore, the singular system (3.2) is exponentially practically stable with respect to \(w(k)\) with \(\eta=\eta_{6}, \lambda =\lambda_{2}\), and \(r=r_{7}\). □

Remark 3.1

In Theorem 3.2, for \(p=1\), we can show that the singular system (3.2) is exponentially practically stable in the pth-moment with respect to \(w(k)\) by considering the explicit form of solution of the system. System (3.2) may be reduced to system (3.3) and (3.4). Moreover, the explicit solution of (3.3) and (3.4) with \(k_{0}=0\) is given as follows:
$$\begin{aligned} & y_{1}(k) = A_{1}^{k}y_{1}(0)+ \sum_{i=0}^{k-1}A_{1}^{k-1-i}G_{1}w(i), \end{aligned}$$
(3.11)
$$\begin{aligned} & y_{2}(k) =-G_{2}w(k). \end{aligned}$$
(3.12)
Thus, from (3.11) and (3.12), we have
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert &\leq \bigl\Vert y_{1}(k) \bigr\Vert + \bigl\Vert y_{2}(k) \bigr\Vert \\ &\leq \Vert A_{1} \Vert ^{k} \bigl\Vert y_{1}(0) \bigr\Vert +\sum_{i=0}^{k-1} \Vert A_{1} \Vert ^{k-1-i} \Vert G_{1} \Vert \bigl\Vert w(i) \bigr\Vert + \Vert G_{2} \Vert \bigl\Vert w(k) \bigr\Vert . \end{aligned}$$
By assuming that \(\Vert A_{1} \Vert < 1\), we obtain
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert &\leq \Vert A_{1} \Vert ^{k} \bigl\Vert y_{1}(0) \bigr\Vert +\overline {w} \Vert G_{1} \Vert { }\frac{1}{1- \Vert A_{1} \Vert }+\overline{w} \Vert G_{2} \Vert \\ &= \Vert A_{1} \Vert ^{k} \bigl\Vert y_{1}(0) \bigr\Vert +r_{0}, \end{aligned}$$
where \(r_{0}=\overline{w} \Vert G_{1} \Vert { }\frac{1}{1- \Vert A_{1} \Vert }+\overline{w} \Vert G_{2} \Vert \). Since \(x(k)=Ny(k)\), we have that
$$\begin{aligned} \bigl\Vert Ex(k) \bigr\Vert &\leq \Vert E \Vert \Vert N \Vert \bigl\Vert y(k) \bigr\Vert \\ &\leq \Vert E \Vert \Vert N \Vert \bigl( \Vert A_{1} \Vert ^{k} \bigl\Vert y_{1}(0) \bigr\Vert +r_{0} \bigr) \\ &\leq \Vert E \Vert \Vert N \Vert \bigl( \Vert A_{1} \Vert ^{k} \Vert M \Vert \Vert E \Vert \bigl\Vert x(0) \bigr\Vert +r_{0} \bigr) \\ &=\overline{\eta} \bigl\Vert x(0) \bigr\Vert \Vert A_{1} \Vert ^{k}+\overline{r}, \end{aligned}$$
where \(\overline{\eta}= \Vert E \Vert ^{2} \Vert N \Vert \Vert M \Vert \) and \(\overline{r}= \Vert E \Vert \Vert N \Vert r_{0}\). Hence, system (3.2) is exponentially practically stable.
Next, we consider the discrete time system with delay and disturbance as follows:
$$\begin{aligned} \textstyle\begin{cases}x(k+1)=f(k,x_{k},w(k)), \\ x(s)=\varphi(s),\quad s\in\mathbb{N}_{k_{0}-\tau}, \end{cases}\displaystyle \end{aligned}$$
(3.13)
where \(x_{k} \) is defined by \(x_{k}(s)=x(k+s)\) for any \(s \in\mathbb {N}_{k_{0}-\tau}\), disturbance \(w(k)\in\Omega\), where Ω is defined as in (2.1), \(f:\mathbb{R}\times\mathbb{R}^{n}\times\Omega \longrightarrow\mathbb{R}^{n}\) is continuous and locally Lipschitz in \((x,w)\), uniformly in k with Lipschitz constant L which satisfies \(f(k,0,0)=0\). Let \(x(k;k_{0},\varphi,w)\) denote the trajectory of system (3.13) with initial condition φ and disturbance signal \(w(k)\in\Omega\).

Definition 3.3

System (3.13) is exponentially practically stable in the pth-moment with respect to \(w(k)\) for some \(p>0\) if, for any \(k\geq k_{0}\), there exist constants \(0< \lambda<1, \eta> 0, r>0\) such that
$$\begin{aligned} \bigl\Vert x(k;k_{0},\phi,w) \bigr\Vert ^{p} \leq\eta \Vert \varphi \Vert ^{p}\lambda^{k-k_{0}}+r, \quad\forall w(k)\in \Omega. \end{aligned}$$

Theorem 3.3

If there exist a Lyapunov–Krasovskii functional\(V(k,x(k))\), aK-functionρ, and positive constants\(c_{1},c_{2},a,p,q,\beta\), where\(q>1, 0<\beta<1, \rho ( \Vert w(k ) \Vert )<\beta a\)such that the following conditions hold for all\(w(k)\in\Omega\):
  1. (i)

    \(c_{1} \Vert x(k) \Vert ^{p}\leq V(k,x(k))\leq c_{2} \Vert x(k) \Vert ^{p}+a\),

     
  2. (ii)
    If\(V(k+s,x(k+s))\leq qV(k+1,x(k+1))\)with\(s \in\mathbb {N}_{k_{0}-\tau}\), then
    $$ \Delta V\bigl(k,x(k)\bigr)=V\bigl(k+1,x(k+1)\bigr)-V\bigl(k,x(k)\bigr)\leq-\beta V\bigl(k,x(k)\bigr)+ \rho \bigl( \bigl\Vert w(k ) \bigr\Vert \bigr). $$
    Then system (3.13) is exponentially practically stable in thepth-moment with\(\eta=\frac{c_{2}}{c_{1}}, q^{-\frac{1}{\tau+1}}\leq \lambda<1\), and\(r=\frac{a}{c_{1}}\).
     

Proof

For \(q>1\), there exists \(0<\lambda<1\) such that \(q\geq \lambda^{-(\tau+1)}\), or equivalently, \(q^{-\frac{1}{\tau+1}}\leq \lambda<1\). By employing a similar approach as in the proof of Theorem (3.1) in [23], it follows from \(0<\beta<1\) and \(\rho( \Vert w(k ) \Vert )<\beta a\) that
$$ V\bigl(k,x(k)\bigr)\leq c_{2} \Vert \varphi \Vert ^{p} \lambda^{k-k_{0}}+a $$
for \(k \geq k_{0}, w(k)\in\Omega\), from which it follows that
$$ \bigl\Vert x(k) \bigr\Vert ^{p}\leq\frac{c_{2}}{c_{1}} \Vert \varphi \Vert ^{p}\lambda^{k-k_{0}}+\frac{a}{c_{1}},\quad k\geq k_{0}, w(k)\in\Omega. $$
Therefore, system (3.13) is exponentially practically stable in the pth-moment with \(\eta=\frac{c_{2}}{c_{1}}, q^{-\frac{1}{\tau+1}}\leq \lambda<1\), and \(r=\frac{a}{c_{1}}\). □

Finally, we consider exponentially practical stability for system (2.1) with delay and disturbance.

Definition 3.4

The discrete time singular system (2.1) is said to be exponentially practically stable in the pth-moment for some \(p>0\) if there exist constants \(0< \lambda<1, \eta>0, r>0\) for each disturbance \(w(k)\in\Omega\) such that
$$\begin{aligned} \bigl\Vert Ex(k;k_{0},\varphi,w) \bigr\Vert ^{p} \leq \eta \Vert \varphi \Vert ^{p}\lambda^{k-k_{0}}+r \end{aligned}$$
for all \(k\geq k_{0}\), where \(x(k;k_{0},\varphi,w)\) is the state trajectory of the system with initial condition φ. In particular, when \(p=2\), the system is said to be exponentially practically stable in the mean square.

In order to proceed with the main result on exponentially practical stability in the pth-moment of a singular system with delay and disturbance (2.1), we make the following assumption; an explanation for this assumption is given in Remark 3.2.

Assumption 3.1

There exist nonsingular matrices \(M,N\) with appropriate dimensions such that \(MEN= \bigl({\scriptsize\begin{matrix}{}I_{r}& 0\cr 0&0_{n-r} \end{matrix}}\bigr) \), \({MAN}= \bigl({\scriptsize\begin{matrix}{} A_{1}& 0\cr0&I_{n-r} \end{matrix}}\bigr) \), \({MBN}= \bigl({\scriptsize\begin{matrix}{}B_{1}& 0\cr B_{3}&B_{4} \end{matrix}}\bigr) \), and \({MG}= \bigl({\scriptsize\begin{matrix}{} G_{1}\cr G_{2} \end{matrix}}\bigr) \), where \(\Vert B_{4} \Vert <1\).

Remark 3.2

For a physical meaning of Assumption 3.1, it implies that there is a plant (\(y_{1}\)) in this situation which does not dynamically depend on the other plant (\(y_{2}\)). For future investigation, we propose to study a more general case in which \({MBN}= \bigl({\scriptsize\begin{matrix}{} B_{1}& B_{2}\cr B_{3}&B_{4} \end{matrix}}\bigr) \), where \(B_{2}\) may not be zero; namely, all plants dynamically interact, and that \(\Vert B_{4} \Vert \) may not be less than 1.

Theorem 3.4

Assume that the singular system (2.1) is regular and causal, and that Assumption 3.1holds. Then the singular system (2.1) is exponentially practically stable in thepth-moment with respect to\(w(k)\), if there exists a Lyapunov–Krasovskii functional\(V(k,x(k))\)such that
  1. (i)

    \(c_{1} \Vert Ex(k) \Vert ^{p}\leq V(k,x(k))\leq c_{2} \Vert Ex(k) \Vert ^{p}+a\),

     
  2. (ii)
    If\(V(k+s,x(k+s))\leq qV(k+1,x(k+1))\)with\(s \in\mathbb {N}_{k_{0}-\tau}\), then
    $$ \Delta V\bigl(k,x(k)\bigr)=V\bigl(k+1,x(k+1)\bigr)-V\bigl(k,x(k)\bigr)\leq-\beta V\bigl(k,x(k)\bigr)+ \rho \bigl( \bigl\Vert w(k ) \bigr\Vert \bigr) $$
    hold for some positive constants\(a, c_{1}, c_{2}, p,q, \beta\), where\(q>1, 0<\beta<1\), and someK-functionρ.
     

Proof

Assume that system (2.1) is regular and causal. Then, from [30] and Assumption 3.1, there exist nonsingular matrices \(M, N\) such that
$$\begin{aligned} &MEN= \begin{pmatrix}I_{r}& 0\\0&0_{n-r} \end{pmatrix} ,\qquad {MAN}= \begin{pmatrix}A_{1}& 0\\0&I_{n-r} \end{pmatrix} ,\\ & {MBN}= \begin{pmatrix}B_{1}&0\\B_{3}&B_{4} \end{pmatrix} ,\qquad {MG}= \begin{pmatrix}G_{1}\\G_{2} \end{pmatrix} , \end{aligned}$$
where \(\Vert B_{4} \Vert <1\). Let \(y(k)=N^{-1}x(k)= \bigl[{\scriptsize\begin{matrix}{}y_{1}(k)\cr y_{2}(k) \end{matrix}}\bigr] \), then system (2.1) is transformed to the following system:
$$\begin{aligned} &y_{1}(k+1)=A_{1}y_{1}(k)+B_{1}y_{1}(k- \tau)+G_{1}w(k), \end{aligned}$$
(3.14)
$$\begin{aligned} & y_{2}(k)=-B_{3}y_{1}(k- \tau)-B_{4}y_{2}(k-\tau)-G_{2}w(k), \\ &y_{1}(s):=\phi_{1}(s)=N^{-1} \varphi_{1}(s),\quad s \in\mathbb{N}_{k_{0}-\tau}, \\ &y_{2}(s):=\phi_{2}(s)=N^{-1}\varphi_{2}(s),\quad s \in\mathbb{N}_{k_{0}-\tau}. \end{aligned}$$
(3.15)
From the assumption, there exists a Lyapunov–Krasovskii functional \(V(k,x(k))\) which satisfies conditions (i) and (ii). Then we obtain the following estimations:
$$\begin{aligned} &c_{1} \bigl\Vert Ex(k) \bigr\Vert ^{p}\leq V \bigl(k,x(k)\bigr)\leq c_{2} \bigl\Vert Ex(k) \bigr\Vert ^{p}+a, \\ &c_{1} \bigl\Vert ENy(k) \bigr\Vert ^{p}\leq V \bigl(k,Ny(k)\bigr)\leq c_{2} \bigl\Vert ENy(k) \bigr\Vert ^{p}+a, \\ &c_{1} \bigl\Vert M^{-1}MEN y(k) \bigr\Vert ^{p}\leq V\bigl(k,Ny(k)\bigr)\leq c_{2} \bigl\Vert M^{-1} MEN y(k) \bigr\Vert ^{p}+a, \\ &c_{1}\Biggl\Vert M^{-1} \begin{bmatrix}y_{1}(k)\\0 \end{bmatrix} \Biggr\Vert ^{p}\leq V\bigl(k,Ny(k)\bigr)\leq c_{2} \Biggl\Vert M^{-1} \begin{bmatrix}y_{1}(k)\\0 \end{bmatrix} \Biggr\Vert ^{p}+a, \\ &c_{1}\Biggl\Vert M^{-1}N^{-1}N \begin{bmatrix}y_{1}(k)\\0 \end{bmatrix} \Biggr\Vert ^{p}\leq V\bigl(k,Ny(k) \bigr)\leq c_{2} \Biggl\Vert M^{-1}N^{-1}N \begin{bmatrix}y_{1}(k)\\0 \end{bmatrix} \Biggr\Vert ^{p}+a. \end{aligned}$$
Let \(\overline{y}(k)=Ny(k), \overline{y_{1}}(k)=N \bigl[{\scriptsize\begin{matrix}{} y_{1}(k)\cr 0 \end{matrix}}\bigr] \). Then we obtain
$$\begin{aligned} c_{1} \bigl\Vert M^{-1}N^{-1} \overline{y_{1}}(k) \bigr\Vert ^{p}\leq V\bigl(k,\overline {y}(k)\bigr)\leq c_{2} \bigl\Vert M^{-1}N^{-1} \overline{y_{1}}(k) \bigr\Vert ^{p}+a, \end{aligned}$$
which gives
$$\begin{aligned} c_{1} \bigl\Vert M^{-1}N^{-1} \overline{y_{1}}(k) \bigr\Vert ^{p}\leq V\bigl(k,\overline {y_{1}}(k)\bigr)\leq c_{2} \bigl\Vert M^{-1}N^{-1} \overline{y_{1}}(k) \bigr\Vert ^{p}+a. \end{aligned}$$
Thus, we get
$$\begin{aligned} V\bigl(k,\overline{y_{1}}(k)\bigr)& \geq c_{1} \bigl( \bigl\Vert M^{-1}N^{-1}\overline {y_{1}}(k) \bigr\Vert ^{2} \bigr) ^{\frac{p}{2}} \\ &= c_{1} \bigl( \bigl\Vert \overline{y_{1}}(k)^{T} \bigl(M^{-1}N^{-1}\bigr)^{T} \bigl(M^{-1}N^{-1} \bigr)\overline{y_{1}}(k) \bigr\Vert \bigr) ^{\frac{p}{2}} \\ &\geq c_{1} \bigl( \lambda_{\mathrm{min}} \bigl( \bigl(M^{-1}N^{-1} \bigr)^{T} \bigl(M^{-1}N^{-1}\bigr) \bigr) \bigr) ^{\frac{p}{2}} \bigl\Vert \overline {y_{1}}(k) \bigr\Vert ^{p}. \end{aligned}$$
Similarly, we have
$$ V\bigl(k,\overline{y_{1}}(k)\bigr)\leq c_{2} \bigl\Vert M^{-1} \bigr\Vert ^{p} \bigl\Vert N^{-1} \bigr\Vert ^{p} \bigl\Vert \overline{y_{1}}(k) \bigr\Vert ^{p}+a. $$
Thus, we obtain
$$\begin{aligned} \overline{c}_{1} \bigl\Vert \overline{y_{1}}(k) \bigr\Vert ^{p}\leq V\bigl(k,\overline {y_{1}}(k)\bigr)\leq \overline{c}_{2} \bigl\Vert \overline{y_{1}}(k) \bigr\Vert ^{p}+a, \end{aligned}$$
where \(\overline{c}_{1} =c_{1} ( \lambda_{\mathrm{min}} ( (M^{-1}N^{-1})^{T} (M^{-1}N^{-1}) ) ) ^{\frac{p}{2}}\) and \(\overline{c}_{2} =c_{2} \Vert M^{-1} \Vert ^{p} \Vert N^{-1} \Vert ^{p}\).
Now, assume that the following inequalities hold:
$$\begin{aligned} &V\bigl(k+s,x(k+s)\bigr)\leq qV\bigl(k+1,x(k+1)\bigr)\quad \mbox{with }s \in\mathbb {N}_{k_{0}-\tau}, \\ &V\bigl(k+s,Ny(k+s)\bigr)\leq qV\bigl(k+1,Ny(k+1)\bigr)\quad \mbox{with }s \in\mathbb {N}_{k_{0}-\tau}, \\ &V\bigl(k+s,\overline{y}(k+s)\bigr)\leq qV\bigl(k+1,\overline{y}(k+1)\bigr) \quad \mbox{with } s \in\mathbb{N}_{k_{0}-\tau}, \\ &V\bigl(k+s,\overline{y_{1}}(k+s)\bigr)\leq qV\bigl(k+1,\overline {y_{1}}(k+1)\bigr)\quad \mbox{with } s \in\mathbb{N}_{k_{0}-\tau}. \end{aligned}$$
Then it follows from (ii) that
$$\begin{aligned} &\Delta V\bigl(k,x(k)\bigr)=V\bigl(k+1,x(k+1)\bigr)-V\bigl(k,x(k)\bigr)\leq- \beta V\bigl(k,x(k)\bigr)+ \rho \bigl( \bigl\Vert w(k) \bigr\Vert \bigr), \\ &\Delta V\bigl(k,Ny(k)\bigr)=V\bigl(k+1,Ny(k+1)\bigr)-V\bigl(k,Ny(k)\bigr)\leq- \beta V\bigl(k,Ny(k)\bigr)+ \rho\bigl( \bigl\Vert w(k) \bigr\Vert \bigr), \\ &\Delta V\bigl(k,\overline{y}(k)\bigr)=V\bigl(k+1,\overline{y}(k+1)\bigr)-V \bigl(k,\overline {y}(k)\bigr)\leq-\beta V\bigl(k,\overline{y}(k)\bigr)+ \rho\bigl( \bigl\Vert w(k) \bigr\Vert \bigr), \\ &\Delta V\bigl(k,\overline{y_{1}}(k)\bigr)=V\bigl(k+1, \overline{y_{1}}(k+1)\bigr)-V\bigl(k,\overline {y_{1}}(k) \bigr)\leq-\beta V\bigl(k,\overline{y_{1}}(k)\bigr)+ \rho\bigl( \bigl\Vert w(k) \bigr\Vert \bigr). \end{aligned}$$
Since \(\overline{y_{1}}(k)=N \bigl[{\scriptsize\begin{matrix}{} y_{1}(k)\cr 0 \end{matrix}}\bigr] \), it follows from (3.14) that
$$\begin{aligned} \overline{y_{1}}(k+1)=\overline{A_{1}} \overline{y_{1}}(k)+\overline {B_{1}}\overline{y_{1}}(k- \tau)+\overline{G_{1}}\overline{w}(k), \end{aligned}$$
(3.16)
where \(\overline{A_{1}}=N \bigl[{\scriptsize\begin{matrix}{}A_{1} & 0 \cr 0 & 0 \end{matrix}}\bigr] N^{-1}, \overline{B_{1}}=N \bigl[{\scriptsize\begin{matrix}{}B_{1} & 0 \cr 0 & 0\end{matrix}}\bigr] N^{-1}, \overline{G_{1}}=N \bigl[{\scriptsize\begin{matrix}{} G_{1} & 0 \cr 0 & 0 \end{matrix}}\bigr] \), and \(\overline{w}(k)= \bigl[{\scriptsize\begin{matrix}{} w(k) \cr 0 \end{matrix}}\bigr] \). Therefore, we may conclude that there exists a Lyapunov–Krasovskii functional \(V(k,\overline{y_{1}}(k))\) for system (3.16) which satisfies the following conditions:
  1. (i)

    \(\bar{c_{1}} \Vert \overline{y_{1}}(k) \Vert ^{p}\leq V(k,\overline {y_{1}}(k))\leq\bar{c_{2}} \Vert \overline{y_{1}}(k) \Vert ^{p}+a\),

     
  2. (ii)
    If \(V(k+s,\overline{y_{1}}(k+s))\leq qV(k+1,\overline{y_{1}}(k+1))\) with \(s \in\mathbb{N}_{k_{0}-\tau}\), then
    $$ \Delta V\bigl(k,\overline{y_{1}}(k)\bigr)=V\bigl(k+1, \overline{y_{1}}(k+1)\bigr)-V\bigl(k,\overline {y_{1}}(k) \bigr)\leq-\beta V\bigl(k,\overline{y_{1}}(k)\bigr)+ \rho\bigl( \bigl\Vert w(k ) \bigr\Vert \bigr). $$
     
Thus, from Theorem 3.3, there exist constants \(0< \lambda<1, \eta _{0}\geq0, r_{0}>0\) such that
$$\begin{aligned} \bigl\Vert \overline{y_{1}}(k) \bigr\Vert ^{p} \leq\eta_{0} \Vert \overline{\phi} _{1} \Vert ^{p}\lambda^{k-k_{0}}+r_{0}, \quad \forall k\geq k_{0}, \end{aligned}$$
(3.17)
where \(\overline{\phi} _{1}=N \bigl[{\scriptsize\begin{matrix}{}\phi_{1}\cr 0\end{matrix}}\bigr] \). It follows that
$$\begin{aligned} \bigl\Vert y_{1}(k) \bigr\Vert ^{p} & \leq \eta_{0} \bigl\Vert N^{-1} \bigr\Vert ^{p} \Vert N \Vert ^{p} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}}+ \bigl\Vert N^{-1} \bigr\Vert ^{p}r_{0} \\ &= \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}+r_{1}, \quad \forall k\geq k_{0}, \end{aligned}$$
(3.18)
where \(\eta_{1}=\eta_{0} \Vert N^{-1} \Vert ^{p} \Vert N \Vert ^{p}, r_{1}= \Vert N^{-1} \Vert ^{p}r_{0}\). Therefore, we obtain
$$\begin{aligned} \bigl\Vert y_{1}(k) \bigr\Vert \leq \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}}. \end{aligned}$$
(3.19)
From (3.19), there are four cases to be considered according to the values of p and \(r_{1}\) as follows.
(Case I) \(0< p<1, 0<r_{1}<1\). Let \(\lfloor\frac{1}{p}\rfloor=n, n\in\mathbb{I}^{+}\). Since \(0<\lambda <1\), we may assume without loss of generality that
$$ \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}+r_{1}< 1 $$
for all \(k\geq k_{0}\). Then, by the binomial theorem, we obtain
$$\begin{aligned} \bigl\Vert y_{1}(k) \bigr\Vert \leq {}&\bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}} \\ \leq{}& \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}}+r_{1} \bigr) ^{\lfloor\frac{1}{p} \rfloor} \\ = {}&\bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}+r_{1} \bigr) ^{n} \\ ={}& \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}} \bigr) ^{n}+ \begin{pmatrix} n\\1 \end{pmatrix} \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{n-1} r_{1}\\ &{}+ \begin{pmatrix} n\\2 \end{pmatrix} \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{n-2} r_{1}^{2} +\cdots+r_{1}^{n} \\ \leq{}& \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}} + \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}} r_{1}+ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}} r_{1} \\ &{}+\cdots+ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1} \\ ={}& \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}} + ( n-1 ) \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}} r_{1} + \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1} \\ ={}&\left [ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} + ( n-1 ) \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1} \right ] \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}} +\left [ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1} \right ] \\ ={}&\eta_{2} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}+r_{2}, \end{aligned}$$
where \(\eta _{2}= \bigl[ \bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) + ( n-1 ) \bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) r_{1} \bigr] \eta_{1}\) and \(r_{2}= \bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) r_{1}\).
(Case II) \(0< p<1, r_{1}\geq1\). Let \(\lceil\frac{1}{p} \rceil=n, n\in\mathbb{I}^{+}\). Since \(0<\lambda <1\), we may assume without loss of generality that
$$ \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}< 1 $$
for all \(k\geq k_{0}\). Then, by the binomial theorem, we obtain
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert \leq{}& \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}} \\ \leq{}& \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}}+r_{1} \bigr) ^{n} \\ ={}& \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}} \bigr) ^{n}+ \begin{pmatrix} n\\1 \end{pmatrix} \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{n-1} r_{1}\\ &{}+ \begin{pmatrix} n\\2 \end{pmatrix} \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{n-2} r_{1}^{2}+\cdots+r_{1}^{n} \\ \leq{}& \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}r_{1}^{n} + \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}r_{1}^{n}\\ &{}+ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}r_{1}^{n}+ \cdots + \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1}^{n} \\ ={}&n \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}r_{1}^{n}+ \begin{pmatrix} n\\ \lceil\frac{n}{2} \rceil \end{pmatrix} r_{1}^{n} \\ ={}&\eta_{3} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}+r_{3}, \end{aligned}$$
where \(\eta_{3}=n \bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) \eta_{1} r_{1}^{n}\) and \(r_{3}= \bigl({\scriptsize\begin{matrix}{} n\cr \lceil\frac{n}{2} \rceil \end{matrix}}\bigr) r_{1}^{n} \).
(Case III) \(p\geq1, 0< r_{1}<1\). Let \(\lfloor p \rfloor=n, n\in\mathbb{I}^{+}\). Since \(0<\lambda<1\), we may assume without loss of generality that
$$ \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}+r_{1}< 1 $$
for all \(k\geq k_{0}\). Then, by the binomial theorem, we obtain
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert &\leq \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}} \\ &\leq \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}}+r_{1} \bigr) ^{ \frac{1}{n} } \\ &\leq \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{ \frac{1}{n} } +r_{1}^{\frac{1}{n}} \\ &\leq\eta_{1}^{\frac{1}{n}} \Vert \phi_{1} \Vert ^{\frac{p}{n}} \lambda ^{\frac{k-k_{0}}{n}}+r_{1}^{\frac{1}{n}} \\ &\leq\eta_{1}^{\frac{1}{n}} \Vert \phi_{1} \Vert ^{\frac{p}{n}-p} \Vert \phi_{1} \Vert ^{p} \bigl( \lambda^{\frac{1}{n}}\bigr) ^{k-k_{0}} +r_{1}^{\frac{1}{n}} \\ &=\eta_{4} \Vert \phi_{1} \Vert ^{p} \lambda_{1}^{k-k_{0}}+r_{4}, \end{aligned}$$
where \(\eta _{4}=\eta_{1}^{\frac{1}{n}} \Vert \phi_{1} \Vert ^{\frac{p}{n}-p}, r_{4}=r_{1}^{\frac{1}{n}}\), and \(\lambda_{1}=\lambda^{\frac{1}{n}}\).
(Case IV) \(p\geq1, r_{1}\geq1\). Let \(\lfloor p \rfloor=n, n\in\mathbb{I}^{+}\). Since \(0<\lambda<1\), we may assume without loss of generality that
$$ \eta_{1} \Vert \phi_{1} \Vert ^{p} \lambda^{k-k_{0}}< 1 $$
for all \(k\geq k_{0}\). Then, by the binomial theorem, we obtain
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert &\leq \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda ^{k-k_{0}}+r_{1} \bigr) ^{\frac{1}{p}} \\ &\leq \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}}+r_{1} \bigr) ^{ \frac{1}{n} } \\ &\leq \bigl( \eta_{1} \Vert \phi_{1} \Vert ^{p}\lambda^{k-k_{0}} \bigr) ^{ \frac{1}{n} } +r_{1}^{\frac{1}{n}} \\ &\leq\eta_{1}^{\frac{1}{n}} \Vert \phi_{1} \Vert ^{\frac{p}{n}} \lambda ^{\frac{k-k_{0}}{n}}+r_{1} \\ &\leq\eta_{1}^{\frac{1}{n}} \Vert \phi_{1} \Vert ^{\frac{p}{n}-p} \Vert \phi_{1} \Vert ^{p} \bigl( \lambda^{\frac{1}{n}}\bigr) ^{k-k_{0}} +r_{1} \\ &=\eta_{4} \Vert \phi_{1} \Vert ^{p} \lambda_{1}^{k-k_{0}}+r_{1}, \end{aligned}$$
where \(\eta _{4}=\eta_{1}^{\frac{1}{n}} \Vert \phi_{1} \Vert ^{\frac{p}{n}-p} \) and \(0<\lambda_{1}=\lambda^{\frac{1}{n}} <1\).
From (Case I)–(Case IV), we obtain that
$$\begin{aligned} \bigl\Vert y_{1}(k) \bigr\Vert &\leq \eta_{5} \Vert \phi_{1} \Vert ^{p} \lambda _{2}^{k-k_{0}}+r_{5} \\ &\leq \eta_{5} \Vert \phi \Vert ^{p} \lambda _{2}^{k-k_{0}}+r_{5}, \end{aligned}$$
(3.20)
where \(\eta_{5}=\max\lbrace\eta_{2},\eta_{3},\eta_{4}\rbrace, r_{5}=\max \lbrace r_{1}, r_{2}, r_{3}, r_{4}\rbrace, \lambda_{2}= \min\lbrace\lambda, \lambda_{1}\rbrace\), \(\Vert \phi \Vert = \max_{s \in\mathbb {N}_{k_{0}-\tau}} \lbrace \Vert \phi_{1} (s) \Vert , \Vert \phi_{2} (s) \Vert \rbrace\).
From (3.15), we have
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert \leq \Vert B_{3} \Vert \bigl\Vert y_{1}(k-\tau) \bigr\Vert + \Vert B_{4} \Vert \bigl\Vert y_{2}(k-\tau) \bigr\Vert + \Vert G_{2} \Vert \bigl\Vert w(k) \bigr\Vert ,\quad \forall k \geq k_{0}. \end{aligned}$$
(3.21)
For \(k\geq k_{0}\), we proceed with the proof as follows:
• For \(k \in[k_{0},k_{0}+\tau]\), we have
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert &\leq \Vert B_{3} \Vert \Vert \phi_{1} \Vert + \Vert B_{4} \Vert \Vert \phi_{2} \Vert + \Vert G_{2} \Vert \bigl\Vert w(k) \bigr\Vert \\ &\leq \Vert B_{3} \Vert \Vert \phi \Vert + \Vert B_{4} \Vert \Vert \phi \Vert + \Vert G_{2} \Vert \bigl\Vert w(k) \bigr\Vert \\ &\leq \bigl( \Vert B_{3} \Vert + \Vert B_{4} \Vert \bigr) \Vert \phi \Vert +\gamma, \end{aligned}$$
where \(\gamma= \Vert G_{2} \Vert \Vert w(k) \Vert \leq \Vert G_{2} \Vert \overline{w}\).
• For \(k \in[k_{0}+\tau,k_{0}+2 \tau]\), we have
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert &\leq \Vert B_{3} \Vert \bigl( \eta_{5} \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}}+r_{5} \bigr) + \Vert B_{4} \Vert \bigl[ \bigl( \Vert B_{3} \Vert + \Vert B_{4} \Vert \bigr) \Vert \phi \Vert +\gamma \bigr] +\gamma \\ &= \eta_{5} \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda _{2}^{k-k_{0}}+ \Vert B_{3} \Vert r_{5} + \bigl( \Vert B_{4} \Vert \Vert B_{3} \Vert + \Vert B_{4} \Vert ^{2} \bigr) \Vert \phi \Vert + \Vert B_{4} \Vert \gamma +\gamma. \end{aligned}$$
• For \(k \in[k_{0}+2 \tau,k_{0}+3 \tau]\), we have
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert \leq{}& \Vert B_{3} \Vert \bigl( \eta_{5} \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}}+ r_{5} \bigr) +\eta_{5} \Vert B_{4} \Vert \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}}+ \Vert B_{4} \Vert \Vert B_{3} \Vert r_{5} \\ &{}+ \bigl( \Vert B_{4} \Vert ^{2} \Vert B_{3} \Vert + \Vert B_{4} \Vert ^{3} \bigr) \Vert \phi \Vert + \Vert B_{4} \Vert ^{2}\gamma+ \Vert B_{4} \Vert \gamma + \gamma. \end{aligned}$$
• For \(k \in[k_{0}+3 \tau,k_{0}+4 \tau]\), we have
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert \leq{}&\eta_{5} \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} + \Vert B_{3} \Vert r_{5} +\eta_{5} \Vert B_{4} \Vert \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} \\ &{}+ \Vert B_{4} \Vert \Vert B_{3} \Vert r_{5} +\eta_{5} \Vert B_{4} \Vert ^{2} \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} + \Vert B_{4} \Vert ^{2} \Vert B_{3} \Vert r_{5} \\ &{}+ \bigl( \Vert B_{4} \Vert ^{3} \Vert B_{3} \Vert + \Vert B_{4} \Vert ^{4} \bigr) \Vert \phi \Vert + \Vert B_{4} \Vert ^{3} \gamma+ \Vert B_{4} \Vert ^{2} \gamma+ \Vert B_{4} \Vert \gamma+\gamma. \end{aligned}$$
• For \(k \in[k_{0}+4 \tau,k_{0}+5 \tau]\), we have
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert \leq{}&\eta_{5} \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} + \Vert B_{3} \Vert r_{5} +\eta_{5} \Vert B_{4} \Vert \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} \\ &{}+ \Vert B_{4} \Vert \Vert B_{3} \Vert r_{5} +\eta_{5} \Vert B_{4} \Vert ^{2} \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} + \Vert B_{4} \Vert ^{2} \Vert B_{3} \Vert r_{5} \\ &{}+\eta_{5} \Vert B_{4} \Vert ^{3} \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} + \Vert B_{4} \Vert ^{3} \Vert B_{3} \Vert r_{5} + \bigl( \Vert B_{4} \Vert ^{4} \Vert B_{3} \Vert + \Vert B_{4} \Vert ^{5} \bigr) \Vert \phi \Vert \\ &{}+ \Vert B_{4} \Vert ^{4} \gamma+ \Vert B_{4} \Vert ^{3} \gamma+ \Vert B_{4} \Vert ^{2} \gamma+ \Vert B_{4} \Vert \gamma+\gamma. \end{aligned}$$
By repeating the above process, for all \(k \in[k_{0}+(h-1) \tau ,k_{0}+h \tau]\), where \(h \in\mathbb{I}^{+}\), we get that
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert \leq{}& \eta_{5} \bigl( 1+ \Vert B_{4} \Vert + \Vert B_{4} \Vert ^{2} +\cdots+ \Vert B_{4} \Vert ^{h-2} \bigr) \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} \\ &{}+ \bigl( 1+ \Vert B_{4} \Vert + \Vert B_{4} \Vert ^{2} +\cdots+ \Vert B_{4} \Vert ^{h-2} \bigr) \Vert B_{3} \Vert r_{5} + \bigl( \Vert B_{4} \Vert ^{h-1} \Vert B_{3} \Vert + \Vert B_{4} \Vert ^{h} \bigr) \Vert \phi \Vert \\ &{}+ \bigl( 1+ \Vert B_{4} \Vert + \Vert B_{4} \Vert ^{2} + \Vert B_{4} \Vert ^{3} +\cdots+ \Vert B_{4} \Vert ^{h-1} \bigr) \gamma. \end{aligned}$$
(3.22)
Thus, from (3.21) and (3.22), for \(k \in[k_{0}+h \tau,k_{0}+(h+1) \tau]\), we obtain
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert \leq{}& \eta_{5} \bigl( 1+ \Vert B_{4} \Vert + \Vert B_{4} \Vert ^{2} + \cdots+ \Vert B_{4} \Vert ^{h-1} \bigr) \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} \\ &{}+ \bigl( 1+ \Vert B_{4} \Vert + \Vert B_{4} \Vert ^{2} +\cdots+ \Vert B_{4} \Vert ^{h-1} \bigr) \Vert B_{3} \Vert r_{5} + \bigl( \Vert B_{4} \Vert ^{h} \Vert B_{3} \Vert + \Vert B_{4} \Vert ^{h+1} \bigr) \Vert \phi \Vert \\ &{}+ \bigl( 1+ \Vert B_{4} \Vert + \Vert B_{4} \Vert ^{2} + \Vert B_{4} \Vert ^{3} + \cdots+ \Vert B_{4} \Vert ^{h} \bigr) \gamma. \end{aligned}$$
Hence, from \(\Vert B_{4} \Vert <1\), we obtain by mathematical induction that
$$\begin{aligned} \bigl\Vert y_{2}(k) \bigr\Vert \leq{}& \eta_{5} \bigl( 1+ \Vert B_{4} \Vert + \Vert B_{4} \Vert ^{2} +\cdots \bigr) \Vert B_{3} \Vert \Vert \phi \Vert ^{p} \lambda _{2}^{k-k_{0}} \\ &{}+ \bigl( 1+ \Vert B_{4} \Vert + \Vert B_{4} \Vert ^{2} +\cdots \bigr) \Vert B_{3} \Vert r_{5}+ \bigl( \Vert B_{3} \Vert + \Vert B_{4} \Vert \bigr) \Vert \phi \Vert \\ &{} + \bigl( 1+ \Vert B_{4} \Vert + \Vert B_{4} \Vert ^{2} + \cdots \bigr) \gamma \\ \leq{}&\frac{\eta_{5} \Vert B_{3} \Vert }{1- \Vert B_{4} \Vert } \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}} +\frac{ \Vert B_{3} \Vert r_{5}}{1- \Vert B_{4} \Vert } + \bigl( \Vert B_{3} \Vert + \Vert B_{4} \Vert \bigr) \Vert \phi \Vert +\frac{\gamma}{1- \Vert B_{4} \Vert } \\ ={}& \eta_{6} \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}}+ r_{6}, \end{aligned}$$
(3.23)
where \(\eta _{6} =\frac{\eta_{5} \Vert B_{3} \Vert }{1- \Vert B_{4} \Vert }\) and \(r_{6}=\frac{ \Vert B_{3} \Vert r_{5}+\gamma}{1- \Vert B_{4} \Vert }+ ( \Vert B_{3} \Vert + \Vert B_{4} \Vert ) \Vert \phi \Vert \).
Thus, it follows from (3.20) and (3.23) that
$$\begin{aligned} \bigl\Vert y(k) \bigr\Vert & \leq \bigl\Vert y_{1}(k) \bigr\Vert + \bigl\Vert y_{2}(k) \bigr\Vert \\ &\leq \eta_{5} \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}}+ r_{5} +\eta_{6} \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}}+r_{6} \\ &= ( \eta_{5}+\eta_{6} ) \Vert \phi \Vert ^{p} \lambda _{2}^{k-k_{0}}+ r_{5} +r_{6} \\ &= \eta_{7} \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}}+ r_{7}, \end{aligned}$$
(3.24)
where \(\eta _{7}=\eta_{5}+\eta_{6}\) and \(r_{7}= r_{5} +r_{6}\).
From \(x(k)=Ny(k)\) and (3.24), we get
$$\begin{aligned} \bigl\Vert Ex(k) \bigr\Vert &\leq \Vert E \Vert \Vert N \Vert \bigl\Vert y(k) \bigr\Vert \\ &\leq \Vert E \Vert \Vert N \Vert \bigl(\eta_{7} \Vert \phi \Vert ^{p} \lambda_{2}^{k-k_{0}}+r_{7} \bigr) \\ &\leq\eta_{7} \Vert E \Vert \Vert N \Vert \bigl\Vert N^{-1} \bigr\Vert \Vert \varphi \Vert ^{p} \lambda_{2}^{k-k_{0}}+ \Vert E \Vert \Vert N \Vert r_{7} \\ &= \eta_{8} \Vert \varphi \Vert \lambda_{2}^{k-k_{0}}+r_{8}, \end{aligned}$$
where \(\eta _{8}=\eta_{7} \Vert E \Vert \Vert N \Vert \Vert N^{-1} \Vert \Vert \varphi \Vert ^{p-1} \) and \(r_{8}= \Vert E \Vert \Vert N \Vert r_{7}\).

Therefore, the discrete time singular system (2.1) is exponentially practically stable with respect to \(w(k)\) with \(\eta=\eta_{8}, \lambda =\lambda_{2}\), and \(r=r_{8}\). □

Remark 3.3

From the method of proof of Theorem 3.4, it is clear that this method can be applied for a discrete time singular system with disturbance and time varying delay \(\tau(k)\) with \(0\leq\tau(k) \leq\tau, \tau>0\).

Remark 3.4

As is known, Razumikhin techniques only require less restrictive assumptions, namely they employ a type of Lyapunov–Krasovskii functional which is required to decrease only if a certain condition on the past state trajectory and the current state is satisfied. However, such Razumikhin-type techniques usually lead to a delay-independent criterion which is less conservative than a delay-dependent result, especially for constant delay systems. To deal with this conservativeness, several mathematical approaches have been considered in recent works, e.g., the LMI approach and the time-dependent Lyapunov functional method. Recently, in [31, 32], the Razumikhin technique was expressed by utilizing the LMI approach and the time-invariant Lyapunov functional method which avoid the conservativeness of the Razumikhin-type techniques. It is our future investigation to apply the above mentioned approaches to obtain less conservative criteria for exponentially practical stability of discrete time singular systems with delay and disturbance.

Remark 3.5

Obviously, exponential stability implies exponentially practical stability but not conversely. However, in several practical applications, it only needs to stabilize a system into the region of a phase space, namely the system may oscillate near the equilibrium point, in which the performance is still acceptable. To the best of our knowledge, the present work is the first result on exponentially practical stability of a discrete time singular system with delay and disturbance. Moreover, compared to [22] which proposed asymptotically practical stability criteria for a discrete time system with delay, we derive an exponentially practical stability condition which is more desirable.

4 Numerical examples

Remark 4.1

We provide an algorithm for the implementation and computational corresponding to Theorem 3.2 and Theorem 3.4 as follows:
  1. 1.

    First, we choose an appropriate Lyapunov functional or Lyapunov–Krasovskii functional candidate according to the assumptions of Theorem 3.2 or Theorem 3.4, respectively. Then, we estimate the values of \(c_{1},c_{2}\), and a which satisfy condition (i) of the corresponding theorems.

     
  2. 2.

    From the estimations of \(c_{1}, c_{2}\), and a obtained in 1, we choose appropriate \(q, \beta\), \(c_{3}\), and ρ which satisfy condition (ii) of the corresponding theorems.

     

Example 4.1

Consider system (3.2) with \(E= \bigl[{\scriptsize\begin{matrix}{}1& 0\cr 0&0 \end{matrix}}\bigr] \), \(A= \bigl[{\scriptsize\begin{matrix}{} 0.5& 0.5\cr 0&1 \end{matrix}}\bigr] \), \(G= \bigl[{\scriptsize\begin{matrix}{} 1\cr 1 \end{matrix}}\bigr] ,w(k)\in\mathbb{R}\), and \(k_{0}=0\) with the initial condition given by \(x(0)=[5,-0.04]^{T}\). We can see that \(\operatorname{det}(zE-A)=-z+0.5\neq0\) for some \(z \in\mathbb{C}\) and \(\operatorname{deg}(\operatorname{det}(zE-A))= \operatorname{rank}(E)=1\). Thus, system (3.2) is regular and causal. For nonsingular matrices \(M= \bigl[{\scriptsize\begin{matrix}{}2& -1\cr 0&2 \end{matrix}}\bigr] , N= \bigl[{\scriptsize\begin{matrix}{}0.5& 0\cr 0&0.5 \end{matrix}}\bigr] \), we obtain
$$\begin{aligned} MEN = \begin{bmatrix}1& 0\\0&0 \end{bmatrix} ,\qquad {MAN}= \begin{bmatrix}0.5& 0\\0&1 \end{bmatrix} , \qquad {MG}= \begin{bmatrix}1\\2 \end{bmatrix} . \end{aligned}$$
We choose a Lyapunov functional as \(V(k,x(k))=x^{T}(k)E^{T}Ex(k)+a\) with \(a>0\). Then we obtain that
  1. (i)

    \(\Vert Ex(k) \Vert ^{2} \leq V(k,x(k)) \leq \Vert Ex(k) \Vert ^{2}+a\),

     
  2. (ii)
    $$\begin{aligned} &\Delta V\bigl(k,x(k)\bigr)\\ &\quad=V\bigl(k+1,x(k+1)\bigr)-V\bigl(k,x(k)\bigr) \\ &\quad= x^{T}(k+1)E^{T}Ex(k+1)+a-x^{T}(k)E^{T}Ex(k)-a \\ &\quad= x^{T}(k)A^{T}Ax(k)+2x^{T}(k)A^{T}Gw(k)+w^{T}(k)G^{T}Gw(k)-x^{T}(k)E^{T}Ex(k) \\ &\quad= \begin{bmatrix}x_{1}(k)\\x_{2}(k) \end{bmatrix} ^{T} \begin{bmatrix}0.5& 0\\0.5&1 \end{bmatrix} \begin{bmatrix}0.5& 0.5\\0&1 \end{bmatrix} \begin{bmatrix}x_{1}(k)\\x_{2}(k) \end{bmatrix} +2 \begin{bmatrix}x_{1}(k)\\x_{2}(k) \end{bmatrix} ^{T} \begin{bmatrix}0.5& 0\\0.5&1 \end{bmatrix} \begin{bmatrix}1\\1 \end{bmatrix} w(k) \\ &\qquad{}+w^{T}(k) \begin{bmatrix}1&1 \end{bmatrix} \begin{bmatrix}1\\1 \end{bmatrix} w(k)- \begin{bmatrix}x_{1}(k)\\x_{2}(k) \end{bmatrix} ^{T} \begin{bmatrix}1& 0\\0&0 \end{bmatrix} \begin{bmatrix}1& 0\\0&0 \end{bmatrix} \begin{bmatrix}x_{1}(k)\\x_{2}(k) \end{bmatrix} \\ &\quad= 0.25x_{1}^{2}(k)+0.5x_{1}(k)x_{2}(k)+1.25x_{2}^{2}(k)+x_{1}(k)w(k)+3x_{2}(k)w(k) \\ &\qquad{}+2w(k)^{2}-x_{1}(k)^{2} \\ &\quad= -0.75x_{1}^{2}(k)+1.25w^{2}(k)+0.5x_{1}(k)w(k)-w(k)^{2} \\ &\quad\leq-0.75x_{1}^{2}(k)+0.25x_{1}^{2}(k)+0.25w^{2}(k)+0.25w(k)^{2} \\ &\quad=-0.75x_{1}^{2}(k)+0.25x_{1}^{2}(k)+0.25x_{2}^{2}(k)+0.25w(k)^{2} \\ &\quad = -0.5x_{1}^{2}(k)+0.25x_{2}^{2}(k)+0.25w(k)^{2} \\ &\quad= -0.5x_{1}^{2}(k)-0.5x_{2}^{2}(k)+0.75x_{2}^{2}(k)+0.25w(k)^{2} \\ &\quad= -0.5 \bigl( x_{1}^{2}(k)+x_{2}^{2}(k) \bigr) +0.75w_{2}^{2}(k)+0.25w(k)^{2} \\ &\quad = -0.5 \bigl\Vert x(k) \bigr\Vert ^{2}+w^{2}(k). \end{aligned}$$
     
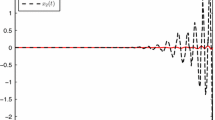
Therefore, by Theorem 3.2, we may show that system (3.2) is exponentially practically stable in the pth-moment with \(\eta=35.6, \lambda=0.5, r=0.5\). For simulation purpose, we let \(a=0.3, \Vert w(k) \Vert \leq0.1\). Then Theorem 3.2 is satisfied with the parameters \(c_{1}=1, c_{2}=1,a=0.3, c_{3}=0.5, p=2,\rho( \Vert w(k) \Vert )=w(k)^{2}\leq 0.01\). Figure 1 shows the trajectories of solution of Example 4.1 with disturbance. Figure 2 shows the trajectories of solution of Example 4.1 without disturbance.
Open image in new window
Figure 1

The trajectory of solution of system (3.2)

Open image in new window
Figure 2

The trajectory of solution of system (3.2) without disturbance

Example 4.2

Consider system (2.1) with \(E= \bigl[{\scriptsize\begin{matrix}{}1& 0\cr 0&0 \end{matrix}}\bigr] \), \(A= \bigl[{\scriptsize\begin{matrix}{} -0.05& 0\cr -0.05&-0.05 \end{matrix}}\bigr] \), \(B= \bigl[{\scriptsize\begin{matrix}{}0.4& 0\cr -0.05&-0.02 \end{matrix}}\bigr] \), \(G= \bigl[{\scriptsize\begin{matrix}{} 0.5\cr 0.5 \end{matrix}}\bigr] ,w(k)\in\mathbb{R},\tau=1\), and \(k_{0}=0\) with the initial conditions given by \(x(-1)=[5,5]^{T}, x(0)=[5,1.75]^{T}\). We can see that \(\operatorname{det}(zE-A)=0.05z+0.0025\neq0\) for some \(z \in\mathbb {C}\) and \(\operatorname{deg}(\operatorname{det}(zE-A))= \operatorname{rank}(E)=1\). Thus, system (2.1) is regular and causal. For nonsingular matrices \(M= \bigl[{\scriptsize\begin{matrix}{} 2& 0\cr 0&2 \end{matrix}}\bigr] , N= \bigl[{\scriptsize\begin{matrix}{} 0.5& 0\cr-0.5&-10 \end{matrix}}\bigr] \), we get
$$\begin{aligned} &MEN = \begin{bmatrix}1& 0\\0&0 \end{bmatrix} ,\qquad {MAN}= \begin{bmatrix}-0.05& 0\\0&1 \end{bmatrix} , \\ & {MBN}= \begin{bmatrix}0.4& 0\\-0.03&0.4 \end{bmatrix},\qquad {MG}= \begin{bmatrix}1\\1 \end{bmatrix} . \end{aligned}$$
We choose a Lyapunov–Krasovskii functional as \(V(k,x(k))= \vert x_{1}(k) \vert +a\) with \(a>0\).
From \(Ex(k)= \bigl[{\scriptsize\begin{matrix}{} 1& 0\cr 0&0 \end{matrix}}\bigr] \bigl[{\scriptsize\begin{matrix}{} x_{1}(k)\cr x_{2}(k) \end{matrix}}\bigr] = \bigl[{\scriptsize\begin{matrix}{} x_{1}(k)\cr 0 \end{matrix}}\bigr] \) and
$$\begin{aligned} Ex(k+1)={}& \begin{bmatrix}1& 0\\0&0 \end{bmatrix} \begin{bmatrix}x_{1}(k+1)\\x_{2}(k+1) \end{bmatrix} \\ ={}& \begin{bmatrix}-0.05& 0\\-0.05&-0.05 \end{bmatrix} \begin{bmatrix}x_{1}(k)\\x_{2}(k) \end{bmatrix} + \begin{bmatrix}0.4& 0\\-0.05&-0.02 \end{bmatrix} \begin{bmatrix}x_{1}(k-\tau)\\x_{2}(k-\tau) \end{bmatrix} + \begin{bmatrix}0.5\\0.5 \end{bmatrix} w(k), \end{aligned}$$
we obtain
$$\begin{aligned} \begin{bmatrix}x_{1}(k+1)\\0 \end{bmatrix} = \begin{bmatrix}-0.05x_{1}(k)+0.4x_{1}(k-\tau)+0.5w(k)\\ -0.05x_{1}(k)-0.05x_{2}(k)-0.05x_{1}(k-\tau)-0.02x_{2}(k-\tau)+0.5w(k) \end{bmatrix} . \end{aligned}$$
Thus, we obtain
  1. (i)

    \(\Vert Ex(k) \Vert \leq V(k,x(k))= \vert x_{1}(k) \vert +a \leq \Vert Ex(k) \Vert +a\),

     
  2. (ii)
    If \(V(k+s,x(k+s))\leq qV(k+1,x(k+1))\) with \(s\in\mathbb{N}_{-\tau }\), then we have
    $$\begin{aligned} &x_{1}(k+1)=-0.05x_{1}(k)+0.4x_{1}(k- \tau)+0.5w(k), \\ &\bigl\vert x_{1}(k+1) \bigr\vert \leq0.05 \bigl\vert x_{1}(k) \bigr\vert +0.4 \bigl\vert x_{1}(k-\tau ) \bigr\vert + 0.5 \bigl\vert w(k) \bigr\vert , \\ &\bigl\vert x_{1}(k+1) \bigr\vert +a-a \leq0.05 \bigl\vert x_{1}(k) \bigr\vert +0.05 a-0.05 a+ 0.4 \bigl\vert x_{1}(k-\tau) \bigr\vert + 0.4 a- 0.4 a \\ &\phantom{\bigl\vert x_{1}(k+1) \bigr\vert +a-a \leq}{}+ 0.5 \bigl\vert w(k) \bigr\vert , \\ &\bigl\vert x_{1}(k+1) \bigr\vert +a \leq0.05 \bigl( \bigl\vert x_{1}(k) \bigr\vert +a \bigr)+ 0.4 \bigl( \bigl\vert x_{1}(k-\tau) \bigr\vert +a \bigr)+0.55a + 0.5 \bigl\vert w(k) \bigr\vert , \\ &V\bigl(k+1,x(k+1)\bigr)\leq0.05V\bigl(k,x(k)\bigr)+0.4V\bigl(k-\tau,x(k-\tau) \bigr)+0.55a + 0.5 \bigl\Vert w(k) \bigr\Vert \\ &\phantom{V\bigl(k+1,x(k+1)\bigr)}\leq0.05V\bigl(k,x(k)\bigr)+0.4qV\bigl(k+1,x(k+1)\bigr)+0.55a + 0.5 \bigl\Vert w(k) \bigr\Vert \\ &\phantom{V\bigl(k+1,x(k+1)\bigr)}\leq\frac{0.05}{1-0.4q}V\bigl(k,x(k)\bigr)+\frac{0.55a + 0.5 \Vert w(k) \Vert }{1-0.4q}. \end{aligned}$$
    Thus,
    $$\begin{aligned} \Delta V\bigl(k,x(k)\bigr)&=V\bigl(k+1,x(k+1)\bigr)-V\bigl(k,x(k)\bigr) \\ &\leq\frac{0.05}{1-0.4q}V\bigl(k,x(k)\bigr)+\frac{0.55a + 0.5 \Vert w(k) \Vert }{1-0.4q}-V\bigl(k,x(k)\bigr)\\ &=- \biggl( 1-\frac{0.05}{1-0.4q} \biggr)V\bigl(k,x(k)\bigr)+\frac{0.55a + 0.5 \Vert w(k) \Vert }{1-0.4q} \\ &=-\beta V\bigl(k,x(k)\bigr)+\rho\bigl( \bigl\Vert w(k) \bigr\Vert \bigr), \end{aligned}$$
    where \(\beta\leq1-\frac{0.05}{1-0.4q}\) and \(\rho( \Vert w(k) \Vert )=\frac{0.55a + 0.5 \Vert w(k) \Vert }{1-0.4q}\).
     
Therefore, by Theorem 3.4, system (2.1) is exponentially practically stable in the pth-moment with \(\eta=82.41, \lambda=0.8\), and \(r=54.58\). For simulation purpose, we let \(a=0.5, \Vert w(k) \Vert \leq 0.1\). Then Theorem 3.4 is satisfied with \(c_{1}=1, c_{2}=1,a=0.5,q=1.6, \beta=0.8, p=1,\rho( \Vert w(k) \Vert ) \leq 0.9\). Figure 3 shows the trajectories of solution of Example 4.2. Figure 4 shows the trajectories of solution of system (2.1) without disturbance.
Open image in new window
Figure 3

The trajectory of solution of system (2.1)

Open image in new window
Figure 4

The trajectory of solution of system (2.1) without disturbance

5 Conclusion

In this paper, exponentially practical stability of a discrete time singular system with delay and disturbance has been investigated. For systems with disturbance but without delay, by using Lyapunov stability theory, we obtained a criterion for exponentially practical stability of a general discrete time system and a linear discrete time singular system, respectively. For systems with delay and disturbances, by using the Razumikhin-type technique, we derived exponentially practical stability criteria for a general discrete time system and a linear singular system, respectively. Numerical examples were given to show effectiveness of our theoretical results.

Notes

Acknowledgements

The first author is supported by student scholarship from the Human Resources Development in Science Project (Science Achievement Scholarship of Thailand SAST). The second author is supported by Chiang Mai University. This research is also (partially) supported by the Center of Excellence in Mathematics, The Commission on Higher Education, Thailand.

Authors’ contributions

All authors read and approved the final manuscript.

Competing interests

The authors declare that they have no competing interests.

References

  1. 1.
    Feng, G., Cao, J.: Stability analysis of impulsive switched singular systems. IET Control Theory Appl. 9(6), 863–870 (2015) MathSciNetCrossRefGoogle Scholar
  2. 2.
    Feng, Z., Li, W., Lam, J.: New admissibility analysis for discrete singular systems with time-varying delay. Appl. Math. Comput. 265, 1058–1066 (2015) MathSciNetGoogle Scholar
  3. 3.
    Gao, C., Liu, X., Li, W.: Input-to-state stability of discrete-time singular systems based on quasi-min-max model predictive control. IET Control Theory Appl. 9(11), 1662–1669 (2015) MathSciNetCrossRefGoogle Scholar
  4. 4.
    Han, Y., Kao, Y., Gao, C.: Robust sliding mode control for uncertain discrete singular systems with time-varying delays and external disturbances. Automatica 75, 210–216 (2017) MathSciNetCrossRefMATHGoogle Scholar
  5. 5.
    Hassanabadi, A.H., Shafiee, M., Puig, V.: UIO design for singular delayed LPV systems with application to actuator fault detection and isolation. Int. J. Syst. Sci. 47(1), 107–121 (2015) MathSciNetCrossRefMATHGoogle Scholar
  6. 6.
    Hien, L.V., Vu, L.H., Phat, V.N.: Improved delay-dependent exponential stability of singular systems with mixed interval time-varying delays. IET Control Theory Appl. 9(9), 1364–1372 (2015) MathSciNetCrossRefGoogle Scholar
  7. 7.
    Li, S., Lin, H.: On \(l_{1}\) stability of switched positive singular systems with time-varying delay. Int. J. Robust Nonlinear Control 27(16), 1–15 (2017) Google Scholar
  8. 8.
    Li, S., Xiang, Z.: Stability \(l_{1}\)-gain and \(l_{\infty}\)-gain analysis for discrete-time positive switched singular delayed systems. Appl. Math. Comput. 275, 95–106 (2016) MathSciNetGoogle Scholar
  9. 9.
    Lin, J., Gao, Z.: Observers design for switched discrete-time singular time-delay systems with unknown inputs. Nonlinear Anal. Hybrid Syst. 18, 85–99 (2015) MathSciNetCrossRefMATHGoogle Scholar
  10. 10.
    Lin, J., et al.: Functional observer for switched discrete-time singular systems with time delays and unknown inputs. IET Control Theory Appl. 9(14), 2146–2156 (2015) MathSciNetCrossRefGoogle Scholar
  11. 11.
    Liu, Y., et al.: Input-to-state stability for discrete-time nonlinear switched singular systems. Inf. Sci. 358(359), 18–28 (2016) CrossRefGoogle Scholar
  12. 12.
    Liu, T., et al.: Finite-time stability of discrete switched singular positive systems. Circuits Syst. Signal Process. 36(6), 1–13 (2017) MathSciNetCrossRefGoogle Scholar
  13. 13.
    Long, S., Zhong, S.: Improved results for stochastic stabilization of a class of discrete-time singular Markovian jump systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 23, 11–26 (2017) MathSciNetCrossRefMATHGoogle Scholar
  14. 14.
    Ma, Y., Zheng, Y.: Delay-dependent stochastic stability for discrete singular neural networks with Markovian jump and mixed time-delays. Neural Comput. Appl. 29(1) 111–122 (2018) MathSciNetCrossRefGoogle Scholar
  15. 15.
    Muoi, N.H., Rajchakit, G., Phat, V.N.: LMI approach to finite-time stability and stabilization of singular linear discrete delay systems. Acta Appl. Math. 146(1), 81–93 (2016) MathSciNetCrossRefMATHGoogle Scholar
  16. 16.
    Niamsup, P., Phat, V.N.: A new result on finite-time control of singular linear time-delay systems. Appl. Math. Lett. 60, 1–7 (2016) MathSciNetCrossRefMATHGoogle Scholar
  17. 17.
    Rami, M.A., Napp, D.: Positivity of discrete singular systems and their stability: an LP-based approach. Automatica 50(1), 84–91 (2014) MathSciNetCrossRefMATHGoogle Scholar
  18. 18.
    Sau, N.H., Niamsup, P., Phat, V.N.: Positivity and stability analysis for linear implicit difference delay equation. Linear Algebra Appl. 510, 25–41 (2016) MathSciNetCrossRefMATHGoogle Scholar
  19. 19.
    Zamani, I., Shafiee, M., Ibeas, A.: Stability analysis of hybrid switched nonlinear singular time-delay systems with stable and unstable subsystems. Int. J. Syst. Sci. 45(5), 1128–1144 (2014) MathSciNetCrossRefMATHGoogle Scholar
  20. 20.
    Zamani, I., Shafiee, M., Ibeas, A.: Switched nonlinear singular systems with time-delay: stability analysis. Int. J. Robust Nonlinear Control 25(10), 1497–1513 (2015) MathSciNetCrossRefMATHGoogle Scholar
  21. 21.
    Zamani, I., Shafiee, M.: Stability analysis of uncertain switched singular time-delay systems with discrete and distributed delays. Optim. Control Appl. Methods 36(1), 1–28 (2015) MathSciNetCrossRefMATHGoogle Scholar
  22. 22.
    Sun, L., Liu, C., Li, X.: Practical stability of impulsive discrete systems with time delays. Abstr. Appl. Anal. 2014, 954121 (2014) MathSciNetGoogle Scholar
  23. 23.
    Wangrat, S., Niamsup, P.: Exponentially practical stability of impulsive discrete time system with delay. Adv. Differ. Equ. 2016, 277 (2016) MathSciNetCrossRefGoogle Scholar
  24. 24.
    Zeng, Z.: Converse Lyapunov theorems for nonautonomous discrete-time systems. J. Math. Sci. 161(2), 337–343 (2009) MathSciNetCrossRefMATHGoogle Scholar
  25. 25.
    Ghanmi, B., Hadj Taieb, N., Hammami, M.A.: Growth conditions for exponential stability of time-varying perturbed systems. Int. J. Control 86(6), 1086–1097 (2013) MathSciNetCrossRefMATHGoogle Scholar
  26. 26.
    Ben Hamed, B., Ellouze, I., Hammami, M.A.: Practical uniform stability of nonlinear differential delay equations. Mediterr. J. Math. 8, 603–616 (2011) MathSciNetCrossRefMATHGoogle Scholar
  27. 27.
    Ben Hamed, B., Hammami, M.A.: Practical stabilization of a class of uncertain time-varying nonlinear delay systems. J. Control Theory Appl. 7(2), 175–180 (2009) MathSciNetCrossRefGoogle Scholar
  28. 28.
    Caraballo, T., Hammami, M.A., Mchiri, L.: Practical exponential stability of impulsive stochastic functional differential equations. Syst. Control Lett. 109, 43–48 (2017) MathSciNetCrossRefMATHGoogle Scholar
  29. 29.
    Ellouze, I., Hammami, M.A.: Practical stability of impulsive control systems with multiple time delays. Dyn. Contin. Discrete Impuls. Syst., Ser. A Math. Anal. 20, 341–356 (2013) MathSciNetMATHGoogle Scholar
  30. 30.
    Dai, L.: Singular Control Systems. Springer, New York (1989) CrossRefMATHGoogle Scholar
  31. 31.
    Chen, W., Lu, X., Zheng, W.: Impulsive stabilization and impulsive synchronization of discrete-time delayed neural networks. IEEE Trans. Neural Netw. Learn. Syst. 26(4), 734–748 (2015) MathSciNetCrossRefGoogle Scholar
  32. 32.
    Li, Z., et al.: Impulsive synchronization of discrete-time networked oscillators with partial input saturation. Inf. Sci. 422, 531–541 (2018) CrossRefGoogle Scholar

Copyright information

© The Author(s) 2018

Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.Department of MathematicsChiang Mai UniversityChiang MaiThailand
  2. 2.Centre of Excellence in MathematicsCHEBangkokThailand

Personalised recommendations