1 Introduction

As far as we are concerned, the theory of fractional partial differential equations (FPDE), as a new and effective mathematical tool, is very popular and important in many scientific and engineering problems. This is due to the fact that they can well describe the memory and hereditary properties of different substances [1–5]. For instance, the multi-term FPDEs have been employed to some models for describing the processes in practice, such as the oxygen delivery through a capillary to tissues [6], the underlying processes with loss [7], the anomalous diffusion in highly heterogeneous aquifers and complex viscoelastic materials [8], and so on. For others, one may refer to [1, 9–13].

Recently, researchers have found that many important dynamic processes exhibit fractional-order behavior that may vary with time and/or space. So it is significant to develop the concept of variable-order calculus. Presently, variable-order calculus has been applied in many fields such as viscoelastic mechanics [14], geographic data [15], signal confirmation [16], and diffusion process [17]. Since the kernel of the variable-order operators has a variable exponent, analytical solutions to variable fractional-order differential equations are more difficult to obtain. Therefore, the development of numerical methods to solve variable-order fractional differential equations is an actual and important problem. Nowadays numerical methods for variable-order fractional differential equations, which mainly cover finite difference methods [18–26], spectral methods [27–29], matrix methods [30, 31], reproducing kernel methods [32, 33], and so on, have been studied extensively by many researchers.

Roughly speaking, the fractional models can be classified into three principal kinds: space-fractional differential equation, time-fractional differential equation, and time-space fractional differential equation. Lately, Shen et al. [18] proposed numerical techniques for the variable-order time fractional diffusion equation. Zhang et al. studied an implicit Euler numerical method for the time variable fractional-order mobile-immobile advection-dispersion model in [19]. Lin et al. [20] investigated the stability and convergence of an explicit finite-difference approximation for the variable-order nonlinear fractional diffusion equation. Zhuang et al. [21] proposed explicit and implicit Euler approximations for the variable-order fractional advection-diffusion equation with a nonlinear source term. Sweilam et al. used an explicit finite difference method to study the variable-order nonlinear space fractional wave equation [22]. Zhuang et al. [23] proposed an implicit Euler approximation for the time and space variable fractional-order advection-dispersion model with first-order temporal and spatial accuracy.

But in the existing literature, there is little work on higher-order numerical methods for the multi-term time-space variable-order fractional differential equations because more numerical analysis is involved.

In this paper, we consider the following multi-term time-space variable-order fractional diffusion equations with initial-boundary value problem:

figure a

Here, the operator \(P_{\alpha,\alpha_{1},\ldots,\alpha_{S}}({}^{C}_{0}D_{t})u(x,t)\) is defined by

$$ P_{\alpha,\alpha_{1},\ldots,\alpha_{S}}({}^{C }_{0}D_{t})u(x,t) ={}^{C }_{0}D^{\alpha_{0}(x,t)}_{t}u(x,t)+\sum^{S}_{s=1}a_{s}(x,t) {}^{C }_{0}D^{\alpha_{s}(x,t)}_{t}u(x,t), $$

where \({}^{C }_{0}D^{\alpha_{s}(x,t)}_{t} (s=0,1,\ldots,S)\) are left-hand side variable-order Caputo fractional derivatives defined by [21]

$$\begin{aligned} {}^{C }_{0}D^{\alpha_{s}(x,t)}_{t}u(x,t) =\frac{1}{\Gamma(1-\alpha_{s}(x,t))} \int^{t}_{0}(t-{z})^{-\alpha_{s}(x,t)}\frac {\partial u(x,{z})}{\partial{z}} \,d{z},\quad 0< \alpha_{s}(x,t)< 1. \end{aligned}$$

\(0<\alpha_{S}(x,t)<\alpha_{S-1}(x,t)<\cdots<\alpha_{1}(x,t)<\alpha_{0}(x,t), 0<\underline{\alpha}\leq\alpha_{0}(x,t)\leq\overline{\alpha}<1, a_{s}(x,t)\geq0\). The space fractional derivatives \(_{x}R^{\beta(x,t)}, _{x}R^{\gamma(x,t)}\) are generalized Riesz fractional derivatives defined by [20, 21]

$$ {}^{}_{x}R^{\zeta(x,t)}u(x,t)=-\operatorname{sec}\bigl(\zeta(x,t)\pi/2\bigr) \bigl( \rho {}^{}_{0}D^{\zeta(x,t)}_{x}+\sigma {}^{}_{x}D^{\zeta(x,t)}_{L}\bigr)u(x,t). $$

Here, left-hand side and right-hand side variable-order Riemann–Liouville fractional derivatives are defined by

$$\begin{aligned} & D^{\zeta(x,t)}_{+}u(x,t)=\biggl[\frac{1}{\Gamma(n-\zeta(x,t))} \frac{d^{n}}{d\theta^{n}} \int^{\theta}_{0}(\theta-\eta)^{n-\zeta (x,t)-1}u(\eta,t) \,d\eta\biggr]_{\theta=x}, \\ & D^{\zeta(x,t)}_{-}u(x,t)=\biggl[\frac{(-1)^{n}}{\Gamma(n-\zeta(x,t))} \frac {d^{n}}{d\theta^{n}} \int^{L}_{\theta} (\eta-\theta)^{n-\zeta(x,t)-1}u(\eta,t) \,d\eta\biggr]_{\theta=x}, \end{aligned}$$

where n is a positive integer and \(n-1<\zeta(x,t)< n\). \(1<\underline{\beta}\leq\beta(x,t)\leq\overline{\beta}< 2, 0<\underline {\gamma}\leq\gamma(x,t)\leq\overline{\gamma}<1, \rho\geq0, \sigma\geq0, \rho+\sigma=1\), \(p(x,t) \geq0, q(x,t)\geq 0, c(x,t)\geq0\). We use L1-algorithm to approximate the temporal direction derivative, the standard and shifted Grünwald method to approximate the spatial direction derivative, and propose an unconditionally stable finite difference scheme. Furthermore, we prove the convergence of the scheme by using errors estimation method, and the convergence rate of order \((\tau+h)\) is obtained.

The remainder of the paper is organized as follows. In Sect. 2, we give some preliminaries, which is necessary for our following analysis. A finite difference scheme for equations (1)–(3) is proposed, and the unconditional stability and convergence of the approximation scheme are proved in Sect. 3. Numerical examples are given in Sect. 4 to demonstrate the effectiveness of the scheme. Finally, we conclude this paper in Sect. 5.

2 Preliminaries and discretization of the diffusion equation

Let \(t_{k}=k\tau, k=0,1, 2, \ldots, n, x_{i}=ih, i=0,1,2,\ldots,m\), where \(\tau= T/n\) and \(h=L/m\) are time and space steps, respectively. For an arbitrary function of two variables \(u(x,t)\), we denote \(u^{k}_{i}=u(x_{i},t_{k})\). Let \(P(x,t)=p(x,t)\times(-\operatorname{sec}\beta(x,t)\pi/2), Q(x,t)=q(x,t)\times (-\operatorname{sec}\gamma(x,t)\pi/2)\).

For a variable-order Caputo derivative, the authors proposed the L1 operator in [19] as follows:

$$L_{\tau}^{\alpha_{i}^{k}}u_{i}^{k}={ \frac{\tau^{-\alpha^{k+1}_{i}}}{\Gamma (2-\alpha^{k+1}_{i})}}\sum^{k}_{j=0} \bigl(u_{i}^{k+1-j}-u_{i}^{k-j} \bigr)G^{\alpha,k+1}_{i,j}, $$

where \(G^{\alpha,k+1}_{i,j}=(j+1)^{1-\alpha^{k+1}_{i}} -j^{1-\alpha^{k+1}_{i}}\), and gave the following approximation result.

Lemma 2.1

([19])

Suppose that \(\frac{\partial^{2}u(x,t)}{\partial t^{2}}\in C(\Omega)\), \(0<\alpha(x,t)< 1\), we have

$$\bigl\vert R^{\alpha_{i}^{k}}_{\tau}\bigr\vert = \bigl\vert {}^{C }_{0}D^{\alpha ^{k}_{i}}_{t}u_{i}^{k}-L_{\tau}^{\alpha_{i}^{k}}u_{i}^{k} \bigr\vert \leq\frac{\max \vert \frac{\partial^{2}u(x_{i},t)}{\partial t^{2}} \vert T^{1-\alpha ^{k+1}_{i}}}{2\Gamma(2-\alpha^{k+1}_{i})}\tau. $$

For a variable-order Grünwald–Letnikov fractional derivative, [21, 34] proposed the following “standard” and “shifted” operators:

$$\begin{aligned} &{}^{}_{+}D_{h}^{\zeta_{i}^{k}}u_{i}^{k}=h^{-\zeta^{k}_{i}} \sum^{i}_{j=0}g^{j}_{\zeta^{k}_{i}} u_{i-j}^{k}, \qquad {}^{}_{-} {D}_{h}^{\zeta_{i}^{k}}u_{i}^{k}=h^{-\zeta^{k}_{i}} \sum^{m-i}_{j=0}g^{j}_{\zeta^{k}_{i}} u_{i+j}^{k}, \\ &{}^{}_{+} {\overline{D}}_{h}^{\zeta_{i}^{k}}u_{i}^{k}=h^{-\zeta ^{k}_{i+1}} \sum^{i+1}_{j=0} g^{j}_{\zeta^{k}_{i+1}}u_{i+1-j}^{k},\qquad {}^{}_{-} {\overline{D}}_{h}^{\zeta_{i}^{k}}u_{i}^{k}=h^{-\zeta^{k}_{i-1}} \sum^{m-i+1}_{j=0}g^{j}_{\zeta^{k}_{i-1}}u_{i-1+j}^{k}, \end{aligned}$$

where \(g^{j}_{\zeta^{k}_{i}}\) is the Grünwald weights defined by \(g^{j}_{\zeta^{k}_{i}}=\frac{{\Gamma(j-\zeta_{i}^{k})}}{ {\Gamma(-\zeta_{i}^{k})}\Gamma(j+1)}, j=0,1,2,\ldots\) .

Suppose that the function \(f(x)\) is \((m-1)\)-continuously differentiable in the interval \([0, L]\) and that \(f^{m}(x)\) is integrable in \([0, L]\). Then, for every \(\zeta(x,t)\ (0\leq m-1<\zeta(x,t)< m)\), the Riemann–Liouville fractional derivative exists and coincides with the Grünwald–Letnikov fractional derivative [1, 35]. So the Grünwald–Letnikov operator can be used to approximate the Riemann–Liouville derivative.

Define the function space as follows:

$$\Theta^{1+\zeta}=\biggl\{ u(x,t)\Big\vert \max_{0\leq t\leq T} \int_{\mathbb {R}}\bigl(1+ \vert \omega \vert \bigr)^{1+\zeta} \bigl\vert F\bigl[u(t,x)\bigr] \bigr\vert \,d\omega< \infty\biggr\} , $$

where \(F[u(t,x)](\omega)=\int\mathrm {e}^{i\omega x}u(x,t)\,dx\). So the following results can be obtained.

Lemma 2.2

([21, 34])

For \(0 \leq n-1<\xi(x,t)< n\), if \(u(x,t)\in\Theta^{1+\zeta}\) and \({}^{R }_{0}D^{\xi(x,t)}_{x}u(x,t), {}^{R }_{x}D^{\xi (x,t)}_{L}u(x,t)\in C^{1}(\Omega)\), then we can obtain the “standard” Grünwald approximation

$$\bigl\vert R^{\zeta_{i}^{k}}_{+} \bigr\vert = \bigl\vert D^{\zeta^{k}_{i}}_{+}u_{i}^{k}- {}^{}_{+}D_{h}^{\zeta _{i}^{k}}u_{i}^{k} \bigr\vert \leq \mathit{Ch},\qquad \bigl\vert R^{\zeta_{i}^{k}}_{-} \bigr\vert = \bigl\vert D^{\zeta^{k}_{i}}_{-}u_{i}^{k}-{}^{}_{-} {D}_{h}^{\zeta _{i}^{k}}u_{i}^{k} \bigr\vert \leq \mathit{Ch} $$

and the “shifted” Grünwald approximation

$$\bigl\vert {\overline{R}}^{\zeta_{i}^{k}}_{+} \bigr\vert = \bigl\vert { \overline{D}}^{\zeta ^{k}_{i}}_{+}u_{i}^{k}- {}^{}_{+} {\overline{D}}_{h}^{\zeta_{i}^{k}}u_{i}^{k} \bigr\vert \leq \mathit{Ch},\qquad \bigl\vert {\overline{R}}^{\zeta_{i}^{k}}_{-} \bigr\vert = \bigl\vert {\overline{D}}^{\zeta ^{k}_{i}}_{-}u_{i}^{k}- {}^{}_{-} {\overline{D}}_{h}^{\zeta_{i}^{k}}u_{i}^{k} \bigr\vert \leq \mathit{Ch}. $$

It was shown in [34] that when \(\beta\in(1,2)\) using the “standard” Grünwald formula will be unconditionally unstable. So we adopt the “shifted” Grünwald formula to approximate the space fractional derivatives \(_{x}R^{\beta(x,t)}u(x,t)\) and the “standard” Grünwald formula to approximate the space fractional derivatives \(_{x}R^{\gamma(x,t)}u(x,t)\).

At the end of this section, we give the following discretization schemes for Eq. (1)–(3):

$$\begin{aligned} \begin{aligned} &L_{\tau}^{\alpha_{0i}^{k+1}}v_{i}^{k+1}+ \sum^{S}_{s=1}a_{si}^{k+1}L_{\tau }^{\alpha_{si}^{k+1}}v_{i}^{k+1}-P_{i}^{k+1} \bigl(\rho {}^{}_{-} {\overline{D}}_{h}^{\beta_{i}^{k+1}}v_{i}^{k+1} +\sigma {}^{}_{+} {\overline{D}}_{h}^{\beta _{i}^{k+1}}v_{i}^{k+1} \bigr) \\ &\quad{}-Q_{i}^{k+1}\bigl(\rho {}^{}_{-}D_{h}^{\gamma_{i}^{k+1}}v_{i}^{k+1}+ \sigma {}^{}_{+} {D}_{h}^{\gamma_{i}^{k+1}}v_{i}^{k+1} \bigr) +c_{i}^{k+1}v_{i}^{k+1}=f_{i}^{k+1}, \\ &\quad i=0,1,2,\ldots,m; k=0,1,2,\ldots,n-1. \\ &v^{0}_{i}=\phi(ih),\quad i=0,1,2,\ldots,m; \\ &v^{k}_{0}=0,\qquad v^{k}_{m}=0,\quad k=0,1,2, \ldots,n-1. \end{aligned} \end{aligned}$$
(4)

These are linear implicit schemes, each layer of iterative needs to solve a system of linear algebraic equations. Now we rewrite algorithm (4) as a vector form. To this end, we give the following notation.

Let \(b^{k+1}_{i}=\tau^{\alpha^{k+1}_{0i}}\Gamma(2-\alpha^{k+1}_{0i})\) and

$$ M^{k+1}_{i,j}=G^{\alpha_{0},k+1}_{i,j}+ \sum^{S}_{s=1}\frac{\Gamma (2-\alpha^{k+1}_{0i})}{\Gamma(2-\alpha^{k+1}_{si})} a^{k+1}_{s_{i}}\tau^{\alpha^{k+1}_{0i}-\alpha^{k+1}_{si}}G^{\alpha _{s},k+1}_{i,j}. $$
(5)

\(E^{k+1}_{i}=(M^{k+1}_{i,0})^{-1}b^{k+1}_{i}P^{k+1}_{i}, F^{k+1}_{i}=(M^{k+1}_{i,0})^{-1}b^{k+1}_{i}Q^{k+1}_{i}, H^{k+1}_{i}=(M^{k+1}_{i,0})^{-1}b^{k+1}_{i}c^{k+1}_{i}\).

For \(i=1,2,\ldots, m-1\), \(j=1,2,\ldots, m-1\), \(k=0,1,2,\ldots, n \),

$$\begin{aligned} A^{k}_{ij}= \textstyle\begin{cases} -E^{k}_{i}\sigma h^{-\beta^{k}_{i-1}}g^{j-i+1}_{\beta ^{k}_{i-1}}-F^{k}_{i}\sigma h^{-\gamma^{k}_{i}}g^{j-i}_{\gamma^{k}_{i}}, & j\geq i+2,\\ -E^{k}_{i}(\rho h^{-\beta^{k}_{i+1}}g^{0}_{\beta^{k}_{i+1}}+\sigma h^{-\beta^{k}_{i-1}}g^{2}_{\beta^{k}_{i-1}}) -F^{k}_{i}\sigma h^{-\gamma^{k}_{i}}g^{1}_{\gamma^{k}_{i}}, & j= i+1,\\ 1-E^{k}_{i}(\rho h^{-\beta^{k}_{i+1}}g^{1}_{\beta^{k}_{i+1}}+\sigma h^{-\beta^{k}_{i-1}}g^{1}_{\beta^{k}_{i-1}})-F^{k}_{i} h^{-\gamma^{k}_{i}}+H^{k}_{i}, & j= i,\\ -E^{k}_{i}(\rho h^{-\beta^{k}_{i+1}}g^{2}_{\beta^{k}_{i+1}}+\sigma h^{-\beta^{k}_{i-1}}g^{0}_{\beta^{k}_{i-1}})-F^{k}_{i} \rho h^{-\gamma^{k}_{i}}g^{1}_{\gamma^{k}_{i}}, & j= i-1,\\ -E^{k}_{i}\rho h^{-\beta^{k}_{i+1}}g^{i-j+1}_{\beta^{k}_{i+1}}-F^{k}_{i} \rho h^{-\gamma^{k}_{i}}g^{i-j}_{\gamma^{k}_{i}}, & j\leq i-2. \end{cases}\displaystyle \end{aligned}$$
(6)

For \(i=1,2,\ldots, m-1, k=1,2,\ldots, n \),

$$ B_{i}^{k}=\bigl(M ^{k}_{i,0} \bigr)^{-1}\sum^{k}_{j=1} \bigl(M^{k}_{i,k-j}-M^{k}_{i,k-j+1} \bigr)v^{j}_{i} +\bigl(M^{k}_{i,0} \bigr)^{-1}M^{k}_{i,k}v^{0}_{i}+ \bigl(M^{k}_{i,0}\bigr)^{-1}b^{k}_{i}f^{k+1}_{i}. $$
(7)

Denote \(A^{k}=(A^{k}_{ij})\), \(B^{k}=(B_{1}^{k},B_{2}^{k},\ldots, B_{m-1}^{k})^{T} \), \(V^{k}=(v^{k}_{1}, v^{k}_{2},\ldots, v^{k}_{m-1})^{T} \), \(\phi=(\phi_{1}, \phi_{2}, \ldots, \phi_{m-1})^{T}\).

Therefore, the discrete scheme (4) can be expressed in the following vector form:

$$\begin{aligned} \textstyle\begin{cases} A^{k+1}V^{k+1}=B^{k+1}, \quad k=0,1,\ldots,n-1, \\ V^{0}=\phi. \end{cases}\displaystyle \end{aligned}$$
(8)

3 Solvability, stability and convergence

In this section, we consider the solvability, stability and convergence of the discrete scheme (4) or (8). For this purpose, we give the following two lemmas.

Lemma 3.1

Suppose \(0<\underline{\alpha}\leq\alpha_{s}(x,t)\leq\overline{\alpha }<1\ (s=0,1,2,\ldots,S)\), and \(M^{k}_{i,j}\) given by (5). Then

$$\begin{aligned} &M^{k}_{i,j}-M^{k}_{i,j+1}>0, \quad i=1,2, \ldots, m, j=0,1,\ldots,k-1, \\ &\bigl(M^{k}_{i,0}\bigr)^{-1}\sum ^{k}_{j=1}\bigl(M^{k}_{i,k-j}-M^{k}_{i,k-j+1} \bigr)+\bigl(M^{k}_{i,0}\bigr)^{-1}M^{k}_{i,k}=1,\quad i=1,2,\ldots, m, \end{aligned}$$

for \(k=1,2,\ldots, n \).

Proof

Let \(f(x)=(x+1)^{1-\alpha(x_{i},t_{k})}-{x}^{1-\alpha(x_{i},t_{k})}\), we have

$$f^{'}(x)=\bigl(1-\alpha(x_{i},t_{k})\bigr) \bigl[(x+1)^{-\alpha(x_{i},t_{k})}-x^{-\alpha (x_{i},t_{k})}\bigr]< 0,\quad x>0, $$

so the function \(f(x)\) is strictly decreasing. Therefore, for \(j>0\), we have \(f(j+1)< f(j)\), namely

$$2(j+1)^{1-\alpha^{k}_{i}}-j^{1-\alpha^{k}_{i}}-(j+2)^{1-\alpha^{k}_{i}}>0. $$

It is easy to see that \(M^{k}_{i,0}>M^{k}_{i,1}\). Moreover, for \(j=1, \ldots , m-1\), we have

$$\begin{aligned} &M^{k}_{i,k-j}-M^{k}_{i,k-j+1} \\ &\quad=2(k-j+1)^{1-{\alpha^{k}_{0i}}}-(k-j)^{1-{\alpha ^{k}_{0i}}}-(k-j+2)^{1-{\alpha^{k}_{0i}}} \\ &\qquad{}+\sum^{S}_{s=1}\frac{\Gamma(2-\alpha^{k}_{0i})}{\Gamma(2-\alpha^{k}_{si})} a^{k}_{si}\tau^{\alpha^{k}_{0i}-\alpha^{k}_{si}}\bigl[2(k-j+1)^{1-\alpha ^{k}_{si}}-(k-j)^{1- \alpha^{k}_{si}}-(k-j+2)^{1-\alpha^{k}_{si}} \bigr] \\ &\quad\geq 0. \end{aligned}$$

In addition, noting that \((M^{k}_{i,0})^{-1}M^{k}_{i,0}=1\), we can obtain the second formula of the lemma. The proof is completed. □

Lemma 3.2

([23])

For \(1<\underline{\beta}\leq\beta(x,t)\leq\overline{\beta}<2, 0<\underline{\gamma}\leq\gamma(x,t)\leq\overline{\gamma}<1\), the coefficients \(g^{j}_{\beta^{k}_{i}}\) and \(g^{j}_{\gamma^{k}_{i}}\) \((i=1,2,\ldots, m, k=1,2,\ldots, n)\) satisfy

$$\begin{aligned} &g^{0}_{\beta^{k}_{i}}=1; \qquad g^{1}_{\beta^{k}_{i}}< 0;\qquad g^{j}_{\beta ^{k}_{i}}>0, \quad (j\geq2); \qquad \sum^{\infty}_{j=0}g^{j}_{\beta^{k}_{i}}=0;\qquad \sum^{l}_{j=0}g^{j}_{\beta ^{k}_{i}}< 0,\quad (l\geq1). \\ &g^{0}_{\gamma^{k}_{i}}=1; \qquad g^{j}_{\gamma^{k}_{i}}< 0,\quad (j \geq1); \qquad \sum^{\infty}_{j=0}g^{j}_{\gamma^{k}_{i}}=0;\qquad \sum^{l}_{j=0}g^{j}_{\gamma^{k}_{i}}>0,\quad (l\geq1). \end{aligned}$$

3.1 Solvability analysis

Using Lemma 3.2 and a simple computation yields

$$\begin{aligned} \begin{aligned} & A^{k}_{ii}\geq1, \qquad A^{k}_{ij} \leq0,\quad (j\neq i),\qquad \sum_{j=1}^{m-1}A^{k}_{ij} \geq1, \quad i=1,\ldots, m-1, \\ &\bigl\vert A^{k}_{ii} \bigr\vert -\sum _{j=1}^{m-1} \bigl\vert A^{k}_{ij} \bigr\vert = A^{k}_{ii}+\sum_{j=1}^{m-1}A^{k}_{ij} \geq1,\quad i=1,\ldots, m-1. \end{aligned} \end{aligned}$$
(9)

Namely, matrix A is strictly diagonally dominant with positive diagonal terms and nonpositive off-diagonal terms. Therefore, matrix A is invertible. So the following theorem can be obtained.

Theorem 3.1

Scheme (8) has a unique solution.

3.2 Stability analysis

Theorem 3.2

Suppose \(V^{k}_{i},\widetilde{V}^{k}_{i}\) are solutions of schemes (4) with the initial values \(V^{k}_{0},\widetilde{V}^{k}_{0}\), respectively. Then

$$\bigl\Vert V^{k}-\widetilde{V}^{k} \bigr\Vert _{\infty} \leq C \bigl\Vert V^{0}-\widetilde{V}^{0} \bigr\Vert _{\infty},\quad k=0, 1, \ldots, $$

where \(\Vert V^{k}-\widetilde{V}^{k} \Vert _{\infty}=\max_{1\leq i \leq m-1} \vert v^{k}_{i}-\widetilde{v}^{k}_{i} \vert \).

Proof

Denote \(X^{k}=V^{k}-\widetilde{V}^{k}=(\varepsilon^{k}_{1}, \ldots, \varepsilon ^{k}_{m-1})^{T}\), then

$$ A^{k+1}X^{k+1}=B^{k+1},\quad k=0,1, \ldots,n-1, $$
(10)

where the component of \(B^{k+1}\) is

$$ B_{i}^{k+1}=\bigl(M ^{k+1}_{i,0} \bigr)^{-1}\sum^{k}_{j=1} \bigl(M^{k+1}_{i,k-j}-M^{k+1}_{i,k-j+1}\bigr) \varepsilon^{j}_{i} +\bigl(M^{k+1}_{i,0} \bigr)^{-1}M^{k+1}_{i,k}\varepsilon^{0}_{i}. $$
(11)

Now we prove this theorem applying mathematical induction method.

For \(k=1\), suppose \(\Vert X^{1} \Vert _{\infty}= \vert \varepsilon ^{1}_{l} \vert \). Considering the lth equation of (10), we have

$$\begin{aligned} \bigl\vert A^{1}_{ll} \bigr\vert \bigl\vert \varepsilon^{1}_{l} \bigr\vert = & \Biggl\vert B^{1}_{l}-\sum_{j=1,j\neq l}^{m-1}A^{1}_{lj} \varepsilon^{1}_{j} \Biggr\vert \leq \bigl\vert B^{1}_{l} \bigr\vert +\sum_{j=1,j\neq l}^{m-1} \bigl\vert A^{1}_{lj} \bigr\vert \bigl\vert \varepsilon^{1}_{l} \bigr\vert , \end{aligned}$$

namely

$$\begin{aligned} \Biggl( \bigl\vert A^{1}_{ll} \bigr\vert -\sum _{j=1,j\neq l}^{m-1} \bigl\vert A_{lj}^{1} \bigr\vert \Biggr) \bigl\vert \varepsilon^{1}_{l} \bigr\vert \leq& \bigl\vert B^{1}_{l} \bigr\vert . \end{aligned}$$

Due to (9) and (11), we can obtain

$$\begin{aligned} \bigl\vert \varepsilon^{1}_{l} \bigr\vert \leq \frac{ \vert B^{1}_{l} \vert }{ \vert A_{ll}^{1} \vert -{\sum_{j=1,j\neq l}^{m-1}} \vert A_{lj}^{1} \vert } \leq \bigl\vert B^{1}_{l} \bigr\vert = \bigl\vert \varepsilon^{0}_{l} \bigr\vert \leq \bigl\Vert X^{0} \bigr\Vert _{\infty}. \end{aligned}$$

Assume that \(\Vert X^{j} \Vert _{\infty}\leq \Vert X^{0} \Vert _{\infty}\ (j=1,\ldots, k)\), similar to the case of \(k=1\). Suppose \(\Vert X^{k+1} \Vert _{\infty}= \vert \varepsilon ^{k+1}_{l} \vert \), according to (9), (11), and Lemma 3.1, we have

$$\begin{aligned} \bigl\vert \varepsilon^{k+1}_{l} \bigr\vert &\leq \bigl\vert B^{k+1}_{l} \bigr\vert \\ &= \bigl(M ^{k+1}_{l,0}\bigr)^{-1}\sum ^{k}_{j=1}\bigl(M^{k+1}_{l,k-j}-M^{k+1}_{l,k-j+1} \bigr) \bigl\vert \varepsilon^{j}_{l} \bigr\vert + \bigl(M^{k+1}_{l,0}\bigr)^{-1}M^{k+1}_{l,k} \bigl\vert \varepsilon^{0}_{l} \bigr\vert \\ &\leq\bigl(M ^{k+1}_{l,0}\bigr)^{-1}\sum ^{k}_{j=1}\bigl(M^{k+1}_{l,k-j}-M^{k+1}_{l,k-j+1} \bigr) \bigl\Vert X^{0} \bigr\Vert _{\infty} + \bigl(M^{k+1}_{l,0}\bigr)^{-1}M^{k+1}_{l,k} \bigl\Vert X^{0} \bigr\Vert _{\infty} \\ &\leq \bigl\Vert X^{0} \bigr\Vert _{\infty}. \end{aligned}$$

Due to the principle of mathematical induction, the proof is completed. □

3.3 Convergence analysis

Theorem 3.3

Suppose that problem (1) has a smooth solution \(u(x, t)\). Let \(v^{k}_{i}\) be the numerical solution computed by (4). Then there is a positive constant C independent of τ and h such that

$$\bigl\Vert u^{k}_{i}-v_{i}^{k} \bigr\Vert _{\infty}\leq C(\tau+h),\quad i=1,2,\ldots,m-1; k=1,2,\ldots,n. $$

Proof

Denote \(Y^{k}=U^{k}-\widetilde{V}^{k}=(\eta^{k}_{1}, \ldots, \eta^{k}_{m-1})^{T}\), then according to (1) and (4), we obtain the following error equation:

$$\begin{aligned} &L_{\tau}^{\alpha_{0i}^{k+1}}\eta_{i}^{k+1}+\sum ^{S}_{s=1}a_{si}^{k+1}L_{\tau}^{\alpha_{si}^{k+1}} \eta_{i}^{k+1}-P_{i}^{k+1} \bigl(\rho {}^{}_{-} {\overline{D}}_{h}^{\beta_{i}^{k+1}} \eta_{i}^{k+1} +\sigma {}^{}_{+} {\overline{D}}_{h}^{\beta_{i}^{k+1}} \eta _{i}^{k+1}\bigr) \\ &\quad{}-Q_{i}^{k+1}\bigl(\rho {}^{}_{-}D_{h}^{\gamma_{i}^{k+1}} \eta _{i}^{k+1}+\sigma {}^{}_{+} {D}_{h}^{\gamma_{i}^{k}} \eta_{i}^{k+1}\bigr) +c_{i}^{k+1} \eta_{i}^{k+1}=R_{i}^{k+1}, \end{aligned}$$

where

$$R_{i}^{k+1}=R^{\alpha_{0i}^{k+1}}_{\tau}+\sum ^{S}_{s=1}a_{si}^{k+1}R^{\alpha_{si}^{k+1}}_{\tau}+ R^{\gamma_{i}^{k+1}}_{+}+R^{\gamma_{i}^{k+1}}_{-} +\overline{R}^{\beta_{i}^{k+1}}_{+}+ \overline{R}^{\beta_{i}^{k+1}}_{-}. $$

We rewrite it in the following vector form:

$$ A^{k+1}Y^{k+1}=B^{k+1},\quad k=0,1, \ldots,n-1, $$
(12)

where the component of \(B^{k+1}\) is

$$ B_{i}^{k+1}=\bigl(M ^{k+1}_{i,0} \bigr)^{-1}\sum^{k}_{j=1} \bigl(M^{k+1}_{i,k-j}-M^{k+1}_{i,k-j+1}\bigr) \eta^{j}_{i} +\bigl(M^{k+1}_{i,0} \bigr)^{-1}b^{k+1}_{i}R^{k+1}_{i}, $$
(13)

similar to the proof of Theorem 3.3.

For \(k=1\), suppose \(\Vert Y^{1} \Vert _{\infty}= \vert \eta^{1}_{l} \vert \). From Lemma 2.1, Lemma 2.2, the definitions of \(M_{i,j}^{k}, b_{i}^{k}\) and (13), we have

$$\begin{aligned} \bigl\vert \eta^{1}_{l} \bigr\vert &\leq \bigl\vert B^{1}_{l} \bigr\vert = \bigl\vert \bigl(M^{1}_{l,0} \bigr)^{-1}b^{1}_{l}R^{1}_{l} \bigr\vert \\ &=\Biggl(1+\sum^{S}_{s=1} \frac{\Gamma(2-\alpha^{1}_{0l})}{\Gamma(2-\alpha_{sl}^{1})} a_{sl}^{1}\tau^{{\alpha^{1}_{0l}}-\alpha^{1}_{sl}}\Biggr) \tau^{\alpha^{1}_{0l}}\Gamma\bigl(2-\alpha^{1}_{0l} \bigr)R^{1}_{l} \\ &\leq C(\tau+h). \end{aligned}$$

Assume that \(\Vert Y^{j} \Vert _{\infty}\leq C (\tau+h)\ (j=1,\ldots,k)\). Suppose \(\Vert Y^{k+1} \Vert _{\infty}= \vert \eta^{k+1}_{l} \vert \). Similar to the case of \(k=1\), we have

$$\begin{aligned} \bigl\vert \eta^{k+1}_{l} \bigr\vert &\leq \bigl\vert B^{k+1}_{l} \bigr\vert \\ &=\bigl(M ^{k+1}_{l,0}\bigr)^{-1}\sum ^{k}_{j=1}\bigl(M^{k+1}_{l,k-j}-M^{k+1}_{l,k-j+1} \bigr) \bigl\vert \eta^{j}_{l} \bigr\vert + \bigl(M^{k+1}_{l,0}\bigr)^{-1}b^{k+1}_{l} \bigl\vert R^{k+1}_{l} \bigr\vert \\ &\leq C\bigl(M ^{k+1}_{l,0}\bigr)^{-1}(\tau+h) \Biggl[\sum^{k}_{j=1}\bigl(M^{k+1}_{l,k-j}-M^{k+1}_{l,k-j+1} \bigr) +b^{k+1}_{l}\Biggr]. \end{aligned}$$
(14)

By the definitions of \(M^{k+1}_{i,k}\) and \(b_{i}^{k+1}\), we have

$$\frac{M^{k+1}_{i,k}}{b_{i}^{k+1}} \geq\frac{(k+1)^{1-{\alpha^{k+1}_{0i}}}-k^{1-{\alpha^{k+1}_{0i}}}}{ \tau^{{\alpha^{k+1}_{0i}}}\Gamma(2-{\alpha^{k+1}_{0i}})} \geq\frac{(1-{\alpha^{k+1}_{0i}})k^{-{\alpha^{k+1}_{0i}}}}{ \tau^{{\alpha^{k+1}_{0i}}}\Gamma(2-{\alpha^{k+1}_{0i}})} = \frac{(1-{\alpha^{k+1}_{0i}})}{t_{k}^{{\alpha^{k+1}_{0i}}}\Gamma(2- {\alpha^{k+1}_{0i}})}, $$

namely

$$ b_{i}^{k+1}\leq C M^{k+1}_{i,k}. $$

Substituting the above inequality into (14), we have

$$\begin{aligned} \bigl\vert \eta^{k+1}_{l} \bigr\vert \leq C (\tau+h) \bigl(M ^{k+1}_{l,0}\bigr)^{-1}\Biggl(\sum ^{k}_{j=1}\bigl(M^{k+1}_{l,k-j}-M^{k+1}_{l,k-j+1} \bigr) +M^{k+1}_{l,k}\Biggr)\leq C (\tau+h). \end{aligned}$$

Due to the principle of mathematical induction, the theorem is proved. □

4 Numerical examples

In this section, three examples are presented to illustrate the practical application of our numerical method. Consider the vectors \(V^{k}=(v_{0}^{k},\ldots,v_{m}^{k})\), where \(v^{k}_{i}\) is the approximate solution for \(x_{i}=i h, i=0,1,\ldots, m\), at a certain time t, and \(U^{k}=(u_{0}^{k},\ldots, u_{m}^{k})\), where \(u_{i}^{k}\) is the exact solution. The error is defined by the \(l_{\infty}\) norms:

$$\bigl\Vert V^{k}-U^{k} \bigr\Vert _{\infty}=\max _{0\leq i\leq m} \bigl\vert v^{k}_{i}-u^{k}_{i} \bigr\vert . $$

Example 4.1

Consider the following fractional differential equation:

$$\begin{aligned} \textstyle\begin{cases} {}^{C}_{0}D^{\alpha(x,t)}_{t}u(x,t)+2\cos(\beta(x,t)\pi /2)_{x}R^{\beta(x,t)}u(x,t)- \cos(\gamma(x,t)\pi/2)_{x}R^{\gamma(x,t)}u(x,t) \\ \quad=f(x,t),\quad (x,t)\in\Omega=(0,1)\times(0,T],\\ u(x,0)=5x^{2}(1-x), \quad 0\leq x \leq1,\\ u(0,t)=0,\qquad u(1,t)=0,\quad 0\leq t \leq T, \end{cases}\displaystyle \end{aligned}$$
(15)

where

$$\begin{aligned} f(x,t)={}&\frac{10x^{2}(1-x)t^{2-\alpha(x,t)}}{\Gamma(3-\alpha (x,t))}-10\bigl(t^{2}+1\bigr)\biggl[ \frac{2x^{2-\beta(x,t)}}{\Gamma(3-\beta(x,t))}-\frac {6x^{3-\beta(x,t)}}{\Gamma(4-\beta(x,t))}\biggr] \\ &{} +5\bigl(t^{2}+1\bigr)\biggl[\frac{2x^{2-\gamma(x,t)}}{\Gamma(3-\gamma(x,t))}-\frac {6x^{3-\gamma(x,t)}}{\Gamma(4-\gamma(x,t))} \biggr]. \end{aligned}$$

We take \(\alpha(x,t)=0.8+0.01 \sin(5xt), \beta(x,t)=1.8+0.01x^{2}t^{2}, \gamma(x,t)=0.8+0.01x^{2}\sin t\), \(\rho=1, \sigma=0, \tau=h=0.1\). The above problem has the exact solution \(u(x,t)=5(t^{2}+1)x^{2}(1-x)\).

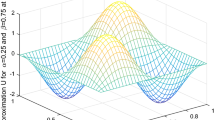
Table 1 lists the maximum errors of the proposed method between the exact solution and the numerical solution for problem (15) at \(T=1\). Figure 1 shows the behavior of the exact solution and the numerical solution of the proposed method at \(t = 0, t = 0.5, t = 1\) for problem (15), respectively. It can be seen that the numerical solution is in good agreement with the exact solution. Figure 2 shows 3D-drawing of the numerical solution and the exact solution of problem (15) at \(T= 1\). We can see that the numerical solution is very similar to the exact solution. From the results displayed in Table 1 and in Figs. 1 and 2, it is obvious that the proposed method is efficient and able to give numerical solutions coinciding with the exact solutions.

Figure 1
figure 1

The solution behavior of (15) at \(t=0\), \(t=0.5\), \(t=1\)

Full size image
Figure 2
figure 2

Three-dimensional numerical solution (left) and the exact solution (right) of (15)

Full size image
Table 1 Numerical solution, exact solution, and absolute error at \(T=1.0\) of (15)
Full size table

Example 4.2

Consider the following fractional differential equation:

$$\begin{aligned} \textstyle\begin{cases} {}^{C}_{0}D^{\alpha(x,t)}_{t}u(x,t)+\cos(\beta(x,t)\pi /2)_{x}R^{\beta(x,t)}u(x,t) +\partial u(x,t)/\partial x \\ \quad =f(x,t), \quad (x,t)\in\Omega=(0,8)\times(0,T],\\ u(x,0)=\frac{x^{2}(8-x)}{80},\quad 0\leq x \leq8,\\ u(0,t)=0, \qquad u(8,t)=0, \quad 0\leq t \leq T, \end{cases}\displaystyle \end{aligned}$$
(16)

where

$$\begin{aligned} f(x,t)={}&\frac{x^{2}(8-x)t^{1-\alpha(x,t)}}{80\Gamma(2-\alpha(x,t))}- \frac{(t+1)}{80}\biggl[\frac{16x^{2-\beta(x,t)}}{\Gamma(3-\beta(x,t))} - \frac{6x^{3-\beta(x,t)}}{\Gamma(4-\beta(x,t))}\biggr]\\ &{}+\frac{(t+1)}{80}x(16-3x). \end{aligned}$$

We take \(\alpha(x,t)=0.5+0.01 \sin(5xt), \beta(x,t)=1.5+0.01x^{2}t^{2}, \gamma(x,t)=1\), \(\rho=1, \sigma=0, \tau=0.05, h=0.1\). The above problem has the exact solution \(u(x,t)=\frac{(t+1)x^{2}(8-x)}{80}\).

A comparison of the numerical solution of the proposed method and the exact solution for problem (16) is listed in Table 2 and is shown in Fig. 3. It can be seen that the proposed method is in excellent agreement with the exact solution.

Figure 3
figure 3

The solution behavior of (16) at \(t=0\), \(t=0.5\), \(t=1\)

Full size image
Table 2 Numerical solution, exact solution, and absolute error at \(T=1.0\) of (16)
Full size table

Example 4.3

Consider the two-term VO fractional differential equation:

$$\begin{aligned} \textstyle\begin{cases} {}^{C}_{0}D^{\alpha(x,t)}_{t}u(x,t)+{}^{C}_{0}D^{\alpha (x,t)/ 2}_{t}u(t)-{}_{x}R^{\beta(x,t)}u(x,t)+u(x,t)=f(x,t),\\ \quad (x,t)\in\Omega=(0,1)\times(0,T],\\ u(x,0)=x^{2}(1-x)^{2},\quad 0\leq x \leq1,\\ u(0,t)=0,\qquad u(1,t)=0,\quad 0\leq t \leq T, \end{cases}\displaystyle \end{aligned}$$
(17)

where

$$\begin{aligned} f(x,t)={}&2x^{2}(1-x)^{2}\biggl[\frac{t^{2-\alpha(x,t)}}{\Gamma(3-\alpha (x,t))}+ \frac{t^{2-\alpha(x,t)/2}}{\Gamma(3-\alpha(x,t)/2)}\biggr]+\frac {\operatorname{sec}(\beta(x,t)\pi/2)}{2}\bigl(1+t^{2}\bigr) \\ &{}\times\biggl[\frac{2(x^{2-\beta(x,t)}+(1-x)^{2-\beta(x,t)})}{\Gamma(3-\beta (x,t))}-\frac{12(x^{3-\beta(x,t)}+(1-x)^{3-\beta(x,t)})}{\Gamma(4-\beta(x,t))} \\ &{}+\frac{24(x^{4-\beta(x,t)}+(1-x)^{4-\beta(x,t)})}{\Gamma(5-\beta (x,t))}\biggr]+\bigl(1+t^{2}\bigr)x^{2}(1-x)^{2}. \end{aligned}$$

We take \(\alpha(x,t)=1-0.5e^{-xt}, \beta(x,t)=1.7+0.1e^{-\frac {x^{2}}{1000}-\frac{t}{50}-1}\), \(\rho=\sigma=\frac{1}{2},\tau=h=0.1\). The above problem has the exact solution \(u(x,t)=(1+t^{2})x^{2}(1-x)^{2}\).

Table 3 gives the numerical solution, the exact solution, and the absolute error at \(T=1\) of (17). Figure 4 shows the solution behavior of (17) at \(t=0.25, t=0.75, t=1\), respectively. It can be seen that the numerical solution is in good agreement with the exact solution.

Figure 4
figure 4

The solution behavior of (17) at \(t=0.25\), \(t=0.75\), \(t=1\)

Full size image
Table 3 Numerical solution,exact solution and absolute error at \(T=1.0\) of (17)
Full size table

5 Conclusion

In this paper, a finite difference scheme has been proposed to solve a multi-term time-space variable-order fractional diffusion equation. The stability and convergence have been analyzed by the mathematical induction method. Numerical examples are provided to show that the finite difference scheme is computationally efficient. The techniques for the numerical schemes and related numerical analysis can be applied to solve variable-order fractional (in space and/or in time) partial differential equations.