1 Introduction

Some mathematical models, for instance, see [1–5], have been employed to describe and understand epidemic transmission dynamics since the work of Kermack and McKendrick [6] was proposed. The classical compartment models were proposed and investigated on the ground of some restrictive assumptions including a constant total population size and a constant recruitment rate for the susceptible individuals. This assumption is relatively reasonable for a short-lasting disease. While in reality, the population sizes of human beings and other creatures are generally variable, instead of keeping constant for a long run. As an example of this phenomenon, Ngonghala et al. pointed out that malaria in developing countries took place with growth of local population size. When it concerns the variable population size, some recent literature works, such as Ngonghala et al. [7], Busenberg and Driessche [8], Wang et al. [9], Zhao et al. [10], Zhu and Hu [11], Li et al. [12], had considered the effect of population size on the epidemic dynamics. We would like to mention the work by Wang et al. [9], in which they constructed an SIS epidemic model under the assumption that the susceptible individuals followed the Logistic growth:

$$ \begin{aligned} &\dot{S}(t)=rS \biggl(1-\frac{S}{a} \biggr)- \beta(I) IS+\gamma I, \\ &\dot{I}(t)=\beta(I) IS-(d+\varepsilon+\gamma)I, \end{aligned} $$
(1)

where \(S(t)\) and \(I(t)\) denote the numbers of the susceptible and the infected individuals at time t, respectively; r is the intrinsic growth rate of the susceptible individuals; a is the carrying capacity of the community in the absence of infection; d is the natural death rate; γ represents the recovery rate of the infected individuals; ε is the disease-induced death rate; \(\beta(I)\) is the transmission rate and is given in the following form:

$$ \beta(I)= \textstyle\begin{cases} \beta, & 0\leq I\leq I_{c}, \\ \beta (\frac{I_{c}}{I} )^{p}, & I>I_{c}. \end{cases} $$
(2)

All the parameters are assumed to be nonnegative. When \(p=0\), \(\beta(I)\) is equal to the constant transmission rate β. In this paper, we shall consider the following deterministic SIS endemic model:

$$ \begin{aligned} &\dot{S}(t)=bS(a-S)-\beta IS+\gamma I, \\ &\dot{I}(t)=\beta IS-(d+\varepsilon+\gamma)I, \end{aligned} $$
(3)

where \(b=r/a\). We set \(N(t)\) is the total population at time t, then

$$ \dot{N}(t)=\dot{S}(t) + \dot{I}(t)=rS \biggl(1-\frac{S}{a} \biggr)-(d+ \varepsilon)I. $$
(4)

Wang et al. [9] showed that the domain

$$ \Pi = \biggl\{ (S,I) \in \mathbb{R}^{2}_{+}\mid N=S+I\leq K_{0}=\frac{(ab+d+\varepsilon)^{2}}{4b^{2}(d+\gamma)}+1 \biggr\} $$
(5)

is a positively invariant set with respect to model (1). Moreover, the disease-free equilibrium \(E_{0}(a,0)\) of model (1) always exists, and if the basic reproductive number

$$ R_{0}=\frac{\beta a}{d+\varepsilon+\gamma}\leq1, $$
(6)

\(E_{0}(a,0)\) is globally asymptotically stable. If \(R_{0}>1\), then \(E_{0}(a,0)\) is unstable, and there is a unique endemic equilibrium \(E^{*}(S^{*},I^{*})\) which is globally asymptotically stable. Here

$$ S^{*}=\frac{d+\varepsilon+\gamma}{\beta},\qquad I^{*}=\frac{S^{*2}b}{d+\varepsilon}(R_{0}-1). $$
(7)

The compartment models are inevitably affected by the environmental noise. We assume that the transmission coefficient β is subject to the environmental white noise, that is,

$$ \beta \rightarrow \beta + \sigma \dot{B}(t), $$
(8)

where \(B(t)\) is a standard Brownian motion, σ is the intensity of environmental white noise. In order to explore the stochastic effect, when the constant transmission rate is replaced by a random variable, we consider the corresponding stochastic SIS epidemic model:

$$ \begin{aligned} &\mathrm{d} {S}(t)=\bigl(bS(a-S)-\beta IS+\gamma I \bigr)\,\mathrm{d}t-\sigma IS\,\mathrm{d}B(t), \\ &\mathrm{d} {I}(t)=\bigl(\beta IS-(d+\varepsilon+\gamma)I\bigr)\,\mathrm{d}t+ \sigma IS\,\mathrm{d}B(t). \end{aligned} $$
(9)

The sum of the two equations for the population size \(N(t)\) of models (3) and (9) is

$$ \dot{N}(t)=bS(a-S)-(d+\varepsilon)I. $$
(10)

Throughout this paper, we will work on the complete probability space \((\Omega, \{\mathcal{F}_{t}\}_{t\geq 0},P)\) with its filtration \(\{\mathcal{F}_{t}\}_{t\geq 0}\) satisfying the usual conditions (i.e., it is right continuous and \(\mathcal{F}_{0}\) contains all P-null sets). We will investigate the dynamical properties of stochastic SIS model from several aspects: the result that stochastic model (9) admits a unique positive solution will be studied in the next section. The sufficient conditions of the persistence for the infected individuals would be derived. Further, we still find a simple condition to reach the extinction for the infected individuals. As a consequence, several illustrative examples are carried out to support the main results of this paper.

2 Existence and uniqueness of positive solution

In this section, we first show that the solution of system (9) is positive and global. Our proof is motivated by the work of Mao et al. [13].

Theorem 1

There exists a unique solution \((S(t),I(t))\) of system (9) on \(t\geq 0\) for any initial value \((S(0),I(0))\in \mathbb{R}^{2}_{+}\), and the solution will remain in \(\mathbb{R}^{2}_{+}\) with probability 1, namely \((S(t),I(t))\in \mathbb{R}^{2}_{+} \) for all \(t\geq 0\) almost surely.

Proof

Since the coefficients of model (9) satisfy local Lipschitz conditions for any initial value \((S(0),I(0))\in \mathbb{R}^{2}_{+}\), there exists a unique local solution on \(t\in[0,\tau_{e})\), where \(\tau_{e}\) is the explosion time. Next, we will show that the solution of model (9) is global. To this end, we need to show that \(\tau_{e}=\infty\) holds almost surely. Let \(k_{0}>0\) be sufficiently large such that \(S(0)\) and \(I(0)\) all lie within the interval \([\frac{1}{k_{0}}, k_{0}]\). For all \(k\geq k_{0}\), we define the stopping time

$$ \tau_{k}=\inf \biggl\{ t\in[0,\tau_{e}): \min \bigl\{ S(t),I(t)\bigr\} \leq \frac{1}{k}~\mbox{or}~\max \bigl\{ S(t),I(t)\bigr\} \geq k \biggr\} . $$
(11)

Throughout this paper, we set \(\inf\emptyset=\infty\). Clearly, \(\tau_{k}\) is an increasing function as \(k\rightarrow\infty\). We set \(\tau_{\infty}=\lim_{k\to \infty} \tau_{k}\), according to the definition of stopping time, we get that \(\tau_{\infty}\leq\tau_{e}\) a.s. If we can show that \(\tau_{\infty}=\infty \) a.s., then \(\tau_{e}=\infty\) a.s. From now on, our proof will go by contradiction. If this statement is false, then there exists a pair of constants \(T>0\) and \(\varepsilon\in(0,1)\) such that \(P\{\tau_{\infty}\leq T\}>\varepsilon\), hence there exists an integer \(k_{1}>k_{0}\) such that

$$ P\{\tau_{k}\leq T\}\geq\varepsilon \quad \mbox{for all } k>k_{1}. $$
(12)

We define a \(C^{2}\)-function \(V:\mathbb{R}^{2}_{+}\rightarrow\mathbb{R}_{+}\) as follows:

$$ V(S,I)=S-k-k\log \frac{S}{k}+I-1-\log I, $$
(13)

where k is a constant determined later. Generalized Itô's formula gives that

$$ \begin{aligned}[b] LV(S,I) ={}& \biggl(1-\frac{k}{S} \biggr) \bigl(bS(a-S)-\beta IS+\gamma I \bigr)+ \biggl(1-\frac{1}{I} \biggr) \bigl( \beta IS-(d+\varepsilon+\gamma)I \bigr) \\ &{}+\frac{k}{2}\sigma^{2} I^{2}+\frac{1}{2} \sigma^{2} S^{2} \\ ={}&(ab+kb-\beta)S-bS^{2}+\bigl(k\beta-(d+\varepsilon)\bigr)I-abk- \frac{k\gamma I}{S}+(d+\varepsilon+\gamma) \\ &{}+\frac{k}{2}\sigma^{2} I^{2}+\frac{1}{2} \sigma^{2} S^{2}. \end{aligned} $$
(14)

Choose the constant

$$ k=\frac{d+\varepsilon}{\beta}, $$
(15)

which implies that

$$ \begin{aligned}[b] LV(S,I) &= (ab+kb-\beta)S-bS^{2}-abk- \frac{k\gamma I}{S}+(d+\varepsilon+\gamma) +\frac{k}{2}\sigma^{2}I^{2}+ \frac{1}{2}\sigma^{2}S^{2} \\ &\leq (ab+kb)K_{0}+(d+\varepsilon+\gamma)+\frac{(1+k)}{2} \sigma^{2}K_{0}^{2}:=M_{0}. \end{aligned} $$
(16)

The remainder of the proof follows that in Zhao et al. [10]. □

3 Persistence in the mean

In this section, we shall investigate the persistence property of model (9). The solution of model (9) is said to be persistent in the mean if

$$ \liminf_{t\rightarrow \infty}\frac{1}{t} \int_{0}^{t}I(s)\,\mathrm{d}s>0\quad \mbox{a.s.} $$
(17)

For convenience, we define the following notation:

$$ \bigl\langle x(t)\bigr\rangle =\frac{1}{t} \int_{0}^{t}x(s)\,\mathrm{d}s. $$
(18)

Lemma 1

([13], Strong law of large numbers)

Let \(M=\{M_{t}\}_{t\geq0}\) be a real-valued continuous local martingale vanishing at \(t=0\). Then

$$ \lim_{t\to \infty}\langle M,M\rangle_{t}=\infty\quad \textit{a.s.}\quad \Rightarrow\quad \lim_{t\to \infty}\frac{M_{t}}{\langle M,M\rangle_{t}}=0 \quad \textit{a.s.}, $$
(19)

and also

$$ \limsup_{t\to \infty}\frac{\langle M,M\rangle_{t}}{t}=\infty\quad \textit{a.s.}\quad \Rightarrow\quad \lim_{t\to \infty}\frac{M_{t}}{t}=0\quad \textit{a.s.} $$
(20)

Theorem 2

Let \((S(t), I(t))\) be a solution of system (9) with any initial value \((S(0),I(0))\in \Pi\). If

$$ b\leq\beta, \quad \tilde{R}_{0}= \frac{ab}{d+\varepsilon+\gamma}- \frac{\sigma^{2}K_{0}^{2}}{2(d+\varepsilon+\gamma)} =\frac{b}{\beta}R_{0}- \frac{\sigma^{2}K_{0}^{2}}{2(d+\varepsilon+\gamma)}>1, $$
(21)

then the density of the infected individuals obeys the following expression:

$$ \liminf_{t\rightarrow \infty}\bigl\langle I(t)\bigr\rangle \geq \frac{(d+\varepsilon+\gamma)(\tilde{R}_{0}-1)}{d+\varepsilon+\gamma+\beta} >0\quad \textit{a.s.} $$
(22)

Proof

Integrating both sides of the second equation of model (9) gives that

$$ \frac{I(t)-I(0)}{t}= \beta\langle IS\rangle -(d+\varepsilon+\gamma) \langle I\rangle +\frac{\sigma}{t} \int_{0}^{t} I(r)S(r)\,\mathrm{d}B(r). $$
(23)

Then generalized Itô's formula acting on model (9) leads to

$$\begin{aligned} &\mathrm{d}\ln S(t)= \biggl(ab-bS-\beta I+\gamma\frac{I}{S}- \frac{\sigma^{2}}{2}I^{2} \biggr)\,\mathrm{d}t-\sigma I\,\mathrm{d}B(t), \end{aligned}$$
(24)
$$\begin{aligned} &\mathrm{d}\ln I(t)= \biggl(\beta S-(d+\varepsilon+\gamma)- \frac{\sigma^{2}}{2}S^{2} \biggr)\,\mathrm{d}t+\sigma S\,\mathrm{d}B(t). \end{aligned}$$
(25)

Integrating both sides of (24) and (25) from 0 to t and dividing by t, we have that

$$\begin{aligned} &\frac{\ln S(t)-\ln S(0)}{t}=ab-b\langle S\rangle-\beta \langle I\rangle+ \gamma \biggl\langle \frac{I}{S} \biggr\rangle -\frac{\sigma^{2}}{2}\bigl\langle I^{2}\bigr\rangle +\frac{\sigma}{t} \int_{0}^{t} I(r)\,\mathrm{d}B(r), \end{aligned}$$
(26)
$$\begin{aligned} &\frac{\ln I(t)-\ln I(0)}{t}=\beta\langle S\rangle-(d+\varepsilon+\gamma) -\frac{\sigma^{2}}{2}\bigl\langle S^{2}\bigr\rangle +\frac{\sigma}{t} \int_{0}^{t} S(r)\,\mathrm{d}B(r). \end{aligned}$$
(27)

We combine (23), (26), and (27) and derive that

$$ \begin{aligned}[b] &\frac{\ln S(t)-\ln S(0)}{t}+\frac{\ln I(t)-\ln I(0)}{t}+\frac{I(t)-I(0)}{t} \\ &\quad =ab-(d+\varepsilon+\gamma)-(d+\varepsilon+\gamma+\beta) \langle I \rangle+(\beta-b)\langle S\rangle+\gamma \biggl\langle \frac{I}{S} \biggr\rangle +\bigl(\beta+\sigma^{2}\bigr)\langle IS\rangle \\ &\qquad {}-\frac{\sigma^{2}}{2}\bigl\langle S^{2}+I^{2}+2SI \bigr\rangle +\frac{\sigma}{t} \int_{0}^{t}\bigl(S(r)-I(r)+ S(r)I(r)\bigr)\, \mathrm{d}B(r) \\ &\quad \geq ab-(d+\varepsilon+\gamma)-\frac{\sigma^{2}}{2}K_{0}^{2}-(d+ \varepsilon+\gamma+\beta) \langle I\rangle \\ &\qquad {}+\frac{\sigma}{t} \int_{0}^{t} \bigl(S(r)-I(r)+ S(r)I(r)\bigr)\, \mathrm{d}B(r), \end{aligned} $$
(28)

then

$$\begin{aligned} (d+\varepsilon+\gamma+\beta)\langle I\rangle \geq&ab-(d+ \varepsilon+\gamma)-\frac{\sigma^{2}}{2}K_{0}^{2} + \frac{\sigma}{t} \int_{0}^{t} \bigl(S(r)-I(r)+ S(r)I(r)\bigr)\, \mathrm{d}B(r) \\ &{}-\frac{\ln S(t)-\ln S(0)}{t}-\frac{\ln I(t)-\ln I(0)}{t}-\frac{I(t)-I(0)}{t}. \end{aligned}$$
(29)

We denote

$$ M_{1}(t)=\sigma \int_{0}^{t} \bigl(S(r)-I(r)+ S(r)I(r)\bigr)\, \mathrm{d}B(r) $$
(30)

by strong law of large numbers for martingales, together with the facts \(0< S(t)\), \(I(t)< K_{0}\), which yields that

$$ \lim_{t\to \infty} \frac{S(t)}{t}=0,\qquad \lim _{t\to \infty} \frac{I(t)}{t}=0,\qquad \lim_{t\to \infty} \frac{M_{1}(t)}{t}=0\quad \mbox{a.s.}, $$
(31)

therefore,

$$ \liminf_{t\rightarrow \infty}\bigl\langle I(t)\bigr\rangle \geq \frac{ab-(d+\varepsilon+\gamma)-\frac{\sigma^{2}}{2}K_{0}^{2}}{d+\varepsilon+\gamma+\beta} =\frac{(d+\varepsilon+\gamma)(\tilde{R}_{0}-1)}{d+\varepsilon+\gamma+\beta}>0\quad \mbox{a.s.} $$
(32)

The proof is complete. □

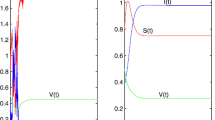
Example 1

Let the parameters of model (9) be

$$ \begin{aligned} &r=0.8,\qquad a=10,\qquad b=0.08,\qquad \beta=0.3,\qquad \gamma=0.35, \\ &d=0.1,\qquad \varepsilon=0.02,\qquad \sigma=0.01 \end{aligned} $$
(33)

and the initial value be \((S(0),I(0))=(5,2)\), then the threshold of model (9) is computed as

$$ \tilde{R}_{0}= 1.1121>1, $$
(34)

which is consistent with the result of Theorem 2 (see Fig. 1).

Figure 1
figure 1

The density of the infected individuals is persistent, where the threshold \(\tilde{R}_{0}>1\)

Full size image

4 Extinction

In the previous section, we have investigated the persistence of the solution to model (9). In this section, we shall prove that the density of the infected individuals will be driven to extinction with a negative exponential power under some simple assumptions.

Theorem 3

Let \((S(t), I(t))\) be the solution of model (9) with the initial value \((S(0),I(0))\in \Pi\). If

$$ \breve{R}_{0}=\frac{\beta K_{0}}{d+\varepsilon+\gamma}=\frac{K_{0}}{a}R_{0}< 1 $$
(35)

or

$$ \sigma^{2}>\frac{\beta^{2}}{2(d+\varepsilon+\gamma)} $$
(36)

holds, then the density of the infected individuals will decline to zero exponentially with probability one. That is to say,

$$ \limsup_{t\to \infty} \frac{\ln I(t)}{t}\leq \biggl( \frac{\beta K_{0}}{d+\varepsilon+\gamma}-1 \biggr) (d+\varepsilon+\gamma) $$
(37)

or

$$ \limsup_{t\to \infty} \frac{\ln I(t)}{t}\leq\frac{\beta^{2}}{2\sigma^{2}}-(d+ \varepsilon+\gamma)\quad \textit{a.s.} $$
(38)

Proof

From the second equation of model (9), we have

$$ \frac{\ln I(t)}{t}=\frac{\ln I(0)}{t} +\frac{1}{t} \int_{0}^{t} \biggl(\beta S(r)-(d+\varepsilon+\gamma)- \frac{\sigma^{2}}{2}S^{2}(r) \biggr)\,\mathrm{d}r+\frac{\sigma}{t} \int_{0}^{t} S(r)\,\mathrm{d}B(r). $$
(39)

The fact \(S\leq K_{0}\) leads to the following result:

$$ \begin{aligned}[b] \frac{\ln I(t)}{t}&\leq\frac{\ln I(0)}{t}+ \frac{1}{t} \int_{0}^{t} \bigl(\beta K_{0}-(d+ \varepsilon+\gamma) \bigr)\,\mathrm{d}r +\frac{\sigma}{t} \int_{0}^{t} S(r)\,\mathrm{d}B(r) \\ &=\frac{\ln I(0)}{t} + \biggl(\frac{\beta K_{0}}{d+\varepsilon+\gamma}-1 \biggr) (d+\varepsilon+ \gamma) +\frac{\sigma}{t} \int_{0}^{t} S(r)\,\mathrm{d}B(r). \end{aligned} $$
(40)

We denote

$$ M_{2}(t)=\sigma \int_{0}^{t} S(r)\,\mathrm{d}B(r) $$
(41)

by the strong law of large numbers for martingales, we then have

$$ \lim_{t\to \infty} \frac{M_{2}(t)}{t}=0\quad \mbox{a.s.} $$
(42)

Condition (35) of Theorem 3 gives that

$$ \limsup_{t\to \infty} \frac{\ln I(t)}{t}\leq \biggl( \frac{\beta K_{0}}{d+\varepsilon+\gamma}-1 \biggr) (d+\varepsilon+\gamma)\leq0\quad \mbox{a.s.} $$
(43)

On the other hand, expression (39) can be computed as follows:

$$ \begin{aligned}[b] \frac{\ln I(t)}{t} ={}&\frac{\ln I(0)}{t}+ \frac{1}{t} \int_{0}^{t} \biggl(-\frac{\sigma^{2}}{2} \biggl(S- \frac{\beta}{\sigma^{2}} \biggr)^{2} +\frac{\beta^{2}}{2\sigma^{2}}-(d+\varepsilon+ \gamma) \biggr)\,\mathrm{d}r \\ &{}+\frac{\sigma}{t} \int_{0}^{t} S(r)\,\mathrm{d}B(r) \\ \leq{}&\frac{\ln I(0)}{t}+\frac{\beta^{2}}{2\sigma^{2}}-(d+\varepsilon+\gamma)+ \frac{M_{2}(t)}{t}. \end{aligned} $$
(44)

By similar discussion, together with condition (36), we take superior limit on both sides of (44) and derive that

$$ \limsup_{t\to \infty} \frac{\ln I(t)}{t}\leq\frac{\beta^{2}}{2\sigma^{2}}-(d+ \varepsilon+\gamma)< 0\quad \mbox{a.s.} $$
(45)

The proof is complete. □

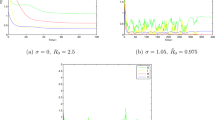
Example 2

We set the parameters of model (9) are

$$ \begin{aligned} &r=0.4,\qquad a=100,\qquad b=0.004,\qquad \beta=0.2,\qquad \gamma=0.3, \\ &d=0.1, \qquad \varepsilon=0.2, \qquad \sigma=0.2, \end{aligned} $$
(46)

and the initial value is \((S(0),I(0))=(35,50)\). It is easy to check that

$$ \sigma^{2}=0.04>\frac{\beta^{2}}{2(d+\varepsilon+\gamma)}=0.0120. $$
(47)

Theorem 3 is satisfied, and the infected individuals will decline to zero according to Fig. 2. If we choose another group of parameters

$$ \begin{aligned} &r=0.8,\qquad a=10,\qquad b=0.08,\qquad \beta=0.02,\qquad \gamma=0.8, \\ &d=0.5,\qquad \varepsilon=0.1,\qquad \sigma=0.01, \end{aligned} $$
(48)

and the initial value \((S(0),I(0))=(1,8)\) in order to meet condition (36), after substitution, we then get that

$$ \frac{\beta K_{0}}{d+\varepsilon+\gamma}=0.8556< 1, $$
(49)

which also means that the infected individuals definitely tend to zero with the rate of a negative exponential power as shown in Fig. 3.

Figure 2
figure 2

The infected individuals are extinct under condition (35)

Full size image
Figure 3
figure 3

The density of the infected individuals approaches zero almost surely under condition (36)

Full size image

5 Conclusion

The dynamical properties of the stochastic SIS model with Logistic growth are paid more attention to in this paper. According to the approach shown in many recent literature works, we still construct a \(C^{2}\)-function to show that the stochastic SIS epidemic model admits a unique positive global solution. Based on the general assumption of this paper, the total population is separated into two compartments: one is the susceptible, another is the infected. We also assume that the transmission rate β is perturbed by a white noise. The two indicators \(\tilde{R}_{0}\) and \(\breve{R}_{0}\) are kind of thresholds of this paper: when \(\tilde{R}_{0}> 1\), under some extra conditions, the density of the infected individuals keeps persistent; when \(\breve{R}_{0}<1\) holds or (36) is valid, the density of the infected individuals declines to zero in a long run. Several illustrative examples support the main results of this paper.