Parameter estimation for nonergodic Ornstein-Uhlenbeck process driven by the weighted fractional Brownian motion

Abstract

In this paper, we consider the nonergodic Ornstein-Uhlenbeck process

$$ X_{0}=0, \quad\quad dX_{t}=\theta X_{t} \,dt+dB_{t}^{a,b},\quad t\geq0, $$

driven by the weighted fractional Brownian motion $B_{t}^{a,b}$ with parameter a and b. Our goal is to estimate the unknown parameter $\theta>0$ based on the discrete observations of the process. We construct two estimators $\hat{\theta}_{n}$ and $\check{\theta}_{n}$ of θ and show their strong consistency and the rate consistency.

1 Introduction

The fractional Brownian motion (fBm for short) has already been widely applied in hydrology, traffic volume prediction, estimation of Hurst exponent of seismic signal, finance, and various other areas due to its properties such as long-range dependence, self-similarity, and stationarity of its increments. However, fBm is not sufficient for some random phenomena, so many researchers have chosen more general stochastic processes to construct stochastic models. For instance, Azzaoui and Clavier [1] studied impulse response of the 60-Ghz channel by using α-stable processes. Lin and Lin [2] studied pricing debt value in stochastic interest rate by using Lévy processes. Meanwhile, the weighted fractional Brownian motion (wfBm), which is a kind of generalizations of the fBm, can be also used for modeling.

We recall that the wfBm $B_{t}^{a,b}$ with parameters $(a,b)$ such that $a>-1$, $\vert b\vert <1$, and $\vert b\vert < a+1$ and long/short-range dependence is a centered self-similar Gaussian process with covariance function

$$\begin{aligned}& R^{a,b}(t,s):=E \bigl[ B^{a,b}_{t}B^{a,b}_{s} \bigr] = \int _{0}^{s\wedge t}u^{a} \bigl[(t-u)^{b}+(s-u)^{b} \bigr]\,du, \quad s,t\geq0. \end{aligned}$$

(1)

Obviously, when $a=b=0$, $B_{t}^{a,b}$ is the standard Brownian motion $B_{t}$. When $a=0$, we have

$$\begin{aligned} E \bigl[ B^{a,b}_{t}B^{a,b}_{s} \bigr] = \frac{1}{b+1} \bigl[t^{b+1}+s^{b+1}-\vert s-t\vert ^{b+1} \bigr], \end{aligned}$$

which is the covariance function of the fBm with Hurst index $\frac{b+1}{2}$ when $-1< b<1$. Therefore, the wfBm is an extension of the fBm. The wfBm has some applications in various areas. It is known that the process $B_{t}^{a,b}$ introduced in Bojdecki et al. [3] is neither a semimartingale nor a Markov process unless $a=0$ and $b=0$, so many useful technical tools of stochastic analysis are ineffective when researchers deal with $B_{t}^{a,b}$. More studies on the wfBm can be found in Bojdecki et al. [4, 5], Garzón [6], Shen, Yan, and Cui [7], Yan, Wang, and Jing [8], and the references therein.

Kleptsyna and LeBreton [9] first studied the maximum likelihood estimator (MLE) of the fractional Ornstein-Uhlenbeck (fOU) process $X_{t}$ and proved the convergence of the MLE. Hu and Nualart [10] studied the drift parameter estimation by a least squares approach and obtained the consistency and the asymptotic properties of the estimator based on continuous observations $\{X_{t}, t \in[0, T]\}$. In the ergodic case, Azmoodeh and Morlanes [11], Azmoodeh and Viitasaari [12], Hu and Song [13], and Jiang and Dong [14] studied the statistical inference for several models. In addition, Belfadli, Es-Sebaiy, and Ouknine [15], El Machkouri, Es-Sebaiy, and Ouknine [16], Es-Sebaiy and Ndiaye [17], Shen, Yin, and Yan [18] studied the parameter estimation in the nonergodic case for fOU processes. Liu and Song [19] considered minimum distance estimation for fOU processes. Xiao et al. [20] considered the fOU processes with discretization procedure of an integral transform.

Thus, motivated by all these studies, the present paper is concerned with the parameter estimation problem for nonergodic O-U process driven by the wfBm

$$\begin{aligned} X_{0}=0,\quad\quad dX_{t}=\theta X_{t}\,dt +dB^{a,b}_{t}, \quad t\geq0, \end{aligned}$$

(2)

where $\theta>0$ is an unknown parameter. Hu and Nualart [10] used the LSE technique to define the estimation of the unknown parameter as follows:

$$\begin{aligned} \widehat{\theta}_{t}=\frac{\int^{t}_{0}X_{s}\, dX_{s}}{\int^{t}_{0}X^{2}_{s}\,ds}, \end{aligned}$$

(3)

where the integral $\int^{t}_{0}X_{s}\,dX_{s}$ is interpreted in the Young sense (see Young [21]). In fact, when $\widehat{\theta }_{t}=\frac{\int^{t}_{0}X_{s}\,dX_{s}}{\int^{t}_{0}X^{2}_{s}\,ds}$, the quadratic function of θ

$$\begin{aligned} \int^{t}_{0}\vert \dot{X}_{s}-\theta X_{s}\vert ^{2}\, ds= \int^{t}_{0} \dot{X}^{2}_{s} \,ds-2\theta \int^{t}_{0}X_{s}\, dX_{s} +\theta^{2} \int_{0}^{t} X_{s}^{2}\,ds \end{aligned}$$

has minimum.

Note that ElOnsy, Es-Sebaiy. and Ndiaye [22] studied the parameter estimation for nonergodic fOU processes of the second kind with discrete observations. They proved the strong consistency of the estimators and obtained the rate consistency of those estimators. In this paper, we study parameter estimation problems for nonergodic OU processes driven by the weighted fractional Brownian motion with discrete observations. We construct two estimators, then prove the consistency of the estimators and get their rate consistency. By comparing ElOnsy, Es-Sebaiy, and Ndiaye [22] with our paper, we obtain both the consistency of the estimators and their rate consistency. However, there is some difference of the processes we study.

From a practical standpoint, it is more realistic and amusing to consider asymptotic properties of the estimator based on discrete observations of $X_{t}$. We suppose that an Ornstein-Uhlenbeck process $X_{t}$ is observed in equidistant times with step size $\Delta_{n}:t_{1}=\Delta_{n}$, $t_{2}=2\bigtriangleup_{n},\dots, t_{n}=T_{n}=n\bigtriangleup_{n}$, where we denote by $T_{n}$ the length of the ‘observation window.’ The goal is to construct two estimators for θ that converge at rate $\sqrt{n\Delta_{n}}$ based on the observational data $X_{t_{i}}$, $i=0,1,\dots,n$.

Since $\int_{0}^{t} X_{s}\,dX_{s}$ is a Young integral (pathwise sense), we have $\int_{0}^{t}X_{s}\,dX_{s}=\frac{1}{2}X_{t}^{2}$, Thus, we obtain

$$\begin{aligned} \tilde{{\theta}}_{T_{n}}=\frac{\int_{0}^{T_{n}}X_{s}\, dX_{s}}{\int_{0}^{T_{n}}X_{s}^{2}\,ds} = \frac{X_{T_{n}}^{2}}{2\int_{0}^{T_{n}}X_{s}^{2}\,ds}. \end{aligned}$$

(4)

In the following, we construct two different discrete version estimators of $\tilde{{\theta}}_{T_{n}}$. In (4), let us replace $\int_{0}^{T_{n}}X_{s}\,dX_{s}$ by $\sum_{i=1}^{n}X_{t_{i-1}}(X_{t_{i}}-X_{t_{i-1}})$ and $\int _{0}^{T_{n}}X_{s}^{2}\,ds$ by $\Delta_{n}\sum_{i=1}^{n}X_{t_{i-1}}^{2}$.

Then the estimators of θ are as follows:

$$\begin{aligned} \hat{\theta}_{n}=\frac{\sum_{i=1}^{n}X_{t_{i-1}}(X_{t_{i}}-X_{t_{i-1}})}{\Delta_{n}\sum_{i=1}^{n}X_{t_{i-1}}^{2}} \end{aligned}$$

(5)

and

$$\begin{aligned} \check{\theta}_{n}=\frac{X_{T_{n}}^{2}}{2 \Delta _{n}\sum_{i=1}^{n}X_{t_{i-1}}^{2}}. \end{aligned}$$

(6)

Denote $S_{n}=\Delta_{n}\sum_{i=1}^{n}X_{t_{i-1}}^{2}$. Then (5) and (6) can be rewritten respectively as

$$\begin{aligned} \hat{\theta}_{n}=\frac{\sum_{i=1}^{n}X_{t_{i-1}}(X_{t_{i}}-X_{t_{i-1}})}{S_{n}} \end{aligned}$$

(7)

and

$$\begin{aligned} \check{\theta}_{n}=\frac{X_{T_{n}}^{2}}{2 S_{n}}. \end{aligned}$$

(8)

The paper is organized as follows. In Section 2, some preliminaries for the wfBm $B_{t}^{a,b}$ and main lemmas are provided. In Section 3 the strong consistency of $\hat{\theta}_{n}$ and $\check{\theta}_{n}$ are proved. In Section 4, we show the rate consistency of $\hat{\theta}_{n}$ and $\check{\theta}_{n}$. Finally, we make simulations to show the performance of two estimators $\hat{\theta }_{n}$ and $\check{\theta}_{n}$.

2 Preliminaries and main lemmas

Let $B_{t}^{a,b}$ be a wfBm defined on a complete probability space $(\Omega,\mathcal{F},P)$ with parameters a, b ($a>-1$, $0< b<1$, $b< a+1$). It is possible for researchers to construct a variety of stochastic calculus with respect to the wfBm $B_{t}^{a,b}$ associated with the Malliavin calculus. More studies and references can be found in Nualart [23] and the references therein. Here, we need to review the basic concepts and some results of the Malliavin calculus.

The crucial ingredient is the canonical Hilbert space $\mathcal{H}$ (also called the reproducing kernel Hilbert space) associated with the wfBm $B_{t}^{a,b}$ defined as the closure of the linear space $\mathcal {E}$ generated by the indicator functions $\{\mathbf{1}_{[0,t]}, t\in [0,T]\}$ with respect to the scalar product

$$\begin{aligned} \langle \mathbf{1}_{[0,t]},\mathbf{1}_{[0,s]} \rangle_{\mathcal{H}}=R^{a,b}(t,s). \end{aligned}$$

The mapping $\mathcal{E} \ni\varphi \mapsto B^{a,b}(\varphi)=\int_{0}^{T} \varphi(s)\,dB_{s}^{a,b}$ ($B^{a,b}(\varphi)$ is a Gaussian process on $\mathcal{H}$, and $E[B^{a,b}(\varphi)B^{a,b}(\psi)]=\langle\varphi, \psi\rangle_{\mathcal{H}}$ for all $\varphi, \psi\in\mathcal{H}$) is an isometry from the space $\mathcal{E}$ to the Gaussian space generated by the wfBm $B_{t}^{a,b}$, and it can be extended to the Hilbert space $\mathcal{H}$.

We can find a linear space of functions contained in $\mathcal{H}$ in the following way. Let $\vert {\mathcal{H}}\vert$ be the linear space of measurable functions φ on $[0, T]$ such that

$$\begin{aligned} \Vert \varphi \Vert ^{2}_{\vert \mathcal {H}\vert }:= \int^{T}_{0} \int^{T}_{0} \bigl\vert \varphi(s) \bigr\vert \bigl\vert \varphi(r) \bigr\vert \phi(s,r)\,ds\,dr< \infty \end{aligned}$$

(9)

with $\phi(s,r)=b(s\wedge r)^{a}(s\vee r-s\wedge r)^{b-1}$.

It can be proved that $(\vert {\mathcal{H}}\vert , \langle \cdot, \cdot\rangle_{\vert {\mathcal{H}}\vert })$ is a Banach space (see Shen et al. [18] and Pipiras and Taqqu [24]. Moreover,

$$\begin{aligned} L^{2} \bigl([0,T] \bigr) \subset L^{\frac{2}{1+a+b}} \subset{ \vert \mathcal {H}\vert } \subset\mathcal{H}. \end{aligned}$$

Furthermore, for all $\varphi, \phi\in{ \vert \mathcal{H}\vert }$ (see Shen et al. [18]),

$$\begin{aligned}& E \biggl( \int_{0}^{T} \varphi_{s} \,dB_{s}^{a,b} \int_{0}^{T} \phi_{s} \,dB_{s}^{a,b} \biggr) \\& \quad=b \int_{0}^{T} \int_{0}^{T} \varphi_{u} \phi_{v} (u\wedge v)^{a}(u\vee v-u\wedge v)^{b-1} \,du\,dv. \end{aligned}$$

(10)

For every $n \geq1$, we denote by $\mathcal{H}_{n}$ the nth Wiener chaos of $B_{t}^{a,b}$. Namely, $\mathcal{H}_{n}$ is the closed linear subspace of $L^{2}(\Omega)$ generated by the random variables $\{ H_{n}(B_{t}^{a,b}(f)),f \in\mathcal{H},{\Vert f \Vert _{\mathcal{H}}=1}\}$, where $H_{n}$ is the nth Hermite polynomial. The mapping $I_{n}(h^{\otimes n})=n!H_{n}(B_{t}^{a,b}(f))$ gives a linear isometry between the symmetric tensor product $\mathcal {H}^{\odot n}$ and $\mathcal{H}_{n}$, where the symmetric tensor product $\mathcal{H}^{\odot n}$ is equipped with the modified norm $\Vert \cdot \Vert _{\mathcal{H}^{\odot n}}=\frac{1}{\sqrt {n!}}\Vert \cdot \Vert _{\mathcal{H}^{\otimes n}}$, where $\mathcal{H}^{\otimes n}$ denotes the tensor product, $h^{\otimes n}\in \mathcal{H}^{\otimes n}$. For every $f,g \in\mathcal{H}^{\odot n}$, we have the following formula:

$$\begin{aligned} E \bigl(I_{n}(f) I_{n}(g) \bigr)=n!\langle f,g \rangle_{\mathcal{H}^{\otimes n}}, \end{aligned}$$

where $I_{n}(f)$ is the multiple stochastic integral of a function f. It has the following property:

$$\begin{aligned} \bigl(E \bigl[ \bigl\vert I_{q}(f) \bigr\vert ^{p} \bigr] \bigr)^{\frac{1}{p}}\leq C_{p,q} \bigl(E \bigl[ \bigl\vert I_{q}(f) \bigr\vert ^{2} \bigr] \bigr)^{\frac{1}{2}} \quad \hbox{for any } p \geq2. \end{aligned}$$

Naturally, for any $F\in\oplus_{i=1}^{q}\mathcal{H}_{i}$, we have

$$\begin{aligned} \bigl(E\vert F\vert ^{p} \bigr)^{\frac{1}{p}}\leq C_{p,q} \bigl(E\vert F\vert ^{2} \bigr)^{\frac{1}{2}} \quad \mbox{for any } p \geq2. \end{aligned}$$

(11)

To prove the consistency of the estimators $\hat{\theta}_{n}$ and $\check{\theta}_{n}$, we will use the following lemmas.

Lemma 1

(Kloeden and Neuenkirch [25])

Let $\gamma>0$ and $P_{0}\in\mathbf{N}$. Moreover, let $\{Z_{n}\}_{n\in \mathbf{N}}$ be a sequence of random variables. Suppose that, for every $p\geq p_{0}$, there exists a constant $c_{p} >0$ such that, for all $n\in\mathbf{N}$,

$$\begin{aligned} \bigl(E\vert Z_{n}\vert ^{p} \bigr)^{\frac{1}{p}} \leq c_{p}\cdot n^{-\gamma}. \end{aligned}$$

Then, for all $\varepsilon>0$, there exists a random variable $\eta _{\varepsilon}$ such that, for any $n\in\mathbf{N}$,

$$\begin{aligned} \vert Z_{n}\vert \leq\eta_{\varepsilon}\cdot n^{-r+\varepsilon} \quad \textit{a.s.} \end{aligned}$$

Moreover, $E\vert \eta_{\varepsilon} \vert ^{p}<\infty$ for all ${p\geq1}$.

Lemma 2

Assume that $-1< a<0$, $0< b< a+1$, $a+b>0$, and $\Delta_{n}\rightarrow0$ and $T_{n}\rightarrow\infty$ as $n\rightarrow\infty$. Then, for any $\alpha>0$,

$$\begin{aligned} e^{-2\theta T_{n}}S_{n}=\frac{\Delta_{n}}{e^{2\theta \Delta_{n}}-1} \eta_{t_{n-1}}^{2} +o \bigl(n^{\alpha}\Delta_{n}^{\frac {a+b-1}{2}} e^{-\theta T_{n}} \bigr) \quad \textit{almost surely.} \end{aligned}$$

(12)

Moreover, if $n\Delta_{n}^{1+\beta}\rightarrow\infty$ for some $\beta>0$ as $n\rightarrow\infty$, then

$$\begin{aligned} e^{-2\theta T_{n}}S_{n}=\frac{\Delta_{n}}{e^{2\theta \Delta_{n}}-1} \eta_{t_{n-1}}^{2} +o(1) \quad \textit{almost surely.} \end{aligned}$$

(13)

In particular, as $n\rightarrow\infty$,

$$\begin{aligned} e^{-2\theta T_{n}}S_{n}\rightarrow\frac{\eta_{\infty }^{2}}{2\theta} \quad \textit{almost surely}, \end{aligned}$$

(14)

where $\eta_{\infty}:=\int_{0}^{\infty}{e^{-\theta s}\, d{B_{s}^{a,b}}}$. Small o-notation $o(\bullet)$ is defined as an infinitesimal of higher order of •.

Proof

First, it is easy to get the solution of SDE (2):

$$\begin{aligned} X_{t}=e^{\theta t} \int_{0}^{t}{e^{-\theta s}\,d{B_{s}^{a,b}}}. \end{aligned}$$

(15)

Denote

$$\begin{aligned} \eta_{t}= \int_{0}^{t}{e^{-\theta s}\,d{B_{s}^{a,b}}}, \quad t>0. \end{aligned}$$

Then

$$\begin{aligned} X_{t}=e^{\theta t} \eta_{t}. \end{aligned}$$

(16)

Applying (16), we have

$$\begin{aligned} S_{n} =\Delta_{n} \sum_{i=1}^{n} X_{t_{i-1}}^{2} = \Delta_{n} \sum _{i=1}^{n}e^{2\theta(i-1)\Delta_{n}} \eta_{t_{i-1}}^{2}. \end{aligned}$$

Next, we need to deal with the term $e^{-2\theta T_{n}}S_{n}$:

$$\begin{aligned} e^{-2\theta T_{n}}S_{n}&=\Delta_{n} e^{-2\theta T_{n}}\sum _{i=1}^{n} e^{2\theta(i-1)\Delta_{n}} \eta_{t_{i-1}}^{2} \\ & =\frac{\Delta_{n}}{e^{2\theta\Delta_{n}}-1}\sum_{i=1}^{n} e^{2\theta(i-n)\Delta_{n}}\frac{e^{2\theta\Delta _{n}}-1}{e^{2\theta\Delta_{n}}}\eta_{t_{i-1}}^{2} \\ & =\frac{\Delta_{n}}{e^{2\theta\Delta_{n}}-1}\sum_{i=1}^{n} e^{2\theta(i-n)\Delta_{n}} \bigl(1-e^{-2\theta\Delta_{n}} \bigr)\eta _{t_{i-1}}^{2} \\ & =\frac{\Delta_{n}}{e^{2\theta\Delta_{n}}-1}\sum_{i=1}^{n} \bigl[ e^{2\theta(i-n)\Delta_{n}}-e^{2\theta(i-1-n)\Delta _{n}} \bigr]\eta_{t_{i-1}}^{2} \\ & =\frac{\Delta_{n}}{e^{2\theta\Delta_{n}}-1} \Biggl[\eta _{t_{n-1}}^{2}- \sum _{i=1}^{n-1} \bigl(\eta_{t_{i}}^{2}- \eta _{t_{i-1}}^{2} \bigr)e^{2\theta(i-n)\Delta_{n}} \Biggr]. \end{aligned}$$

Hence,

$$\begin{aligned} e^{-2\theta T_{n}}S_{n}-\frac{\Delta_{n}}{e^{2\theta\Delta _{n}}-1}\eta_{t_{n-1}}^{2} =-\frac{\Delta_{n}}{e^{2\theta\Delta_{n}}-1} \Biggl[\sum_{i=1}^{n-1} \bigl( \eta_{t_{i}}^{2}-\eta_{t_{i-1}}^{2} \bigr)e^{2\theta (i-n)\Delta_{n}} \Biggr]. \end{aligned}$$

Because $e^{2\theta\Delta_{n}}-1=2\theta\Delta_{n}+o(\Delta_{n})$, we have

$$\begin{aligned} e^{-2\theta T_{n}}S_{n}-\frac{\Delta_{n}}{e^{2\theta \Delta_{n}}-1} \eta_{t_{n-1}}^{2}=-\frac{1}{2\theta+\frac{o(\Delta _{n})}{\Delta_{n}}}F_{n}, \end{aligned}$$

(17)

where $F_{n}:=\sum_{i=1}^{n-1}(\eta_{t_{i}}^{2}-\eta _{t_{i-1}}^{2})e^{2\theta(i-n)\Delta_{n}}$. From the equality

$$\begin{aligned} \sqrt{\Delta_{n}}e^{\theta T_{n}}F_{n}=\sqrt{ \Delta_{n}}\sum_{i=1}^{n-1}e^{\theta i\Delta_{n}}e^{\theta(i-n)\Delta_{n}} \bigl(\eta _{t_{i}}^{2}-\eta_{t_{i-1}}^{2} \bigr), \end{aligned}$$

applying the Minkowski inequality, we have

$$\begin{aligned} \bigl(E \bigl\vert \sqrt{\Delta_{n}}e^{\theta T_{n}}F_{n} \bigr\vert ^{2} \bigr)^{\frac{1}{2}}\leq\sqrt{\Delta_{n}} \sum_{i=1}^{n-1}e^{\theta i\Delta_{n}}e^{\theta(i-n)\Delta_{n}} \bigl[E \bigl(\eta _{t_{i}}^{2}-\eta_{t_{i-1}}^{2} \bigr)^{2} \bigr]^{\frac{1}{2}}. \end{aligned}$$

(18)

By the Cauchy-Schwarz inequality we can rewrite (18) as

$$\begin{aligned}& \bigl(E \bigl\vert \sqrt{\Delta_{n}}e^{\theta T_{n}}F_{n} \bigr\vert ^{2} \bigr)^{\frac{1}{2}} \\& \quad \leq2 \sqrt{\Delta_{n}} \bigl(E\eta_{\infty }^{4} \bigr)^{\frac{1}{4}}\sum_{i=1}^{n-1}e^{\theta i\Delta_{n}}e^{\theta (i-n)\Delta_{n}} \bigl[E(\eta_{t_{i}}-\eta_{t_{i-1}})^{4} \bigr]^{\frac{1}{4}} \\& \quad =2\sqrt{3}\sqrt{\Delta_{n}} \bigl(E\eta_{\infty}^{2} \bigr)^{\frac {1}{2}}\sum_{i=1}^{n-1}e^{\theta i\Delta_{n}}e^{\theta(i-n)\Delta _{n}} \bigl[E(\eta_{t_{i}}-\eta_{t_{i-1}})^{2} \bigr]^{\frac{1}{2}} \\& \quad =2\sqrt{3}\sqrt{\Delta_{n}} \biggl[\frac{b}{2^{a}\theta^{1+a+b}}\Gamma (1+a) \Gamma(b) \biggr]^{\frac{1}{2}} \sum_{i=1}^{n-1}e^{\theta i\Delta_{n}}e^{\theta(i-n)\Delta _{n}} \bigl[E(\eta_{t_{i}}-\eta_{t_{i-1}})^{2} \bigr]^{\frac{1}{2}}. \end{aligned}$$

According to (10), we can calculate

$$\begin{aligned}& \bigl[E(\eta_{t_{i}}-\eta_{t_{i-1}})^{2} \bigr] \\& \quad =E \biggl( \int_{t_{i-1}}^{t_{i}}e^{-\theta s}\,dB_{s}^{a,b} \biggr)^{2} \\& \quad = b \int_{t_{i-1}}^{t_{i}} \int_{t_{i-1}}^{t_{i}}e^{-\theta s}e^{-\theta r}(s \wedge r)^{a}(s\vee r-s\wedge r)^{b-1}\,ds\,dr. \end{aligned}$$

Letting $s=(u+i-1)\Delta_{n}$ and $r=(v+i-1)\Delta_{n}$ ($i=1,2,3,\dots ,n$), we have

$$\begin{aligned}& \bigl[E \bigl(e^{\theta i\Delta_{n}}(\eta_{t_{i}}- \eta_{t_{i-1}}) \bigr)^{2} \bigr] \\& \quad=b\Delta_{n}^{a+b+1}e^{2\theta\Delta_{n}} \int_{0}^{1} \int _{0}^{1}e^{-\theta u\Delta_{n}}e^{-\theta v\Delta_{n}} \bigl((u+i-1)\wedge (v+i-1) \bigr)^{a} \\& \quad\quad{}\times \bigl((u\vee v)-(u \wedge v) \bigr)^{b-1}\,du\,dv \\& \quad\leq b\Delta_{n}^{a+b+1}e^{2\theta\Delta_{n}} \int _{0}^{1} \int_{0}^{1} \bigl((u+i-1)\wedge(v+i-1) \bigr)^{a} \\& \quad\quad{}\times \bigl((u\vee v)-(u \wedge v) \bigr)^{b-1}\,du\,dv \\& \quad=2b\Delta_{n}^{a+b+1}e^{2\theta\Delta_{n}} \int_{0}^{1} \int _{v}^{1}(v+i-1)^{a}(u-v)^{b-1} \,du\,dv \\& \quad\leq2b\Delta_{n}^{a+b+1}e^{2\theta\Delta_{n}} \int _{0}^{1} \int_{v}^{1}v^{a}(u-v)^{b-1} \,du\,dv \\& \quad=2\Delta_{n}^{a+b+1}e^{2\theta\Delta_{n}} \int _{0}^{1}v^{a}(1-v)^{b} \,dv \\& \quad=2\Delta_{n}^{a+b+1}e^{2\theta\Delta_{n}}B(a+1,b+1) \\& \quad:=M\Delta_{n}^{a+b+1}e^{2\theta\Delta_{n}}, \end{aligned}$$

(19)

where $M=2B(a+1,b+1)$. Hence,

$$\begin{aligned}& \bigl(E \bigl\vert \sqrt{\Delta_{n}}e^{\theta T_{n}}F_{n} \bigr\vert ^{2} \bigr)^{\frac{1}{2}} \\& \quad\leq2\sqrt{3M} \bigl(E\eta_{\infty}^{2} \bigr)^{\frac{1}{2}}\Delta _{n}^{\frac{a+b}{2}+1}e^{\theta\Delta_{n}} \sum _{i=1}^{n-1}e^{\theta(i-n)\Delta_{n}} \\& \quad=2\sqrt{3M} \bigl(E\eta_{\infty}^{2} \bigr)^{\frac{1}{2}} \Delta _{n}^{\frac{a+b}{2}+1}e^{\theta(1-n)\Delta_{n}} \sum _{i=1}^{n-1}e^{i\theta\Delta_{n}} \\& \quad=2\sqrt{3M} \bigl(E\eta_{\infty}^{2} \bigr)^{\frac{1}{2}} \Delta _{n}^{\frac{a+b}{2}+1}\frac{1-e^{\theta(1-n)\Delta_{n}}}{1-e^{-\theta \Delta_{n}}} \\& \quad\leq2\sqrt{3M} \bigl(E\eta_{\infty}^{2} \bigr)^{\frac{1}{2}}\Delta _{n}^{\frac{a+b}{2}+1}\frac{1}{1-e^{-\theta\Delta_{n}}} \\& \quad\leq2\sqrt{3M} \bigl(E\eta_{\infty}^{2} \bigr)^{\frac{1}{2}}\frac{\Delta _{n}}{1-e^{-\theta\Delta_{n}}}\Delta_{n}^{\frac{a+b}{2}} \\& \quad\leq c(a,b,\theta) \Delta_{n}^{\frac{a+b}{2}}, \end{aligned}$$

(20)

where $c(a,b,\theta)$ is a positive constant depending on a, b, θ, and its value may be different in different cases. Therefore, for any $\alpha> 0$,

$$\begin{aligned} \bigl[E \bigl\vert n^{-\alpha}\Delta_{n}^{\frac{1-(a+b)}{2}} e^{\theta T_{n}}F_{n} \bigr\vert ^{2} \bigr]^{\frac{1}{2}} \leq c(a,b,\theta) n^{-\alpha}. \end{aligned}$$

According to (11) and Lemma 1, there exists a random variable $X_{\alpha}$ such that

$$\begin{aligned} \bigl\vert n^{-\alpha}\Delta_{n}^{\frac{1-(a+b)}{2}} e^{\theta T_{n}}F_{n} \bigr\vert \leq \vert X_{\alpha} \vert n^{-\frac{\alpha}{2}} \quad \mbox{a.s.} \end{aligned}$$

(21)

for all $n \in N$. Moreover, $[E\vert X_{\alpha} \vert ^{p}]< \infty$ for all $p\geq1$. Therefore equality (12) is satisfied.

For the convergence (13), we assume that $n\Delta _{n}^{1+\beta}\rightarrow\infty$ for some $\beta>0$ as $n\rightarrow\infty$. Then

$$\begin{aligned} \bigl(n\Delta_{n}^{1+\beta} \bigr)^{\frac{2\alpha+1-(a+b)}{2\beta }}\rightarrow \infty. \end{aligned}$$

Note that $T_{n}^{\alpha+\frac{2\alpha+1-(a+b)}{2\beta}}e^{-\theta T_{n}}\rightarrow0$ as $n\rightarrow\infty$ and

$$\begin{aligned} n^{\alpha}\Delta_{n}^{\frac{a+b-1}{2}} e^{-\theta T_{n}}= \frac{T_{n}^{\alpha+\frac{2\alpha+1-(a+b)}{2\beta}}e^{-\theta T_{n}}}{(n\Delta_{n}^{1+\beta})^{\frac{2\alpha+1-(a+b)}{2\beta}}}. \end{aligned}$$

Hence, using (12), we get the convergence (13).

For the convergence (14), note that $\frac{\Delta_{n}}{e^{2\theta\Delta_{n}}-1} \rightarrow 2\theta$ as $n \rightarrow\infty$, and using $\eta_{t} \rightarrow \eta_{\infty}: =\int_{0}^{\infty}e^{-\theta s}\,dB_{s}^{a,b}$ as $t\rightarrow\infty$, we can easily obtain it by (13). □

3 Establishment and strong consistency of the estimators

In this section, we construct two estimators $\hat{\theta}_{n}$ and $\check{\theta}_{n}$ and prove the strong consistency.

Using $t_{i}=i \Delta_{n}$ ($i=1,2,\dots,n$) and (16), we have

$$\begin{aligned} X_{t_{i-1}}=e^{\theta t_{i-1}}\eta_{t_{i-1}} \end{aligned}$$

(22)

and

$$\begin{aligned} X_{t_{i}}=e^{\theta t_{i}}\eta_{t_{i}}. \end{aligned}$$

(23)

Applying (22) and (23), we can write the estimator $\hat {\theta}_{n}$ in (7) as

$$\begin{aligned} \hat{\theta}_{n}&=\frac{\sum_{i=1}^{n}e^{\theta t_{i}}\eta_{t_{i}}X_{t_{i-1}}-\sum_{i=1}^{n}X_{t_{i-1}}^{2}}{S_{n}} \\ & =\frac{\sum_{i=1}^{n}e^{\theta t_{i}}(\eta_{t_{i}}-\eta _{t_{i-1}})X_{t_{i-1}}+(\sum_{i=1}^{n}e^{\theta t_{i}}\eta _{t_{i-1}}X_{t_{i-1}}-\sum_{i=1}^{n}X_{t_{i-1}}^{2})}{S_{n}} \\ & =\frac{\sum_{i=1}^{n}e^{\theta t_{i}}(\eta_{t_{i}}-\eta _{t_{i-1}})X_{t_{i-1}}+(e^{\theta\Delta_{n} }-1)\sum_{i=1}^{n}X_{t_{i-1}}^{2}}{S_{n}} \\ & =\frac{G_{n}}{S_{n}}+\frac{e^{\theta\Delta_{n}}-1}{\Delta_{n}}, \end{aligned}$$

(24)

where $G_{n}:=\sum_{i=1}^{n}e^{\theta t_{i}}(\eta_{t_{i}}-\eta _{t_{i-1}})X_{t_{i-1}}$.

Substituting (16) into (8), we can write the other estimator $\check{\theta}_{n}$ of θ as

$$\begin{aligned} \check{\theta}_{n} =\frac{e^{2\theta T_{n}}\eta _{T_{n}}^{2}}{2S_{n}} = \frac{\eta_{T_{n}}^{2}}{2e^{-2\theta T_{n}}S_{n}}. \end{aligned}$$

(25)

Theorem 1

Let $-1< a<0$, $0< b< a+1$, $a+b>0$. Assume that $\theta>0$ and that $\Delta_{n}\rightarrow0$ and $n\Delta _{n}^{1+\beta}\rightarrow\infty$ for some $\beta>0$ as $n\rightarrow\infty$. Then

$$\begin{aligned} \hat{\theta}_{n}\rightarrow\theta \quad \textit{a.s.} \end{aligned}$$

(26)

and

$$\begin{aligned} \check{\theta}_{n}\rightarrow\theta \quad \textit{a.s.} \end{aligned}$$

(27)

Proof

To prove (26), we need to show that $\frac {G_{n}}{S_{n}}\rightarrow0$ a.s. as $n\rightarrow\infty$.

According to (14), it suffices to show that

$$\begin{aligned} e^{-2\theta T_{n}}G_{n}\rightarrow0 \quad \mbox{a.s.}, n \rightarrow\infty. \end{aligned}$$

(28)

By the Minkowski inequality and (20) we have

$$\begin{aligned}& \bigl(E \bigl\vert e^{-2\theta T_{n}}G_{n} \bigr\vert ^{2} \bigr)^{\frac{1}{2}} \\& \quad= e^{-2\theta T_{n}} \Biggl\{ E \Biggl[\sum_{i=1}^{n}e^{\theta t_{ i} }( \eta_{t_{i}}-\eta_{t_{i-1}})X_{t_{i-1}} \Biggr]^{2} \Biggr\} ^{\frac {1}{2}} \\& \quad\leq e^{-2\theta T_{n}}\sum_{i=1}^{n}e^{\theta i \Delta_{n} } \bigl(EX_{t_{i-1}}^{2} \bigr)^{\frac{1}{2}} \bigl[E( \eta_{t_{i}}-\eta _{t_{i-1}})^{2} \bigr]^{\frac{1}{2}} \\& \quad\leq e^{-2\theta T_{n}}\sqrt{M}\Delta_{n}^{\frac {a+b+1}{2}}e^{\theta\Delta_{n} } \sum_{i=1}^{n} \bigl(EX_{t_{i-1}}^{2} \bigr)^{\frac{1}{2}}v \\& \quad\leq\sqrt{M}e^{\theta\Delta_{n} } \bigl(E{\eta_{\infty }^{2}} \bigr)^{\frac{1}{2}}\Delta_{n}^{\frac{a+b+1}{2}}e^{-2\theta T_{n}} \sum _{i=1}^{n}e^{\theta(i-1)\Delta_{n}} \\& \quad=\sqrt{M}e^{\theta\Delta_{n} } \bigl(E{\eta_{\infty}^{2}} \bigr)^{\frac {1}{2}}\Delta_{n}^{\frac{a+b+1}{2}}e^{-2\theta T_{n}} \frac{1-e^{\theta T_{n}}}{1-e^{\theta\Delta_{n}}} \\& \quad\leq\sqrt{M}e^{\theta\Delta_{n} } \bigl(E{\eta_{\infty }^{2}} \bigr)^{\frac{1}{2}}\Delta_{n}^{\frac{a+b+1}{2}}e^{-\theta T_{n}} \frac {1-e^{-\theta T_{n}}}{e^{\theta\Delta_{n}}-1} \\& \quad\leq\sqrt{M}e^{\theta\Delta_{n} } \bigl(E{\eta_{\infty }^{2}} \bigr)^{\frac{1}{2}}\Delta_{n}^{\frac{a+b+1}{2}}e^{-\theta T_{n}} \frac {1}{e^{\theta\Delta_{n}}-1} \\& \quad\leq c(a,b,\theta)\Delta_{n}^{\frac{a+b-1}{2}}e^{-\theta T_{n}}. \end{aligned}$$

(29)

Noting that $\Delta_{n}^{\frac{a+b-1}{2}}e^{-\theta T_{n}}=o(n^{-\alpha})$, $\alpha>0$, as $n \rightarrow\infty$, we have that, for any $\gamma>0$,

$$\begin{aligned} \Delta_{n}^{\frac{a+b-1}{2}}e^{-\theta T_{n}}=n^{-\alpha-\gamma}, \end{aligned}$$

and thus (29) can be written as follows:

$$\begin{aligned} \bigl(E \bigl\vert e^{-2\theta T_{n}}G_{n} \bigr\vert ^{2} \bigr)^{\frac {1}{2}}\leq c(a,b,\theta)n^{-\alpha-\gamma}. \end{aligned}$$

By (11) and Lemma 1 there exists a random variable $X_{\alpha}$ such that

$$\begin{aligned} \bigl\vert e^{-2\theta T_{n}}G_{n} \bigr\vert \leq \vert X_{\alpha} \vert n^{-\alpha} \quad \mbox{a.s.} \end{aligned}$$

for all $n \in N$. Moreover, $[E\vert X_{\alpha} \vert ^{p}]< \infty$ for all $p\geq1$. Hence, the convergence (28) is satisfied. Observe that $\frac{e^{\theta\Delta_{n}}-1}{\Delta_{n}}\rightarrow \theta$ as $n \rightarrow\infty$, and then the convergence (26) is proved.

Now, it remains to show that the convergence (27) is satisfied.

Since $\eta_{t} \rightarrow\eta_{\infty}: =\int_{0}^{\infty }e^{-\theta s}\,dB_{s}^{a,b}$ a.s. as $t\rightarrow\infty$, the convergence (27) is easily proved from (14) and (25). This completes proof. □

4 Rate consistency of the estimators

In this section, we show that $\sqrt{T_{n}}(\hat{\theta}_{n}-\theta)$ and $\sqrt{T_{n}}(\check{\theta}_{n}-\theta)$ are bounded in probability.

Theorem 2

Let $-1< a<0$, $0< b< a+1$, $a+b>0$. Assume that $\Delta_{n}\rightarrow0$, $T_{n}\rightarrow\infty$, and $n\Delta_{n}^{1+\beta }\rightarrow\infty$ for some $\beta>0$ as $n\rightarrow\infty$,

• (1) for any $q\geq0$,

  $$\begin{aligned} \Delta_{n}^{q} e^{\theta T_{n}}(\hat{ \theta}_{n}-\theta) \textit{ is not bounded in probability}. \end{aligned}$$

  (30)

• (2) if $n\Delta_{n}^{3}\rightarrow0$ as $n\rightarrow\infty$, then

  $$\begin{aligned} \sqrt{T_{n}}(\hat{\theta}_{n}-\theta) \textit{ is bounded in probability}. \end{aligned}$$

  (31)

Proof

(1) Firstly, we consider the case of $q=1$.

According to (24), we have

$$\begin{aligned} \Delta_{n} e^{\theta T_{n}}(\hat{\theta}_{n}- \theta )=e^{\theta T_{n}} \bigl(e^{\theta\Delta_{n}}-1-\theta\Delta_{n} \bigr)+\frac {\Delta_{n} e^{-\theta T_{n}}G_{n}}{e^{-2\theta T_{n}}S_{n}}. \end{aligned}$$

(32)

Because $e^{\theta\Delta_{n}}-1-\theta\Delta_{n}\sim\frac{\theta ^{2}}{2}\Delta_{n}^{2}$ as $\Delta_{n}\rightarrow0$, we have

$$\begin{aligned} \lim_{n\rightarrow\infty}e^{\theta T_{n}} \bigl(e^{\theta\Delta _{n}}-1-\theta \Delta_{n} \bigr) =&\lim_{n\rightarrow\infty}\frac{\theta ^{2}}{2} \Delta_{n}^{2}e^{\theta T_{n}} \\ =&\lim_{n\rightarrow\infty}\frac{\theta^{2}}{2} \bigl(n\Delta _{n}^{1+\beta} \bigr)^{\frac{2}{\beta}}\frac{e^{\theta T_{n}}}{T_{n}^{\frac {2}{\beta}}}. \end{aligned}$$

Because $n\Delta_{n}^{1+\beta}\rightarrow\infty$ as $n\rightarrow \infty$ for some $\beta>0$ and $\frac{e^{\theta T_{n}}}{T_{n}^{\frac {2}{\beta}}} \rightarrow\infty$ as $n\rightarrow\infty$, we obtain that, as $n\rightarrow\infty$,

$$\begin{aligned} e^{\theta T_{n}} \bigl(e^{\theta\Delta_{n}}-1-\theta\Delta _{n} \bigr)\rightarrow\infty. \end{aligned}$$

(33)

Applying (29), we have that, as $n\rightarrow\infty$,

$$\begin{aligned} E \bigl\vert \Delta_{n} e^{-\theta T_{n}}G_{n} \bigr\vert \leq c(a,b,\theta)\Delta_{n}^{\frac{{a+b+1}}{2}}\rightarrow0. \end{aligned}$$

(34)

Therefore we get the result (30) when $q=1$ by combining (14), (32), (33), and (34). Next, we consider the case of $q>1$.

According to (32), we have

$$\begin{aligned} \Delta_{n}^{q} e^{\theta T_{n}}(\hat{ \theta}_{n}-\theta )=\Delta_{n}^{q-1}e^{\theta T_{n}} \bigl(e^{\theta\Delta_{n}}-1-\theta \Delta_{n} \bigr)+ \Delta_{n}^{q-1} \frac{\Delta_{n} e^{-\theta T_{n}}G_{n}}{e^{-2\theta T_{n}}S_{n}}. \end{aligned}$$

(35)

Because $e^{\theta\Delta_{n}}-1-\theta\Delta_{n}\sim\frac{\theta ^{2}}{2}\Delta_{n}^{2}$ as $\Delta_{n}\rightarrow0$, we have

$$\begin{aligned} \lim_{n\rightarrow\infty}\Delta_{n}^{q-1}e^{\theta T_{n}} \bigl(e^{\theta \Delta_{n}}-1-\theta\Delta_{n} \bigr) =&\lim _{n\rightarrow\infty}\frac {\theta^{2}}{2}\Delta_{n}^{q+1}e^{\theta T_{n}} \\ =&\lim_{n\rightarrow\infty}\frac{\theta^{2}}{2} \bigl(n\Delta _{n}^{1+\beta} \bigr)^{\frac{1+q}{\beta}}\frac{e^{\theta T_{n}}}{T_{n}^{\frac{1+q}{\beta}}}. \end{aligned}$$

Because $n\Delta_{n}^{1+\beta}\rightarrow\infty$ as $n\rightarrow \infty$ for some $\beta>0$ and $\frac{e^{\theta T_{n}}}{T_{n}^{\frac {1+q}{\beta}}}\rightarrow\infty$ as $n\rightarrow\infty$, we obtain that, as $n\rightarrow\infty$,

$$\begin{aligned} \Delta_{n}^{q-1}e^{\theta T_{n}} \bigl(e^{\theta\Delta _{n}}-1-\theta\Delta_{n} \bigr)\rightarrow\infty. \end{aligned}$$

(36)

Then by using (14), (34), (35), and (36) the result (30) is obtained when $q>1$.

Finally, the case of $0\leq q<1$ is a direct result. Thus the proof of (30) is completed.

(2) According to (32), we have

$$\begin{aligned} \sqrt{T_{n}}(\hat{\theta}_{n}-\theta) =& \sqrt{n\Delta _{n}^{3}}\frac{e^{\theta\Delta_{n}}-1-\theta\Delta_{n}}{\Delta _{n}^{2}}+ \frac{\sqrt{T_{n}}e^{-2\theta T_{n}}G_{n}}{e^{-2\theta T_{n}}S_{n}} \\ =&\sqrt{n\Delta_{n}^{3}}\frac{o(\Delta_{n}^{2})}{\Delta _{n}^{2}}+ \frac{\sqrt{T_{n}}e^{-2\theta T_{n}}G_{n}}{e^{-2\theta T_{n}}S_{n}}, \end{aligned}$$

(37)

where $o(\Delta_{n}^{2})$ is an infinitesimal of higher order than $\Delta_{n}^{2}$ as $n\rightarrow\infty$.

Because $\Delta_{n}\rightarrow0$ and $n\Delta_{n}^{3}\rightarrow 0$ as $n\rightarrow\infty$, we have

$$\begin{aligned} \sqrt{n\Delta_{n}^{3}} \frac{o(\Delta_{n}^{2})}{\Delta _{n}^{2}}\rightarrow0. \end{aligned}$$

(38)

Let us now show that, as $n\rightarrow\infty$,

$$\begin{aligned} \frac{\sqrt{T_{n}}e^{-2\theta T_{n}}G_{n}}{e^{-2\theta T_{n}}S_{n}}\rightarrow0 \quad \mbox{in probability}. \end{aligned}$$

Applying (14), it remains to prove $\sqrt{T_{n}}e^{-2\theta T_{n}}G_{n}\rightarrow0$ as $n\rightarrow\infty$ in probability.

Using (37), we have

$$\begin{aligned} E \bigl\vert e^{-2\theta T_{n}}G_{n} \bigr\vert \leq \bigl(E \bigl\vert e^{-2\theta T_{n}}G_{n} \bigr\vert ^{2} \bigr)^{\frac{1}{2}}\leq c(a,b,\theta )\Delta_{n}^{\frac{a+b-1}{2}}e^{-\theta T_{n}}. \end{aligned}$$

Then

$$\begin{aligned}& E \bigl\vert \sqrt{T_{n}}e^{-2\theta T_{n}}G_{n} \bigr\vert \leq c(a,b,\theta)\Delta_{n}^{\frac{a+b-1}{2}}e^{-\theta T_{n}} \sqrt{T_{n}} \\& \quad=c(a,b,\theta)\frac{T_{n}^{\frac{1}{2}+\frac{1-(a+b)}{2\beta }}e^{-\theta T_{n}}}{(n\Delta_{n}^{1+\beta})^{\frac{1-(a+b)}{2\beta }}} \\& \quad\rightarrow0 \quad \mbox{as } n\rightarrow\infty. \end{aligned}$$

(39)

The last convergence (39) follows from $n\Delta_{n}^{1+\beta }\rightarrow\infty$ as $n\rightarrow\infty$. Applying the Markov inequality, as $n\rightarrow\infty$, we have

$$\begin{aligned} \sqrt{T_{n}}e^{-2\theta T_{n}}G_{n}\rightarrow0 \quad \mbox{in probability}. \end{aligned}$$

Thus, combining (14), (38), and (39), we deduce the conclusion (2). □

Theorem 3

Let $-1< a<0$, $0< b< a+1$, $a+b>0$. Assume that $\Delta_{n}\rightarrow0$, $T_{n}\rightarrow\infty$, and $n\Delta_{n}^{1+\beta}\rightarrow \infty$ for some $\beta>0$ as $n\rightarrow\infty$,

• (1) for any $q\geq0$,

  $$\begin{aligned} \Delta_{n}^{q} e^{\theta T_{n}}(\check{{ \theta }}_{n}-\theta) \textit{ is not bounded in probability}. \end{aligned}$$

  (40)

• (2) If $n\Delta_{n}^{3}\rightarrow0$ as $n\rightarrow\infty$, then

  $$\begin{aligned} \sqrt{T_{n}}(\check{{\theta}}_{n}-\theta) \textit{ is bounded in probability}. \end{aligned}$$

  (41)

Proof

(1) First, we shall prove the case of $q=\frac{1}{2}$. By using (33) we calculate

$$\begin{aligned}& \sqrt{\Delta_{n}}e^{\theta T_{n}}(\check{\theta }_{n}-\theta) \\& \quad=\sqrt{\Delta_{n}}e^{\theta T_{n}} \biggl(\frac{\eta _{T_{n}}^{2}}{2e^{-2\theta T_{n}}S_{n}}- \theta \biggr) \\& \quad=\frac{\sqrt{\Delta_{n}}e^{\theta T_{n}}}{2e^{-2\theta T_{n}}S_{n}} \bigl(\eta_{T_{n}}^{2}-2\theta e^{-2\theta T_{n}}S_{n} \bigr) \\& \quad=\frac{\sqrt{\Delta_{n}}e^{\theta T_{n}}}{2e^{-2\theta T_{n}}S_{n}} \biggl[ \bigl(\eta_{t_{n}}^{2}- \eta_{t_{n-1}}^{2} \bigr)+ \biggl(1-\frac{2\theta \Delta_{n}}{e^{2\theta\Delta_{n}}-1} \biggr) \eta_{t_{n-1}}^{2} \\& \quad\quad{} -2\theta \biggl(e^{-2\theta T_{n}}S_{n}- \frac{\Delta _{n}}{e^{2\theta\Delta_{n}}-1}\eta_{t_{n-1}}^{2} \biggr) \biggr] \\& \quad=\frac{\sqrt{\Delta_{n}}e^{\theta T_{n}}}{2e^{-2\theta T_{n}}S_{n}} \biggl[ \bigl(\eta_{t_{n}}^{2}- \eta_{t_{n-1}}^{2} \bigr)+\frac{2\theta }{2\theta+\frac{o(\Delta_{n})}{\Delta_{n}}}F_{n} \\& \quad\quad{} + \biggl(1-\frac{2\theta\Delta_{n}}{e^{2\theta\Delta _{n}}-1} \biggr)\eta_{t_{n-1}}^{2} \biggr], \end{aligned}$$

(42)

where (42) comes from (17).

Using the Minkowski and Cauchy inequalities, by (20) and (21) we have

$$\begin{aligned}& E \biggl\vert \sqrt{\Delta_{n}}e^{\theta T_{n}} \biggl[ \bigl(\eta _{t_{n}}^{2}-\eta_{t_{n-1}}^{2} \bigr)+ \frac{2\theta}{2\theta+\frac {o(\Delta_{n})}{\Delta_{n}}}F_{n} \biggr] \biggr\vert \\& \quad\leq E \bigl\vert \sqrt{\Delta_{n}}e^{\theta T_{n}} \bigl(\eta _{t_{n}}^{2}-\eta_{t_{n-1}}^{2} \bigr) \bigr\vert +E \biggl\vert \frac{2\theta }{2\theta+\frac{o(\Delta_{n})}{\Delta_{n}}}\sqrt{\Delta _{n}}e^{\theta T_{n}}F_{n} \biggr\vert \\& \quad\leq 2E \bigl(\eta_{\infty}^{2} \bigr)^{\frac{1}{2}} \bigl\{ E \bigl[\sqrt{\Delta _{n}}e^{\theta T_{n}}(\eta_{t_{n}}- \eta_{t_{n-1}}) \bigr]^{2} \bigr\} ^{\frac {1}{2}}+E \biggl\vert \frac{2\theta}{2\theta+\frac{o(\Delta _{n})}{\Delta_{n}}}\sqrt{\Delta_{n}}e^{\theta T_{n}}F_{n} \biggr\vert \\ & \quad\leq c(a,b,\theta)\Delta_{n}^{\frac{a+b+2}{2}}e^{\theta \Delta_{n}}+c(a,b, \theta)\Delta_{n}^{\frac{{a+b}}{2}}. \end{aligned}$$

The last inequality converges to 0 a.s. as $n\rightarrow\infty$.

Thus by the Markov inequality and (14) we that, as $n\rightarrow\infty$,

$$\begin{aligned} \frac{\sqrt{\Delta_{n}}e^{\theta T_{n}}}{2e^{-2\theta T_{n}}S_{n}} \biggl[ \bigl(\eta_{t_{n}}^{2}- \eta_{t_{n-1}}^{2} \bigr)+\frac{2\theta }{2\theta+\frac{o(\Delta_{n})}{\Delta_{n}}}F_{n} \biggr] \rightarrow0 \quad \mbox{in probability}. \end{aligned}$$

(43)

Furthermore,

$$\begin{aligned}& \sqrt{\Delta_{n}}e^{\theta T_{n}} \biggl(1-\frac{2\theta\Delta _{n}}{e^{2\theta\Delta_{n}}-1} \biggr) \\ & \quad=\sqrt{\Delta_{n}}e^{\theta T_{n}}\frac{e^{2\theta\Delta _{n}}-1-2\theta\Delta_{n}}{e^{2\theta\Delta_{n}}-1} \\ & \quad=\Delta_{n}^{\frac{3}{2}}e^{\theta T_{n}}\frac{e^{2\theta \Delta_{n}}-1-2\theta\Delta_{n}}{\Delta_{n}^{2}} \frac{\Delta _{n}}{e^{2\theta\Delta_{n}}-1} \\ & \quad= \bigl(n\Delta_{n}^{1+\beta} \bigr)^{\frac{3}{2\beta}} \frac{e^{\theta T_{n}}}{T_{n}^{\frac{3}{2\beta}}}\frac{e^{2\theta\Delta _{n}}-1-2\theta\Delta_{n}}{\Delta_{n}^{2}}\frac{\Delta _{n}}{e^{2\theta\Delta_{n}}-1}. \end{aligned}$$

Noting that $n\Delta_{n}^{1+\beta}\rightarrow\infty$ as $n\rightarrow\infty$ for some $\beta>0$, $\frac{e^{\theta T_{n}}}{T_{n}^{\frac{3}{2\beta}}}\rightarrow\infty$ as $n\rightarrow \infty$, and $\frac{e^{2\theta\Delta_{n}}-1-2\theta\Delta _{n}}{\Delta_{n}^{2}}\rightarrow2\theta^{2}$ and $\frac{\Delta _{n}}{e^{2\theta\Delta_{n}}-1}\rightarrow\frac{1}{2\theta}$ as $\Delta_{n}\rightarrow0$, we obtain that, as $n\rightarrow\infty$,

$$\begin{aligned} \sqrt{\Delta_{n}}e^{\theta T_{n}} \biggl(1- \frac{2\theta\Delta _{n}}{e^{2\theta\Delta_{n}}-1} \biggr)\rightarrow\infty. \end{aligned}$$

(44)

Then we get (40) when $q=\frac{1}{2}$ by combining (14), (43), and (44).

Similarly, we can prove (40) when $q>\frac{1}{2}$ and $0\leq q<\frac{1}{2}$.

Thus we have the conclusion (1) of Theorem 3.

(2) Now, we calculate

$$\begin{aligned}& \sqrt{T_{n}}(\check{\theta}_{n}-\theta) \\ & \quad=\sqrt{T_{n}} \biggl(\frac{\eta_{T_{n}}^{2}}{2e^{-2\theta T_{n}}S_{n}}-\theta \biggr) \\ & \quad=\frac{\sqrt{T_{n}}}{2e^{-2\theta T_{n}}S_{n}} \bigl(\eta _{T_{n}}^{2}-2\theta e^{-2\theta T_{n}}S_{n} \bigr) \\ & \quad=\frac{\sqrt{T_{n}}}{2e^{-2\theta T_{n}}S_{n}} \biggl[ \bigl(\eta _{t_{n}}^{2}- \eta_{t_{n-1}}^{2} \bigr)+ \biggl(1-\frac{2\theta\Delta _{n}}{e^{2\theta\Delta_{n}}-1} \biggr) \eta_{t_{n-1}}^{2} \\ & \qquad{}-2\theta \biggl(e^{-2\theta T_{n}}S_{n}-\frac{\Delta _{n}}{e^{2\theta\Delta_{n}}-1} \eta_{t_{n-1}}^{2} \biggr) \biggr] \\ & \quad=\frac{\sqrt{T_{n}}}{2e^{-2\theta T_{n}}S_{n}} \biggl[ \bigl(\eta _{t_{n}}^{2}- \eta_{t_{n-1}}^{2} \bigr)+\frac{2\theta}{2\theta+\frac {o(\Delta_{n})}{\Delta_{n}}}F_{n} \\ & \qquad{}+ \biggl(1-\frac{2\theta\Delta_{n}}{e^{2\theta\Delta _{n}}-1} \biggr)\eta_{t_{n-1}}^{2} \biggr], \end{aligned}$$

(45)

where equation (45) comes from (17).

Using the Minkowski and Cauchy inequalities, from (20) and (21) we have

$$\begin{aligned}& E \biggl\vert \sqrt{T_{n}} \biggl[ \bigl(\eta_{t_{n}}^{2}- \eta_{t_{n-1}}^{2} \bigr)+\frac {2\theta}{2\theta+\frac{o(\Delta_{n})}{\Delta_{n}}}F_{n} \biggr] \biggr\vert \\& \quad\leq E \bigl\vert \sqrt{T_{n}} \bigl(\eta_{t_{n}}^{2}- \eta _{t_{n-1}}^{2} \bigr) \bigr\vert +E \biggl\vert \frac{2\theta}{2\theta+\frac {o(\Delta_{n})}{\Delta_{n}}}\sqrt{T_{n}}F_{n} \biggr\vert \\& \quad\leq2E \bigl(\eta_{\infty}^{2} \bigr)^{\frac{1}{2}} \bigl\{ E \bigl[\sqrt {T_{n}}(\eta_{t_{n}}-\eta_{t_{n-1}}) \bigr]^{2} \bigr\} ^{\frac{1}{2}} +E \biggl\vert \frac{2\theta}{2\theta+\frac{o(\Delta_{n})}{\Delta _{n}}} \sqrt{T_{n}}F_{n} \biggr\vert \\& \quad\leq c_{1}(a,b,\theta)\Delta_{n}^{\frac{a+b-1}{2}}e^{\theta \Delta_{n}}e^{-\theta T_{n}} \sqrt{n\Delta_{n}^{3}}+c_{2}(a,b,\theta ) \Delta_{n}^{\frac{a+b-1}{2}}e^{-\theta T_{n}}\sqrt{T_{n}} \\& \quad=c_{1}(a,b,\theta)\frac{T_{n}^{\frac{1}{2}+\frac {1-(a+b)}{2\beta}}e^{-\theta T_{n}}}{(n\Delta_{n}^{1+\beta})^{\frac {1-(a+b)}{2\beta}}}e^{\theta\Delta_{n}} \Delta_{n}+c_{2}(a,b,\theta )\frac{T_{n}^{\frac{1}{2}+\frac{1-(a+b)}{2\beta}}e^{-\theta T_{n}}}{(n\Delta_{n}^{1+\beta})^{\frac{1-(a+b)}{2\beta}}}. \end{aligned}$$

The last term converges to 0 almost surely since $n\Delta _{n}^{1+\beta}\rightarrow\infty$ as $n\rightarrow\infty$. Thus by the Markov inequality and (14) we have that, as $n\rightarrow\infty$,

$$\begin{aligned} \frac{\sqrt{T_{n}}}{2e^{-2\theta T_{n}}S_{n}} \biggl[ \bigl(\eta _{t_{n}}^{2}- \eta_{t_{n-1}}^{2} \bigr)+\frac{2\theta}{2\theta+\frac {o(\Delta_{n})}{\Delta_{n}}}F_{n} \biggr] \rightarrow0 \quad \mbox{in probability}. \end{aligned}$$

(46)

Next, we consider the convergence of $\sqrt{T_{n}}(1-\frac{2\theta \Delta_{n}}{e^{2\theta\Delta_{n}}-1})$:

$$\begin{aligned}& \sqrt{T_{n}} \biggl(1-\frac{2\theta\Delta_{n}}{e^{2\theta\Delta _{n}}-1} \biggr) \\& \quad=\frac{\sqrt{n\Delta_{n}^{3}}}{\Delta_{n}}\frac{e^{2\theta \Delta_{n}}-1-2\theta\Delta_{n}}{e^{2\theta\Delta_{n}}-1} \\& \quad=\sqrt{n\Delta_{n}^{3}}\frac{e^{2\theta\Delta_{n}}-1-2\theta \Delta_{n}}{\Delta_{n}^{2}} \frac{\Delta_{n}}{e^{2\theta\Delta_{n}}-1}. \end{aligned}$$

Because $n\Delta_{n}^{3}\rightarrow0$, $\frac{e^{2\theta\Delta _{n}}-1-2\theta\Delta_{n}}{\Delta_{n}^{2}}\rightarrow2\theta^{2}$, and $\frac{\Delta_{n}}{e^{2\theta\Delta_{n}}-1}\rightarrow\frac {1}{2\theta}$ as $n\rightarrow\infty$, we obtain that, as $n\rightarrow\infty$,

$$\begin{aligned} \sqrt{T_{n}} \biggl(1-\frac{2\theta\Delta_{n}}{e^{2\theta \Delta_{n}}-1} \biggr) \rightarrow0. \end{aligned}$$

(47)

Therefore, combining (14), (46), and (47), we have the conclusion (2) of Theorem 3. □

5 Numerical simulations

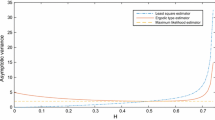
In this section, we study the efficiency of the estimators $\hat{\theta }_{n}$ and $\check{\theta}_{n}$ of θ based on the simulated path of $X_{t}$ for different values of a, b, θ. We simulate 200 sample paths of $X_{t}$ on the time interval $[0,1]$ with the equidistant time $\Delta_{n}=0.0001$. At the end, we get a series of data sets about the two estimators $\hat{\theta}_{n}$ and $\check {\theta}_{n}$ by (5) and (6). The simulation of $\hat {\theta}_{n}$ and $\check{\theta}_{n}$ is given in Table 1.

Table 1 The means, medians, and standard deviations of estimators

According to Table 1, we can easily see that the standard deviations of the estimators $\hat{\theta}_{n}$ and $\check{\theta }_{n}$ are small. Also, we see that the means and medians of the constructed parameter estimators are close to the true parameter values. Therefore, the numerical simulations confirm the theoretical research.