Abstract
We discuss a novel epidemic SIRS model with time delay on a scale-free network in this paper. We give an equation of the basic reproductive number \(R_{0}\) for the model and prove that the disease-free equilibrium is globally attractive and that the disease dies out when \(R_{0}<1\), while the disease is uniformly persistent when \(R_{0}>1\). In addition, by using a suitable Lyapunov function, we establish a set of sufficient conditions on the global attractiveness of the endemic equilibrium of the system.
Similar content being viewed by others
1 Introduction
Following both the seminal work on small-world network phenomena by Watts and Strogatz [1] and the scale-free network, in which the probability of \(p(k)\) for any node with k links to other nodes is distributed according to the power law \(p(k)=Ck^{-\gamma}\) (\(2<\gamma \le3\)), suggested by Barabási and Albert [2], the spreading of an epidemic disease on heterogeneous networks, i.e., scale-free networks, has been studied by many researchers [3–22].
Realistic epidemic models should include some past states of the system, and time delay plays an important role in the spreading process of the epidemic. For instance, it can simulate the incubation period of the infectious disease, the infectious period of patients, and the immunity period of recovery of the disease with time delay [21, 23]. However, only little attention has been given to the epidemic models with time delays on heterogeneous networks. Liu and Xu presented a functional differential equation SEIRS epidemic model, in which time delay represents the latent period and the immune period [19]. Liu and Deng et al. discussed a functional differential equation SIS model, in which time delay represents the average infectious period [20], obtained the basic reproduction number, and discussed the persistence of the disease. Wang and Wang et al. presented a functional differential equation SIR model, in which time delay represents the incubation period, and discussed the global stability of equilibria of the system [21]. Kang and Fu also established a functional differential equation SIS model with an infective vector and analyzed the global stability of the endemic equilibrium, the disease-free equilibrium [22], and so on.
Considering the fact that the immune individual may become the susceptible individual, Chen and Sun discussed an SIRS epidemic model without delay [15]. In [21], Wang and Wang et al. presented a delayed SIR model, in which time delay represents the incubation period during which the infectious agents develop in the vector, and discussed the global stability of equilibria of the system. Motivated by the work of Chen [15] and Wang [21], we will present a novel functional differential equation SIRS model in which time delay represents the incubation period of an infective vector to investigate the epidemic spreading on a heterogeneous network.
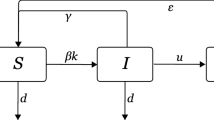
Assuming the size of the network is a constant N during the period of epidemic spreading, we also suppose that the degree of each node is time-invariant and \(p(k)\) denotes the degree distribution of the network. Let \(S_{k}(t)\), \(I_{k}(t)\), and \(R_{k}(t)\) be the relative density of susceptible nodes, infected nodes, and recovered nodes of connectivity k at time t, respectively, where \(k=m, m+1,\ldots, n\), in which m and n are the minimum and maximum degree in network topology, respectively. Since the number of total nodes with degree k is a constant \(p(k)N\) during the period of epidemic spreading, the following normalization conditions hold:
In propagation processes of the epidemic via a vector (such as the mosquito), when a susceptible vector is infected by an infected one, there is a delay τ during which the infectious agents develop in the vector and the infected vector becomes itself infectious after the delay. At the same time, the vector’s usual activities are in a limited range, and the vector population size is large enough such that at any time t a number of the infectious vector population in the vicinity of the infected nodes with degree k (\(k=m, m+1,\ldots, n\)) at any time t is simply proportional to the number of the infected nodes with degree k. The dynamical equations for the density \(S_{k}(t)\), \(I_{k}(t)\), and \(R_{k}(t)\), at the mean-field level, satisfy the following set of functional differential equations when \(t>0\) [20, 21, 24]:
where \(\lambda(k)\) is a transmission coefficient of the disease between the susceptible nodes and infected nodes and r is the recovery rate from the infected nodes to the recovered nodes because the infected nodes (patients) are cured. δ is the removal rate from the susceptible nodes to the recovered nodes because the susceptible nodes acquire temporary immunity. μ is the removal rate from the recovered nodes to the susceptible nodes because the recovered nodes lose temporary immunity. The dynamics of n groups of SIRS subsystems are coupled through the function \(\Theta(t)\), which represents the probability that any given link points to an infected node at time t. Considering the uncorrelated network [3, 11], we have
where \(\langle k\rangle=\sum_{k=m}^{n} p(k)k\) stands for the average node degree. \(\lambda(k)\) is the correlated (k-dependent) infection rate, such as λk, \(\lambda c(k)\) [11], and so on. \(\varphi(k)\) denotes an infected node, with degree k, occupied edges which can transmit the disease, while \(\varphi(k)=ak^{\alpha}/(1+bk^{\alpha})\), \(0\leq \alpha<1\), \(a>0\), \(b\geq0\) [7]. With different parameters, \(\varphi(k)\) can be divided into different cases, such as \(\varphi(k)=k\) [3] when \(\alpha=1\), \(b=0\), and \(a=1\); \(\varphi(k)=A\) [5] when \(a=A\), \(\alpha=0\), and \(b=0\); \(\varphi(k)=k^{\alpha}\) [6] when \(a=1\) and \(b=0\). Specially, if \(b\neq0\), \(\varphi(k)\) will become gradually saturated as degree k increases, i.e., \(\lim_{k\rightarrow\infty}\varphi(k)=b/a\).
The initial conditions of system (1) are the following:
where \(\omega=(\zeta_{m}(\theta), \psi_{m}(\theta), \phi_{m}(\theta),\ldots, \zeta_{n}(\theta), \psi_{n}(\theta), \phi_{n}(\theta))\in C\) are nonnegative continuous on \([-\tau, 0]\) and \(\zeta_{k}(0)>0\), \(\psi_{k}(0)>0\) for \(\theta =0\). C denotes the Banach space \(C([-\tau, 0], R^{3(n-m+1)})\) with the norm
where
It is well known, by the fundamental theory of functional differential equations [25], that system (1) has a unique solution \((S_{m}(t), \ldots, S_{n}(t), I_{m}(t), \ldots, I_{n}(t), R_{m}(t), \ldots, R_{n}(t))\) satisfying the initial conditions (3). It is easy to show that all solutions of system (1) with initial conditions (3) are defined on \([0, +\infty)\) due to the boundedness of \(S_{k}\), \(I_{k}\), and \(R_{k}\). In addition, using similar arguments as in [26], it is easy to show that all solutions of system (1) with initial conditions (3) remain positive for all \(t\geq0\).
The rest of this paper is organized as follows. The dynamical behaviors of the SIRS model are discussed in Section 2. Numerical simulations and discussions are given to demonstrate the main results in Section 3. Finally, the main conclusions of this work are summarized in Section 4.
2 Dynamical behaviors of the model
Note that \(S_{k}(t)+I_{k}(t)+R_{k}(t)=1\). If we discuss the dynamical behaviors of system (1), we only discuss the following equivalent system of model (1):
Denote
where \(\langle f(k)\rangle=\sum_{k} f(k) p(k)\), in which \(f(k)\) is a function.
Note that we obtain from the first equation of system (4) the following equation:
By the standard comparison theorem in the theory of differential equations, we have
Hence we know
is positively invariant with respect to system (4), and every forward orbit in \(R_{+}^{2(n-m+1)}\) eventually enters \(D_{0}\).
Theorem 1
System (4) always has a disease-free equilibrium \(E_{0}( {\frac{\mu}{\mu+\delta }},\ldots, {\frac{\mu}{\mu+\delta}},0,\ldots,0)\). System (4) has a unique endemic equilibrium \(E_{*}(S_{m}^{*}, S_{m+1}^{*},\ldots , S_{n}^{*}, I_{m}^{*},I_{m+1}^{*},\ldots,I_{n}^{*})\) when \(R_{0}>1\).
Proof
Obviously, the disease-free equilibrium \(E_{0}\) of system (4) always exists. Now we discuss the existence of the endemic equilibrium of system (4). Note that the equilibrium \(E_{*}\) should satisfy
where
From (7), we obtain
Substituting this into (8), we obtain the self-consistency equality
similar to the proof of Theorem 1 in [20]. Equation (10) has a unique positive solution when \(R_{0}>1\) and consequently, system (4) has a unique endemic equilibrium \(E_{*}\) since (7) and (9) hold. □
Remark 1
We know that the basic reproductive number for system (1) is \(R_{0}\). If \(\varphi(k)=k\) and \(\tau=0\), system (1) reduces to the SIRS model (1.2) without delay in [15], and \(R_{0}\) in this paper consists/coincides with one of the model in [15].
Theorem 2
If \(R_{0}<1\), the disease-free equilibrium \(E_{0}\) of system (4) is globally attractive.
Proof
Obviously, we need only to discuss the global attractiveness of system (4) in \(D_{0}\).
Consider the following Lyapunov function:
where η is a constant to be determined.
Calculating the derivative of \(V(t)\) along the solution of (4), we get
Note that \(0< S_{k}(t)\leq\mu/(\mu+\delta)\) according to the positive invariance of \(D_{0}\). We have
Let \(\eta= {\frac{1}{2}\frac{\mu}{\mu+\delta}\frac{\langle \lambda(k)\varphi(k)\rangle}{\langle k\rangle}}\). We have
Thus \(\dot{V}(t) \vert _{\text{(4)}}\leq0\) when \(R_{0}< 1\) and \(\dot {V}(t) \vert _{\text{(4)}}=0\) if and only if \(\Theta=0\). Note that the fact that \(\Theta=0\) means that \(I_{k}=0\). Moreover, \(\lim_{t\rightarrow+\infty }S_{k}(t)=\mu/(\mu+\delta)\), the largest invariant set of \(\dot {V}(t) \vert _{\text{(1)}}=0\) is a singleton \(E_{0}\). Therefore, by the LaSalle invariance principle (see [27, Chapter 2, Theorem 5.3]), the disease-free equilibrium \(E_{0}\) is globally attractive. □
Lemma 1
[28]
Consider the following equation:
where \(a_{1},a_{2},\tau>0\); \(x(t)>0\) for \(-\tau\leq t\leq0\). We have
-
(i)
if \(a_{1}< a_{2}\), then \(\lim_{t\rightarrow+\infty}x(t)=0\),
-
(ii)
if \(a_{1}>a_{2}\), then \(\lim_{t\rightarrow+\infty}x(t)=+\infty\).
Theorem 3
For system (4), if \(R_{0}>1\), the disease-free equilibrium \(E_{0}\) is unstable, and the disease is uniformly persistent, i.e., there exists a positive constant ϵ such that \(\lim_{t\rightarrow+\infty}\inf I_{k}(t)\geq\epsilon \), \(k=m,m+1,\ldots,n\).
Proof
Denote
Consequently, we have
where \((\bar{S}, \bar{\psi})=(S_{m},S_{m+1},\ldots, S_{n}, \psi_{m}, \psi _{m+1}, \ldots, \psi_{n})\).
Let \((S_{m}(t), I_{m}(t), \ldots, S_{n}, I_{n}(t))=(S_{m}(t,\omega), I_{m}(t,\omega ),\ldots, S_{n}(t,\omega), I_{n}(t,\omega))\) be the solution of (4) with initial function \(\omega=(\zeta_{m}(\theta), \psi_{m}(\theta), \ldots, \psi _{n}(\theta), \phi_{n}(\theta))\) and
Obviously, X and \(X^{0}\) are positively invariant sets for \(T(t)\). \(T(t)\) is completely continuous for \(t>0\). Also, it follows from \(0< S_{k}(t), I_{k}(t)\leq1\) for \(t>0\) that \(T(t)\) is point-dissipative. \(E_{0}\) is the unique equilibrium of system (4) on \(\partial X^{0}\) and it is globally stable on \(\partial X^{0}\), \(\tilde{A_{\partial}}=\{E_{0}\}\), and \(E_{0}\) is isolated and acyclic. Finally, the proof will be complete if we prove \(W^{s}(E_{0})\cap X^{0}=\emptyset\), where \(W^{s}(E_{0})\) is the stable manifold of \(E_{0}\). Suppose it is not true. Then there exists a solution \((\bar{S},\bar{I})\) in \(X^{0}\) such that
Since \(R_{0}>1\), we may choose \(0<\eta<1\) such that \({\frac {\mu(1-\eta)}{(\lambda(k)\eta+\mu+\delta)r}\frac{\langle\lambda (k)\varphi(k)\rangle}{\langle k\rangle}}>1\). At the same time, there exists a \(T_{2}>0\) such that \(0\leq I_{k}(t)<\eta\) for \(t>T_{2}\) due to \(\lim_{t\rightarrow+\infty}\inf I_{k}(t)=0\).
When \(t>T_{2}\), we obtain from the first equation of system (4)
Hence there exists a \(T_{3}>T_{2}\) such that the following equality holds when \(t>T_{2}\):
For \(t>T_{2}\), we have from (2) and (10)
Note that \({\frac{\mu(1-\eta)}{(\lambda(k)\eta+\mu+\delta )r}} {\frac{\langle\lambda(k)\varphi(k)\rangle}{\langle k\rangle}}>1\). It follows that \({\frac{\mu(1-\eta )}{\lambda(k)\eta+\mu+\delta}} {\frac{\langle\lambda (k)\varphi(k)\rangle}{\langle k\rangle}}>r\). Hence we deduce from (10) that \(\lim_{t\rightarrow+\infty}\Theta(t)=+\infty\) according to Lemma 1, contradicting \(\lim_{t\rightarrow+\infty}\Theta(t)=0\) due to \(\lim_{t\rightarrow+\infty}I_{k}(t)=0\). Hence \(\lim_{t\rightarrow+\infty}\inf \Theta(t)\neq0\). Moreover, there exists a \(k_{0}\in\{m, m+1,\ldots, n\}\) such that \(\lim_{t\rightarrow+\infty}\inf I_{k_{0}}(t)\neq0\), contradicting \(\lim_{t\rightarrow+\infty}\inf I_{k}(t)=0\), \({k=m, m+1,\ldots , n}\).
Hence, the infection is uniformly persistent according to Theorem 2.4 in [27, Chapter 8], i.e., there exists an ϵ, being a positive constant, such that \(\lim_{t\rightarrow+\infty}\inf I_{k}(t)\geq \epsilon\) and \(\lim_{t\rightarrow+\infty}\inf S_{k}(t)\geq\epsilon\). The disease-free equilibrium \(E_{0}\) is unstable accordingly. This completes the proof. □
Furthermore, we obtain the following Theorem 4 about the global attractiveness of the endemic equilibrium \(E_{*}\) of system (4) by constructing a suitable Lyapunov function.
Theorem 4
If \(R_{0}>1\), \(\delta< r\), and \(I_{k}^{*}<\mu /(\mu+\delta)(\delta/r)\), \(k=m,m+1,\ldots, n\), then the endemic equilibrium \(E_{*}\) of system (4) is globally attractive.
Proof
For convenience, we still discuss system (1).
In accordance with (6) and \(S_{k}(t)+I_{k}(t)+R_{k}(t)=1\), \(k=m,m+1,\ldots,n\), we know
is positively invariant with respect to system (4), and every forward orbit in \(R_{+}^{3(n-m+1)}\) eventually enters \(\tilde{D}_{0}\).
Thus we just need to discuss the global attractiveness of system (1) in \(\tilde{D}_{0}\).
Denote \(R_{k}^{*}=1-S_{k}^{*}-I_{k}^{*}\). Then \(E^{*}(S_{m}^{*}, I_{m}^{*}, R_{m}^{*}, S_{m+1}^{*}, I_{m+1}^{*},R_{m+1}^{*},\ldots, S_{n}^{*}, I_{n}^{*},R_{n}^{*},)\) is the endemic equilibrium of system (1). System (1) may be rewritten as the following system:
where \({\beta_{kl}=\frac{\lambda(l)\varphi(l)p(l)}{\langle k\rangle}}\), \(l=m, m+1,\ldots, n\).
Note that the endemic equilibrium of system (1) satisfies
We have from (13) and (14) that
Let us consider
Calculating the derivative of \(V_{k}(t)\) along a solution of (15), we get
Note that
in which \(G(a)=a-1-\ln a \geq0\) and
in which \(H(a)=-a+\ln a\).
Thus we deduce from (14), (17), (18), and (19) that
Furthermore, since \(S_{k}(t)\leq {\frac{\mu}{\mu+\delta}}\), we deduce from the last equation of system (15) that
Since \(I_{k}^{*}<\delta/(\mu+\delta)(\mu/r)\), we take \(\varepsilon=\delta /(\mu+\delta)-I_{k}^{*}r/\mu>0\). It follows from (23) that there exists a \(T_{4}>T_{1}\) such that \(R_{k}(t)\geq\delta/(\mu+\delta)-\varepsilon\) when \(t>T_{4}\). Hence \(-\mu R_{k}+rI_{k}^{*}\leq -\mu(\delta/(\mu+\delta)-\varepsilon )+rI_{k}^{*}=0\) when \(t>T_{4}\), i.e.,
In addition, the matrix
is irreducible, so the following matrix is irreducible:
Hence there exists a positive vector \(C=(c_{m}, c_{m+1},\ldots, c_{n})\) such that \(BC=0\), in which \(c_{k}\) is the cofactor of the kth diagonal entry of B and \(m\leq k\leq n\) [29, Lemma 2.1].
It follows from \(BC=0\) that
Consequently, we have
i.e.,
Define a Lyapunov function as follows:
and we deduce from (20), (22), and (23) that
Moreover, \(\dot{V}(t) \vert _{\text{(17)}}= 0\) if and only if \(S_{k}=S_{k}^{*}\), \(I_{k}=I_{k}^{*}\), and \(R_{k}=R_{k}^{*}\). Therefore, by the LaSalle invariance principle (see [27, Chapter 2, Theorem 5.3]), the endemic equilibrium \(E^{*}\) is globally attractive when \(R_{0}>1\), \(\delta< r\) and \(I_{k}^{*}<\mu/(\mu+\delta)(\delta/r)\), \(k=m,m+1,\ldots, n\). The proof is completed. □
3 Numerical simulations and discussions
The basic reproductive number for system (4) (or (1)) is
The equilibrium \(E_{0}\) is globally attractive and the infection eventually disappears when \(R_{0}<1\). The infection will always exist when \(R_{0}>1\). Note that \(R_{0}\) is irrelative to τ.
Now we present numerical simulations to demonstrate the above mentioned theorems. Note that we obtain the equilibria from system (4). The simulations are based on system (4) and a scale-free network in which the degree distribution is \(p(k)=Ck^{-\gamma}\) and C satisfies \(\sum_{k=m}^{n}p(k)=1\). Assuming the network is finite, the maximum connectivity n of any node is related to the network age, measured as the number of nodes N [5, 8]. We have
Let \(n=100\) and \(m=1\) be suitable assumptions. Let \(\phi(k)=ak^{\alpha}/(1+bk^{\alpha})\) in which \(a=0.5\), \(\alpha=0.75\), \(b=0.02\), and \(\lambda (k)=\lambda k\). The initial functions are \(I_{k}(s)=0.45\), \(k=2,3,4,5\), and \(I_{k}=0\), \(k\neq2,3,4,5\) for \(s\in[0,\tau]\).
Denote
Obviously, \(I(t)\) is the relative average density of the infected nodes.
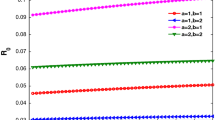
Case 1: Let \(\lambda=0.03\), \(r=0.06\), \(\delta=0.03\), \(\mu=0.06\), \(\gamma=2.5\), and \(\tau=2\). We obtain from (25) that \(R_{0}=0.5064<1\). Figure 1 shows the dynamic behaviors of system (4). The numerical simulation shows that \(\lim_{t\rightarrow+\infty}I(t)=0\). It follows that \(\lim_{t\rightarrow+\infty}I_{k}(t)=0\) and the infection eventually disappears. The numerical result is consistent with Theorem 2.
Dynamical behaviors of system ( 4 ) with \(\pmb{R_{0}=0.5046}\) .
Case 2: Let \(\lambda=0.1\), \(r=0.06\), \(\delta=0.05\), \(\mu=0.06\), \(\gamma=2.5\), \(\tau =2\), and \(\delta< r\). We obtain from (25) that \(R_{0}=1.4596>1\) and \(\max I_{k}^{*}=0.2930<\mu/(\mu+\delta)(\delta/r)=0.4545\). Figure 2 shows the dynamic behaviors of system (4). The average densities \(I_{k}(t)\) and \(I(t)\) converge to a positive constant as \(t\rightarrow+\infty\) and the infection is uniformly persistent. The numerical result is consistent with Theorems 3 and 4.
Dynamical behaviors of system ( 4 ) with \(\pmb{R_{0}=1.4596}\) .
Although the time delay τ has no effects on both the spreading threshold and the density of infected nodes at the stationary state according to (7) and (25), we find that the delay τ has much impact on the density \(I(t)\) of the infected nodes; the slower the relative density of infected nodes converges to the stationary state, the larger τ gets. Thus the delay cannot be ignored. The numerical simulations in Figure 1 and Figure 2 verify it.
Moreover, let \(\lambda=0.1\), \(r=0.06\), \(\delta=0.03\), \(\mu=0.06\), \(\gamma=2.5\), \(\tau=2\), and \(\delta< r\). We obtain from (25) that \(R_{0}=1.7806>1\) but \(I_{k}^{*}\geq\mu/(\mu+\delta)(\delta/r)=0.3333\), \(40\leq k\leq100\). Figure 3 shows the dynamic behaviors of system (4). The parameters of system (4) do not satisfy Theorem 4, but the relative density \(I_{k}(t)\) and the relative average density \(I(t)\) still converge to a positive constant as \(t\rightarrow+\infty\). At the same time, no Hopf bifurcation occurs, so Theorem 4 has room for improvement.
Dynamical behaviors of system ( 4 ) with \(\pmb{\tau=2}\) and \(\pmb{R_{0}=1.5793}\) .
4 Conclusions
An SIRS model with time delay on a scale-free network has been proposed, in which time delay describes the incubation period of the infective vector. We obtained the basic reproduction number \(R_{0}\), which is irrelative to τ. The disease-free equilibrium is globally attractive and infection may disappear when \(R_{0}<1\), while the infection is uniformly persistent when \(R_{0}>1\). Moreover, the endemic equilibrium is globally attractive if \(R_{0}>1\), \(\delta< r\), and \(I_{k}^{*}<\mu/(\mu+\delta)(\delta/r)\), \(k=m,m+1,\ldots, n\). However, numerical simulations (Figure 3) show that the endemic equilibrium is still globally attractive even if \(\delta< r\) and \(I_{k}^{*}<\mu/(\mu+\delta )(\delta/r)\), \(k=m,m+1,\ldots, n\) do not hold when \(R_{0}>1\). Therefore, improvement of the sufficient condition in Theorem 4 on the global attractiveness of the endemic equilibrium of system (4) is an interesting but challenging problem.
References
Watts, DJ, Strogatz, SH: Collective dynamics of small world networks. Nature 393, 440-442 (1998)
Barabási, AL, Alber, R: Emergence of scaling in random networks. Science 286, 509-512 (1999)
Pastor-Satorras, R, Vespignani, A: Epidemic dynamics in finite size scale-free networks. Phys. Rev. E 65, Article ID 035108 (2002)
Balthrop, J, Forrest, S, Newman, M, Williamson, M: Technological networks and the spread of computer viruses. Science 304, 527-529 (2004)
Yang, R, Wang, B, Ren, J, Bai, W, Shi, Z, Wang, W, Zhou, T: Epidemic spreading on heterogeneous networks with identical infectivity. Phys. Lett. A 364, 189-193 (2007)
Cheng, X, Liu, X, Chen, Z, Yuan, Z: Spreading behavior of SIS model with non-uniform transmission on scale-free networks. J. China Univ. Post Telecommun. 16, 27-31 (2009)
Zhang, H, Fu, X: Spreading of epidemics on scale-free networks with nonlinear infectivity. Nonlinear Anal. 70, 3273-3278 (2009)
Li, K, Small, M, Zhang, H, Fu, X: Epidemic outbreaks on networks with effective contacts. Nonlinear Anal., Real World Appl. 11, 1017-1025 (2010)
Fu, X, Michael, S, David, M, Zhang, H: Epidemic dynamics on scale-free networks with piecewise linear infectivity and immunization. Phys. Rev. E 77, Article ID 036113 (2008)
Zhang, J, Jin, Z: The analysis of an epidemic model on networks. Appl. Math. Comput. 217, 7053-7064 (2011)
Zhu, G, Fu, X, Chen, G: Global attractivity of a network-based epidemics SIS model with nonlinear infectivity. Commun. Nonlinear Sci. Numer. Simul. 17, 2588-2594 (2013)
Gong, Y, Song, Y, Jiang, G: Epidemic spreading in scale-free networks including the effect of individual vigilance. Chin. Phys. B 21, Article ID 010205 (2012)
Li, T, Wang, Y, Guan, Z: Spreading dynamics of a SIQRS epidemic model on scale-free networks. Commun. Nonlinear Sci. Numer. Simul. 19, 686-692 (2014)
Liu, J, Zhang, T: Epidemic spreading of an SEIRS model in scale-free networks. Commun. Nonlinear Sci. Numer. Simul. 16, 3375-3384 (2011)
Chen, L, Sun, J: Global stability and optimal control of an SIRS epidemic model on heterogeneous networks. Physica A 10, 196-204 (2014)
Yu, R, Li, K, Chen, B, Shi, D: Dynamical analysis of an SIRS network model with direct immunization and infective vector. Adv. Differ. Equ. 2015, Article ID 116 (2015)
Xu, X, Chen, G: The SIS model with time delay on complex networks. Int. J. Bifurc. Chaos 19, 623-628 (2009)
Xia, C, Wang, Z, Sanz, J, Meloni, S, Moreno, Y: Effects of delayed recovery and nonuniform transmission on the spreading of diseases in complex networks. Physica A 392, 1577-1585 (2013)
Liu, X, Xu, D: Analysis of SEτIRωS epidemic disease models with vertical transmission in complex networks. Acta Math. Appl. Sin. Engl. Ser. 28, 63-74 (2012)
Liu, Q, Deng, C, Sun, M: The analysis of an epidemic model with time delay on scale-free networks. Physica A 410, 79-87 (2014)
Wang, J, Wang, J, Liu, M, Li, Y: Global stability analysis of an SIR epidemic model with demographics and time delay on networks. Physica A 410, 268-275 (2014)
Kang, H, Fu, X: Epidemic spreading and global stability of an SIS model with an infective vector on complex networks. Commun. Nonlinear Sci. Numer. Simul. 27, 30-39 (2015)
Ma, Z, Li, J: Dynamical Modelling and Analysis of Epidemics. World Scientific, Singapore (2009)
Cooke, K: Stability analysis for a vector disease model. Rocky Mt. J. Math. 9, 31-42 (1979)
Hale, J: Theory of Functional Differential Equations. Springer, New York (1977)
Busenberg, S, Cooke, K: The effect of integral conditions in certain equations modeling epidemics and population growth. J. Math. Biol. 10, 13-32 (1980)
Kuang, Y: Delay Differential Equations with Applications in Population Dynamics. Academic Press, Boston (1993)
Smith, HL: Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems. Mathematical Surveys and Monographs, vol. 41. Am. Math. Soc., Providence (1995)
Guo, H, Li, M, Shuai, Z: Global stability of endemic equilibrium of multigroup SIR epidemic models. Can. Appl. Math. Q. 14, 259-284 (2006)
Acknowledgements
The authors are very grateful to the anonymous referees for their valuable suggestions, which greatly led to significant improvement of the original manuscript. This research was supported by the Hebei Provincial Natural Science Foundation of China under Grant No. A2016506002 and the Innovation Foundation of Shijiazhuang Mechanical Engineering College under Grant No. YSCX1201.
Author information
Authors and Affiliations
Contributions
All authors contributed to the expression of the model and the discussion of results. They read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, Q., Sun, M. & Li, T. Analysis of an SIRS epidemic model with time delay on heterogeneous network. Adv Differ Equ 2017, 309 (2017). https://doi.org/10.1186/s13662-017-1367-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1367-z