Abstract
In this paper, a predator-prey model with Holling type-I functional response and multi state impulsive feedback control is established, where the intensity of pesticide spraying and the release amount of natural enemies are linearly dependent on the given threshold in the second impulse. Firstly, the existence of order-1 periodic solution of the system is investigated by successor functions and Bendixson theorem of impulsive differential equations, then the stability of periodic solutions is proved by the analogue of the Poincaré criterion. Furthermore, in order to reduce the actual total cost and obtain the best economic benefit, the optimal economic threshold is obtained, which provides the optimal strategy for the practical application. Finally, numerical simulations for specific examples are carried out to illustrate the feasibility of the above conclusions.
Similar content being viewed by others
1 Introduction
Differential equation is the most basic mathematical theory and method to study the movement, evolution and change of things, objects and phenomena in natural sciences and social sciences. Many principles and laws in the fields of biology, chemistry, physics, aerospace, medicine, economics and finance can all be described by appropriate differential equations [1–12]. In [4], Meng et al. analyzed the dynamic behavior of a stochastic biological system; in [1], Bai et al. investigated the dynamic behavior of the boundary value problem fractional nonlinear system, and in the research articles [2, 3], Wang et al. paid attention to the control problems of nonlinear systems. Moreover, in the fields of natural sciences and engineering technology partial differential equations have been extensively used (see, for examples, [13–15]).
In recent decades, scholars have paid more and more attention to the impulsive differential equations which have played an important role in the field of life sciences [16, 17]. In addition, by modeling impulsive differential equations, external effects of various possible changes in the population can be included in the proposed model. The impulse of the classical impulsive differential equation can be divided into two types: fixed time impulse and state impulse. In particular, the former type has been developed and widely used in various fields [18–23]. Ballinger and Liu [18] proposed a population dynamics model with fixed time impulse and discussed the persistence of the model. Liu et al. [20] established a predator-prey model considering Holling type-I functional response with time impulse, and the authors completely established the stability properties of the relevant equilibria of the model. A pest management control model with continuous time impulse was presented and the global asymptotic stability properties of its positive equilibrium were studied by Zhang et al. [21].
In recent years, it can be seen that many scholars are interested in application in mathematical biology; many practical problems, such as injecting insulin, vaccination and spraying pesticides, need to be treated including state feedback control strategy [24–27]. The state feedback control is a threshold strategy which is used in impulsive semi-dynamic systems. The impulse starts to be effective when the abundance of a particular species reaches a certain threshold. The threshold strategy is widely used in the fields of ecology, life science and medicine. Therefore, it is crucial to describe and study impulsive differential equations; for instance, authors in the research articles [28–34] have formulated mathematical models in pest management to study the dynamic behavior. It is well known that in order to prevent the destruction by pests on some crops, it is required to spray pesticides in a timely manner; as a result, it could quickly destroy the important proportion of pest population also. In order to minimize the damage of using pesticides on the crops, cultivators adopt the biological control method to control or eradicate the pest from the crops. In this case, cultivators release natural enemies, the integrated impulse control to be implemented when a given threshold is reached. Integrated pest management is the most effective way to minimize the use of pesticides and to eliminate pests under the premise of ensuring food safety and maintaining ecological balance. In [31], Cheng et al. established a pest control model with Holling type-I functional response and studied its existence and attractiveness of order-1 periodic solution. In [32], Tang et al. presented a semi-dynamic predator-prey model with Holling type-II functional response and studied the global stability of boundary order-1 limit cycle. In [34], Zhang et al. considered a pest management model with nonlinear state impulsive control and Holling type-II functional response and focused their attention on geometric analysis. For further information, the readers are directed to read the references [35–37].
It is worthy to note that most scholars study the single state feedback control on impulsive differential equation, that is, they consider only the case when the density of population reaches a given threshold. We can take preventive measures, but this method is not consistent with the facts. To avoid the economic and practical issues, it is required to adopt different controlling methods under different thresholds. It can be considered under three cases. Firstly, when the density of pest population \(x(t)\) reaches the slightly harmful threshold \(h_{1}\), releasing the natural enemy population \(y(t)\) may help avoid the damage. Secondly, when the density of pest population \(x(t)\) is at the economic threshold \(h_{2}\) (\(0< h_{1}< h_{2}\)), only releasing the natural enemy cannot reduce the damage. Therefore, certain pesticide has to be sprayed and the natural enemy released at the same time. Finally, if control measures are taken at the economic injury threshold \(h_{3}\) (\(h_{3}>h_{2}\)), high intensity pesticide will kill a large number of natural enemies, pollute the environment and cause serious economic losses. It can be seen that the pest controlling method of multi state pulse has important research value in practical application [38, 39].
The claim that the impulsive differential equations have been well developed can be accepted; however, more improvements are needed to cope with the real world applications. For instance, we should not only consider the stability properties of the system under a given time or threshold in the real life, but also consider how to minimize the loss caused on crops by the pests. Therefore, the optimization problem incorporating both the effects of biological control and chemical control has an important theoretical value as well as practical significance. However, it can be seen from the literature that the optimization problem has not been extensively studied. Tang et al. [40] established an integrated pest management model and obtained the optimal pulse time. In [41], Liu et al. studied a stochastic model with delays and the optimal harvesting effort, and the authors obtained an expression for the maximum expected value of sustainable yield. Sun et al. [42, 43] investigated dynamics analysis and obtained the optimal pest control level of a pest management predator-prey system. However, in the above articles, although authors have obtained excellent results, they have considered the optimization problems neglecting multi state impulsive effect on the predator-prey system.
Based on the above works and the analysis, the state-dependent impulsive predator-prey system with Holling type-I functional response can be written as
where the density of the pest population and the natural enemy population are expressed by \(x(t)\) and \(y(t)\), respectively. The intrinsic growth rate of pest, the predation coefficient and the death rate of natural enemy are denoted by a, b and c, respectively. \(0< r<1\) means the conversion coefficient, q is the release amount of natural enemy at time \(t_{h_{1}}\), while δ is the release amount of natural enemy at time \(t_{h_{2}}\). \(a,b,r,c,d,q,h_{1},h_{2}\) are all positive constants, \(y^{*}=\frac{a}{b}\), \(\alpha,\beta\) represent the proportion of pests and natural enemies which are killed by pesticides, respectively. In this paper, \(\alpha(x),\beta(x)\) and \(\delta(x)\) are continuous functions defined on [\(h_{1},h_{3}\)], which satisfies \(\delta (h_{1})=\delta_{\max}\) and \(\delta(h_{3})=\delta_{\min}\), \(\alpha (h_{1})=0\) and \(\alpha(h_{3})=\alpha_{\max}\), \(\beta(h_{1})=0\) and \(\beta (h_{3})=\beta_{\max}\). \(\alpha(x), \beta(x)\) and \(\delta(x)\) are expressed as follows using the same notation as in [42], i.e.,
The main organization of the paper is as follows. Some important concepts and lemmas are presented in Section 2. In Section 3, the existence of order-1 periodic solution of system (1) is discussed by the successor function method and Bendixson theorem of impulsive differential equations. In Section 4, sufficient conditions for the stability of periodic solutions of system (1) obtained by analogue of the Poincaré criterion are presented. In Section 5, it is shown that the conclusions are verified by numerical simulation, and the optimization problem is considered in order to minimize the total cost of pest control. Finally, a summary is made.
2 Preliminaries
At first, we consider the free system of system (1)
Define the following function:
It is easy to know that \(\Lambda(x,y)\) is positive definite in the first quadrant and it satisfies all conditions of the Lyapunov function.
The derivative of \(\Lambda(x,y)\) is
We can obtain that \(\Lambda'(x,y)\equiv0\) if \(x\leq x_{0}\), then all solutions of system (3) constitute a set \(\{(x,y)|\Lambda (x,y)\leq\Lambda(x_{0},y^{*})\}\), which is a closed orbit \(\Lambda (x,y)=\Sigma\), where \(0<\Sigma<\Lambda(x_{0},y^{*})\).
If \(x>x_{0}\), we have \(\Lambda'(x,y)>0\), then the orbit of system (3) always passes through the closed curve \(\Lambda(x,y)=\Sigma\) at \(x>x_{0}\) and out of the curve \(\Lambda(x,y)=\Lambda(x_{0},y^{*})\).
Thus, we observe the line
where h is a threshold of system (1). The derivative of \(l(x,y)\) is as follows:
Then we get that \(l'\vert_{l=0}<0\) on condition of \(m>\frac {(ax+bx_{0}+c-rbx_{0})h}{bx_{0}+c-rbx_{0}}\). Therefore, the following lemma is obtained.
Lemma 2.1
-
(i)
System (3) has two stable states: saddle point \(O(0,0)\) and stable center \(E(\frac{c}{rb},\frac{a}{b})\) when \(x \leq x_{0}\) and satisfies \(x_{0}\geq\frac{c}{rb}\).
-
(ii)
The orbits of system (3) go across the line \(l=0\) from the right to the left, which satisfies \(x_{0}< x \leq h \) and \(m>\frac {(ax+bx_{0}+c-rbx_{0})h}{bx_{0}+c-rbx_{0}}\), and intersect the line \(x=x_{0}\).
Some basic definitions and lemmas are given as follows.
Definition 2.1
[44]
Consider the general model with state-dependent impulse
where \(M(x,y)\) is called an impulsive set, and let N be the corresponding phase set. \(M(x,y)\) and \(N(x,y)\) represent the curve line or straight line on the plane. There exists a continuous impulse mapping \(I: I(M)=N\). We define a dynamic system constituted by the definition of solution of state impulsive differential equation (5) as semi-continuous dynamic systems, which is denoted as \((\Omega,f,I,M)\).
Definition 2.2
[30]
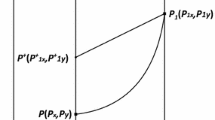
Assume that the pulse set M and the phase set N are both straight lines, as shown in Figure 1. For any point \(B\in N\), then \(\Pi(B,t)=C\in M\), \(I(C)=B^{+}\in N\), we denote the ordinates of points B and \(B^{+}\) by \(y_{B}\) and \(y_{B^{+}}\), respectively. Then \(B^{+}\) is defined as the successor point of B, and \(f(B)=y_{B^{+}}-y_{B}\) is the successor function of point B.
Definition 2.3
[30]
An orbit \(\widetilde{\Pi }(Q_{0},T)\) is called order-1 periodic solution with period T if there exists a point \(Q_{0}\in N\) and \(T>0\) such that \(Q=\Pi (Q_{0},T)\in M\) and \(Q^{+}=I(Q)=Q_{0}\).
Definition 2.4
[39]
For system (5), the orbit starting from the point A reaches the point \(A_{1}\) on \(L_{M}\), and then jumps onto the point \(A_{1}^{+}\) on \(L_{N}\), that is, the orbit moves from A to \(A_{1}\), and then to \(A_{1}^{+}\). Similarly, the orbit moves from B to \(B_{1}\), and then to \(B_{1}^{+}\). Thus the region k encircled by the closed curve \(\widehat{ABB_{1}A_{1}}\) is an invariant set of system (5). k is called the Bendixson region of system (5).
Lemma 2.2
[45]
The successor function defined in Definition 2.4 is continuous.
Lemma 2.3
[44]
In system (5), if there exist \(A\in N,B\in N\) satisfying the successor function \(f(A)f(B)<0\), then there must exist a point \(Q (Q\in N)\) satisfying Q between the point A and the point B such that \(f(Q)=0\), then system (5) has an order-1 periodic solution.
Lemma 2.4
[39] Bendixson theorem of impulsive differential equations
Assume that k is a Bendixson region of system (5), if k does not contain any critical points of system (5), then system (5) has an order-1 periodic solution in k.
Lemma 2.5
[16] Analogue of the Poincaré criterion
The T-periodic solution \(x=\xi(t),y=\eta(t)\) of the system
is orbitally asymptotically stable if the multiplier \(\mu_{2}\) satisfies the condition \(|\mu_{2}|<1\), where
and \(P,Q,\frac{\partial U}{\partial x},\frac{\partial U}{\partial y},\frac{\partial V}{\partial x},\frac{\partial V}{\partial y},\frac {\partial\varphi}{\partial x},\frac{\partial\varphi}{\partial y}\) are calculated at the point \((\xi(T_{i}),\eta(T_{i}))\) and \(P_{+}=P(\xi (T_{i}^{+}), \eta(T_{i}^{+})), Q_{+}=Q(\xi(T_{i}^{+}),\eta(T_{i}^{+}))\).
In this paper, we assume that the condition \(c\leq rbx_{0}\) holds. Based on the biological significance of system (1), we only consider \(D=\{(x,y)|x\geq0,y\geq0\}\).
3 Existence of order-1 periodic solution
In this section, the existence of order-1 periodic solution of system (1) is investigated by using the differential equation geometry theory and Bendixson theorem of impulsive differential equations. Here we denote
where the lines \(M_{1}\) and \(M_{2}\) are the first impulsive set and the second impulsive set of system (1), respectively, the lines \(N_{1}\) and \(N_{2}\) are the phase set corresponding to the impulsive set \(M_{1}\) and the impulsive set \(M_{2}\), respectively.
Isoclinic lines of system (1) are denoted as follows:
For convenience, the coordinate of any point C is defined as (\(x_{c}\),\(y_{c}\)). If the point \(Q(h,y_{Q})\in M\), pulse occurs at the point Q, the impulsive function transfers the point Q into \(Q^{+}\in N\).
By Lemma 2.1, the orbit with any initiating point of \(D=\{ (x,y)|x\geq0,y\geq0\}\) will intersect the set \(N_{1}\) or \(N_{2}\) with time increasing; therefore, we consider the following cases.
3.1 The orbit starting from the point of \(N_{1}\)
In this case, we have \(x\leq x_{0}\), \(0< h_{1}<\frac{c}{rb}<x_{0}\). For convenience, we denote the intersection of \(L_{1}\) and \(L_{2}\) by \(E(\frac{c}{rb},\frac{a}{b})\), and the point \(F_{1}(h_{1},\frac{a}{b})\) is the intersection of \(L_{1}\) and \(N_{1}\). The orbit \(\Gamma_{1}\) of system (1) passes through the point \(B(h_{1},\frac {a}{b}+\varepsilon)\in N_{1}\) above \(F_{1}\), where \(\varepsilon>0\), and intersects with the pulse set \(M_{1}\) at \(B_{1}(h_{1},y_{B_{1}})\). Then the orbit jumps back to \(N_{1}\) at \(B_{1}^{+}(h_{1},y_{B_{1}}+q)\) from \(M_{1}\) due to the pulse action.
By regulating q, the position of \(B_{2}^{+}\) has the following three subcases.
Case I \(y_{B}< y_{B_{1}}+q\).
In this case, the point \(B_{1}^{+}\) is above B, thus the successor function of B is \(f(B)=y_{B_{1}}+q -(\frac{a}{b}+\varepsilon)>0\). On the other hand, the orbit \(\Gamma_{2}\) passing through the point \(B_{1}^{+}\) intersects with \(M_{1}\) at \(B_{2}(h_{1},y_{B_{2}})\) because any two orbits are disjoint, then we have \(y_{B_{2}}< y_{B_{1}}<\frac {a}{b}\). The point \(B_{2}\) is mapped to \(B_{2}^{+}(h_{1},y_{B_{2}}+q)\) after impulsive effect. The point \(B_{2}^{+}\) is located above \(F_{1}\) and under \(B_{1}^{+}\), thus the successor function of \(B_{1}^{+}\) is \(f(B_{1}^{+})=y_{B_{2}}+q -(y_{B_{1}}+q)<0\). Therefore, \(f(B)f(B_{1}^{+})<0\).
From the above discussion, it is easy to know that the region \(G_{1}\) encircled by the closed curve \(\widehat{B_{1}^{+}B_{2}B_{1}B}\) is a positive invariant set of system (1) and it contains no equilibrium point. By Lemma 2.4, there exists an order-1 periodic solution of system (1) (see Figure 2(a)).
The orbit starting from the phase set \(\pmb{N_{1}}\) (cases in Section 3.1 ). (a) Case I. (b) Case II. (c) Case III.
Case II \(y_{B}=y_{B_{1}}+q\).
In this case, the successor point \(B_{1}^{+}\) is exactly B, then \(f(B)=y_{B_{1}}+q -(\frac{a}{b}+\varepsilon)=0\), thus the curve \(\widehat{BB_{1}B_{1}^{+}}\) forms a periodic solution of system (1) (see Figure 2(b)).
Case III \(y_{B}>y_{B_{1}}+q\).
In this case, the point \(B_{1}^{+}\) is below the point B, thus the successor function of B is \(f(B)=y_{B_{1}}+q -(\frac{a}{b}+\varepsilon )<0\). On the other hand, the orbit \(\Gamma_{2}\) passing through the point \(B_{1}^{+}\) intersects with \(M_{1}\) at \(B_{2}(h_{1},y_{B_{2}})\) because any two orbits are disjoint, then we have \(y_{B_{1}}< y_{B_{2}}<\frac{a}{b}\). The point \(B_{2}\) is mapped to \(B_{2}^{+}(h_{1},y_{B_{2}}+q)\) after impulsive effect. The point \(B_{1}^{+}\) is located above \(F_{1}\) and under \(B_{2}^{+}\), then the successor function of \(B_{1}^{+}\) is \(f(B_{1}^{+})=y_{B_{2}}+q -(y_{B_{1}}+q)>0\). Therefore, \(f(B)f(B_{1}^{+})<0\). Thus there exists an order-1 periodic solution of system (1) by Lemma 2.4 (see Figure 2(c)).
Based on the above analysis, we get the following theorem.
Theorem 3.1
If \(x\leq x_{0}\) and \(0< h_{1}<\frac{c}{rb}<x_{0}\), there exists an order-1 periodic solution of system (1).
3.2 The orbit starting from the point of \(N_{2}\)
In this subsection, we assume the line \(L_{1}\) intersects with \(L_{2}\), \(N_{2}\) and \(M_{2}\) at points \(E(\frac{c}{rb},\frac{a}{b})\), \(B((1-\alpha)h_{2},\frac{a}{b})\) and \(F_{2}(h_{2},\frac{a}{b})\), respectively. By Lemma 2.3 and qualitative analysis, there exists a unique closed orbit Γ of system (1) which contains the point E and tangents to \(M_{2}\) at the point \(F_{2}\). There is an orbit \(\Gamma_{1}\) that tangents to \(N_{2}\) at the point B and intersects \(M_{2}\) at the point \(B_{1}(h_{2},y_{B_{1}})\). The orbit \(\Gamma_{1}\) jumps back to \(B_{1}^{+}((1-\alpha)h_{2},(1-\beta )y_{B_{1}}+\delta)\in N_{2}\) after impulsive effect. By regulating δ, if \((1-\alpha)h_{2}\leq h_{1}\), the case can be discussed like the case in Section 3.1. And if \((1-\alpha)h_{2}> h_{1}\), two cases should be discussed.
Case I The orbit Γ and the phase set \(N_{2}\) are disjoint and \(x\leq x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<\frac{c}{rb}<h_{2}\leq x_{0}\). For this case, we have three subcases to be discussed.
Case I(a) \(y_{B_{1}}+q< y_{B}\).
If the point \(B_{1}^{+}\) is below the point B, we have \(f(B)=y_{B_{1}^{+}}-y_{B}<0\). Then we choose another orbit \(\Gamma_{2}\) which is very close to the x axis and intersects with \(N_{2}\) at one point denoted by \(C((1-\alpha)h_{2},y_{C})\), then intersects with \(M_{2}\) at the point \(B_{2}(h_{2},y_{B_{2}})\). The orbit \(\Gamma_{2}\) jumps back to \(B_{2}^{+}((1-\alpha)h_{2},(1-\beta)y_{B_{2}}+\delta)\in N_{2}\) after a pulse action, and it is above C, then the successor function of point C is \(f(C)=y_{B_{2}^{+}}-y_{C}>0\). Therefore, \(f(B)f(C)<0\). According to Lemma 2.3, there must be Q which meets \(y_{C}< Q< y_{B}\) in the phase set \(N_{1}\) to make \(f(Q)=y_{Q^{+}}-y_{Q}=0\), then there is an order-1 periodic solution of system (1) (see Figure 3(a)).
The orbit starting from the phase set \(\pmb{N_{2}}\) (cases in Section 3.2 ). (a) Case I(a). (b) Case I(b). (c) Case I(c). (d) Case II(a). (e) Case II(b). (f) Case II(c). (g) Case III(a). (h) Case III(b). (i) Case III(c). (j) Case IV(a). (k) Case IV(b). (l) Case IV(c).
Case I(b) \(y_{B_{1}}+q=y_{B}\).
In this subcase, the successor point \(B_{1}^{+}\) is exactly B, then \(f(B)=y_{B_{1}^{+}}-y_{B}=0\), thus the curve \(\widehat {BB_{1}B_{1}^{+}}\) forms a periodic solution of system (1) (see Figure 3(b)).
Case I(c) \(y_{B_{1}}+q>y_{B}\).
If the point \(B_{1}^{+}\) lies above the point B, there is \(f(B)=y_{B_{1}^{+}}-y_{B}>0\). We select the orbit \(\Gamma_{2}\) which tangents to \(F_{1}\) and intersects with \(N_{2}\) and \(M_{2}\) at \(C((1-\alpha)h_{2},y_{C})\) and \(B_{2}(h_{2},y_{B_{2}})\). The point \(B_{2}\) is influenced by pulse to \(B_{2}^{+}(h_{1},y_{B_{2}}+q)\in N_{2}\). By the existence and uniqueness of impulsive differential equations, we have \(y_{B_{2}}< y_{B_{1}}\). Then we get \(f(C)=y_{B_{2}^{+}}-(y_{C}) <0\). Thus, \(f(B)f(B_{1}^{+})<0\). According to Lemma 2.3, there must be Q which meets \(y_{B}< Q< y_{C}\) in the phase set \(N_{1}\) to make \(f(Q)=y_{Q^{+}}-y_{Q}=0\), then there is an order-1 periodic solution of system (1) (see Figure 3(c)).
Case II The orbit Γ crosses the phase set \(N_{2}\) and \(x\leq x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<\frac{c}{rb}<h_{2}\leq x_{0}\).
In this case, we assume Γ intersects \(N_{2}\) at \(P_{1}((1-\alpha )h_{2},y_{P_{1}})\) and \(P_{2}((1-\alpha)h_{2},y_{P_{2}})\), where \(y_{P_{1}}>y_{P_{2}}\), and tangents to \(M_{2}\) at the point \(F_{2}\), then jumps back to \(N_{2}\) at one point denoted by \(F_{2}^{+}\). According to the position of the point \(F_{2}^{+}\), the following subcases are given.
Case II(a) \(y_{F_{2}^{+}}< y_{{P_{2}}}\) or \(y_{F_{2}^{+}}>y_{P_{1}}\).
In this subcase, the point \(F_{2}^{+}\) is below \(P_{2}\) or above \(P_{1}\). By following similar analysis as that in Case I(a) or Case I(c), we can prove there exists an order-1 periodic solution of system (1) (see Figure 3(d)).
Case II(b) \(y_{F_{2}^{+}}=y_{P_{1}}\) or \(y_{F_{2}^{+}}=y_{{P_{2}}}\).
In this subcase, the point \(F_{2}^{+}\) coincides with \(P_{1}\) or \(P_{2}\), then we get \(f(P_{1})=y_{F_{2}^{+}}-y_{P_{1}}=0\) or \(f(P_{2})=y_{F_{2}^{+}}-y_{P_{2}}=0\), thus an order-1 periodic solution of system (1) is existent (see Figure 3(e)).
Case II(c) \(y_{P_{2}}< y_{F_{2}^{+}}< y_{P_{1}}\).
If the point \(F_{2}^{+}\) is between \(P_{1}\) and \(P_{2}\), because any two trajectories are disjoint, then the orbit \(\Gamma_{1}\) crosses the phase set \(N_{2}\) at \(F_{2}^{+}\) and does not intersect with the impulse set \(M_{2}\), thus there is no order-1 periodic solution. According to the biological background, there are not a lot of pests in the farmland, crop damage is very small, therefore, it does not need pulse (see Figure 3(f)).
On the other hand, the line \(L_{1}\) intersects with \(L_{2}\) and \(N_{2}\) at points \(E(\frac{c}{rb},\frac{a}{b})\) and \(B((1-\alpha )h_{2},\frac{a}{b})\), respectively, the line \(L_{3}\) intersects with \(M_{2}\) at \(F_{2}(h_{2},\frac{ah_{2}}{bx_{0}})\). According to Lemma 2.3 and qualitative analysis, there exists a unique closed orbit Γ of system (1) which contains the point E and tangents to \(M_{2}\) at the point \(F_{2}\). There is an orbit \(\Gamma _{1}\) that tangents to \(N_{2}\) at the point B and intersects \(M_{2}\) at the point \(B_{1}(h_{2},y_{B_{1}})\). The orbit \(\Gamma_{1}\) jumps back to \(B_{1}^{+}((1-\alpha)h_{2},(1-\beta)y_{B_{1}}+\delta)\in N_{2}\) after impulsive effect. By regulating δ, if \((1-\alpha)h_{2}\leq h_{1}\), the case can be discussed like the case in Section 3.1. And if \((1-\alpha)h_{2}> h_{1}\), we have two subcases to be discussed as follows.
Case III The orbit Γ and the phase set \(N_{2}\) are disjoint and \(x> x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<\frac{c}{rb}\leq x_{0}<h_{2}\).
The method of proof is similar to Case I, here we omit it (see Figures 3(g), 3(h) and 3(i)).
Case IV The orbit Γ crosses the phase set \(N_{2}\) and \(x> x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<\frac{c}{rb}\leq x_{0}<h_{2}\).
The method of proof is similar to that in Case II, here we omit it (see Figures 3(j), 3(k) and 3(l)).
Moreover, if \(x< x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<h_{2}<\frac{c}{rb}\leq x_{0}\), the proof process is similar to that in Case I, there is no longer detailed description and graphic analysis.
From the above analysis, we get the following theorems.
Theorem 3.2
-
(1)
If the orbit Γ and the phase set \(N_{2}\) are disjoint and \(x\leq x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<\frac{c}{rb}<h_{2}\leq x_{0}\), there exists an order-1 periodic solution of system (1).
-
(2)
If the orbit Γ crosses the phase set \(N_{2}\) and \(x\leq x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<\frac{c}{rb}<h_{2}\leq x_{0}\), there are the following two conditions:
Theorem 3.3
-
(1)
If the orbit Γ and the phase set \(N_{2}\) are disjoint and \(x>x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<\frac{c}{rb}\leq x_{0}<h_{2}\), there exists an order-1 periodic solution of system (1).
-
(2)
If the orbit Γ crosses the phase set \(N_{2}\) and \(x>x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<\frac{c}{rb}\leq x_{0}<h_{2}\), there are the following two conditions:
Theorem 3.4
If \(x< x_{0}\), \(0< h_{1}<(1-\alpha)h_{2}<h_{2}<\frac{c}{rb}\leq x_{0}\), there exists an order-1 periodic solution in system (1).
4 Stability of order-1 periodic solution
In this section, under the existence condition of periodic solution of system (1), we discuss its stability by Lemma 2.5.
4.1 The orbit starting from the phase set \(N_{1}\)
Let \(x=\xi(t),y=\eta(t)\) be a T-periodic solution of system (1) and \(\xi_{1}=\xi(T),\eta_{1}=\eta(T);\xi_{0}=\xi(0),\eta_{0}=\eta (0);\xi_{1}^{+}=\xi(T^{+}),\eta_{1}^{+}=\eta(T^{+})\), then we have
Let \(P(x,y)=x(t)(a-by(t)),Q(x,y)=y(t)(-c+rbx(t)),U(x,y)=0,V(x,y)=q ,\varphi(x,y)=x-h_{1}\). Then
and
Therefore,
Thus we get the following theorem.
Theorem 4.1
If \(c< rbx_{0}\) and \(\frac{a+bq-\sqrt{a^{2}+b^{2}q^{2}}}{2b}\leq\eta _{0}\leq\frac{a+bq+\sqrt{a^{2}+b^{2}q^{2}}}{2b}\) hold, then the order-1 periodic solution of system (1) is stable.
4.2 The orbit starting from the phase set \(N_{2}\)
Let \(x=u(t),y=v(t)\) be a T-periodic solution of system (1) and \(u_{1}=u(T)=h_{2},v_{1}=v(T);u_{0}=u(0),v_{0}=v(0);u_{1}^{+}=u(T^{+}),v_{1}^{+}=v(T^{+})\), then we have
Let \(P(x,y)=x(t)(a-by(t)),Q(x,y)=y(t)(-c+rbx(t)),U(x,y)=-\alpha x,V(x,y)=-\beta y+\delta,\varphi(x,y)=x-h_{2}\).
Then
and
Thus
The following theorem is obtained.
Theorem 4.2
If \(c< rbx_{0}\) and \(\frac{\omega-\sqrt{\omega^{2}-4ab\delta}(1-\beta )(2-\beta)}{2b(2-\beta)}< v_{0}<\frac{\omega+\sqrt{\omega^{2}-4ab\delta }(1-\beta) (2-\beta)}{2b(2-\beta)}\) hold, where \(\omega=2a(1-\beta)+b\delta(2-\beta )\), then the order-1 periodic solution of system (1) is stable.
5 Numerical simulations and optimization
5.1 Numerical simulations
In this section, specific examples are given to verify the feasibility of the conclusions. Let \(a=0.8\), \(b=c=r=0.6\), \(x_{0}=1.9\), \(h_{3}=7.2\), \(\alpha_{\max}=0.9\), \(\beta_{\max}=0.75\), \(\delta_{\max}=0.78\), \(\delta _{\min}=0.03\), then the equilibrium point of free system is \(E(1.67,1)\). Inserting these parameter values into system (1), we get
Example 1
Let \(q=1.5\), \(h_{1}=0.6\) and the initial value be \((1.5,0.6)\). Figures 4(a), 4(b) and 4(c) show that system (6) has an order-1 periodic solution which is stable.
Numerical simulation of Example 1 . (a) Phase portrait of \(x(t)\) and \(y(t)\) on \(h_{1}=0.6\). (b) Time series of \(x(t)\). (c) Time series of \(y(t)\).
Example 2
Let \(h_{2}=1.88\) and the initial value be \((0.6,1.15)\). By a direct calculation, we have \(\alpha=0.175\), \(\beta =0.145\) and \(\delta=0.635\). Figures 5(a), 5(b) and 5(c) show that system (6) has a stable order-1 periodic solution. By observing carefully from Figure 5(b), we can estimate that the period of order-1 periodic solution is \(T=5.19\).
Numerical simulation of Example 2 . (a) Phase portrait of \(x(t)\) and \(y(t)\) on \(h_{2}=1.88\). (b) Time series of \(x(t)\). (c) Time series of \(y(t)\).
Example 3
When \(h_{2}=5\), let the initial value be \((2,0.6)\), then \(\alpha=0.6\), \(\beta=0.5\) and \(\delta=0.28\). Figures 6(a), 6(b) and 6(c) show that system (6) has an order-1 periodic solution with period \(T=1.73\) which is stable.
Numerical simulation of Example 3 . (a) Phase portrait of \(x(t)\) and \(y(t)\) on \(h_{2}=5\). (b) Time series of \(x(t)\). (c) Time series of \(y(t)\).
Example 4
Let \(h_{2}=1\) and the initial value \((1.2,0.5)\) be given. By a direct computation, we have \(\alpha=0.055\), \(\beta=0.045\) and \(\delta=0.735\). The phase diagram and time series diagram of \(x(t)\) and \(y(t)\) are shown in Figure 7. Figures 7(a), 7(b) and 7(c) show that system (6) has a stable order-1 periodic solution. By observing carefully from Figure 7(b), we can estimate that the period of order-1 periodic solution is \(T=1.965\).
Numerical simulation of Example 4 . (a) Phase portrait of \(x(t)\) and \(y(t)\) on \(h_{2}=1\). (b) Time series of \(x(t)\). (c) Time series of \(y(t)\).
5.2 Determination and optimization of economic threshold \(h_{2}\)
The integrated control method of spraying pesticides and releasing natural enemies not only speeds up the death rate of pests, but also avoids the excessive damage to the crops; at the same time, the ecological balance is ensured. In order to ensure the best use of the material, the shortest time and the highest efficiency, the following optimal problem is investigated to find the best economic threshold.
Assume that \(d_{1}\) is the unit cost of the use of pesticides and the damage to crops, \(d_{2}\) is the unit cost of releases of natural enemy. Our objective is to maximize the control of pests and reduce unit costs in the process of integrated pest control. Let F be the total cost in a period of system (6) under the control of economic threshold \(h_{2}\), which is a function of intensity of pesticide spraying \(\alpha (h_{2})\), and the released amount of natural enemies are given by \(\delta(h_{2})\). Then we have \(F(h_{2})=d_{1}\alpha(h_{2})+d_{2}\delta (h_{2})\), and the optimization model is established as follows:
The objective function is solved to find out the best economic threshold \(h_{2}^{*}\), so as to obtain the optimal pesticide control intensity \(\delta^{*}=\delta(h_{2}^{*})\), to find an optimal release amount of natural enemies \(\alpha^{*}=\alpha(h_{2}^{*})\), and to find an optimal control period of pest \(T^{*}=T(h_{2}^{*})\). Figure 8 illustrates the variation of period T and the cost per unit time \(F/T\) with the economic threshold \(h_{2}\), where \(d_{1}=d_{2}=1{,}000\), i.e., \(d_{1}/d_{2}=1\). From Figures 8(a) and 8(b), we can see that the optimal economic threshold is \(h_{2}^{*}=1.88\), the optimal pesticide control intensity is \(\alpha^{*}=0.175\), the optimal release amount of natural enemy is \(\delta^{*}=0.635\), and the optimal control period of the pest is \(T^{*}=5.19\).
6 Conclusion
In this paper, according to the different degrees of damage on crops, feedback control with two state dependent impulses is adopted on the pest management. When the density of pests reaches the slightly harmful threshold \(h_{1}\), only the biological control method is adopted; when the density of pests reaches the economic threshold \(h_{2}\), the method of combining biological and chemical control is used, which can make the density of pests less than a given threshold and maintain the ecological balance. Analysis shows that this method is effective. Finally, numerical simulations are carried out to verify effectiveness of the control strategy. In addition, an optimization problem is proposed and solved, the optimal economic threshold is determined under the condition that the total cost is minimum. However, there are some deviations in the results, which need to be improved.
References
Bai, Z, Zhang, S, Sun, S, Yin, C: Monotone iterative method for fractional differential equations. Electron. J. Differ. Equ. 2016(6), 1 (2016)
Wang, F, Liu, Z, Zhang, Y, Chen, CLP: Adaptive fuzzy control for a class of stochastic pure-feedback nonlinear systems with unknown hysteresis. IEEE Trans. Fuzzy Syst. 24(1), 140-152 (2016)
Wang, F, Liu, Z, Zhang, Y, Chen, CLP: Adaptive quantized controller design via backstepping and stochastic small-gain approach. IEEE Trans. Fuzzy Syst. 24(2), 330-343 (2016)
Meng, X, Zhao, S, Feng, T, Zhang, T: Dynamics of a novel nonlinear stochastic SIS epidemic model with double epidemic hypothesis. J. Math. Anal. Appl. 433(1), 227-242 (2016)
Guo, S, Ma, W: Global behavior of delay differential equations model of HIV infection with apoptosis. Discrete Contin. Dyn. Syst., Ser. B 21(1), 103-119 (2016)
Zhang, T, Meng, X, Zhang, T: Global analysis for a delayed SIV model with direct and environmental transmissions. J. Appl. Anal. Comput. 6(2), 479-491 (2016)
Wang, W, Ma, W, Lai, X: Repulsion effect on superinfecting virions by infected cells for virus infection dynamic model with absorption effect and chemotaxis. Nonlinear Anal., Real World Appl. 33, 253-283 (2017)
Wang, W, Ma, W, Lai, X: A diffusive virus infection dynamic model with nonlinear functional response, absorption effect and chemotaxis. Commun. Nonlinear Sci. Numer. Simul. 42, 585-606 (2017)
Jiang, Z, Ma, W: Permanence of a delayed SIR epidemic model with general nonlinear incidence rate. Math. Methods Appl. Sci. 38(3), 505-516 (2014)
Braverman, E, Chatzarakis, GE, Stavroulakis, IP: Iterative oscillation tests for differential equations with several non-monotone arguments. Adv. Differ. Equ. 2016(1), 87 (2016)
Miao, A, Zhang, J, Zhang, T, Pradeep, BGSA: Threshold dynamics of a stochastic SIR model with vertical transmission and vaccination. Comput. Math. Methods Med. 2017, 1-10 (2017)
Zhang, T, Zhang, T, Meng, X: Stability analysis of a chemostat model with maintenance energy. Appl. Math. Lett. 68, 1-7 (2017)
Xu, X: A deformed reduced semi-discrete Kaup-Newell equation, the related integrable family and Darboux transformation. Appl. Math. Comput. 251, 275-283 (2015)
Zhang, Y, Dong, H, Zhang, X, Yang, H: Rational solutions and lump solutions to the generalized-dimensional Shallow Water-like equation. Comput. Math. Appl. 73(2), 246-252 (2017)
Wang, W, Ma, W: A diffusive HIV infection model with nonlocal delayed transmission. Appl. Math. Lett. 75, 96-101 (2018)
Bainov, D, Simeonov, P: Impulsive Differential Equations: Periodic Solutions and Applications. Chapman & Hall/CRC, Boca Raton (1993)
Nieto, JJ, O’Regan, D: Variational approach to impulsive differential equations. Nonlinear Anal., Real World Appl. 10(2), 680-690 (2009)
Ballinger, G, Liu, X: Permanence of population growth models with impulsive effects. Math. Comput. Model. 26(12), 59-72 (1997)
Zhao, W, Li, J, Meng, X: Dynamical analysis of SIR epidemic model with nonlinear pulse vaccination and lifelong immunity. Discrete Dyn. Nat. Soc. 2015, Article ID 848623 (2015)
Liu, B, Zhang, Y, Chen, L: Dynamic complexities of a Holling I predator-prey model concerning periodic biological and chemical control. Chaos Solitons Fractals 22(1), 123-134 (2004)
Zhang, H, Jiao, J, Chen, L: Pest management through continuous and impulsive control strategies. Biosystems 90(2), 350-361 (2007)
Meng, X, Zhang, L: Evolutionary dynamics in a Lotka-Volterra competition model with impulsive periodic disturbance. Math. Methods Appl. Sci. 39(2), 177-188 (2016)
Zhang, T, Ma, W, Meng, X: Global dynamics of a delayed chemostat model with harvest by impulsive flocculant input. Adv. Differ. Equ. 2017, 115 (2017)
Pang, G, Chen, L: Periodic solution of the system with impulsive state feedback control. Nonlinear Dyn. 78(1), 743-753 (2014)
Li, Z, Wang, T, Chen, L: Periodic solution of a chemostat model with Beddington-DeAnglis uptake function and impulsive state feedback control. J. Theor. Biol. 261(1), 23-32 (2009)
Zhao, Z, Wang, T, Chen, L: Dynamic analysis of a turbidostat model with the feedback control. Commun. Nonlinear Sci. Numer. Simul. 15(4), 1028-1035 (2010)
Yang, J, Tang, G, Tang, S: Modelling the regulatory system of a chemostat model with a threshold window. Math. Comput. Simul. 132, 220-235 (2017)
Jiang, G, Lu, Q: Impulsive state feedback control of a predator-prey model. J. Comput. Appl. Math. 200(1), 193-207 (2007)
Tang, S, Xiao, Y, Chen, L, Cheke, RA: Integrated pest management models and their dynamical behaviour. Bull. Math. Biol. 67(1), 115-135 (2005)
Liu, B, Tian, Y, Kang, B: Existence and attractiveness of order one periodic solution of a Holling II predator-prey model with state-dependent impulsive control. Int. J. Biomath. 5(3) (2012)
Cheng, H, Zhang, T, Wang, F: Existence and attractiveness of order one periodic solution of a Holling I predator-prey model. Abstr. Appl. Anal. 2012, Article ID 126018 (2012)
Tang, S, Tang, B, Wang, A, Xiao, Y: Holling II predator-prey impulsive semi-dynamic model with complex Poincar map. J. Differ. Equ. 81(3), 1575-1596 (2015)
Zhang, T, Ma, W, Meng, X, Zhang, T: Periodic solution of a prey-predator model with nonlinear state feedback control. Appl. Math. Comput. 266, 95-107 (2015)
Zhang, T, Zhang, J, Meng, X, Zhang, T: Geometric analysis of a pest management model with Holling’s type III functional response and nonlinear state feedback control. Nonlinear Dyn. 84(3), 1529-1539 (2016)
Tian, Y, Zhang, T, Sun, K: Dynamics analysis of a pest management prey-predator model by means of interval state monitoring and control. Nonlinear Anal. Hybrid Syst. 23, 122-141 (2017)
Zhang, H, Georgescu, P, Zhang, L: Periodic patterns and Pareto efficiency of state dependent impulsive controls regulating interactions between wild and transgenic mosquito populations. Commun. Nonlinear Sci. Numer. Simul. 31(1-3), 83-107 (2016)
Tian, Y, Sun, K, Chen, L: Modelling and qualitative analysis of a predator-prey system with state-dependent impulsive effects. Math. Comput. Simul. 82(2), 318-331 (2011)
Cheng, H, Wang, F, Zhang, T: Multi-state dependent impulsive control for pest management. J. Appl. Math. 2012, Article ID 381503 (2012)
Zhao, L, Chen, L, Zhang, Q: The geometrical analysis of a predator-prey model with two state impulses. Math. Biosci. 238(2), 55-64 (2012)
Tang, S, Tang, G, Cheke, RA: Optimum timing for integrated pest management: modelling rates of pesticide application and natural enemy releases. J. Theor. Biol. 264(2), 623-638 (2010)
Liu, L, Meng, X: Optimal harvesting control and dynamics of two-species stochastic model with delays. Adv. Differ. Equ. 2017(1), 18 (2017)
Sun, K, Zhang, T, Tian, Y: Theoretical study and control optimization of an integrated pest management predator-prey model with power growth rate. Math. Biosci. 279, 13-26 (2016)
Sun, K, Zhang, T, Tian, Y: Dynamics analysis and control optimization of a pest management predator-prey model with an integrated control strategy. Appl. Math. Comput. 292, 253-271 (2017)
Chen, L: Pest control and geometric theory of semi-continuous dynamical system. J. Beihua Univ. Nat. Sci. 12(1), 1-12 (2011)
Liu, Q, Huang, L, Chen, L: A pest management model with state feedback control. Adv. Differ. Equ. 2016(1), 292 (2016)
Acknowledgements
The paper was supported by the National Natural Science Foundation of China (No. 11371230), Shandong Provincial Natural Science Foundation, China (No. ZR2015AQ001), SDUST Research Fund (2014TDJH102), and Joint Innovative Center for Safe and Effective Mining Technology and Equipment of Coal Resources, Shandong Province of China.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors read and approved the final manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, J., Cheng, H., Meng, X. et al. Geometrical analysis and control optimization of a predator-prey model with multi state-dependent impulse. Adv Differ Equ 2017, 252 (2017). https://doi.org/10.1186/s13662-017-1300-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1300-5