Abstract
The multilevel augmentation method with the anti-derivatives of the Daubechies wavelets is presented for solving nonlinear two-point boundary value problems. The anti-derivatives of the Daubechies wavelets are applied as the multilevel bases for the subspaces of approximate solutions. This process results in a full nonlinear system that can be solved by the multilevel augmentation method for reducing computational cost. The convergence rate of the present method is shown. It is the order of \(2^{s}\), \(0\leq s\leq p\) when p is the order of the Daubechies wavelets. Various examples of the Dirichlet boundary conditions are shown to confirm the theoretical results.
Similar content being viewed by others
1 Introduction
Many problems in science and engineering can be modeled by nonlinear differential equations. Due to their complexities of both differential equation forms and boundary condition types, analytical solutions are available for only simple problems. Efficient and accurate numerical solutions are then usually required in general. One of the most effective numerical methods relies on variational formulations; see [1, 2], and [3].
The multilevel basis method can be applied with the variational formulation to obtain the approximate solutions of nonlinear problem. This formulation results in the discretization of nonlinear systems with unknown coefficients in the approximate subspace of each basis level. A nonlinear solver such as the Newton iterative method can be used to find approximate solutions for each level required. In order to obtain more accurate results, the number of applied basis levels must be increased, resulting in large nonlinear systems. The computational time increases exponentially with only a small increase in the basis levels. In order to reduce the computational time, we apply the advantage of multilevel bases by connecting the information among basis levels. This approach, the augmentation method, was first introduced by [1, 2, 4]. The fully nonlinear system is divided into two smaller systems and then solved separately.
In multi-scale decompositions, multi-scale piecewise polynomials can be applied in variational formulation (see [1, 4]). These basis types are easily presented and implemented as a numerical algorithm. They can be used for specific types of boundary conditions, and in this case they can represent Dirichlet conditions with zero boundary values while the modified approximation technique can be applied for non-zero Dirichlet conditions. To extend to a more general class of multilevel basis for solving various types of boundary conditions, the anti-derivatives of Daubechies wavelets introduced by Xu and Shann [5] can be applied to solve many kinds of boundary conditions: Dirichlet and Neumann types. Reference [6] has presented the case of the linear boundary value problem and shown that the Daubechies wavelets can be applied in conjunction with the augmentation method to save computational time for Dirichlet boundary value problem.
This study extends the multi-scale decomposition to a nonlinear boundary value problem. We apply the anti-derivatives of the Daubechies wavelets to solving nonlinear boundary value problems. The discretization of the nonlinear differential problem is represented by a nonlinear system that can be solved iteratively by the Newton method. To save computational time, the augmentation method presented by Chen, Chen, Wu and Xu (see e.g. [2, 4, 7, 8]) will be applied to solving the nonlinear system under the Daubechies wavelets. Combining these two concepts, as presented here, results in a new numerical method. The rate of convergence is also proved. It is of the order \(2^{s}\), \(0\leq s\leq p\) when p is the order of the Daubechies wavelets applied.
Given the interval \((a,b)\), we use the notation \(L^{2}(a,b)\) to denote the space of square integrable functions on \((a,b)\) with standard inner product \((\cdot, \cdot)\) defined by
and associated norm \(\Vert \cdot \Vert \).
Let \(H^{s}(a,b)\) denote the standard Sobolev space with the norm \(\Vert \cdot \Vert _{s}\) given by
and the seminorm \(|\cdot|_{s}\) given by
For Dirichlet boundary conditions, we work on the solution space
equipped with the inner product
and associated norm \(|\cdot|_{1}\). It is well known that the norm \(|\cdot|_{1}\) is equivalent to the standard norm \(\Vert \cdot \Vert _{1}\) in this space.
We consider the following nonlinear differential equation:
where \(\beta(x) \in L^{\infty}(a,b)\) and \(\varphi(x,u) \in C ([a,b] \times\mathbb{R} )\), with Dirichlet boundary conditions:
To solve numerically the nonlinear problem, the formulation can be summarized as follows.
-
1.
Formulate the variational form of the considering problem. We determine approximate solution, if the variational form has a unique solution. Because it is not our main consideration in this work, we assume that the nonlinear boundary value problem and its variational form have the same isolated solution \(u^{*} \in H_{0}^{1}(a,b)\).
-
2.
Choose a sequence \(\{S_{n}\}\) of nested finite-dimensional subspaces of the solution space \(H_{0}^{1}(a,b)\) such that \(\overline {\bigcup_{n\in\mathbb{N}} S_{n}} = H_{0}^{1}(a,b)\). At this step, such finite-dimensional subspaces have anti-derivatives of Daubechies wavelets as their orthonormal bases.
-
3.
Apply the multilevel augmentation method (MAM) to obtain the nth level approximation, which is composed of two smaller systems. One is a linear system. Another one is a nonlinear system. The nonlinear system will be solved iteratively using the Newton method.
This work is organized as follows. In Section 2, we introduce the anti-derivatives of the Daubechies wavelets and the finite-dimensional subspaces of the solution subspaces of \(H^{1}(a,b)\). The concept of multilevel augmentation method is presented in Section 3. The estimations of the optimal error rate are shown in Section 4. Some numerical examples are demonstrated in Section 5. Conclusions are finally drawn in Section 6.
2 Bases for subspaces of \(H^{1}_{0}(a,b)\)
To apply our method for solving the nonlinear boundary value problem, we construct a sequence \(\{S_{n}\}\) of nested finite-dimensional subspaces of the solution space such that \(\bigcup_{n\in\mathbb{N}} S_{n}\) is dense in the solution space. In this section, we will give a brief introduction to the anti-derivatives of wavelets that are the orthonormal bases for the finite-dimensional subspaces of the solution space \(H^{1}_{0}(a,b) \).
Assume that p is a positive integer. For \(j \geq-1\) and \((j,k) \in \mathbb{Z}\times\mathbb{Z}\), let
be the Daubechies wavelets of order p (see e.g. [5, 9] for the details of the construction and additional properties of the wavelets). We shift the interval \([0, 2p-1]\) to \([a,b]\) by the transformation
Note that the support of the wavelet \(\psi_{jk}(y)\) is the interval
Set
The wavelets \(\{\psi_{jk} | j\geq-1, k\in I_{j} \}\) form a frame for \(L^{2}(a,b)\), that is, the set consisting of all linear expansions is equal to \(L^{2}(a,b)\).
In [5], Xu and Shann introduced the anti-derivatives of the Daubechies wavelets that form orthonormal bases for the finite-dimensional subspaces of solution spaces.
For \(j\geq-1\) and \(k\in I_{j}\), the anti-derivatives of wavelets are defined by
Note that \(\Psi_{jk} \in H^{1}_{0}(a,b)\). For \(n\in\mathbb{N}_{0}\), define the finite-dimensional subspace
Let
The set \(\{\Psi_{jk} | -1\leq j < n, k\in D_{j}\}\) is a basis for \(S_{n}\). Applying the Gram-Schmidt process, the resulting set,
is an orthonormal basis for \(S_{n}\) with the inner product \([\cdot,\cdot ]\) in \(H_{0}^{1}(a,b)\). For the sake of simplicity when we consider the algebraic system, we will enumerate the double indices lexicographically. The resulting set \(\{\overline{\Psi}_{j} | 1\leq j \leq\dim S_{n}\}\) is an orthonormal basis for \(S_{n}\).
3 Multilevel augmentation method
In this section, we summarize the main concepts of multilevel augmentation method for solving the nonlinear boundary value problems. Readers can refer to [2, 4, 7, 8] for details.
The variational form of the nonlinear differential equation (1) is: Find \(u\in H^{1}_{0}(a,b)\)
where
Suppose that \(u^{*} \in H^{1}_{0}(a,b)\) is the common isolated solution of given differential equation and its variational form. We will solve the variational form (2). Let \(S_{n}\) be a nested sequence of finite-dimensional subspaces of such that \(\bigcup_{n\in\mathbb{N}} S_{n}\) is dense in H. Let \(\{\overline {\Psi}_{j} | j=1, 2, \ldots, \dim S_{n}\}\) be an orthonormal basis for \(S_{n}\) and the nth level approximate solution \(u_{n} \in S_{n}\) be of the form
satisfying
Note that by the orthonormal property of the basis, we have
Suppose that \(u_{n}\) is already solved. Instead of solving \(u_{n+1}\) directly from the nonlinear system of \(\dim S_{n+1} \), we apply the multilevel augmentation method to find an approximate solution in the next level, \(u_{n,1}\). There are two main steps here. Firstly, we solve for \(u^{H}_{n+1}= \sum_{j=\dim S_{n}+1}^{\dim S_{n+1}}\alpha ^{1}_{j}\overline{\Psi}_{j} \in S_{n+1}\setminus S_{n}\) from the system
We then obtain
Secondly, we solve for \(u^{L}_{n+1}= \sum_{j=1}^{\dim S_{n}}\alpha ^{1}_{j}\overline{\Psi}_{j} \in S_{n}\) from the nonlinear system
That is, we solve for \(\alpha_{j}^{1}\) where \(j=1, \ldots, \dim S_{n}\) from
Finally, we obtain the approximate solution at this level by setting
For \(i\in\mathbb{N}\), suppose that \(u_{n,i}\) is already solved, say,
The \((n+i+1)\)th multilevel augmentation solution, \(u_{n,i+1}\), can be solved inductively. We begin with solving for \(u^{H}_{n+i+1}= \sum_{j=\dim S_{n}+1}^{\dim S_{n+i+1}}\alpha^{i+1}_{j}\overline{\Psi}_{j} \in S_{n+i+1}\setminus S_{n}\) from the system
Then we solve \(u^{L}_{n+i+1}= \sum_{j=1}^{\dim S_{n}}\alpha ^{i+1}_{j}\overline{\Psi}_{j} \in S_{n}\) from the nonlinear system
That is, we obtain \(\alpha_{j}^{i+1}\) where \(j=1, \ldots, \dim S_{n}\) from
Finally, we obtain the approximate solution at this level by setting
It should be noted that the original full nonlinear system of \(\dim S_{n+i+1} \) can be solved in the augmentation method by just solving the smaller nonlinear system of the fixed size \(\dim S_{n}\). The increasing number of unknown coefficients when increasing the level approximation can be solved by the corresponding linear systems. Specially for our presented orthonormal basis, the linear system is easy to solve. The unknown coefficients in the higher level are obtained directly. Overall, the computational time can then be reduced greatly by this method.
Algorithm: The multilevel augmentation method based on the Galerkin method.
Let \(n, i\) be two fixed positive integers.
Step 1: Solve the nonlinear system
and obtain the solution \(u_{n}\). Let \(u_{n,0}:=u_{n}\) and \(m:=1\).
Step 2: Compute
Define \(u^{H}_{n,m}:= \sum_{j=\dim S_{n}+1}^{\dim S_{n+m}}\alpha ^{m}_{j}\overline{\Psi}_{j}\).
Step 3: Solve the nonlinear system
Define \(u^{L}_{n,m} := \sum_{j=1}^{\dim S_{n}}\alpha^{m}_{j}\overline {\Psi}_{j}\) and let \(u_{n,m}=u^{L}_{n,m}+u^{H}_{n,m}\).
Step 4: Set \(m \leftarrow m+1\) and go back to Step 2 until \(m=i\).
The computational complexity which is measured by the number of multiplications and functional evaluations used in the computation of the above algorithm is of the order \(\mathcal{O}(\dim S_{n+m})\). More details of complexity analysis can be found in [4] and [2].
4 Error analysis
In this section, we will show the convergent rate of the multilevel augmentation method in conjunction with the anti-derivatives of the Daubechies wavelets. Let \(u^{*}\) be the isolated solution of (2), \(u_{n}\in S_{n}\) be the nth (standard) multilevel solution obtained from the wavelets of order p and \(u_{n, i}\) be the \((n+i)\)th multilevel augmentation solution of (2).
Throughout this section, we assume that φ satisfies the following conditions:
-
(i)
\(\varphi(x,u)\) is a real continuous function in \((x,u) \in[a,b] \times\mathbb{R}\), and satisfies the Lipschitz condition with respect to u for \(|u|\leq R, R\geq0\), that is,
$$\bigl\vert \varphi(x,v)-\varphi(x,v) \bigr\vert \leq M_{1}|u-w|,\quad |v|\leq R, |w|\leq R, $$for some positive constant \(M_{1}\).
-
(ii)
\(\varphi(x,u)\) is continuously differentiable with respect to u for all \(x\in[a,b]\), and all \(v \in B(u^{*},\rho):=\{v | |v-u^{*}|\leq\rho\}\), for some \(\rho>0\), and there exists a positive constant \(M_{2}\) such that
$$\bigl\vert \varphi_{u}(x,v)-\varphi_{u}(x,w) \bigr\vert \leq M_{2}|v-w|, \quad\text{for all } v, w \in B\bigl(x^{*},\rho\bigr). $$
The following lemma was proved in Section 3 of [4] but for convenience of the reader, we have reproduced and included its proof for ready reference.
Lemma 4.1
Suppose that \(\varphi(x,u)\) satisfies the conditions (i) and (ii). Then there exists a continuous and compact operator \(\mathcal{K} : H^{1}_{0}(a,b) \rightarrow H^{1}_{0}(a,b)\) such that
and that \(\mathcal{K}\) is Fréchet differentiable on the closed ball \(B(u^{*},\rho)\) and the Fréchet derivative \(\mathcal{K}'\) satisfies the Lipschitz condition, that is, there exists a positive constant C
Proof
For a given \(u\in H^{1}_{0}(a,b)\), the operators \(f_{u}(\cdot) := (\beta (x)u' , \cdot) \) and \(g_{u}(\cdot) := (\varphi(x,u) , \cdot) \) are bounded linear functionals on \(H^{1}_{0}(a,b)\). By the Riesz representation theorem, there exist \(\mathcal{K}_{1}u, \mathcal{K}_{2}u \in H^{1}_{0}(a,b)\) such that
and
We define the linear operator \(\mathcal{K}_{1} : H^{1}_{0}(a,b) \rightarrow H^{1}_{0}(a,b)\) by
and define the nonlinear operator \(\mathcal{K}_{2} : H^{1}_{0}(a,b) \rightarrow H^{1}_{0}(a,b)\) by
The operator \(\mathcal{K}_{1}\) is compact. By the linearity of \(\mathcal {K}_{1}\), we see that \(\mathcal{K}_{1}\) is continuous (or bounded) and its Fréchet derivative is itself. Then there exists a positive constant \(c_{1}\) such that
By Proposition 3.1 in [4], the nonlinear \(\mathcal{K}_{2}\) is continuous, compact and Fréchet differentiable on the closed ball \(B(u^{*},\rho)\). Moreover, for any \(v , w \in B(u^{*},\rho)\), there exists a positive constant \(c_{2}\) such that
Define \(\mathcal{K}=\mathcal{K}_{1}+\mathcal{K}_{2}\). Then \(\mathcal {K}\) continuous, compact and Fréchet differentiable on the closed ball \(B(u^{*},\rho)\). Set \(C:=c_{1}+c_{2}\), the Fréchet derivative \(\mathcal{K}'\) therefore satisfies the Lipschitz condition. □
Next, we consider the difference between the isolated solution \(u^{*}\) and the \((n+i)\)th multilevel augmentation solution, \(u_{n, i}\), of (1).
Theorem 4.2
Let \(u^{*}\) be an isolated solution of (1) and \(u_{n,i}\) be the \((n+i)\) th multilevel augmentation solution. Let \(\mathcal{K}'(u^{*})\) be the Fréchet derivative of \(\mathcal{K}\) at \(u^{*}\). If 1 is not an eigenvalue of \(\mathcal{K}'(u^{*})\) and if \(u^{*}\in H^{s+1}(a,b)\), then there exist a positive constant β and a positive integer N such that, for all \(n\geq N\), and \(i\in\mathbb{N}_{0}\),
Proof
The variational form of (1) can be written in the form of \((\mathcal{I}-\mathcal{K})u =0\). By Lemma 4.1, the operator \(\mathcal{K}\) is completely continuous and Fréchet differentiable on the closed ball \(B(u^{*},\rho)\) and the Fréchet derivative \(\mathcal{K}'\) satisfies the Lipschitz condition.
Let \(E_{n} := \inf\{|u^{*}-v|_{1} | v\in S_{n}\}\). By Theorem 3.1 in [5],
where C is a constant depending on n and s. Fix \(0\leq s\leq p\). For \(n\in\mathbb{N}\), set \(\gamma_{n} = C2^{-(n+1)s}|u^{*}|_{s+1}\). Then \(\gamma_{n+1}/\gamma_{n} \geq\sigma:= 2^{-s} > 0\). Referring to Lemma 2.2 in [4], there exist a positive constant ρ and a positive integer N such that, for all \(n\geq N\), and \(i\in\mathbb{N}_{0}\),
Thus
Since the norm \(|\cdot|_{1}\) is equivalent to the standard norm \(\Vert \cdot \Vert _{1}\), \(\Vert u \Vert \leq \Vert u \Vert _{1}\), and \(|u|_{s+1} \leq \Vert u \Vert _{s+1}\), there exists a positive constant c such that
□
The above estimation suggests that, if we apply the wavelet of order p, the solution \(u\in H^{1}_{0}(a,b) \cap H^{s+1}(a,b) \). If we apply the multilevel augmentation method from level \(n+i-1\) to \(n+i\) by the anti-derivatives wavelets of order p, the errors measured in \(L^{2}\)-norm decrease at most by a factor of \(2^{p}\). Consequently, the errors obtained by the standard multilevel and the multilevel augmentation methods decrease with the same order.
5 Numerical examples
In this section, we illustrate the accuracy of the multilevel augmentation method in conjunction with the anti-derivatives of the Daubechies wavelets of order p for solving nonlinear boundary value problems with Dirichlet boundary conditions.
Example 5.1
Consider the boundary value problem [4]
with boundary conditions
The isolated solution is \(u^{*}(x) = -\ln2 +2\ln [ c\sec\{ c(x-1/2)/2\} ]\), with \(c \approx1.3360557\ldots\) .
The variational form is
where the inner product \((f,g) =\int_{0}^{1}fg \,dx\). Equivalently,
where \(\{\overline{\Psi}_{j}\}\) is an orthonormal basis for \(H^{1}_{0}(0,1)\).
Find the first level of approximate solution: standard multilevel method. For \(p=1\), the set \(\{\overline{\Psi}_{00} \}\) is a basis for the subspace \(S_{1}\). Suppose that the approximate solution \(u_{1}\in S_{1}\) is of the form
We need to know \(a_{00}\). It can be approximated from
This becomes a nonlinear equation with one unknown, \(a_{00}\). It can be solved by the Newton method. At this step, we obtain the first level approximate solution.
Find the second level of approximate solution: standard multilevel method. For \(p=1\), the set of \(\{\overline{\Psi}_{00} , \overline{\Psi }_{10} , \overline{\Psi}_{11}\}\) is represented as the multilevel bases for the subspace \(S_{2}\). Suppose that the approximate solution \(u_{2}\in S_{2}\) is in the form of
We will find approximate solution \(u_{2}\in S_{2}\) by solving for \(b_{00}, b_{10} , b_{11}\) from
or
We obtain the system of nonlinear equations with three unknown \(b_{00}, b_{10} \), and \(b_{11}\). We can solve by the Newton method. At this step, we obtain the second level of approximate solution by the standard multilevel method.
Find the third level of approximate solution: standard multilevel method. For \(p=1\), the set \(\{\overline{\Psi}_{00} , \overline{\Psi}_{10} , \overline{\Psi}_{11} , \overline{\Psi}_{20} , \overline{\Psi }_{21} , \overline{\Psi}_{22} , \overline{\Psi}_{23} \}\) is represented as the multilevel basis for the subspace \(S_{3}\). Suppose that the approximate solution \(u_{3}\in S_{3}\) is of the form
We will find approximate solution \(u_{3}\in S_{3}\) by solving for \(c_{00}, c_{10} , c_{11} , c_{20} , c_{21} , c_{22} , c_{23} \) from
We obtain a system of nonlinear equations with seven unknowns that can be solved by the Newton method. At this step, we obtain the third level of approximation by the standard multilevel method. The calculations can be extended to any number of levels, depending on the numerical accuracy required.
Next, we will show the calculation steps of the multilevel augmentation method. Assume that we have obtained \(u_{2}\in S_{2}\): \(u_{2}= b_{00}\overline{\Psi}_{00} + b_{10}\overline{\Psi}_{10} + b_{11}\overline{\Psi}_{11}\) from the second level of the standard multilevel method. The third level of approximation can be obtained by the multilevel augmentation method as follows.
Find the third level of approximate solution: multilevel augmentation method. Next, we will show how to find \(u_{2,1}\), which is the approximation of \(u_{3}\) in the third level. Assume that we have already obtained the second level of the approximate solution. The approximate solution \(u_{2,1} \in S_{3}\) is of the form
where \(u_{2,1}^{L} \in S_{2}\) and \(u_{2,1}^{H} \in S_{3}\setminus S_{2}\). Suppose that
There are two sub-steps to find \(u_{2,1}^{L}\) and \(u_{2,1}^{H}\).
We first solve for \(\alpha^{1}_{20} , \alpha^{1}_{21} , \alpha^{1}_{22} , \alpha^{1}_{23} \) from
Next, we can solve for \(\alpha^{1}_{00}, \alpha^{1}_{1,0}, \alpha ^{1}_{1,1}\) from
At this step, we solved iteratively by the Newton method. This procedure shows that the present scheme can reduce the computational time when solving the nonlinear systems.
The approximate solution \(u_{1,2} \in S_{3}\) is finally obtained,
Find the fourth level of approximate solution: multilevel augmentation method. Next, we will show how to find \(u_{2,2}\), which is the approximation of \(u_{4}\) in the third level. Assume that we have already obtained the second level of approximate solution. The approximate solution \(u_{2,2} \in S_{4}\) is of the form
where \(u_{2,2}^{L} \in S_{2}\) and \(u_{2,2}^{H} \in S_{4}\setminus S_{2}\). Suppose that
There are two sub-steps to find \(u_{2,2}^{L}\) and \(u_{2,2}^{H}\).
We first solve for \(\alpha^{2}_{20} , \ldots , \alpha^{2}_{23}, \alpha^{2}_{30} , \alpha^{2}_{31} , \ldots , \alpha^{2}_{37}\), from
Next, we can solve for \(\alpha^{2}_{00}, \alpha^{2}_{1,0}, \alpha ^{2}_{1,1}\) from
The approximate solution \(u_{2,2} \in S_{4}\) is finally obtained,
The multilevel augmentation method for calculating higher levels can be performed using the same procedure. The accuracy of the numerical solution depends on the starting level of the augmentation method.
Since we have to calculate the inner product of functions and bases, we perform it numerically by the trapezoidal rule in all of the examples. The derivatives are approximated using the central difference formula.
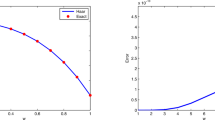
In Example 5.1, we apply the Daubechies wavelets of order \(p=1\) and \(p=2\) to solve the problem. The numerical results are shown in Tables 1 and 2, respectively. The column of \(\Vert u-u_{n} \Vert \) shows the error in the \(L^{2}\) norm obtained from the standard multilevel method. The \(L^{2}\) error decreases by the factor of 21 when the applied level increases. The next column, \(\text{Time}_{n}\), is the computing time in seconds run on the machine processor 2.3 GHz, Intel Core i7, memory 4 GB, 1600 MHz. It takes exponential order when the number of level increases. The \(L^{2}\) error when starting with the levels 2 and 3 are also shown. The decreasing in \(L^{2}\) error agrees with the theoretical results. Moreover, when we augment one more level, the computing time of our algorithm increases slightly, which is consistent with the linear complexity estimate.
The \(L^{2}\) errors by the augmentation method are of the same order as those of the standard multilevel method, when applied at the same level. When comparing the results between \(p=1\) and \(p=2\), the \(L^{2}\) errors for \(p=2\) decrease faster than those for \(p=1\). The rate of convergence decreases by the factor of C22, for some constants C. The results from Tables 1 and 2 confirm the theoretical results of our main theorem.
Example 5.2
Consider the boundary value problem
with Dirichlet boundary conditions
The isolated solution is \(u^{*}(x) = \sin(\pi x) \).
Numerical results for \(p=1\) is shown in Table 3. The \(L^{2}\) norm of the error decreases by a factor of 2. The \(L^{2}\) errors of the multilevel augmentation method are slightly greater than those of the multilevel method at the same level and decrease in the same order as the standard multilevel method.
In our last example, we will test our present method to solve the nonlinear boundary value problem with non-zero Dirichlet boundary conditions.
Consider
with the Dirichlet boundary condition
We assume that \(\beta\in L^{\infty}(a,b)\), \(\varphi\in C([a,b],\mathbb {R})\) and u is the unknown to be determined. Assume the solution u as
The variational formulation of (5) is to find \(w \in H_{0}^{1}(a,b)\) such that
By applying this technique, we can solve the nonlinear problem with non-zero Dirichlet conditions.
Example 5.3
Consider the boundary value problem
with Dirichlet boundary conditions
The isolated solution is \(u^{*}(x) = \sin(\pi x) + x\).
The variational form of this problem is
Equivalently,
Numerical results for the wavelet basis of order \(p=1\) are shown in Table 4. At the same level, the \(L^{2}\) errors of the multilevel augmentation method are slightly greater than those of the standard multilevel method. The rate of convergence in the \(L^{2}\) error agrees well with the theoretical results. The computing time of the augmentation method is of the same order when the number of augmented levels increases.
6 Conclusions
This study extends the multi-scale decomposition to a nonlinear boundary value problem. We apply the anti-derivatives of the Daubechies wavelets of order p to solve nonlinear two-point boundary value problems. The augmentation method is employed in a variational formulation for multilevel constructions. The present method can reduce computational time when solving the discretization of the full nonlinear system. The nonlinear system from the standard multilevel method can be separated or augmented into two smaller systems. One is linear and the other is a nonlinear one that can be solved iteratively by the Newton method. The numerical accuracy can be improved by increasing the resolutions or the level of approximations. The rate of convergence was shown to be at most on the order of \(2^{p}\) where p is the order of the wavelet basis. We illustrate numerically in our examples that the \(L^{2}\) error decreases when the number of basis levels increases. The rate of convergence from our estimations has been confirmed by many examples. Due to its advantages, the anti-derivatives of the Daubechies wavelets can be used to solve various kinds of boundary conditions. We are extending this study to apply this basis type with the augmentation method for solving Neumann type and mixed boundary conditions, without any modifications in the assumed form of approximate solution; these results will be reported elsewhere.
References
Chen, M, Chen, Z, Chen, G: Approximate Solutions of Operator Equations. World Scientific, Singapore (1997)
Chen, X, Chen, Z, Wu, B, Xu, Y: Fast multilevel augmentation methods for a nonlinear boundary integral equation. SIAM J. Numer. Anal. 49, 2231-2255 (2011)
Yavneh, I, Dardyk, G: A multilevel nonlinear method. SIAM J. Sci. Comput. 28(1), 24-46 (2006)
Chen, J: Fast multilevel augmentation methods for nonlinear boundary value problems. Comput. Math. Appl. 61, 612-619 (2011)
Xu, JC, Shann, WC: Galerkin-wavelet methods for two point boundary value problems. Numer. Math. 63, 123-144 (1992)
Utudee, S, Maleewong, M: Wavelet multilevel augmentation method for linear boundary value problems. Adv. Differ. Equ. 2015, 126 (2015). doi:10.1186/s13662-015-0464-0
Chen, X, Chen, Z, Wu, B, Xu, Y: Multilevel augmentation methods for nonlinear boundary integral equations II: accelerated quadratures and Newton iterations. J. Integral Equ. Appl. 24(4), 545-574 (2012)
Chen, Z, Wu, B, Xu, Y: Fast multilevel augmentation methods for solving Hammerstein equations. SIAM J. Numer. Anal. 47, 2321-2346 (2009)
Daubechies, I: Orthonormal bases of compactly supported wavelets. Commun. Pure Appl. Math. 41, 909-996 (1988)
Acknowledgements
This research was supported by the Faculty of Science, Chiang Mai University as regards the first author, and the Faculty of Science, Kasetsart University as regards the second author.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Utudee, S., Maleewong, M. Multilevel anti-derivative wavelets with augmentation for nonlinear boundary value problems. Adv Differ Equ 2017, 100 (2017). https://doi.org/10.1186/s13662-017-1156-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-017-1156-8