1 Introduction

In population ecology, the dynamics of species populations and the way these populations interact with the environment have raised widespread concerns [1]. It is the study of how the population sizes of species change over time and space. Among these interactions, the predator-prey interaction is the most basic one, and plenty of mathematical models have been established since the pioneering work by Lotka and Volterra [2, 3].

To better understand the relationship between predator and prey, a functional response is utilized to model the intake rate of a consumer as a function of food density, such as Holling types I-IV [4, 5], Beddington-DeAngelis type [6], Hassell-Varley type [7], Leslie-Gower type [8], Crowley-Martin type [9], and so on [10, 11]. In many situations, when predators have to search, share or compete for their resources, the so-called ratio-dependent functional response is reasonable. It means that the per capita predator growth rate is a function of the ratio of prey to predator abundance. This is strongly supported by numerous fields and laboratory experiments and observations [12]. Such ratio-dependent models can present rich dynamic behaviors, see [13–15]. In addition, the environmental carrying capacity of predator is proportional to the number of prey; consequently, the Leslie-Gower type functional response was proposed in [16, 17].

For most populations, they do not always stay in a fixed place and usually move from a higher concentration region to a lower concentration one. Thus, the spatial diffusive factor should be considered in modeling the predator-prey system. Given all this, a nondimensional diffusive Leslie-Gower predator-prey model with ratio-dependent Holling type III functional response was considered in [18] as follows:

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t}-d_{1} \Delta u(x,t)=u(x,t)(1-u(x,t))-\frac{\beta u^{2}(x,t)v(x,t)}{u^{2}(x,t)+mv^{2}(x,t)}, \quad x\in\Omega, t>0, \\ \frac{\partial v(x,t)}{\partial t}-d_{2} \Delta v(x,t)=rv(x,t) ( 1-\frac {v(x,t)}{u(x,t)} ), \quad x\in\Omega, t>0. \end{cases} $$

Here, \(u(x,t)\) and \(v(x,t)\) represent the density of the prey and predator at time t and location \(x\in\Omega\), respectively. The region \(\Omega\subset\mathbb{R}^{N}\) (\(N\leq3\)) is a bounded domain with smooth boundary ∂Ω. The nonnegative continuous initial conditions and homogeneous Neumann boundary conditions are imposed. All the coefficients are positive constants, \(d_{1}\) and \(d_{2}\) are diffusion coefficients, and more detailed ecological meanings can be found in [18].

As is well known, time delay, especially the maturation delay of the predator, is ubiquitous in an ecological system. Hence, in this paper, by taking account of the combined effects of spatial diffusion and time delay, we mainly consider the following modified predator-prey model:

$$ \textstyle\begin{cases} \frac{\partial u(x,t)}{\partial t}-d_{1} \Delta u(x,t)=u(x,t)(1-u(x,t))-\frac{\beta u^{2}(x,t)v(x,t)}{u^{2}(x,t)+mv^{2}(x,t)}, \quad x\in\Omega, t>0, \\ \frac{\partial v(x,t)}{\partial t}-d_{2} \Delta v(x,t)=rv(x,t) ( 1-\frac {v(x-\tau,t)}{u(x-\tau,t)} ), \quad x\in\Omega, t>0, \\ \frac{\partial u(x,t)}{\partial\nu}=\frac{\partial v(x,t)}{\partial \nu}=0, \quad x\in\partial\Omega, t>0, \\ u(x,t)=u_{1}(x,t)\geq0, \quad\quad v(x,t)=v_{1}(x,t)\geq0, \quad x\in\overline{\Omega },t\in[-\tau,0], \end{cases} $$
(1)

where all the coefficients are positive constants, time delay \(\tau>0\) is the mature time of the predator. The initial functions \(u_{1}(x,t)\) and \(v_{1}(x,t)\) are continuous, \(\partial/\partial\nu\) represents the outward normal derivative on the boundary ∂Ω. The system is subject to no-flux boundary conditions, and it means that the ecology system is self-contained. In fact, there have been some significant results about the simplifications of system (1). In detail, the spatiotemporal dynamics have been studied without time delay. For example, Shi and Li [18] focused on the local and global stability of positive constant steady state by using the linearization method and the Lyapunov functional method. In [19], Shi et al. derived the existences of Turing bifurcation, Hopf bifurcation, and Turing-Hopf bifurcation by regarding r as the bifurcation parameter. In [20], Zhou also investigated the existence of Turing pattern and nonexistence of nonconstant steady state solutions by the bifurcation method and the energy method. Besides, Song et al. [21] considered the corresponding delay system without diffusion and ratio-dependent functional response and established the existence of local and global Hopf bifurcations by choosing time delay as the bifurcation parameter. For some other related results, refer to [22–25].

However, to the best of our knowledge, there are no results on the joint effects of diffusion and delay on the spatiotemporal dynamics of the delayed reaction-diffusion system (1). As a consequence, our major goal is to investigate the basic properties of system (1), the stability of constant steady states and the time periodic solutions generated by diffusion and delay. The rest of this paper is arranged as follows. In Section 2, we give some preliminary results on the well-posedness of solutions and the dissipativeness of the system. In Section 3, we derive sufficient conditions for the stability of nonnegative constant steady states and the existence of Hopf bifurcation. In Section 4, we compute the formulae for determining the Hopf bifurcation properties. In Section 5, we conduct some numerical simulations to illustrate our theoretical results. Finally, we give some conclusions and biological interpretations.

2 Elementary results

Here, we establish some basic properties of the solutions of system (1), specifically, the well-posedness of solutions and the dissipativeness of system (1).

For convenience, we first restate a useful lemma from [26] as follows.

Lemma 1

Consider the equation

$$ \textstyle\begin{cases} \frac{\partial w}{\partial t}=\overline{D} \Delta w + wg(w(x,t-\tau)), \quad x\in\Omega, t>0, \\ \frac{\partial w}{\partial\nu}=0, \quad x\in\partial\Omega, t>0, \\ w(x,s)\geq0,\quad\quad w(x,0) \not\equiv0, \quad x\in\overline{\Omega},s\in[-\tau,0]. \end{cases} $$
(2)

If the function g satisfies \(g(w)\leq\alpha(1-w/d)\), then the solution of (2) has the property

$$ \limsup_{t\rightarrow+\infty}\max_{\overline{\Omega}} w(\cdot,t)\leq de^{\alpha\tau}. $$

Theorem 1

System (1) has a unique global solution, and the solution remains nonnegative and uniformly bounded for all \(t > 0\).

Proof

Following the process in [27, 28], we can similarly get the local existence and uniqueness of solution \((u(x,t), v(x,t))\) with \(x\in\overline{\Omega}\) and \(t\in[0,T)\), where T is the maximal existence time of the solution.

In order to conform to the comparison theorem and the standard theory of semilinear parabolic system in [29], we only need to construct a pair of coupled lower-upper solutions \(\mathbf{0}=(0,0)\) and \(\mathbf{M}=(M_{1},M_{2})\), where

$$\begin{aligned}& M_{1}=\max\Bigl\{ 1, \sup_{-\tau\leq s\leq0} \bigl\Vert u_{1}(\cdot,s) \bigr\Vert _{C(\bar{\Omega},\mathbb{R})} \Bigr\} , \\& M_{2}=\max\Bigl\{ M_{1}e^{r\tau}, \sup _{-\tau\leq s\leq0} \bigl\Vert v_{1}(\cdot ,s) \bigr\Vert _{C(\bar{\Omega},\mathbb{R})} \Bigr\} . \end{aligned}$$

Then the proof can be completed. □

In the following, we will show that any nonnegative solution of system (1) is bounded as \(t\rightarrow+\infty\) for all \(x\in\Omega\).

Theorem 2

Dissipativeness

The system (1) is dissipative. That is, the nonnegative solution \((u, v)\) of system (1) satisfies

$$\limsup_{t\rightarrow+\infty} u(x,t)\leq1, \quad\quad \limsup_{t\rightarrow+\infty } v(x,t)\leq e^{r\tau}. $$

Proof

On the basis of positivity of solutions in Theorem 1, we have

$$\frac{\partial u(x,t)}{\partial t}-d_{1}\Delta u(x,t)\leq u(x,t) \bigl( 1-u(x,t) \bigr)\quad \mbox{for } (x,t)\in\Omega\times[0,+\infty). $$

Then we can estimate the upper limit of \(u(x,t)\) due to the standard comparison principle:

$$\limsup_{t\rightarrow+\infty} u(x,t) \leq 1. $$

In other words, for an arbitrary \(\varepsilon_{1}>0\), there exists a positive constant \(T_{1}\) such that for any \(t\geq T_{1}\),

$$u(x,t)\leq1+\varepsilon_{1}. $$

Analogously, for any \(T\in[T_{1}+\tau,+\infty)\), we have

$$\frac{\partial v(x,t)}{\partial t}-d_{2}\Delta v(x,t)\leq rv(x,t) \biggl( 1- \frac{v(x,t-\tau)}{1+\varepsilon_{1}} \biggr). $$

Therefore, the following estimation can be deduced by Lemma 1:

$$\limsup_{t\rightarrow+\infty} v(x,t)\leq e^{r\tau}. $$

The proof is complete. □

3 The stability of positive steady states and the existence of Hopf bifurcation

Setting the right sides of the first two equations in system (1) equal to zero and solving the algebraic equations of u and v, we can obtain the two constant steady states: \(E_{1}=(1,0)\) and \(E_{\ast}=(u_{\ast},v_{\ast})\), where \(u_{\ast}=v_{\ast}=1-\frac{\beta}{1+m}\). Apparently, \(E_{\ast}\) is positive when the following assumption holds:

(H1):

\(\beta< 1+m \).

So, we always expect assumption (H1) to be true. For the convenience of research, in the remainder of this paper, we only consider the one-dimensional region \(\Omega=(0,l\pi)\).

We know that the eigenvalues of the operator −Δ on Ω under the homogeneous Neumann boundary conditions are \(\mu_{n}=n^{2}/l^{2}\), \(n=0,1,2,\ldots\) . Let \(E(\mu_{n})\) be the eigenfunction space corresponding to \(\mu_{n}\) in \(C^{1}(\Omega)\), \(\{ \varphi_{nj}: j=1,2,\ldots,\dim E(\mu_{n}) \}\) be an orthonormal basis of \(E(\mu_{n})\), \(X=[C^{1}(\Omega)]^{2}\), and \(X_{nj}=\{ \mathbf{c}\cdot\varphi_{nj}: \mathbf{c}\in\mathbb{R}^{2} \}\). Then

$$X=\bigoplus_{n=1}^{\infty}X_{n} \quad\mbox{and} \quad X_{n}=\bigoplus_{j=1}^{\dim E(\mu_{n})}X_{nj}. $$

For each \(n\geq0\), \(X_{n}\) is invariant under the linearized operator of system (1), and the characteristic equation at \(E_{1}=(1, 0)\) is given by

$$\left \vert \textstyle\begin{array}{c@{\quad}c} \lambda+d_{1}\frac{n^{2}}{l^{2}}+\frac{(1+m)^{2}-2\beta}{(1+m)^{2}} & \frac{\beta (1-m)}{(1+m)^{2}}\\ -r & \lambda+d_{2}\frac{n^{2}}{l^{2}}+r \end{array}\displaystyle \right \vert =0, $$

which is equivalent to

$$ \biggl( \lambda+d_{1}\frac{n^{2}}{l^{2}}+1 \biggr) \biggl( \lambda-d_{2}\frac{n^{2}}{l^{2}}-r \biggr)=0. $$
(3)

The constant steady state is asymptotically stable if all the characteristic values have negative real parts for any \(n\geq0\). It is evident that characteristic equation (3) has a positive value \(\lambda=r\) when \(n=0\). Then the semi-trivial steady state \(E_{1}=(1,0)\) is always unstable. From the ecological point of view, we are more interested in the stability of positive constant steady state \(E_{\ast}=(u_{\ast}, v_{\ast})\), and the corresponding characteristic equation is

$$\left \vert \textstyle\begin{array}{c@{\quad}c} \lambda+d_{1}\frac{n^{2}}{l^{2}}+\frac{(1+m)^{2}-2\beta}{(1+m)^{2}} & \frac{\beta (1-m)}{(1+m)^{2}}\\ -re^{-\lambda\tau} & \lambda+d_{2}\frac{n^{2}}{l^{2}}+re^{-\lambda\tau} \end{array}\displaystyle \right \vert =0, $$

and

$$ \lambda^{2}+A_{n}\lambda+B_{n}+e^{-\lambda\tau}(C \lambda+F_{n})=0, $$
(4)

where

$$\begin{aligned}& A_{n}=(d_{1}+d_{2})\frac{n^{2}}{l^{2}}+\frac{(1+m)^{2}-2\beta}{(1+m)^{2}}, \\& B_{n}=d_{1}d_{2}\frac{n^{4}}{l^{4}}+d_{2}\frac{(1+m)^{2}-2\beta}{(1+m)^{2}}\frac{n^{2}}{l^{2}}, \\& C=r, \\& F_{n}=rd_{1}\frac{n^{2}}{l^{2}}+\frac{r(1+m-\beta)}{1+m}. \end{aligned}$$

In the following, we shall explore the effect of spatial diffusion and time delay on the dynamic behaviors of system (1), respectively.

3.1 The effect of diffusion

In this subsection, we regard coefficient β as the bifurcation parameter and discuss the effect of spatial diffusion on the stability of positive steady state \(E_{\ast}\) without time delay. Then the characteristic equation (4) can be reduced to

$$ \lambda^{2}-T_{n}\lambda+D_{n}=0, $$
(5)

where

$$\begin{aligned}& T_{n}= \frac{2\beta-(1+m)^{2}}{(1+m)^{2}}-r-(d_{1}+d_{2}) \frac{n^{2}}{l^{2}}, \\& D_{n}=d_{1}d_{2}\frac{n^{4}}{l^{4}}+ \biggl[ d_{1}r+d_{2} \biggl( 1-\frac{2\beta}{(1+m)^{2}} \biggr) \biggr] \frac{n^{2}}{l^{2}}+\frac{\beta r(1-m)}{(1+m)^{2}}+r\frac{(1+m)^{2}-2\beta}{(1+m)^{2}}. \end{aligned}$$

Through direct computation, we can obtain the following inequality when the positive constant steady state exists:

$$\frac{\beta r(1-m)}{(1+m)^{2}}+r\frac{(1+m)^{2}-2\beta}{(1+m)^{2}}=\frac {r(1+m-\beta)}{1+m}>0. $$

For any \(n\geq0\) with \(\tau=0\), the necessary condition for the existence of Hopf bifurcation at \(E_{\ast}\) is \(T_{n}=0\), that is,

$$\frac{2\beta-(1+m)^{2}(1+r)}{(1+m)^{2}}=(d_{1}+d_{2})\frac{n^{2}}{l^{2}}. $$

Denote

$$\beta_{n}=\frac{(1+m)^{2}(d_{1}+d_{2})\frac{n^{2}}{l^{2}}+(1+m)^{2}(1+r)}{2},\quad n=0,1,2,\ldots, $$

then the positive steady state \(E_{\ast}\) is asymptotically stable when \(\beta<\beta_{0}\) and the potential Hopf bifurcation may occur when \(\beta >\beta_{0}\).

Next, we need to verify the transversality condition. Suppose that the root of equation (5) has the form \(\lambda(\beta)=a(\beta )+ib(\beta)\). Substituting it into (5) and separating the real and negative parts, we get

$$2a(\beta)b(\beta)i=T_{n}b(\beta)i, $$

and

$$\operatorname{Re}\bigl(\lambda' (\beta)\bigr)= a'( \beta)=\frac{T_{n}'(\beta )}{2}=\frac{1}{(1+m)^{2}}>0. $$

We further make the following assumption:

(H2):

\((1+m)(1+r) < 2 \).

With the previous analysis, the following conclusions can be drawn by the Hopf bifurcation theory in [29].

Theorem 3

When hypotheses (H1) and (H2) are satisfied, we have

  1. (i)

    If \(\beta\in(0,\beta_{0})\), then the positive steady state \(E_{\ast}\) is asymptotically stable.

  2. (ii)

    If \(\beta\in(\beta_{0}, m+1)\), then the positive steady state \(E_{\ast}\) is unstable.

  3. (iii)

    The periodic solutions bifurcating from \(\beta=\beta_{0}\) are spatially homogeneous, and the periodic solutions bifurcating from \(\beta=\beta_{n}\) (\(1\leq n\leq N_{1}, \beta_{N_{1}}< m+1, \beta_{N_{1}+1} \geq m+1\)) are spatially inhomogeneous.

3.2 The effect of delay

Next, we discuss the dynamic behaviors of \(E_{\ast}\) by taking time delay τ as the bifurcation parameter.

Let \(\pm i\omega\) (\(\omega>0\)) be the roots of equation (4), then we get

$$-\omega^{2}+i\omega A_{n}+B_{n}+(\cos\omega \tau-i\sin\omega\tau) (i\omega C+F_{n})=0. $$

Separating the real and imaginary parts can lead to

$$ \textstyle\begin{cases} \omega^{2}-B_{n}=F_{n}\cos\omega\tau+\omega C \sin\omega\tau, \\ -\omega A_{n} =\omega C \cos\omega\tau- F_{n} \sin\omega\tau, \end{cases} $$
(6)

and

$$ \omega^{4}+P_{n}\omega^{2}+Q_{n}=0, $$
(7)

where

$$\begin{aligned}& P_{n}=A_{n}^{2}-2B_{n}-C^{2}, \\& \begin{aligned} Q_{n}&=(B_{n}+F_{n})(B_{n}-F_{n}) \\ & =D_{n} \biggl[ d_{1}d_{2}\frac{n^{4}}{l^{4}}+ \biggl( d_{2}\frac{(1+m)^{2}-2\beta}{(1+m)^{2}}-rd_{1} \biggr) \frac{n^{2}}{l^{2}} -\frac{r(1+m-\beta)}{1+m} \biggr]. \end{aligned} \end{aligned}$$

Then \(Q_{0}=-D_{0}\frac{r(1+m-\beta)}{1+m}<0\) when (H1) holds. Moreover, based on the property of parabola, there exists a nonnegative integer \(N_{2}\), such that \(Q_{n}<0\) for \(0\leq n\leq N_{2}\). Further, equation (7) has the unique positive root \(\omega_{n}\), and the characteristic equation (4) has purely imaginary roots \(\pm i\omega_{n}\), where

$$\omega_{n}=\sqrt{\frac{-P_{n}+\sqrt{P_{n}^{2}-4Q_{n}}}{2}}, \quad n=0,1,2,\ldots , N_{2}. $$

By solving equations (6), we get

$$ \textstyle\begin{cases} \cos\omega\tau= \frac{(F_{n}-A_{n}C)\omega_{n}^{2}-B_{n}F_{n}}{F_{n}^{2}+C^{2}\omega_{n}^{2}} ,\\ \sin\omega\tau= \frac{C\omega_{n}^{3}+(A_{n}F_{n}-B-nC)\omega_{n}}{F_{n}^{2}+C^{2}\omega _{n}^{2}} , \end{cases} $$
(8)

and then obtain the corresponding values of τ as follows:

$$\tau=\tau_{j}^{(n)}=\frac{1}{\omega_{n}} \biggl[ \arccos \frac{(F_{n}-A_{n}C)\omega _{n}^{2}-B_{n}F_{n}}{F_{n}^{2}+C^{2}\omega_{n}^{2}}+2j\pi\biggr] ,\quad j=0,1,2,\ldots. $$

Specially, we define

$$\tau_{0}=\min\bigl\{ \tau_{j}^{(n)} \bigr\} ,\quad j=0,1,2,\ldots, n=0,1,2,\ldots,N_{2}. $$

To verify the transversality condition, we take the derivative of equation (4) with respect to τ and have

$$2\lambda\frac{\mathrm{d}\lambda}{\mathrm{d}\tau}+A_{n}\frac{\mathrm {d}\lambda}{\mathrm{d}\tau}+e^{-\lambda\tau}C \frac{\mathrm{d}\lambda }{\mathrm{d}\tau}-(C\lambda+F_{n})e^{-\lambda\tau} \biggl( \lambda+ \tau\frac {\mathrm{d}\lambda}{\mathrm{d}\tau} \biggr)=0. $$

It can be simplified to

$$\begin{aligned} \biggl( \frac{\mathrm{d}\lambda}{\mathrm{d}\tau} \biggr)^{-1} =& \frac {2\lambda+A_{n}+Ce^{-\lambda\tau}-\tau e^{-\lambda\tau}(C\lambda +F_{n})}{\lambda e^{-\lambda\tau}(C\lambda+F_{n})} \\ =& \frac{(2\lambda+A_{n})e^{\lambda\tau}+C}{\lambda(C\lambda+F_{n})} -\frac {\tau}{\lambda} , \end{aligned}$$

and

$$\operatorname{Re} \biggl( \frac{\mathrm{d}\lambda}{\mathrm{d} \tau} \biggr) ^{-1}_{\tau=\tau_{j}^{(n)}}= \frac{\omega_{n}^{4}+F_{n}^{2}-B_{n}^{2}}{(F_{n}\omega _{n})^{2}+(C\omega_{n}^{2})^{2}}. $$

Denote

(H3):

\(\beta<\min\{ m+1,(1+m)^{2}/2 \}\).

If condition (H3) holds, then \(F_{n}+B_{n}=D_{n}>0\). Moreover, from

$$F_{n}-B_{n}=-d_{1}d_{2} \frac{n^{4}}{l^{4}}+ \biggl( rd_{1}-d_{2}+\frac{2d_{2}\beta}{(1+m)^{2}} \biggr) \frac{n^{2}}{l^{2}} +\frac{r(1+m-\beta)}{1+m}, $$

we can always find the greatest nonnegative integer \(N_{3}\), such that

$$F_{n}-B_{n}>0,\quad\mbox{for } n=0,1,2, \ldots,N_{3}. $$

Therefore, we get

$$\operatorname{Re} \biggl( \frac{\mathrm{d}\lambda}{\mathrm{d} \tau} \biggr)^{-1}_{\tau=\tau_{j}^{(n)}} >0. $$

From above, we can establish the existence of Hopf bifurcation induced by time delay.

Theorem 4

When hypothesis (H3) is satisfied, we have

  1. (i)

    For \(\tau\in[0,\tau_{0})\), the positive steady state \((u_{\ast},v_{\ast})\) is asymptotically stable.

  2. (ii)

    or \(\tau>\tau_{0}\), the positive steady state \((u_{\ast},v_{\ast})\) is unstable. Furthermore, \(\tau=\tau_{j}^{(n)}\) (\(j=0,1,2,\ldots\) ; \(n=0,1,2,\ldots,\min\{ N_{2}, N_{3} \}\)) are Hopf bifurcation values.

4 Bifurcation properties

In this section, we mainly analyze the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions obtained in Theorem 4. The methods here are based on the center manifold theorem and normal form theory for partial functional differential equations in [29, 30].

In general, we use \(\tau^{\ast}\) to denote an arbitrary value of \(\tau _{j}^{(n)}\) with \(j\in\mathbb{N}_{0}\) and \(n\in\{0,1,2,\ldots,\min\{{N_{2}, N_{3}}\}\}\). And we also use \(\pm i\omega^{\ast}\) to denote the corresponding simply purely imaginary roots \(\pm i\omega_{n}\).

Setting \(\tilde{u}(\cdot,t)=u(\cdot,\tau t)\), \(\tilde{v}(\cdot ,t)=v(\cdot,\tau t)\), \(\tilde{U}(t)=(\tilde{u}(\cdot,t),\tilde{v}(\cdot ,t))\), and \(\tau=\tau^{\ast}+\alpha\) with \(\alpha\in\mathbb{R}\), then \(\alpha=0\) is the Hopf bifurcation value of system (1). For simplicity, we drop the tilde and rewrite system (1) in the form

$$ \frac{\mathrm{d}U(t)}{\mathrm{d}t}=\tau D\Delta U(t)+L(\alpha) (U_{t})+f(U_{t},\alpha), $$
(9)

where \(D=\operatorname{diag}\{d_{1}, d_{2}\}\), \(\varphi=(\varphi_{1},\varphi_{2})^{T}\in\mathcal{C}\), and \(L(\alpha)(\cdot): \mathcal{C}\rightarrow X\), \(f: \mathcal{C}\times\mathbb{R}\rightarrow X\) are given by

$$\begin{aligned}& L(\alpha) (\varphi)=\bigl(\tau^{\ast}+\alpha\bigr)\left ( \textstyle\begin{array}{c} \frac{2\beta-(1+m)^{2}}{(1+m)^{2}}\varphi_{1}(0)- \frac{\beta (1-m)}{(1+m)^{2}}\varphi_{2}(0) \\ r\varphi_{1}(-1)-r\varphi_{2}(-1) \end{array}\displaystyle \right ), \\& f(\varphi,\alpha)=\bigl(\tau^{\ast}+\alpha\bigr)\left ( \textstyle\begin{array}{c} \sum_{i+j\geq2}\frac{1}{i!j!}F_{ij} \varphi_{1}^{i}(0)\varphi_{2}^{j}(0) \\ \sum_{i+j+l\geq2} \frac{1}{i!j!l!}G_{ijl} \varphi_{2}^{i}(0)\varphi _{1}^{j}(-1)\varphi_{2}^{l}(-1) \end{array}\displaystyle \right ), \end{aligned}$$

and

$$\begin{aligned}& F(u,v)=u-u^{2}-\frac{\beta u^{2}v}{u^{2}+mv^{2}},\quad \quad G(v,w,z)=rv- \frac{rvz}{w}, \\& F_{ij}=\frac{\partial^{i+j}F}{\partial u^{i}\, \partial v^{j}}(u_{\ast},v_{\ast}), \quad \quad G_{ijl}=\frac{\partial^{i+j+l}G}{\partial v^{i} \,\partial w^{j}\, \partial z^{l}}(v_{\ast},u_{\ast},v_{\ast}). \end{aligned}$$

From Section 3, we can know that \(\pm i\omega^{\ast}\tau^{\ast}\) is a pair of simple purely imaginary eigenvalues of the following linear differential equation:

$$ \dot{U}(t)=\tau D\Delta U(t)+L(\alpha) (U_{t}). $$
(10)

Next, we discuss the following differential equation:

$$ \dot{Y}(t)=-\tau D n^{2} Y(t)+L(\alpha) (Y_{t}). $$
(11)

By the Riesz representation theorem here, there exists a \(2\times2\) matrix function \(\eta(\theta, \alpha)\) (\(-1\leq\theta\leq0\)) whose elements are of bounded variation such that

$$-\tau D \frac{n^{2}}{l^{2}} \varphi(0)+L(\alpha) (\varphi)= \int_{-1}^{0}\mathrm{d} \eta(\theta, \alpha)\varphi( \theta), $$

where

$$\eta(\theta,\alpha)= \textstyle\begin{cases} (\tau^{\ast}+\alpha) \bigl( {\scriptsize\begin{matrix}{} -d_{1}\frac{n^{2}}{l^{2}}+\frac{2\beta-(1+m)^{2}}{(1+m)^{2}} & -\frac{\beta(1-m)}{(1+m)^{2}} \cr 0 & -d_{2}\frac{n^{2}}{l^{2}} \end{matrix}} \bigr) , & \theta=0, \\ 0, & \theta\in(-1,0),\\ (\tau^{\ast}+\alpha)\bigl( {\scriptsize\begin{matrix}{} 0 & 0 \cr r & -r \end{matrix}} \bigr), & \theta=-1. \end{cases} $$

For \(\Phi\in C^{1}([-1,0],\mathbb{R}^{2})\), \(\Psi\in C^{1}([0,1],\mathbb {R}^{2})\), we define

$$\begin{aligned}& A_{1}\bigl(\Phi(\theta)\bigr)= \textstyle\begin{cases} \frac{\mathrm{d}\Phi(\theta)}{\mathrm{d}\theta}, & \theta\in[-1,0),\\ \int_{-1}^{0}\mathrm{d}\eta(\theta,0)\Phi(\theta), & \theta=0, \end{cases}\displaystyle \\& A_{1}^{\ast}\bigl(\Psi(s)\bigr)= \textstyle\begin{cases} -\frac{\mathrm{d}\Psi(s)}{\mathrm{d}s}, & s\in(0,1],\\ \int_{-1}^{0}\mathrm{d}\eta^{T}(\theta,0)\Psi(-\theta), & s=0. \end{cases}\displaystyle \end{aligned}$$

Then \(A_{1}^{\ast}\) and \(A_{1}\) are adjoint operators under the bilinear form

$$\begin{aligned} (\Psi,\Phi)_{0} =& \overline{\Psi}(0)\Phi(0)- \int_{-1}^{0} \int_{0}^{\theta}\overline{\Psi}(\zeta-\theta)\, \mathrm{d} \eta(\theta,0)\Phi(\zeta)\,\mathrm{d}\zeta \\ =& \overline{\Psi}(0)\Phi(0)+\tau^{\ast}\int_{-1}^{0} \overline{\Psi}(\zeta+1) \left ( \textstyle\begin{array}{c@{\quad}c} 0 & 0 \\ r & -r \end{array}\displaystyle \right ) \Phi(\zeta)\,\mathrm{d}\zeta. \end{aligned}$$

It can be verified that \(q(\theta)=q(0)\cdot e^{i\omega^{\ast}\tau^{\ast}\theta}=(1,\eta)^{T} e^{i\omega^{\ast}\tau^{\ast}\theta}\) (\(\theta\in[-1,0]\)) and \(q^{\ast}(s)=Mq^{\ast}(0)e^{i\omega^{\ast}\tau^{\ast}s}=M(\xi,1)^{T} e^{i\omega^{\ast}\tau^{\ast}s}\) (\(s\in[0,1]\)) are eigenvectors of \(A_{1}\) and \(A_{1}^{\ast}\) corresponding to \(i\omega^{\ast}\tau^{\ast}\) and \(-i\omega ^{\ast}\tau^{\ast}\), respectively, where

$$\begin{aligned}& \eta=\frac{re^{-i\omega^{\ast}\tau^{\ast}}}{i\omega^{\ast}+d_{2}\frac {n^{2}}{l^{2}}+re^{-i\omega^{\ast}\tau^{\ast}}}, \\& \xi=\frac{(1+m)^{2}}{\beta(1-m)} \biggl( i\omega^{\ast}-d_{2} \frac{n^{2}}{l^{2}}-re^{i\omega^{\ast}\tau^{\ast}} \biggr), \\& M= \bigl[ \xi+r\tau^{\ast}e^{-i\omega^{\ast}\tau^{\ast}} +\overline{\eta} \bigl(1-r \tau^{\ast}e^{-i\omega^{\ast}\tau^{\ast}} \bigr) \bigr]^{-1}. \end{aligned}$$

Then the center subspace of system (1) is \(P=\operatorname{span}\{ q(\theta ),\overline{q(\theta)} \}\), and the adjoint subspace is \(P^{\ast}=\operatorname{span}\{ q^{\ast}(s),\overline{q^{\ast}(s)} \}\).

Let \(h\cdot f_{n}=h_{1}\beta_{n}^{1}+h_{2}\beta_{n}^{2}\), \(f_{n}=(\beta_{n}^{1},\beta_{n}^{2})\) and \(\beta_{n}^{1}=(\cos\frac{nx}{l},0)^{T}\), \(\beta_{n}^{2}=(0,\cos\frac{nx}{l})^{T}\). The complex-valued \(L^{2}\) inner product on the Hilbert space \(X_{C}\) is

$$ \langle U_{1},U_{2} \rangle= \frac{1}{l\pi} \int_{0}^{l\pi} (u_{1}\overline{v_{1}}+u_{2} \overline{v_{2}})\,\mathrm{d}x $$
(12)

for \(U_{1}=(u_{1},u_{2}), U_{2}=(v_{1},v_{2})\in X_{C}\). And \(\langle\beta_{0}^{i}, \beta_{0}^{i} \rangle=1\), \(\langle \beta_{n}^{i}, \beta_{n}^{i} \rangle=\frac{1}{2}\), \(i=1,2\), \(n=1,2,\ldots\) ,

$$ \langle\Phi, f_{n} \rangle= \bigl( \bigl\langle \Phi, \beta_{n}^{1} \bigr\rangle , \bigl\langle \Phi, \beta_{n}^{2} \bigr\rangle \bigr), $$
(13)

where \(\Phi\in C([-1,0],X)\). Then the center subspace of system (10) at \(\alpha=0\) is given by

$$ P_{\mathrm{CN}}\mathcal{L}= \bigl\{ \bigl(q(\theta)z+ \overline{q( \theta)}\bar{z} \bigr)\cdot f_{n}, z\in\mathbb{C} \bigr\} . $$
(14)

Setting \(\alpha=0\), we can obtain the center manifold

$$ W(z,\bar{z},\theta)=W_{20}\frac{z^{2}}{2}+W_{11}z \bar{z}+W_{02}\frac{\bar{z}^{2}}{2}+\cdots. $$
(15)

The flow of system (9) on the center manifold can be written as follows:

$$U_{t}=\bigl(q(\theta)z(t)+\overline{q(\theta)}\bar{z}(t)\bigr)\cdot f_{n}+W\bigl(z(t),\bar {z}(t),\theta\bigr). $$

Moreover, for \(U_{t}\in C_{0}\) of (9) at \(\tau=\tau^{\ast}\), we have \(\dot{z}=i\omega^{\ast}\tau^{\ast}z+g(z,\bar{z})\), where

$$ g(z,\bar{z})=\overline{q^{\ast}(0)} \bigl\langle f(U_{t}, 0), f_{n} \bigr\rangle =g_{20} \frac{z^{2}}{2}+g_{11}z\bar{z}+g_{02}\frac{\bar{z}^{2}}{2}+g_{21} \frac{z^{2}\bar{z}}{2}+\cdots. $$
(16)

Following the calculation procedures in [29] and [30], we can get

$$\begin{aligned}& g_{20}= \textstyle\begin{cases} 0, & n=1,2,\ldots, \\ \tau^{\ast}\overline{M} [ \overline{\xi}( F_{20}+F_{02}\eta^{2}+2F_{11}\eta ) +(G_{020} e^{-2i\omega^{\ast}\tau^{\ast}} & \\ \quad{} +G_{002}\eta e^{-2i\omega^{\ast}\tau^{\ast}}+2G_{110}\eta e^{-i\omega^{\ast}\tau^{\ast}} & \\ \quad{} +2G_{101}\eta^{2} e^{-i\omega^{\ast}\tau^{\ast}} +2G_{011}\eta e^{-2i\omega^{\ast}\tau^{\ast}} ) ], & n=0, \end{cases}\displaystyle \\& g_{11}= \textstyle\begin{cases} 0, & n=1,2,\ldots, \\ \tau^{\ast}\overline{M} [ \overline{\xi}( F_{20}+F_{02}\vert \eta \vert ^{2}+F_{11}(\eta+\overline{\eta} )) + (G_{200} \vert \eta \vert ^{2} & \\ \quad{} +G_{020} +G_{002}\vert \eta \vert ^{2} +G_{110}(\overline {\eta} e^{-i\omega^{\ast}\tau^{\ast}}+\eta e^{i\omega^{\ast}\tau^{\ast}}) & \\ \quad{} + G_{101}\eta\overline{\eta}(e^{i\omega^{\ast}\tau^{\ast}}+e^{-i\omega^{\ast}\tau^{\ast}})+G_{011}(\eta+\overline{\eta})) ], & n=0, \end{cases}\displaystyle \\& g_{02}=\overline{g_{20}}, \\& \begin{aligned} g_{21} &= \frac{\tau^{\ast}\overline{M}}{l\pi} \biggl\{ \int_{0}^{l\pi}\cos^{4}\frac{nx}{l}\, \mathrm{d}x \bigl[ F_{30}+F_{03}\eta \vert \eta \vert ^{2} +F_{21}(2\eta+\overline{\eta}) +F_{12} \bigl(2\eta\overline{ \eta}+\eta^{2} \bigr) \bigr] \\ &\quad{} + \int_{0}^{l\pi}\cos^{4}\frac{nx}{l}\, \mathrm{d}x \bigl[ G_{300}\eta \vert \overline{\eta} \vert ^{2} +G_{030}e^{-i\omega^{\ast}\tau^{\ast}} +G_{003}\eta \vert \overline{\eta} \vert ^{2}e^{-i\omega^{\ast}\tau^{\ast}} \\ &\quad{} +G_{210} \bigl(2\eta\overline{\eta}e^{-i\omega^{\ast}\tau^{\ast}}+ \eta^{2} e^{i\omega^{\ast}\tau^{\ast}} \bigr) +G_{201} \bigl(2 \eta^{2}\overline{\eta}e^{-i\omega^{\ast}\tau^{\ast}}+\eta^{2}\overline{ \eta}e^{i\omega^{\ast}\tau^{\ast}} \bigr) \\ &\quad{} + G_{120} \bigl(2\eta+\overline{\eta}e^{-2i\omega^{\ast}\tau^{\ast}} \bigr)+ G_{021} \bigl(2\eta e^{-i\omega^{\ast}\tau^{\ast}} +\overline{\eta} e^{-i\omega^{\ast}\tau^{\ast}} \bigr) \\ &\quad{} + G_{102} \bigl(2\eta^{2}\overline{\eta} + \eta^{2} \overline{\eta} e^{-2i\omega^{\ast}\tau^{\ast}} \bigr) + G_{012} \bigl(2\eta\overline{\eta}e^{-i\omega^{\ast}\tau^{\ast}}+\eta^{2} e^{-i\omega ^{\ast}\tau^{\ast}} \bigr) \\ &\quad{} + 2G_{111} \bigl(\eta\overline{\eta} +\eta\overline{\eta} e^{-2i\omega^{\ast}\tau^{\ast}} +\eta^{2} \bigr) \bigr] \\ &\quad{} + \int_{0}^{l\pi} \cos^{2}\frac{nx}{l} \overline{\xi} \bigl[ F_{20} \bigl(W_{20}^{(1)}(0) +2W_{11}^{(1)}(0) \bigr) +F_{02} \bigl(\overline{ \eta}W_{20}^{(2)}(0) +2\eta W_{11}^{(2)}(0) \bigr) \\ &\quad{} + F_{11} \bigl( W_{20}^{(2)}(0)+\overline{ \eta}W_{20}^{(1)}(0) +2\eta W_{11}^{(1)}(0)+2W_{11}^{(20)}(0) \bigr) \bigr]\,\mathrm{d}x \\ &\quad{} + \int_{0}^{l\pi} \cos^{2}\frac{nx}{l} \bigl[ G_{200} \bigl(\overline{\eta}W_{20}^{(2)}(0) + 2\eta W_{11}^{(2)}(0) \bigr) \\ &\quad{} + G_{020} \bigl(W_{20}^{(1)}(-1)e^{i\omega^{\ast}\tau^{\ast}}+2W_{11}^{(1)}(-1)e^{-i\omega^{\ast}\tau^{\ast}} \bigr) \\ &\quad{} + G_{002} \bigl(\overline{\eta} W_{20}^{(2)}(-1) e^{i\omega^{\ast}\tau^{\ast}} +2\eta W_{11}^{(2)}(-1)e^{-i\omega^{\ast}\tau ^{\ast}} \bigr) \\ &\quad{} + G_{110} \bigl( \overline{\eta} W_{20}^{(1)}(-1)+W_{20}^{(2)}(0) e^{i\omega^{\ast}\tau^{\ast}} +2\eta W_{11}^{(1)}(-1)+2W_{11}^{(2)}(0) e^{-i\omega^{\ast}\tau^{\ast}} \bigr) \\ &\quad{} + G_{101} \bigl( \overline{\eta} W_{20}^{(2)}(0)e^{i\omega^{\ast}\tau^{\ast}} +\overline{\eta} W_{20}^{(2)}(-1) +2\eta W_{11}^{(2)}(0)e^{-i\omega^{\ast}\tau^{\ast}}+2 \eta W_{11}^{(2)}(-1) \bigr) \\ &\quad{} + G_{011} \bigl( \overline{\eta} W_{20} ^{(1)}(-1)e^{i\omega^{\ast}\tau^{\ast}}+ W_{20}^{(2)}(-1)e^{i\omega^{\ast}\tau ^{\ast}} +2\eta W_{11}^{(1)}(-1)e^{-i\omega^{\ast}\tau^{\ast}} \\ &\quad{} + 2W_{11}^{(2)}(-1)e^{-i\omega^{\ast}\tau^{\ast}} \bigr) \bigr]\, \mathrm{d}x \biggr\} , \end{aligned} \end{aligned}$$

where \(n=0,1,2,\ldots\) and

$$\begin{aligned}& W_{20}(\theta)= \biggl( \frac{ig_{20}}{\omega^{\ast}\tau^{\ast}}q(\theta) + \frac{i\overline{g_{02}}}{3\omega^{\ast}\tau^{\ast}}\overline{q(\theta)} \biggr) \cdot f_{n}+E_{1} e^{2i\omega^{\ast}\tau^{\ast}\theta}, \\& W_{11}(\theta)= \biggl( -\frac{ig_{11}}{\omega^{\ast}\tau^{\ast}}1(\theta) + \frac{i\overline{g_{11}}\overline{q(\theta)}}{\omega^{\ast}\tau^{\ast}} \biggr) \cdot f_{n}+E_{2}, \\& E_{1}=E_{1}'\times \left ( \textstyle\begin{array}{c} F_{20}+F_{02}\eta^{2}+2F_{11}\eta \\ E_{12} \end{array}\displaystyle \right ) \cos^{2}\frac{nx}{l}, \\& E_{12}=(G_{020} e^{-2i\omega^{\ast}\tau^{\ast}} + \eta e^{-2i\omega^{\ast}\tau ^{\ast}}( G_{002}+2G_{011}) + 2\eta e^{-i\omega^{\ast}\tau^{\ast}}(G_{110}+G_{101} \eta), \\& E_{1}'=\left ( \textstyle\begin{array}{c@{\quad}c} 2i\omega^{\ast}+d_{1}\frac{n^{2}}{l^{2}}-\frac{2\beta -(1+m)^{2}}{(1+m)^{2}} & \frac{\beta(1-m)}{(1+m)^{2}} \\ -re^{-2i\omega^{\ast}\tau^{\ast}} & 2i\omega^{\ast}+ d_{2}\frac {n^{2}}{l^{2}}+re^{-2i\omega^{\ast}\tau^{\ast}} \end{array}\displaystyle \right ) ^{-1}, \end{aligned}$$

and

$$\begin{aligned}& E_{2}=E_{2}'\times \left ( \textstyle\begin{array}{c} F_{20}+F_{02}\vert \eta \vert ^{2}+F_{11}(\eta +\overline{\eta} ) \\ E_{22} \end{array}\displaystyle \right )\cos^{2}\frac{nx}{l}, \\& \begin{aligned} E_{22} &= \vert \eta \vert ^{2}(G_{200} +G_{002}) +G_{020}+2G_{110}\operatorname{Re} \bigl\{ \eta e^{i\omega^{\ast}\tau^{\ast}} \bigr\} \\ &\quad{} +2\vert \eta \vert ^{2}G_{101} \operatorname{Re} \bigl\{ e^{i\omega^{\ast}\tau^{\ast}} \bigr\} +2G_{011} \operatorname{Re}\{\eta\}, \end{aligned} \\& E_{2}'=\left ( \textstyle\begin{array}{c@{\quad}c} d_{1}\frac{n^{2}}{l^{2}}-\frac{2\beta -(1+m)^{2}}{(1+m)^{2}} & \frac{\beta(1-m)}{(1+m)^{2}} \\ -r & d_{2}\frac{n^{2}}{l^{2}}+r \end{array}\displaystyle \right ) ^{-1}. \end{aligned}$$

From the above analysis, we can compute the following quantities which determine the direction of bifurcation and the stability of periodic solutions:

$$\begin{aligned}& c_{1}(0)=\frac{i}{2\omega^{\ast}\tau^{\ast}} \biggl( g_{20}g_{11}-2 \vert g_{11}\vert ^{2}-\frac{1}{3}\vert g_{02}\vert ^{2} \biggr) +\frac{g_{21}}{2}, \\& \ell_{2}=-\frac{\operatorname{Re}(c_{1}(0))}{\operatorname{Re}(\lambda' (\tau^{\ast}))}, \\& \iota_{2}=2\operatorname{Re} \bigl(c_{1}(0) \bigr), \\& \chi_{2}=-\frac{1}{\omega^{\ast}\tau^{\ast}} \bigl(\operatorname{Im} \bigl(c_{1}(0) \bigr)+\ell_{2} \operatorname{Im} \bigl( \lambda' \bigl( \tau^{\ast}\bigr) \bigr) \bigr). \end{aligned}$$

Theorem 5

For system (1),

  1. (i)

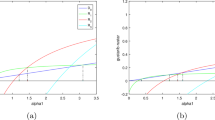
    \(\ell_{2}\) determines the bifurcation direction: if \(\ell _{2}>0\), then the bifurcation is supercritical and the periodic solution exists for \(\tau>\tau_{0}\); if \(\ell_{2}<0\), then the bifurcation is subcritical and the periodic solution exists for \(\tau<\tau_{0}\).

  2. (ii)

    \(\iota_{2}\) determines the stability of bifurcating periodic solutions: the periodic solutions are orbitally asymptotically stable if \(\iota_{2}<0\), or unstable if \(\iota_{2}>0\).

  3. (iii)

    \(\chi_{2}\) determines the period of the bifurcating periodic solutions: the period is monotonically increasing at time delay τ when \(\chi_{2}>0\), or is monotonically decreasing at time delay τ when \(\chi_{2}<0\).

5 Numerical simulations

In this section, to illustrate the analytic results, we will conduct some numerical examples by the aid of MATLAB.

For system (1), we set

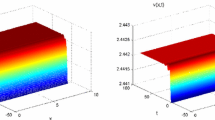
$$\Omega=(0,\pi),\quad\quad m=0.1, \quad\quad r=0.08, \quad\quad d_{1}=1, \quad\quad d_{2}=0.5, $$

and choose the initial functions \(u_{1}=0.6+0.4 \sin(x+t)\) and \(v_{1}=1+0.6\sin(x+t)\), then we can get the unique Hopf bifurcation value \(\beta_{0}=0.6534\). Thus, the bifurcating periodic solutions are spatially homogeneous. From Theorem 3, we can find that the positive equilibrium solution \(E_{\ast}\approx(0.4309, 0.4309)\) is asymptotically stable when \(\beta =0.626<\beta_{0}\) (see Figure 1), and the periodic solution bifurcates from \(E_{\ast}\approx(0.3818, 0.3818)\) when \(\beta=0.68>\beta_{0}\) (see Figure 2). From Figure 3, the solutions converge to zero, and a periodic phenomenon vanishes when β is slightly away from the critical value \(\beta_{0}\) because the Hopf bifurcation obtained in Theorem 3 is only local.

Figure 1
figure 1

The equilibrium solution \(\pmb{E_{\ast}}\) is stable when \(\pmb{\beta =0.626<\beta_{0}}\) .

Full size image
Figure 2
figure 2

Periodic solution exists when \(\pmb{\beta=0.68>\beta_{0}}\) .

Full size image
Figure 3
figure 3

Solution converges to zero when \(\pmb{\beta=0.8>\beta_{0}}\) .

Full size image

Next, to meet the assumption (H3), we rechoose

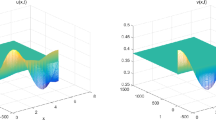
$$m=3, \quad\quad \beta=0.5,\quad\quad r=0.6, \quad\quad d_{1}=1, \quad\quad d_{2}=0.5, $$

and the initial functions \(u_{1}=0.6\) and \(v_{1}=1\). Then the positive equilibrium solution is \(E_{\ast}=(0.875,0.875)\). By direct computation, we have the Hopf bifurcation critical value \(\tau _{0}\approx2.5181\) when \(n=0\) and \(\omega_{0}\approx0.635415\). From Figures 4 and 5, we can observe that the positive equilibrium solution \(E_{\ast}\) is asymptotically stable when time delay \(\tau=1.85\) is smaller than the Hopf bifurcation critical value \(\tau_{0}\); on the other hand, \(E_{\ast}\) is unstable, and a periodic phenomenon appears when \(\tau=3>\tau_{0}\).

Figure 4
figure 4

The equilibrium solution \(\pmb{E_{\ast}}\) is stable when \(\pmb{\tau =1.85<\tau_{0}}\) .

Full size image
Figure 5
figure 5

The equilibrium solution \(\pmb{E_{\ast}}\) is unstable, and a periodic solution occurs when \(\pmb{\tau=3>\tau_{0}}\) .

Full size image

Finally, from Figure 6, we can also observe the existence of spatially inhomogeneous periodic solution when

$$m=3, \quad\quad \beta=0.5, \quad\quad r=0.6, \quad\quad d_{1}=0.0008, \quad\quad d_{2}=0.008, \quad\quad \tau=3 $$

with initial values \(u_{1}=0.8+0.2\cos(4x+t)\) and \(u_{2}=1+0.5\cos(3x+t)\).

Figure 6
figure 6

The spatially inhomogeneous periodic solution exists.

Full size image

6 Conclusions

In this paper, we have considered a ratio-dependent predator-prey system with spatial diffusion and time delay and have investigated the joint effects of spatial diffusion and time delay. The well-posedness of solutions and the dissipativeness of the system have been established based on inequality techniques. Hopf bifurcation conditions have also been derived by choosing different bifurcation parameters respectively. It is observed that a periodic phenomenon appears when the bifurcation parameter passes through some critical value.

It is shown that the parameter β, which reflects the specific predation rate or the interaction strength between two species, can make the equilibrium solution \(E_{\ast}=(u_{\ast}, v_{\ast})\) asymptotically stable or unstable without time delay. From Theorem 3, we can control the parameter β sufficiently small to achieve the stabilization. For example, some measures can be adopted to decrease the value of β, such as founding a refuge for prey species or increasing the interference with interaction between two species. On the other hand, the numerical examples indicate that a spatially homogeneous periodic solution will exist when the parameter β is larger than the Hopf bifurcation value. Nevertheless, when β is far away from the critical value, the two species will be extinct. It reflects that over-hunting or denudation may seriously destroy the ecological environment.

Our results also show that time delay has a vital impact on the dynamics of system (1). The second group of parameters we choose in Section 5 also satisfy the conditions of Theorem 2.7 in [18]. That is to say, the equilibrium solution \(E_{\ast}\) is globally asymptotically stable when time delay is equal to zero. However, the asymptotic behavior is not able to always keep stable when time delay varies. If time delay τ is sufficiently small, then the equilibrium solution \(E_{\ast}\) is still asymptotically stable. When τ is slightly larger than a certain critical value, the equilibrium solution \(E_{\ast}\) is no longer stable and a spatially periodic solution may appear. Furthermore, if we choose other diffusion coefficients, we can find spatially inhomogeneous periodic solutions, which are not included in [19, 20], without time delay.

Well, due to the local existence of Hopf bifurcation, the periodic solutions only exist in a small neighborhood of bifurcation value. It is interesting and significant to further explore the global continuation of local Hopf bifurcation, which can ensure the existence of periodic solutions when the parameter is much larger or less than the bifurcation value. We will continue this research in the near future. Still, the methods and results in the present paper have supplemented the ones in [18–20] and can also be applied to other reaction-diffusion systems without or with time delay. We hope that our work could be useful to study the effects of spatial diffusion and time delay on the population dynamics.