1 Introduction

In this work, we present an iterative reproducing kernel Hilbert spaces method (IRKHSM) for investigating the fractional Riccati differential equation of the following form [1, 2]:

$$ { }^{c}D_{0+}^{\alpha}u(\eta)=p(\eta)u^{2}( \eta)+q(\eta)u(\eta )+r(\eta) ,\quad 0 \leq\eta\leq T, $$
(1)

with the initial condition

$$ u(0)=0, $$
(2)

where \(p ( \eta ) \), \(q ( \eta )\), \(r ( \eta )\) are real continuous functions, and \(u ( \eta )\in W_{2}^{2} [ {0, T} ]\).

The Riccati differential equation is named after the Italian nobleman Count Jacopo Francesco Riccati (1676-1754). The book of Reid [1] includes the main theories of Riccati equation, with implementations to random processes, optimal control, and diffusion problems [2].

Fractional Riccati differential equations arise in many fields, although discussions on the numerical methods for these equations are rare. Odibat and Momani [3] investigated a modified homotopy perturbation method for fractional Riccati differential equations. Khader [4] researched the fractional Chebyshev finite difference method for fractional Riccati differential equations. Li et al. [5] have solved this problem by quasi-linearization technique.

There has been much attention in the use of reproducing kernels for the solutions to many problems in the recent years [6, 7]. Those papers show that this method has many outstanding advantages [8]. Cui has presented the Hilbert function spaces. This useful framework has been utilized for obtaining approximate solutions to many nonlinear problems [9]. Convenient references for this method are [10–13].

This paper is arranged as follows. Reproducing kernel Hilbert space theory is given in Section 2. Implementation of the IRKHSM is shown in Section 3. Exact and approximate solutions of the problems are presented in Section 4. Some numerical examples are given in Section 5. A summary of the results of this investigation is given in Section 6.

2 Preliminaries

The fractional derivative has good memory influences compared with the ordinary calculus. Fractional differential equations are attained in model problems in fluid flow, viscoelasticity, finance, engineering, and other areas of implementations.

Definition 2.1

The Riemann-Liouville fractional integral operator of order α is determined as [14]

$$ J_{0+}^{\alpha}y(x)=\frac{1}{\Gamma(\alpha)} \int_{0}^{x} {(x-r)^{\alpha -1}y(r)\,dr}, $$
(3)

where \(\Gamma(\cdot)\) is the gamma function, \(\alpha\geq0\) and \(x>0\).

Definition 2.2

The Caputo derivative of order α is given as [14]

$$ { }^{c}D_{0+}^{\alpha}y(x)=\frac{1}{\Gamma(n-\alpha)} \int _{0}^{x}\frac{\partial^{n}}{\partial x^{n}}\frac {y(r)}{(x-r)^{n-\alpha}} \,dr, $$
(4)

where \(n-1<\alpha\leq n\) and \(x>0\).

We need the following properties:

$$\begin{aligned}& \mathrm{(i)}\quad J_{0+}^{\alpha}{ }^{c}D_{0+}^{\alpha}y(x)=y(x)- \sum_{k=0}^{m-1}y^{k} \bigl(0^{+}\bigr)\frac{x^{k}}{k!}. \\& \mathrm{(ii)}\quad { }^{c}D_{0+}^{\alpha}J_{0+}^{\alpha}y(x)=y(x). \end{aligned}$$

3 Reproducing kernel functions

We describe the notion of reproducing kernel Hilbert spaces, show some particular instances of these spaces, which will play an important role in this work, and define some well-known properties of these spaces in this section.

Definition 3.1

Let \(S\neq\emptyset\), \(B:S\times S \to{C}\) is a reproducing kernel function of the Hilbert space H iff [10]

$$\begin{aligned}& \mathrm{(i)} \quad \forall\tau\in S, \quad B (\cdot,\tau ) \in H; \\& \mathrm{(ii)} \quad \forall\tau\in S, \forall\phi\in H, \quad \bigl\langle \phi ( \cdot ),B ( {\cdot, \tau} )\bigr\rangle = \phi ( \tau ). \end{aligned}$$

Definition 3.2

The inner product space \(W_{2}^{2} [ {0, T} ]\) is presented as [15]

$$\begin{aligned} W_{2}^{2} [ {0, T} ] &= \bigl\{ f ( t ) | f, {f}' \text{ are absolutely continuous (AC) real-valued functions}, \\ &\quad {f}'' \in L^{2} [ {0, T} ], f ( 0 ) = 0 \bigr\} , \end{aligned} $$

where \(L^{2} [ {0,T} ] = \{ {f } | \int_{0}^{T} {f^{2} ( t )\,dt < \infty} \}\),

$$ \bigl\langle f ( t ),g ( t )\bigr\rangle _{W_{2}^{2}[0,T] } = f ( 0 )g ( 0 ) + f ( T )g ( T ) + \int_{0}^{T} {{f}'' ( t ){g}'' ( t )\,dt} $$
(5)

and

$$\Vert f \Vert _{W_{2}^{2} } = \sqrt{\langle f,f\rangle _{W_{2}^{2} } } ,\quad f,g \in W_{2}^{2} [ {0, T} ], $$

are the inner product and norm in \(W_{2}^{2} [ {0, T} ]\).

Theorem 3.1

\(W_{2}^{2} [ {0, T} ]\) is an RKHS. There exist \(R_{x} ( t ) \in W_{2}^{2} [ {0, T} ]\) for any \(f ( t ) \in W_{2}^{2} [ {0, T} ]\) and each fixed \(x \in [ {0, T} ]\), \(t \in [ {0, T} ]\), such that \(\langle f ( t ),R_{x} ( t )\rangle _{W_{2}^{2} } = f ( x )\). The reproducing kernel \(R_{x} ( t )\) can be written as [15]

$$ R_{x} ( t ) = \textstyle\begin{cases} R_{1} (x,t), &t \le x,\\ R_{1} (t,x) , &t > x, \end{cases} $$
(6)

where

$$\begin{aligned} R_{1} (x,t) = t\bigl((x - T)Tt^{2} + x\bigl(2T^{3} - 3xT^{2} + x^{2}T + 6\bigr)\bigr) / \bigl(6T^{2} \bigr). \end{aligned}$$

Definition 3.3

\(W_{2}^{1} [ {0, T} ]\) is given as [15]

$$ \begin{gathered} W_{2}^{1} [ {0, T} ] = \bigl\{ f ( x )| f \mbox{ is AC real-valued function}, {f}' \in L^{2} [ {0, T} ] \bigr\} , \\ \bigl\langle f ( t ),g ( t )\bigr\rangle _{W_{2}^{1}[0,T]} = f ( 0 )g ( 0 ) + \int_{0}^{T} {{f}' ( t ){g}' ( t )\,dt}, \end{gathered} $$
(7)

and

$$\Vert f \Vert _{W_{2}^{1} } = \sqrt{\langle f,f\rangle _{W_{2}^{1} } } ,\quad f,g \in W_{2}^{1} [ {0, T} ], $$

are the inner product and norm in \(W_{2}^{1} [ {0, T} ]\).

\(W_{2}^{1} [ {0, T} ]\) is am RKHS, and its reproducing kernel function is obtained as

$$ T_{x} ( t ) = \textstyle\begin{cases} 1 + t ,& t \le x,\\ 1 + x ,& t > x. \end{cases} $$
(8)

4 Solutions to the fractional Riccati differential equations in RKHS

The solution of (1)-(2) has been obtained in the RKHS \(W_{2}^{2} [ {0, T} ]\). To get through with the problem, we investigate equation (1) as

$$\begin{aligned} u(\eta)=f\bigl(\eta,u(\eta)\bigr), \quad 0< \eta< T, \end{aligned}$$
(9)

where

$$\begin{aligned} f\bigl(\eta,u(\eta)\bigr)=\frac{1}{\Gamma(\alpha)} \int_{0}^{\eta}(\eta -\tau)^{\alpha-1}\bigl(p( \tau)u^{2}(\tau)+q(\tau)u(\tau)+r(\tau)\bigr)\,d\tau , \quad 0< \alpha\leq1. \end{aligned}$$

Let \(L:W^{2}_{2}[0,T]\rightarrow W_{2}^{1}[0,T]\) be such that \(Lu(\eta )= u(\eta)\). Then L is a bounded linear operator. We define \(\varphi_{i} ( \eta ) = T_{\eta_{i} } ( \eta )\) and \(\psi_{i} ( \eta ) = L^{\ast}\varphi_{i} ( \eta )\). By the Gram-Schmidt orthogonalization process we obtain

$$ \bar{\psi}_{i} ( \eta ) = \sum_{k = 1}^{i} {\beta_{ik} \psi_{k} ( \eta )} \quad ( {\beta_{ii} > 0, i = 1,2,\ldots} ). $$
(10)

Theorem 4.1

If \(\{ {\eta_{i} } \}_{i = 1}^{\infty}\) is dense on \([ {0, T} ]\), then \(\{ {\psi_{i} ( \eta )} \}_{i = 1}^{\infty}\) is a complete system of \(W_{2}^{2} [ {0, T} ]\), and we have \(\psi_{i} ( \eta ) = {L_{t} R_{\eta}( t )} | _{t = \eta_{i} } \).

Proof

We obtain

$$\begin{aligned} \psi_{i} ( \eta ) &= \bigl( {L^{\ast}\varphi_{i} } \bigr) ( \eta ) = \bigl\langle \bigl( {L^{\ast}\varphi_{i} } \bigr) ( t ),R_{\eta}( t )\bigr\rangle \\ &= \langle\varphi_{i} ( t ),L_{t} R_{\eta}( t )\rangle= {L_{t} R_{\eta}( t )} | _{t = \eta_{i} } . \end{aligned} $$

It appears that \(\psi_{i} ( \eta ) \in W_{2}^{2} [ {0, T} ]\). For each fixed \(u ( \eta ) \in W_{2}^{2} [ {0, T} ]\), let \(\langle u ( \eta ),\psi_{i} ( \eta )\rangle= 0\) (\({i = 1,2,\ldots} \)), which means that

$$ \bigl\langle u ( \eta ),L^{\ast}\varphi_{i} ( \eta )\bigr\rangle = \bigl\langle Lu (\cdot ),\varphi_{i} ( \cdot )\bigr\rangle = ( {Lu} ) ( {\eta_{i} } ) = 0. $$
(11)

Remark that \(\{ {\eta_{i} } \}_{i = 1}^{\infty}\) is dense on \([ {0, T} ]\), and hereby \(( {Lu} ) ( \eta ) = 0\). We obtain \(u \equiv0\) by \(L^{ - 1}\). So, the proof of Theorem 4.1 is complete. □

Theorem 4.2

If \(\{ {\eta_{i} } \}_{i = 1}^{\infty}\) is dense on \([ {0, T} ]\) and the solution of (9) is unique, then the solution of (1)-(2) is obtained as

$$ u ( \eta ) = \sum_{i = 1}^{\infty}{\sum _{k = 1}^{i} {\beta _{ik} f \bigl( { \eta_{k} ,u(\eta_{k}) } \bigr)} } \bar{\psi}_{i} ( \eta ). $$
(12)

Proof

\(\{ {\bar{\psi }_{i} ( \eta )} \}_{i = 1}^{\infty}\) is a complete orthonormal basis of \(W_{2}^{2} [ {0, T} ]\) by Theorem 4.1. Therefore, we acquire

$$\begin{aligned} u ( \eta ) =& \sum_{i = 1}^{\infty}{\bigl\langle u ( \eta ),\bar{\psi}_{i} ( \eta )\bigr\rangle _{W_{2}^{2}[0,T] } } \bar{ \psi}_{i} ( \eta ) \\ =& \sum_{i = 1}^{\infty}{\sum _{k = 1}^{i} {\beta_{ik} \bigl\langle u ( \eta ),L^{\ast}T_{\eta_{k} } ( \eta )\bigr\rangle _{W_{2}^{2}[0,T] } } } \bar{\psi}_{i} ( \eta ) \\ = &\sum_{i = 1}^{\infty}{\sum _{k = 1}^{i} {\beta_{ik} \bigl\langle Lu ( x ),T_{\eta_{k} } ( \eta )\bigr\rangle _{W_{2}^{1}[0,T] } } } \bar { \psi}_{i} ( \eta ) \\ =& \sum_{i = 1}^{\infty}{\sum _{k = 1}^{i} {\beta_{ik} \bigl\langle f \bigl( {\eta,u(\eta)} \bigr),T_{\eta_{k} } ( \eta )\bigr\rangle _{W_{2}^{1}[0,T] } } } \bar {\psi}_{i} ( \eta ) \\ =& \sum_{i = 1}^{\infty}{\sum _{k = 1}^{i} {\beta_{ik} f \bigl( { \eta_{k} ,u(\eta_{k}) } \bigr)} } \bar{\psi}_{i} ( \eta ). \end{aligned}$$

This completes the proof. □

The approximate solution \(u_{n} ( \eta )\) can be gained by the n-term intercept of the exact solution \(u ( \eta )\) as

$$ u_{n} ( \eta ) = \sum_{i = 1}^{n} { \sum_{k = 1}^{i} {\beta _{ik} f \bigl( {\eta_{k} ,u(\eta_{k}) } \bigr)} } \bar{ \psi}_{i} ( \eta ). $$
(13)

Remark 4.1

We notice the following two cases in order to solve equations (1)-(2) by using RKHS.

Case 1: If equation (1) is linear, that is, \(p(\eta )=0\), then an approximate solution can be obtained directly from equation (12) .

Case 2: If equation (1) is nonlinear, that is, \(p(\eta)\neq0\), then an approximate solution can be obtained by using the following iterative method. According to equation (13), the exact solution of equation (1) can be denoted by

$$ u(\eta) = \sum_{i = 1}^{\infty}{A_{i} \bar{\psi}_{i} ( \eta )} , $$
(14)

where \(A_{i} = \sum_{k = 1}^{i} {\beta_{ik} f ( {\eta_{k} ,u ( {\eta_{k} } )} )} \). In fact, \(A_{i} \), \(i = 1,2,\ldots\) , in (14) are unknown, and we will approximate \(A_{i} \) using known \(B_{i} \). For a numerical computation, we define the initial function \(u_{0} ( {\eta_{1} } ) = 0\) (we can choose any fixed \(u_{0} ( {\eta_{1} } ) \in W_{2}^{2} [ {0, T} ]\)) and the n-term approximation to \(u ( \eta )\) by

$$ u_{n} (\eta) = \sum_{i = 1}^{n} {B_{i} \bar{\psi}_{i} ( \eta )} , $$
(15)

where the coefficients \(B_{i} \) of \(\bar{\psi}_{i} ( \eta )\) are given as

$$\begin{aligned}& B_{1} = \beta_{11} f \bigl( {\eta_{1} ,u_{0} ( {\eta_{1} } )} \bigr), \\& u_{1} ( \eta ) = B_{1} \bar{\psi}_{1} ( \eta ), \\& B_{2} = \sum_{k = 1}^{2} { \beta_{2k} } f \bigl( {\eta_{k} ,u_{k - 1} ( { \eta_{k} } )} \bigr), \\& u_{2} ( \eta ) = \sum_{i = 1}^{2} {B_{i} \bar{\psi}_{i} ( \eta )} , \\& \vdots \\& u_{n - 1} ( \eta ) = \sum_{i = 1}^{n - 1} {B_{i} \bar{\psi}_{i} ( \eta )} , \\& B_{n} = \sum_{k = 1}^{n} { \beta_{nk} } f \bigl( {\eta_{k} ,u_{k - 1} ( { \eta_{k} } )} \bigr). \end{aligned}$$
(16)

In equation (15), we can see that the approximation \(u_{n} ( \eta )\) satisfies the initial condition (2). The approximate solution is computed from 15:

$$ u_{n}^{N} ( \eta ) = \sum_{i = 1}^{N} {\sum_{k = 1}^{i} {\beta_{ik} f \bigl( {\eta_{k} ,u_{n - 1} ( {\eta_{k} } )} \bigr)} } \bar{\psi}_{i} ( \eta ). $$
(17)

Theorem 4.3

If \(u(\eta)\in W_{2}^{2}[0,T]\), then there exist \(E > 0\) and \(\Vert u(\eta)\Vert _{C[0,T]} = {\max} _{\eta\in[0,T]}\vert u(\eta)\vert \) such that \(\Vert u^{(i)}(\eta)\Vert _{C[0,T]}\le E\Vert u(\eta )\Vert _{W_{2}^{2}[0,T]}\), \(i =0,1\).

Proof

We obtain \(u^{(i)} ( \eta ) = \langle u ( t ),\partial_{\eta}^{i} R_{\eta}( t )\rangle_{W_{2}^{2}[0,T] } \) for any η, \(t \in [ {0, T} ]\) and \(i = 0, 1\). Then, we get \(\Vert {\partial_{\eta}^{i} R_{\eta}( t )} \Vert _{W_{2}^{2}[0,T] } \le E_{i} \), \(i = 0,1\), by \(R_{\eta}( t )\).

Therefore, we acquire

$$\begin{aligned} \bigl\vert {u^{(i)} ( \eta )} \bigr\vert =& \bigl\vert {\bigl\langle u ( \eta ),\partial_{\eta}^{i} R_{\eta}( x ) \bigr\rangle _{W_{2}^{2}[0,T] } } \bigr\vert \\ \le& \bigl\Vert {u ( \eta )} \bigr\Vert _{W_{2}^{2}[0,T] } \bigl\Vert { \partial_{\eta}^{i} R_{\eta}( \eta )} \bigr\Vert _{W_{2}^{2}[0,T] } \\ \le& E_{i} \bigl\Vert {u ( \eta )} \bigr\Vert _{W_{2}^{2}[0,T] } \end{aligned}$$

for \(i=0, 1\).

Thus, we get \(\Vert {u^{(i)} ( \eta )} \Vert _{C[0,T]} \le\max\{E_{0} , E_{1} \}\Vert {u ( \eta )} \Vert _{W_{2}^{2}[0,T] }\) for \(i=0, 1\). This completes the proof. □

Theorem 4.4

The approximate solution \(u_{n} ( \eta )\) and its first derivative \({u}'_{n} ( \eta )\) are uniformly convergent in \([0,T]\).

Proof

From Theorem 4.3, for any \(\eta\in [ {0,T} ]\), we get

$$\begin{aligned} \bigl\vert {u_{n}^{ ( i )} ( \eta ) - u^{ ( i )} ( \eta )} \bigr\vert = &\bigl\vert {\bigl\langle u_{n} ( \eta ) - u ( \eta ),\partial_{\eta}^{i} R_{\eta}( \eta )\bigr\rangle _{W_{2}^{2}[0,T] } } \bigr\vert \\ \le& \bigl\Vert {\partial_{\eta}^{i} R_{\eta}( \eta )} \bigr\Vert _{W_{2}^{2}[0,T] } \bigl\Vert {u_{n} ( \eta ) - u ( \eta )} \bigr\Vert _{W_{2}^{2}[0,T] } \\ \le& E_{i} \bigl\Vert {u_{n} ( \eta ) - u ( \eta )} \bigr\Vert _{W_{2}^{2}[0,T]} , \quad i = 0,1, \end{aligned}$$

where \(E_{0} \) and \(E_{1} \) are positive constants. Hence, if \(u_{n} ( \eta ) \to u ( \eta )\) in the sense of the norm of \(W_{2}^{2} [0,T]\) as \(n \to\infty\), then the approximate solutions \(u_{n} ( \eta )\) and \({u}'_{n} ( \eta )\) uniformly converge to the exact solution \(u ( \eta )\) and its derivative \({u}' ( \eta )\), respectively. □

5 Numerical examples

To give a clear overview of this technique, we give the following informative examples. All of the computations have been applied by utilizing the Maple software package. The results attained by the method are compared with the exact solution of each example and are found to be in good agreement.

Example 5.1

We debate the fractional Riccati differential equation

$$\begin{aligned}& { }^{c}D_{0+}^{\alpha}u(\eta) = 1 -u^{2} ( \eta ), \quad 0 \leq \eta\leq T, \end{aligned}$$
(18)
$$\begin{aligned}& u ( 0 ) = 0. \end{aligned}$$
(19)

The exact solution of (18)-(19) is given by

$$ u ( \eta ) = \frac{e^{2 \eta} - 1}{e^{2 \eta} + 1} $$
(20)

when \(\alpha=1\). Using IRKHSM for equations (18)-(19) and taking \(T=1\), \(\eta_{i} = \frac{i}{N}\), \(i = 1, 2,\ldots,N\), the numerical solution \(u_{n}^{N} ( \eta )\) is computed. Comparison of our result with other methods at some selected grid points for \(N = 10\), \(n = 8\), and \(\alpha=1\), \(\alpha=0.9\), \(\alpha=0.75\) are given in Tables 1-3, respectively.

Table 1 Comparison of IRKHSM solution with other methods for Example  5.1 ( \(\pmb{\alpha=1}\) )
Full size table
Table 2 Comparison of IRKHSM solution with other methods for Example  5.1 ( \(\pmb{\alpha=0.9}\) )
Full size table
Table 3 Comparison of IRKHSM solution with other methods for Example  5.1 ( \(\pmb{\alpha=0.75}\) )
Full size table

Example 5.2

We investigate the fractional Riccati differential equation as

$$\begin{aligned}& { }^{c}D_{0+}^{\alpha}u(\eta)= 1 + 2u ( \eta )-u^{2} ( \eta ), \quad 0 \leq\eta\leq T, \end{aligned}$$
(21)
$$\begin{aligned}& u ( 0 ) = 0. \end{aligned}$$
(22)

The exact solution of (21)-(22) is given as

$$ u ( \eta ) = 1 + \sqrt{2} \tanh \biggl( {\sqrt{2} \eta+ \frac{\log ( { ( { - 1 + \sqrt{2} } ) / ( {1 + \sqrt{2} } )} )}{2}} \biggr) $$
(23)

when \(\alpha=1\). Using IRKHSM for equations (21)-(22) and taking \(T=1\), \(\eta_{i} = \frac{i}{N}\), \(i = 1, 2,\ldots,N\), the numerical solution \(u_{n}^{N} ( \eta )\) is computed. The absolute errors of some methods are given in Table 4. Comparison of our result with other methods at some selected grid points for \(N = 13\), \(n = 6\), and \(\alpha=0.9\), \(\alpha=0.75\) are given in Tables 5 and 6, respectively.

Table 4 Comparison of absolute errors for some methods for Example  5.2 ( \(\pmb{\alpha=1}\) )
Full size table
Table 5 Comparison of IRKHSM solution with other methods for Example  5.2 ( \(\pmb{\alpha=0.9}\) )
Full size table
Table 6 Comparison of IRKHSM solution with other methods for Example  5.2 ( \(\pmb{\alpha=0.75}\) )
Full size table

Example 5.3

We solve the fractional Riccati differential equation

$$\begin{aligned}& { }^{c}D_{0+}^{\alpha}u(\eta) = \eta^{3} u^{2} ( \eta ) - 2 \eta^{4} u ( \eta ) + \eta^{5}, \end{aligned}$$
(24)
$$\begin{aligned}& u ( 0 ) = 0. \end{aligned}$$
(25)

The exact solution of (24)-(25) is given as

$$ u ( \eta ) = \eta $$
(26)

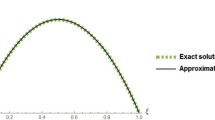
when \(\alpha=1\). Using IRKHSM for equations (24)-(25) and taking \(T=1\), \(\eta_{i} = \frac{i}{N}\), \(i = 1, 2,\ldots,N\), the numerical solution \(u_{n}^{N} ( \eta )\) is computed. Comparison of the IRKHSM solutions \(u_{3}^{4}(\eta)\) for Example 5.3 with different values of α is given in Figure 1. The absolute error of IRKHSM solution \(u_{3}^{4}(\eta)\) for Example 5.3 with \(\alpha=1\) is shown in Figure 2.

Figure 1
figure 1

Comparison of the IRKHSM solutions for Example 5.3 .

Full size image
Figure 2
figure 2

Absolute error of IRKHSM solution for Example 5.3 .

Full size image

6 Conclusion

IRKHSM were successfully implemented to get approximate solutions of the fractional Riccati differential equations. Numerical results were compared with the existing methods to prove the efficiency of the method. The IRKHSM is very powerful and accurate in obtaining approximate solutions for wide classes of the problem. The approximate solution attained by the IRKHSM is uniformly convergent. The series solution methodology can be implemented to much more complicated nonlinear equations. This method can be extended to solve the other fractional differential equations.