1 Introduction

The fractional calculus is a mathematical discipline that is 300 years old, and it has developed progressively up to now. The concept of differentiation to fractional order was defined in the 19th century by Riemann and Liouville. In various problems of physics, mechanics, and engineering, fractional differential equations and fractional integral equations have been proved to be a valuable tool in modeling many phenomena [1, 2]. However, most fractional-order equations do not have analytic solutions. Therefore, there has been significant interest in developing numerical schemes for the solutions of fractional-order differential equations.

In the past 40 years, the theory and applications of the fractional-order partial differential equations (FPDEs) have become of increasing interest for the researchers to generalize the integer-order differential equations. Conventionally various technologies, e.g. modified homotopy analysis transform method (MHATM) [3], modified homotopy analysis Laplace transform method [4], homotopy analysis transform method (HATM) [5, 6], fractional homotopy analysis transform method (FHATM) [7], local fractional variational iteration algorithms [8] were used for the solutions of the FPDEs. Meanwhile, local fractional similarity solution for the diffusion equation was discussed in [9]. The inverse problems for the fractal steady heat transfer described by the local fractional Volterra integro-differential equations were considered in [10].

Recently, many effective methods for obtaining approximations or numerical solutions of fractional-order integro-differential equations have been presented. These methods include the variational iteration method [11–13], the adomian decomposition method [14], the fractional differential transform method [15], the reproducing kernel method [16], the collocation method [17, 18], and the wavelet method [19–24].

Wavelet theory is a relatively new and an emerging area in the field of applied science and engineering. Wavelets permit the accurate representation of a variety of functions and operators. Moreover, wavelets establish a connection with fast numerical algorithms [25]. So the wavelet method is a new numerical method for solving the fractional equations and it needs a small amount of calculation. However, the method will produce a singularity in the case of certain increased resolutions. Using wavelet numerical method has several advantages: (a) the main advantage is that after discretizing the coefficient matrix of the algebraic equation shows sparsity; (b) the wavelet method is computer oriented, thus solving a higher-order equation becomes a matter of dimension increasing; (c) the solution is a multi-resolution type; (d) the solution is convergent, even the size of the increment may be large [24]. Many researchers started using various wavelets for analyzing problems of high computational complexity. It is proved that wavelets are powerful tools to explore new directions in solving differential equations and integral equations.

In this paper, the main purpose is to introduce the Euler wavelet operational matrix method to solve the nonlinear Volterra integro-differential equations of fractional order. The Euler wavelet is first presented and it is constructed by Euler polynomials. The method is based on reducing the equation to a system of algebraic equations by expanding the solution as Euler wavelet with unknown coefficients. The characteristic of the operational method is to transform the integro-differential equations into the algebraic one. It not only simplifies the problem but also speeds up the computation. It is worth noting that the Euler polynomials are not based on orthogonal functions, nevertheless, they possess the operational matrix of integration. Also the Euler wavelet is superior to the Legendre wavelet and the Chebyshev wavelet for approximating an arbitrary function, which can be verified by numerical examples.

The structure of this paper is as follows: In Section 2, we recall some basic definitions and properties of the fractional calculus theory. In Section 3, the Euler wavelets are constructed and the operational matrix of the fractional integration is derived. In Section 4, we summarize the application of the Euler wavelet operational matrix method to the solution of the fractional integro-differential equations. Some numerical examples are provided to clarify the approach in Section 5. The conclusion is given in Section 6.

2 Fractional calculus

There are various definitions of fractional integration and derivatives. The widely used definition of a fractional integration is the Riemann-Liouville definition and the definition of a fractional derivative is the Caputo definition.

Definition 1

The Rieman-Liouville fractional integral operator \(I^{\alpha}_{t}\) of order α is defined as [26]

$$ \bigl(I^{\alpha}_{t} f\bigr) (t)=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} \frac{1}{\Gamma (\alpha)}\int^{t}_{0} (t-\tau)^{\alpha-1}f(\tau)\,\mathrm{d}\tau,& \alpha>0, t>0,\\ f(t),& \alpha=0. \end{array}\displaystyle \right . $$
(1)

For the Riemann-Liouville fractional integral we have

$$ I^{\alpha}_{t} t^{v}= \frac{\Gamma(v+1)}{\Gamma(v+1+\alpha)}t^{v+\alpha}, \quad v>-1. $$
(2)

Definition 2

The Caputo definition of fractional differential operator is given by

$$ \bigl(D^{\alpha}_{t} f\bigr) (t)=\frac{1}{\Gamma(n-\alpha)} \int^{t}_{0} \frac{f^{(n)}(\tau)}{(t-\tau)^{\alpha+1-n}}\,\mathrm{d}\tau, \quad n-1< \alpha \leq n, n\in N, $$
(3)

where \(\alpha> 0\) is the order of the derivative and n is the smallest integer greater than α if \(\alpha\notin N\) or equal to α if \(\alpha\in N\).

For the Caputo derivative we have the following two basic properties:

$$ \bigl(D^{\alpha}_{t} I^{\alpha}_{t} \bigr) (t)=f(t) $$
(4)

and

$$ \bigl(I^{\alpha}_{t} D^{\alpha}_{t} f\bigr) (t)=f(t)-\sum_{k=0}^{n-1}f^{(k)} \bigl(0^{+}\bigr)\frac{t^{k}}{k!}, \quad t>0, $$
(5)

where \(f^{(k)}(0^{+}):=\lim_{t\rightarrow {0^{+}}}D^{k}f(t)\), \(k=0,1,\ldots,n-1\).

3 Euler wavelet operational matrix of the fractional integration

3.1 Wavelets and Euler wavelet

Wavelets constitute a family of functions constructed from dilation and translation of a single function \(\psi(x)\) called the mother wavelet. When the dilation parameter a and the translation parameter b vary continuously we have the following family of continuous wavelets [27, 28]:

$$\psi_{ab}(t)=|{a}|^{-\frac{1}{2}}\psi \biggl(\frac{t-b}{a} \biggr),\quad a, b\in R, a\neq0. $$

If we restrict the parameters a and b to discrete values as \(a=a_{0}^{-k}, b=nb_{0}a_{0}^{-k}, a_{0}>1, b_{0}>0\), we have the following family of discrete wavelets:

$$\psi_{kn}(t)=|a_{0}|^{\frac{k}{2}}\psi \bigl(a_{0}^{k}t-nb_{0}\bigr), \quad k,n\in Z, $$

where \(\psi_{kn}\) form a wavelet basis for \(L^{2}(R)\). In particular, when \(a_{0}=2\) and \(b_{0}=1\) then \(\psi _{kn}(t)\) form an orthonormal basis.

The Euler wavelet \(\psi_{nm}(t)=\psi(k,n,m,t)\) involves four arguments, \(n=1,\ldots,2^{k-1}\), k is assumed to be any positive integer, m is the degree of the Euler polynomials, and t is the normalized time. They are defined on the interval \([0,1)\) as

$$ \psi_{nm}(t)=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} 2^{\frac{k-1}{2}}\tilde{\mathrm{E}}_{m}(2^{k-1}t-n+1),& {\frac {n-1}{2^{k-1}}\leq t< \frac{n}{2^{k-1}}},\\ 0,& \mbox{otherwise}, \end{array}\displaystyle \right . $$
(6)

with

$$ \tilde{\mathrm{E}}_{m}(t)=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} 1,& m=0,\\ \frac{1}{\sqrt{\frac {2{(-1)}^{m-1}{(m{!})}^{2}}{{(2m)}{!}}E_{2m+1}(0)}}\mathrm{E}_{m}(t),& m >0. \end{array}\displaystyle \right . $$
(7)

The coefficient \(\frac{1}{\sqrt{\frac {2{(-1)}^{m-1}{(m{!})}^{2}}{{(2m)}{!}}E_{2m+1}(0)}}\) is for normality, the dilation parameter is \(a=2^{-(k-1)}\), and the translation parameter \(b=(n-1)2^{-(k-1)}\). Here, \(E_{m}(t)\) are the well-known Euler polynomials of order m which can be defined by means of the following generating functions [29]:

$$\frac{2e^{ts}}{e^{s}+1}=\sum_{m=0}^{\infty}E_{m}(t)\frac{s^{m}}{m!} \quad \bigl(\vert s\vert < \pi\bigr). $$

In particular, the rational numbers \(E_{m}=2^{m}E_{m}(1/2)\) are called the classical Euler numbers. Also, the Euler polynomials of the first kind for \(k=0,\ldots, m\) can be constructed from the following relation:

$$\sum_{k=0}^{m} \bigl({}_{k}^{m} \bigr)E_{k}(t)+E_{m}(t)=2t^{m}, $$

where \(({}_{k}^{m})\) is a binomial coefficient. Explicitly, the first basic polynomials are expressed by

$$E_{0}(t)=1, \qquad E_{1}(t)=t-\frac{1}{2}, \qquad E_{2}(t)=t^{2}-t, \qquad E_{3}(t)=t^{3}- \frac {2}{3}t^{2}+\frac{1}{4},\qquad\cdots. $$

These polynomials satisfy the following formula:

$$ \int_{0}^{1} E_{m}(t)E_{n}(t) \,\mathrm{d}t={(-1)}^{n-1}\frac {m!(n+1)!}{(m+n+1)!}E_{m+n+1}(0), \quad m,n\geq1, $$
(8)

and the Euler polynomials form a complete basis over the interval \([0, 1]\). Furthermore, when \(t=0\), we have

$$E_{0}(0)=1, \qquad E_{1}(0)=-\frac{1}{2}, \qquad E_{3}(0)=\frac{1}{4}, \qquad E_{5}(0)=- \frac {1}{2},\qquad\cdots. $$

3.2 Function approximation

A function \(f(t)\), square integrable in \([0,1]\), may be expressed in terms of the Euler wavelet as

$$ f(t)=\sum_{n=0}^{\infty}\sum _{m\in Z}c_{nm}\psi_{nm}(t), $$
(9)

and we can approximate the function \(f(t)\) by the truncated series

$$ f(t)\simeq \sum_{n=1}^{2^{k-1}} \sum_{m=0}^{M-1}c_{nm} \psi_{nm}(t)=C^{\mathrm{T}}\Psi(t), $$
(10)

where the coefficient vector C and the Euler function vector \(\Psi(t)\) are given by

$$\begin{aligned}& C=[c_{10},c_{11},\dots,c_{1{(M-1)}},c_{20}, \dots,c_{2{(M-1)}},\dots ,c_{2^{k-1}0},\dots,c_{2^{k-1}(M-1)}]^{\mathrm{T}}, \end{aligned}$$
(11)
$$\begin{aligned}& \Psi(t)=[\psi_{10},\psi_{11},\dots,\psi_{1{(M-1)}}, \psi_{20},\dots,\psi _{2{(M-1)}},\dots,\psi_{2^{k-1}0},\dots, \psi_{2^{k-1}(M-1)}]^{\mathrm{T}}. \end{aligned}$$
(12)

Taking the collocation points as follows:

$$t_{i}=\frac{2i-1}{2^{k}M}, \quad i=1,2,\ldots,2^{k-1}M, $$

we define the Euler wavelet matrix \(\Phi_{\hat{m}\times \hat{m}}\) as

$$\Phi_{\hat{m}\times \hat{m}}= \biggl[\Psi \biggl(\frac{1}{2\hat{m}} \biggr), \Psi \biggl(\frac {3}{2\hat{m}} \biggr), \ldots, \Psi \biggl(\frac{2\hat{m}-1}{2\hat{m}} \biggr) \biggr], $$

where \(\hat{m}=2^{k-1}M\). Notation: from now we define \(\hat{m}=2^{k-1}M\).

To evaluate C, we let

$$a_{ij}= \int_{0}^{1}\psi_{ij}(t)f(t) \, \mathrm{d}t. $$

Using equation (10) we obtain

$$a_{ij}=\sum_{n=1}^{2^{k-1}}\sum _{m=0}^{M-1}c_{nm} \int_{0}^{1}\psi _{nm}(t) \psi_{ij}(t)f(t) \,\mathrm{d}t=\sum_{n=1}^{2^{k-1}} \sum_{m=0}^{M-1}c_{nm}d_{nm}^{ij}, $$

where \(d_{nm}^{ij}=\int_{0}^{1}\psi_{nm}(t)\psi_{ij}(t)f(t) \mathrm {d}t\) and \(i=1,2,\ldots,2^{k-1}, j=0,1,\ldots,M-1\).

Therefore,

$$A^{\mathrm{T}}=C^{\mathrm{T}}D, $$

with

$$A=[a_{10},a_{11},\dots,a_{1{(M-1)}},a_{20}, \dots,a_{2{(M-1)}},\dots ,a_{2^{k-1}0},\dots,a_{2^{k-1}(M-1)}]^{\mathrm{T}} $$

and

$$D=\bigl[d_{nm}^{ij}\bigr], $$

where D is a matrix of order \(2^{k-1}M\times2^{k-1}M\) and is given by

$$ D= \int_{0}^{1}\Psi(t)\Psi^{T}(t) \, \mathrm{d}t. $$
(13)

The matrix D in equation (13) can be calculated by using equation (8) in each interval \(n=1,2,\ldots,2^{k-1}\). For example, with \(k=2\) and \(M=2\), D the identity matrix, and for \(k=2\) and \(M=3\) we have

$$D= \begin{bmatrix} 1& 0& -\frac{\sqrt{30}}{6}& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ -\frac{\sqrt{30}}{6}& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 0& -\frac{\sqrt{30}}{6}\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& -\frac{\sqrt{30}}{6}& 0& 1 \end{bmatrix}. $$

Hence, \(C^{T}\) in equation (10) is given by

$$ C^{T}=A^{T}D^{-1}. $$
(14)

Similarly, we can approximate the function \(k(s,t) \in L^{2}([0,1]\times [0,1])\) as

$$ k(s,t)=\Psi(s)^{\mathrm{T}}K\Psi(t), $$
(15)

where K is a \(2^{k-1}M\times2^{k-1}M\) matrix given by [30]

$$K=D^{-1} \biggl[ \int_{0}^{1} \int_{0}^{1} k(s,t)\Psi(s)\Psi(t) \mathrm {d}t \biggr]D^{-1}. $$

3.3 Convergence of Euler wavelets basis

We first state some basic results as regards Euler polynomials approximations. The important properties will enable us to establish the convergence theorem of the Euler wavelets basis. The Euler polynomials of degree m are defined by [29]. Now we defined \(\Lambda(t)={[E_{0}(t),E_{1}(t),\ldots,E_{N}(t)]}^{T}\), so a function \(f(t) \in L^{2}[0,1]\) can be expressed in terms of the Euler polynomials basis \(\Lambda(t)\). Hence,

$$f(t)\simeq\sum_{i=0}^{N}e_{i}E_{i}(t) = E^{T} \Lambda(t), $$

where \(E={[e_{0},e_{1},\ldots,e_{N}]}^{T}\).

Lemma 3

Suppose that the function \(f: [0,1]\rightarrow R\) is \(m+1\) times continuously differentiable, and \(f \in C^{m+1}[0,1]\), \(\mathrm{Y}=\operatorname{span}\{E_{0}, E_{1},\ldots, E_{N}\}\) is vector space. If \(E^{T} \Lambda(t)\) is the best approximation of f out of Y, then the mean error bound is presented as follows:

$$\bigl\Vert f-E^{t}\Lambda\bigr\Vert _{2} \leq \frac{\sqrt{2}\tilde{M}S^{\frac {2m+3}{2}}}{(m+1)!\sqrt{2m+3}}, $$

where \(\tilde{M}=\max_{t \in[0,1]}|f^{(m+1)}(t)|\), \(S=\max\{1-t_{0},t_{0}\} \).

Proof

Consider the Taylor polynomials

$$\hat{f}(t)=f(t_{0})+f'(t_{0}) (t-t_{0})+f{''}(t_{0}) \frac{{(t-t_{0})}^{2}}{2!}+\cdots +f^{(m)}(t_{0})\frac{{(t-t_{0})}^{m}}{m!}, $$

where we have

$$\bigl\vert f(t)-\hat{f}(t)\bigr\vert =\biggl\vert f^{(m+1)}(\zeta) \frac{{(t-t_{0})}^{m+1}}{{(m+1)}!}\biggr\vert ,\quad \exists\zeta\in(0,1). $$

Since \(E^{T}\Lambda(t)\) is the best approximation of \(f(t)\), we have

$$\begin{aligned} \bigl\Vert f-E^{T}\Lambda\bigr\Vert ^{2}_{2} \leq& \|f-\hat{f}\|^{2}_{2}= \int^{1}_{0}\bigl[f(t)-\hat {f}(t) \bigr]^{2}\,\mathrm{d}t \\ =& \int^{1}_{0}\biggl[f^{(m+1)}(\zeta) \frac{{(t-t_{0})}^{m+1}}{{(m+1)}!}\biggr]^{2}\mathrm {d}t \\ \leq&\frac{{\tilde{M}}^{2}}{[(m+1)!]^{2}} \int^{1}_{0}{(t-t_{0})}^{2m+2} \mathrm {d}t \\ \leq&\frac{2{\tilde{M}}^{2}S^{2m+3}}{[(m+1)!]^{2}(2m+3)}. \end{aligned}$$

 □

Theorem 4

Suppose that the function \(f: [0,1]\rightarrow \mathrm{R}\) is \(m+1\) times continuously differentiable and \(f\in C^{m+1}[0,1]\). Then \(\tilde{f}(t)=C^{T}\Psi(t)\) approximates \(f(t)\) with mean error bounded as follows:

$$\bigl\Vert f(t)-\tilde{f}(t)\bigr\Vert _{2}\leq\frac{\sqrt{2}\tilde {M}}{2^{(k-1)(m+1)}(m+1)!\sqrt{2m+3}}, $$

where \(\tilde{M}=\max_{t \in[0,1]}|f^{(m+1)}(t)|\).

Proof

We divide the interval \([0,1]\) into subintervals \(I_{k,n}= [\frac{n-1}{2^{k-1} },\frac{n}{2^{k-1}} ]\), \(n=1,\ldots \) , \(2^{k-1}\) with the restriction that \(\tilde{f}(t)\) is a polynomial of degree less than \(m+1\) that approximates f with minimum mean error. The approximation approaches the exact solution as k approaches ∞. We use Lemma 3, to obtain

$$\begin{aligned} \bigl\Vert f(t)-\tilde{f}(t)\bigr\Vert ^{2}_{2} =& \int^{1}_{0}\bigl[f(t)-\tilde{f}(t) \bigr]^{2}\mathrm {d}x \\ =&\sum_{n} \int_{I_{k,n}}\bigl[f(t)-\tilde{f}(t)\bigr]^{2}\, \mathrm{d}t \\ \leq&\sum_{n} \biggl[\frac{\sqrt{2}\tilde{M_{n}}{(\frac{1}{2^{k-1}})}^{\frac {2m+3}{2}}}{(m+1)!\sqrt{2m+3}} \biggr]^{2} \\ \leq&\frac{2\tilde{M}^{2}}{2^{(k-1)(2m+2)}[(m+1)!]^{2}(2m+3)}, \end{aligned}$$

where \(\tilde{M_{n}}=\max_{t \in I_{k,n}}|f^{(m+1)}(t)|\). By taking the square roots we arrive at the upper bound. The error of the approximation \(\tilde{f}(t)\) of \(f(t)\) therefore decays like \(2^{-(m+1)(k-1)}\). □

3.4 Operational matrix of the fractional integration

We first give the definition of block pulse functions (BPFs): an m-set of BPFs on \([0,1)\) is defined as

$$ b_{i}(t)=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} 1,& i/m\leq t< (i+1)/m,\\ 0,& \mbox{otherwise}, \end{array}\displaystyle \right . $$
(16)

where \(i=0, 1, 2,\ldots, m-1\). The BPFs have disjointness and orthogonality as follows:

$$b_{i}(t)b_{j}(t)= \left \{ \textstyle\begin{array}{@{}l@{\quad}l} 0,& i\neq j,\\ b_{i}(t),& i=j, \end{array}\displaystyle \right . $$

and

$$\int_{0}^{1} b_{i}(\tau)b_{j}( \tau)\,\mathrm{d}\tau=\left \{ \textstyle\begin{array}{@{}l@{\quad}l} 0,& i\neq j,\\ 1/m,& i=j. \end{array}\displaystyle \right . $$

Every function \(f(t)\) which is square integrable in the interval \([0,1)\) can be expanded in terms of BPFs series as

$$ f(t)\approx\sum_{i=0}^{m-1}f_{i}b_{i}(t)=F^{\mathrm{T}}B_{m}(t), $$
(17)

where \(F=[f_{0}, f_{1}, \ldots, f_{m-1}]^{\mathrm{T}}\), \(B_{m}(t)=[b_{0}(t), b_{1}(t), \ldots, b_{m-1}(t)]^{\mathrm{T}}\). By using the orthogonality of BPFs, for \(i=0,1,\ldots, m-1\), the coefficients \(f_{i}\) can be obtained:

$$f_{i}=m \int_{0}^{1}b_{i}(t)f(t)\,\mathrm{d}t. $$

By using the disjointness of the BPFs and the representation of \(B_{m}(t)\), we have

$$ B_{m}(t)B_{m}^{\mathrm{T}}(t)= \begin{bmatrix} b_{0}(t)& &\mathbf{0}\\ & b_{1}(t)& \\ &\ddots&\\ \mathbf{0}&&b_{{m}-1}(t) \end{bmatrix}. $$
(18)

The block pulse operational matrix of the fractional integration \(F^{\alpha}\) has been given in [31],

$$ I^{\alpha}\bigl(B_{\hat{m}}(t)\bigr)\approx F^{\alpha}B_{\hat{m}}(t), $$
(19)

where

$$ F^{\alpha}=\frac{1}{{\hat{m}}^{\alpha}}\frac{1}{\Gamma(\alpha+2)} \begin{bmatrix} 1&\xi_{1}&\xi_{2}&\xi_{3}&\cdots&\xi_{\hat{m}-1}\\ 0&1&\xi_{1}&\xi_{2}&\cdots&\xi_{\hat{m}-2}\\ 0&0&1&\xi_{1}&\cdots&\xi_{\hat{m}-3}\\ \vdots&\vdots&\ddots&\ddots& \ddots&\vdots\\ 0&0&\cdots&0&1&\xi_{1}\\ 0&0&0&\cdots&0&1 \end{bmatrix} $$
(20)

and

$$\xi_{\kappa}=(\kappa+1)^{\alpha+1}-2\kappa^{\alpha+1}+( \kappa-1)^{\alpha+1}. $$

Note that, for \(\alpha=1\), \(F^{\alpha}\) is BPF’s operational matrix of integration.

There is a relation between the block pulse functions and Euler wavelets,

$$ \Psi(t)=\Phi B_{\hat{m}}(t). $$
(21)

If \(I^{\alpha}_{t}\) is fractional integration operator of Euler wavelet, we can get

$$ I^{\alpha}_{t}\bigl(\Psi(t)\bigr)\approx P^{\alpha}\Psi(t), $$
(22)

where matrix \(P^{\alpha}\) is called the Euler wavelet operational matrix of fractional integration. Using equations (19) and (21), we have

$$ I^{\alpha}_{t}\bigl(\Psi(t)\bigr)\approx I^{\alpha}_{t}\bigl(\Phi B_{\hat{m}}(t)\bigr)=\Phi I^{\alpha}_{t}\bigl(B_{\hat{m}}(t)\bigr)\approx \Phi F^{\alpha}B_{\hat{m}}(t). $$
(23)

Combining equation (22) and equation (23), we can get

$$ P^{\alpha}=\Phi F^{\alpha}\Phi^{-1}. $$
(24)

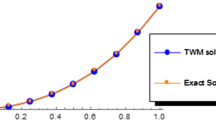
We select the function t to verify the correctness of fractional integration operational matrix \(P^{\alpha}\). The fractional integration of order α for the function \(f(t)=t\) is given by

$$ I^{\alpha}_{t} f(t)=\frac{\Gamma(2)}{\Gamma(\alpha+2)}t^{\alpha+1}. $$
(25)

The comparison results are shown in Figure 1 (\(\alpha=0.5\), \(\hat{m}=32\)).

Figure 1
figure 1

\(\pmb{1/2}\) order integration of t .

Full size image

4 Method of numerical solution

Consider the nonlinear fractional-order integro-differential equation

$$ D^{\alpha}_{t}y(x)=\lambda \int_{0}^{x} k(x,t)\bigl[y(t)\bigr]^{p} \,\mathrm{d}t+g(x), $$
(26)

subject to the initial conditions

$$ y^{(i)}(0)=\delta_{i}, \quad i=0,1,\dots,r-1, r \in N, $$
(27)

where \(y^{(i)}(x)\) stands for the ith-order derivative of \(y (x)\), \(D^{\alpha}_{t} \) (\(r-1<\alpha\leq r\)) denotes the Caputo fractional-order derivative of order α, \(g(x) \in L^{2}[0,1], k\in L^{2}({[0,1])}^{2}\) are given functions, \(y (x)\) is the solution to be determined, λ is a real constant, and \(p \in N\). The given functions \(g, k\) are assumed to be sufficiently smooth.

Now we approximate \(D^{\alpha}_{t}y(x), k(x,t)\), and \(g(x)\) in terms of Euler wavelets as follows:

$$ D^{\alpha}_{t}y(x)\approx Y^{\mathrm{T}} \Psi(x), \qquad k(x,t)=\Psi(x)^{\mathrm{T}}K\Psi(t) $$
(28)

and

$$ g(x)\approx G^{\mathrm{T}}\Psi(x), $$
(29)

where \(K=[k_{ij}]\), \(i, j = 1, 2,\ldots,\hat{m}\), and \(G = {[g_{1}, g_{2}, \ldots, g_{\hat{m}}]}^{T}\).

Using equations (5) and (28), we have

$$ y(x)\approx Y^{\mathrm{T}}P^{\alpha}\Psi(x)+\sum _{k=0}^{{\hat {m}}-1}y^{(k)}\bigl(0^{+}\bigr) \frac{x^{k}}{k!}. $$
(30)

In the above summation, we substitute the supplementary conditions (27) and approximate it with the Euler wavelet, we can get

$$ y(x)\approx\bigl(Y^{\mathrm{T}}P^{\alpha}+ \tilde{Y}^{\mathrm{T}}\bigr)\Psi(x), $$
(31)

where Ỹ is an m̂-vector. According to equation (21), the above equation can be written as

$$ y(x)\approx Y^{\mathrm{T}}P^{\alpha}\Phi B_{{\hat{m}}}(x)+\tilde {Y}^{\mathrm{T}}\Phi B_{\hat{m}}(x). $$
(32)

Let \(E=[e_{0}, e_{1}, \ldots, e_{{\hat{m}}-1}]=(Y^{\mathrm{T}}P^{\alpha }+\tilde{Y}^{\mathrm{T}})\Phi\). Then equation (32) becomes

$$y(x)\approx E B_{\hat{m}}(x). $$

By using the disjointness property of the BPFs, we have

$$\begin{aligned} \bigl[y(x)\bigr]^{2} \approx&\bigl[EB_{\hat{m}}(x) \bigr]^{2}=\bigl[e_{0}b_{0}(x)+e_{1}b_{1}(x)+ \cdots +e_{{\hat{m}}-1}b_{{\hat{m}}-1}(x)\bigr]^{2} \\ =&e_{0}^{2}b_{0}(x)+e_{1}^{2}b_{1}(x)+ \cdots+e_{{\hat{m}}-1}^{2}b_{{\hat {m}}-1}(x) \\ =&\bigl[e_{0}^{2},e_{1}^{2}, \ldots, e_{{\hat{m}}-1}^{2}\bigr]B_{\hat{m}}(x)=E_{2}B_{\hat{m}}(x), \end{aligned}$$

where \(E_{2}=[e_{0}^{2}, e_{1}^{2}, \ldots, e_{{\hat{m}}-1}^{2}]\). By induction we can get

$$ \bigl[y(x)\bigr]^{p}\approx\bigl[e_{0}^{p},e_{1}^{p}, \ldots, e_{{\hat{m}}-1}^{p}\bigr]B_{\hat{m}}(x)=E_{p}B_{\hat{m}}(x), $$
(33)

where p is any positive integer. Using equations (19), (28), and (33) we will have

$$\begin{aligned} \int_{0}^{x} k(x,t)\bigl[y(t)\bigr]^{p} \,\mathrm{d}t =& \int_{0}^{x} \Psi^{\mathrm{T}}(x)K \Psi(t)B_{\hat{m}}^{\mathrm{T}}(t) E_{p}^{\mathrm{T}}\, \mathrm{d}t \\ =& \int_{0}^{x} \Psi^{\mathrm{T}}(x)K\Phi B_{\hat{m}}(t)B_{\hat{m}}^{\mathrm {T}}(t)E_{p}^{\mathrm{T}} \,\mathrm{d}t \\ =&\Psi^{\mathrm{T}}(x)K\Phi \int_{0}^{x} B_{\hat{m}}(t)B_{\hat{m}}^{\mathrm{T}}(t)E_{p}^{\mathrm{T}} \mathrm {d}t \\ =&\Psi^{\mathrm{T}}(x)K\Phi \int_{0}^{x} \operatorname{diag}(E_{p})B_{\hat{m}}(t) \,\mathrm{d}t \\ =&\Psi^{\mathrm{T}}(x)K\Phi \operatorname{diag}(E_{p}) \int_{0}^{x}B_{\hat {m}}(t)\,\mathrm{d}t \\ =&\Psi^{\mathrm{T}}(x)K\Phi \operatorname{diag}(E_{p})F^{1}B_{\hat {m}}(x) \\ =& B_{\hat{m}}^{\mathrm{T}}(x)\Phi^{\mathrm{T}}K\Phi \operatorname{diag}(E_{p})F^{1}B_{\hat{m}}(x) \\ =&\tilde{Q}^{\mathrm{T}}B_{\hat{m}}(x), \end{aligned}$$
(34)

where Q̃ is an m̂-vector with elements equal to the diagonal entries of the following matrix:

$$Q= \Phi^{\mathrm{T}}K\Phi \operatorname{diag}(E_{q})F^{1}. $$

Substituting the above equations into equation (26), we have

$$ Y^{\mathrm{T}}\Phi B_{\hat{m}}(x)=\lambda \tilde{Q}^{\mathrm{T}}B_{\hat{m}}(x)+G^{\mathrm{T}}\Phi B_{\hat{m}}(x). $$
(35)

Using \(B_{\hat{m}}(x)\) to multiply two sides of equation (35) and integration in the interval \([0,1]\), according to orthogonality of the BPFs we can get

$$ Y^{\mathrm{T}}\Phi=\lambda \tilde{Q}^{\mathrm{T}}+G^{\mathrm{T}} \Phi, $$
(36)

which is a nonlinear system of algebraic equations. By solving this system we can obtain the approximation of equation (26), and we solve the nonlinear system by using the Newton iterative method.

5 Numerical examples

In this section, six examples are given to demonstrate the applicability and accuracy of our method. Examples 1-5 have smooth solutions, while Example 6 has a non-smooth and singular solution. In all examples the package of Matlab 7.0 has been used to solve the test problems considered in this paper.

Using equation (36) the absolute error function is defined as

$$R_{\hat{m}}(x)=\bigl\vert Y^{\mathrm{T}}\Phi B_{\hat{m}}(x)- \lambda \tilde{Q}^{\mathrm{T}}B_{\hat{m}}(x) -G^{\mathrm{T}}\Phi B_{\hat {m}}(x)\bigr\vert , $$

where \(\hat{m}=2^{k-1}M\); M is the degree of the Euler polynomials and usually takes small values in a computation. Since the truncated Euler wavelet series is an approximate solution of equation (26), we must have \(R_{\hat{m}}(x)\approx0\). In the following examples, we can find that when M is fixed, the larger the value of k, the more accurate the approximation solution of equation. So the optimum value of k is determined by the prescribed accuracy.

To demonstrate the effectiveness of this method, we will adopt the same error definition as [20]. The approximate norm-2 of the absolute error is given by

$$\bigl\Vert e_{\hat{m}}(x)\bigr\Vert _{2}=\bigl\Vert y(x)-y_{\hat{m}}(x)\bigr\Vert _{2}\approx \Biggl( \frac {1}{N}\sum_{i=0}^{N} \bigl(y(x_{i})-y_{\hat{m}}(x_{i})\bigr)^{2} \Biggr)^{1/2}, $$

where \(y(x)\) is the exact solution and \(y_{\hat{m}}(x)\) is the approximation solution obtained.

Example 1

Let us consider the following fractional nonlinear integro-differential equation:

$$D^{\frac{4}{5}}_{t}y(x)= \int_{0}^{x} (x-t)\bigl[y(t)\bigr]^{2}\, \mathrm{d}t+g(x), \quad 0\leq x< 1, $$

where \(g(x)=\frac{1}{\Gamma(1/5)} (\frac{25}{3}x^{6/5}-5x^{1/5} )-\frac{1}{30}x^{6}+\frac{x^{5}}{10} -\frac{x^{4}}{12}\), and the equation is subject to the initial conditions \(y(0)=0\). The exact solution of this equation is \(y(x)=x^{2}-x\). Table 1 shows the absolute errors obtained by Euler wavelets and SCW [22], respectively. Table 2 shows the approximate norm-2 of absolute errors obtained by the Euler wavelet and SCW methods.

Table 1 The absolute errors of different k and \(\pmb{M=3}\) for Example  1
Full size table
Table 2 Approximate norm-2 of absolute errors for some k of the Euler and SCW
Full size table

From Table 1, we find that the absolute errors become smaller and smaller with k increasing. Table 2 shows that the Euler wavelet method can reach a higher degree of accuracy than the SCW method.

Example 2

Consider the nonlinear fractional-order Volterra integro-differential equation

$$D^{\frac{6}{5}}_{t}y(x)= \int_{0}^{x} {(x-t)}^{2}\bigl[y(t) \bigr]^{3}\mathrm {d}t+g(x), \quad 0\leq x< 1, $$

where \(g(x)=\frac{5}{2\Gamma(4/5)}x^{4/5}-\frac{x^{9}}{252}\), and subject to the initial conditions \(y(0)=y'(0)=0\). The exact solution of this equation is \(y(x)=x^{2}\).

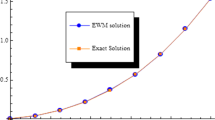
Table 2 shows the approximate norm-2 of absolute errors obtained by the Euler wavelet and SCW methods. The comparisons between approximate and exact solutions for various k and \(M=2\) are shown in Figure 2. With the value of k increasing, the numerical results become more accurate and we infer that the approximate solutions converge to the exact solution.

Figure 2
figure 2

The approximate solution of Example  2 for some k .

Full size image

Example 3

Consider the nonlinear Volterra integro-differential equation

$$D^{\frac{3}{4}}_{t}y(x)- \int_{0}^{x} xt\bigl[y(t)\bigr]^{4}\, \mathrm{d}t=g(x), 0\leq x< 1, $$

where \(g(x)=\frac{1}{\Gamma(1/4)} (\frac{32}{5}x^{5/4}-4x^{1/4} )+\frac{1}{10}x^{11}+\frac{4}{9}x^{10} -\frac{4}{3}x^{9}+\frac{4}{7}x^{8}+\frac{1}{6}x^{7}\), and the equation is subject to the initial conditions \(y(0)=y'(0)=0\). The exact solution of this equation is \(y(x)=x^{2}-x\). Table 3 shows the approximate solution obtained by our method (\(\hat {m}=2^{(k-1)}M\)), reproducing the kernel method (\(\hat{m}=2^{k}(2M+1)\)) [16] and CAS wavelet methods (\(\hat{m}=2^{k}(2M+1)\)) [20]. To make each method having the same number of wavelet bases, we select \(M=3\) for the Euler wavelet. Under the condition of the same error, our method is closer to the exact solution.

Table 3 Comparison of approximate norm-2 of absolute errors with reproducing kernel and CAS
Full size table

Example 4

Consider this equation:

$$D^{\frac{5}{3}}_{t}y(x)- \int_{0}^{x} {(x+t)}^{2}\bigl[y(t) \bigr]^{3}\mathrm {d}t=g(x),\quad 0\leq x< 1, $$

where \(g(x)=\frac{6}{\Gamma(\frac{1}{3})}\sqrt[3]{x}-\frac{x^{2}}{7}-\frac {x}{4}-\frac{1}{9}\), and the supplementary condition \(y(0)=y'(0)=0\). The exact solution is \(y(x)=x^{2}\). Table 3 shows the approximate solution obtained by the Euler wavelet method, reproducing the kernel method and CAS wavelet methods. From Table 3 we can see our method is closer to the exact solution.

Example 5

In the following we consider the fourth-order equation [20]

$$D^{\alpha}_{t}y(x)- \int_{0}^{x} e^{-t}\bigl[y(t) \bigr]^{2}\,\mathrm{d}t=1,\quad 0\leq x< 1, 3< \alpha\leq4, $$

such that \(y(0)=y'(0)=y''(0)=y^{(3)}(0)=1\), and when \(\alpha= 4\), the exact solution is \(y(x) = e^{x}\). The numerical results, for some α between 3 and 4, are presented in Table 4 with a comparison with [20]. Table 4 shows the Euler wavelet numerical solution to be in excellent agreement with the solution of CAS method in [20].

Table 4 Numerical results for Example  5 with comparison to CAS
Full size table

It is worth noticing that the method introduced above only can solve equation (26) for \(x \in[0,1]\). That is because the Euler wavelet is defined on the interval \([0,1]\). However, the variable x of equation (26) is defined on the interval \([0,4]\), so we should turn \(\Psi(x)\) into \(\Psi(x/4)\) in the discrete procedure. The numerical result with \(\alpha= 4\) for \(x \in[0,4]\) is shown in Figure 3. The numerical solution is in perfect agreement with the exact solutions.

Figure 3
figure 3

Numerical and exact solution of Example  5 for \(\pmb{\hat{m}=8}\) .

Full size image

Let us consider examples with non-smooth and singular solutions.

Example 6

Consider the following equation:

$$D^{\alpha}_{t}y(x)=- \int_{0}^{x} \frac{{[y(t)]}^{2}}{(x-t)^{1/2}}\,\mathrm{d}t+g(x), $$

which has \(y(x) = x^{-1/4}\) as the exact solution, with this supplementary condition \(y(0) = 0\), where \(g(x)=-\frac{\Gamma(-1/4)x^{-1/2}}{4\Gamma (1/2)}+\pi\). In this case, there is a singularity at point \(x = 0\). The solution around this point is not good (see Figure 4 with \(k=4\), \(M = 2\)). The Euler wavelet method can be combined with the definition of Riemann-Liouville fractional integral operator to deal with the weakly singular integral. As observed, our method provides a reasonable estimate even in this case with singular solution.

Figure 4
figure 4

The approximate solution of Example  6 for \(\pmb{k=4, M=2}\) .

Full size image

In the examples above, we do not show the computational times of the different methods. In fact, the Euler wavelet method has the faster computing speed, compared with the CAS wavelet method and the second Chebyshev wavelet method. In Example 1, for instance, when \(k = 4,5,6\), the computational times of the second Chebyshev wavelet are 1.71 s, 1.94 s, and 4.21 s, while the computational times of the Euler wavelet are 0.79 s, 1.25 s, and 3.57 s. The same conclusion can be drawn from the other examples.

6 Conclusion

In this paper, we construct the Euler wavelet and derive the wavelet operational matrix of the fractional integration, and we use it to solve the fractional integro-differential equations. By solving the nonlinear system, approximate solutions are got. Graphical illustrations and tables of the numerical results with the aid of Euler wavelets indicate that the numerical results are well in agreement with exact solutions and superior to other results. Also the proposed method can be efficiently applied to a large number of similar fractional problems. Of course, the convergence of this algorithm has not been derived, which will be future research work.