1 Introduction

State feedback plays an important role in solving all kinds of complex problems in the control systems. Many control system problems can be realized by introducing proper state feedback, such as stabilization, decoupling, non-static error tracking, and optimal control. But because the system state cannot be measured directly, or due to the limitation of measuring equipment in economic or use, leading to the impossibility to actually get all information of the system state variables, it is very difficult to realize a physical form of state feedback. So the requirement of the state feedback in performance is incompatible with a physical implementation. One of the ways to solve this problem is through the reconstruction of the state of systems, and make the reconstruction of the state take the place of the real state of systems, to satisfy the requirement of the state feedback. The state reconstruction problem, namely the problem of observer design, is the way to solve these problems. In this paper, we are able to design effective state observers for nonlinear systems using the T-S fuzzy control method.

In the past 20 years, scholars have made a lot of research on the design of nonlinear observers. In the early 1960s, the famous Kalman filter [2] and Luenberger observer [3] led to the linear system state observer complete design method. Unlike the linear system, nonlinear observer design is more complex. For nonlinear systems, there have no unified analysis method until now. A currently popular method is to classify the system, firstly. Then the existence and the design of state observer for different types of nonlinear systems are studied. For example, in accordance with the degree of nonlinearity of the system, which system has been well studied, Lipschitz nonlinear systems [4, 5] only depend on nonlinear systems of the output [6, 7], nonlinear systems of the multivariable meet the circle criterion [8], and we have the strict feedback stochastic nonlinear system [9].

At present, the design of the nonlinear system is aimed at the particular nonlinear system. Yi and Zhang [10] developed an extended updated-gain high gain observer to make a tradeoff between reconstruction speed and measurement noise attenuation. Huang et al. [11] propose a new method to design observers for Lur’e differential inclusion systems. Generally speaking, the structure of the observer for nonlinear systems can be summarized as follows by several methods: the class of Lyapunov function method [12, 13], differential geometric methods for designing [14, 15], the extended Luenberger observer method [16, 17], and the extended Kalman filtering method [18, 19]. Chadli and Karimi dealt with the observer design for Takagi-Sugeno (T-S) fuzzy models subject to unknown inputs and disturbance affecting both states and outputs of the system [20]. Yin et al. presented an approach for data-driven design of fault diagnosis system [21]. Aouaouda et al. were concerned with robust sensor fault detection observer (SFDO) design for uncertain and disturbed discrete-time Takagi-Sugeno (T-S) systems using the \(H_{-} /H_{\infty}\) criterion [22]. Zhao et al. proposed an input-output approach to the stability and stabilization of uncertain Takagi-Sugeno (T-S) fuzzy systems with time-varying delay [23].

Singular systems are also called differential algebraic systems, one has many theories of research results in nearly 30 years, and one has many applications in the aviation, aerospace, robotics, power system, electronic network, chemistry, biology, economy, and other fields [24–26] at present; the study of the singular system is still an area of control theory research of great interest at home and abroad. Singular systems describe a class of more extensive actual system models. In particular, singular systems have an impulse behavior, and they make relevant research becoming more complex and novel. Therefore, it has important academic value and broad application background. At 1999, Taniguchi et al. made the normal fuzzy system extend to more general situations and put forward the fuzzy singular system [27, 28], which use multiple local linear singular systems to approximate a global nonlinear system, and it is easy to solve the problem of the control of global nonlinear singular systems with the help of linear system analysis and the control method.

In this paper, firstly, we apply the T-S fuzzy method in nonlinear singular systems and form a T-S fuzzy singular system. Secondly, in order to get a better state feedback, we use the method of Lyapunov functions to design an observer with T-S fuzzy form. Then we prove the parameters and state estimation errors are globally stable of the T-S fuzzy observer, we give the sufficient condition that the fuzzy control fuzzy system is globally exponentially stable, and we give the controller gains. Finally, simulation results are given to illustrate the correctness of results and the effectiveness of the observer.

Notations

The symbol R denotes the set of real numbers. \(R^{n}\) denotes the n-dimensional Euclidean space. The superscript ‘T’ stands for matrix transposition. \(A > 0\), \(A < 0\) denote symmetric positive definite and symmetric negative definite, respectively. For a matrix A, \(A^{ - 1}\), \(\Vert A \Vert \), \(\lambda_{\min} (A)\), and \(\lambda _{\max}(A)\) denote its inverse, the induced norm, the minimum eigenvalues, and maximum eigenvalues, respectively. \(C^{0}\) and \(C^{1}\) represent the continuous and differentiable functions, respectively. \(\Sigma^{ +}\) represent the generalized inverse matrix of the matrix Σ.

2 Preliminaries

Lemma 1

For proper dimension matrix \(v_{1}\) and \(v_{2}\), there is a positive k and arbitrary matrix norm \(\Vert \bullet \Vert \) leading to the following equalities:

$$v_{1}^{T}v_{2} + v_{2}^{T}v_{1} \le k\Vert v_{1} \Vert ^{2} + \frac{1}{k}\Vert v_{2} \Vert ^{2}. $$

Lemma 2

[29]

The singular value decomposition of \(C^{*}\) is

$$C^{*} = U\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \Sigma& 0_{r_{c} \times(n - r_{c})} \\ 0_{(q - r_{c}) \times r_{c}} & 0_{(q - r_{c}) \times(n - r_{c})} \end{array}\displaystyle \right ]H^{T}, $$

where \(U \in R^{q \times q}\) is an orthogonal matrix, \(\Sigma= \operatorname{diag} [ \sigma_{1}(C^{*} ), \ldots,\sigma_{r_{c}}(C^{*} ) ]\), \(\sigma_{k}(C^{*} )\), \(k = 1,2, \ldots,r_{c}\), refer to the singular value of \(C^{*}\), \(r_{c} = \operatorname{rank}(C^{*} ) \le q\), and \(H \in R^{n \times n}\) represents an orthogonal matrix. Then the pseudo-inverse \(C^{*}\), which is denoted by \(C^{+}\), is

$$C^{ +} = H\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} \Sigma^{ - 1} & 0_{r_{c} \times(n - r_{c})} \\ 0_{(q - r_{c}) \times r_{c}} & 0_{(q - r_{c}) \times(n - r_{c})} \end{array}\displaystyle \right ]U^{T}. $$

Lemma 3

For any positive a, b, the following equation holds true:

$$0 \le\frac{ab}{a + b} \le a. $$

Lemma 4

Rayleigh-Ritz theorem

Let \(A^{*} \in R^{n \times n}\) be a positive definite, real, and symmetric matrix. Then \(\forall x \in R^{n}\), the following inequality holds:

$$\lambda_{\min} \bigl(A^{*} \bigr)\Vert x \Vert ^{2} \le x^{T}A^{*} x \le \lambda_{\max} \bigl(A^{*} \bigr)\Vert x \Vert ^{2}. $$

3 Problem statement

Consider a singular nonlinear system described by

$$ \left \{ \textstyle\begin{array}{l} E\dot{x}(t) = Ax(t) + Bu(t) + Df(x(t),u(t),t), \\ y = Cx(t), \end{array}\displaystyle \right . $$
(3.1)

where \(x(t) \in R^{n}\) is the state variable, \(y(t) \in R^{p}\) is the measured output, \(u(t) \in R^{m}\) is the control input. \(f:R^{n} \times R^{m} \times R \to R^{f}\) is an unknown continuous nonlinear function, \(E \in R^{n \times n}\) is a singular matrix, \(A \in R^{n \times n}\), \(B \in R^{n \times m}\), \(C \in R^{p \times n}\), and \(D \in R^{n \times f}\) are indicative of the known constant matrices.

System (3.1) is a classic nonlinear model and the nonlinear model is more troublesome dealing with many problems, so we use the linear system to approximate the nonlinear system according to the characteristics of T-S fuzzy control, so that the problem of the nonlinear system is transformed into the problem of a linear system.

  • Model rule i:

    If \(\xi_{1}(t)\) is \(M_{i1}\) and ⋯ and \(\xi_{q}(t)\) is \(M_{iq}\)

    then

    $$ \left \{ \textstyle\begin{array}{l} E\dot{x}(t) = A_{i}x(t) + B_{i}u(t), \\ y = C_{i}x(t), \end{array}\displaystyle \right .\quad i = 1,2, \ldots,r, $$
    (3.2)

where \(M_{ij}\) is a fuzzy set and r is the number of rules, \(A_{i} \in R^{n \times n}\), \(B_{i} \in R^{n \times m}\), \(C_{i} \in R^{p \times n}\), \(\xi_{1}(t),\xi_{2}(t), \ldots,\xi_{i}(t)\) are known premise variables that may be functions of the state variables, we will use \(\xi(t)\) to denote the vector containing all individual elements \(\xi_{1}(t),\xi_{2}(t), \ldots,\xi_{i}(t)\). \(\beta_{i}(\xi(t)) = \prod_{j = 1}^{l} M_{ij}(\xi_{j})\) is the membership function of the system (3.2) with respect to the ith plant rules.

According to the characteristics of T-S fuzzy approximation, we can approximate the global nonlinear function with a number of local linear functions. So we can get the following model:

$$ \left \{ \textstyle\begin{array}{l} E\dot{x}(t) = \sum_{i = 1}^{r} \lambda_{i}(\xi (t)) \{ A_{i}x(t) + B_{i}u(t) \}, \\ y(t) = \sum_{i = 1}^{r} \lambda_{i}(\xi(t))C_{i}x(t), \end{array}\displaystyle \right . $$
(3.3)

where

$$\left \{ \textstyle\begin{array}{l} \lambda_{i}(\xi(t)) = \frac{\beta_{i}(\xi (t))}{\sum_{i = 1}^{r} \beta_{i}(\xi(t))}, \\ \lambda_{i}(\xi(t)) \ge0, \\ \sum_{i = 1}^{r} \lambda_{i}(\xi(t)) = 1. \end{array}\displaystyle \right . $$

According to the system (3.3), the following augmented system is considered:

$$ \begin{aligned} &\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} I_{n} & 0 \\ 0 & 0 \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{@{}c@{}} \dot{x}(t) \\ \ddot{x}(t) \end{array}\displaystyle \right ] = \sum _{i = 1}^{r} \lambda_{i}\bigl(\xi(t)\bigr) \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} 0 & I_{n} \\ A_{i} & - E \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{@{}c@{}} x(t) \\ \dot{x}(t) \end{array}\displaystyle \right ] + \left [ \textstyle\begin{array}{@{}c@{}} 0 \\ B_{i} \end{array}\displaystyle \right ]u(t), \\ &\bar{y}(t) = \sum_{i = 1}^{r} \lambda_{i}\bigl(\xi(t)\bigr)\left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} C_{i} & 0 \\ 0 & C_{i} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{@{}c@{}} x(t) \\ \dot{x}(t) \end{array}\displaystyle \right ] \end{aligned} $$
(3.4)

and its compact form is defined by

$$ \left \{ \textstyle\begin{array}{l} \overline{E}\dot{z}(t) = \sum_{i = 1}^{r} \lambda_{i}(\xi(t)) \{ \overline{A}_{i}z(t) + \overline{B}_{i}u(t) \}, \\ \bar{y}(t) = \sum_{i = 1}^{r} \lambda_{i}(\xi(t))\overline{C}_{i}z(t), \end{array}\displaystyle \right . $$
(3.5)

where \(z(t) = [ x(t) \ \dot{x}(t)]^{T} \in R^{2n}\) is the augmented state. \(\overline{E} = \bigl [{\scriptsize\begin{matrix}{} I_{n} & 0 \cr 0 & 0\end{matrix}} \bigr ] \in R^{2n \times2n}\), \(\overline{A}_{i} = \bigl [{\scriptsize\begin{matrix}{}0 & I_{n} \cr A_{i} & - E\end{matrix}} \bigr ] \in R^{2n \times2n}\), \(\overline{B}_{i} = \bigl [{\scriptsize\begin{matrix}{} 0 \cr B_{i}\end{matrix}} \bigr ] \in R^{2n \times m}\), \(\overline{C}_{i} = \bigl [{\scriptsize\begin{matrix}{} C_{i} & 0 \cr 0 & C_{i}\end{matrix}} \bigr ] \in R^{2p^{*}2n}\), \(i = 1,2, \ldots,r\).

In order to facilitate the design of the observer, we have the following assumptions:

  1. 1.

    The T-S fuzzy augmented system (3.5) is solvable and impulse free.

  2. 2.

    The first-order derivative of the output vector is available.

  3. 3.

    \(\operatorname{rank}\Bigl[ {\scriptsize\begin{matrix}{} \overline{E} \cr \Gamma\overline{A}_{i} \cr \overline{C}_{i}\end{matrix}} \Bigr] = 2n\), \(i = 1,2, \ldots,r\), the matrix \(\Gamma\in R^{r_{1} \times2n}\) is a full row rank, and \(\Gamma[ \overline{E} \ 0 \ 0] = 0\) where \(\operatorname{rank}([ \overline{E} \ 0 \ 0]) = n + p\).

4 Main results

In 2008, Karimi [30] presented a convex optimization method for observer-based mixed \(H_{2}/H_{\infty}\) control design of linear systems with time-varying state, input and output delays and gave the delay dependent sufficient conditions for the design of a desired observer-based control, that is, the linear matrix inequalities. Kao et al. [31] focused on designing a sliding-mode control for a class of neutral-type stochastic systems with Markovian switching parameters and nonlinear uncertainties.

Consider the following continuous observer for the ‘subsystem’ of the augmented system (3.5):

$$ \left \{ \textstyle\begin{array}{l} \dot{\theta} (t) = \sum_{i = 1}^{r} \lambda_{i}(\xi(t)) \{ N_{i}\theta(t) + H_{i}u(t) + L_{i}(a,b,c,\bar{y}(t)) + J_{i}\bar{y}(t) \}, \\ \bar{z} = \sum_{i = 1}^{r} \lambda_{i}(\xi(t)) \{ P_{i}\theta(t) - Q_{i}\Gamma\overline{B}_{i}u(t) + F_{i}\bar{y}(t) \}. \end{array}\displaystyle \right . $$
(4.1)

Below we will explain the meaning of the parameters of system (4.1):

\(\theta(t) \in R^{q}\) is the observer state vector, \(\bar{z}(t)\) represents the estimation of \(\bar{y}(t)\). \(L_{i}\) is the estimator gain and continuous:

$$ L_{i} = - \frac{\gamma_{1}\Vert X_{i}^{ - 1} \Vert ^{2}S_{i}\tilde{\bar{y}}\Vert S_{i}\tilde{\bar{y}} \Vert ^{2}}{2\Vert S_{i}\tilde{\bar{y}} \Vert ^{2} - 2\dot{h}_{1}(t)h_{2i}(t)} - \frac{\Vert T_{i} \Vert S_{i}\tilde{\bar{y}}\bar{z}^{T}\bar{z}}{\Vert S_{i}\tilde{\bar{y}} \Vert \Vert \bar{z} \Vert - \dot{h}_{1}(t)h_{2i}(t)}, $$
(4.2)

where \(\tilde{\bar{y}}(t) = \bar{z}(t) - \bar{y}(t)\) is the output reconstruction error,

$$\begin{aligned}& h_{1}:R^{ +} \to R^{ +},\quad h_{1} \in C^{1},\forall t \in R^{ +},\qquad \sup h_{1}(t) < \infty,\qquad \sup\dot{h}_{1}(t) < 0, \\& h_{2i}:R^{+} \to R^{ +},\quad h_{2} \in C^{0},\forall t \in R^{ +},\qquad h_{2 i}(t) \le \frac{1}{\Vert X_{i}^{ - 1} \Vert ^{2}\gamma_{1}a^{2} + 2\Vert T_{i} \Vert c^{2}} \end{aligned}$$

and the \(\gamma_{1}\) satisfy the following conditions:

$$N_{i}^{T}X_{i} + X_{i}N_{i} + \frac{1}{\gamma_{1}}X_{i}T_{i}^{T}T_{i}X_{i} \le- Q_{1},\quad i = 1,2, \ldots,r, $$

where \(N_{i}\) is the Hurwitz matrix, \(X_{i}\) and \(Q_{1}\) are symmetric positive definite matrices.

According to the literature [32], we get the relevant parameters:

\(R \in R^{q \times2n}\) is a full row rank matrix,

$$\begin{aligned}& \Omega_{i} = \left [ \textstyle\begin{array}{@{}c@{}} \overline{E} \\ \Gamma\overline{A}_{i} \\ \overline{C}_{i} \end{array}\displaystyle \right ], \qquad \Sigma_{i} = \left [ \textstyle\begin{array}{@{}c@{}} R \\ \Gamma\overline{A}_{i} \\ \overline{C}_{i} \end{array}\displaystyle \right ], \\& \sigma_{i} = T_{i}\overline{A}_{i} \Sigma^{ +} \left [ \textstyle\begin{array}{@{}c@{}} 0_{q \times(r_{1} + 2p)} \\ I_{r_{1} + 2p} \end{array}\displaystyle \right ] + Y_{i}\bigl(I_{q + r_{1} + 2p} - \Sigma\Sigma^{ +} \bigr)\left [ \textstyle\begin{array}{@{}c@{}} 0_{q \times(r_{1} + 2p)} \\ I_{r_{1} + 2p} \end{array}\displaystyle \right ], \\& P_{i} = R\Omega^{ +} \left [ \textstyle\begin{array}{@{}c@{}} 0_{2n \times(r_{1} + 2p)} \\ I_{r_{1} + 2p} \end{array}\displaystyle \right ] + Z_{i}\bigl(I_{2n + r_{1} + 2p} - \Omega \Omega^{ +} \bigr)\left [ \textstyle\begin{array}{@{}c@{}} 0_{2n \times(r_{1} + 2p)} \\ I_{r_{1} + 2p} \end{array}\displaystyle \right ], \\& T_{i} = R\Omega^{ +} \left [ \textstyle\begin{array}{@{}c@{}} I_{2n} \\ 0_{(r_{1} + 2p) \times2n} \end{array}\displaystyle \right ] + Z_{i}\bigl(I_{2n + r_{1} + 2p} - \Omega \Omega^{ +} \bigr)\left [ \textstyle\begin{array}{@{}c@{}} I_{2n} \\ 0_{(r_{1} + 2p) \times2n} \end{array}\displaystyle \right ], \\& N_{i} = T_{i}\overline{A}_{i} \Sigma^{ +} \left [ \textstyle\begin{array}{@{}c@{}} I_{q} \\ 0_{(r_{1} + 2p) \times q} \end{array}\displaystyle \right ] + Y_{i}\bigl(I_{q + r_{1} + 2p} - \Sigma\Sigma^{ +} \bigr)\left [ \textstyle\begin{array}{@{}c@{}} I_{q} \\ 0_{(r_{1} + 2p) \times q} \end{array}\displaystyle \right ], \\& K_{i} = \Sigma^{ +} \left [ \textstyle\begin{array}{@{}c@{}} I_{q} \\ 0_{(r_{1} + 2p) \times q} \end{array}\displaystyle \right ] + W_{i} \bigl( I_{q + r_{1} + 2\mathrm{p}} - \Sigma \Sigma^{ +} \bigr)\left [ \textstyle\begin{array}{@{}c@{}} I_{q} \\ 0_{(r_{1} + 2p) \times q} \end{array}\displaystyle \right ], \\& \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{}} Q_{i} & F_{i} \end{array}\displaystyle \bigr] = \Sigma^{ +} \left [ \textstyle\begin{array}{@{}c@{}} P_{i} \\ I_{r_{1} + 2p} \end{array}\displaystyle \right ] + W_{i} \bigl( I_{q + r_{1} + 2\mathrm{p}} - \Sigma \Sigma^{ +} \bigr)\left [ \textstyle\begin{array}{@{}c@{}} P_{i} \\ I_{r_{1} + 2p} \end{array}\displaystyle \right ], \\& \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{}} - \varphi& J_{i} \end{array}\displaystyle \bigr] = \sigma_{i} + N_{i}P_{i}, \\& H_{i} = T_{i}\overline{B}_{i}, \\& \quad i = 1,2, \ldots,r, \end{aligned}$$

where \(r_{1} = n - p\), Y, Z, W are arbitrary matrices of appropriate dimension.

Theorem 1

For the T-S fuzzy observer (4.1), the parameters and state estimation errors are globally stable, if the following equations (4.3)-(4.5) hold:

$$\begin{aligned}& N_{i}T_{i}\overline{E} - T_{i} \overline{A}_{i} + J_{i}\overline{C}_{i} = 0, \end{aligned}$$
(4.3)
$$\begin{aligned}& \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} P_{i} & Q_{i} & F_{i} \end{array}\displaystyle \bigr]\left [ \textstyle\begin{array}{@{}c@{}} T_{i}\overline{E} \\ \Gamma\overline{A}_{i} \\ \overline{C}_{i} \end{array}\displaystyle \right ] = I_{2n}, \end{aligned}$$
(4.4)

and there exist positive \(\gamma_{1}\), \(X_{i} = X_{i}^{T} > 0\), satisfying the following matrix inequality:

$$ \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} N_{i}^{T}X + XN_{i} & XT_{i} \\ T_{i}^{T}X & - \gamma_{1}I \end{array}\displaystyle \right ] < 0. $$
(4.5)

Proof

First we define ε as the error of θ and \(T_{i}\overline{E}z\). That is \(\varepsilon= \theta- T_{i}\overline{E}z\). According to (3.5) and (4.1), we can obtain

$$\begin{aligned}& \dot{\varepsilon}_{j} = \sum_{i = 1}^{r} \lambda _{i}\bigl(\xi (t)\bigr) \bigl\{ N_{i} \varepsilon_{j} + (N_{i}T_{i}\overline{E} + J_{i}\overline {C}_{i} - T_{i} \overline{A}_{i})z + (H_{i} - T_{i} \overline{B}_{i})u(t) + L_{i}(a,b,c,\bar{y}) \bigr\} , \\& \quad j = 1,2, \ldots,r. \end{aligned}$$
(4.6)

According to (4.3) and the process of solving \(H_{i}\), we can get

$$ \dot{\varepsilon}_{j} = \sum_{i = 1}^{r} \lambda_{i}\bigl(\xi(t)\bigr) \bigl\{ N_{i} \varepsilon_{j} + L_{i}(a,b,c,\bar{y}) \bigr\} ,\quad j = 1,2, \ldots,r. $$
(4.7)

By considering the equation

$$\Gamma \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \overline{E} & 0 & 0 \end{array}\displaystyle \bigr]\left [ \textstyle\begin{array}{@{}c@{}} \dot{z} \\ 0 \\ 0 \end{array}\displaystyle \right ] = \sum_{i = 1}^{r} \Gamma\overline{A}_{i}z(t) + \Gamma \overline{B}_{i}u(t) $$

we have the equation

$$\Gamma \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \overline{E} & 0 & 0 \end{array}\displaystyle \bigr] = 0. $$

So

$$\sum_{i = 1}^{r} \Gamma\overline{A}_{i}z(t) + \Gamma\overline{B}_{i}u(t),\quad i = 1,2, \ldots,r. $$

That is,

$$ \Gamma\overline{A}_{i}z(t) = - \Gamma\overline{B}_{i}u(t), \quad i = 1,2, \ldots,r. $$
(4.8)

Using equation (4.8), θ and z̄, we can get

$$ \bar{z} - z = \sum_{i = 1}^{r} \lambda_{i}\bigl(\xi(t)\bigr) \bigl\{ K_{i}\varepsilon + (K_{i}T_{i}\overline{E} + Q_{i}\Gamma \overline{A}_{i} + F_{i}\overline{C}_{i} - 1)z \bigr\} , $$
(4.9)

which can be rewritten as

$$ \bar{z} - z = \sum_{i = 1}^{r} \lambda_{i}\bigl(\xi(t)\bigr)\left \{ K_{i} \varepsilon_{i} + \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} P_{i} & Q_{i} & F_{i} \end{array}\displaystyle \bigr]\left [ \textstyle\begin{array}{@{}c@{}} T_{i}\overline{E} \\ F_{i}\overline{A}_{i} \\ \overline{C}_{i} \end{array}\displaystyle \right ]z - z \right \}. $$
(4.10)

According to equation (4.4), the augmented state observation error is obtained:

$$ \tilde{z} = \sum_{i = 1}^{r} \lambda_{i}\bigl(\xi(t)\bigr)K_{i}\varepsilon_{i}, $$
(4.11)

where \(\tilde{z} = \bar{z} - z\).

Here we are going to have a stability analysis. First, we construct a positive definite function as a Lyapunov function:

$$ V(t) = \sum_{i = 1}^{r} \bigl\{ \lambda_{i}\bigl(\xi (t)\bigr)\varepsilon_{i}^{T}X_{i} \varepsilon_{i} + \eta_{1}a^{2} + \eta_{3}c^{2} + h_{1}(t) \bigr\} . $$
(4.12)

By using (4.6), the time derivative of V is written:

$$\dot{V}(t) = \sum_{i = 1}^{r} \sum _{j = 1}^{r} \lambda_{i}^{2} \bigl\{ \varepsilon_{i}^{T}\bigl(N_{j}^{T}X_{j} + X_{j}N_{j}\bigr)\varepsilon_{i} + 2 \varepsilon_{i}^{T}X_{j}L_{i} + 2 \eta_{1}a\dot{a} + 2\eta_{3}c\dot{c} + \dot{h}_{1}(t) \bigr\} . $$

According to Lemma 1, we can get

$$\begin{aligned} \dot{V}(t) \le&\sum_{i = 1}^{r} \sum _{j = 1}^{r} \lambda_{i}^{2} \biggl\{ \varepsilon_{i}^{T}\biggl(N_{j}^{T}X_{j} + X_{j}N_{j} + \frac{1}{\gamma_{1}}X_{j}T_{j}T_{j}^{T}X_{j} \biggr)\varepsilon_{i} \\ &{}+ 2\varepsilon_{i}^{T}X_{j}L_{i} + 2\eta_{1}a\dot{a} + 2\eta_{3}c\dot{c} + \dot{h}_{1}(t) \biggr\} . \end{aligned}$$

Then \(X_{i} = S_{i}\overline{C}_{i}K_{i}\), \(i = 1,2, \ldots,r\), where \(S_{i}\) is computed using Lemma 2. So

$$\begin{aligned} \dot{V}(t) \le&\sum_{i = 1}^{r} \sum _{j = 1}^{r} \lambda_{i}^{2} \biggl\{ \varepsilon_{i}^{T}\biggl(N_{j}^{T}X_{j} + X_{j}N_{j} + \frac{1}{\gamma_{1}}X_{j}T_{j}T_{j}^{T}X_{j} \biggr)\varepsilon_{i} \\ &{}+ 2\tilde{\bar{y}}S_{i}^{T}L_{i} + 2\eta_{1}a\dot{a} + 2\eta_{2}c\dot{c} + \dot{h}_{1}(t) \biggr\} . \end{aligned}$$

Using equation (4.2), we can obtain

$$\begin{aligned} \dot{V}(t) \le&\sum_{i = 1}^{r} \sum _{j = 1}^{r} \lambda_{i}^{2} \biggl\{ \varepsilon_{i}^{T}\biggl(N_{j}^{T}X_{j} + X_{j}N_{j} + \frac{1}{\gamma_{1}}X_{j}T_{j}T_{j}^{T}X_{j} \biggr)\varepsilon_{i} \\ &{}- \frac{\gamma_{1}a^{2}\dot{h}_{1}(t)h_{2 i}(t)\Vert X_{i}^{ - 1} \Vert ^{2}\Vert S_{i}\tilde{\bar{y}} \Vert ^{2}}{\Vert S_{i}\tilde{\bar{y}} \Vert ^{2} - \dot{h}_{1}(t)h_{2 i}(t)} - \frac{2c^{2}\dot{h}_{1}(t)h_{2 i}(t)\Vert T_{i} \Vert \Vert S_{i}\tilde{\bar{y}} \Vert \Vert \hat{z} \Vert }{\Vert S_{i}\tilde{\bar{y}} \Vert \Vert \bar{z} \Vert - \dot{h}_{1}(t)h_{2i}(t)} + \dot{h}_{1}(t) \biggr\} . \end{aligned}$$

Because of \(h_{2i}(t) > 0\) and \(\sup\dot{h}_{1}(t) < 0\), we combine with Lemma 3:

$$\begin{aligned} \dot{V}(t) \le&\sum_{i = 1}^{r} \sum _{j = 1}^{r} \lambda_{i}^{2} \biggl\{ \varepsilon_{i}^{T}\biggl(N_{j}^{T}X_{j} + X_{j}N_{j} + \frac{1}{\gamma_{1}}X_{j}T_{j}T_{j}^{T}X_{j} \biggr)\varepsilon_{i} \\ &{}+ \dot{h}_{1}(t) \bigl(1 - \gamma_{1}\bigl\Vert X_{i}^{ - 1} \bigr\Vert ^{2}a^{2}h_{2i}(t) - 2\Vert T_{i} \Vert c^{2}h_{2i}(t)\bigr) \biggr\} ; \end{aligned}$$

\(h_{2i}(t)\) should satisfy this inequality:

$$h_{2i}(t) \le\frac{1}{\Vert X_{i}^{ - 1} \Vert a^{2}\gamma_{1} + 2\Vert T_{i} \Vert c^{2}},\quad i = 1,2, \ldots,r. $$

The result is the following inequality:

$$\dot{V}(t) \le\sum_{i = 1}^{r} \sum _{j = 1}^{r} \lambda_{i}^{2} \biggl\{ \varepsilon_{i}^{T}\biggl(N_{j}^{T}X_{j} + X_{j}N_{j} + \frac{1}{\gamma_{1}}X_{j}T_{j}T_{j}^{T}X_{j} \biggr)\varepsilon_{i} \biggr\} . $$

Because

$$\left \{ \textstyle\begin{array}{l} N_{i}^{T}X_{i} + X_{i}N_{i} + \frac{1}{\gamma_{1}}X_{i}T_{i}^{T}T_{i}X_{i} \le- Q_{1},\quad i = 1,2, \ldots,r, \\ \Bigl[ {\scriptsize\begin{matrix}{} N_{i}^{T}X + XN_{i} & XT_{i} \cr T_{i}^{T}X & - \gamma_{1}I\end{matrix}} \Bigr] < 0 \end{array}\displaystyle \right . $$

and by applying Schur lemma and Rayleigh-Ritz theorem, we can get

$$ \dot{V}(t) \le- \lambda_{\min} (Q_{1})\sum _{i = 1}^{r} \lambda_{i}^{2} \Vert \varepsilon_{i} \Vert ^{2} \le0. $$
(4.13)

Therefore, the derivative of V is negative semi definite. According to the Lyapunov theorem, we can get the ε, z̃ and the parameters estimation errors are globally stable.

According to the above analysis, we proved the theorem. □

In view of the system (4.1), we give a kind of fuzzy control scheme.

  • Model rule i:

    If \(\xi_{1}(t)\) is \(M_{i1}\) and ⋯ and \(\xi_{q}(t)\) is \(M_{iq}\)

    then \(u(t) = K_{l}x(t)\),

where \(l \in L: = \{ 1,2, \ldots,r\}\), which can be rewritten as

$$ u(t) = \sum_{l = 1}^{r} u_{l} \bigl(\xi(t)\bigr)K_{l}x(t). $$
(4.14)

The fuzzy control system consisting of the fuzzy system (4.1) and smooth controller (4.14) can be rewritten as

$$ \dot{\theta} = \sum_{i = 1}^{r} \sum _{l = 1}^{r} \lambda_{i}u_{l} \bigl[ (N_{l} + H_{l}K_{j})\theta(t) + L_{l}\bigl(a,b,c,\bar{y}(t)\bigr) + J_{l}\bar{y}(t) \bigr]. $$
(4.15)

Theorem 2

The fuzzy control system (4.15) is globally exponentially stable if there a set of matrices \(Q_{l}\), \(l \in L\), a set of symmetric matrices \(\Phi_{l}\), \(l \in L\), a set of matrices \(\Phi_{li} = \Phi_{il}^{T}\), \(i,l \in L\), \(l < i\), and a positive definite matrix X meets the following LMIs:

$$\begin{aligned}& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} - X + \Phi_{l} & XN_{l}^{T} + Q_{l}^{T}H_{l}^{T} \\ N_{l}X + H_{l}Q_{l} & - X \end{array}\displaystyle \right ] < 0,\quad l \in L, \end{aligned}$$
(4.16)
$$\begin{aligned}& \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} - X + \Phi_{li} & XN_{l}^{T} + Q_{i}^{T}H_{l}^{T} \\ N_{l}X + H_{l}Q_{i} & - X \end{array}\displaystyle \right ] \\& \quad {}+ \left [ \textstyle\begin{array}{@{}c@{\quad}c@{}} - X + \Phi_{il} & XN_{i}^{T} + Q_{l}^{T}H_{i}^{T} \\ N_{i}X + H_{i}Q_{l} & - X \end{array}\displaystyle \right ] < 0,\quad l,i \in L,l < i, \end{aligned}$$
(4.17)
$$\begin{aligned}& \Phi: = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} \Phi_{1} & \Phi_{12} & \cdots& \Phi_{1r} \\ \Phi_{21} & \Phi_{2} & \cdots& \Phi_{2r} \\ \vdots& \vdots& \ddots& \vdots\\ \Phi_{r1} & \Phi_{r2} & \cdots& \Phi_{rl} \end{array}\displaystyle \right ] > 0, \end{aligned}$$
(4.18)

and the controller gains can be determined by

$$ K_{l} = Q_{l}X^{ - 1},\quad l \in L. $$
(4.19)

Proof

First of all, we defined the Lyapunov function

$$ V(x) = x^{T}X^{ - 1}x, $$
(4.20)

where the matrix X is positive definite [33].

By applying the Schur complement to (4.16) and (4.17), respectively, one has

$$\begin{aligned}& (N_{l}X + H_{l}Q_{l})^{T}X^{ - 1}(N_{l}X + H_{l}Q_{l}) - X + \Phi_{l} < 0, \end{aligned}$$
(4.21)
$$\begin{aligned}& \frac{1}{2}(N_{l}X + H_{l}Q_{i} + N_{i}X + H_{i}Q_{l})^{T}X^{ - 1}(N_{l}X + H_{l}Q_{i} + N_{i}X + H_{i}Q_{l}) \\& \quad {}- 2X + \Phi_{li} + \Phi_{il} < 0. \end{aligned}$$
(4.22)

We define \(A_{li} = N_{l} + H_{l}K_{i}\) and \(B = L_{l}(a,b,c,\bar{y}) + J_{l}\bar{y}\), and we consider the Lyapunov function defined in (4.20). Because the form of the following function is a sum, in order to facilitate the subsequent proof, we give the discrete form for the Lyapunov function:

$$\begin{aligned} \Delta V(t) =& V\bigl(\theta(t + 1)\bigr) - V\bigl(\theta(t)\bigr) \\ =& \Biggl[ \sum_{l = 1}^{r} u_{l}A_{li}\theta(t) \Biggr]^{T}X^{ - 1} \Biggl[ \sum_{l = 1}^{r} u_{l}A_{li} \theta(t) \Biggr] - \theta(t)^{T}X^{ - 1}\theta(t) \\ =& \sum_{l = 1}^{r} \sum _{i = 1}^{r} \lambda_{i}u_{l} \theta (t)^{T}A_{li}^{T}X^{ - 1}A_{il} \theta(t) - \theta(t)^{T}X^{ - 1}\theta (t) \\ =& \sum_{l = 1}^{r} \sum _{i = 1}^{r} u_{l}^{2}\theta (t)^{T}\bigl(A_{ll}^{T}X^{ - 1}A_{ll} - X^{ - 1}\bigr)\theta(t) \\ &{}+ \sum_{l = 1}^{r} \sum _{i = 1}^{r} \lambda_{i}u_{l} \theta (t)^{T}\bigl(A_{li}^{T}X^{ - 1}A_{il} + A_{il}^{T}X^{ - 1}A_{li} - 2X^{ - 1}\bigr)\theta(t) \\ =& \sum_{l = 1}^{r} \sum _{i = 1}^{r} u_{l}^{2}\theta (t)^{T}\bigl(A_{ll}^{T}X^{ - 1}A_{ll} - X^{ - 1}\bigr)\theta(t) \\ &{}+ \sum_{l = 1}^{r} \sum _{l < i}^{r} \lambda_{i}u_{l} \theta(t)^{T} \biggl[ \frac{1}{2}(A_{li} + A_{il})^{T}X^{ - 1}(A_{li} + A_{il}) - 2X^{ - 1} \biggr]\theta(t). \end{aligned}$$
(4.23)

Then using (4.21) and (4.22),

$$\begin{aligned} \Delta V(t) \le&- \sum_{l = 1}^{r} \sum _{i = 1}^{r} u_{l}^{2} \theta(t)^{T}X^{ - 1}\Phi_{l}X^{ - 1}\theta(t) \\ &{}- \sum_{l = 1}^{r} \sum _{l < i}^{r} u_{l}\lambda_{i} \theta(t)^{T}\bigl(X^{ - 1}\Phi_{li}X^{ - 1} + X^{ - 1}\Phi_{il}X^{ - 1}\bigr)\theta(t) \\ \le&- \left [ \textstyle\begin{array}{@{}c@{}} u_{1}\theta\\ \vdots\\ u_{r}\theta \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} X^{ - 1}\Phi_{1}X^{ - 1} & \cdots& X^{ - 1}\Phi_{1r}X^{ - 1} \\ \vdots& \ddots& \vdots\\ X^{ - 1}\Phi_{r1}X^{ - 1} & \cdots& X^{ - 1}\Phi_{r}X^{ - 1} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{@{}c@{}} u_{1}\theta\\ \vdots\\ u_{r}\theta \end{array}\displaystyle \right ] \\ \le&- k\sum_{l = 1}^{r} u_{l}^{2}\theta(t)^{T}\theta(t) \\ \le&- k\bigl\Vert \theta(t) \bigr\Vert ^{2}, \end{aligned}$$
(4.24)

where \(k > 0\).

Thus the fuzzy control system (4.15) is globally exponentially stable and the controller gains can be determined by (4.8). The proof is thus completed. □

5 Examples

Example 1

In 1984, Mikania micrantha first appeared in Shenzhen. Mikania micrantha is in vines and has the super ability to reproduce, climbing shrubs and trees, can quickly form whole plant coverage, and the plants by destroying the photosynthesis suffocate. Mikania micrantha can produce allelochemicals to inhibit the growth of other plants.

According to [34], we give the model of the invasion of Mikania micrantha:

$$ \left \{ \textstyle\begin{array}{l} \dot{x}(t) = r_{1}x(t) ( 1 - \frac{x(t) + y(t)}{k} ), \\ \dot{y}(t) = r_{2}y(t) - E(t)y(t), \\ 0 = E(t)y(t)c - m, \end{array}\displaystyle \right . $$
(5.1)

where \(x(t)\), \(y(t)\), \(E(t)\) denote the density of native species, the density of alien species (Mikania micrantha), and the capture of the alien species (Mikania micrantha), respectively; \(r_{1}\) and \(r_{2}\) denote the intrinsic growth rate of native species and Mikania micrantha, respectively; k represents environmental capacity of native species; m represents the cost of artificial capture of Mikania micrantha; c represents unit capture cost of Mikania micrantha.

The values of the settings in [34] are \(r_{2} = 0.1\), \(k = 20\), \(c = 0.03\), \(r_{1} = 0.5\), \(m = 4\). So we can get

$$ \left \{ \textstyle\begin{array}{l} \dot{x}(t) = 0.5x(t) ( 1 - \frac{x(t) + y(t)}{20} ), \\ \dot{y}(t) = 0.1y(t) - E(t)y(t), \\ 0 = 0.03E(t)y(t) - 4. \end{array}\displaystyle \right . $$
(5.2)

On account of the presence of saturation for the species population density, it is reasonable to suppose \(x(t) \in[ - d_{1},d_{1}]\), \(y(t) \in[- d_{2},d_{2}]\), \(d_{1} = 10\), \(d_{2} = 10\), and then the fuzzy state model can be written as follows, which is appropriate for describing model system (4.15) as \(x(t) \in[ - d_{1},d_{1}]\), \(y(t) \in[ - d_{2},d_{2}]\):

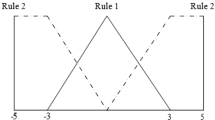
Rule 1: If \(x(t)\) is \(M_{1}\) and \(y(t)\) is \(M_{3}\), then

$$\widetilde{E}\dot{X}(t) = \widetilde{A}_{1}X(t) + \widetilde{B}_{1}\tilde{u}(t). $$

Rule 2: If \(x(t)\) is \(M_{1}\) and \(y(t)\) is \(M_{4}\), then

$$\widetilde{E}\dot{X}(t) = \widetilde{A}_{2}X(t) + \widetilde{B}_{2}\tilde{u}(t). $$

Rule 3: If \(x(t)\) is \(M_{2}\) and \(y(t)\) is \(M_{3}\), then

$$\widetilde{E}\dot{X}(t) = \widetilde{A}_{3}X(t) + \widetilde{B}_{3}\tilde{u}(t). $$

Rule 4: If \(x(t)\) is \(M_{2}\) and \(y(t)\) is \(M_{4}\), then

$$\widetilde{E}\dot{X}(t) = \widetilde{A}_{4}X(t) + \widetilde{B}_{4}\tilde{u}(t). $$

Here

$$\begin{aligned}& X(t) = \bigl[x(t),y(t),E(t)\bigr]^{T}, \\& \widetilde{E} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ], \\& \widetilde{A}_{1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 2r_{1} - \frac{2d_{1}r_{1}}{k} & - \frac{2r_{1}}{k} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.5 & - 0.05 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ], \\& \widetilde{A}_{2} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 2r_{1} + \frac{2d_{1}r_{1}}{k} & \frac{2r_{1}}{k} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1.5 & 0.05 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\displaystyle \right ], \\& \widetilde{A}_{3} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 \\ 0 & 2r_{2} & - 2d_{2} \\ 0 & 0 & 2d_{2}c \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 \\ 0 & 0.2 & - 20 \\ 0 & 0 & 0.6 \end{array}\displaystyle \right ], \\& \widetilde{A}_{4} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 \\ 0 & 2r_{2} & 2d_{2} \\ 0 & 0 & - 2d_{2}c \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 \\ 0 & 0.2 & 20 \\ 0 & 0 & - 0.6 \end{array}\displaystyle \right ], \\& \widetilde{B}_{1} = \widetilde{B}_{2} = \widetilde{B}_{3} = \widetilde{B}_{4} = \left [ \textstyle\begin{array}{@{}c@{}} 0 \\ 0 \\ m \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{@{}c@{}} 0 \\ 0 \\ 4 \end{array}\displaystyle \right ]. \end{aligned}$$

In order to observe the state variables, we add an output variable:

$$y(t) = \sum_{i = 1}^{4} \tilde{ \lambda}_{i}\bigl(X(t)\bigr)\widetilde{C}_{i}X(t), $$

where

$$\widetilde{C}_{1} = \widetilde{C}_{2} = \widetilde{C}_{3} = \widetilde{C}_{4} = \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1 & 1 & 1 \end{array}\displaystyle \bigr]^{T}. $$

According to the definitions and results of fuzzy models, the integral fuzzy model is inferred as follows:

$$ \left \{ \textstyle\begin{array}{l} \widetilde{E}\dot{X}(t) = \sum_{i = 1}^{4} \tilde{\lambda}_{i}(X(t))[\widetilde{A}_{i}X(t) + \widetilde{B}_{i}\tilde{u}(t)], \\ y(t) = \sum_{i = 1}^{4} \tilde{\lambda}_{i}(X(t))\widetilde{C}_{i}X(t), \end{array}\displaystyle \right . $$
(5.3)

where \(\tilde{\lambda}_{1}(X(t)) = \frac{1}{4}(1 - \frac{x(t)}{d_{1}})\), \(\tilde{\lambda}_{2}(X(t)) = \frac{1}{4}(1 + \frac{x(t)}{d_{1}})\), \(\tilde{\lambda}_{3}(X(t)) = \frac{1}{4}(1 - \frac{y(t)}{d_{2}})\), \(\tilde{\lambda}_{4}(X(t)) = \frac{1}{4}(1 + \frac{y(t)}{d_{2}})\).

According to (3.5), we can obtain matrices \(\overline{A}_{i}\), E̅, \(\overline{B}_{i}\), \(\overline{C}_{i}\), R, and Γ, \(i = 1,2,3,4\),

$$\begin{aligned}& \overline{A}_{1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0.5 & - 0.05 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\displaystyle \right ],\qquad \overline{A}_{2} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 1.5 & 0.05 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\displaystyle \right ], \\& \overline{A}_{3} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0.2 & - 20 & 0 & 1 & 0 \\ 0 & 0 & 0.6 & 0 & 0 & 0 \end{array}\displaystyle \right ],\qquad \overline{A}_{4} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0.2 & 20 & 0 & 1 & 0 \\ 0 & 0 & - 0.6 & 0 & 0 & 0 \end{array}\displaystyle \right ], \\& \textstyle\begin{array}{l} \overline{E} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\displaystyle \right ],\qquad \overline{B}_{i} = \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 0 & 0 & 4 \end{array}\displaystyle \bigr]^{T}, \\ \overline{C}_{i} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 1 \end{array}\displaystyle \right ]^{T},\quad i = 1,2,3,4, \end{array}\displaystyle \\& R = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \end{array}\displaystyle \right ],\qquad \Gamma= \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \end{array}\displaystyle \right ]. \end{aligned}$$

The application of fourth chapter results in \(N_{i}\), \(H_{i}\), \(L_{i}\), \(J_{i}\), \(K_{i}\), \(F_{i}\), \(S_{i}\), and \(Q_{i}\), \(i = 1,2,3,4\).

In addition, the following Xand γ must obey the Schur lemma:

$$X = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.145 & - 0.003 & 0 \\ - 0.033 & 0.138 & 0 \\ 0 & 0 & 0.074 \end{array}\displaystyle \right ] \quad \mbox{and}\quad \gamma= 0.947. $$

Below we give the functions \(h_{1}(t)\), \(h_{2i}(t)\) (\(i = 1,2,3,4\)) and the initial value:

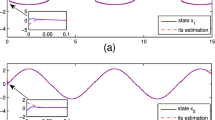
$$\begin{aligned}& h_{1}(t) = e^{ - 0.1t}, \\& h_{2i}(t) = 0.295e^{ - 0.1t},\quad i = 1,2,3,4, \\& x_{0} = \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 4 & 1 & 0.7 \end{array}\displaystyle \bigr]^{T}, \\& \theta= \bigl[ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.2 & 0.2 & 0.2 \end{array}\displaystyle \bigr]^{T}. \end{aligned}$$

We give the state response diagram of the system, as shown in Figures 1, 2, and 3. The red line in Figure 1 represents the state response of the \(x(t)\), and the blue line indicates the observer’s estimation. Figure 2 shows the state response of \(y(t)\), and the value of the blue line indicates the observer’s estimation. Figure 3, the red line, indicates the state response of \(E(t)\), and the blue line indicates the observer’s estimation.

Figure 1
figure 1

The comparison of the actual and estimated states of \(\pmb{x(t)}\) by our observer.

Full size image
Figure 2
figure 2

The comparison of the actual and estimated states of \(\pmb{y(t)}\) by our observer.

Full size image
Figure 3
figure 3

The comparison of the actual and estimated states of \(\pmb{E(t)}\) by our observer.

Full size image

To illustrate the superiority of our design of the observer, we use for the state observer of [1] three state estimation of nonlinear singular systems. The red lines in Figure 4 show the actual state response of the \(x(t)\), and the blue line the literature observer on the estimate of the \(x(t)\); in Figure 5 red lines represent actual state response of the \(y(t)\), and the blue line shows the literature observer estimate states of \(y(t)\). In Figure 6 the red line shows the actual state of \(E(t)\), and the blue line shows the literature observer on the estimate of \(E(t)\).

Figure 4
figure 4

The comparison of the actual and estimated states of \(\pmb{x(t)}\) by the observer of [ 1 ].

Full size image
Figure 5
figure 5

The comparison of the actual and estimated states of \(\pmb{y(t)}\) by the observer of [ 1 ].

Full size image
Figure 6
figure 6

The comparison of the actual and estimated states of \(\pmb{E(t)}\) by the observer of [ 1 ].

Full size image

Example 2

In view of system (5.2), we give the controller of the system (4.15).

Rule 1: If \(x(t)\) is \(M_{1}\) and \(y(t)\) is \(M_{3}\), then

$$u_{1} = K_{1}X(t). $$

Rule 2: If \(x(t)\) is \(M_{1}\) and \(y(t)\) is \(M_{4}\), then

$$u_{2} = K_{2}X(t). $$

Rule 3: If \(x(t)\) is \(M_{2}\) and \(y(t)\) is \(M_{3}\), then

$$u_{3} = K_{3}X(t). $$

Rule 4: If \(x(t)\) is \(M_{2}\) and \(y(t)\) is \(M_{4}\), then

$$u_{4} = K_{4}X(t). $$

Here

$$\begin{aligned}& X(t) = \bigl[x(t),y(t),E(t)\bigr]^{T}, \\& X = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1.5 & 0.8 & 1 \\ 0.8 & 2.1 & 2.3 \\ 1 & 2.3 & 1.7 \end{array}\displaystyle \right ], \\& Q_{1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1.4 & 1 & 0 \\ 1 & 0.7 & 0 \\ 0 & 0 & 0.5 \end{array}\displaystyle \right ],\qquad Q_{2} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1.4 & 0.5 & 0 \\ 0.5 & 0.7 & 0 \\ 0 & 0 & 0.5 \end{array}\displaystyle \right ], \\& Q_{3} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1.4 & 1 & 0 \\ 1 & 0.3 & 0 \\ 0 & 0 & 0.2 \end{array}\displaystyle \right ], \qquad Q_{4} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1.4 & 0.5 & 0 \\ 0.5 & 0.3 & 0 \\ 0 & 0 & 0.2 \end{array}\displaystyle \right ], \\& K_{1} = Q_{1}X^{ - 1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.7031 & - 1.3726 & 1.4435 \\ 0.5086 & - 0.9698 & 1.0129 \\ 0.0623 & 0.6346 & - 0.6011 \end{array}\displaystyle \right ], \\& K_{2} = Q_{2}X^{ - 1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.9282 & - 1.0014 & 0.8089 \\ 0.0967 & - 0.7447 & 0.9507 \\ 0.0623 & 0.6346 & - 0.6011 \end{array}\displaystyle \right ], \\& K_{3} = Q_{3}X^{ - 1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.7031 & - 1.3726 & 1.4435 \\ 0.6887 & - 0.6729 & 0.5053 \\ 0.0249 & 0.2538 & - 0.2404 \end{array}\displaystyle \right ], \\& K_{3} = Q_{3}X^{ - 1} = \left [ \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.9282 & - 1.0014 & 0.8089 \\ 0.2768 & - 0.4478 & 0.4430 \\ 0.0249 & 0.2538 & - 0.2404 \end{array}\displaystyle \right ]. \end{aligned}$$

After adding the controller, the graphics of the system (5.2) state variables are given in Figures 7, 8, and 9.

Figure 7
figure 7

The comparison of the error states of \(\pmb{x(t)}\) by adding the controller.

Full size image
Figure 8
figure 8

The comparison of the error states of \(\pmb{y(t)}\) by adding the controller.

Full size image
Figure 9
figure 9

The comparison of the error states of \(\pmb{E(t)}\) by adding the controller.

Full size image

6 Conclusions

In this paper, we mainly design the state observer-based T-S fuzzy singular system. We use the T-S fuzzy control method to form a T-S fuzzy singular system. Then we give an augmented system and T-S fuzzy compact form of singular system. Then we design a T-S fuzzy observer for the system. In order to verify the global stability of the T-S fuzzy observer with parameter and state estimation error, we construct a Lyapunov function of the T-S fuzzy form. Finally, we consider two numerical examples, comparing in the simulation observation the actual state and our observer is designed to estimate the state. From the comparison of the results we see that our design for the observer is effective. In future work, we intend to consider the following two main approaches of the literature. Kao et al. [35] devoted their work to investigating the problem of robust sliding-mode control for a class of uncertain Markovian jump linear time-delay systems with generally uncertain transition rates (GUTRs) and Noroozi et al. [36] gave semiglobal practical integral input-to-state stability (SP-iISS) for a feedback interconnection of two discrete-time subsystems.