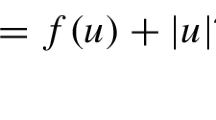1 Introduction

Let us consider the following semilinear asymmetric Duffing equation:

$$ x''+\alpha x^{+}-\beta x^{-}+f(t,x)=0, $$
(1.1)

where \(x^{\pm }=\max \{\pm x,0\}\), α and β are positive constants satisfying

$$ \frac{1}{\sqrt{\alpha }}+\frac{1}{\sqrt{\beta }}=\frac{2}{\omega } $$
(1.2)

with \(\omega \in \mathbb{R}^{+} \), \(f(t,x)\in C^{0,1}(\mathbf{S}^{1}\times \mathbb{R})\) is a continuous function, 2π-periodic in the first argument and has continuous derivative in the second one, where \(\mathbf{S}^{1}= \mathbb{R}/2\pi \mathbb{Z}\).

As one of the simplest but non-trivial conservative systems, equation (1.1) has been extensively and intensively studied by many researchers as regards its dynamic behavior such as periodic solutions [1–10], and the existence of bounded or unbounded solutions [11–16]. In the existing literature, a lot of work has been done to prove the existence of the periodic solutions, such as [1–10] and the references given therein, but there is little information as regards the dynamics behavior of its periodic solution. On the other hand, Aubry-Mather theory about twist maps heavily indicates that equation (1.1) most likely possesses at least some ‘good’ periodic solutions as well as some generalized quasi-periodic solutions. This is the main objective of this paper and we will prove the existence of Aubry-Mather sets for equation (1.1) under some suitable assumptions.

In the early 1980s, Aubry [17] and Mather [18] have proved independently that invariant curves of integral system will be broken if its perturbation increased gradually and/or the smoothness of integrable system is weakened, when they, respectively, studied a one dimensional liquid crystal model of solid state physics and the qualitative properties of the orbits of an area-preserving twist map of the annulus. They also found that when invariant curves break, they do not disappear completely, some special invariant sets still exist. Today, these invariant sets are called the Aubry-Mather sets. For the planar differential system, Aubry-Mather theory suggests that for its Poincaré mapping if there exist Aubry-Mather sets \(M_{\sigma }\) with a rotation number σ, then the planar differential system possesses Aubry-Mather type solutions \(z_{\sigma }(t)=(x_{\sigma }(t),y_{\sigma }(t))\), such that \(M_{\sigma }\equiv \overline{\{z_{\sigma }(2\pi i),i\in Z\}}\) satisfying the following geometrical properties:

\((1)\) if \(\sigma =\frac{n}{m}\in {\mathbb{Q}}\) with \((n,m)=1\), then \(z_{\sigma }(t)\) is a Birkhoff periodic solution with periodic \(2m\pi \) and \(\arg (z_{\sigma }(t)+m)=\arg (z_{\sigma }(t))+n\), the m solutions \(z_{\sigma }(t+2\pi i), 0\leq i\leq m-1\), can be homotopically transformed to m distinct parallel lines;

\((2)\) if \(\sigma \in {{\mathbb{R}}\backslash {\mathbb{Q}}}\), then \(M_{\sigma }\) is either an invariant circle and its orbits are just usual quasi-periodic orbits, or an invariant Cantor set and its orbits become generalized ones. For further interpretations, we refer to the recent work of [19] and [20].

In general, we note that the existence of Birkhoff type periodic solution is very difficult to prove, see, for example, Bernstein and Katok work [21]. But Aubry-Mather theory has provided a powerful tool for complete qualitative description of the dynamic behavior of differential equations due to their applications in many fields such as differential geometry, dynamical systems, and solid physics (see [22, 23]). In the last two decades, there has been an increasing interest in obtaining sufficient conditions for the existence of Aubry-Mather sets for different classes of nonlinear second order differential equations. We refer to the recent papers [24–33], and references therein. Especially, in [29], Capietto and Liu have studied the following piecewise linear equation:

$$ x''+\alpha x^{+}-\beta x^{-}+\psi (x)=e(t), $$
(1.3)

where \(\psi (x)\in C^{2}(\mathbb{R})\) is bounded and \(e(t)\in C^{2}(\mathbf{S}^{1})\) is 2π-periodic. Under some additional hypotheses on \(\psi (x)\) and in the resonant case

$$ \frac{1}{\sqrt{\alpha }}+\frac{1}{\sqrt{\beta }}=\frac{2}{\omega } $$
(1.4)

with \(\omega \in \mathbb{Q}^{+}\), they used an exchange of the role of time and angle variables and proved the existence of Aubry-Mather sets for equation (1.3), by means of a version of the Aubry-Mather theorem on a cylinder with the monotone twist assumption given by Pei [25], in which the author gave some sufficient conditions for the existence of Aubry-Mather sets for a class of semilinear Duffing equations,

$$ x''+\lambda ^{2} x+\psi (x)=p(t), $$
(1.5)

where \(\lambda >0\) is a constant, \(p(t)\in C^{0}(\mathbf{S}^{1})\) is a periodic function and \(\psi (x)\in C^{2}(\mathbb{R})\) is an unbounded function satisfying some other growth conditions.

Now a natural and open question is whether equation (1.3) still possesses Aubry-Mather sets when the smoothness of \(\psi (x)\) and \(e(t)\) is further weakened. Our Theorem 1.1 in the following will answer this question and we will deal with a more general case (1.1) than that of (1.3). Owing to the appearance of weak smoothness nonlinearity, the methods in [25–31] are no longer valid. To overcome this difficulty, we first introduce a suitable action and angle variable transformation similar to [29] so that the transformed system of (1.1) is a perturbation of an integral Hamiltonian system, and then apply a new estimate approach developed by the present author (see the recent papers [32–34]) to directly prove the Poincaré map of the transformed system satisfying monotone twist property. Furthermore, the Aubry-Mather theorem on a cylinder with monotone twist assumption by Pei [25] guarantees the existence of Aubry-Mather sets for (1.1), which leads to our desired results. The results of this paper are new and they are natural generalizations and refinements of previously known results obtained in [25, 29].

More exactly, the following theorem is proved.

Theorem 1.1

Assume that the condition (1.2) holds true. Let \(f(t,x)\in C^{0,1}(\mathbf{S}^{1}\times \mathbb{R})\) satisfy the following conditions:

\((A_{1})\) :

the limit \(\lim_{\vert x \vert \to +\infty }f_{x}(t,x)=0\), uniformly in \(t\in [0,2\pi ]\);

\((A_{2})\) :

there exist constants \(d\geq 0, \mu >0\), such that

$$ \operatorname{sgn}(x) \bigl[f(t,x)-xf_{x}(t,x) \bigr]>\mu ,\quad\textit{for } \vert x \vert \geq d. $$

Then there exists \(\varepsilon _{0}>0\), such that, for any \(\sigma \in (2\omega \pi ,2\omega \pi +\varepsilon _{0})\), equation (1.1) possesses an Aubry-Mather type solution \(z_{\sigma }(t)=(x_{\sigma }(t),x'_{\sigma }(t))\) with rotation number σ, namely,

  1. (i)

    when \(\sigma =\frac{n}{m}\) is rational, and \((n,m)=1\), the solutions \(z_{\sigma }^{i}(t)=z_{\sigma }(t+2\pi i) , 0\leq i\leq m-1\), are mutually unlinked periodic solutions of period m;

  2. (ii)

    when σ is irrational, the solution \(z_{\sigma }(t)\) is either a usual quasi-periodic solution or a generalized one exhibiting a Denjoy minimal set (see the definition in [35])

    $$ M_{\sigma }\equiv \overline{ \bigl\{ z_{\sigma }(2\pi i),i\in { \mathbb{Z}} \bigr\} }. $$

Remark 1.1

Applying the rule of L’Hospital to condition \((A_{1})\), it is easy to see that

$$ \lim_{\vert x \vert \to +\infty }\frac{f(t,x)}{x}=0,\quad \text{uniformly in } t\in[0,2\pi ].\hspace{150pt} (f_{0}) $$

The rest of the paper is organized as follows: The proof of Theorem 1.1 will be given in Section 4. Section 2 introduces some basic results which are necessary for the proof of Theorem 1.1. In Section 2.1, we introduce a polar coordinate type action-angle variable which transform equation (1.1) into a perturbation of an integral Hamiltonian system, and then in Section 2.2, we will give some estimates on the corresponding action and angle variables functions. Section 3 deals with the proof of monotone twist property of the Poincaré map P of the new system around infinity. Finally, Section 5 presents some examples and remarks on Theorem 1.1.

2 Some basic results

2.1 Action-angle variables

Introducing a new variable y as \(x'=-y\), then equation (1.1) is equivalent to the following system:

$$ x'=-y, \qquad y'=\alpha x^{+}-\beta x^{-}+f(t,x). $$
(2.1)

Let \((C(t),S(t))\) be the solution of the autonomous system

$$ x'=-y, \qquad y'=\alpha x^{+}- \beta x^{-} $$
(2.2)

satisfying the initial condition \((C(0),S(0))=(1,0)\). Then it is well known that \(S(t)\in C^{1}(\mathbb{R})\) and \(C(t)\in C^{2}(\mathbb{R})\) are \(\frac{2\pi }{\omega }\)-periodic and the even function \(C(t)\) can be expressed as

$$ C(t)= \textstyle\begin{cases} \cos \sqrt{\alpha }t, &0\leq \vert t \vert \leq \frac{\pi }{2\sqrt{\alpha }},\\ -\sqrt{\frac{\alpha }{\beta }}\sin \sqrt{\beta }(t-\frac{\pi }{2\sqrt{\alpha }}),& \frac{\pi }{2\sqrt{\alpha }}\leq \vert t \vert \leq \frac{\pi }{\omega }. \end{cases} $$

It is easy to see that the functions \(C(t)\) and \(S(t)\) are very similar to the cosine and the sine. Moreover, it is not difficult to prove that

  1. (i)

    \(C'(t)=-S(t), S'(t)=\alpha C^{+}(t)-\beta C^{-}(t)\);

  2. (ii)

    \((S(t))^{2}+\alpha (C^{+}(t))^{2}+\beta (C^{-}(t))^{2}\equiv \alpha \);

  3. (iii)

    \(\vert C(t) \vert \leq \max \{1,\sqrt{\frac{\alpha }{\beta }}\}:=C_{\infty }, \vert S(t) \vert \leq \sqrt{\alpha }\).

For \(r>0\) and \(\theta (\operatorname{mod} 2\pi )\), we introduce the action and angle variables transformation \(T:(r,\theta )\rightarrow (x,y)\) as

$$ x=\sqrt{2\lambda r}C \biggl(\frac{\theta }{\omega } \biggr),\qquad y= \sqrt{2\lambda r}S \biggl(\frac{\theta }{\omega } \biggr) $$
(2.3)

with \(\lambda =\frac{\omega }{\alpha }\). Then its Jacobian

$$ \det T'(r,\theta )= \begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta } \cr \frac{\partial y}{\partial r}& \frac{\partial y}{\partial \theta } \end{vmatrix}=1, $$

where \(x_{r}=\frac{\partial x}{\partial r}=\frac{x}{2r}, x_{\theta }=\frac{\partial x}{\partial \theta }=-\frac{y}{\omega }, y_{r}=\frac{\partial y}{\partial r}=\frac{y}{2r}, y_{\theta }=\frac{\partial y}{\partial \theta }=\frac{\alpha x^{+}}{\omega }-\frac{\beta x^{-}}{\omega }\). Therefore the map T is symplectic.

2.2 Some estimates on action and angle variables functions

Under (2.3), (2.1) becomes

$$ \frac{d\theta }{dt}=\Phi _{1}(t,\theta ,r),\qquad \frac{dr}{dt}=\Phi _{2}(t,\theta ,r), $$
(2.4)

where \(\Phi _{1}(t,\theta ,r)=\omega +\frac{x(\theta ,r)f(t,x(\theta ,r) )}{2r},\Phi _{2}(t,\theta ,r)=\frac{y(\theta ,r)f(t,x(\theta ,r) )}{\omega }\).

According to the assumptions of \((A_{1})\) and \((A_{2})\), it is easy to prove the existence and uniqueness of the solution of the initial value problem associated with (2.4). Moreover, this solution has continuous derivatives with respect to initial data.

Let \(\theta (t)=\theta (t;\theta _{0},r_{0}),r(t)=r(t;\theta _{0},r_{0})\) be the solution of initial value problem \(\theta (0)=\theta _{0},r(0)=r_{0}\), then

$$ x(t;\theta _{0},r_{0})=x \bigl(\theta (t;\theta _{0},r_{0}),r(t;\theta _{0},r_{0}) \bigr)= \sqrt{2\lambda r(t;\theta _{0},r_{0}})C \biggl( \frac{\theta (t;\theta _{0},r_{0})}{\omega } \biggr) $$

and

$$ y(t;\theta _{0},r_{0})=y \bigl(\theta (t;\theta _{0},r_{0}),r(t;\theta _{0},r_{0}) \bigr)= \sqrt{2\lambda r(t;\theta _{0},r_{0}})S \biggl( \frac{\theta (t;\theta _{0},r_{0})}{\omega } \biggr) $$

are the solutions of (2.1) with initial data \(x(0)=x(0;\theta _{0},r_{0}),y(0)=y(0;\theta _{0},r_{0})\). So the Poincaré map P of (2.4) is of the form

$$ P:(\theta _{0},r_{0})\mapsto \bigl(\theta (2 \pi ,\theta _{0},r_{0}),r(2\pi ,\theta _{0},r_{0}) \bigr). $$
(2.5)

For notional convenience, hereinafter, we write x, y, θ, r instead of \(x(\theta (t;\theta _{0},r_{0}),r(t;\theta _{0}, r_{0}))\), \(y(\theta (t;\theta _{0},r_{0}),r(t;\theta _{0},r_{0})),\theta (t;\theta _{0},r_{0}), r(t;\theta _{0},r_{0})\), respectively.

Now in the following, we will give some growth estimation properties with respect to the action and angle variables functions \(r(t;\theta _{0},r_{0})\) and \(\theta (t;\theta _{0},r_{0})\).

Proposition 2.1

Assume that \((A_{1})\) holds. Then the limit

$$ \lim_{r_{0}\to +\infty }r(t;\theta _{0},r _{0})=+\infty $$

holds uniformly with respect to \(t\in [0,2\pi ]\).

Proof

By \((f_{0})\) and the action and angle variables transformation (2.3), there exist constants \(B>0, F>0\), such that

$$\bigl\vert r'(t) \bigr\vert = \biggl\vert \frac{yf(t,x)}{\omega } \biggr\vert \leq Br(t)+F,\quad \forall r\neq 0. $$

Then, by the Gronwall inequality, we obtain

$$ e^{-2\pi B}r_{0}-\frac{F}{B} \bigl(1-e^{-2\pi B} \bigr)\leq r(t)\leq e^{2\pi B}r_{0}+ \frac{F}{B} \bigl(e^{2\pi B}-1 \bigr) $$
(2.6)

for all \(t\in [0,2\pi ]\).

Consequently, by (2.6), \(r(t;\theta _{0},r _{0})\to +\infty \) as \(r_{0}\to +\infty \) uniformly for \(t\in [0,2\pi ]\). □

By (2.6), we can easily verify the following.

Proposition 2.2

Suppose that \((A_{1})\) holds. Then there exist constants \(\beta _{2}>\beta _{1}>0\) and \(\bar{r}>0\), such that, for any \(r_{0}\geq \bar{r}\), we have

$$ \beta _{1}r_{0}\leq r(t;\theta _{0},r_{0}) \leq \beta _{2}r_{0}, $$

for \(\forall \theta _{0}\in \mathbb{R}\) and \(\forall t\in[0,2\pi ]\).

Proposition 2.3

Let \((A_{1})\) hold. Then, for any \(\theta _{0}\in \mathbb{R}\) and \(t\in [0,2\pi ]\), there exists \(\bar{r}>0\), such that

$$ \frac{\omega }{2}\leq \theta '(t;\theta _{0},r_{0})\leq 2\omega $$
(2.7)

as long as \(r_{0}\geq \bar{r}\).

Proof

Since \((f_{0})\) holds, for every \(\varepsilon >0\), there exists \(X=X(\varepsilon )>0\), such that

$$\begin{aligned} \bigl\vert f(t,x) \bigr\vert \leq \varepsilon \vert x \vert \end{aligned}$$

if \(\vert x \vert \geq X\) and \(\forall t\in [0,2\pi ]\). Hence,

$$\begin{aligned} \frac{d\theta }{dt}=\omega +\frac{xf(t,x)}{2r} \geq \omega -\frac{\varepsilon x^{2}}{2r}. \end{aligned}$$

Thus, in view of (2.3) and Proposition 2.1, there exists \(\bar{r_{1}}>0\) such that

$$\frac{d\theta }{dt}\geq \frac{\omega }{2} $$

if \(r_{0}\geq \bar{r_{1}}\).

If \(\vert x \vert \leq X\), we may assume that \(\vert f(t,x) \vert \leq f_{\infty }\), where \(f_{\infty }= \max \{\vert f(t,x) \vert :t\in [0,2\pi ],\vert x \vert \leq X\}\), then

$$ \frac{d\theta }{dt}=\omega +\frac{xf(t,x)}{2r} \geq \omega - \frac{f_{\infty }\vert x \vert }{2r}. $$

Hence, by (2.3) and Proposition 2.1, there exists a constant \(\bar{r_{2}}>0\), such that \(\frac{d\theta }{dt}\geq \frac{\omega }{2}\) if \(r_{0}\geq \bar{r_{2}}\).

If we choose \(\bar{r}=\max \{\bar{r_{1}},\bar{r_{2}}\}\), then \(r_{0}\geq \bar{r}\) implies \(\frac{d\theta }{dt}\geq \frac{\omega }{2}\).

Using the same arguments as above, one can prove that the inequality on the right side of (2.7) holds. □

3 Monotone twist property

In this section, we will prove

$$\begin{aligned} \frac{\partial \theta (2\pi ;\theta _{0},r_{0}) }{\partial r_{0}}< 0 \end{aligned}$$

if \(r_{0}\gg 1\). This implies the Poincaré map P given by (2.5) has monotone twists around infinity.

Now in the following, we will start to examine the behavior of \(\frac{\partial \theta (2\pi ;\theta _{0},r_{0}) }{\partial r_{0}} \) when \(r_{0}\gg 1\).

Let us consider the variational equation of (2.4) with respect to the initial value \(r_{0}\). One can verify that, for any \(t\in [0, 2\pi ]\),

$$ \begin{aligned} &\dot{\theta }_{r_{0}}=a_{1}(t) \frac{\partial r}{\partial r_{0}}+ a_{2}(t)\frac{\partial \theta }{\partial r_{0}}, \\ &\dot{r}_{r_{0}}=-a_{2}(t) \frac{\partial r}{\partial r_{0}}+ a_{3}(t) \frac{\partial \theta }{\partial r_{0}}, \end{aligned} $$
(3.1)

where

$$\begin{aligned}& a_{1}(t)=\frac{\partial \Phi _{1}(t,\theta ,r)}{\partial r} =\frac{-x[f(t,x)-xf_{x}(t,x)]}{4r^{2}}, \\& a_{2}(t)=\frac{\partial \Phi _{1}(t,\theta ,r)}{\partial \theta }=\frac{-y}{2\omega r} \bigl[f(t,x)+xf_{x}(t,x) \bigr], \\& a_{3}(t)=\frac{\partial \Phi _{2}(t,\theta ,r)}{\partial \theta }=\frac{(\alpha x^{+}-\beta x^{-})f(t,x)}{\omega ^{2}}-\frac{y^{2}f_{x}(t,x)}{\omega ^{2}}. \end{aligned}$$

Then we have the following.

Lemma 3.1

For \(r_{0}\gg 1\) and \(\forall t,s \in [0,2\pi ]\), the following conclusions hold:

  1. (i)

    \(a_{1}(t)=o(\frac{1}{r_{0}})\);

  2. (ii)

    \(a_{2}(t)=o(1)\);

  3. (iii)

    \(a_{1}(t)\cdot a_{3}(s)=o(1)\).

Proof

By using Lemma 3.2, the proof can be obtained immediately. □

Next we are going to give a detailed proof of Lemma 3.2.

Lemma 3.2

As \(r_{0}\rightarrow +\infty \), the following convergences hold uniformly on \(t\in [0,2\pi ]\):

  1. (i)

    \(\frac{xf(t,x)}{r}\rightarrow 0\), \(\frac{x^{2}f_{x}(t,x)}{r}\rightarrow 0\);

  2. (ii)

    \(\frac{yf(t,x)}{r}\rightarrow 0\), \(\frac{yxf_{x}(t,x)}{r}\rightarrow 0\), \(\frac{y^{2}xf(t,x)f_{x}(t,x)}{r^{2}}\rightarrow 0\).

Proof

If \((A_{1})\) and \((f_{0})\) hold, then to each \(\varepsilon >0\) there corresponds a positive number \(X=X(\varepsilon )>0\), such that

$$\begin{aligned} \bigl\vert f_{x}(t,x) \bigr\vert \leq \frac{\varepsilon }{4\lambda C_{\infty }^{2}} \end{aligned}$$

and

$$ \bigl\vert f(t,x) \bigr\vert \leq \frac{\varepsilon }{4\lambda C_{\infty }^{2}} \vert x \vert $$

if \(\vert x \vert \geq X\) and \(t\in[0,2\pi ]\), here \(C_{\infty }\) is defined in Section 2.1.

Set \(F_{1}(\varepsilon )=\max \{\vert f(t,x) \vert :t\in [0,2\pi ],\vert x \vert \leq X\}, F_{2}(\varepsilon )=\max \{\vert f_{x}(t,x) \vert :t\in [0,2\pi ],\vert x \vert \leq X\}\).

(i) According to the action and angle variables transformation (2.3), one has

$$\begin{aligned}& \biggl\vert \frac{xf(t,x)}{r} \biggr\vert \leq \frac{XK_{1}(\varepsilon )}{r}+ \frac{\varepsilon x^{2}}{4\lambda C_{\infty }^{2}r} \leq \frac{XK_{1}(\varepsilon )}{r}+\frac{\varepsilon }{2} ; \\& \biggl\vert \frac{x^{2}f_{x}(t,x)}{r} \biggr\vert \leq \frac{X^{2}F_{2}(\varepsilon )}{r}+ \frac{\varepsilon x^{2}}{4\lambda C_{\infty }^{2}r} \leq \frac{X^{2}F_{2}(\varepsilon )}{r}+\frac{\varepsilon }{2}. \end{aligned}$$

Then, given \(\bar{r}>0\), choose \(r_{0}\) so that \(r_{0}\geq \bar{r}\), by using Proposition 2.2, provided

$$ r(t)\geq \max \biggl\{ \frac{2XK_{1}(\varepsilon )}{\varepsilon };\frac{2X^{2}F_{2}(\varepsilon )}{\varepsilon } \biggr\} , $$

we have

$$ \biggl\vert \frac{xf(t,x)}{r} \biggr\vert \leq \varepsilon ;\qquad \biggl\vert \frac{x^{2}f_{x}(t,x)}{r} \biggr\vert \leq \varepsilon . $$

Since \(\varepsilon >0\) is arbitrary, the proof of (i) is complete.

(ii) Corresponding to (2.3), one can see that

$$\begin{aligned}& \biggl\vert \frac{yf(t,x)}{r} \biggr\vert \leq \frac{\varepsilon \vert y \vert \vert x \vert }{4\lambda C_{\infty }^{2}r}+ \frac{F_{1}(\varepsilon )\vert y \vert }{r} \leq \frac{\sqrt{\alpha }\varepsilon }{2C_{\infty }}+\frac{\sqrt{2\omega }F_{1}(\varepsilon )}{\sqrt{r}}; \\& \biggl\vert \frac{yxf_{x}(t,x)}{r} \biggr\vert \leq \frac{\varepsilon \vert y \vert \vert x \vert }{4\lambda C_{\infty }^{2}r}+ \frac{X\vert y \vert F_{2}(\varepsilon )}{r} \leq \frac{\sqrt{\alpha }\varepsilon }{2C_{\infty }}+\frac{\sqrt{2\omega }XK_{2}(\varepsilon )}{\sqrt{r}}; \\& \biggl\vert \frac{y^{2}xf(t,x)f_{x}(t,x)}{r^{2}} \biggr\vert \leq \frac{2\lambda \alpha F_{1}(\varepsilon )F_{2}(\varepsilon )X}{r}+ \frac{2\lambda \vert x \vert ^{2}\varepsilon ^{2}}{4\lambda C_{\infty }^{4}r}\leq \frac{2\lambda \alpha F_{1}(\varepsilon )F_{2}(\varepsilon )X}{r}+\frac{\alpha \varepsilon ^{2}}{4C_{\infty }^{2}}. \end{aligned}$$

Then, given \(\bar{r}>0\), choose \(r_{0}\) so that \(r_{0}\geq\bar{r}\), by using Proposition 2.2, provided

$$ r(t)\geq \max \biggl\{ \frac{8\omega F_{1}^{2}(\varepsilon )}{\varepsilon ^{2}}; \frac{8\omega X^{2} F_{2}^{2}(\varepsilon )}{\varepsilon ^{2}}; \frac{2\omega F_{1}(\varepsilon )F_{2}(\varepsilon )X}{\varepsilon } \biggr\} , $$

we have

$$\biggl\vert \frac{yf(t,x)}{r} \biggr\vert \leq \frac{\sqrt{\alpha }\varepsilon }{2C_{\infty }}+ \frac{\varepsilon }{2}; \qquad \biggl\vert \frac{yxf_{x}(t,x)}{r} \biggr\vert \leq \frac{\sqrt{\alpha }\varepsilon }{2C_{\infty }}+\frac{\varepsilon }{2}; \qquad \biggl\vert \frac{y^{2}xf(t,x)f_{x}(t,x)}{r^{2}} \biggr\vert \leq \varepsilon +\frac{\alpha \varepsilon ^{2}}{4C_{\infty }^{2}}. $$

Since \(\varepsilon >0\) is arbitrary, (ii) is proved. □

Combining the previous lemmas, we have the following.

Lemma 3.3

For all \(t \in (0,2\pi ]\), as \(r_{0}\rightarrow +\infty \), we have

  1. (i)

    \(\theta _{r_{0}}(t;\theta _{0}, r_{0})\rightarrow 0\);

  2. (ii)

    \(r_{r_{0}}(t;\theta _{0}, r_{0})=1+o(1)\);

  3. (iii)

    \(\theta _{\theta _{0}}(t;\theta _{0}, r_{0})=1+o(1)\).

Proof

By the variational equations (3.1) and Lemma 3.2, we have

$$\begin{aligned} \theta _{r_{0}}(t)&=e^{\int _{0}^{t}a_{2}(s)\,ds}\cdot \int _{0}^{t} e^{-\int _{0}^{s}a_{2}(t)\,dt} a_{1}(s) \cdot r_{r_{0}}(s)\,ds \\ &= \bigl(1+o(1) \bigr) \int _{0}^{t}a_{1}(s)\cdot r_{r_{0}}(s)\,ds, \\ r_{r_{0}}(t)&=e^{-\int _{0}^{t}a_{2}(s)\,ds}\cdot \biggl(1+ \int _{0}^{t} e^{\int _{0}^{s}a_{2}(t)\,dt} a_{3}(s) \cdot \theta _{r_{0}}(s)\,ds \biggr) \\ &=1+o(1)+ \bigl(1+o(1) \bigr) \int _{0}^{t}a_{3}(s)\cdot \biggl( \int _{0}^{s}a_{1}(t)\cdot r_{r_{0}}(t)\,dt \biggr)\,ds \\ &=1+o(1)+o(1) \int _{0}^{t} \int _{0}^{s}I_{r_{0}}(t)\,dt\,ds, \end{aligned}$$

where we have used \(\theta _{r_{0}}(0)=0\) and \(r_{r_{0}}(0)=1\).

Therefore, for all \(t\in (0,2\pi ]\), sending \(r_{0}\rightarrow +\infty \), we have \(r_{r_{0}}(t)=1+o(1)\) and \(\theta _{r_{0}}(t)=(1+o(1))\int _{0}^{t}a_{1}(s)\,ds\rightarrow 0\). This completes the proof of (i) and (ii).

To prove (iii), we consider the variational equation of (2.4) about \(\theta _{0}\)

$$ \dot{\theta }_{\theta _{0}}=a_{1}(t) \frac{\partial r}{\partial \theta _{0}}+ a_{2}(t)\frac{\partial \theta }{\partial \theta _{0}}, \qquad \dot{r}_{\theta _{0}}=-a_{2}(t) \frac{\partial r}{\partial \theta _{0}}+ a_{3}(t) \frac{\partial \theta }{\partial \theta _{0}}. $$
(3.2)

Similar to the proof of (ii), one can see that \(\theta _{\theta _{0}}(t;\theta _{0}, r_{0})=1+o(1)\) for \(\forall t\in (0,2\pi ]\), as \(r_{0}\rightarrow +\infty \). This completes the proof of Lemma 3.3. □

Now, we will give an estimate of upper bound and lower bound for \(a_{1}(t)\).

Lemma 3.4

Let \(d\geq 0\) satisfy \((A_{2})\).

  1. (i)

    If \(\vert x(t;\theta _{0},r_{0}) \vert \leq d\) for all \(t \in [0,2\pi ]\), then there exists a constant \(K_{d}>0\), such that \(\vert a_{1}(t) \vert \leq \frac{K_{d}}{r^{2}(t)}\).

  2. (ii)

    If \(\vert x(t;\theta _{0},r_{0}) \vert \geq d\) for all \(t \in [0,2\pi ]\), then there exists a constant \(L_{d}>0\), such that \(\vert a_{1}(t) \vert \geq \frac{L_{d}}{r^{2}(t)}\). Moreover, \(\vert x(t;\theta _{0},r_{0}) \vert \geq d\) implies that \(a_{1}(t)<0\).

Proof

(i) If \(\vert x(t;\theta _{0},r_{0}) \vert \leq d\), we take \(f_{d}=\max_{\vert x \vert \leq d, t\in [0,2\pi ]}\vert f(x,t)-xf_{x}(x,t) \vert \).

Then

$$\bigl\vert a_{1}(t) \bigr\vert =\biggl\vert \frac{-x[f(x,t)-xf_{x}(x,t)]}{4r^{2}} \biggr\vert \leq \frac{\vert x \vert f_{d}}{4r^{2}(t)}\leq \frac{df_{d}}{4r^{2}(t)}. $$

Set \(K_{d}= \frac{df_{d}}{4}\), we get \(\vert a_{1}(t) \vert \leq \frac{K_{d}}{r^{2}(t)}\).

(ii) If \(\vert x(t;\theta _{0},r_{0}) \vert \geq d\), then from the condition of \((A_{2})\), one can see that \(xf(x,t)-x^{2}f_{x}(x,t)>\mu x\) when \(x\geq d\), and \(xf(x,t)-x^{2}f_{x}(x,t)>-\mu x\) when \(x\leq -d\). Hence, \(a_{1}(t)<0\). Further,

$$\bigl\vert a_{1}(t) \bigr\vert = \biggl\vert \frac{-x[f(x,t)-xf_{x}(x,t)]}{4r^{2}} \biggr\vert \geq \frac{\vert x \vert \mu }{4r^{2}(t)} \geq \frac{d\mu }{4r^{2}(t)} . $$

Choosing \(L_{d}=\frac{d\mu }{4}\), it yields

$$\bigl\vert a_{1}(t) \bigr\vert \geq \frac{L_{d}}{r^{2}(t)}. $$

Denote \(a_{1}(t)=a_{1}^{+}(t)-a_{1}^{-}(t)\), where \(a_{1}^{\pm }(t)=\max \{\pm a_{1}(t),0\}\). To estimate the integral of \(a_{1}^{+}(t)\) on \([0,2\pi ]\) is smaller than the integral of \(a_{1}^{-}(t)\) on \([0,2\pi ]\), we need the following lemma. □

Lemma 3.5

Let \(d\geq 0\) be as in Theorem  1.1. Define \(\Delta t=\{t\in [0,2\pi ]\mid \vert x(t;\theta _{0},r_{0}) \vert \leq d\}\). Then there exist \(\bar{r_{0}}>0,D>0\), such that

$$ \vert \Delta t \vert \leq \frac{D}{\sqrt{r_{0}}}, $$

for all \(r_{0}\geq \bar{r_{0}}\).

Proof

By Proposition 2.3, we know that \(\Delta t\rightarrow 0\) if and only if \(\Delta \theta \rightarrow 0\).

According to the action and angle variables transformation (2.3), we see that there exists \(\gamma >0\) such that \(\vert \tan \Delta \theta \vert \leq \frac{\gamma d}{\sqrt{2\lambda r(t)}}\) when \(\Delta \theta \rightarrow 0 \). Therefore, by using Proposition 2.2, we know that there exist \(\bar{r_{0}}>0, D>0\), such that

$$ \vert \Delta t \vert \leq \frac{D}{\sqrt{r_{0}}}, $$

for all \(r_{0}\geq \bar{r_{0}}\). Lemma 3.5 follows. □

In the following, we will give an estimate of \(\frac{\partial \theta (2\pi ;\theta _{0},r_{0}) }{\partial r_{0}}\) if \(r_{0}\gg 1\).

Lemma 3.6

For \(r_{0}\gg 1\), we have \(\theta _{r_{0}}(2\pi )<0\).

Proof

Combining Lemma 3.4, Lemma 3.5 and Proposition 2.2, we can make it clear that

$$\begin{aligned} \theta _{r_{0}}(2\pi ) &= \bigl(1+o(1) \bigr) \int _{0}^{2\pi }a_{1}(s)\,ds \\ &= \bigl(1+o(1) \bigr) \biggl( \int _{a_{1}(t)\leq 0}a_{1}(s)\,ds+ \int_{a_{1}(t)\geq 0} a_{1}(s)\,ds \biggr) \\ &\leq - \bigl(1+o(1) \bigr) \biggl( \frac{L_{d}}{\beta _{2}^{2}r_{0}^{2}} \bigl(2\pi -\vert \Delta t \vert \bigr)-\frac{K_{d}}{\beta _{1}^{2}r_{0}^{2}}\vert \Delta t \vert \biggr) \\ &\leq \bigl(1+o(1) \bigr) \biggl( \frac{(\beta _{1}^{2} L_{d} +\beta _{2}^{2}K_{d})D}{\beta _{1}^{2}\beta _{2}^{2}r_{0}^{2}\sqrt{r_{0}}}-\frac{2\pi L_{d}}{\beta _{2}^{2}r_{0}^{2}} \biggr). \end{aligned}$$

Consequently, if \(\sqrt{r_{0}}>\frac{(\beta _{1}^{2} L_{d} +\beta _{2}^{2}K_{d})D}{2\pi L_{d}\beta _{1}^{2}}\), then \(\theta _{r_{0}}(2\pi )<0\). □

4 Proof of Theorem 1.1

Now we are in a position to prove Theorem 1.1.

Proof of Theorem 1.1.

According to Lemma 3.6 and the Aubry-Mather theory framework developed by Pei [25], we know that the Poincaré map P of system (2.4) is a monotone twist map if \(r_{0}\gg 1\). At last, using similar arguments as in [25], one may extend the Poincaré map P to a new map P̂ which is a global monotone twist homeomorphism of the cylinder \(\mathbf{S}^{1}\times \mathbb{R}\) and coincides with P on \(\mathbf{S}^{1}\times [r_{0},+\infty )\) with a fixed constant \(r_{0}\gg 1\). Therefore, the existence of Aubry-Mather sets \(M_{\sigma }\) of P̂ is guaranteed by the Aubry-Mather theorem by Pei [25]. Moreover, for some small \(\varepsilon _{0}>0\), all those Aubry-Mather sets with rotation number \(\sigma \in (2\omega \pi ,2\omega \pi +\varepsilon _{0}) \) lie in the domain \(\mathbf{S}^{1}\times [r_{0},+\infty )\). Hence they are just the Aubry-Mather sets of the Poincaré map of P. From the above discussions, we have showed the existence of Aubry-Mather sets, this implies that equation (1.1) has a solution \(z_{\sigma }(t)=(x_{\sigma }(t),x'_{\sigma }(t))\) with rotation number σ. Thus, the proof of Theorem 1.1 is completed. □

5 Examples and remarks

As an application, let us consider the following equation:

$$ x''+\alpha x^{+}-\beta x^{-}+f(t,x)=0, $$
(5.1)

where \(x^{\pm }=\max \{\pm x,0\}\), α and β are positive constants satisfying

$$ \frac{1}{\sqrt{\alpha }}+\frac{1}{\sqrt{\beta }}=\frac{2}{\omega } $$
(5.2)

with \(\omega \in \mathbb{R}^{+} \), \(f(t,x)\in C^{0,1}(\mathbf{S}^{1}\times \mathbb{R})\) and \(\mathbf{S}^{1}= \mathbb{R}/2\pi \mathbb{Z}\).

Example 5.1

Bounded perturbation

Consider \(f(t, x) =\operatorname{sgn}(x)\arctan x\cdot (1+\vert p(t) \vert )\), where \(p(t)\) is a continuous function satisfying \(p(t +2\pi ) = p(t)\). We can easily check \(f(t, x)\in C^{0,1}(\mathbf{S}^{1}\times \mathbb{R})\) is a bounded function satisfying conditions \((A_{1})\) and \((A_{2})\) in Theorem 1.1 when \(d=1\) and \(\mu =\frac{\pi }{4}-\frac{1}{2}\) for any \(\alpha \neq \beta \) in (5.2). But \(f(t, x)\) does not satisfy the conditions \((H_{1})\)-\((H_{4})\) of Theorem 1 in [29]. Therefore, the results obtained in this paper can be viewed as natural generalizations and refinements of the results in [29].

Example 5.2

Unbounded perturbation

Let \(\alpha =\beta =\lambda \) in (5.2) and \(f(t,x)=\operatorname{sgn}(x)\ln (1+\vert x \vert )\cdot (1+\vert p(t) \vert )\), where \(p(t)\) is a continuous function satisfying \(p(t +2\pi ) = p(t)\). It is obvious that \(f(t, x)\in C^{0,1}(\mathbf{S}^{1}\times \mathbb{R})\) is an unbounded function satisfying conditions \((A_{1})\) and \((A_{2})\) in Theorem 1.1 if \(d=e^{2}\) and \(\mu =1\). It is clear that the conditions \((D_{1})\) and \((D_{2})\) of Theorem B in [25] are not satisfied. Thus our situation is more general than the results obtained in [25].

Remark 5.1

Comparing the estimation method in this paper with [25, 29], it seems that our estimation processes are much simpler than those used in [25, 29] to some degree. Moreover, it is easy to see that the results of this paper generalize and refine the early results published so far, our results are new and not covered by any known work in the literature.

Remark 5.2

Finally, let us note that our method could be useful in more general situations such as equations depending nonlinearly on the derivative, Hamiltonian or more general second order differential equations. These extensions should be developed elsewhere.