1 Introduction

According to a study, a discrete time system is a more natural way to represent systems such as networked control system, numerical analysis, and population models [1–9]. In most physical dynamic systems, abrupt state changes at certain moments often occur. It is natural to assume these changes to happen instantaneously. Such dynamical systems with these changes are called impulsive systems. Impulsive systems arise in many fields and there are several studies on stability of impulsive systems [3–5, 8, 10–15]. Moreover, the real processes in our world always involve time delay systems; for example, manufacturing processes, digital control systems, population dynamics, and the electronic implementation of analog neural networks, etc. It is well known that time delay might cause instability, divergence behavior, and oscillation of dynamic systems. Therefore, the stability of impulsive system with time delay has been investigated extensively over the past decades [1–22].

Recently, the stability analysis of time delay system has been investigated extensively in many areas [1–4, 6, 8, 9, 13, 23]. There are important types of stability of dynamical systems, namely exponential stability and practical stability. In the case of exponential stability, it is required that all solutions starting near an equilibrium point not only stay nearby, but tend to the equilibrium point very fast with exponential decay rate; see [2–4, 6, 12, 14, 15, 23]. Meanwhile, for practical stability, one only needs to stabilize a system in a region of phase space, namely the system may oscillate close to the state, in which the performance is still acceptable. There are several results on the practical stability for continuous time systems with delay [10, 16, 17] and without delay [12, 24, 25]. On the other hand, there are few results on practical stability for discrete time systems with delay [5, 7]. Moreover, there are several practical applications of impulsive discrete time system with delay such as BAM neural networks [18], Nicholson’s blowflies model [3], and switched systems with delays [19–21]. Therefore, it is important to investigate the practical stability problem of impulsive discrete time system with delay. In [3, 4], the authors have studied discrete time delayed dynamic systems with impulsive effects. By employing Lyapunov stability theory and a Razumikhin type technique, exponential stability criteria of impulsive discrete time system with delay have been derived. In [5], an asymptotically practical stability condition of impulsive discrete systems with time delays has been provided by using Lyapunov stability theory and a Razumikhin type technique. However, the stability criteria depend on τ, namely, \(\tau\triangleq\sup_{m \in\mathbb{Z}^{+}}\lbrace k_{m+1}-k_{m}\rbrace<+\infty\), where \(k_{m}\) are impulsive moments. Obviously, exponential stability implies exponentially practical stability but not conversely. However, in several practical applications, one only needs to stabilize a system in a region of phase space, namely the system may oscillate near the equilibrium point, in which the performance is still acceptable. Motivated by the above discussions, in this paper, we derive novel exponentially practical stability criteria of impulsive discrete time systems with delay by using Lyapunov stability theory and a Razumikhin type technique. To the best of our knowledge, it is the first result on the exponentially practical stability of impulsive discrete time systems with delay. Moreover, comparing to [5] which proposed an asymptotically practical stability condition, our technique can be used to derive an exponentially practical stability condition if it is more desirable. Furthermore, the obtained condition is not required that \(\sup_{m\in \mathbb{Z}^{+}}\lbrace k_{m+1}-k_{m}\rbrace<+ \infty\), where \(k_{m}\) are impulsive moments which is imposed in [5]. The paper is organized as follows. In Section 2, we introduce some notations, definitions, and a proposition. In Section 3, we give new criteria for exponentially practical stability of impulsive discrete time systems with delay. In Section 4, a numerical example is given to show the effectiveness of our theoretical results. Our conclusion is given in Section 5.

2 Preliminaries

Let \(\mathbb{R}^{n}\) denote the n dimensional Euclidean space, \(\Vert x \Vert \) is the Euclidean norm of vector x. Given a positive integer τ, for any function \(\phi: \mathbb{N}_{-\tau} \longrightarrow\mathbb{R}^{n}\), we define \(\Vert \phi \Vert =\max_{\theta\in\mathbb{N}_{-\tau}}\lbrace \Vert \phi(\theta) \Vert \rbrace\), \(\mathbb{N}=\{0,1,2,\ldots\}\) and \(\mathbb{N}_{-\tau}=\{ -\tau ,-\tau-1,\ldots,-1,0\}\).

Consider the following impulsive discrete time system with delay:

$$ \textstyle\begin{cases} x(k+1)=f(k,\overline{x}_{k}), \quad k\geq k_{0},\\ \overline{x} (k)= \textstyle\begin{cases} x(k_{m})+I_{m}(k_{m},x(k_{m})),\quad k= k_{m}, \\ x(k),\quad k\neq k_{m}, m\in\mathbb{N,} \end{cases}\displaystyle \\ x(s)=\phi(s),\quad s\in\mathbb{N}_{k_{0}-\tau}, \end{cases} $$
(2.1)

where \(x(k)\in\mathbb{R}^{n}\), \(\overline{x}_{k} \) is defined by \(\overline{x}_{k}(s)=\overline{x}(k+s)\) for any \(s \in\mathbb {N}_{-\tau }\). We assume \(f : \mathbb{N}\times\mathbb{N}_{k_{0}-\tau}\rightarrow \mathbb{R}^{n}\) and \(I_{m} : \mathbb{N}\times\mathbb{R}^{n} \rightarrow \mathbb{R}^{n}\) for \(m \in\mathbb{N}\), and the impulsive moments satisfy \(0\leq k_{0}< k_{1}< k_{2}<\cdots,k_{m}\rightarrow\infty\) for \(m\rightarrow\infty\). Furthermore, we assume \(f(k,0)=0, I_{m}(k,0)=0\), which implies that (2.1) admits the trivial solution. Let \(x(k;k_{0},\phi)\) denote the trajectory of system (2.1) with initial condition ϕ.

Definition 2.1

[2, 23]

The trivial solution of system (2.1) is exponentially practically stable in the pth moment, if, for any \(k\geq k_{0}\) there exist constants \(\lambda>0, M\geq0, r>0\) such that

$$\bigl\Vert x(k;k_{0},\phi) \bigr\Vert ^{p} \leq M \Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+r. $$

The following proposition will be used in the proof of our main results. The proofs are straightforward and will be omitted.

Proposition 2.1

Let \(\gamma, \beta\) be positive real numbers and \(0<\lambda<1\). If one of the following conditions holds:

  1. (i)

    \(\gamma\geq1\) and \(\frac{\gamma e -1}{\gamma e} <\beta<1\),

  2. (ii)

    \(\gamma< 1\) and \(\frac{ e -1}{ e} <\beta<1\),

then \(\max\{(1-\beta) e^{\lambda}, (1-\beta)\gamma e^{\lambda}\}<1\).

3 Main results

We first consider the exponentially practical stability problem of system (2.1) in the case \(\gamma\geq1\).

Theorem 3.1

If there exist positive numbers \(a, c_{1}, c_{2}, p, \gamma, q, \beta, \eta;q> \gamma\geq1, \frac {\gamma e -1}{\gamma e} <\beta<1, \frac{1}{\gamma}>1-\beta, \eta< \min\lbrace\frac{a-a \gamma+a \gamma\beta}{\gamma} , \beta a \rbrace\) and a Lyapunov function \(V(k,\overline{x}(k))\) such that the following conditions hold:

  1. (i)

    \(c_{1}\Vert \overline{x}(k) \Vert ^{p}\leq V(k,\overline{x}(k))\leq c_{2}\Vert \overline{x}(k) \Vert ^{p}+a, \forall k\geq k_{0}-\tau, x\in \mathbb{R}^{n} \),

  2. (ii)

    if \(V(k+s,\overline{x}(k+s))< qV(k+1,x(k+1))\) with \(s \in \mathbb {N}_{-\tau}\), then \(\Delta V(k,\overline {x}(k))=V(k+1,x(k+1))-V(k,\overline{x}(k))\leq-\beta V(k,\overline {x}(k))+ \eta\) holds,

  3. (iii)

    \(V(k_{m},\overline {x}(k_{m}))=V(k_{m},x(k_{m}))+I_{m}(k_{m},x(k_{m}))\leq \gamma V(k_{m},x(k_{m})),m\in\mathbb{N},x\in\mathbb{R}^{n}\),

then the trivial solution of system (2.1) is exponentially practically stable in the pth moment.

Proof

Since \(q>\gamma\geq1\), there exists \(0<\lambda<1\) such that

$$q>\gamma e^{\lambda(\tau+1)}\geq e^{\lambda(\tau+1)}. $$

From (i), for \(k \in[k_{0}-\tau,k_{0}]\), we get

$$\begin{aligned} V \bigl(k,x(k) \bigr)\leq c_{2}\Vert x \Vert ^{p}+a \leq c_{2}\Vert x \Vert ^{p}e^{-\lambda(k-k_{0})}+a \leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+a. \end{aligned}$$
(3.1)

We claim that

$$\begin{aligned} V \bigl(k,\overline{x}(k) \bigr)\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda (k-k_{0})}+a, \quad k \in[k_{m-1}+1,k_{m}]. \end{aligned}$$
(3.2)

Now, we will prove (3.2) by using mathematical induction.

First, we show that (3.2) holds for \(m=1\), namely

$$\begin{aligned} V \bigl(k,\overline{x}(k) \bigr)\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda (k-k_{0})}+a,\quad k \in[k_{0}+1,k_{1}]. \end{aligned}$$
(3.3)

We assume (3.3) were not true, then there exists \(k \in [k_{0}+1,k_{1}]\) such that \(V(k,\overline{x}(k))> c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+a\). Let \(k^{*}=\min\{k \in [k_{0}+1,k_{1}]/V(k,\overline{x}(k))> c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+a\}\). From (3.1) and the definition of \(k^{*}\), we have

$$ V \bigl(k,\overline{x}(k) \bigr)\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda (k-k_{0})}+a,\quad k \in \bigl[k_{0}- \tau,k^{*}-1 \bigr]. $$

We will consider two possible cases for \(k^{*} \in[k_{0}+1,k_{1}]\).

  1. (I)

    \(k^{*} \in[k_{0}+1,k_{1}-1]\).

In this case, for any \(s \in\mathbb{N}_{-\tau}\), we have

$$\begin{aligned} V \bigl(k^{*}-1+s,x \bigl(k^{*}-1+s \bigr) \bigr)&\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-1+s-k_{0})}+a \\ &=c_{2}\Vert \phi \Vert ^{p} e^{-\lambda(s-1)}e^{-\lambda(k^{*}-k_{0})}+a \\ &\leq c_{2} e^{\lambda (\tau+1)}\Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-k_{0})}+ae^{\lambda (\tau+1)}\\ & = e^{\lambda(\tau +1)} \bigl[ c_{2} \Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-k_{0})}+a \bigr] \\ &< qV \bigl(k^{*},x \bigl(k^{*} \bigr) \bigr). \end{aligned}$$

Let \(\overline{k}=k^{*}-1\), then we get \(V(\overline{k}+s,x(\overline {k}+s))\leq qV(\overline{k}+1,x(\overline{k}+1))\). By (ii), we have \(\Delta V(\overline{k},x(\overline{k}))\leq-\beta V(\overline {k},x(\overline{k}))+\eta\) holds. Thus, we have

$$\begin{aligned} V \bigl(k^{*},x \bigl(k^{*} \bigr) \bigr)&\leq(1-\beta)\ V \bigl(k^{*}-1,x \bigl(k^{*}-1 \bigr) \bigr)+\eta \\ & \leq(1-\beta ) \bigl[c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-1-k_{0})}+a \bigr]+\eta \\ &\leq(1-\beta )e^{\lambda}c_{2} \Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-k_{0})}+a-\beta a+\eta. \end{aligned}$$

By assumption of η and Proposition 2.1, we get \(V(k^{*},x(k^{*}))\leq(1-\beta)e^{\lambda}c_{2} \Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-k_{0})}+a-\beta a+\eta\), which contradicts the definition of \(k^{*}\). Hence (3.3) holds.

  1. (II)

    \(k^{*}=k_{1}\).

In this case, we have \(V(k_{1},\overline{x}(k_{1}))> c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k_{1}-k_{0})}+a\) and for any \(s \in\mathbb {N}_{-\tau}\), we get

$$\begin{aligned} V \bigl(k_{1}-1+s,x(k_{1}-1+s) \bigr)&\leq c_{2} \Vert \phi \Vert ^{p}e^{-\lambda(k_{1}-1+s-k_{0})}+a \\ & =c_{2}\Vert \phi \Vert ^{p} e^{-\lambda(s-1)}e^{-\lambda(k_{1}-k_{0})}+a \\ &\leq c_{2} e^{\lambda (\tau+1)}\Vert \phi \Vert ^{p}e^{-\lambda(k_{1}-k_{0})}+ae^{\lambda (\tau+1)} \\ & = e^{\lambda(\tau +1)} \bigl[ c_{2} \Vert \phi \Vert ^{p}e^{-\lambda(k_{1}-k_{0})}+a \bigr] \\ & < e^{\lambda(\tau +1)}V \bigl(k_{1},\overline{x}(k_{1}) \bigr) \\ & < e^{\lambda(\tau +1)} \gamma V \bigl(k_{1},x(k_{1}) \bigr) \\ & < qV \bigl(k_{1},x(k_{1}) \bigr). \end{aligned}$$

Let \(\overline{k}=k_{1}-1\), then we get \(V(\overline{k}+s,x(\overline {k}+s))\leq qV(\overline{k}+1,x(\overline{k}+1))\). By (ii), we have \(\Delta V(\overline{k},x(\overline{k}))\leq-\beta V(\overline {k},x(\overline{k}))+\eta\), which gives

$$ \frac{1}{\gamma}V \bigl(k_{1},\overline{x}(k_{1}) \bigr) \leq V \bigl(k_{1},x(k_{1}) \bigr)\leq (1-\beta) V \bigl(k_{1}-1,x(k_{1}-1) \bigr)+\eta. $$

Thus, we obtain

$$\begin{aligned} V \bigl(k_{1},\overline{x}(k_{1}) \bigr)&\leq (1-\beta) \gamma V \bigl(k_{1}-1,x(k_{1}-1) \bigr)+\eta\gamma \\ &\leq(1-\beta)\gamma \bigl[c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k_{1}-1-k_{0})}+a \bigr]+\eta\gamma \\ &\leq(1-\beta )\gamma e^{\lambda}c_{2} \Vert \phi \Vert ^{p}e^{-\lambda (k_{1}-k_{0})}+a\gamma-a \gamma\beta+\eta\gamma. \end{aligned}$$

By assumption of η and Proposition 2.1, we get \(V(k^{*},x(k^{*}))\leq(1-\beta)\gamma e^{\lambda}c_{2} \Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-k_{0})}+a\gamma-a \gamma\beta+\eta\gamma\), which contradicts the definition of \(k^{*}=k_{1}\). Hence (3.3) holds.

Next, we assume (3.2) holds for \(m \in\mathbb{N}\), namely

$$ V \bigl(k,\overline{x}(k) \bigr)\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda (k-k_{0})}+a, \quad k \in[k_{m-1}+1,k_{m}]. $$

Then we will show that

$$ V \bigl(k,\overline{x}(k) \bigr)\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda (k-k_{0})}+a, \quad k \in[k_{m}+1,k_{m+1}]. $$
(3.4)

We assume (3.4) were not true, then there exists

$$ k^{*}=\min \bigl\{ k \in[k_{m}+1,k_{m+1}]/V \bigl(k, \overline{x}(k) \bigr)> c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+a \bigr\} . $$

For \(k \in[k_{m}+1,k^{*}-1]\), we have \(V(k,\overline{x}(k))\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+a\). We will consider two possible cases for \(k^{*} \in[k_{m}+1,k_{m+1}]\).

  1. (I)

    \(k^{*} \in[k_{m}+1,k_{m+1}-1]\).

In this case, for any \(s \in\mathbb{N}_{-\tau}\), we have

$$\begin{aligned} V \bigl(k^{*}-1+s,x \bigl(k^{*}-1+s \bigr) \bigr)&\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-1+s-k_{0})}+a \\ &=c_{2}\Vert \phi \Vert ^{p} e^{-\lambda(s-1)}e^{-\lambda(k^{*}-k_{0})}+a \\ &\leq c_{2} e^{\lambda (\tau+1)}\Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-k_{0})}+ae^{\lambda (\tau+1)} \\ & = e^{\lambda(\tau +1)} \bigl[ c_{2} \Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-k_{0})}+a \bigr] \\ &< qV \bigl(k^{*},x \bigl(k^{*} \bigr) \bigr), \end{aligned}$$

thus \(V(\overline{k}+s,x(\overline{k}+s))\leq qV(\overline {k}+1,x(\overline{k}+1))\) and from (ii), we have \(\Delta V(\overline {k},x(\overline{k}))\leq-\beta V(\overline{k}, x(\overline{k}))+\eta\), which contradicts the definition of \(k^{*}\). Hence (3.4) holds.

  1. (II)

    \(k^{*}=k_{m+1}\).

In this case, we have \(V(k_{m+1},\overline{x}(k_{m+1}))> c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k_{m+1}-k_{0})}+a\). Then, for any \(s \in\mathbb {N}_{-\tau}\), we get

$$\begin{aligned} V \bigl(k_{m+1}-1+s,\overline{x}(k_{m+1}-1+s) \bigr)&\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k_{m+1}-1+s-k_{0})}+a \\ &=c_{2}\Vert \phi \Vert ^{p} e^{-\lambda(s-1)}e^{-\lambda(k_{m+1}-k_{0})}+a \\ &\leq c_{2} e^{\lambda (\tau+1)}\Vert \phi \Vert ^{p}e^{-\lambda(k_{m+1}-k_{0})}+ae^{\lambda (\tau+1)} \\ &= e^{\lambda(\tau +1)} \bigl[ c_{2} \Vert \phi \Vert ^{p}e^{-\lambda(k_{m+1}-k_{0})}+a \bigr] \\ &< e^{\lambda(\tau +1)}V \bigl(k_{1},\overline{x}(k_{m+1}) \bigr) \\ &< e^{\lambda(\tau +1)} \gamma V \bigl(k_{1},x(k_{m+1}) \bigr) \\ &< qV \bigl(k_{1},x(k_{m+1}) \bigr). \end{aligned}$$

Let \(\overline{k}=k_{m+1}-1\), then we get \(V(\overline{k}+s,\overline {x}(\overline{k}+s))\leq qV(\overline{k}+1,x(\overline{k}+1))\). By (ii), we have \(\Delta V(\overline{k},\overline{x}(\overline {k}))\leq -\beta V(\overline{k},\overline{x}(\overline{k}))+\eta\), which gives

$$ \frac{1}{\gamma}V \bigl(k_{m+1},\overline{x}(k_{m+1}) \bigr) \leq V \bigl(k_{m+1},x(k_{m+1}) \bigr)\leq(1-\beta) V \bigl(k_{m+1}-1,\overline {x}(k_{m+1}-1) \bigr)+\eta. $$

Thus, we obtain

$$\begin{aligned} V \bigl(k_{m+1},\overline{x}(k_{m+1}) \bigr)&\leq (1-\beta) \gamma V \bigl(k_{m+1}-1,\overline{x}(k_{m+1}-1) \bigr)+\eta \gamma \\ &\leq(1-\beta)\gamma \bigl[c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k_{m+1}-1-k_{0})}+a \bigr]+\eta\gamma \\ &\leq(1-\beta )\gamma e^{\lambda}c_{2} \Vert \phi \Vert ^{p}e^{-\lambda (k_{m+1}-k_{0})}+a\gamma-a \gamma\beta+\eta\gamma. \end{aligned}$$

By assumption on η and Proposition 2.1, we get \(V(k^{*},x(k^{*}))\leq(1-\beta)\gamma e^{\lambda}c_{2} \Vert \phi \Vert ^{p}e^{-\lambda(k^{*}-k_{0})}+a\gamma-a \gamma\beta+\eta\gamma\), which contradicts the definition of \(k^{*}=k_{m+1}\). Hence (3.4) holds.

Thus, for all \(k\geq k_{0}\), we have

$$ V \bigl(k,\overline{x}(k) \bigr)\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+a. $$

From (i), we obtain

$$ c_{1} \bigl\Vert \overline{x}(k) \bigr\Vert ^{p}\leq V \bigl(k,\overline{x}(k) \bigr)\leq c_{2}\Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+a, $$

which implies that

$$ \bigl\Vert \overline{x}(k) \bigr\Vert ^{p}\leq\frac{c_{2}}{c_{1}} \Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+\frac{a}{c_{1}}. $$

Therefore, the trivial solution of system (2.1) is exponentially practically stable in the pth moment. □

Next, we give an exponentially practical stability condition of system (2.1) for the case \(0<\gamma<1\).

Theorem 3.2

If there exist positive numbers \(a, c_{1}, c_{2}, p, \gamma, q, \beta, \eta;q>1>\gamma>0, \frac{ e -1}{ e} <\beta<1,\ \frac{1}{\gamma}>1-\beta, \eta< \min\lbrace\frac{a-a \gamma+a \gamma\beta}{\gamma} , \beta a \rbrace\) and a Lyapunov function \(V(k,\overline{x}(k))\) such that the following conditions hold:

  1. (i)

    \(c_{1}\Vert \overline{x}(k) \Vert ^{p}\leq V(k,\overline{x}(k))\leq c_{2}\Vert \overline{x}(k) \Vert ^{p}+a, \forall k\geq k_{0}-\tau, x\in \mathbb{R}^{n} \),

  2. (ii)

    if \(V(k+s,\overline{x}(k+s))< qV(k+1,x(k+1))\) with \(s \in \mathbb {N}_{-\tau}\), then \(\Delta V(k,\overline {x}(k))=V(k+1,x(k+1))-V(k,\overline{x}(k))\leq-\beta V(k,\overline {x}(k))+ \eta\) hold,

  3. (iii)

    \(V(k_{m},\overline {x}(k_{m}))=V(k_{m},x(k_{m}))+I_{m}(k_{m},x(k_{m}))\leq \gamma V(k_{m},x(k_{m})),m\in\mathbb{N} ,x\in\mathbb{R}^{n}\),

then the trivial solution of system (2.1) is exponentially practically stable in the pth moment.

Proof

Since \(q>1>\gamma>0\), there exists \(0<\lambda<1\) such that

$$q>e^{\lambda(\tau+1)}\geq\gamma e^{\lambda(\tau+1)}. $$

From assumption of η and Proposition 2.1, by using a similar argument as in the proof of Theorem 3.1, we may show that \(\Vert \overline{x}(k) \Vert ^{p}\leq\frac{c_{2}}{c_{1}}\Vert \phi \Vert ^{p}e^{-\lambda(k-k_{0})}+\frac{a}{c_{1}}, \forall k\geq k_{0}\). Therefore, the trivial solution of system (2.1) is exponentially practically stable in the pth moment. □

Remark 3.1

From the methods of proof of Theorem 3.1 and Theorem 3.2, it is clear that these methods can be applied for an impulsive discrete time system with time varying delay \(\tau(k)\) with \(0\leq\tau(k) \leq\tau, \tau>0\).

Remark 3.2

We now provide a direct and effective solving algorithm corresponding to Theorems 3.1 and 3.2 as follows:

  1. 1.

    First, we choose an appropriate Lyapunov function candidate. Then we make an estimate for \(c_{1} ,c_{2}\) and a satisfying condition (i).

  2. 2.

    Next, find an estimation of γ which satisfies (iii).

  3. 3.

    Finally, with estimates of \(c_{1}, c_{2}, a\) and γ in 1 and 2, we choose appropriate \(q, \beta\), and η which satisfy condition (ii).

4 Numerical example

Example 4.1

Consider the following impulsive discrete time system with delay:

$$ \textstyle\begin{cases} x(k+1)=cx(k)+dx(k-1),\quad k\geq0,\\ \overline{x} (k)= \textstyle\begin{cases} \gamma x(k_{m}), \quad k= k_{m}, \\ x(k),\quad k\neq k_{m}, m\in\mathbb{N}, \end{cases}\displaystyle \\ x(s)=\phi(s),\quad s\in\mathbb{N}_{-1}, \end{cases} $$
(4.1)

where \(c, d\) are arbitrary constants and γ is positive constant, which is considered in [4]. Let \(a>0\) be given. If there exist positive numbers \(c_{1}, c_{2}, p, \gamma, q, \beta, \eta\) such that \(\eta = (1-\vert c\vert -\vert d\vert )a, \beta\leq\min\lbrace1-\frac {\vert c\vert }{1-\vert d\vert q}, \gamma-\frac{\vert c\vert }{1-\vert d\vert q} \rbrace\), then the trivial solution of system (4.1) is exponentially practically stable in the pth moment.

Proof

We choose a Lyapunov function \(V(k,\overline{x}(k))=\vert \overline{x}(k) \vert +a\); then we have

(i) \(c_{1}\Vert \overline{x}(k)\Vert \leq V(k,\overline {x}(k))=\vert \overline{x}(k) \vert +a \leq c_{2}\Vert \overline {x}(k)\Vert +a,\forall k\geq k_{0}-1\).

(ii) Assume \(V(k+s,\overline{x}(k+s))< qV(k+1,x(k+1))\) with \(s \in\mathbb{N}_{-1}\), then we have

$$\begin{aligned} V \bigl(k+1,x(k+1) \bigr)&=\bigl\vert x(k+1)\bigr\vert +a \\ &=\bigl\vert cx(k)+dx(k-1)\bigr\vert +a \\ &= \vert c\vert \bigl\vert x(k)\bigr\vert +\vert d\vert \bigl\vert x(k-1)\bigr\vert +a \\ &=\vert c\vert \bigl\vert x(k)\bigr\vert +\vert c\vert a -\vert c \vert a +\vert d\vert \bigl\vert x(k-1)\bigr\vert +\vert d\vert a - \vert d\vert a +a \\ &=\vert c\vert V \bigl(k,x(k) \bigr)+\vert d\vert V \bigl(k-1 ,x(k-1) \bigr) +\bigl(1- \vert c\vert -\vert d\vert \bigr)a \\ &\leq \vert c\vert V \bigl(k,x(k) \bigr)+\vert d\vert qV \bigl(k+1,x(k+1) \bigr) +\bigl(1- \vert c\vert -\vert d\vert \bigr)a \\ &\leq\frac{\vert c\vert }{1-\vert d\vert q} V \bigl(k,x(k) \bigr) +\bigl(1-\vert c\vert -\vert d\vert \bigr)a. \end{aligned}$$

We have two cases as follows.

Case I. \(k \neq k_{m}\). In this case, we have

$$\begin{aligned} \Delta V \bigl(k,\overline {x}(k) \bigr)&=V \bigl(k+1,x(k+1) \bigr)-V \bigl(k, \overline{x}(k) \bigr) \\ &=V \bigl(k+1,x(k+1) \bigr)-V \bigl(k,x(k) \bigr) \\ &\leq\frac{\vert c\vert }{1-\vert d\vert q} V \bigl(k,x(k) \bigr) +\bigl(1-\vert c\vert -\vert d\vert \bigr)a-V \bigl(k,x(k) \bigr) \\ &= \biggl(\frac{\vert c\vert }{1-\vert d\vert q} -1 \biggr)V \bigl(k,x(k) \bigr) +\bigl(1-\vert c \vert -\vert d\vert \bigr)a \\ &=- \biggl(1-\frac{\vert c \vert }{1-\vert d \vert q} \biggr)V \bigl(k,x(k) \bigr) +\bigl(1-\vert c \vert - \vert d \vert \bigr)a \\ &=- \biggl(1-\frac{\vert c\vert }{1-\vert d\vert q} \biggr)V \bigl(k,x(k) \bigr)+\eta;\quad\eta= \bigl(1- \vert c \vert -\vert d\vert \bigr)a. \end{aligned}$$

Case II. \(k = k_{m}\). In this case, we have

$$\begin{aligned} \Delta V \bigl(k,\overline {x}(k) \bigr)&=V \bigl(k+1,x(k+1) \bigr)-V \bigl(k, \overline{x}(k) \bigr) \\ &\leq\frac{\vert c\vert }{1-\vert d\vert q} V \bigl(k,x(k) \bigr) +\bigl(1-\vert c\vert -\vert d\vert \bigr)a- \gamma V \bigl(k,x(k) \bigr) \\ &= \biggl(\frac{\vert c\vert }{1-\vert d\vert q} -\gamma \biggr)V \bigl(k,x(k) \bigr) +\bigl(1- \vert c\vert - \vert d\vert \bigr)a \\ &=- \biggl(\gamma-\frac{\vert c\vert }{1-\vert d\vert q} \biggr)V \bigl(k,x(k) \bigr) +\bigl(1- \vert c\vert - \vert d\vert \bigr)a \\ &=- \biggl(\gamma-\frac{\vert c\vert }{1-\vert d\vert q} \biggr)V \bigl(k,x(k) \bigr)+\eta;\quad\eta= \bigl(1- \vert c\vert -\vert d\vert \bigr)a. \end{aligned}$$

From the assumptions, we get

$$\begin{aligned} \Delta V \bigl(k,\overline{x}(k) \bigr)\leq-\beta V \bigl(k,\overline{x}(k) \bigr)+ \eta. \end{aligned}$$

(iii) For \(k=k_{m}\), we have

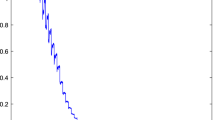
$$\begin{aligned} V \bigl(k_{m},\overline{x}(k_{m}) \bigr)&=\bigl\vert \overline {x}(k_{m})\bigr\vert +a \\ &=\bigl\vert \gamma x(k_{m})\bigr\vert +a \\ &=\gamma \biggl[\bigl\vert x(k_{m})\bigr\vert +\frac{a}{\gamma} \biggr] \\ &\leq\gamma \bigl[\bigl\vert x(k_{m})\bigr\vert +a \bigr] \\ &=\gamma V \bigl(k_{m},x(k_{m}) \bigr). \end{aligned}$$

Therefore, from Theorem 3.2, we conclude that the system (4.1) is exponentially practically stable in the pth moment. For simulation purposes, we let \(a=0.5, \vert c \vert =0.04, \vert d \vert =0.43,\lambda =0.05, q=1.4,\gamma=0.9 \). We choose the Lyapunov function \(V(k,\overline{x}(k))=\vert \overline{x}(k) \vert +0.5\). Then Theorem 3.2 is satisfied with the parameters \(c_{1}=c_{2}=1,a=0.5,p=1,\beta =0.8,\gamma=0.9\), and \(\eta=0.27\). Therefore, we have \(\Vert \overline{x}(k) \Vert \leq1.8e^{-0.05 k}+0.5, \forall k\geq0\). In Figure 1 and Figure 2, with initial conditions given by \(x(-1)=1.8, x(0)=1.6\), the trajectories of solutions of (4.1) with impulsive moments \(k_{m}=4k+3, m\in \mathbb{N}\) in which \(\sup_{m\in\mathbb{Z}^{+}}\lbrace k_{m+1}-k_{m}\rbrace=4 <+ \infty \) and \(k_{m}=\lbrace4,6,9,13,18,24,\ldots\rbrace\) in which \(\sup_{m\in \mathbb{Z}^{+}}\lbrace k_{m+1}-k_{m}\rbrace= \infty\), are shown, respectively. It is worth noting that, in [4], the asymptotically practically stable criterion requires \(\tau\triangleq\sup_{m \in \mathbb{Z}^{+}}\lbrace k_{m+1}-k_{m}\rbrace<+ \infty\). On the other hand, this restriction is not required in Theorem 3.2. Therefore, our result is less conservative than the result obtained in [4].

Figure 1
figure 1

Numerical simulation of Example  4.1 with \(\pmb{\sup_{m\in\mathbb{Z}^{+}}\lbrace k_{m+1}-k_{m}\rbrace<+\infty }\) .

Full size image
Figure 2
figure 2

Numerical simulation of Example  4.1 with \(\pmb{\sup_{m\in\mathbb{Z}^{+}}\lbrace k_{m+1}-k_{m}\rbrace= \infty }\) .

Full size image

 □

5 Conclusion

In this paper the exponentially practical stability is derived for an impulsive discrete time system with delay by using Lyapunov stability theory and a Razumikhin type technique. Comparing to some existing results in the literature the obtained criterion is not required that \(\sup_{m\in\mathbb{Z}^{+}}\lbrace k_{m+1}-k_{m}\rbrace<+ \infty\), where \(k_{m}\) are impulsive moments. A numerical example is given to show the effectiveness of our theoretical results.