1 Introduction

In 2011, Matsumoto and Szidarovszky [1] first introduced the following delay differential neoclassical growth model:

$$ x'(t)=-\alpha x(t)+s F\bigl(x(t-\tau)\bigr) $$
(1.1)

to show the emergence of erratic fluctuations in the capital accumulation process, where x is the capital per labor, \(s\in(0,1)\) is the average propensity to save, \(\alpha=n+s \mu\) with μ being the depreciation ratio of capital and n the growth rate of the labor, the production function \(F(x)=Cx^{a}(1-x)^{b}\) is unimodal (\(a,b\), and C are positive parameters) and τ is the delay in the production process. Two years later, in [2] they modified (1.1) as follows:

$$ x'(t)=-\alpha x(t)+\beta x^{\gamma}(t-\tau)e^{-\delta x(t-\tau)}. $$
(1.2)

Here \(\alpha,\gamma,\delta\), and β are positive parameters, δ reflects the strength of a ‘negative effect’ caused by increasing concentration of capital, γ is a proxy for measuring returns to scale of the production function and \(\beta=sc\), where c is a positive constant. As regards the seminal and early work of neoclassical growth model, we refer to Day [3–5], Solow [6], Swan [7], Puu [8] and Bischi et al. [9]. Recently, Matsumoto and Szidarovszky [2] have studied the local stability of (1.2) by considering the corresponding characteristic equation in three different cases: \(\gamma<1\), \(\gamma=1\), and \(\gamma>1\). Clearly, equation (1.2) with \(\gamma=1\) is the famous Nicholson blowflies model [10], which has been researched by a lot of academics [11–18]. When \(\gamma<1\) and \(\gamma>1\), Chen and Wang [19] and Wang [20] have investigated the exponential stability of the unique positive equilibrium and two positive equilibriums, respectively. Furthermore, Wang [20] have put forward an open problem: Obtain the existence of two positive periodic solutions of (1.2) with variable coefficients and delays.

Moreover, since periodicity phenomenon is very common in economic, engineering and biological fields, one of the most interesting themes in the qualitative theory of functional differential equations is the existence of periodic solutions for its significance in real world. Up to now, there have been a number of important and remarkable results (see [21–25] and the references therein) concerning the existence of periodic solutions. Although much has been done, results on the existence of multi-periodic solutions of the delay differential neoclassical growth model are scarce. Hence, the main aim of this paper is to deal with the existence of two positive periodic solutions for the following generalized delay differential neoclassical growth model:

$$ x'(t)=-\alpha(t) x(t)+\beta(t) x^{\gamma}\bigl(t-\tau(t) \bigr)e^{-\delta(t) x(t-\tau(t))}, $$
(1.3)

where \(\beta, \delta\in C(\mathrm{R}, (0,+\infty))\), \(\tau\in C(\mathrm{R}, [0,+\infty))\), and \(\alpha\in C(\mathrm{R}, \mathrm {R})\) are all ω-periodic functions, \(\int_{0}^{\omega}\alpha (t)\,dt>0\), γ and ω are positive constants.

For convenience and simplicity, we introduce a few notations and assumptions. Let

$$G(t,s)=\frac{e^{\int_{t}^{s}\alpha(r)\,dr}}{e^{\int_{0}^{\omega}\alpha (r)\,dr}-1}, $$

\(0< A=\min\{G(t,s):0\leq t,s\leq\omega\}<\max\{G(t,s):0\leq t,s\leq \omega\}=B\), and \(\sigma=\frac{A}{B}\in(0,1)\). For an ω-periodic function \(f\in C(\mathrm{R}, \mathrm{R})\), we define

$$f_{m}=\min _{t\in[0,\omega]}\bigl\{ f(t) \bigr\} ,\qquad f_{M}=\max _{t\in [0,\omega]} \bigl\{ f(t)\bigr\} . $$

Let \(g(x)=x^{\gamma}e^{-\delta_{M} x}\). Then it is obvious that \(g(x)\) increases strictly on \([0, \frac{\gamma}{\delta_{M}}]\) and decreases strictly on \([\frac{\gamma}{\delta_{M}},+\infty]\). Thus, there exists unique \(r_{0}\in(\frac{\gamma}{\delta_{M}},+\infty )\) such that \(g(r_{0})=g(\sigma\frac{\gamma}{\delta_{M}})\).

We also make the following assumption:

  1. (S)

    \(A\omega\beta_{m} g(r_{0})>r_{0}\).

The proof of the main result is based on the Krasnoselskii fixed point theorem in a cone [26]. First of all, we introduce the definition of a cone in the Banach space.

Definition 1.1

Let X be a Banach space. K is called a cone if it is a closed and nonempty subset of X such that

  1. (i)

    \(ax+by\in K\) for all \(x,y\in K\) and \(a,b>0\);

  2. (ii)

    \(x, -x\in K\) implies \(x=0\).

The Krasnoselskii fixed point theorem in a cone (see [26]) is as follows.

Lemma 1.1

Let X be a Banach space and \(K\subset X\) be a cone in X. Suppose \(\Omega_{1}\) and \(\Omega_{2}\) are open subsets of X with \(0\in\Omega_{1},\overline{\Omega}_{1}\subset\Omega_{2}\), and let

$$\Psi: K\cap(\overline{\Omega}_{2}\setminus\Omega_{1}) \rightarrow K $$

be a completely continuous operator such that one of the following conditions holds:

  1. (i)

    \(\Vert \Psi x\Vert \geq \Vert x\Vert , \forall x\in K\cap\partial\Omega_{1}\) and \(\Vert \Psi x\Vert \leq \Vert x\Vert , \forall x\in K\cap\partial \Omega_{2}\);

  2. (ii)

    \(\Vert \Psi x\Vert \geq \Vert x\Vert , \forall x\in K\cap\partial\Omega_{2}\) and \(\Vert \Psi x\Vert \leq \Vert x\Vert , \forall x\in K\cap\partial \Omega_{1}\).

Then Ψ has a fixed point in \(K\cap(\overline{\Omega }_{2}\setminus\Omega_{1})\).

2 Existence of two positive periodic solutions

In this section, we establish some sufficient conditions on the existence of two positive periodic solutions of model (1.3).

Let \(X=\{x(t)\in C(\mathrm{R},\mathrm{R}), x(t)=x(t+\omega), \forall t\in R \}\) and define \(\Vert x\Vert =\sup_{t\in[0,\omega]}|x(t)|\). Then X is a Banach space with the norm \(\Vert \cdot \Vert \). Let

$$K=\bigl\{ x(t)\in X| x(t)\geq0, x(t)\geq\sigma \Vert x\Vert \mbox{ for } t\in R \bigr\} . $$

It is easy to confirm that K is a cone in X.

Define an operator on X as follows:

$$ (\Psi x) (t)= \int_{t}^{t+\omega}G(t,s)\beta(s)x^{\gamma}\bigl(s- \tau (s)\bigr)e^{-\delta(s)x(s-\tau(s))}\,ds $$
(2.1)

for \(x\in X\). Obviously, Ψ is a completely continuous operator on X and the existence of an ω-periodic solution of (1.3) is equivalent to find the fixed point of operator Ψ on X.

Lemma 2.1

\(\Psi(K)\subset K\).

Proof

For any \(x\in K\), we have

$$\Vert \Psi x\Vert \leq B \int_{0}^{\omega}\beta(s)x^{\gamma}\bigl(s-\tau (s)\bigr)e^{-\delta(s)x(s-\tau(s))}\,ds $$

and

$$(\Psi x) (t)\geq A \int_{0}^{\omega}\beta(s)x^{\gamma}\bigl(s-\tau (s)\bigr)e^{-\delta(s)x(s-\tau(s))}\,ds, $$

from which we deduce that

$$(\Psi x) (t)\geq\frac{A}{B}\Vert \Psi x\Vert =\sigma \Vert \Psi x \Vert . $$

This implies that \(\Psi x \in K\) for any \(x\in K\), i.e., \(\Psi(K)\subset K\). □

Theorem 2.1

Suppose that \((S)\) holds. Then (1.3) has at least two ω-positive periodic solutions.

Proof

Since \(\lim_{x\rightarrow0}\beta(t)x^{\gamma}e^{-\delta(t)x}=\lim_{x\rightarrow+\infty}\beta(t)x^{\gamma}e^{-\delta(t)x}=0\), \(\forall t\in[0,\omega]\), for any sufficiently small constant \(\varepsilon>0\) such that \(B\omega \varepsilon<1\), there are two constants \(r_{1},r_{2}(r_{1}<\frac{\gamma }{\delta_{M}}<r_{0}<r_{2})\) such that

$$ \beta(t)x^{\gamma}e^{-\delta(t)x} \leq\varepsilon r_{1},\quad (t,x)\in [0,\omega]\times[0,r_{1}] $$
(2.2)

and

$$ \beta(t)x^{\gamma}e^{-\delta(t)x} \leq\varepsilon x, \quad (t,x)\in [0,\omega] \times[r_{2},\infty]. $$
(2.3)

Define

$$\begin{aligned} \Omega_{1} =&\bigl\{ x|x\in X, \Vert x\Vert < r_{1}\bigr\} ,\qquad \Omega_{2}=\biggl\{ x|x\in X, \Vert x\Vert < \frac {\gamma}{\delta_{M}} \biggr\} , \\ \Omega_{3} =&\bigl\{ x|x\in X, \Vert x\Vert < r_{0}\bigr\} ,\qquad \Omega_{4}=\bigl\{ x|x\in X, \Vert x\Vert < r_{3}\bigr\} , \end{aligned}$$

where \(r_{3}=\max\{r_{2}+\frac{\gamma}{\delta_{M}}, \frac{B\widetilde {M}\omega}{1-B\omega\varepsilon} \}\) and \(\widetilde{M}=\max _{t\in[0,\omega],x\in[0,r_{2}]}\{\beta(t)x^{\gamma}e^{-\delta (t)x} \}\).

If \(x\in K\cap\partial\Omega_{1}\), then \(\Vert x\Vert =r_{1}\) and \(x(t)\geq \sigma r_{1}\). From (2.1) and (2.2), we have

$$(\Psi x) (t)\leq B \int_{t}^{t+\omega}\beta(s)x^{\gamma}\bigl(s-\tau (s)\bigr)e^{-\delta(s)x(s-\tau(s))}\,ds\leq B\omega\varepsilon r_{1}< r_{1}, $$

which implies that \(\Vert \Psi x\Vert <\Vert x\Vert \) for \(x\in K\cap\partial\Omega_{1}\).

If \(x\in K\cap\partial\Omega_{2}\), then \(\Vert x\Vert =\frac{\gamma}{\delta _{M}}\) and \(x(t)\geq\sigma\frac{\gamma}{\delta_{M}}\). In view of \((S)\), (2.1), and the fact that \(\min_{x\in[\sigma\frac{\gamma}{\delta_{M}},\frac{\gamma }{\delta_{M}}]}g(x)=g(\sigma\frac{\gamma}{\delta_{M}})=g(r_{0})\), we obtain

$$\begin{aligned} (\Psi x) (t) \geq&A \int_{t}^{t+\omega}\beta(s)x^{\gamma}\bigl(s-\tau (s)\bigr)e^{-\delta(s)x(s-\tau(s))}\,ds \\ \geq&A \int_{t}^{t+\omega}\beta_{m} g(x\bigl(s-\tau(s) \bigr)\,ds \\ \geq&A \int_{t}^{t+\omega}\beta_{m}g\biggl(\sigma \frac{\gamma}{\delta _{M}}\biggr)\,ds \\ =&A\omega\beta_{m} g(r_{0}) \\ >&r_{0}>\frac{\gamma}{\delta_{M}}. \end{aligned}$$

This implies that \(\Vert \Psi x\Vert >\Vert x\Vert \) for \(x\in K\cap\partial\Omega_{2}\).

If \(x\in K\cap\partial\Omega_{3}\), then \(\Vert x\Vert =r_{0}\) and \(x(t)\geq \sigma r_{0}>\sigma\frac{\gamma}{\delta_{M}}\). Due to (2.1), (2.3), and the fact that \(\min_{x\in[\sigma r_{0},r_{0}]}g(x)=g(r_{0})\), we get

$$\begin{aligned} (\Psi x) (t) \geq&A \int_{t}^{t+\omega}\beta(s)x^{\gamma}\bigl(s-\tau (s)\bigr)e^{-\delta(s)x(s-\tau(s))}\,ds \\ \geq&A \int_{t}^{t+\omega}\beta_{m} g(x\bigl(s-\tau(s) \bigr)\,ds \\ \geq&A \int_{t}^{t+\omega}\beta_{m}g(r_{0})\,ds \\ =&A\omega\beta_{m} g(r_{0}) \\ >&r_{0}, \end{aligned}$$

which implies that \(\Vert \Psi x\Vert >\Vert x\Vert \) for \(x\in K\cap\partial\Omega_{3}\).

If \(x\in K\cap\partial\Omega_{4}\), then \(\Vert x\Vert =r_{3}\) and \(x(t)\geq \sigma r_{3}\). From (2.1) and (2.3), we have

$$\begin{aligned} (\Psi x) (t) \leq&B \int_{t}^{t+\omega}\beta(s)x^{\gamma}\bigl(s-\tau (s)\bigr)e^{-\delta(s)x(s-\tau(s))}\,ds \\ \leq&B \int_{E_{1} }\beta(s)x^{\gamma}\bigl(s-\tau(s) \bigr)e^{-\delta (s)x(s-\tau(s))}\,ds \\ &{}+B \int_{E_{2} }\beta(s)x^{\gamma}\bigl(s-\tau(s) \bigr)e^{-\delta(s)x(s-\tau (s))}\,ds \\ \leq&B\widetilde{M}\omega+B\omega\varepsilon r_{3}< r_{3}, \end{aligned}$$

which implies that \(\Vert \Psi x\Vert <\Vert x\Vert \) for \(x\in K\cap\partial\Omega _{4}\), where \(E_{1}=\{s|s\in[t,t+\omega], 0\leq x(s-\tau(s))\leq r_{2} \}\) and \(E_{2}=\{s|s\in[t,t+\omega], r_{2}< x(s-\tau(s))\leq r_{3} \}\).

Clearly, \(\overline{\Omega}_{1}\subset\Omega_{2}\), \(\overline{\Omega }_{2}\subset\Omega_{3}\), and \(\overline{\Omega}_{3}\subset\Omega_{4}\). Since \(\Psi(K)\subset K\) and Ψ is a completely continuous operator on X, it follows from Lemma 1.1 that Ψ has one fixed point \(x_{1}\in K\cap(\overline{\Omega }_{2}\setminus\Omega_{1})\) and another fixed point \(x_{2}\in K\cap(\overline{\Omega}_{4}\setminus \Omega_{3})\), which are obviously different. Moreover, \(x_{1}(t)\geq \sigma r_{1}>0\) and \(x_{2}(t)\geq\sigma r_{0}>0\). Therefore, \(x_{1}\) and \(x_{2}\) are two positive periodic solutions of (1.3). The proof of Theorem 2.1 is completed. □

Remark 2.1

It is worth mentioning that although the authors of [27] considered the existence of two positive periodic solutions for equation (1.3) with \(\gamma=2\), it is neglected that the two positive periodic solutions might merge into one when they are on the boundary of \(\Omega_{2}\). Here, we have proved that there exist two distinct positive periodic solutions for equation (1.3), which generalizes and improves the result of [27].

3 An example

In this section, we give an example to support the results obtained in the previous section.

Example 3.1

Consider the following delay differential neoclassical growth model:

$$ x'(t)=-(0.05+\sin t)x(t)+(6+\sin t)x^{3}\bigl(t-2|\cos t|\bigr)e^{-(2+\cos t)x(t-2|\cos t|)}. $$
(3.1)

Obviously, \(\alpha(t)=0.05+\sin t\), \(\beta(t)=6+\sin t\), \(\delta (t)=2+\cos t\), and \(\tau(t)=2|\cos t|\) are all 2π-periodic functions, \(\int_{0}^{\omega}\alpha(t)\,dt=0.1\pi>0 \), \(g(x)=x^{3}e^{-3x}\), and \(\gamma=3,\omega=2\pi\).

Note that \(A=\frac{e^{-0.1\pi}}{e^{0.1\pi}-1}\), \(B=\frac{e^{0.1\pi }}{e^{0.1\pi}-1}\), \(\sigma=A/B=e^{-0.2\pi}\), \(\frac{\gamma}{\delta _{M}}=1\), \(\beta_{m}=5\), \(r_{0}\approx1.6815\). Then we verify conditions (S) as follows:

$$A\omega\beta_{m}g(r_{0})\approx1.9048 >r_{0}. $$

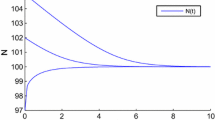
Therefore, it follows from Theorem 2.1 that (3.1) has at least two 2π-positive periodic solutions.

Remark 3.1

To the best of our knowledge, few authors have considered the existence of two positive periodic solutions for the generalized delay differential neoclassical growth model (1.3). It is clear that all the results in [1, 2, 10, 11, 24] and the references therein cannot be applicable to prove that there exist two 2π-positive periodic solutions for model (3.1). So the results of this paper are essentially new and complement some existing ones in [1, 2, 10, 11, 24].

4 Conclusions

In this paper, we study the generalized delay differential neoclassical growth model with periodic coefficients and delays. By using the Krasnoselskii fixed point theorem, we have derived conditions on the existence of two positive periodic solutions, which gives a satisfying answer to the open problem mentioned in the Introduction. In the future, we will consider the stability of the two positive periodic solutions for model (1.3), which is an interesting and challenging work.