Analysis of a predator-prey model with Lévy jumps

Abstract

This paper deals with a predator-prey model of Beddington-DeAngelis type functional response with Lévy jumps. The proposed mathematical model consists of a system of two stochastic differential equations to stimulate the interactions between predator population and prey population. The dynamics of the system is discussed mainly from the point of view of persistence and extinction. To begin with, the global positivity, stochastically boundedness and other asymptotic properties have been derived. In addition, sufficient conditions for extinction, nonpersistence in the mean and weak persistence are obtained. It is proved that the variation of Lévy jumps can affect the asymptotic property of the system.

1 Introduction

In mathematical ecology, the relationship between prey and predator is one of the most intriguing and significant topics due to its universal existence. One significant component of the predator-prey relationship is the predator’s functional response. It has long been and will continue to be a dominant theme in ecosystem theory. The predator-prey systems with different kinds of functional responses (see Hassell-Varley [1], Beddington-DeAngelis [2, 3] and Crowley-Martin [4]) and references therein) have been investigated by mathematicians and ecologists. However, due to many reasons (such as environmental pollution, over predation, over exploitation, extensive and unregulated harvesting), the birth/death rates, carrying capacities, competition coefficients and other parameters involved in this system perform random fluctuations. Then we need to take the environmental noise into account, for example, consider the stochastic perturbation of the death rate of the predator and birth rate of the prey. In some cases, the scholars prefer the Beddington-DeAngelis type functional response because predator-prey model with Beddington-DeAngelis functional response can describe the species and the ecological systems more reasonably. It has desirable qualitative features of ratio dependent form and overcomes some unexpected behaviors at low prey population level. Also, it has an extra term in the denominator modeling mutual interference among predators. There is much excellent work on the predator-prey system with Beddington-DeAngelis functional response, for example, [5–8]. Liu-Wang [5] studied the global asymptotic stability, Qiu et al. [6] investigated some dynamical properties, Liu-Wang [7] discussed stochastically asymptotic stability, etc. Their work stimulated much of our work. Our consideration in this work is a generalization of the model in [7]. A basic problem concerning predator-prey model is the existence and uniqueness of global positive solutions. One of the main approaches in the literature to date is to construct different types of Lyapunov functions to investigate how the solutions behave in $\mathbb {R}_{+}^{2}$. In our work, we proved the system (1.1) has a unique global positive solution by the method of variable transformation. Moreover, we obtained the result that almost all sample paths of any solution starting from a positive state will never be nonpositive, which can ensure the precise mathematical form and bring about more definite practical significance.

On the other hand, from the viewpoint of biology, large and sudden environmental disturbance, such as earthquakes, tsunamis, hurricanes, floods, droughts may have important consequences on the system. As a result, the systems become very complex and the sample paths are discontinuous. These phenomena cannot be exactly described by Brownian motion. To explain these phenomena, introducing a jump process into this system is one of the important methods [9]. There is a large number of literature on this topic, for example, [9–21], and the references therein. Especially, in [18] Liu-Wang investigated stochastic logistic models with Lévy noise and gave sufficient and necessary conditions for the stochastic permanence and extinction; Liu [19] established the sufficient conditions for the stability in mean and extinction of stochastic predator-prey system with modified Leslie-Gower and Holling-type II schemes with Lévy jumps. As a result of the mentioned themes, this paper puts forward a predator-prey model of Beddington-DeAngelis type functional response with Lévy jumps of the form

$$ \left \{ \textstyle\begin{array}{l} \mathrm{d}x(t)= x(t-) [ (a_{11}(t)-a_{12}(t)x(t-)-\frac {a_{13}(t)y(t-)}{b_{1}(t)+b_{2}(t)x(t-)+b_{3}(t)y(t-)} )\,\mathrm{d}t \\ \hphantom{\mathrm{d}x(t)={}}{}+\sigma_{1}(t)dB_{1}(t) ]+\int_{\mathbb{Y}}h_{1}(t,u)x(t-)\tilde {N}(\mathrm{d}t,\mathrm{d}u), \\ \mathrm{d}y(t)= y(t-) [ (-a_{21}(t)-a_{22}(t)y(t-)+\frac {a_{23}(t)x(t-)}{b_{1}(t)+b_{2}(t)x(t-)+b_{3}(t)y(t-)} )\,\mathrm{d}t \\ \hphantom{\mathrm{d}y(t)={}}{}+\sigma_{2}(t)dB_{2}(t) ]+\int_{\mathbb{Y}}h_{2}(t,u)y(t-)\tilde {N}(\mathrm{d}t,\mathrm{d}u), \end{array}\displaystyle \right . $$

(1.1)

with $x(0)=x_{0}>0$ and $y(0)=y_{0}>0$, where $x(t-)$ and $y(t-)$ denote the left limit of $x(t)$ and $y(t)$, respectively. $(B_{1}(t))$ and $(B_{2}(t))$ are Brownian motions, N is a Poisson counting measure with characteristic measure λ on a measurable subset $\mathbb {Y}$ of $[0,\infty)$ with $\lambda(\mathbb{Y})<\infty$ and $\tilde {N}(\mathrm{d}t,\mathrm{d}u):=N(\mathrm{d}t,\mathrm{d}u)-\lambda(\mathrm{d}u)\,\mathrm{d}t$, and the functions $h_{i}: \mathbb {Y}\times(0, \infty)\rightarrow\mathbb{R}$ ($i=1,2$) are bounded and continuous with respect to λ and are $\mathfrak{B}(\mathbb {Y})\times\mathscr{F}_{t}$ measurable. Throughout this paper, the process $(B_{1}(t))$ and $(B_{2}(t))$ are defined on a complete probability space $(\Omega, \mathscr{F}, \{\mathscr{F}_{t}\}_{t>0}, \mathbb{P})$. The parameters $a_{ij}(\cdot)$ ($i, j=1,2,3$), $b_{k}(\cdot)$ ($k=1,2,3$), $\sigma_{m}(\cdot)$ and $h_{m}(\cdot)$ ($m=1,2$) are all positive bounded function on $\mathbb{R}_{+}$.

Although there is much literature about predator-prey systems with Lévy noise, this study is mainly involved in estimate to the sample Lyapunov exponents. On one hand, we prove that the system (1.1) has a unique global positive solution. Our method is a little similar to the one in [19]. But we do not use comparison theorem to prove the global solution, instead came out with Lyapunov functions. On the other hand, we study the long-term behaviors of solution to stochastic nonautonomous system (1.1). Moreover, we establish the result $\limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t}\leq0$ by an exponential martingale inequality with jumps, which plays an important role in this work and is different from that of [18] and [19] in the proof. In [18] and [19], they mainly showed the stability in the mean and extinction of the solutions. Different from those results obtained in [18] and [19], by establishing the estimation to the sample Lyapunov exponents, we show more long behaviors such as weakly persistence, nonpersistence in the mean and extinction of solution to system (1.1). Meanwhile, it is important to point out that the proof of the properties of the solution is not a direct generalization for systems without Lévy noise and some new techniques are devised to deal with the difficulties due to Lévy noise.

We need the following technical result from Bao [10] for the jump-diffusion coefficient.

Assumption A

For any $t\geq0$, $u\in\mathbb{Y}$ and $i=1,2$,

$$ h_{i}(t,u)>-1, $$

(1.2)

when $-1< h_{i}(t,u)<0$, the disturbance denotes decreasing of the community, while $h_{i}(t,u)>0$, it respects increasing.

For notational simplicity, we introduce the following symbols:

$$\begin{aligned}& c_{1}(t)=a_{11}(t)-\frac{\sigma_{1}^{2}(t)}{2}- \int_{\mathbb {Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u), \\& c_{2}(t)=-a_{21}(t)-\frac{\sigma_{2}^{2}(t)}{2}- \int_{\mathbb {Y}} \bigl[h_{2}(t,u)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u), \\& f(t)=\frac{a_{13}(t)y(t)}{b_{1}(t)+b_{2}(t)x(t)+b_{3}(t)y(t)},\qquad g(t)=\frac{a_{23}(t)x(t)}{b_{1}(t)+b_{2}(t)x(t)+b_{3}(t)y(t)}, \\& \hat{\varphi}=\inf_{t\in\mathbb{R}_{+}}\varphi(t),\qquad \check{\varphi }= \sup_{t\in\mathbb{R}_{+}}\varphi(t). \end{aligned}$$

The organization of this paper is as follows. In Section 2 we study some properties of the solution of model (1.1) with noise consisting of Brownian motion and jumps. On this basis, in Section 3 we show the long-time behaviors of the model and reveal the effect of the intensities of the noises on the model by means of theoretical derivation, which is the core part of this paper. Finally, we introduce a numerical example to verify intuitively the results in the rest of the paper.

2 Properties of the solution

Since the $x(t)$, $y(t)$ in (1.1) are the population sizes of the prey and predator at time t, respectively, and they should be nonnegative. By the biological explanation of model, only positive solutions are meaningful, which will be proved theoretically in mathematics analysis in Lemma 2.1. In the following, first we should ensure the existence of positive solutions. Moreover, in order to guarantee that the model has a unique global solution (i.e., no explosion in a finite time) for any given initial value, the coefficients of the model are generally required to satisfy the linear growth condition and local Lipschitz condition (mentioned in [22]). However, the coefficients of (1.1) neither fulfil the linear growth condition, nor local Lipschitz continuity. It is therefore necessary to use another method to prove that the solution of system (1.1) is not only positive but also will not explode to infinity at any finite time. The transformations $e^{X(t)}=x(t)$ and $e^{Y(t)}=y(t)$ result in the corresponding coefficients satisfying a local Lipschitz condition, which is motivated by [19]. In the following, we shall prove the system (1.1) has a unique global positive global solution by the method of variable transformation.

Theorem 2.1

Under Assumption  A, for any initial values $(x_{0}, y_{0})\in\mathbb {R}^{2}_{+}$, there is a unique global positive solution $(x(t), y(t))$ for any $t\geq0$ almost surely.

Proof

The proof is divided into two steps.

Step 1: consider the following equations:

$$ \left \{ \textstyle\begin{array}{l} \mathrm{d}X(t)= (c_{1}(t)-a_{12}(t)e^{X(t)}-\frac {a_{13}(t)e^{Y(t)}}{b_{1}(t)+b_{2}(t)e^{X(t)}+b_{3}(t)e^{Y(t)}} )\,\mathrm{d}t \\ \hphantom{\mathrm{d}X(t)={}}{}+\sigma_{1}(t)\,\mathrm{d}B_{1}(t)+\int_{\mathbb{Y}}\ln(1+h_{1}(t,u))\tilde {N}(\mathrm{d}t,\mathrm{d}u), \\ \mathrm{d}Y(t)= (c_{2}(t)-a_{22}(t)e^{Y(t)}+\frac {a_{23}(t)e^{X(t)}}{b_{1}(t)+b_{2}(t)e^{X(t)}+b_{3}(t)e^{Y(t)}} )\,\mathrm{d}t \\ \hphantom{\mathrm{d}Y(t)={}}{}+\sigma_{2}(t)\,\mathrm{d}B_{2}(t)+\int_{\mathbb{Y}}\ln(1+h_{2}(t,u))\tilde {N}(\mathrm{d}t,\mathrm{d}u), \end{array}\displaystyle \right . $$

(2.1)

on $t\geq0$ with initial value $(X(0),Y(0))=(\ln x_{0}, \ln y_{0})$. It is easy to find that the coefficients of (2.1) satisfy the local Lipschitz condition, then there is a unique local solution $(X(t), Y(t))$ for $t\in[0, \tau_{e})$, where $\tau_{e}$ is the explosion time. Therefore, by Itô’s formula, $(x(t), y(t))=(e^{X(t)}, e^{Y(t)})$ is the unique positive local solution of (1.1) with initial value $(x_{0}, y_{0})\in\mathbb{R}^{2}_{+}$.

Step 2: we shall show this solution is global, i.e. $\tau _{e}=+\infty$ a.s. Let $k_{0}>0$ be sufficiently large for $x_{0}\in (\frac{1}{k_{0}},k_{0} )$, $y_{0}\in (\frac{1}{k_{0}},k_{0} )$. For each integer $k\geq k_{0}$, define the stopping time

$$\tau_{k}=\inf \biggl\{ t\in [0,\tau_{e} ): x_{t} \notin \biggl(\frac{1}{k},k \biggr) \mbox{ or }y_{t}\notin \biggl(\frac{1}{k},k \biggr) \biggr\} . $$

Obviously, $\tau_{k}$ is increasing as $k\uparrow+\infty$ a.s. Set $\tau _{+\infty}:= \lim_{k\rightarrow+\infty}\tau_{k}$, therefore $\tau _{+\infty}\leq\tau_{e}$ a.s. If we can show that $\tau_{+\infty}=+\infty$ is true, then $\tau_{e}=+\infty$ and $(x(t), y(t))\in\mathbb {R}^{2}_{+}$ for all $t\geq0$, a.s. Consequently, we only need to show $\tau_{+\infty}=+\infty$ a.s. To illustrate this statement, let us define a $C^{2}$-function by

$$V(x, y)=(x-1-\ln x)+(y-1-\ln y). $$

The nonnegativity of this function can be seen from the fact that $f(u)=u-v-\ln\frac{u}{v}\geq0$, for all $u,v>0$. Using Itô’s formula, we obtain

$$\begin{aligned} \mathrm{d}V(x,y) =&LV \bigl(x(t),y(t) \bigr)\,\mathrm{d}t+ \bigl(x(t)-1 \bigr) \sigma_{1}(t)\,\mathrm{d}B_{1}(t)+ \bigl(y(t)-1 \bigr) \sigma_{2}(t)\,\mathrm{d}B_{2}(t) \\ &{}+ \int_{\mathbb{Y}} \bigl[h_{1}(t,u)x(t)-\ln \bigl(1+h_{1}(t,u) \bigr)+h_{2}(t,u)y(t)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr]\tilde{N}(\mathrm{d}t,\mathrm{d}u), \end{aligned}$$

where

$$\begin{aligned} LV \bigl(x(t),y(t) \bigr) \leq&-a_{12}(t) \biggl(x(t)- \frac{a_{11}(t)+a_{12}(t)}{2a_{12}(t)} \biggr)^{2}+\frac{(a_{11}(t)+a_{12}(t))^{2}}{4a_{12}(t)} \\ &{}+\frac{a_{13}(t)}{b_{3}(t)}-a_{22}(t) \biggl(y(t)-\frac {a_{23}(t)+b_{2}(t)a_{22}(t)-b_{2}(t)a_{21}(t)}{2b_{2}(t)a_{22}(t)} \biggr)^{2} \\ &{}+\frac{ (a_{23}(t)+b_{2}(t)a_{22}(t)-b_{2}(t)a_{21}(t) )^{2}}{4b_{2}^{2}(t)a_{22}(t)}+a_{21}(t)-a_{11}(t) \\ &{}+\frac{1}{2}\sigma_{1}^{2}(t)+\frac{1}{2} \sigma_{2}^{2}(t) \\ &{}+ \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr)+h_{2}(t,u)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr] \lambda( \mathrm{d}u) \\ \leq&\frac{(a_{11}(t)+a_{12}(t))^{2}}{4a_{12}(t)}+\frac{ (a_{23}(t)+b_{2}(t)a_{22}(t)-b_{2}(t)a_{21}(t) )^{2}}{4b_{2}^{2}(t)a_{22}(t)} \\ &{}+a_{21}(t)+\frac{a_{13}(t)}{b_{3}(t)}-a_{11}(t)+ \frac{1}{2}\sigma _{1}^{2}(t)+\frac{1}{2} \sigma_{2}^{2}(t) \\ &{}+ \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr)+h_{2}(t,u)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr] \lambda( \mathrm{d}u) \\ \leq&\frac{(\check{a}_{11}+\check{a}_{12})^{2}}{4\hat{a}_{12}}+\frac {\check{a}_{13}}{\hat{b}_{3}}+\frac{ (\check{a}_{23}+\check {b}_{2}\check{a}_{22}-\hat{b}_{2}\hat{a}_{21} )^{2}}{4\hat {b}_{2}^{2}\hat{a}_{22}}+ \check{a}_{21}+\frac{1}{2}\check{\sigma }_{1}^{2}+ \frac{1}{2}\check{\sigma}_{2}^{2}- \hat{a}_{11} \\ &{}+ \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr)+h_{2}(t,u)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr] \lambda( \mathrm{d}u). \end{aligned}$$

Here we have used the fact $0\leq f(t)\leq\frac{a_{13}(t)}{b_{3}(t)}$, $0\leq g(t)\leq\frac{a_{23}(t)}{b_{2}(t)}$ and the inequality $x-\ln (x+1)\geq0$ ($x>-1$). Therefore, we have

$$LV \bigl(x(t),y(t) \bigr)\leq K_{1}+2K_{2}=:K, $$

where

$$\begin{aligned}& K_{1}=\frac{(\check{a}_{11}+\check{a}_{12})^{2}}{4\hat{a}_{12}}+\frac {\check{a}_{13}}{\hat{b}_{3}}+\frac{ (\check{a}_{23}+\check {b}_{2}\check{a}_{22}-\hat{b}_{2}\hat{a}_{21} )^{2}}{4\hat {b}_{2}^{2}\hat{a}_{22}}+ \check{a}_{21}+\frac{1}{2}\check{\sigma }_{1}^{2}+ \frac{1}{2}\check{\sigma}_{2}^{2}- \hat{a}_{11}, \\& K_{2}=\max \biggl\{ \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda (\mathrm{d}u), \int_{\mathbb{Y}} \bigl[h_{2}(t,u)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u) \biggr\} . \end{aligned}$$

Then

$$\begin{aligned} \mathrm{d}V \bigl(x(t),y(t) \bigr) \leq&K\,\mathrm{d}t+ \bigl(x(t)-1 \bigr)\sigma_{1}(t)\,\mathrm{d}B_{1}(t)+ \bigl(y(t)-1 \bigr) \sigma_{2}(t)\,\mathrm{d}B_{2}(t) \\ &{}+ \int_{\mathbb{Y}} \bigl[h_{1}(t,u)x(t)-\ln \bigl(1+h_{1}(t,u) \bigr)+h_{2}(t,u)y(t) \\ &{}-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr]\tilde{N}(\mathrm{d}t, \mathrm{d}u). \end{aligned}$$

(2.2)

Integrating both sides of (2.2) from 0 to $\tau_{k}\wedge T$, we deduce

$$\begin{aligned}& \int_{0}^{\tau_{k}\wedge T}\,\mathrm{d}V \bigl(x(t),y(t) \bigr) \\& \quad \leq \int_{0}^{\tau_{k}\wedge T}K\,\mathrm{d}t+ \int_{0}^{\tau_{k}\wedge T} \bigl(x(t)-1 \bigr) \sigma_{1}(t) \,\mathrm{d}B_{1}(t)+ \int_{0}^{\tau_{k}\wedge T} \bigl(y(t)-1 \bigr) \sigma_{2}(t) \,\mathrm{d}B_{2}(t) \\& \qquad {}+ \int_{0}^{\tau_{k}\wedge T} \int_{\mathbb{Y}} \bigl[h_{1}(t,u)x(t)-\ln \bigl(1+h_{1}(t,u) \bigr)+h_{2}(t,u)y(t) \\& \qquad {}-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr]\tilde{N}(\mathrm{d}t, \mathrm{d}u). \end{aligned}$$

(2.3)

Taking the expectation of both sides of (2.3), we obtain

$$ \mathrm{E}V \bigl(x(\tau_{k}\wedge T),y( \tau_{k}\wedge T) \bigr)\leq V(x_{0},y_{0})+KT. $$

(2.4)

Define a function, for each $v>1$,

$$ \mu(v)=\inf \biggl\{ V(x_{1},x_{2}): x_{i}\geq v \mbox{ or }x_{i}\leq\frac{1}{v}, i=1,2 \biggr\} . $$

Due to the property of the function $g(x)=x-1-\ln x$, $x>0$, we deduce that

$$ \lim_{x\rightarrow+\infty}g(x)=+\infty \quad \mbox{and} \quad \lim _{x\rightarrow 0^{+}}g(x)=+\infty $$

and hence

$$ \lim_{v\rightarrow+\infty}\mu(v)=+\infty. $$

(2.5)

Set $\Omega_{k}=\{\tau_{k}\leq T\}$. Then we obtain from (2.4)

$$\begin{aligned} \mu(k)P(\Omega_{k}) \leq& E \bigl[I_{\Omega_{k}}V \bigl(x( \tau_{k}),y(\tau_{k}) \bigr) \bigr] \\ \leq& EV \bigl(x(\tau_{k}\wedge T),y(\tau_{k}\wedge T) \bigr) \\ \leq& V(x_{0},y_{0})+KT, \end{aligned}$$

where $I_{\Omega_{k}}$ is the indicator function of $\Omega_{k}$. Recalling (2.5) and letting $k\rightarrow+\infty$ yield $P(\tau_{+\infty}\leq T)=0$. Since T is arbitrary, we must have $P(\tau_{+\infty}=+\infty)=1$. The proof is therefore completed. □

Theorem 2.2

Under Assumption  A, for any $0\leq p\leq1$, there is a constant K such that

$$ \sup_{t\in\mathbb{R}_{+}}\mathrm{E} \bigl(x^{p}(t)+y^{p}(t) \bigr)\leq K. $$

And assume further that there is a constant $M(p)$ such that, for some $p>1$, $t\geq0$, $i=1,2$,

$$ \int_{\mathbb{Y}} \bigl\vert h_{i}(t,u) \bigr\vert ^{p}\lambda\,\mathrm{d}(u)\leq M(p), $$

(2.6)

then there is a $K(p)$ such that

$$ \sup_{t\in\mathbb{R}_{+}}\mathrm{E} \bigl(x^{p}(t)+y^{p}(t) \bigr)\leq K(p). $$

(2.7)

Proof

The following idea goes to back to that of [10].

Applying Itô’s formula for $p>1$, we obtain

$$\begin{aligned} \mathrm{d}\mathrm{e}^{t}x^{p}(t) \leq& \mathrm{e}^{t} \biggl[-p\hat{a}_{12}x^{p+1}(t)+ \biggl(1+p \biggl(\check {a}_{11}+\frac{p-1}{2}\check{ \sigma}_{1}^{2} \biggr) \biggr)x^{p}(t) \biggr]\, \mathrm{d}t \\ &{}+px^{p}(t)\sigma_{1}(t)\,\mathrm{d}B_{1}(t)+ \int_{\mathbb{Y}}\mathrm{e}^{t}x^{p}(t) \bigl[ \bigl(1+\check{h}_{1}(u) \bigr)^{p}-1 \\ &{}-p\hat{h}_{1}(u) \bigr]\lambda(\mathrm{d}u)\,\mathrm{d}t+ \int_{\mathbb{Y}}\mathrm{e}^{t}x^{p}(t) \bigl[ \bigl(1+h_{1}(t,u) \bigr)^{p}-1 \bigr]\tilde{N}(\mathrm{d}t, \mathrm{d}u). \end{aligned}$$

(2.8)

By Assumption A and the condition (2.6), we deduce that there exists a constant $K_{1}(p)$ such that

$$\begin{aligned}& -p\hat{a}_{12} x^{p+1}(t)+ \biggl(1+p \biggl( \check{a}_{11}+\frac {p-1}{2}\check{\sigma}_{1}^{2} \biggr) \biggr)x^{p}(t) \\& \qquad {}+ \int_{\mathbb {Y}} \bigl[ \bigl(1+\check{h}_{1}(u) \bigr)^{p}-1-p\hat{h}_{1}(u) \bigr]\lambda( \mathrm{d}u)x^{p}(t) \\& \quad \leq K_{1}(p). \end{aligned}$$

Taking the expectation on both sides of the (2.8) and rearranging yield

$$\mathrm{E} \bigl(\mathrm{e}^{t}x^{p}(t) \bigr)\leq x_{0}^{p}+ \int^{t}_{0}K_{1}(p) \mathrm{e}^{s}\,\mathrm{d}s=x_{0}^{p}+K_{1}(p) \bigl(\mathrm{e}^{t}-1 \bigr). $$

From the above inequality, we deduce that there exists a constant $\bar {K}_{1}(p)>0$ such that

$$\sup_{t\in\mathbb{R}_{+}}\mathrm{E} \bigl(x^{p}(t) \bigr)\leq \bar{K}_{1}(p). $$

In the same way, we can deduce that there exists a constant $\bar {K}_{2}(p)>0$ such that

$$\sup_{t\in\mathbb{R}_{+}}\mathrm{E} \bigl(y^{p}(t) \bigr)\leq \bar{K}_{2}(p). $$

Hence $\sup_{t\in\mathbb{R}_{+}}\mathrm{E}(x^{p}(t)+y^{p}(t))\leq\bar {K}_{1}(p)+\bar{K}_{2}(p)=:K(p)$, which yields the desired assertion (2.7). For $0\leq p\leq1$, utilizing the Young inequality yields

$$\int_{\mathbb{Y}} \bigl[ \bigl(1+h_{i}(t,u) \bigr)^{p}-1-ph_{i}(t,u) \bigr]\lambda(\mathrm{d}u)\leq0, \quad i=1,2. $$

Consequently,

$$\begin{aligned}& -p\hat{a}_{12}x^{p+1}(t)+ \biggl(1+p \biggl( \check{a}_{11}+\frac {p-1}{2}\check{\sigma}_{1}^{2} \biggr) \biggr)x^{p}(t) \\& \qquad {}+ \int_{\mathbb {Y}} \bigl[ \bigl(1+h_{i}(t,u) \bigr)^{p}-1-ph_{i}(t,u) \bigr]\lambda(\mathrm{d}u)x^{p}(t) \\& \quad \leq-p\hat{a}_{12}x^{p+1}(t)+ \biggl(1+p \biggl( \check{a}_{11}+\frac {p-1}{2}\check{\sigma}_{1}^{2} \biggr) \biggr)x^{p}(t), \end{aligned}$$

which has an upper bound. Then the conclusion follows immediately. □

As an application of Theorem 2.2, together with Chebyshev’s inequality, we establish the following result.

Theorem 2.3

Let the conditions of Theorem  2.2 hold. Then the solution $z(t)=(x(t),y(t))$ of (1.1) is stochastically bounded, that is to say, for any $\varepsilon\in(0,1)$, there is a constant $H:=H(\varepsilon)$ such that, for any $z_{0}=(x_{0},y_{0})\in\mathbb{R}^{2}_{+}$,

$$\limsup_{t\rightarrow+\infty}\mathbb{P} \bigl\{ \bigl|z(t) \bigr|\leq H \bigr\} \geq1- \varepsilon. $$

The next results are instrumental for obtaining the long-time behaviors of the system (1.1).

Lemma 2.1

Let Assumption  A hold. Then, for all initial values $(x_{0},y_{0})\in \mathbb{R}^{2}_{+}$,

$$ \mathbb{P} \bigl\{ x(t)>0, \forall t>0 \bigr\} =1 \quad \textit{and} \quad \mathbb{P} \bigl\{ y(t)>0, \forall t>0 \bigr\} =1. $$

(2.9)

Proof

We shall only prove the result for $(x(t))$ since the result for $(y(t))$ can be done in the same way. Denote

$$\tau_{K}:=\inf \bigl\{ t>0; x(t)\geq K \bigr\} ,\quad K\geq1 \quad \mbox{and} \quad \rho_{U}:= \bigl\{ t>0; x(t)\leq U \bigr\} , \quad U>0. $$

By Theorem 2.1, $(x(t))$ is nonexplosive, that is, $\lim_{K\rightarrow\infty}\tau_{K}=\infty$ with probability 1. By Itô’s formula, for $p>0$ such that $-\hat{a}_{11}+\frac{\check{a}_{13}}{\hat {b}_{3}}+\frac{p+1}{2}\check{\sigma}_{1}^{2}>0$, we deduce

$$\begin{aligned} x^{-p}(t\wedge\rho_{U}\wedge\tau_{K}) \leq&x_{0}^{-p}+ \int_{0}^{t\wedge\rho_{U}\wedge\tau_{K}} \biggl\{ p \biggl(- \hat{a}_{11}+\check{a}_{12}K+\frac{\check{a}_{13}}{\hat{b}_{3}} \biggr)+ \frac{p(p+1)}{2}\check{\sigma}_{1}^{2} \\ &{}+ \int_{\mathbb{Y}} \bigl[(1+\hat{h}_{1})^{-p}-1+p \check{h}_{1} \bigr]\lambda(\mathrm{d}u) \biggr\} x^{-p}(s)\, \mathrm{d}s \\ &{}+ \int_{0}^{t\wedge\rho_{U}\wedge\tau_{K}}-px^{-p}(s) \sigma_{1}(s)\,\mathrm{d}B_{1}(t) \\ &{}+ \int_{0}^{t\wedge\rho_{U}\wedge\tau_{K}} \int_{\mathbb {Y}}x^{-p}(s) \bigl[ \bigl(1+h_{1}(s,u) \bigr)^{-p}-1 \bigr]\tilde{N}(\mathrm{d}s,\mathrm{d}u). \end{aligned}$$

Taking the expectations of both sides and utilizing Gronwall’s inequality yield

$$\begin{aligned} \mathbb{E}x^{-p}(t\wedge\rho_{U}\wedge\tau_{K}) \leq&x_{0}^{-p}\exp \biggl\{ \biggl[p \biggl(- \hat{a}_{11}+\check{a}_{12}K+\frac{\check{a}_{13}}{\hat {b}_{3}}+ \frac{p+1}{2}\check{\sigma}_{1}^{2} \biggr) \\ &{}+ \int_{\mathbb{Y}} \bigl[(1+\hat{h}_{1})^{-p}-1+p \check{h}_{1} \bigr]\lambda(\mathrm{d}u) \biggr]t \biggr\} . \end{aligned}$$

Let $\rho_{0}=\inf\{t>0; x(t)=0\}$, then $\rho_{U}\uparrow\rho_{0}$ as $U\downarrow0$. If the statement (2.9) is false, that is, $\mathbb{P}(\rho_{0}<\infty)>0$, we can choose a pair of constants t and K large enough such that $\mathbb{P}(\rho_{0}< t\wedge\tau _{K})>0$. Then, for any $U>0$,

$$\begin{aligned} 0 < &\mathbb{P}(\rho_{0}< t\wedge\tau_{K})\leq\mathbb{P}( \rho_{U}< t\wedge \tau_{K}) \\ \leq& U^{p}\mathbb{E} \bigl[x^{-p}(t\wedge \rho_{U}\wedge\tau _{K}) \mathbf{I}_{\{\rho_{U}< t\wedge\tau_{K}\}} \bigr] \\ \leq& U^{p}\mathbb{E} \bigl[x^{-p}(t\wedge \rho_{U}\wedge\tau_{K}) \bigr] \\ \leq&U^{p}x_{0}^{-p}\exp \biggl\{ \biggl[p \biggl(-\hat{a}_{11}+\check {a}_{12}K+\frac{\check{a}_{13}}{\hat{b}_{3}}+ \frac{p+1}{2}\check{\sigma }_{1}^{2} \biggr) \\ &{}+ \int_{\mathbb{Y}} \bigl[(1+\hat{h}_{1})^{-p}-1+p \check {h}_{1} \bigr]\lambda(\mathrm{d}u) \biggr]t \biggr\} . \end{aligned}$$

Letting $U\downarrow0$, we get a contradiction. Therefore, it implies $\mathbb{P}(\rho_{0}<\infty)=0$. We complete the proof. □

Lemma 2.2

Let Assumption  A hold. Assume in addition that there exists a constant $c>0$ such that

$$ \int_{\mathbb{Y}} \bigl[\ln \bigl(1+h_{i}(t,u) \bigr) \bigr]^{2}\lambda(\mathrm{d}u)\leq c. $$

(2.10)

Then, for any initial value $(x_{0},y_{0})\in\mathbb{R}^{2}_{+}$, the solution of $(x(t),y(t))$ of (1.1) has the property

$$ \limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t}\leq0 \quad \textit{and} \quad \limsup_{t\rightarrow\infty}\frac{\ln y(t)}{t}\leq0 \quad \textit{a.s.} $$

Proof

In this section we use the transform $\ln x(t)$. By Lemma 2.1, this transform make sense for all $t\geq0$. Then, for any $t\geq0$, applying Itô’s formula we deduce

$$\begin{aligned} \mathrm{e}^{t}\ln x(t) =&\ln x_{0}+ \int_{0}^{t}\mathrm{e}^{s} \bigl[\ln x(s)+c_{1}(s)-a_{12}(s)x(s)-f(s) \bigr]\,\mathrm{d}s \\ &{}+ \int_{0}^{t}\mathrm{e}^{s} \sigma_{1}(s)\,\mathrm{d}B_{1}(s)+ \int_{0}^{t} \int _{\mathbb{Y}}\mathrm{e}^{s}\ln \bigl(1+h_{1}(s,u) \bigr)\tilde{N}(\mathrm{d}s,\mathrm{d}u). \end{aligned}$$

It follows from the inequality $\ln x\leq x-1$ that

$$\begin{aligned} \mathrm{e}^{t}\ln x(t) \leq&\ln x_{0}+ \int_{0}^{t}\mathrm{e}^{s} \biggl[\ln x(s)+a_{11}(t)-\frac{\sigma_{1}^{2}(t)}{2}-a_{12}(s)x(s)-f(s) \biggr]\, \mathrm{d}s \\ &{}+ \int_{0}^{t}\mathrm{e}^{s} \sigma_{1}(s)\,\mathrm{d}B_{1}(s)+ \int_{0}^{t} \int _{\mathbb{Y}}\mathrm{e}^{s}\ln \bigl(1+h_{1}(s,u) \bigr)\tilde{N}(\mathrm{d}s,\mathrm{d}u). \end{aligned}$$

Due to the property of the function $\ln x-cx$ ($c,x>0$) that it has maximum value $-1-\ln c$ on $x=\frac{1}{c}$, we deduce that

$$\begin{aligned} \mathrm{e}^{t}\ln x(t) \leq&\ln x_{0}+ \int_{0}^{t}\mathrm{e}^{s} \biggl[-1-\ln a_{12}(s)+a_{11}(s)-\frac{\sigma_{1}^{2}(s)}{2}-f(s) \biggr]\, \mathrm{d}s \\ &{}+ \int_{0}^{t}\mathrm{e}^{s} \sigma_{1}(s)\,\mathrm{d}B_{1}(s)+ \int_{0}^{t} \int _{\mathbb{Y}}\mathrm{e}^{s}\ln \bigl(1+h_{1}(s,u) \bigr)\tilde{N}(\mathrm{d}s,\mathrm{d}u). \end{aligned}$$

(2.11)

Let $M_{1}(t)=\int_{0}^{t}\mathrm{e}^{s}\sigma_{1}(s)\,\mathrm{d}B_{1}(s)$, $M_{2}(t)=\int_{0}^{t}\int_{\mathbb{Y}}\mathrm{e}^{s}\ln (1+h_{1}(s,u))\tilde{N}(\mathrm{d}s,\mathrm{d}u)$, then the quadratic variation of $M_{1}(t)$ and $M_{2}(t)$ are

$$\bigl\langle M_{1}(t) \bigr\rangle (t)= \int_{0}^{t}\mathrm{e}^{2s}\sigma ^{2}_{1}(s)\,\mathrm{d}s\leq\frac{\check{\sigma}^{2}_{1}}{2} \bigl( \mathrm{e}^{2t}-1 \bigr)< \infty \quad \mbox{a.s.} $$

and

$$\bigl\langle M_{2}(t) \bigr\rangle (t)= \int_{0}^{t} \int_{\mathbb{Y}}\mathrm{e}^{2s} \bigl\vert \ln \bigl(1+h_{1}(s,u) \bigr) \bigr\vert ^{2}\lambda( \mathrm{d}u) \, \mathrm{d}s\leq\frac {c(\mathrm{e}^{2t}-1)}{2}< \infty\quad \mbox{a.s.} $$

In view of Lemma 4.3 in [10], for any positive number α, β, T,

$$\begin{aligned} \begin{aligned} &\mathbb{P} \biggl\{ \sup_{0\leq t\leq T} \biggl[M_{1}(t)- \frac{\alpha}{2} \bigl\langle M_{1}(t) \bigr\rangle (t)+M_{2}(t)- \frac{1}{\alpha} \int_{0}^{t} \int_{\mathbb {Y}} \bigl[\mathrm{e}^{\alpha\mathrm{e}^{s}\ln(1+h_{1}(u,\Lambda(s)))}-1 \\ &\quad {} -\alpha\mathrm{e}^{s}\ln \bigl(1+h_{1}(s,u) \bigr) \bigr]\lambda(\mathrm{d}u)\mathrm{d}s \biggr]\geq \beta \biggr\} \leq \mathrm{e}^{-\alpha\beta}. \end{aligned} \end{aligned}$$

Choose $T=n\gamma$, $\alpha=\varepsilon\mathrm{e}^{-n\gamma}$, and $\beta =\frac{\theta\mathrm{e}^{n\gamma\ln n}}{\varepsilon}$, where $n\in\mathbb {N}$, $0<\varepsilon<1$, $\gamma>0$, and $\theta>1$. By the Borel-Cantelli lemma, we see that there exists an $\Omega_{i}\subseteq \Omega$ with $\mathbb{P}(\Omega_{i})=1$ such that, for any $\omega\in \Omega_{i}$, there is an integer $n_{0}=n_{0}(\omega)$ such that

$$\begin{aligned} M_{1}(t)+M_{2}(t) \leq&\frac{\theta\mathrm{e}^{n\gamma}\ln n}{\varepsilon }+ \frac{\varepsilon\mathrm{e}^{-n\gamma}}{2} \int_{0}^{t}\mathrm{e}^{2s} \sigma^{2}_{1}(s)\,\mathrm{d}s+\frac{\mathrm{e}^{n\gamma}}{\varepsilon } \int_{0}^{t} \int_{\mathbb{Y}} \bigl[ \bigl(1+h_{1}(s,u) \bigr)^{\varepsilon\mathrm{e}^{s-n\gamma}} \\ &{}-1-\varepsilon\mathrm{e}^{s-n\gamma}\ln \bigl(1+h_{1}(s,u) \bigr) \bigr]\lambda(\mathrm{d}u)\,\mathrm{d}s, \end{aligned}$$

where $n>n_{0}$, $0\leq t\leq n\gamma$. Furthermore, from the inequality $x^{p}\leq1+p(x-1)$ ($x\geq0$, $0\leq p\leq1$), we get

$$\begin{aligned}& \frac{\mathrm{e}^{n\gamma}}{\varepsilon} \int_{0}^{t} \int_{\mathbb {Y}} \bigl[ \bigl(1+h_{1}(s,u) \bigr)^{\varepsilon\mathrm{e}^{s-n\gamma}}-1-\varepsilon\mathrm{e}^{s-n\gamma}\ln \bigl(1+h_{1}(s,u) \bigr) \bigr]\lambda(\mathrm{d}u)\,\mathrm{d}s \\& \quad \leq \int_{0}^{t} \int_{\mathbb{Y}}e^{s} \bigl(h_{1}(s,u)-\ln \bigl(1+h_{1}(s,u) \bigr) \bigr)\lambda(\mathrm{d}u)\,\mathrm{d}s. \end{aligned}$$

Substituting the above inequality into (2.11) yields

$$\begin{aligned} \mathrm{e}^{t}\ln x(t) \leq&\ln x_{0}+ \int_{0}^{t}\mathrm{e}^{s} \biggl[-1-\ln a_{12}(s)+a_{11}(s)-\frac{\sigma_{1}^{2}(s)}{2}-f(s) \biggr]\, \mathrm{d}s+\frac {\theta\mathrm{e}^{n\gamma}\ln n}{\varepsilon} \\ &{}+\frac{\varepsilon\mathrm{e}^{-n\gamma}}{2} \int_{0}^{t}\mathrm{e}^{2s} \sigma^{2}_{1}(s)\,\mathrm{d}s + \int_{0}^{t} \int_{\mathbb{Y}}\mathrm{e}^{s} \bigl(h_{1}(s,u)- \ln \bigl(1+h_{1}(s,u) \bigr) \bigr)\lambda(\mathrm{d}u)\,\mathrm{d}s \\ \leq&\ln x_{0}+\frac{\theta\mathrm{e}^{n\gamma}\ln n}{\varepsilon}+ \int _{0}^{t}\mathrm{e}^{s} \biggl(-1- \ln\hat{a}_{12}+\check{a}_{11}-\frac{\sigma _{1}^{2}(s)}{2} \biggr)\, \mathrm{d}s \\ &{}+\frac{\varepsilon\mathrm{e}^{-n\gamma }}{2} \int_{0}^{t}\mathrm{e}^{2s} \sigma^{2}_{1}(s)\,\mathrm{d}s+ \int_{0}^{t} \int_{\mathbb{Y}}\mathrm{e}^{s} \bigl( \bigl\vert \check{h}_{1}(u) \bigr\vert + \bigl\vert \ln \bigl(1+ \check{h}_{1}(u) \bigr) \bigr\vert \bigr)\lambda(\mathrm{d}u)\, \mathrm{d}s \\ \leq&\ln x_{0}+\frac{\theta\mathrm{e}^{n\gamma}\ln n}{\varepsilon}+ \int _{0}^{t}\mathrm{e}^{s} \biggl(-1- \ln\hat{a}_{12}+\check{a}_{11}-\frac {(1-\varepsilon\mathrm{e}^{s-n\gamma})\hat{\sigma}^{2}_{1}}{2} \biggr)\, \mathrm{d}s \\ &{}+ \int_{0}^{t} \int_{\mathbb{Y}}\mathrm{e}^{s} \bigl( \bigl\vert \check{h}_{1}(u) \bigr\vert + \bigl\vert \ln \bigl(1+ \check{h}_{1}(u) \bigr) \bigr\vert \bigr)\lambda(\mathrm{d}u)\, \mathrm{d}s. \end{aligned}$$

Then, for any $\omega\in\Omega_{i}$ and $(n-1)\gamma\leq t\leq n\gamma$ with $n\geq n_{0}+1$, we have

$$\begin{aligned} \ln x(t) \leq&\frac{\ln x_{0}}{\mathrm{e}^{t}}+\frac{\theta\mathrm{e}^{\gamma }\ln n}{\varepsilon}+ \int_{0}^{t}\mathrm{e}^{s-t} \biggl(-1-\ln \hat {a}_{12}+\check{a}_{11}-\frac{(1-\varepsilon\mathrm{e}^{s-n\gamma})\hat {\sigma}^{2}_{1}}{2} \biggr)\, \mathrm{d}s \\ &{}+ \int_{0}^{t} \int_{\mathbb{Y}}\mathrm{e}^{s-t} \bigl( \bigl\vert \check{h}_{1}(u) \bigr\vert + \bigl\vert \ln \bigl(1+ \check{h}_{1}(u) \bigr) \bigr\vert \bigr)\lambda(\mathrm{d}u)\, \mathrm{d}s. \end{aligned}$$

By Assumption A, it is readily seen that, for any $0\leq s\leq n\gamma$, there exists a constant K which is independent of n such that

$$\frac{\ln x(t)}{t}\leq\frac{\ln x_{0}}{t\mathrm{e}^{t}}+\frac{\theta\mathrm{e}^{\gamma}\ln n}{t\varepsilon}+K \biggl( \frac{1}{t}-\frac{1}{t\mathrm{e}^{t}} \biggr). $$

Setting $n\uparrow\infty$, $\varepsilon\uparrow1$, $\gamma\downarrow0$ and $\theta\downarrow1$ leads to

$$\limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t}\leq0. $$

On the other hand, the result for $(y(t))$ can be proved in the same way and so we omit it. □

3 Persistence and extinction

In the previous section, we have discussed some properties of the solution to the system (1.1). In this section we will investigate how jump process affects the persistence and extinction of the system (1.1).

Theorem 3.1

Let Assumption  A and (2.10) hold, for any initial value $(x_{0}, y_{0})\in\mathbb{R}^{2}_{+}$, the solution of $(x(t),y(t))$ of (1.1) has the property

$$\begin{aligned}& \limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t}\leq\limsup _{t\rightarrow \infty}\frac{1}{t} \int^{t}_{0}c_{1}(s)\,\mathrm{d}s\quad \textit{and} \\& \limsup_{t\rightarrow\infty}\frac{\ln y(t)}{t}\leq\limsup _{t\rightarrow\infty }\frac{1}{t} \int^{t}_{0} \biggl(c_{2}(s)+ \frac{a_{23}(s)}{b_{2}(s)} \biggr)\,\mathrm{d}s. \end{aligned}$$

Proof

According to Lemma 2.1, it suffices to show that $x(t)>0$ for all $t\geq0$ almost everywhere. Then using Itô’s formula we have

$$ \ln x(t) \leq\ln x_{0}+ \int_{0}^{t}c_{1}(s)\,\mathrm{d}s+ \int_{0}^{t}\sigma _{1}(s)\, \mathrm{d}B_{1}(s)+ \int_{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{1}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u). $$

This further shows

$$\begin{aligned} \frac{\ln x(t)}{t} \leq&\frac{\ln x_{0}}{t}+\frac{1}{t} \int _{0}^{t}c_{1}(s)\,\mathrm{d}s+ \frac{1}{t} \int_{0}^{t}\sigma_{1}(s)\, \mathrm{d}B_{1}(s) \\ &{}+\frac{1}{t} \int_{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{1}(s,u) \bigr)\tilde {N}( \mathrm{d}s,\mathrm{d}u). \end{aligned}$$

(3.1)

Let $M_{3}(t)=\int_{0}^{t}\sigma_{1}(s)\,\mathrm{d}B_{1}(s)$, $M_{4}(t)=\int _{0}^{t}\int_{\mathbb{Y}}\ln(1+h_{1}(s,u))\tilde{N}(\mathrm{d}s,\mathrm{d}u)$, then the quadratic variations of $M_{3}(t)$ and $M_{4}(t)$ are

$$\bigl\langle M_{3}(t) \bigr\rangle (t)= \int_{0}^{t}\sigma^{2}_{1}(s) \,\mathrm{d}s\leq \check{\sigma}^{2}_{1}t $$

and

$$\bigl\langle M_{4}(t) \bigr\rangle (t)= \int_{0}^{t} \int_{\mathbb{Y}} \bigl\vert \ln \bigl(1+h_{1}(s ,u) \bigr) \bigr\vert ^{2}\lambda(\mathrm{d}u)\,\mathrm{d}s\leq ct. $$

We have

$$\int_{0}^{t}\frac{1}{(1+s)^{2}}\,\mathrm{d}s= \frac{t}{1+t}< \infty, $$

and utilizing the strong law of large numbers for local martingales (see [23]), we get

$$ \lim_{t\rightarrow\infty}\frac{M_{i}(t)}{t}=0 \quad \mbox{a.s. }, i=3,4. $$

(3.2)

Combining the above equalities with (3.1), we obtain

$$\limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t}\leq\limsup _{t\rightarrow \infty}\frac{\ln x_{0}}{t}+\limsup_{t\rightarrow\infty} \frac{1}{t} \int _{0}^{t}c_{1}(s)\,\mathrm{d}s. $$

Hence the result for $(y(t))$ can be proved in the same way and so we omit it. □

If the jump noise intensities are sufficiently large, all the species will become extinct with probability one. The following conclusion illustrates this point.

Theorem 3.2

Assume the conditions of Theorem  3.1. If

$$ \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}c_{1}(s)\,\mathrm{d}s< 0 $$

and

$$\begin{aligned}& \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \int_{\mathbb {Y}} \bigl[h_{1}(s,u)-\ln \bigl(1+h_{1}(s,u) \bigr) \bigr]\lambda(\mathrm{d}u)\,\mathrm{d}s \\& \quad > \limsup_{t\rightarrow\infty} \frac{1}{t} \int_{0}^{t} \biggl(a_{11}(s)- \frac{\sigma _{1}^{2}(s)}{2} \biggr)\,\mathrm{d}s, \end{aligned}$$

then all the species go to extinction, namely, $\lim_{t\rightarrow\infty }x(t)=0$ and $\lim_{t\rightarrow\infty}y(t)=0$.

Proof

In the light of Theorem 3.1, we have $\limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t}<0$ a.s. This further implies that $\lim_{t\rightarrow\infty}x(t)=0$ a.s.

From the view point of biological significance, when the prey dies out, the predator must die out too. Using Itô’s formula we have

$$\begin{aligned} \limsup_{t\rightarrow\infty}\frac{\ln y(t)}{t} \leq&\limsup _{t\rightarrow \infty} \biggl[\frac{\ln y_{0}}{t}+\frac{1}{t} \int_{0}^{t} \biggl(c_{2}(s)-a_{22}(s)y(s)+ \frac{a_{23}(s)x(s)}{b_{1}(s)} \biggr)\,\mathrm{d}s \\ &{}+\frac{1}{t} \int_{0}^{t}\sigma_{2}(s)\, \mathrm{d}B_{2}(s)+\frac{1}{t} \int _{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{2}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u) \biggr] \\ \leq&\limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}c_{2}(s)\,\mathrm{d}s< 0 \quad \mbox{a.s.} \end{aligned}$$

This also implies that $\lim_{t\rightarrow\infty}y(t)=0$ a.s. □

Theorem 3.3

Let Assumption  A and (2.10) hold.

• (1) If $\limsup_{t\rightarrow\infty}\frac{1}{t}\int_{0}^{t}c_{1}(s)\,\mathrm{d}s=0$, then the prey $(x(t))$ is nonpersistent in the mean, namely, $\limsup_{t\rightarrow\infty}\frac{1}{t}\int_{0}^{t}x(s)\,\mathrm{d}s=0$.

• (2) If $\limsup_{t\rightarrow\infty}\frac{1}{t}\int_{0}^{t} [c_{2}(s)+\frac{a_{23}(s)}{b_{2}(s)} ]\,\mathrm{d}s=0$, then the predator $(y(t))$ is nonpersistent in the mean, namely, $\limsup_{t\rightarrow\infty}\frac{1}{t}\int_{0}^{t}y(s)\,\mathrm{d}s=0$.

Proof

Our proof is motivated by the work of Liu and Wang [24]. In view of the fact that $\lim_{t\rightarrow\infty}\frac{1}{t}\int _{0}^{t}c_{1}(s)\,\mathrm{d}s\leq\limsup_{t\rightarrow\infty}\frac{1}{t}\int _{0}^{t}c_{1}(s)\,\mathrm{d}s$ and (3.2), for $\forall\varepsilon >0$, there exists a constant T such that $\frac{1}{t}\int _{0}^{t}c_{1}(s)\,\mathrm{d}s\leq\limsup_{t\rightarrow\infty}\frac{1}{t}\int _{0}^{t}c_{1}(s)\,\mathrm{d}s+\frac{\varepsilon}{2}=\frac{\varepsilon}{2}$, $\frac{M_{3}(t)}{t}\leq\frac{\varepsilon}{4}$, $\frac{M_{4}(t)}{t}\leq \frac{\varepsilon}{4}$, $t\geq T$.

Consequently, for any $\varepsilon>0$ and sufficiently large $t>T$ we deduce that

$$\begin{aligned} \ln x(t) \leq&\ln x_{0}+ \int_{0}^{t} \bigl[c_{1}(s)-a_{12}(s)x(s) \bigr]\,\mathrm{d}s+M_{3}(t)+M_{4}(t) \\ \leq&\ln x_{0}+\varepsilon t-\hat{a}_{12} \int_{0}^{t}x(s)\,\mathrm{d}s. \end{aligned}$$

Define, for $t\geq0$, $\varphi(t)=\int_{0}^{t}x(s)\,\mathrm{d}s$. Then it is easy to see that, for any $t>T$,

$$\ln \biggl(\frac{\mathrm{d}\varphi}{\mathrm{d}t} \biggr)\leq\ln x_{0}+\varepsilon t-\hat {a}_{12}\varphi(t). $$

This further shows, for any $t>T$,

$$\mathrm{e}^{\hat{a}_{12}\varphi(t)}\frac{\mathrm{d}\varphi}{\mathrm{d}t}\leq x_{0} \mathrm{e}^{\varepsilon t}. $$

Integrating the inequality from T to t results in

$$\hat{a}_{12}^{-1} \bigl(\mathrm{e}^{\hat{a}_{12}\varphi(t)}- \mathrm{e}^{\hat {a}_{12}\varphi(T)} \bigr)\leq x_{0}\varepsilon^{-1} \bigl(\mathrm{e}^{\varepsilon t}-\mathrm{e}^{\varepsilon T} \bigr), $$

which yields immediately

$$\mathrm{e}^{\hat{a}_{12}\varphi(t)}\leq\mathrm{e}^{\hat{a}_{12}\varphi (T)}+\hat{a}_{12}x_{0} \varepsilon^{-1} \bigl(\mathrm{e}^{\varepsilon t}-\mathrm{e}^{\varepsilon T} \bigr). $$

Taking the logarithm on both sides yields

$$\varphi(t)\leq\hat{a}_{12}^{-1}\ln \bigl[ \mathrm{e}^{\hat{a}_{12}\varphi (T)}+\hat{a}_{12}x_{0} \varepsilon^{-1} \bigl(\mathrm{e}^{\varepsilon t}-\mathrm{e}^{\varepsilon T} \bigr) \bigr]. $$

Then using L’Hospital’s rule yields

$$\limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}x(s)\,\mathrm{d}s\leq\hat {a}_{12}^{-1}\limsup_{t\rightarrow\infty} \frac{1}{t}\ln\hat {a}_{12}x_{0}\varepsilon^{-1} \mathrm{e}^{\varepsilon t}=\hat {a}_{12}^{-1}\varepsilon\quad \mbox{a.s.} $$

Letting ε tend to 0 in the previous inequality, we obtain $\limsup_{t\rightarrow\infty}\frac{1}{t}\int_{0}^{t}x(s)\,\mathrm{d}s\leq 0$. The corresponding result for $(y(t))$ can be proved with the same technique and we omit it. The proof is completed. □

Theorem 3.4

Let Assumption  A and (2.10) hold.

• (1) If $\limsup_{t\rightarrow\infty}\frac{1}{t}\int_{0}^{t} [c_{1}(s)-\frac{a_{13}(t)}{b_{3}(t)} ]\,\mathrm{d}s>0$, then the prey $(x(t))$ is weakly persistent, namely, $\limsup_{t\rightarrow\infty }x(t)>0$.

• (2) If $\limsup_{t\rightarrow\infty}\frac{1}{t}\int_{0}^{t}c_{1}(s)\,\mathrm{d}s>0$, $\limsup_{t\rightarrow\infty}\frac{1}{t}\int _{0}^{t}c_{2}(s)\,\mathrm{d}s+\frac{\hat{a}_{23}}{b}>\frac{\hat {a}_{23}}{b}\limsup_{t\rightarrow\infty}\frac{1}{t}\int_{0}^{t}\frac {1}{\phi(s)}\,\mathrm{d}s$, then the predator $(y(t))$ is weakly persistent, namely, $\limsup_{t\rightarrow\infty}y(t)>0$, where $b=\max\{\check{b}_{1},\check{b}_{2}\}$ and $\frac{1}{\phi(t)}$ is defined by (3.3).

Proof

To complete the proof, we first show that the prey $(x(t))$ is weakly persistent, that is to say, $\limsup_{t\rightarrow \infty}x(t)>0$. If $\mathbb{P}(\lim_{t\rightarrow\infty}x(t)=0)>0$, there exists a measurable subset $\Omega'$ of Ω such that $\mathbb{P}(\Omega')>0$ and $\lim_{t\rightarrow\infty}x(t,\omega)=0$ for any $\omega\in\Omega'$. Then, by Itô’s formula,

$$\frac{\ln x(t)}{t}=\frac{\ln x_{0}}{t}+\frac{1}{t} \int _{0}^{t} \bigl[c_{1}(s)-a_{12}(s)x(s)-f(s) \bigr]\,\mathrm{d}s+\frac{M_{3}(t)}{t}+\frac {M_{4}(t)}{t}. $$

Combining this with (3.2), for all $\omega\in\Omega'$ we obtain

$$\begin{aligned} \limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t} =&\limsup_{t\rightarrow \infty} \frac{1}{t} \int_{0}^{t} \biggl[c_{1}(s)- \frac {a_{13}(s)y(s)}{b_{1}(s)+b_{3}(s)y(s)} \biggr]\,\mathrm{d}s \\ \geq&\limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \biggl[c_{1}(s)- \frac {a_{13}(s)}{b_{3}(s)} \biggr]\,\mathrm{d}s>0. \end{aligned}$$

This contradicts the fact that $\limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t}\leq0$ in Lemma 2.2. So $(x(t))$ is weakly persistent.

In the following, we need to show that the predator $(y(t))$ is weakly persistent. Now consider the following auxiliary process with jumps:

$$\begin{aligned}& \mathrm{d}\phi(t)=\phi(t-) \bigl[ \bigl(a_{11}(t)-a_{12}(t) \phi(t-) \bigr)\,\mathrm{d}t+\sigma_{1}(t)\,\mathrm{d}B_{1}(t) \bigr] \\& \hphantom{\mathrm{d}\phi(t)={}}{}+ \int_{\mathbb{Y}}h_{1}(t,u)\phi(t-)\tilde{N}(\mathrm{d}t, \mathrm{d}u), \\& \phi(0)=x_{0}. \end{aligned}$$

Then by the comparison theorem [25], $\phi(t)\geq x(t)$ a.s. for all $t>0$, hence $\phi(t)$ will never reach 0. Then applying Itô’s formula, we have

$$\begin{aligned} \mathrm{d}\frac{1}{\phi(t)} =& \biggl[ \biggl(-a_{11}(t)+ \sigma_{1}^{2}(t)+ \int _{\mathbb{Y}} \biggl(\frac{1}{1+h_{1}(t,u)}-1+h_{1}(t,u) \biggr)\lambda(\mathrm{d}u) \biggr)\frac{1}{\phi(t)}+a_{12}(t) \biggr] \,\mathrm{d}t \\ &{}-\frac{1}{\phi(t)}\sigma_{1}(t)\,\mathrm{d}B_{1}(t)+ \int_{\mathbb{Y}}\frac{1}{\phi(t)} \biggl(\frac {1}{1+h_{1}(t,u)}-1 \biggr) \tilde{N}(\mathrm{d}t,\mathrm{d}u). \end{aligned}$$

By Lemma 4.1 in [10], we have

$$\begin{aligned} \frac{1}{\phi(t)} =&\exp \biggl( \int_{0}^{t}-c_{1}(s)\,\mathrm{d}s- \int _{0}^{t}\sigma_{1}(s)\, \mathrm{d}B_{1}(s)- \int_{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{1}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u) \biggr) \\ &{}\times \biggl[\frac{1}{x_{0}}+ \int_{0}^{t}\exp \biggl( \int _{0}^{s}c_{1}(r)\,\mathrm{d}r+ \int_{0}^{s}\sigma_{1}(r)\, \mathrm{d}B_{1}(r) \\ &{}+ \int_{0}^{s} \int_{\mathbb{Y}}\ln \bigl(1+h_{1}(r,u) \bigr)\tilde{N}( \mathrm{d}r,\mathrm{d}u) \biggr)a_{12}(s)\,\mathrm{d}s \biggr]. \end{aligned}$$

(3.3)

Furthermore, in view of the condition $\limsup_{t\rightarrow\infty}\frac {1}{t}\int_{0}^{t}c_{1}(s)\,\mathrm{d}s>0$, together with Theorem 4.4 in [10], there exists a constant T such that, for any $t\geq T$, $\frac{1}{\phi(t)}$ has an upper bound. On the other hand, applying Itô’s formula, we obtain

$$ \mathrm{d} \bigl(\ln\phi(t)-\ln x(t) \bigr)= \biggl(-a_{12}(t) \bigl( \phi(t)-x(t) \bigr)+\frac {a_{13}(t)y(t)}{b_{1}(t)+b_{2}(t)x(t)+b_{3}(t)y(t)} \biggr)\,\mathrm{d}t. $$

This further shows

$$ 0\leq\ln\phi(t)-\ln x(t)\leq-\hat{a}_{12} \int_{0}^{t} \bigl(\phi(s)-x(s) \bigr)\, \mathrm{d}s+ \int_{0}^{t}\frac{\check{a}_{13}}{\hat{b}_{1}}y(s)\,\mathrm{d}s, $$

that is,

$$ \int_{0}^{t} \bigl(\phi(s)-x(s) \bigr)\,\mathrm{d}s \leq\frac{\check{a}_{13}}{\hat {a}_{12}\hat{b}_{1}} \int_{0}^{t}y(s)\,\mathrm{d}s. $$

(3.4)

For the process $(y(t))$, together with (3.4), we have

$$\begin{aligned} \frac{\ln y(t)}{t} =&\frac{\ln y_{0}}{t}-\frac{1}{t} \int _{0}^{t}a_{22}(s)y(s)\,\mathrm{d}s+ \frac{1}{t} \int_{0}^{t} \biggl(c_{2}(s)+ \frac{a_{23}(s)\phi(s)}{b_{1}(s)+b_{2}(s)\phi(s)} \biggr)\,\mathrm{d}s \\ &{}-\frac{1}{t} \int_{0}^{t} \biggl(\frac{a_{23}(s)\phi (s)}{b_{1}(s)+b_{2}(s)\phi(s)}- \frac {a_{23}(s)x(s)}{b_{1}(s)+b_{2}(s)x(s)} \biggr)\,\mathrm{d}s \\ &{}-\frac{1}{t} \int_{0}^{t} \biggl(\frac {a_{23}(s)x(s)}{b_{1}(s)+b_{2}(s)x(s)}-g(s) \biggr) \,\mathrm{d}s \\ &{}+\frac{1}{t} \int_{0}^{t}\sigma_{2}(s)\, \mathrm{d}B_{2}(s)+\frac{1}{t} \int _{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{2}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u) \\ \geq&\frac{\ln y_{0}}{t}-\frac{1}{t} \int_{0}^{t} \biggl(a_{22}(s)+ \frac {a_{23}(s)b_{3}(s)}{b_{1}(s)b_{2}(s)} \biggr)y(s)\,\mathrm{d}s \\ &{}+\frac{1}{t} \int_{0}^{t} \biggl(c_{2}(s)+ \frac{a_{23}(s)\phi (s)}{b_{1}(s)+b_{2}(s)\phi(s)} \biggr)\,\mathrm{d}s-\frac{1}{t} \int_{0}^{t}\frac{a_{23}(s)(\phi (s)-x(s))}{b_{1}(s)+b_{2}(s)\phi(s)}\,\mathrm{d}s \\ &{} + \frac{1}{t} \int_{0}^{t}\sigma_{2}(s)\, \mathrm{d}B_{2}(s)+\frac{1}{t} \int _{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{2}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u) \\ \geq&\frac{\ln y_{0}}{t}-\frac{1}{t} \int_{0}^{t} \biggl(\check {a}_{22}+ \frac{\check{a}_{23}\check{b}_{3}}{\hat{b}_{1}\hat{b}_{2}} \biggr)y(s)\,\mathrm{d}s+\frac{1}{t} \int_{0}^{t}c_{2}(s)\,\mathrm{d}s+ \frac{\hat {a}_{23}}{b}\frac{1}{t} \int_{0}^{t}\frac{\phi(s)}{1+\phi(s)}\,\mathrm{d}s \\ &{}-\frac{1}{t} \int_{0}^{t}\frac{\check{a}_{23}(\phi(s)-x(s))}{\hat {b}_{1}}\,\mathrm{d}s+ \frac{1}{t} \int_{0}^{t}\sigma_{2}(s)\, \mathrm{d}B_{2}(s) \\ &{}+\frac{1}{t} \int_{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{2}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u) \\ \geq&\frac{\ln y_{0}}{t}-\frac{1}{t} \int_{0}^{t} \biggl(\check {a}_{22}+ \frac{\check{a}_{23}\check{b}_{3}}{\hat{b}_{1}\hat {b}_{2}}+\frac{\check{a}_{13}\check{a}_{23}}{\hat{a}_{12}\hat {b}^{2}_{1}} \biggr)y(s)\,\mathrm{d}s+\frac{1}{t} \int_{0}^{t}c_{2}(s)\,\mathrm{d}s \\ &{}+ \frac{\hat{a}_{23}}{b}\frac{1}{t} \int_{0}^{t}\frac{\phi(s)}{1+\phi (s)}\,\mathrm{d}s+ \frac{1}{t} \int_{0}^{t}\sigma_{2}(s)\, \mathrm{d}B_{2}(s) \\ &{}+\frac{1}{t} \int _{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{2}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u), \end{aligned}$$

from which it follows that

$$\begin{aligned}& \liminf_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \biggl(\check {a}_{22}+ \frac{\check{a}_{23}\check{b}_{3}}{\hat{b}_{1}\hat {b}_{2}}+\frac{\check{a}_{13}\check{a}_{23}}{\hat{a}_{12}\hat {b}^{2}_{1}} \biggr)y(s)\,\mathrm{d}s \\& \quad \geq \limsup_{t\rightarrow\infty} \biggl(\frac{1}{t} \int_{0}^{t}c_{2}(s)\,\mathrm{d}s+ \frac{\hat{a}_{23}}{b}\frac {1}{t} \int_{0}^{t}\frac{\phi(s)}{1+\phi(s)}\,\mathrm{d}s \biggr) -\limsup_{t\rightarrow\infty}\frac{\ln y(t)}{t}, \end{aligned}$$

where $b=\max\{\check{b}_{1},\check{b}_{2} \}$.

Here we have used the facts that

$$ \lim_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}\sigma_{2}(s)\, \mathrm{d}B_{2}(s)=0\quad \mbox{a.s.} $$

(3.5)

and

$$ \lim_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{2}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u)=0 \quad \mbox{a.s.}, $$

(3.6)

which are obtained in the same way for (3.2). By Lemma 2.2, we get

$$\begin{aligned}& \liminf_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \biggl(\check {a}_{22}+ \frac{\check{a}_{23}\check{b}_{3}}{\hat{b}_{1}\hat {b}_{2}}+\frac{\check{a}_{13}\check{a}_{23}}{\hat{a}_{12}\hat {b}^{2}_{1}} \biggr)y(s)\,\mathrm{d}s \\& \quad \geq \limsup_{t\rightarrow\infty} \biggl(\frac{1}{t} \int _{0}^{t}c_{2}(s)\,\mathrm{d}s+ \frac{\hat{a}_{23}}{b}\frac{1}{t} \int _{0}^{t}\frac{\phi(s)}{1+\phi(s)}\,\mathrm{d}s \biggr) \\& \quad \geq \limsup_{t\rightarrow\infty} \biggl(\frac{1}{t} \int _{0}^{t}c_{2}(s)\,\mathrm{d}s+ \frac{\hat{a}_{23}}{b}-\frac{\hat {a}_{23}}{b}\frac{1}{t} \int_{0}^{t}\frac{1}{\phi(s)}\,\mathrm{d}s \biggr) \\& \quad = \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}c_{2}(s)\,\mathrm{d}s+ \frac{\hat{a}_{23}}{b}-\limsup_{t\rightarrow\infty}\frac{\hat {a}_{23}}{b} \frac{1}{t} \int_{0}^{t}\frac{1}{\phi(s)}\,\mathrm{d}s. \end{aligned}$$

And furthermore

$$\begin{aligned} \liminf_{t\rightarrow\infty}\frac{1}{t} \int _{0}^{t}y(s)\,\mathrm{d}s \geq& \biggl( \check{a}_{22}+\frac{\check{a}_{23}\check{b}_{3}}{\hat{b}_{1}\hat {b}_{2}}+\frac{\check{a}_{13}\check{a}_{23}}{\hat{a}_{12}\hat {b}^{2}_{1}} \biggr)^{-1} \biggl(\limsup_{t\rightarrow\infty}\frac{1}{t} \int _{0}^{t}c_{2}(s)\,\mathrm{d}s+ \frac{\hat{a}_{23}}{b} \\ &{}-\limsup_{t\rightarrow\infty}\frac{\hat{a}_{23}}{b}\frac{1}{t} \int _{0}^{t}\frac{1}{\phi(s)}\,\mathrm{d}s \biggr) \\ >&0, \end{aligned}$$

which implies that we must have $\limsup_{t\rightarrow\infty}y(t)>0$ a.s. The proof is completed. □

Theorem 3.5

Let Assumption  A and (2.10) hold. If $\limsup_{t\rightarrow \infty}\frac{1}{t}\int_{0}^{t} [c_{1}(s)-\frac {a_{13}(s)}{b_{3}(s)} ]\,\mathrm{d}s>0$ and $\limsup_{t\rightarrow \infty}\frac{1}{t}\int_{0}^{t} [c_{2}(s)+\frac {a_{23}(s)}{b_{2}(s)} ]\,\mathrm{d}s<0$, then $\lim_{t\rightarrow\infty }y(t)=0$ and $\limsup_{t\rightarrow\infty}x(t)>0$.

Proof

First we show that $(y(t))$ goes to extinction. By Itô’s formula we have

$$\begin{aligned} \ln y(t) \leq&\ln y_{0}+ \int_{0}^{t} \biggl(c_{2}(s)+ \frac {a_{23}(s)}{b_{2}(s)} \biggr)\,\mathrm{d}s+ \int_{0}^{t}\sigma_{2}(s)\,\mathrm{d}B(s) \\ &{}+ \int_{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{2}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u) \end{aligned}$$

and, by (3.5) and (3.6),

$$ \limsup_{t\rightarrow\infty}\frac{\ln y(t)}{t}\leq \limsup _{t\rightarrow \infty}\frac{1}{t} \int_{0}^{t} \biggl(c_{2}(s)+ \frac {a_{23}(s)}{b_{2}(s)} \biggr)\,\mathrm{d}s< 0. $$

Hence $\lim_{t\rightarrow\infty}y(t)=0$ a.s.

Next, under the condition that $\lim_{t\rightarrow\infty}y(t)=0$ a.s., we shall show that we must have $\limsup_{t\rightarrow\infty}x(t)>0$ a.s. If this is not true, then $\mathbb{P}(\lim_{t\rightarrow\infty }x(t)=0)>0$ and there exists a measurable subset $\Omega_{0}$ of Ω such that $\mathbb{P}(\Omega_{0})>0$ and $\lim_{t\rightarrow\infty }x(t,\omega)=0$ for any $\omega\in\Omega_{0}$. On the flip side, for all $\omega\in\Omega_{0}$,

$$\begin{aligned} \limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t} =&\limsup_{t\rightarrow \infty} \frac{1}{t} \int_{0}^{t} \bigl(c_{1}(s)-a_{12}(s)x(s)-f(s) \bigr)\,\mathrm{d}s \\ =&\limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \biggl(c_{1}(s)- \frac{a_{13}(s)}{b_{3}(s)} \biggr)\,\mathrm{d}s>0, \end{aligned}$$

which implies that we must have $\limsup_{t\rightarrow\infty}x(t)>0$ a.s. The proof is completed. □

Remark 3.1

Theorems 3.2-3.5 have some interesting biological interpretations. It is readily to see that the extinction and persistence of the predator and prey have close relations with the jumps noise. The $\limsup_{t\rightarrow\infty}\frac{1}{t}\int _{0}^{t}c_{1}(s)\,\mathrm{d}s$ is the threshold between extinction and persistence for the predator-prey models. If $\limsup_{t\rightarrow \infty}\frac{1}{t}\int_{0}^{t}c_{1}(s)\,\mathrm{d}s<0$, i.e. the jump is relatively large

$$\biggl( \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)>a_{11}(t)-\frac{\sigma_{1}^{2}(t)}{2} \biggr), $$

the prey population goes to extinction, and then the predator population goes to extinction. That is to say, if the prey population goes to extinction, the predator will also go to extinction, which is consistent with biological significance. If $\limsup_{t\rightarrow\infty }\frac{1}{t}\int_{0}^{t}c_{1}(s)\,\mathrm{d}s=0$, i.e. the jump is relatively small,

$$\biggl( \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)=a_{11}(t)-\frac{\sigma_{1}^{2}(t)}{2} \biggr), $$

the prey population is nonpersistent in the mean. On the other hand, since $c_{2}(t)<0$, in order to see that the predator population is nonpersistent in the mean, the jump noise is required to satisfy

$$\limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \biggl(c_{2}(s)+ \frac {a_{23}(s)}{b_{2}(s)} \biggr)\,\mathrm{d}s=0. $$

Remark 3.2

When $\limsup_{t\rightarrow\infty}\frac{1}{t}\int_{0}^{t} (c_{1}(s)-\frac{a_{13}(s)}{b_{3}(s)} )\,\mathrm{d}s>0$, the prey population is weakly persistent. This shows that when the jump noise is smaller than the above, the prey population will not go extinct. The weak persistence of predator has close ties to the process $(\phi(t))$ expected for the jump noise. In fact, from a viewpoint of biology, this is reasonable. If the predator population is weakly persistent, the prey population is weakly persistent. In Theorem 3.4, note the following facts:

$$\begin{aligned}& \frac{\ln y(t)}{t}= \frac{\ln y_{0}}{t}+\frac{1}{t} \int _{0}^{t} \bigl[c_{2}(s)-a_{22}(s)y(s)+g(s) \bigr]\,\mathrm{d}s+\frac{1}{t} \int _{0}^{t}\sigma_{2}(s)\, \mathrm{d}B(s) \\& \hphantom{\frac{\ln y(t)}{t}={}}{}+\frac{1}{t} \int_{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{2}(s,u) \bigr)\tilde {N}( \mathrm{d}s,\mathrm{d}u), \\& \lim_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}\sigma_{2}(s)\, \mathrm{d}B(s)=0\quad \mbox{a.s.}, \end{aligned}$$

and

$$ \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \int_{\mathbb{Y}}\ln \bigl(1+h_{2}(s,u) \bigr)\tilde{N}( \mathrm{d}s,\mathrm{d}u)=0\quad \mbox{a.s.} $$

If $\mathbb{P}(\lim_{t\rightarrow\infty}x(t)=0)>0$, then we must have $\mathbb{P}(\limsup_{t\rightarrow\infty}\frac{\ln y(t)}{t}<0)>0$. Therefore, the predator $(y(t))$ is weakly persistent implies that the prey $(x(t))$ is weakly persistent.

Remark 3.3

When

$$\limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \biggl(c_{1}(s)- \frac{a_{13}(s)}{b_{3}(s)} \biggr)\,\mathrm{d}s>0 $$

and

$$\limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \biggl(c_{2}(s)+ \frac {a_{23}(s)}{b_{2}(s)} \biggr)\,\mathrm{d}s< 0, $$

the predator population goes to extinction, and then the prey population will be weakly persistent. In real life, when one or more predator animals become extinct, there is an increase of the animals that they use for food.

Remark 3.4

There is another definition of persistence for stochastic population models, which has attracted a lot of authors. Liu-Bai [26] proposed the concept of stochastically persistent in probability: there is a unique invariant probability measure μ such that $\mu(\Delta _{0})=0$ and the distribution of $X(t)$ converges to μ as $t \rightarrow\infty$ whenever $X(0) \in\mathbb{R}_{+}^{n}$, where $\Delta _{0}=\{a\in\mathbb{R}_{+}^{n}|a_{i}=0\mbox{ for some }i, 1\leq i\leq n\}$. We can refer to Tong et al. [27] with regard to the stochastically persistent in probability of (1.1). For any initial value $Z(0)=(x_{0},y_{0})\in\mathbb{R}^{2}_{+}$, let $p(t, Z(0), \cdot)$ be the transition probability of $X(t)$. According to Chebyshev’s inequality, Theorem 2.2, and the Krylov-Bogoliubov theorem [28], there exists an invariant probability measure μ for the solution $Z(t)=(x(t), Y(t))$ of Eq. (1.1) such that

$$ p \bigl(t, Z(0), \cdot \bigr)\rightarrow\mu(\cdot), \quad \mbox{as }t\rightarrow \infty. $$

On the other hand, under the conditions of Theorem 2.2, using the truncation technique as [27] and Theorem 5.1 in [29], the model (1.1) has the Feller property. Moreover, by the same discussion as that of Theorem 3.1 in Tong et al. [27], one can easily infer that μ is unique. Consequently, the model (1.1) is also stochastically persistent in probability.

4 Numerical simulations

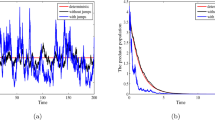
In this section, in order to testify the validity of the main results, the following example and simulations are introduced. Let $x_{0}=2.5$, $y_{0}=2.2$, $a_{11}(t)=0.81$, $a_{12}(t)=a_{22}(t)=0.45+0.2\sin(t)$, $a_{13}(t)=0.06$, $b_{1}(t)=0.1$, $b_{2}(t)=0.2$, $b_{3}(t)=1$, $\sigma _{1}(t)=1.2$, $\sigma_{2}(t)=0.8$, $a_{21}(t)=0.21$, $a_{23}(t)=0.1876$, $\lambda(\mathbb{Y})=1$, and the step size $\Delta t=0.01$. The only difference between Figures 1-4 is that the values of $h_{i}$ ($i=1,2$) are different. In Figure 1, we choose $h_{1}(t,u)=\mathrm{e}-1$, then by a simple calculation, we have

$$ \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)=\mathrm{e}-2 $$

and

$$ c_{1}(t)=a_{11}(t)-\frac{\sigma_{1}^{2}(t)}{2}- \int_{\mathbb {Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)=-0.61< 0. $$

Then in virtue of Theorem 3.2, all the species go to extinction, and Figure 1 confirms this. In Figure 2, we choose $h_{1}(t,u)=0.4863$ and $h_{2}(t,u)=1.1935$, then by a simple calculation, we have

$$\begin{aligned}& \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)=0.09, \\& \int_{\mathbb{Y}} \bigl[h_{2}(t,u)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)=0.408, \end{aligned}$$

and

$$\begin{aligned}& c_{1}(t) =a_{11}(t)-\frac{\sigma_{1}^{2}(t)}{2}- \int_{\mathbb {Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)=0, \\& c_{2}(t) =a_{21}(t)-\frac{\sigma_{2}^{2}(t)}{2}- \int_{\mathbb {Y}} \bigl[h_{2}(t,u)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)=0. \end{aligned}$$

In view of Theorem 3.3, it is readily seen that the prey $(x(t))$ and the predator $(y(t))$ will be nonpersistent in the mean. In Figure 3, we choose $h_{1}(t,u)=h_{2}(t,u)=0.2406$, then by a simple calculation, we have

$$ \int_{\mathbb{Y}} \bigl[h_{i}(t,u)-\ln \bigl(1+h_{i}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)=0.025,\quad i=1,2, $$

and

$$\begin{aligned}& c_{1}(t)-\frac{a_{13}(t)}{b_{3}(t)}=a_{11}(t)-\frac{\sigma _{1}^{2}(t)}{2}- \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda (\mathrm{d}u)-\frac{a_{13}(t)}{b_{3}(t)} \\& \hphantom{c_{1}(t)-\frac{a_{13}(t)}{b_{3}(t)}}=0.005>0, \\& c_{2}(t)+\frac {a_{23}(t)}{b}=a_{21}(t)-\frac{\sigma_{2}^{2}(t)}{2}- \int_{\mathbb {Y}} \bigl[h_{2}(t,u)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)\frac {a_{23}(t)}{b}=0.383, \\& \frac{\hat{a}_{23}}{b}\limsup_{t\rightarrow\infty}\frac{1}{t} \int _{0}^{t}\frac{1}{\phi(s)}\,\mathrm{d}s \leq0.938\times0.4=0.3752. \end{aligned}$$

Then it confirms the conditions of Theorem 3.4. And it is easy to see that the prey $(x(t))$ and the predator $(y(t))$ will be weakly persistent from Figure 3. In Figure 4, we choose $h_{1}(t,u)=0.2406$, $h_{2}(t,u)=\mathrm{e}-1$, by a simple calculation, we have

$$ \int_{\mathbb{Y}} \bigl[h_{i}(t,u)-\ln \bigl(1+h_{i}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)=0.025,\quad i=1,2, $$

and

$$\begin{aligned}& c_{1}(t)-\frac{a_{13}(t)}{b_{3}(t)}=a_{11}(t)-\frac{\sigma _{1}^{2}(t)}{2}- \int_{\mathbb{Y}} \bigl[h_{1}(t,u)-\ln \bigl(1+h_{1}(t,u) \bigr) \bigr]\lambda (\mathrm{d}u)-\frac{a_{13}(t)}{b_{3}(t)} \\& \hphantom{c_{1}(t)-\frac{a_{13}(t)}{b_{3}(t)}}=0.005>0, \\& c_{2}(t)+\frac {a_{23}(t)}{b_{3}(t)}=a_{21}(t)-\frac{\sigma_{2}^{2}(t)}{2}- \int _{\mathbb{Y}} \bigl[h_{2}(t,u)-\ln \bigl(1+h_{2}(t,u) \bigr) \bigr]\lambda(\mathrm{d}u)\frac {a_{23}(t)}{b_{3}(t)} \\& \hphantom{c_{2}(t)+\frac {a_{23}(t)}{b_{3}(t)}}=2.408-\mathrm{e}< 0. \end{aligned}$$

Then by Theorem 3.5, it is easy to see that the prey $(x(t))$ will be weakly persistent and the predator $(y(t))$ will be extinctive from Figure 4.

Figure 1

Solutions of system ( 1.1 ) for $\pmb{x_{0}=2.5}$ , $\pmb{y_{0}=2.2}$ , $\pmb{a_{11}(t)=0.81}$ , $\pmb{a_{12}(t)=a_{22}(t)=0.45+0.2\sin(t)}$ , $\pmb{a_{13}(t)=0.06}$ , $\pmb{b_{1}(t)=0.1}$ , $\pmb{b_{2}(t)=0.2}$ , $\pmb{b_{3}(t)=1}$ , $\pmb{\sigma_{1}(t)=1.2}$ , $\pmb{\sigma_{2}(t)=0.8}$ , $\pmb{a_{21}(t)=0.21}$ , $\pmb{a_{23}(t)=0.1876}$ , $\pmb{h_{1}(t,u)=\mathrm{e}-1}$ , $\pmb{\lambda(\mathbb{Y})=1}$ , and the step size $\pmb{\Delta t=0.01}$ .

Figure 2

Solutions of system ( 1.1 ) for $\pmb{x_{0}=2.5}$ , $\pmb{y_{0}=2.2}$ , $\pmb{a_{11}(t)=0.81}$ , $\pmb{a_{12}(t)=a_{22}(t)=0.45+0.2\sin(t)}$ , $\pmb{a_{13}(t)=0.06}$ , $\pmb{b_{1}(t)=0.1}$ , $\pmb{b_{2}(t)=0.2}$ , $\pmb{b_{3}(t)=1}$ , $\pmb{\sigma_{1}(t)=1.2}$ , $\pmb{\sigma_{2}(t)=0.8}$ , $\pmb{a_{21}(t)=0.21}$ , $\pmb{a_{23}(t)=0.1876}$ , $\pmb{\lambda (\mathbb{Y})=1}$ , and the step size $\pmb{\Delta t=0.01}$ , $\pmb{h_{1}(t,u)=0.4863}$ and $\pmb{h_{2}(t,u)=1.1935}$ .

Figure 3

Solutions of system ( 1.1 ) for $\pmb{x_{0}=2.5}$ , $\pmb{y_{0}=2.2}$ , $\pmb{a_{11}(t)=0.81}$ , $\pmb{a_{12}(t)=a_{22}(t)=0.45+0.2\sin(t)}$ , $\pmb{a_{13}(t)=0.06}$ , $\pmb{b_{1}(t)=0.1}$ , $\pmb{b_{2}(t)=0.2}$ , $\pmb{b_{3}(t)=1}$ , $\pmb{\sigma_{1}(t)=1.2}$ , $\pmb{\sigma_{2}(t)=0.8}$ , $\pmb{a_{21}(t)=0.21}$ , $\pmb{a_{23}(t)=0.1876}$ , $\pmb{\lambda (\mathbb{Y})=1}$ , and the step size $\pmb{\Delta t=0.01}$ , $\pmb{h_{1}(t,u)=h_{2}(t,u)=0.2406}$ .

Figure 4

Solutions of system ( 1.1 ) for $\pmb{x_{0}=2.5}$ , $\pmb{y_{0}=2.2}$ , $\pmb{a_{11}(t)=0.81}$ , $\pmb{a_{12}(t)=a_{22}(t)=0.45+0.2\sin(t)}$ , $\pmb{a_{13}(t)=0.06}$ , $\pmb{b_{1}(t)=0.1}$ , $\pmb{b_{2}(t)=0.2}$ , $\pmb{b_{3}(t)=1}$ , $\pmb{\sigma_{1}(t)=1.2}$ , $\pmb{\sigma_{2}(t)=0.8}$ , $\pmb{a_{21}(t)=0.21}$ , $\pmb{a_{23}(t)=0.1876}$ , $\pmb{\lambda (\mathbb{Y})=1}$ , and the step size $\pmb{\Delta t=0.01}$ , $\pmb{h_{1}(t,u)=0.2406}$ , $\pmb{h_{2}(t,u)=\mathrm{e}-1}$ .

5 Conclusion

In this work we propose a predator-prey model of a Beddington-DeAngelis type functional response with Lévy jumps. We show that the model admits a unique global positive solution, and we study the stochastically boundedness and other asymptotic properties of solutions. Moreover, we provide the sufficient conditions for extinction, nonpersistence in the mean and weak persistence of this models. The results confirm that the intensity of jump noise has a grave impact on the properties of this model. In the future, we will propose some more practical and complex models such as considering the hybrid system driven by continuous time Markov chains into the system (see e.g. [16]). More specifically, consider the following regime-switching predator-prey model of Beddington-DeAngelis type functional response with Lévy jumps:

$$ \left \{ \textstyle\begin{array}{l} \mathrm{d}x(t)= x(t-) [ (a_{11}(\Lambda(t))-a_{12}(\Lambda(t))x(t-)-\frac {a_{13}(\Lambda(t))y(t-)}{b_{1}(\Lambda(t))+b_{2}(\Lambda (t))x(t-)+b_{3}(\Lambda(t))y(t-)} )\,\mathrm{d}t \\ \hphantom{\mathrm{d}x(t)={}}{}+\sigma_{1}(\Lambda(t))dB_{1}(t) ]+\int_{\mathbb{Y}}h_{1}(\Lambda (t),u)x(t-)\tilde{N}(\mathrm{d}t,\mathrm{d}u), \\ \mathrm{d}y(t)= y(t-) [ (-a_{21}(\Lambda(t))-a_{22}(\Lambda(t))y(t-)+\frac {a_{23}(\Lambda(t))x(t-)}{b_{1}(\Lambda(t))+b_{2}(\Lambda (t))x(t-)+b_{3}(\Lambda(t))y(t-)} )\,\mathrm{d}t \\ \hphantom{\mathrm{d}y(t)={}}{}+\sigma_{2}(\Lambda(t))dB_{2}(t) ]+\int_{\mathbb{Y}}h_{2}(\Lambda (t),u)y(t-)\tilde{N}(\mathrm{d}t,\mathrm{d}u). \end{array}\displaystyle \right . $$