1 Introduction

The role played by second-order system in the dynamics of physical and biological systems has been an issue of growing interest and discussion. Recent research has also focused on the relative dominance of existence, uniqueness, and stability behavior of second-order systems [1–5].

In the real world, noise plays an important role in comprehending phenomena that can be very hard to describe by deterministic systems. The dynamical behavior of stochastic partial differential systems (SPDSs) has been discussed [6–11]. Sakthivel et al. [12, 13] studied pseudo almost automorphic mild solutions to stochastic fractional equations by a fixed point strategy and discussed complete controllability of stochastic evolution equations with jumps, respectively. Recently, [14, 15] discussed the existence, uniqueness, and stability of mild solutions to stochastic neutral partial functional systems (SNPFSs). Meanwhile, second-order SPDSs [16] are often used to model charge on a condenser, mechanical vibrations, etc. Liang and Guo [17] discussed the asymptotic behavior for second-order stochastic evolution equations with memory. Sakthivel and Ren [18] studied exponential stability of second-order stochastic evolution equations with Poisson jumps by fixed point theory. In addition, since sudden variations often exist in practice, it is necessary to model the noise source by a sequence of impulses. For instance, the stability for first-order impulsive SPDSs was discussed by using integral inequalities in [19–21]. The authors in [22–24] discussed the existence, controllability, and stability of mild solutions of second-order impulsive stochastic systems.

The papers mentioned above focus on stochastic systems with finite delays. Recently, the study of stochastic systems with infinite delay [25–29] has also been reported. For example, Ren and Sakthivel [30] discussed existence, uniqueness, and stability of a mild solution for second-order neutral stochastic evolution systems with infinite delay and Poisson jumps by fixed point theory. Yue [31] discussed the existence of mild solutions of second-order neutral impulsive stochastic evolution systems with infinite delay by contraction theory. The authors in [32, 33] extended second-order stochastic systems with infinite delay to second-order jump systems and second-order integro-differential systems.

With motivation from the above discussions, in order to overcome the difficulty of impulses and infinite delays, in this paper we first establish a new integral inequality with respect to impulses and infinite delays, which makes an important contribution to stability analysis of the second-order SNPFSs subject to infinite delays and impulses. The integral inequality is new and different from the above papers since the impulses and infinite delays exist in the system. The inequality with finite delays in [19–21, 24] is extended to the inequality with infinite delays and impulses such that it is effective for the stochastic systems with infinite delays and impulses. By the new inequality, together with the stochastic analysis technique, some sufficient conditions for stability are obtained.

The rest of this paper is organized as follows. In Section 2, some preliminaries are introduced. Section 3 presents stability results by establishing a new integral inequality with impulses and infinite delays and stochastic analysis technique. In Section 4, we give an example to show the effectiveness of the obtained results.

2 Preliminaries

In this paper, \((\Omega,\mathfrak{F},\{\mathfrak{F}_{t}\}_{t\geq0},\mathcal{P})\) is a complete probability space equipped with some filtration \(\mathfrak{F}_{t}\) (\(t\geq0\)) satisfying the usual conditions, i.e., the filtration is right continuous and \(\mathfrak{F}_{0}\) contains all \(\mathfrak{F}\)-null sets. Let \({\Xi_{1}}\) and \({\Xi_{2}}\) be two real separable Hilbert spaces and \(L({\Xi_{2}},{\Xi_{1}})\) be the space of bounded linear operators from \({\Xi_{2}}\) to \({\Xi_{1}}\). \(\|\cdot\|\) denotes the norms in \({\Xi_{1}}, {\Xi_{2}}\), and \(L({\Xi _{2}},{\Xi_{1}})\). \(\mathcal{C}((-\infty,0], {\Xi_{1}})\) is the space of all bounded and continuous functions φ from \((-\infty,0]\) to \({\Xi_{1}}\) with the norm \(\|\cdot\|_{\mathcal{C}}=\sup_{-\infty< \theta\leq 0}\|\varphi(\theta)\|\). \(\frak {J}\) is the family of all \(\mathfrak{F}_{t}\) (\(t\geq0\))-measurable and \(\mathcal{C}((-\infty,0],{\Xi_{1}})\)-valued random variables. Let the stochastic process \(w(t)\) be a Q-Wiener process and \(\sigma\in L({\Xi_{2}},{\Xi_{1}})\) be a Q-Hilbert-Schmidt operator with \(\|\sigma\|_{L_{2}^{0}}^{2}=\operatorname{tr}(\sigma Q\sigma^{*})<+\infty\). \(L_{2}^{0}({\Xi _{2}},{\Xi_{1}})\) denotes the space of all Q-Hilbert- Schmidt operators \(\sigma: {\Xi _{2}}\rightarrow {\Xi_{1}}\). For details, we can refer to [6] and the references therein.

Consider the following second-order stochastic neutral partial functional systems (SNPFSs) subject to infinite delays and impulses:

$$ \left \{ \textstyle\begin{array}{@{}l} d[y'(t)-\mu(t,y_{t})]=[Ay(t)+f(t, y_{t})]\,dt +g(t, y_{t})\,dw(t),\quad t\ge0, t\neq t_{j}, j=1,2,\ldots,\\ \Delta y(t_{j})=I_{j}(y(t_{j}^{-})),\quad j=1,2,\ldots,\\ \Delta y'(t_{j})={\widetilde{I}}_{j}(y(t_{j}^{-})),\quad j=1,2,\ldots,\\ y_{0}(\cdot)=\varphi\in\frak {J}, \qquad y'(0)=\Phi, \end{array}\displaystyle \right . $$
(1)

where Φ is also an \(\mathfrak{F}_{0}\)-measurable \({\Xi_{1}}\)-valued random variable independent of the Wiener process \(w(t)\). \(A: D(A)\subset{\Xi_{1}}\rightarrow{\Xi_{1}}\) is the infinitesimal generator of a strongly continuous cosine family on \({\Xi_{1}}\); \(f, \mu: [0,+\infty)\times\frak {J}\rightarrow{\Xi_{1}}\), \(g: [0,+\infty)\times\frak {J}\rightarrow L_{2}^{0}({\Xi_{2}},{\Xi_{1}})\), \(y_{t}: (-\infty,0]\rightarrow{\Xi_{1}}\), \(y_{t}(\theta)=y(t+\theta)\) (\(t\geq 0\)), \(0< t_{1}< t_{2}<\cdots<t_{j}<\cdots\), and \(\lim_{j\rightarrow+\infty}t_{j}=+\infty\). \(I_{j}, {\widetilde{I}}_{j}: \frak {J}\rightarrow H\), \(\vartriangle\xi(t)=\xi(t^{+})-\xi(t^{-})\), where \(\xi(t^{+})\) and \(\xi(t^{-})\) denote the right and left limits of ξ at t, respectively.

Let \(\{C(t): t\in R\}\subset L({\Xi_{1}},{\Xi_{1}})\) be a strongly continuous cosine family (see [5] and the references therein) and the corresponding strongly continuous sine family \(\{S(t): t\in R\}\subset L({\Xi_{1}},{\Xi_{1}})\) be defined by \(S(t)y=\int _{0}^{t}C(s)y\,ds, t\in R, y\in{\Xi_{1}}\). The generator \(A: {\Xi_{1}}\rightarrow{\Xi_{1}}\) of \(\{C(t): t\in R\}\) is defined by \(Ay=\frac{d^{2}}{dt^{2}}C(t)y|_{t=0}\) for all \(y\in D(A)=\{y\in{\Xi_{1}}: C(\cdot)y\in C^{2}(R,{\Xi_{1}})\}\).

Lemma 1

([31])

Let A be the infinitesimal generator of a cosine family of operators \(\{C(t): t\in R\}\). Then:

  1. (i)

    There exist \(\delta^{*}\geq1\) and \(\beta\geq0\) such that \(\Vert C(t)\Vert \leq\delta^{*}e^{\beta t}\) and hence \(\Vert S(t)\Vert \leq\delta^{*} e^{\beta t}\).

  2. (ii)

    For \(0\leq s\leq r<+\infty\), \(A\int_{s}^{r}S(u)y\,du=[C(r)-C(u)]y\).

  3. (iii)

    There exists \(\delta^{**}\geq1\) such that for \(0\leq r\leq s<+\infty\) \(\Vert S(s)-S(r)\Vert \leq \delta^{**} |\int_{r}^{s}e^{\beta|\theta|}\,d\theta|\).

Lemma 2

([6])

For any \(p\geq1\) and for an \(L^{0}_{2}({\Xi_{2}},{\Xi_{1}})\)-valued predictable process \(y(\cdot)\) we have

$$\sup_{s\in[0,t]}E\biggl\Vert \int_{0}^{s}y(v)\,dw(v)\biggr\Vert ^{p} \leq c_{p} \biggl( \int_{0}^{t}\bigl(E\bigl\Vert y(v)\bigr\Vert _{L_{2}^{0}}^{p}\bigr)^{\frac{2}{p}}\,dv \biggr)^{p/2}, \quad t\in[0,+\infty), $$

where \(c_{p}=(p(p-1)/2)^{p/2}\).

Definition 1

An \({\Xi_{1}}\)-value stochastic process \(y(t)\) (\(t\in R\)) is called a mild solution of system (1), if

  1. (i)

    \(y(t)\) is adapted to \(\mathfrak{F}_{t} \) (\(t\geq0\)) and has a càdlàg path on \(t\geq0\) almost surely.

  2. (ii)

    For \(t\in[0,+\infty)\), almost surely

    $$\begin{aligned} y(t) =&C(t)\varphi+S(t) \bigl(\xi-\mu(0,{\varphi})\bigr)+ \int_{0}^{t}C(t-\nu)\mu(\nu ,y_{\nu})\,d\nu \\ &{}+ \int_{0}^{t}S(t-\nu)f(\nu,y_{\nu})\,d\nu+ \int_{0}^{t}S(t-\nu)g(\nu,y_{\nu})\,dw(\nu ) \\ &{}+\sum_{0< t_{j}< t}C(t-t_{j})I_{j} \bigl(y\bigl(t_{j}^{-}\bigr)\bigr)+\sum_{0< t_{j}< t}S(t-t_{j}){ \widetilde{I}}_{j}\bigl(y\bigl(t_{j}^{-}\bigr)\bigr). \end{aligned}$$
    (2)

Definition 2

We say there is a mild solution of system (1), or for simplicity system (1) is said to be pth (\(p\geq2\)) moment exponentially stable, if there exist constants \(\gamma>0\) and \(N_{1}> 0\) such that

$$E\bigl\Vert y(t)\bigr\Vert ^{p}\leq N_{1} e^{-\gamma t}, \quad t\geq0, p\geq2, $$

for the initial data \(\varphi\in\frak {J}\).

3 Main results

In the section, we will establish exponential stability of system (1) by some integral inequalities. Thus we need to employ the following assumptions:

(A1):

For some constants \(\alpha\geq1\), \(a>0\), and \(b>0\), \(\Vert C(t)\Vert \leq\alpha e^{-bt}\) and \(\Vert S(t)\Vert \leq\alpha e^{-at}\), \(t\geq0\).

(A2):

There exist constants \(L_{i}>0\) (\(i=0,1,2\)) and a function \(\kappa: (-\infty,0]\rightarrow[0,+\infty)\) with \(\int _{-\infty}^{0}\kappa(t)\,dt=1\) and \(\int_{-\infty}^{0}\kappa(t)e^{-\hbar t}\,dt<+\infty \) for \(\hbar>0\), such that

$$\begin{aligned}& \bigl\Vert \mu(t,y_{1})-\mu(t,y_{2})\bigr\Vert \leq L_{0} \int_{-\infty}^{0}\kappa(\vartheta)\bigl\Vert y_{1}(t+\vartheta)-y_{2}(t+\vartheta)\bigr\Vert \,d \vartheta, \\& \bigl\Vert f(t,y_{1})-f(t,y_{2})\bigr\Vert \leq L_{1} \int_{-\infty}^{0}\kappa(\vartheta)\bigl\Vert y_{1}(t+\vartheta)-y_{(}t+\vartheta)\bigr\Vert \,d\vartheta, \\& \bigl\Vert g(t,y_{1})-g(t,y_{2})\bigr\Vert _{\frak {L}_{2}^{0}}\leq L_{2} \int_{-\infty}^{0}\kappa (\vartheta)\bigl\Vert y_{1}(t+\vartheta)-y_{2}(t+\vartheta)\bigr\Vert \,d \vartheta, \end{aligned}$$

and \(\mu(t,0)=f(t,0)= g(t,0)=0\) for any \(y_{1},y_{2}\in\frak {J}\) and \(t\geq0\).

(A3):

For \(y_{1}, y_{2}\in{\Xi_{1}}\) and \(\sum_{j=1}^{+\infty}\alpha_{j}<+\infty, \sum_{j=1}^{+\infty}\beta_{j}<+\infty\), there exist positive numbers \(\alpha_{j}, \beta_{j} \) (\(j=1,2,\ldots\)) such that

$$\begin{aligned}& \bigl\Vert I_{j}(y_{1})-I_{j}(y_{2}) \bigr\Vert \le\alpha_{j}\Vert y_{1}-y_{2} \Vert , \\& \bigl\Vert {\widetilde{I}}_{j}(y_{1})-{ \widetilde{I}}_{j}(y_{2})\bigr\Vert \le\beta_{j} \Vert y_{1}-y_{2}\Vert , \end{aligned}$$

and \(I_{j}(0)={\widetilde{I}}_{j}(0)=0\).

Remark 1

References [8, 31] discussed the existence of mild solutions of second-order stochastic neutral partial functional equations with infinite delay or with finite delay, respectively. Similarly, we can show that for system (1) there exists a unique mild solution under the conditions (A1)-(A3). Also, it is obvious that system (1) has a unique trivial mild solution when the initial value \(\varphi=0\).

To obtain exponential stability of system (1), we first establish the following integral inequality with impulses and infinite delays.

Lemma 3

Suppose that \(\eta_{1}, \eta_{2}\in(0, \hbar]\) and there exist constants \(\zeta_{i}>0 \) (\(i=1,2,3,4\)) and a function \(\Psi: R \rightarrow[0,+\infty)\) such that \(\frac{\zeta_{3}}{\eta_{1}}+\frac{\zeta_{4}}{\eta_{2}}+\sum_{j=1}^{+\infty}(a_{j}+b_{j})<1\), and

$$ \Psi(t)\leq \left \{ \textstyle\begin{array}{@{}l} \zeta_{1} e^{-\eta_{1} t}+\zeta_{2}e^{-\eta_{2} t}+\zeta_{3} \int_{0}^{t}e^{-\eta_{1}(t-s)}\int_{-\infty}^{0}\kappa(\vartheta)\Psi (s+\vartheta)\,d\vartheta\,ds\\ \quad{} +\zeta_{4}\int_{0}^{t}e^{-\eta_{2}(t-s)} \int_{-\infty}^{0}\kappa(\vartheta)\Psi(s+\vartheta)\,d\vartheta \,ds\\ \quad{} + \sum_{t_{j}< t}a_{j}e^{-\eta_{1} (t-t_{j})}\Psi (t_{j}^{-}) + \sum_{t_{j}< t}b_{j}e^{-\eta_{2} (t-t_{j})}\Psi(t_{j}^{-}), \quad t\geq 0,\\ \zeta_{1} e^{-\eta_{1} t} +\zeta_{2}e^{-\eta_{2} t}, \quad t\in(-\infty,0], \end{array}\displaystyle \right . $$
(3)

holds. Then \(\Psi(t)\leq N_{2}e^{-\delta t}, t\in(-\infty,+\infty)\), where \(\delta\in(0,\eta_{1}\wedge\eta_{2})\) is a root of the integral equation: \((\frac{\zeta_{3}}{\eta_{1}-\delta}+\frac{\zeta_{4}}{\eta_{2}-\delta } )\int_{-\infty}^{0}\kappa(\vartheta)e^{-\delta\vartheta}\,d\vartheta +\sum_{j=1}^{+\infty}(a_{j}+b_{j})=1\) \(and\) \(N_{2}=\max \{\zeta_{1}+\zeta_{2}, \frac{\zeta_{1}(\eta_{1}-\delta)}{\zeta _{3}\int_{-\infty}^{0}\kappa(\vartheta)e^{-\delta\vartheta}\,d\vartheta}, \frac{\zeta_{2}(\eta_{2}-\delta)}{\zeta_{4}\int_{-\infty}^{0}\kappa(\vartheta )e^{-\delta\vartheta}\,d\vartheta} \}>0\).

Proof

Let \(F(\zeta)= (\frac{\zeta_{3}}{\eta_{1}-\zeta}+\frac{\zeta_{4}}{\eta _{2}-\zeta} )\int_{-\infty}^{0}\kappa (\vartheta)e^{-\zeta\vartheta}\,d\vartheta +\sum_{j=1}^{+\infty}(a_{j}+b_{j})-1\), then it is obvious that there exists a positive constant \(\delta\in(0,\eta_{1}\wedge\eta_{2})\), such that \(F(\delta)=0\).

For any \(\varepsilon>0\) and let

$$\begin{aligned} N_{\varepsilon} =\max \biggl\{ \zeta_{1}+ \zeta_{2}+\varepsilon,\frac{(\eta_{1}-\delta)(\zeta _{1}+\varepsilon)}{\zeta_{3}\int_{-\infty}^{0}\kappa (\vartheta)e^{-\delta\vartheta}\,d\vartheta}, \frac{(\eta_{2}-\delta)(\zeta_{2}+\varepsilon)}{\zeta_{4}\int_{-\infty }^{0}\kappa (\vartheta)e^{-\delta\vartheta}\,d\vartheta} \biggr\} >0. \end{aligned}$$
(4)

Now we only need to claim that (3) implies

$$\begin{aligned} \Psi(t)\leq N_{\varepsilon}e^{- \delta t}, \quad t\in(- \infty,+\infty). \end{aligned}$$
(5)

Obviously, for \(t\in(-\infty,0]\), (5) holds. Next we will prove (5) by the contradiction method. Assume that there exists a \(t_{1}>0\) such that

$$\begin{aligned} \Psi(t)< N_{\varepsilon}e^{-\delta t}, \quad t\in(- \infty,t_{1}),\qquad \Psi (t_{1})=N_{\varepsilon}e^{-\delta t_{1}}. \end{aligned}$$
(6)

Note that \(\delta\in(0,\eta_{1}\wedge\eta_{2})\), from (3) we have

$$\begin{aligned} \Psi(t_{1}) \leq&\zeta_{1} e^{-\eta_{1} t_{1}}+ \zeta_{2}e^{-\eta_{2} t_{1}}+\zeta_{3}N_{\varepsilon}\int_{0}^{t_{1}} e^{-\eta_{1}(t_{1}-s)} \int_{-\infty}^{0}\kappa(\vartheta)e^{-\delta (s+\vartheta)}\,ds \\ &{} +\zeta_{4}N_{\varepsilon}\int_{0}^{t_{1}}e^{-\eta_{2} (t_{1}-s)} \int_{-\infty }^{0} \kappa(\vartheta)e^{-\delta(s+\vartheta)}\,d \vartheta \,ds \\ &{}+ N_{\varepsilon}\sum_{t_{j}< t}a_{j}e^{-\eta_{1} (t_{1}-t_{j})}e^{-\delta t_{j}} + N_{\varepsilon}\sum_{t_{j}< t}b_{j}e^{-\eta_{2} (t_{1}-t_{j})}e^{-\delta t_{j}} \\ \le& \biggl(\zeta_{1}-\frac{N_{\varepsilon}\zeta_{3}}{\eta_{1}-\delta} \int _{-\infty}^{0}\kappa (\vartheta)e^{-\delta\vartheta}\,d \vartheta \biggr) e^{-\eta_{1}t_{1}}+ \biggl(\zeta_{2}-\frac{N_{\varepsilon}\zeta_{4}}{\eta_{2}-\delta } \int_{-\infty}^{0}\kappa(\vartheta)e^{-\delta\vartheta}\,d \vartheta \biggr)e^{-\eta_{2}t_{1}} \\ &{}+ \Biggl(\frac{\zeta_{3}}{\eta_{1}-\delta} \int_{-\infty}^{0}\kappa (\vartheta)e^{-\delta\vartheta}\,d \vartheta +\frac{\zeta_{4}}{\eta_{2}-\delta} \int_{-\infty}^{0}\kappa(\vartheta )e^{-\delta\vartheta}\,d \vartheta \\ &{}+ \sum_{j=1}^{+\infty}(a_{j}+b_{j}) \Biggr)N_{\varepsilon}e^{-\delta t_{1}}. \end{aligned}$$
(7)

By (4), we have

$$\begin{aligned} \zeta_{1}-\frac{\zeta_{3}N_{\varepsilon}}{\eta_{1}-\delta} \int_{-\infty }^{0}\kappa(\vartheta) e^{-\delta\vartheta}\,d \vartheta \le&\zeta_{1}-\frac{\zeta_{3}}{\eta_{1}-\delta} \int_{-\infty}^{0}\kappa (\vartheta)e^{-\delta\vartheta}\,d \vartheta\frac{(\eta_{1}-\delta)(\zeta _{1}+\varepsilon)}{\zeta_{3}\int_{-\infty}^{0}\kappa(\vartheta)e^{-\delta \vartheta}\,d\vartheta} < 0 \end{aligned}$$

and

$$\begin{aligned} \zeta_{2}-\frac{N_{\varepsilon}\zeta_{4}}{\eta_{2}-\delta} \int_{-\infty }^{0}\kappa(\vartheta)e^{-\delta\vartheta}\,d \vartheta \le& \zeta_{2}-\frac{\zeta_{4}}{\eta_{2}-\delta} \int_{-\infty}^{0}\kappa(\vartheta )e^{-\delta\vartheta}\,d \vartheta\frac{(\eta_{2}-\delta)(\zeta_{2}+\varepsilon )}{\zeta_{4}\int_{-\infty}^{0}\kappa(\vartheta)e^{-\delta\vartheta }\,d\vartheta} < 0. \end{aligned}$$

Thus, (7) yields \(\Psi(t_{1})< N_{\varepsilon}e^{-\delta t_{1}}\), which contradicts (6), that is, (5) holds. Since \(\varepsilon>0\) is small enough, by (5), we have \(\Psi(t)\leq N_{2} e^{-\delta t}, t\geq0\), where \(N_{2}=\max \{\zeta_{1}+\zeta_{2},\frac{\zeta_{1}(\eta_{1}-\delta)}{\zeta _{3}\int_{-\infty}^{0}\kappa (\vartheta)e^{-\delta\vartheta}\,d\vartheta}, \frac{\zeta_{2}(\eta_{2}-\delta)}{\zeta_{4}\int_{-\infty}^{0}\kappa (\vartheta)e^{-\delta\vartheta}\,d\vartheta} \}>0\). The proof is completed. □

Remark 2

Lemma 1, which is different from the lemmas of [21, 24, 29], plays an important role here. The main lemmas in [21, 24, 29] cannot be applied in the present study because of the effects of impulses and infinite delays. The main lemma of [21] aims at first-order stochastic systems, while that of [24] focuses on finite constant delay. Our lemma is effective to establish the stability of system (1). It is clear that the lemma can deal with impulses and infinite delay terms.

Theorem 1

Assume that (A1)-(A3) hold and \(a,b\in(0,\hbar]\), and for \(p\geq2\),

$$\begin{aligned} &7^{p-1} {\alpha}^{p} L_{0}^{p} b^{-p}+7^{p-1} {\alpha}^{p} L_{1}^{p} a^{-p}+ 7^{p-1} {\alpha}^{p}L^{p}_{2}a^{-\frac{p}{2}} \biggl(\frac{p(p-1)}{2} \biggr)^{\frac{p}{2}} \biggl(\frac{2(p-1)}{p-2} \biggr)^{1-\frac{p}{2}} \\ &\quad{}+7^{p-1} {\alpha}^{p}\Biggl(\sum _{j=1}^{+\infty} \beta_{j}\Biggr)^{p} +7^{p-1} {\alpha}^{p}\Biggl(\sum_{j=1}^{+\infty} \alpha_{j}\Biggr)^{p}< 1. \end{aligned}$$
(8)

Then system (1) is pth moment exponentially stable. Especially, when \(p=2\) system (1) is mean square exponentially stable provided \({\alpha}^{2} L_{0}^{2} b^{-2}+ {\alpha}^{2} L_{1}^{2} a^{-2}+ {\alpha}^{2}L^{2}_{2}a^{-1} + {\alpha}^{2}(\sum_{j=1}^{+\infty} \beta_{j})^{2} + {\alpha}^{2}(\sum_{j=1}^{+\infty} \alpha_{j})^{2}<1/7\).

Proof

By (2), we have

$$\begin{aligned} E \bigl\Vert y(t)\bigr\Vert ^{p} =&E\biggl\| C(t) \varphi+S(t) \bigl(\Phi-\mu(0,{\varphi})\bigr)+ \int _{0}^{t}C(t-{\varpi})\mu({\varpi},y_{\varpi})\,d{ \varpi} \\ &{}+ \int_{0}^{t}S(t-{\varpi })f({\varpi},y_{\varpi})\,d{ \varpi} + \int_{0}^{t}S(t-{\varpi})g({\varpi},y_{\varpi}) \,dw({\varpi}) \\ &{}+\sum_{0< t_{j}< t}C(t-t_{j})I_{j} \bigl(y\bigl(t_{j}^{-}\bigr)\bigr)+\sum_{0< t_{j}< t}S(t-t_{j}){ \widetilde{I}}_{j}\bigl(y\bigl(t_{j}^{-}\bigr)\bigr) \biggr\| ^{p} \\ \leq&7^{p-1}{\alpha}^{p}E\Vert \varphi \Vert ^{p}e^{-bt}+7^{p-1}{\alpha}^{p}E\bigl\Vert \Phi -\mu(0,{\varphi})\bigr\Vert ^{p}e^{-at} \\ &{}+7^{p-1}E \biggl\Vert \int_{0}^{t}C(t-{\varpi})\mu({\varpi },y_{\varpi})\,d{\varpi}\biggr\Vert ^{p} \\ &{}+7^{p-1}E\biggl\Vert \int_{0}^{t}S(t-{\varpi})f({\varpi},y_{\varpi})\,d{ \varpi}\biggr\Vert ^{p} \\ &{}+7^{p-1}\biggl\Vert \int_{0}^{t}S(t-{\varpi})g({\varpi},y_{\varpi}) \,dw({\varpi})\biggr\Vert ^{p} \\ &{}+7^{p-1}E\biggl\Vert \sum_{0< t_{j}< t}C(t-t_{j})I_{j} \bigl(y\bigl(t_{j}^{-}\bigr)\bigr) \biggr\Vert ^{p} +7^{p-1}E \biggl\Vert \sum_{0< t_{j}< t}S(t-t_{j}){ \widetilde{I}}_{j}\bigl(y\bigl(t_{j}^{-}\bigr)\bigr) \biggr\Vert ^{p}. \end{aligned}$$
(9)

By (A1), (A2), (A3), and the Hölder inequality, we have

$$\begin{aligned} &E\biggl\Vert \int_{0}^{t}C(t-{\varpi})\mu({\varpi},y_{\varpi})\,d{ \varpi}\biggr\Vert ^{p} \\ &\quad\le {\alpha}^{p} \biggl( \int_{0}^{t}\bigl( e^{-b(t-{\varpi})(p+1)/p} \bigr)^{\frac {p}{p-1}}\,d{\varpi}\biggr)^{p-1} \int_{0}^{t} e^{{-b(t-{\varpi})}}E\bigl\Vert \mu({ \varpi}, y_{\varpi} )\bigr\Vert ^{p}d{\varpi} \\ &\quad\le {\alpha}^{p} b^{1-p} \int_{0}^{t} e^{{-b(t-{\varpi})}}E\bigl\Vert \mu({ \varpi}, y_{\varpi} )-\mu({\varpi}, 0)+\mu({\varpi}, 0)\bigr\Vert ^{p}d{\varpi} \\ &\quad\le {\alpha}^{p} L_{0}^{p} b^{1-p} \int_{0}^{t} e^{{-b(t-{\varpi})}}E \biggl( \int_{-\infty}^{0}\kappa(\vartheta)\bigl\Vert y({ \varpi}+\vartheta)\bigr\Vert \,d\vartheta \biggr)^{p}d{\varpi}. \end{aligned}$$

Similarly, we have

$$\begin{aligned} &E\biggl\Vert \int_{0}^{t}S(t-{\varpi})f({\varpi},y_{\varpi})\,d{ \varpi}\biggr\Vert ^{p} \\ &\quad\le {\alpha}^{p} L_{1}^{p} a^{1-p} \int_{0}^{t} e^{{-a(t-{\varpi})}}E \biggl( \int_{-\infty}^{0}\kappa(\vartheta)\bigl\Vert y({ \varpi}+\vartheta)\bigr\Vert \,d\vartheta \biggr)^{p}d{\varpi}. \end{aligned}$$

By (A1) and (A3), we have

$$\begin{aligned} \biggl\Vert \sum_{0< t_{j}< t}C(t-t_{j})I_{j} \bigl(y\bigl(t_{j}^{-}\bigr)\bigr) \biggr\Vert ^{p} \le& { \alpha}^{p} E\biggl(\sum_{0< t_{j}< t}e^{-b(t-t_{j})} \alpha_{j}\bigl\Vert y\bigl(t_{j}^{-}\bigr)\bigr\Vert \biggr)^{p} \\ \le& {\alpha}^{p}E \Biggl(\sum_{j=1}^{+\infty} \alpha_{j}^{\frac{p-1}{p}}\alpha _{j}^{\frac{1}{p}}e^{-b (t-t_{j})} \bigl\Vert y\bigl(t_{j}^{-}\bigr)\bigr\Vert \Biggr)^{p} \\ \le& {\alpha}^{p} \Biggl(\sum_{j=1}^{+\infty} \alpha_{j} \Biggr)^{p-1} \sum_{0< t_{j}< t}q_{j}e^{-pb(t-t_{j})}E \bigl\Vert y\bigl(t_{j}^{-}\bigr)\bigr\Vert ^{p} \\ \le&{\alpha}^{p} \Biggl(\sum_{j=1}^{+\infty} \alpha_{j}\Biggr)^{p-1} \sum_{0< t_{j}< t} \alpha_{j} e^{-b (t-t_{j})}E\bigl\Vert y\bigl(t_{j}^{-} \bigr)\bigr\Vert ^{p} \end{aligned}$$

and

$$\biggl\Vert \sum_{0< t_{j}< t}S(t-t_{j}){ \widetilde{I}}_{j}\bigl(y\bigl(t_{j}^{-}\bigr)\bigr) \biggr\Vert ^{p} \le {\alpha}^{p} \Biggl(\sum _{j=1}^{+\infty} \beta_{j}\Biggr)^{p-1} \sum_{0< t_{j}< t} \beta_{j} e^{-a (t-t_{j})}E \bigl\Vert y\bigl(t_{j}^{-}\bigr)\bigr\Vert ^{p}. $$

From Lemma 2, we obtain

$$\begin{aligned} &E\biggl\Vert \int_{0}^{t}S(t-{\varpi})g({\varpi},y_{\varpi}) \,dw({\varpi})\biggr\Vert ^{p} \\ &\quad\leq c_{p} {\alpha}^{p} \biggl( \int_{0}^{t}\bigl(e^{-a p(t-{\varpi})}E\bigl\Vert g({ \varpi },y_{\varpi})\bigr\Vert _{L^{0}_{2}}^{p} \bigr)^{\frac{2}{p}}\,d{\varpi} \biggr)^{\frac{p}{2}} \\ &\quad=c_{p}{\alpha}^{p} \biggl( \int_{0}^{t}e^{-2a(t-{\varpi})}\bigl(E\bigl\Vert g({ \varpi },y_{\varpi})\bigr\Vert _{L^{0}_{2}}^{p} \bigr)^{\frac{2}{p}}\,d{\varpi} \biggr)^{\frac{p}{2}} \\ &\quad\leq c_{p}{\alpha}^{p} \biggl( \int_{0}^{t}e^{-\frac{2a(p-1)}{p-2}(t-{\varpi })}\,d{\varpi} \biggr)^{\frac{p}{2}-1} \int_{0}^{t}e^{-a(t-{\varpi})}E\bigl\Vert g({ \varpi},y_{\varpi})\bigr\Vert _{L^{0}_{2}}^{p}d{\varpi } \\ &\quad\leq c_{p}{\alpha}^{p}L^{p}_{2} \biggl(\frac{2a(p-1)}{p-2} \biggr)^{1-\frac {p}{2}} \int_{0}^{t}e^{-a(t-{\varpi})} E \biggl( \int_{-\infty}^{0}\kappa(\vartheta)\bigl\Vert y({ \varpi}+\vartheta)\bigr\Vert \,d\vartheta \biggr)^{p}d{\varpi}. \end{aligned}$$

These together with (9) yield

$$\begin{aligned} & E\bigl\Vert y(t)\bigr\Vert ^{p} \\ &\quad\leq 7^{p-1}{\alpha}^{p}E\Vert \varphi \Vert ^{p}e^{-bt}+7^{p-1}{\alpha}^{p}E\bigl\Vert \Phi -\mu(0,{\varphi})\bigr\Vert ^{p}e^{-at} \\ & \qquad{}+7^{p-1} {\alpha}^{p} L_{0}^{p} b^{1-p} \int_{0}^{t} e^{{-b(t-{\varpi})}} \int_{-\infty}^{0}\kappa(\vartheta)E\bigl\Vert y({\varpi }+\vartheta)\bigr\Vert ^{p}\,d\vartheta \,d{\varpi} \\ & \qquad{}+7^{p-1} {\alpha}^{p} L_{1}^{p} a^{1-p} \int_{0}^{t} e^{{-a(t-{\varpi})}} \int_{-\infty}^{0}\kappa(\vartheta)E\bigl\Vert y({\varpi }+\vartheta)\bigr\Vert ^{p}\,d\vartheta \,d{\varpi} \\ & \qquad{}+7^{p-1}c_{p}{\alpha}^{p}L^{p}_{2} \biggl(\frac{2a(p-1)}{p-2} \biggr)^{1-\frac{p}{2}} \int_{0}^{t}e^{-a(t-{\varpi})} \int_{-\infty}^{0}\kappa(\vartheta)E\bigl\Vert y({ \varpi}+\vartheta)\bigr\Vert ^{p}\,d\vartheta \,d{\varpi} \\ & \qquad{}+7^{p-1}{\alpha}^{p} \Biggl(\sum _{j=1}^{+\infty} \alpha_{j}\Biggr)^{p-1} \sum_{0< t_{j}< t} \alpha_{j} e^{-b (t-t_{j})}E \bigl\Vert y\bigl(t_{j}^{-}\bigr)\bigr\Vert ^{p} \\ & \qquad{}+ 7^{p-1} {\alpha}^{p} \Biggl(\sum _{j=1}^{+\infty} \beta_{j}\Biggr)^{p-1} \sum_{0< t_{j}< t} \beta_{j} e^{-a (t-t_{j})}E \bigl\Vert y\bigl(t_{j}^{-}\bigr)\bigr\Vert ^{p}. \end{aligned}$$
(10)

Obviously, from (10) there exist two positive numbers \({\alpha}'\) and \({\alpha}''\) such that \(E\Vert y(t)\Vert ^{2}\leq {\alpha}'e^{-b t}+{\alpha}''e^{-at}\), for any \(t\in(-\infty,0]\).

Let \(\breve{\zeta}_{1}=7^{p-1}{\alpha}^{p}E\Vert \varphi \Vert ^{p}\), \(\breve{\zeta}_{2}=7^{p-1}{\alpha}^{p}E\Vert \Phi-\mu(0,{\varphi})\Vert ^{p}\), \(\breve{\zeta}_{3}=7^{p-1} {\alpha}^{p} L_{0}^{p} b^{1-p} \), \(\breve{\zeta}_{4}=7^{p-1} {\alpha}^{p} L_{1}^{p} a^{1-p}+ 7^{p-1}c_{p}{\alpha}^{p}L^{p}_{2} (\frac {2a(p-1)}{p-2} )^{1-\frac{p}{2}}\), \(\check{\eta}_{j}=7^{p-1} {\alpha}^{p}(\sum_{j=1}^{+\infty} \alpha_{j})^{p-1}\alpha_{j}\), \(\breve{\eta}_{j}=7^{p-1} {\alpha}^{p}(\sum_{j=1}^{+\infty} \beta_{j})^{p-1}\beta_{j}\), If \(\frac{\breve{\zeta_{3}}}{b}+\frac{\breve{\zeta_{4}}}{a} +\sum_{j=1}^{+\infty} \breve{\eta} +\sum_{j=1}^{+\infty} \check{\eta} <1\), i.e. (8) holds, then by Lemma 3, we obtain \(E\Vert y(t)\Vert ^{2}\leq\hat{M}e^{-\hat{\delta } t}, t\in[0,+\infty) \), where \(\hat{\delta} \in(0,\eta_{1}\wedge\eta_{2})\) and δ̂ is a positive root of the equation \((\frac{\breve{\zeta}_{3}}{b-\delta}+\frac{\breve{\zeta}_{4}}{a-\delta } )\int_{-\infty}^{0}\kappa (\vartheta) e^{-\delta\vartheta}\,d\vartheta +\sum_{j=1}^{+\infty}(\alpha_{j}+\beta_{j})=1\), \(\hat{M}= \{7^{p-1}{\alpha}^{p}(E\Vert \varphi \Vert ^{p} +E\Vert \Phi-\mu(0,{\varphi })\Vert ^{p}), 7^{p-1}{\alpha}^{p}b^{-p}L_{0}^{p}, 7^{p-1}{\alpha}^{p} (a^{-p}L_{1}^{p}+c_{p}L^{p}_{2}a^{-\frac{p}{2}} (\frac{2(p-1)}{p-2} )^{1-\frac{p}{2}} ) \}>0\). The proof is completed. □

If \(D(t, y_{t})\equiv0\), system (1) becomes the following second-order SPFDSs subject to infinite delays and being impulsive:

$$ \left \{ \textstyle\begin{array}{@{}l} dy'(t)=[Ay(t)+f(t, y_{t})]\,dt +g(t, y_{t})\,dw(t),\quad t\ge0, t\neq t_{j}, j=1,2,\ldots,\\ \Delta y(t_{j})=I_{j}(y(t_{j}^{-})), \qquad \Delta y'(t_{j})={\widetilde {I}}_{j}(y(t_{j}^{-})),\quad j=1,2,\ldots,\\ y_{0}(\cdot)=\varphi\in\frak {J}, \qquad y'(0)=\Phi, \end{array}\displaystyle \right . $$
(11)

Corollary 1

Under (A1)-(A3), and \(a,b\in(0,\hbar]\), system (11) is pth (\(p\geq2\)) moment exponentially stable provided

$$\begin{aligned} &6^{p-1} {\alpha}^{p} L_{1}^{p} a^{-p}+ 6^{p-1} {\alpha}^{p}L^{p}_{2}a^{-\frac{p}{2}} \biggl(\frac{p(p-1)}{2} \biggr)^{\frac{p}{2}} \biggl(\frac{2(p-1)}{p-2} \biggr)^{1-\frac{p}{2}} \\ &\quad{}+6^{p-1} {\alpha}^{p}\Biggl(\sum _{j=1}^{+\infty} \beta_{j}\Biggr)^{p} +6^{p-1} {\alpha}^{p}\Biggl(\sum_{j=1}^{+\infty} \alpha_{j}\Biggr)^{p}< 1. \end{aligned}$$
(12)

Moreover, if \(p=2\) system (1) is mean square exponentially stable provided \(6 {\alpha}^{2} L_{1}^{2} a^{-2}+ 6 {\alpha}^{2}L^{2}_{2}a^{-1} +6 {\alpha}^{2}(\sum_{j=1}^{+\infty} \beta_{j})^{2} +6 {\alpha}^{2}(\sum_{j=1}^{+\infty} \alpha_{j})^{2}<1\).

If system (1) is not subject to impulses, system (1) becomes the following second-order SNPFSs:

$$ \left \{ \textstyle\begin{array}{@{}l} d[y'(t)-\mu(t,y_{t})]=[Ay(t)+f(t, y_{t})]\,dt +g(t, y_{t})\,dw(t),\quad t\ge0, t\neq t_{j}, j=1,2,\ldots,\\ y_{0}(\cdot)=\varphi\in\frak {J}, \qquad y'(0)=\Phi, \end{array}\displaystyle \right . $$
(13)

Corollary 2

Under (A1)-(A2), and \(a,b\in(0,\hbar]\), system (13) is pth (\(p\geq2\)) moment exponentially stable provided

$$\begin{aligned} 5^{p-1} {\alpha}^{p} L_{0}^{p} b^{-p}+5^{p-1} {\alpha}^{p} L_{1}^{p} a^{-p}+ 5^{p-1} {\alpha}^{p}L^{p}_{2}a^{-\frac{p}{2}} \biggl(\frac{p(p-1)}{2} \biggr)^{\frac{p}{2}} \biggl(\frac{2(p-1)}{p-2} \biggr)^{1-\frac{p}{2}}< 1. \end{aligned}$$
(14)

Moreover, if \(p=2\) system (1) is mean square exponentially stable provided \(5 {\alpha}^{2} L_{0}^{2} b^{-2}+5 {\alpha}^{2} L_{1}^{2} a^{-2}+ 5 {\alpha}^{2}L^{2}_{2}a^{-1}<1\).

Remark 3

System (1) with finite delays or without impulses has been discussed in [8, 22] and [29], respectively. In this paper, we discuss the second-order stochastic neutral partial functional differential equations subject to infinite delays and impulses, which is more general. In addition, the method of establishing stability in [9, 18, 28, 30, 31] is fixed point theory. However, the method different from the above papers is to establish a new integral inequality with respect to impulses and infinite delays. Although [10, 19–21, 24, 29] also utilize the integral inequalities techniques to study stochastic partial differential systems, these inequalities cannot be applied in this paper. In the sense, Theorem 1 is a generalization and development of these existing results. Finally, it should be pointed out that the results are valid for system (1) with finite delays. Our results can easily be extended to second-order stochastic systems driven by a Lévy process.

Remark 4

If \(4^{p-1} {\alpha}^{p} L_{1}^{p} a^{-p}+ 4^{p-1} {\alpha}^{p}L^{p}_{2}a^{-\frac{p}{2}} (\frac{p(p-1)}{2} )^{\frac{p}{2}} (\frac{2(p-1)}{p-2} )^{1-\frac{p}{2}}<1\), system (13) without neutral term is also pth moment exponentially stable. If \({\alpha}^{2} L_{0}^{2} b^{-2}+5 {\alpha}^{2} L_{1}^{2} a^{-2}+ {\alpha }^{2}L^{2}_{2}a^{-1}<1/4\), system (13) without neutral term is mean square exponentially stable.

4 An example

In this section, we will discuss an example to show the theoretical results. Consider the following second-order stochastic neutral partial functional systems subject to infinite delays and impulses:

$$ \begin{aligned} & d \biggl[\frac{\partial}{\partial t}y(t,x)- \mu(t,y_{t}) \biggr] = \biggl[\frac{\partial^{2}}{\partial x^{2}}y(t,x)+f(t,y_{t}) \biggr]\,dt +g(t,y_{t})\,dw(t),\\ &\quad t\geq 0, x\in[0,\pi], \\ &\Delta y(t_{j})=\frac{u_{3}}{{j}^{2}}y\bigl(t_{j}^{-}\bigr), \quad j=1,2,\ldots, \\ &\Delta y'(t_{j})=\frac{u_{4}}{{j}^{2}}y \bigl(t_{j}^{-}\bigr),\quad j=1,2,\ldots, \end{aligned} $$
(15)

with \(y(s)=\varphi(s)\in\frak {J}, y'(0)=\xi, y(t, 0)=y(t, \pi)=0, t\geq0\), \(u_{i}>0, i=0, 1, 2\), and \(u_{3}\ge0, u_{4}\ge0\).

Let \(\Xi_{1}=\mathfrak{L}^{2}[0,\pi]\) and \(\Xi_{2}=R^{1}\) with the norm \(\Vert \cdot \Vert \). Let \(A=\frac{\partial^{2}}{\partial x^{2}}: \Xi_{1}\rightarrow\Xi_{1}\) with \(\mathfrak{D}(A)=\{y\in\Xi_{1}: y, \frac{\partial}{\partial x}y\mbox{ be absolutely continuous}, \frac{\partial^{2} }{\partial x^{2}}y\in\Xi_{1}, y(0)=y(\pi)=0\}\). Thus it is clear that \(\Vert C(t)\Vert \leq e^{-\pi^{2} t}\) and \(\Vert S(t)\Vert \leq e^{-\pi^{2} t}, t\geq0\).

Now let

$$\begin{aligned}& \mu(t,y_{t})\triangleq\frac{u_{0}\pi^{2}}{7} \int_{-\infty}^{0}(-\varpi )^{-\frac{1}{2}} e^{\pi^{2}\varpi}y(t+\varpi,x)\,d\varpi, \\& f(t,y_{t})\triangleq\frac{u_{1}\pi^{2}}{7} \int_{-\infty}^{0}(-\varpi)^{-\frac{1}{2}} e^{\pi^{2}\varpi}y(t+\varpi,x)\,d\varpi, \\& g(t,y_{t})\triangleq\frac{u_{2} \pi}{7} \int_{-\infty}^{0}(-\varpi)^{-\frac{1}{2}}e^{\pi^{2}\varpi }y \bigl((t+\varpi),x\bigr)\,d\varpi, \end{aligned}$$

for any \(y_{t}\in\frak {J}\). It is clear that the conditions of Theorem 1 hold with \(\alpha=1, b=a=\pi^{2}, L_{0}=\frac{u_{0}\pi^{2}}{7}, L_{1}=\frac{u_{1}\pi^{2}}{7}, L_{2}=\frac{u_{2} \pi}{7}, a_{j}=\frac{u_{3}}{7{j}^{2}}, \beta_{j}=\frac{u_{4}}{7{j}^{2}} \) (\(j=1,2,\ldots\)). Then, by Theorem 1, system (15) is pth moment exponentially stable provided

$$\begin{aligned} u_{0}^{p} + u_{1}^{p} + u_{2}^{p} \biggl(\frac{p(p-1)}{2} \biggr)^{\frac{p}{2}} \biggl(\frac{2(p-1)}{p-2} \biggr)^{1-\frac{p}{2}} + \biggl(\frac{u_{3} \pi^{2}}{6} \biggr)^{p} +\biggl(\frac{u_{4} \pi^{2}}{6}\biggr)^{p}< 7. \end{aligned}$$
(16)

Especially, when \(p=2\), system (15) is mean square exponentially stable provided \(u_{0}^{2} + u_{1}^{2} + u_{2}^{2} + \frac{u_{3}^{2} \pi^{4}}{36} + \frac{u_{4}^{2} \pi^{4}}{36} <7\).

If system (15) has no impulse term, i.e. \(u_{3}=u_{4}=0\), then system (15) becomes one of the second-order neutral stochastic systems with infinite delays. Now let \(\alpha=1, b=a=\pi^{2}, L_{0}=\frac{u_{0}\pi^{2}}{5}, L_{1}=\frac{u_{1}\pi^{2}}{5}, L_{2}=\frac{u_{2} \pi}{5}\). Then, by Corollary 2, system (15) without impulses is pth moment exponentially stable provided

$$\begin{aligned} u_{0}^{p} + u_{1}^{p} + u_{2}^{p} \biggl(\frac{p(p-1)}{2} \biggr)^{\frac{p}{2}} \biggl(\frac{2(p-1)}{p-2} \biggr)^{1-\frac{p}{2}} < 5; \end{aligned}$$

and if \(u_{0}^{2} + u_{1}^{2} + u_{2}^{2} <5\), system (15) without impulses is mean square exponentially stable.

Remark 5

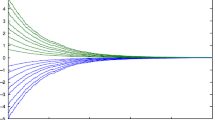
It is clear that the algebraic conditions of stability in the example are easily computed. The example also shows that the results of this paper are effective.

5 Conclusions

In this paper we have studied second-order stochastic neutral partial functional systems subject to infinite delays and impulses. We first established a new integral inequality with respect to impulses and then give some algebraic criteria to ensure pth moment exponential stability of the second-order stochastic impulsive systems. The results show some earlier results are generalized and improved. Finally, an example was given to illustrate the effectiveness of the theoretical results. Further research will be to study controller design and noise stabilization as well as its possible extension to second-order stochastic systems driven by Lévy jumps.