1 Introduction

In recent years, spectral methods (see [1–8]) have often turned out to be efficient and highly accurate schemes when compared with the local methods. The speed of convergence is one of the great advantages of spectral methods. Besides, spectral methods have exponential rates of convergence; they also have a high level of accuracy. The main idea of all versions of spectral methods is to express the approximate solution of the problem as a finite sum of certain basis functions (orthogonal polynomials or a combination of them) and then choose the coefficients in order to minimize the difference between the exact and approximate solutions as well as possible. The spectral collocation method is a specific type of spectral methods, which is more applicable and widely used to solve almost all types of the differential equations [9–12].

The Stokes’ problem based on the Navier-Stokes theory was studied in several articles; see for example [13–21]. Recently, the first problem of Stokes has become more significant due to its applications. The flow of an Oldroyd-B fluid over a suddenly moved flat plate has been described by Stokes’ first problem in [22]. The first problem of Stokes for Oldroyd-B fluid in a porous half-space and a heated boundary second grade fluid in a porous half-space has been discussed by Tan et al. [23, 24]. Shen et al. [25] introduced the fractional derivative model of the Rayleigh-Stokes problem for a heated generalized second grade. The numerical study based on Laguerre-Galerkin method [26] has been introduced for the first problem of Stokes, which describes a Newtonian fluid in a non-Darcian porous half-space.

Fractional calculus [27–36] is a branch of calculus theory, which makes partial differential equations more convenient to describe many phenomena in several fields such as fluid mechanics, chemistry [33, 34], biology [35], viscoelasticity [36], engineering, finance, and physics [37] fields. Bhrawy et al. [38] proposed an accurate Jacobi collocation algorithm for the systems of high-order linear differential-difference equations with mixed initial conditions. The Jacobi pseudospectral method has been discussed by Bhrawy et al. [39] to solve a class of functional-differential equations. Moreover, Bhrawy et al. [40] introduced a combination of Jacobi Gauss-Lobatto and Gauss-Radau collocation algorithms for solving the fractional Fokker-Planck equations. In this paper, the SJ-GL-C and SJ-GR-C methods are proposed to solve multi-dimensional FSFP-HGSGF. The solution of such equation is approximated by means of a finite expansion of shifted Jacobi polynomials for independent variables. The proposed collocation scheme is investigated for both temporal and spatial discretizations. Then we evaluate the residuals of the FSFP-HGSGF at the shifted Jacobi-Gauss-Lobatto (SJ-GL) and shifted Jacobi-Gauss-Radau (SJ-GR) quadrature points. Thereby, the problem is reduced to a system of algebraic equations which is far easier to solve. Indeed, with the freedom to select the shifted Jacobi indices \(\alpha >-1\) and \(\beta >-1\), the method can be calibrated for a wide variety of problems. To the best of our knowledge, there are no results on SJ-GL-C and SJ-GR-C methods for FSFP-HGSGF.

This paper is organized as follows. A few facts of shifted Jacobi polynomials and fractional calculus are listed in Section 2. In Section 3, we introduce a new collocation method for the one-dimensional space FSFP-HGSGF. In Section 4, the proposed scheme is successfully extended to solve the two-dimensional space FSFP-HGSGF. Section 5 is used to solve several problems. A conclusion is given in the last section.

2 Mathematical preliminaries

2.1 Fractional calculus

The fractional integration definition of order \(\nu>0\), can be expressed by several formulas and in general they are not equal to each other. The most often used definitions are the Caputo and Riemann-Liouville definitions.

Definition 2.1

The operator \(J^{\nu}\) of Riemann-Liouville fractional integral is defined as

$$ \begin{aligned} &J^{\nu}f(x)=\frac{1}{\Gamma(\nu)} \int_{0}^{x}{(x-\zeta)}^{\nu-1} f(\zeta) \,d \zeta,\quad\nu>0, x>0, \\ &J^{0} f(x)=f(x), \end{aligned} $$
(2.1)

where

$$\Gamma(\nu)= \int_{0}^{\infty}x^{\nu-1} e^{-x} \,dx. $$

The properties listed below are satisfied for the operator \(J^{\nu}\)

$$ \begin{aligned} &J^{\nu}J^{\mu}f(x)=J^{\nu+\mu} f(x), \\ &J^{\nu}J^{\mu}f(x)=J^{\mu}J^{\nu}f(x), \\ &J^{\nu}x^{\beta}= \frac {\Gamma{(\beta+1)}}{\Gamma{(\beta+1+\nu)}} x^{\beta+\nu}. \end{aligned} $$
(2.2)

Definition 2.2

The next equation defines the Riemann-Liouville fractional derivative \(D^{\nu}\) of order ν

$$ D^{\nu}f(x)=\frac{1}{\Gamma(m-\nu)} \frac{d^{m}}{dx^{m}} \biggl( \int _{0}^{x}{(x-t)}^{m-\nu-1} f(t) \,dt \biggr), \quad m-1< \nu\leq m, x>0, $$
(2.3)

where m is the ceiling function of ν.

Definition 2.3

The Caputo fractional derivative of order ν is defined as

$$ D_{c}^{\nu}f(x)=\frac{1}{\Gamma(m-\nu)} \int_{0}^{x}{(x-\zeta )}^{m-\nu-1} \frac{d^{m}}{dt^{m}}f(\zeta) \,d\zeta, \quad m-1< \nu\leq m, x>0, $$
(2.4)

where m is the ceiling function of ν.

2.2 Properties of shifted Jacobi polynomials

Some few properties of shifted Jacobi polynomials are presented in this subsection. In the following, a few relations related to Jacobi polynomials are listed:

$$ \begin{aligned} & P_{k + 1}^{(\alpha, \vartheta)} (x) = \bigl(a_{k}^{(\alpha, \beta)} x - b_{k}^{(\alpha, \beta)} \bigr) P_{k}^{(\alpha, \beta)} (x) - c_{k}^{(\alpha, \beta)} P_{k - 1}^{(\alpha, \beta)} (x), \quad k \geq1, \\ & P_{0}^{(\alpha, \beta)} (x) = 1, \quad \quad P_{1}^{(\alpha, \beta)} (x) = \frac{1}{2} (\alpha+ \beta+ 2) x + \frac{1}{2} (\alpha- \beta), \\ &P_{k}^{(\alpha,\beta)}(-x) =(-1)^{k}P_{k}^{(\alpha,\beta)}(x), \quad \quad P_{k}^{(\alpha,\beta)}(-1)= \frac{(-1)^{k}\Gamma(k+\beta +1)}{k!\Gamma(\beta+1)}, \end{aligned} $$
(2.5)

where \(\alpha, \beta>-1\), \(x\in[-1,1]\), and

$$\begin{aligned}& a_{k}^{(\alpha, \beta)} = \frac{(2 k + \alpha+ \beta+1) (2 k + \alpha+ \beta+ 2)}{2 (k +1) (k + \alpha+ \beta+ 1)}, \\& b_{k}^{(\alpha, \beta)} = \frac{(\beta^{2}-\alpha^{2})(2 k + \alpha+ \beta+ 1)}{2 (k + 1) (k + \alpha+ \beta+1) (2 k + \alpha+ \beta )}, \\& c_{k}^{(\alpha, \beta)} = \frac{(k + \alpha)(k + \beta)(2 k + \alpha+ \beta+ 2)}{(k +1) (k + \alpha+ \beta+ 1) (2 k + \alpha+ \beta)}. \end{aligned}$$

Moreover, the rth derivative (r is an integer) of \(P_{j}^{(\alpha ,\beta)}(x)\) may be obtained from

$$ \begin{aligned} D^{r}P_{j}^{(\alpha, \beta)}(x) =\frac{\Gamma(j+\alpha+\beta +q+1)}{2^{r}\Gamma(j+\alpha+\beta+1)}P_{j-r}^{(\alpha+r,\beta+r )}(x). \end{aligned} $$
(2.6)

For the shifted Jacobi polynomial \(P_{L,k}^{(\alpha,\beta )}(x)=P_{k}^{(\alpha,\beta)}(\frac{2x}{L}-1)\), \(L>0\), the explicit analytic form is written as

$$ \begin{aligned}[b] P^{(\alpha,\beta)}_{L,k}{(x)}&= \sum_{j=0}^{k}{(-1)}^{k-j} \frac{\Gamma{(k+\beta+1)}\Gamma{(j+k+\alpha+\beta+1)}}{\Gamma (j+\beta+1)\Gamma(k+\alpha+\beta+1)(k-j)!j!L^{j}}x^{j} \\ &=\sum_{j=0}^{k} \frac{\Gamma(k+\alpha+1) \Gamma(k+j+\alpha+\beta +1)}{j! (k-j)! \Gamma(j+\alpha+1) \Gamma(k+\alpha+\beta+1)L^{j}}(x-L)^{j}. \end{aligned} $$
(2.7)

Thus, we can derive the following properties

$$\begin{aligned}& \begin{aligned} &P^{(\alpha,\beta)}_{L,k}(0)={(-1)}^{k} \frac{\Gamma(k+\beta +1)}{\Gamma(\beta+1) k!}, \\ &P_{L,k}^{(\alpha,\beta)}(L)=\frac{\Gamma(k+\alpha+1)}{\Gamma (\alpha+1) k!}, \end{aligned} \end{aligned}$$
(2.8)
$$\begin{aligned}& D^{r}P_{L,k}^{(\alpha,\beta)}(0)= \frac{(-1)^{k-r} \Gamma(k+\beta +1) (k+\alpha+\beta+1 )_{r}}{L^{r}\Gamma(k-r+1) \Gamma(r+\beta+1)}, \end{aligned}$$
(2.9)
$$\begin{aligned}& D^{r}P_{L,k}^{(\alpha,\beta)}(L)= \frac{ \Gamma(k+\alpha+1) (k+\alpha+\beta+1 )_{r}}{L^{r}\Gamma(k-r+1) \Gamma(r+\alpha+1)}, \end{aligned}$$
(2.10)
$$\begin{aligned}& D^{r}P_{L,k}^{(\alpha,\beta)}(x)= \frac{\Gamma (r+k+\alpha+\beta +1)}{L^{r}\Gamma (k+\alpha+\beta+1)}P_{L,k-r}^{(\alpha+r ,\beta+r )}(x). \end{aligned}$$
(2.11)

Assuming that \(w_{L}^{(\alpha,\beta)}(x)=(L-x)^{\alpha}x^{\beta}\), we can define the norm and inner product for the weighted space \(L_{w_{L}^{(\alpha,\beta)}}^{2}[0,L]\) as

$$ (u,v)_{w_{L}^{(\alpha,\beta)}}= \int _{0}^{L}u(x) v(x) w_{L}^{(\alpha,\beta)}(x) \,dx,\qquad \Vert v\Vert _{w_{L}^{(\alpha,\beta)}}= (v,v)_{w_{L}^{(\alpha,\beta )}}^{\frac{1}{2}}. $$
(2.12)

The set of shifted Jacobi polynomials forms a complete \(L_{w_{L}^{(\alpha,\beta)}}^{2}[0,L]\)-orthogonal system. Moreover, and due to (2.12), we have

$$ \bigl\Vert P_{L,k}^{(\alpha,\beta)} \bigr\Vert ^{2}_{w_{L}^{(\alpha,\beta)}}= \biggl(\frac{L}{2} \biggr)^{\alpha+\beta+1}h_{k}^{(\alpha,\beta)}= h^{(\alpha,\beta)}_{L,k}. $$
(2.13)

We used \(x^{(\alpha,\beta)}_{N,j}\), and \(\varpi^{(\alpha ,\beta)}_{N,j}\), \(0\leqslant j\leqslant N\), as the nodes and Christoffel numbers of the standard Jacobi-Gauss interpolation on the interval \([-1, 1]\).

The corresponding nodes and corresponding Christoffel numbers of the shifted Jacobi-Gauss interpolation on the interval \([0,L]\) can be given by

$$\begin{aligned}& x^{(\alpha,\beta)}_{L,N,j} =\frac{L}{2} \bigl(x^{(\alpha,\beta)}_{N,j} +1 \bigr), \\& \varpi^{(\alpha,\beta)}_{L,N,j} = \biggl(\frac{L}{2} \biggr)^{\alpha+\beta +1}\varpi^{(\alpha,\beta)}_{N,j} ,\quad 0\leqslant j \leqslant N. \end{aligned}$$

For any \(\phi\in S_{2N+1}[0,L]\) and using the Jacobi-Gauss quadrature property, we have

$$ \begin{aligned}[b] \int _{0}^{L}(L-x)^{\alpha}x^{\beta}\phi(x)\,dx&= \biggl(\frac{L}{2} \biggr)^{\alpha+\beta+1} \int _{-1}^{1}(1-x)^{\alpha}(1+x)^{\beta}\phi \biggl(\frac{L}{2}(x+1) \biggr)\,dx \\ &= \biggl(\frac{L}{2} \biggr)^{\alpha+\beta+1}\sum _{j=0}^{N}\varpi^{(\alpha,\beta)}_{N,j} \phi \biggl(\frac{L}{2} \bigl(x^{(\alpha,\beta)}_{N,j}+1 \bigr) \biggr) \\ &=\sum_{j=0}^{N}\varpi^{(\alpha,\beta)}_{L,N,j} \phi \bigl(x^{(\alpha,\beta)}_{L,N,j} \bigr). \end{aligned} $$
(2.14)

3 One-dimensional space of fractional Stokes problem

In this section, we introduce a numerical algorithm based on the SJ-GR-C and SJ-GL-C methods for solving numerically one-dimensional FSFP-HGSGF. The collocation points are selected at the SJ-GR and SJ-GL interpolation nodes for temporal and spatial variables, respectively. The core of the proposed method consists of discretizing the one-dimensional FSFP-HGSGF to create a system of algebraic equations of the unknown coefficients. This system can then easily be solved with a standard numerical scheme.

In particular, we consider the following FSFP-HGSGF:

$$ \begin{aligned} \frac{\partial u(x,t)}{\partial t}=D^{1-\gamma}_{t} \biggl(\frac {\partial^{2} u(x,t)}{\partial x^{2}} \biggr)+\frac{\partial^{2} u(x,t)}{\partial x^{2}}+H(x,t), \quad(x, t)\in[0,L] \times[0,T], \end{aligned} $$
(3.1)

with the initial-boundary conditions

$$ \begin{aligned} &u(x,0)=g_{1}(x),\quad\quad u(0,t)=g_{2}(t), \\ &u(L,t)=g_{3}(t),\quad(x, t)\in [0,L]\times[0,T], \end{aligned} $$
(3.2)

where \(H(x,t)\), \(g_{1}(x)\), \(g_{2}(t)\), and \(g_{3}(t)\) are given functions, \(0<\gamma<1\) and \(D^{1-\gamma}_{t}u(x,t)\) is the temporal fractional derivative of order \(1-\gamma\) in the Riemann-Liouville sense.

We are interested in using the SJ-GL-C and SJ-GR-C methods to transform the previous FSFP-HGSGF into a system of algebraic equations. In order to do this, we approximate the independent space variable x using the SJ-GL-C method at the \(x^{(\alpha_{1},\beta_{1})}_{L,N,i}\) nodes, while the independent temporal variable t was approximated by the SJ-GR-C methods. The nodes are the set of points in a specified domain where the dependent variable values are to be approximated. In general, the choice of the location of the nodes is optional. However, taking the roots of the shifted Jacobi orthogonal polynomials, referred to as shifted Jacobi collocation points, gives particularly accurate solutions for the spectral methods.

Now, we outline the main steps of the mixed SJ-GL-C and SJ-GR-C methods for solving the one-dimensional space FSFP-HGSGF. We choose the approximate solution to be of the form

$$ \begin{aligned}[b] u_{N,M}(x,t)&=\sum _{i=0}^{N}\sum_{j=0}^{M}a_{i,j} P_{L,i}^{(\alpha_{1},\beta_{1})}(x)P_{T,j}^{(\alpha_{2},\beta_{2})}(t) \\ &=\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j}f^{i,j}_{0}(x,t), \end{aligned} $$
(3.3)

where \(f^{i,j}_{0}(x,t)=P_{L,i}^{(\alpha_{1},\beta_{1})}(x)P_{T,j}^{(\alpha _{2},\beta_{2})}(t)\).

Then the spatial partial derivatives \(\frac{\partial u(x,t)}{\partial x}\) and \(\frac{\partial^{2} u(x,t)}{\partial x^{2}}\) were computed as

$$\begin{aligned}& \begin{aligned}[b]\frac{\partial u(x,t)}{\partial x}&=\sum _{i=0}^{N}\sum_{j=0}^{M}a_{i,j} \frac{\partial P_{L,i}^{(\alpha_{1},\beta_{1})}(x)}{\partial x}P_{T,j}^{(\alpha_{2},\beta_{2})}(t) \\ &=\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j}f^{i,j}_{1}(x,t), \end{aligned} \end{aligned}$$
(3.4)
$$\begin{aligned}& \begin{aligned}[b]\frac{\partial^{2} u(x,t)}{\partial x^{2}}&=\sum _{i=0}^{N}\sum_{j=0}^{M}a_{i,j} \frac{\partial^{2} P_{L,i}^{(\alpha_{1},\beta_{1})}(x)}{\partial x^{2}}P_{T,j}^{(\alpha_{2},\beta_{2})}(t) \\ &=\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j} f^{i,j}_{2}(x,t), \end{aligned} \end{aligned}$$
(3.5)

where \(f^{i,j}_{1}(x,t)=\frac{\partial P_{L,i}^{(\alpha_{1},\beta _{1})}(x)}{\partial x}P_{T,j}^{(\alpha_{2},\beta_{2})}(t)\) and \(f^{i,j}_{2}(x,t)=\frac{\partial^{2} P_{L,i}^{(\alpha_{1},\beta _{1})}(x)}{\partial x^{2}}P_{T,j}^{(\alpha_{2},\beta_{2})}(t)\).

Furthermore, the temporal derivative \(\frac{\partial u(x,t)}{\partial t}\) is evaluated as

$$ \begin{aligned}[b]\frac{\partial u(x,t)}{\partial t}&=\sum _{i=0}^{N}\sum_{j=0}^{M}a_{i,j} P_{L,i}^{(\alpha_{1},\beta_{1})}(x)\frac{\partial P_{T,j}^{(\alpha _{2},\beta_{2})}(t)}{\partial t} \\ &=\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j} f^{i,j}_{3}(x,t), \end{aligned} $$
(3.6)

where \(f^{i,j}_{3}(x,t)=P_{L,i}^{(\alpha_{1},\beta_{1})}(x)\frac{\partial P_{T,j}^{(\alpha_{2},\beta_{2})}(t)}{\partial t}\).

Moreover, the Riemann-Liouville fractional partial derivative \(D^{1-\gamma}_{t} \frac{\partial^{2} u(x,t)}{\partial x^{2}}\) is given by

$$ \begin{aligned}[b] D^{1-\gamma}_{t} \frac{\partial^{2} u(x,t)}{\partial x^{2}}&=\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j} \frac{\partial^{2} P_{L,i}^{(\alpha_{1},\beta_{1})}(x)}{\partial x^{2}}D^{1-\gamma }_{t} \bigl(P_{T,j}^{(\alpha_{2},\beta_{2})}(t) \bigr) \\ &=\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j} f^{i,j}_{4}(x,t), \end{aligned} $$
(3.7)

where \(f^{i,j}_{4}(x,t)=\frac{\partial^{2} P_{L,i}^{(\alpha_{1},\beta _{1})}(x)}{\partial x^{2}}D^{1-\gamma}_{t}(P_{T,j}^{(\alpha_{2},\beta_{2})}(t))\).

Now, adopting (3.3)-(3.7) enables one to write (3.1) in the form

$$ \begin{aligned}[b] &\sum_{i=0}^{N} \sum_{j=0}^{M}a_{i,j} f^{i,j}_{3}(x,t)=\sum_{i=0}^{N} \sum_{j=0}^{M}a_{i,j} f^{i,j}_{4}(x,t)+\sum_{i=0}^{N} \sum_{j=0}^{M}a_{i,j} f^{i,j}_{2}(x,t)+H(x,t), \\ &\quad (x, t)\in[0,L]\times[0,T]. \end{aligned} $$
(3.8)

The initial condition immediately gives

$$ \begin{aligned} u(x,0)&=\sum _{i=0}^{N}\sum_{j=0}^{M}a_{i,j} f^{i,j}_{0}(x,0)=g_{1}(x), \end{aligned} $$
(3.9)

while the numerical treatments of the boundary conditions are

$$ \begin{aligned} &u(0,t)=\sum _{i=0}^{N}\sum_{j=0}^{M}a_{i,j} f^{i,j}_{0}(0,t)=g_{2}(t), \\ &u(L,t)=\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j} f^{i,j}_{0}(L,t)=g_{3}(t). \end{aligned} $$
(3.10)

In the proposed mixed SJ-GL-C and SJ-GR-C methods, the residual of (3.8) is set to zero at \(M (N-1)\) of SJ-GL and SJ-GR points. Consequently, we find

$$ \begin{aligned}\sum_{i=0}^{N} \sum_{j=0}^{M}F^{i,j}_{r,s} a_{i,j} =&H \bigl(x^{(\alpha_{1},\beta_{1})}_{L,N,r},t^{(\alpha_{2},\beta _{2})}_{T,M,s} \bigr), \quad r=1,\ldots,N-1; s=1,\ldots,M, \end{aligned} $$
(3.11)

where

$$F^{i,j}_{r,s}= f^{i,j}_{3} \bigl(x^{(\alpha_{1},\beta_{1})}_{L,N,r},t^{(\alpha _{2},\beta_{2})}_{T,M,s} \bigr)- f^{i,j}_{4} \bigl(x^{(\alpha_{1},\beta_{1})}_{L,N,r},t^{(\alpha_{2},\beta_{2})}_{T,M,s} \bigr)- f^{i,j}_{2} \bigl(x^{(\alpha_{1},\beta_{1})}_{L,N,r},t^{(\alpha_{2},\beta_{2})}_{T,M,s} \bigr). $$

For the dependence on equations (3.9) and (3.10), we obtain

$$\begin{aligned}& \begin{aligned} \sum_{i=0}^{N} \sum_{j=0}^{M}a_{i,j} f^{i,j}_{0} \bigl(x^{(\alpha_{1},\beta_{1})}_{L,N,r},0 \bigr)=g_{1} \bigl(x^{(\alpha_{1},\beta _{1})}_{L,N,r} \bigr),\quad r=1, \ldots,N-1, \end{aligned} \end{aligned}$$
(3.12)
$$\begin{aligned}& \begin{aligned}\sum_{i=0}^{N} \sum_{j=0}^{M}a_{i,j} f^{i,j}_{0} \bigl(L,t^{(\alpha_{2},\beta_{2})}_{T,M,s} \bigr)=g_{2} \bigl(t^{(\alpha_{2},\beta _{2})}_{T,M,s} \bigr), \quad s=0, \ldots,M, \end{aligned} \end{aligned}$$
(3.13)

and

$$ \begin{aligned}\sum_{i=0}^{N} \sum_{j=0}^{M}a_{i,j} f^{i,j}_{0} \bigl(L,t^{(\alpha_{2},\beta_{2})}_{T,M,s} \bigr)=g_{3} \bigl(t^{(\alpha_{2},\beta _{2})}_{T,M,s} \bigr),\quad s=0, \ldots,M. \end{aligned} $$
(3.14)

Combining equations (3.11), (3.12), (3.13), and (3.14), we obtain

$$ \begin{aligned} &\sum_{i=0}^{N} \sum_{j=0}^{M}F^{i,j}_{r,s} a_{i,j} =H \bigl(x^{(\alpha_{1},\beta_{1})}_{L,N,r},t^{(\alpha_{2},\beta _{2})}_{T,M,s} \bigr),\quad r=1,\ldots,N-1; s=1,\ldots,M, \\ &\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j} f^{i,j}_{0} \bigl(x^{(\alpha_{1},\beta_{1})}_{L,N,r},0 \bigr)=g_{1} \bigl(x^{(\alpha_{1},\beta _{1})}_{L,N,r} \bigr),\quad r=1,\ldots,N-1, \\ &\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j} f^{i,j}_{0} \bigl(L,t^{(\alpha_{2},\beta _{2})}_{T,M,s} \bigr)=g_{2} \bigl(t^{(\alpha_{2},\beta_{2})}_{T,M,s} \bigr), \quad s=0,\ldots,M, \\ &\sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j} f^{i,j}_{0} \bigl(L,t^{(\alpha_{2},\beta_{2})}_{T,M,s} \bigr)=g_{3} \bigl(t^{(\alpha_{2},\beta _{2})}_{T,M,s} \bigr),\quad s=0,\ldots,M, \end{aligned} $$
(3.15)

the previous system of algebraic equations can easily be solved. After the coefficients \(a_{i,j}\) are determined, it is straightforward to compute the approximate solution \(u_{N,M}(x,t)\) at any value of \((x,t)\) in the given domain from the following equation:

$$ \sum_{i=0}^{N}\sum _{j=0}^{M}a_{i,j} P_{L,i}^{(\alpha_{1},\beta_{1})}(x)P_{T,j}^{(\alpha_{2},\beta_{2})}(t). $$
(3.16)

4 Two-dimensional space of fractional Stokes problem

In the present section, we extend the previous algorithm to numerically solve the two-dimensional space FSFP-HGSGF in the following form:

$$\begin{aligned}& \frac{\partial u(x,y,t)}{\partial t}=D^{1-\gamma}_{t} \biggl(\frac {\partial^{2} u(x,y,t)}{\partial x^{2}}+\frac{\partial^{2} u(x,y,t)}{\partial y^{2}} \biggr)+\frac{\partial^{2} u(x,y,t)}{\partial x^{2}}+ \frac{\partial^{2} u(x,y,t)}{\partial y^{2}}+H(x,y,t), \\& \quad (x,y, t)\in[0,L_{1}]\times[0,L_{2}]\times[0,T], \end{aligned}$$
(4.1)

subject to the initial-boundary conditions

$$ \begin{aligned} &u(x,y,0)=g_{0}(x,y), \quad(x,y)\in[0,L_{1}]\times[0,L_{2}], \\ &u(0,y,t)=g_{1}(y,t),\quad \quad u(L_{1},y,t)=g_{2}(y,t), \quad(y,t)\in [0,L_{2}]\times [0,T], \\ & u(x,0,t)=g_{3}(x,t),\quad \quad u(x,L_{2},t)=g_{4}(x,t), \quad(x,t)\in [0,L_{1}]\times[0,T], \end{aligned} $$
(4.2)

where \(H(x,y,t)\), \(g_{0}(x,y)\), \(g_{1}(y,t)\), \(g_{2}(y,t)\), \(g_{3}(x,t)\), and \(g_{4}(x,t)\) are given real valued functions and \(u(x,y,t)\) is an unknown function. Therefore, the SJ-GL-C and SJ-GR-C methods will be applied to transform the previous two-dimensional FSFP-HGSGF into a system of algebraic equations. The SJ-GL-C and SJ-GR-C have been used for the space \((x,y)\) and time t approximations, respectively.

Now, we outline the main steps of the collocation method for solving the two-dimensional FSFP-HGSGF. Let

$$ \begin{aligned}[b] u_{N,M,K}(x,y,t)&=\sum _{i=0}^{N}\sum_{j=0}^{M} \sum_{k=0}^{K}a_{i,j,k} P_{L_{1},i}^{(\alpha_{1},\beta_{1})}(x)P_{L_{2},j}^{(\alpha_{2},\beta _{2})}(y)P_{T,k}^{(\alpha_{3},\beta_{3})}(t) \\ &=\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{j=0}^{K}a_{i,j,k}f^{i,j,k}_{0}(x,y,t), \end{aligned} $$
(4.3)

where \(f^{i,j,k}_{0}(x,y,t)=P_{L_{1},i}^{(\alpha_{1},\beta _{1})}(x)P_{L_{2},j}^{(\alpha_{2},\beta_{2})}(y)P_{T,k}^{(\alpha_{3},\beta_{3})}(t)\).

Then the first spatial and temporal partial derivatives \(\frac {\partial u(x,y,t)}{\partial x}\), \(\frac{\partial u(x,y,t)}{\partial y}\), and \(\frac{\partial u(x,y,t)}{\partial t}\) can be computed as

$$\begin{aligned}& \begin{aligned}[b]\frac{\partial u(x,y,t)}{\partial x} &=\sum _{i=0}^{N}\sum_{j=0}^{M} \sum_{k=0}^{K}a_{i,j,k} \frac {\partial P_{L_{1},i}^{(\alpha_{1},\beta_{1})}(x)}{\partial x}P_{L_{2},j}^{(\alpha_{2},\beta_{2})}(y)P_{T,k}^{(\alpha_{3},\beta_{3})}(t) \\ &=\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{j=0}^{K}a_{i,j,k}f^{i,j,k}_{1}(x,y,t), \end{aligned} \end{aligned}$$
(4.4)
$$\begin{aligned}& \begin{aligned}[b]\frac{\partial u(x,y,t)}{\partial y} &=\sum _{i=0}^{N}\sum_{j=0}^{M} \sum_{k=0}^{K}a_{i,j,k} P_{L_{1},i}^{(\alpha_{1},\beta_{1})}(x)\frac{\partial P_{L_{2},j}^{(\alpha _{2},\beta_{2})}(y)}{\partial y} P_{T,k}^{(\alpha_{3},\beta_{3})}(t) \\ &=\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{j=0}^{K}a_{i,j,k}f^{i,j,k}_{2}(x,y,t), \end{aligned} \end{aligned}$$
(4.5)
$$\begin{aligned}& \begin{aligned}[b]\frac{\partial u(x,y,t)}{\partial t} &=\sum _{i=0}^{N}\sum_{j=0}^{M} \sum_{k=0}^{K}a_{i,j,k} P_{L_{1},i}^{(\alpha_{1},\beta_{1})}(x)P_{L_{2},j}^{(\alpha_{2},\beta _{2})}(y) \frac{\partial P_{T,k}^{(\alpha_{3},\beta_{3})}(t)}{\partial t} \\ &=\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{j=0}^{K}a_{i,j,k}f^{i,j,k}_{3}(x,y,t), \end{aligned} \end{aligned}$$
(4.6)

where

$$\begin{aligned}& f^{i,j,k}_{1}(x,y,t)=\frac{\partial P_{L_{1},i}^{(\alpha_{1},\beta _{1})}(x)}{\partial x}P_{L_{2},j}^{(\alpha_{2},\beta_{2})}(y)P_{T,k}^{(\alpha _{3},\beta_{3})}(t), \\& f^{i,j,k}_{2}(x,y,t)=P_{L_{1},i}^{(\alpha_{1},\beta_{1})}(x) \frac{\partial P_{L_{2},j}^{(\alpha_{2},\beta_{2})}(y)}{\partial y}P_{T,k}^{(\alpha _{3},\beta_{3})}(t), \\& f^{i,j,k}_{3}(x,y,t)=P_{L_{1},i}^{(\alpha_{1},\beta _{1})}(x))P_{L_{2},j}^{(\alpha_{2},\beta_{2})}(y) \frac{\partial P_{T,k}^{(\alpha_{3},\beta_{3})}(t)}{\partial t}. \end{aligned}$$

The second spatial partial derivatives \(\frac{\partial^{2} u(x,y,t)}{\partial x^{2}}\) and \(\frac{\partial^{2} u(x,y,t)}{\partial y^{2}}\) are given by

$$\begin{aligned}& \begin{aligned}\frac{\partial^{2} u(x,y,t)}{\partial x^{2}} &=\sum _{i=0}^{N}\sum_{j=0}^{M} \sum_{j=0}^{K}a_{i,j,k}f^{i,j,k}_{4}(x,y,t), \end{aligned} \end{aligned}$$
(4.7)
$$\begin{aligned}& \begin{aligned}\frac{\partial^{2} u(x,y,t)}{\partial y^{2}} &=\sum _{i=0}^{N}\sum_{j=0}^{M} \sum_{j=0}^{K}a_{i,j,k}f^{i,j,k}_{5}(x,y,t), \end{aligned} \end{aligned}$$
(4.8)

where

$$\begin{aligned}& f^{i,j,k}_{4}(x,y,t)=\frac{\partial^{2} P_{L_{1},i}^{(\alpha_{1},\beta _{1})}(x)}{\partial x^{2}}P_{L_{2},j}^{(\alpha_{2},\beta _{2})}(y)P_{T,k}^{(\alpha_{3},\beta_{3})}(t), \\& f^{i,j,k}_{5}(x,y,t)=P_{L_{1},i}^{(\alpha_{1},\beta_{1})}(x) \frac{\partial ^{2} P_{L_{2},j}^{(\alpha_{2},\beta_{2})}(y)}{\partial y^{2}}P_{T,k}^{(\alpha _{3},\beta_{3})}(t). \end{aligned}$$

Moreover, the Riemann-Liouville fractional derivatives \(D^{1-\gamma }_{t} \frac{\partial^{2} u(x,y,t)}{\partial x^{2}}\) and \(D^{1-\gamma}_{t} \frac{\partial^{2} u(x,y,t)}{\partial y^{2}}\) are given by

$$\begin{aligned}& \begin{aligned} D^{1-\gamma}_{t} \frac{\partial^{2} u(x,y,t)}{\partial x^{2}}&=\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{j=0}^{K}a_{i,j,k}f^{i,j,k}_{6}(x,y,t), \end{aligned} \end{aligned}$$
(4.9)
$$\begin{aligned}& \begin{aligned} D^{1-\gamma}_{t} \frac{\partial^{2} u(x,y,t)}{\partial y^{2}}&=\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{j=0}^{K}a_{i,j,k}f^{i,j,k}_{7}(x,y,t), \end{aligned} \end{aligned}$$
(4.10)

where

$$\begin{aligned}& f^{i,j,k}_{6}(x,y,t)=\frac{\partial^{2} P_{L_{1},i}^{(\alpha_{1},\beta _{1})}(x)}{\partial x^{2}}P_{L_{2},j}^{(\alpha_{2},\beta_{2})}(y)D^{1-\gamma }_{t} P_{T,k}^{(\alpha_{3},\beta_{3})}(t), \\& f^{i,j,k}_{7}(x,y,t)=P_{L_{1},i}^{(\alpha_{1},\beta_{1})}(x) \frac{\partial ^{2} P_{L_{2},j}^{(\alpha_{2},\beta_{2})}(y)}{\partial y^{2}}D^{1-\gamma}_{t} P_{T,k}^{(\alpha_{3},\beta_{3})}(t). \end{aligned}$$

Therefore, adopting (4.3)-(4.6) enables one to write (4.1) in the form

$$\begin{aligned}& \sum_{i=0}^{N} \sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} f^{i,j,k}_{3}(x,y,t) \\& \quad = \sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} f^{i,j,k}_{4}(x,y,t)+\sum_{i=0}^{N} \sum_{j=0}^{M}\sum _{k=0}^{K}a_{i,j,k} f^{i,j,k}_{5}(x,y,t) \\& \quad \quad{} +\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} f^{i,j,k}_{6}(x,y,t)+\sum_{i=0}^{N} \sum_{j=0}^{M}\sum _{k=0}^{K}a_{i,j,k} f^{i,j,k}_{7}(x,y,t) \\& \quad \quad{} +H(x,y,t), \quad (x,y, t)\in [0,L_{1}] \times[0,L_{2}]\times[0,T]. \end{aligned}$$
(4.11)

Moreover, the collocation treatments of the initial-boundary conditions immediately give

$$ \begin{aligned} &u(x,y,0)=\sum _{i=0}^{N}\sum_{j=0}^{M} \sum_{k=0}^{K}a_{i,j,k} f^{i,j,k}_{0}(x,y,0)=g_{0}(x,y), \\ &u(0,y,t)=\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} f^{i,j,k}_{0}(0,y,t)=g_{1}(y,t), \\ &u(L_{1},y,t)=\sum_{i=0}^{N} \sum_{j=0}^{M}\sum _{k=0}^{K}a_{i,j,k} f^{i,j,k}_{0}(L_{1},y,t)=g_{2}(y,t), \\ &u(x,0,t)=\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} f^{i,j,k}_{0}(x,0,t)=g_{3}(x,t), \\ &u(x,L_{2},t)=\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} f^{i,j,k}_{0}(x,L_{2},t)=g_{4}(x,t). \end{aligned} $$
(4.12)

In the proposed method, the residual of (4.1) is set to be zero at \((N-1)\times(M-1)\times K\) of the collocation points

$$ \begin{aligned} \sum_{i=0}^{N} \sum_{j=0}^{M}\sum _{k=0}^{K}F^{i,j,k}_{r,s,\varsigma} a_{i,j,k}&=H \bigl(x^{(\alpha_{1},\beta _{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},t^{(\alpha_{3},\beta _{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} r=1,\ldots,N-1,\\ s=1,\ldots,M-1,\\ \varsigma=1,\ldots,K, \end{array}\displaystyle \right . \end{aligned} $$
(4.13)

where

$$ \begin{aligned}[b]F^{i,j,k}_{r,s,\varsigma} &= f^{i,j,k}_{3} \bigl(x^{(\alpha _{1},\beta_{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr)-f^{i,j,k}_{4} \bigl(x^{(\alpha_{1},\beta _{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},t^{(\alpha_{3},\beta _{3})}_{T,M,\varsigma} \bigr) \\ &\quad{} -f^{i,j,k}_{5} \bigl(x^{(\alpha_{1},\beta_{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta _{2})}_{L_{2},M,s},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma } \bigr)-f^{i,j,k}_{6} \bigl(x^{(\alpha_{1},\beta_{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta _{2})}_{L_{2},M,s},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr) \\ &\quad{}-f^{i,j,k}_{7} \bigl(x^{(\alpha_{1},\beta_{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta _{2})}_{L_{2},M,s},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr), \end{aligned} $$
(4.14)

and from the initial conditions, we have, namely, \((1 + N + 2 K N + M (1 + 2 K + N))\) algebraic equations

$$\begin{aligned}& \sum_{i=0}^{N} \sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} f^{i,j,k}_{0} \bigl(x^{(\alpha_{1},\beta _{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},0 \bigr)= g_{0} \bigl(x^{(\alpha _{1},\beta_{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s} \bigr),\quad \left \{ \textstyle\begin{array}{l} r=1,\ldots,N-1,\\ s=1,\ldots,M-1, \end{array}\displaystyle \right . \\& \sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} ^{i,j}f^{i,j,k}_{0} \bigl(0,y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr)= g_{1} \bigl(y^{(\alpha_{2},\beta _{2})}_{L_{2},M,s},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} s=0,\ldots,M,\\ \varsigma=0,\ldots,K, \end{array}\displaystyle \right . \\& \sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} ^{i,j}f^{i,j,k}_{0} \bigl(L_{1},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr)= g_{2} \bigl(y^{(\alpha_{2},\beta _{2})}_{L_{2},M,s},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} s=0,\ldots,M,\\ \varsigma=0,\ldots,K, \end{array}\displaystyle \right . \\& \sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} ^{i,j}f^{i,j,k}_{0} \bigl(x^{(\alpha_{1},\beta_{1})}_{L_{1},N,r},0,t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr)= g_{3} \bigl(x^{(\alpha_{1},\beta _{1})}_{L_{1},N,r},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} r=1,\ldots,N-1,\\ \varsigma=0,\ldots,K, \end{array}\displaystyle \right . \\& \sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} ^{i,j}f^{i,j,k}_{0} \bigl(x^{(\alpha_{1},\beta_{1})}_{L_{1},N,r},L_{2},t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr)= g_{4} \bigl(x^{(\alpha_{1},\beta _{1})}_{L_{1},N,r},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} r=1,\ldots,N-1,\\ \varsigma=0,\ldots,K, \end{array}\displaystyle \right . \end{aligned}$$
(4.15)

and this, in turn, yields \((M+1)\times(N+1)\times(K+1)\) algebraic equations

$$ \begin{aligned}&\sum_{i=0}^{N} \sum_{j=0}^{M}\sum _{k=0}^{K}F^{i,j,k}_{r,s,\varsigma} a_{i,j,k}=H \bigl(x^{(\alpha _{1},\beta_{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} r=1,\ldots,N-1,\\ s=1,\ldots,M-1,\\ \varsigma=1,\ldots,K, \end{array}\displaystyle \right . \\ &\sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} f^{i,j,k}_{0} \bigl(x^{(\alpha_{1},\beta _{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},0 \bigr)=g_{0} \bigl(x^{(\alpha _{1},\beta_{1})}_{L_{1},N,r},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s} \bigr),\quad \left \{ \textstyle\begin{array}{l} r=1,\ldots,N-1,\\ s=1,\ldots,M-1, \end{array}\displaystyle \right . \\ & \sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} ^{i,j}f^{i,j,k}_{0} \bigl(0,y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr)=g_{1} \bigl(y^{(\alpha_{2},\beta _{2})}_{L_{2},M,s},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} s=0,\ldots,M,\\ \varsigma=0,\ldots,K, \end{array}\displaystyle \right . \\ & \sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} ^{i,j}f^{i,j,k}_{0} \bigl(L_{1},y^{(\alpha_{2},\beta_{2})}_{L_{2},M,s},t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr)=g_{2} \bigl(y^{(\alpha_{2},\beta _{2})}_{L_{2},M,s},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} s=0,\ldots,M,\\ \varsigma=0,\ldots,K, \end{array}\displaystyle \right . \\ & \sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} ^{i,j}f^{i,j,k}_{0} \bigl(x^{(\alpha_{1},\beta_{1})}_{L_{1},N,r},0,t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr)=g_{3} \bigl(x^{(\alpha_{1},\beta _{1})}_{L_{1},N,r},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} r=1,\ldots,N-1,\\ \varsigma=0,\ldots,K, \end{array}\displaystyle \right . \\ & \sum_{i=0}^{N}\sum _{j=0}^{M}\sum_{k=0}^{K}a_{i,j,k} ^{i,j}f^{i,j,k}_{0} \bigl(x^{(\alpha_{1},\beta_{1})}_{L_{1},N,r},L_{2},t^{(\alpha _{3},\beta_{3})}_{T,M,\varsigma} \bigr)=g_{4} \bigl(x^{(\alpha_{1},\beta _{1})}_{L_{1},N,r},t^{(\alpha_{3},\beta_{3})}_{T,M,\varsigma} \bigr),\quad \left \{ \textstyle\begin{array}{l} r=1,\ldots,N-1,\\ \varsigma=0,\ldots,K. \end{array}\displaystyle \right . \end{aligned} $$
(4.16)

The previous system of algebraic equations can easily be solved. After the coefficients \(a_{i,j,k}\) are determined, we compute the approximate solution \(u_{N,M,K}(x,y,t)\) at any value of \((x,y,t)\) in the given domain.

5 Numerical results and comparisons

This section listed several numerical examples to demonstrate the accuracy of the proposed method. Also, we compare our numerical results with the existing numerical results [41–44]. The obtained results of these examples show that the proposed method, by selecting a few number nodes, has a high level of accuracy.

The difference between the measured value of the approximate solution and the exact solution is defined as the absolute error (AE), given by

$$ \begin{aligned} E(x,t)=\bigl\vert u(x,t)-u_{N,M}(x,t) \bigr\vert , \end{aligned} $$
(5.1)

where \(u(x,t)\) and \(u_{N,M}(x,t)\) are the exact and the approximate solutions at the point \((x,t)\), respectively.

Moreover, the maximum absolute error (MAE) is given by

$$ \begin{aligned} \mathrm{MAE}=\operatorname {Max}\bigl\{ E(x,t): \forall(x,t)\in[0,L]\times[0,T] \bigr\} . \end{aligned} $$
(5.2)

Example 1

Consider the FSFP-HGSGF of the following form [41]:

$$ \begin{aligned} &\frac{\partial u(x,t)}{\partial t}=D_{t}^{1-\gamma} \biggl(\frac {\partial^{2}u(x,t)}{\partial x^{2}} \biggr)+ \frac{\partial ^{2}u(x,t)}{\partial x^{2}} \\ &\hphantom{\frac{\partial u(x,t)}{\partial t}=}{}+e^{x} \biggl(( \gamma+2)t^{1+\gamma}-\frac {\Gamma(\gamma+3)}{\Gamma(2\gamma+2)}t^{2\gamma+1}-t^{\gamma +2} \biggr), \\ &u(0,t) = t^{\gamma+2}, \quad\quad u(1,t)=e t^{\gamma+2}, \quad t\in [0,1], \\ &u(x,0) =0,\quad x\in[0,1], \end{aligned} $$
(5.3)

where the exact solution is given by \(u(x,t) = e^{x} t^{\gamma+2}\).

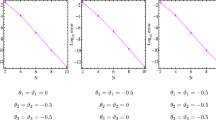
In Table 1, we display a comparison based on the MAEs between our results at \(\alpha _{1}=\beta _{1}=\frac{1}{2}\), \(\alpha _{2}=\beta _{2}=0\) with various choices of N, M, and γ and those in [41]. Figure 1 compares graphically the curves of numerical and exact solutions of problem (5.3) for the different values of t at \(N=8\), \(M=32\), \(\alpha _{1}=\beta _{1}=\alpha _{2}=\beta _{2}=0\), and \(\gamma=0.4\). Moreover, we represent in Figure 2 the logarithmic graphs of MAEs (i.e., \(\log_{10} M_{E}\)) obtained by the present method with different values of N (\(N=M=4, 6, \ldots, 26\)) where \(\alpha _{1}=\beta _{1}=\alpha _{2}=\beta _{2}=0\). This demonstrates that the proposed method leads to an accurate approximation and yields exponential convergence rates.

Figure 1
figure 1

t -direction curves of exact and numerical solutions of problem ( 5.3 ).

Full size image
Figure 2
figure 2

\(\pmb{M_{E}}\) convergence of problem ( 5.3 ).

Full size image
Table 1 The MAEs of Example  1
Full size table

Example 2

Here, we test the following FSFP-HGSGF [42]:

$$ \begin{aligned} &\frac{\partial u(x,t)}{\partial t}=D_{t}^{1-\gamma} \biggl(\frac {\partial^{2}u(x,t)}{\partial x^{2}} \biggr)+ \frac{\partial ^{2}u(x,t)}{\partial x^{2}}+e^{x} t^{\gamma} \biggl(\gamma-\frac {\Gamma(\gamma+2) t^{\gamma}}{\Gamma(2 \gamma+1)}-t+1 \biggr),\quad \\ &u(0,t) = t^{\gamma+1}, \quad\quad u(1,t)=e t^{\gamma+1}, \quad t\in [0,1], \\ &u(x,0) =0,\quad x\in[0,1]. \end{aligned} $$
(5.4)

The exact solution of this problem has the form

$$u(x,t) = t^{\gamma+1} e^{x}. $$

Table 2, displays the MAEs using the present method together with the results obtained in [42] for different choices of N, M. From the results of this example, we observe that the approximate solution by our method is better than those obtained in [42].

Table 2 The MAEs of Example  2
Full size table

Example 3

Finally, we introduce the two-dimensional FSFP-HGSGF [43, 44]:

$$ \begin{aligned} &\frac{\partial u(x,y,t)}{\partial t}= D_{t}^{1-\gamma} \biggl(\frac {\partial^{2}u(x,y,t)}{\partial x^{2}}+\frac{\partial ^{2}u(x,y,t)}{\partial y^{2}} \biggr)+ \frac{\partial ^{2}u(x,y,t)}{\partial x^{2}}+ \frac{\partial^{2}u(x,y,t)}{\partial y^{2}} \\ &\hphantom{\frac{\partial u(x,y,t)}{\partial t}=}{} +\frac{t^{\gamma} e^{x+y} (\Gamma(2 \gamma+2) (\gamma-2 t+1)-2 (2 \gamma+1) \Gamma(\gamma+2) t^{\gamma} )}{\Gamma(2 \gamma+2)},\quad \\ &u(0,y,t) = e^{y}t^{\gamma+1}, \quad\quad u(1,y,t)=e^{y+1} t^{\gamma+1}, \quad(y, t)\in[0,1]\times[0,1], \\ &u(x,0,t) = e^{x}t^{\gamma+1}, \quad\quad u(x,1,t)=e^{x+1} t^{\gamma+1}, \quad(x, t)\in[0,1]\times[0,1], \\ &u(x,y,0) =0,\quad (x,y) \in[0,1]\times[0,1]. \end{aligned} $$
(5.5)

The exact solution of this problem has the form

$$u(x,y,t) = t^{1+\gamma} e^{x+y}. $$

In the last example, a comparison is listed in Table 3 between the MAEs for Example 3 obtained in [43] and the results obtained in this paper at different choices of N, M. The results confirm the high accuracy of the present scheme. A comparison between the results obtained by the novel method with the corresponding results obtained by the compact finite difference scheme [44] is displayed in Table 4, with \(\alpha_{1}=\beta_{1}=\alpha_{2}=\beta_{2}=\frac{1}{2}\), and \(\alpha _{3}=\beta_{3}=0\).

Table 3 The MAEs of Example  3
Full size table
Table 4 The MAEs of Example 3
Full size table

In Figure 3, we plot the space graph of the AE for Example 3 for \(N=M=6\), \(K=24\), and \(\alpha_{1}=\beta_{1}=\alpha_{2}=\beta_{2}=\frac {1}{2}\), \(\alpha_{3}=\beta_{3}=0\) at \(t=0.5\). The AE curve of Example 3 for \(N=M=6\), \(K=24\), and \(\alpha_{1}=\beta_{1}=\alpha_{2}=\beta_{2}=\frac {1}{2}\), \(\alpha_{3}=\beta_{3}=0\) is sketched in Figure 4 at \(x=0.5\) and \(y=0.25\).

Figure 3
figure 3

Space graph of the AE for Example  3 .

Full size image
Figure 4
figure 4

The AE versus t in Example  3 .

Full size image

6 Conclusion

We have presented a new space-time spectral algorithm based on the shifted Jacobi-Gauss-Lobatto and the shifted Jacobi-Gauss-Radau collocation schemes. Based on the numerical results given in Section 5, it has been concluded that the obtained results are excellent in terms of accuracy for all tested problems. We have outlined the implementation of spectral collocation method for solving similar problems with a one- or two-dimensional space. In addition, this method may be extended to related problems. Furthermore, the proposed spectral method might be further developed by considering the generalized Laguerre or modified generalized Laguerre polynomials to solve similar problems in semi-infinite spatial intervals.