Existence and exponential stability of pseudo almost automorphic solutions for Cohen-Grossberg neural networks with mixed delays

Abstract

In this paper, we consider a class of Cohen-Grossberg neural networks with mixed delays. Different from the previous literature, we study the existence and exponential stability of pseudo almost automorphic solutions for the suggested system. Our method is mainly based on the Banach fixed point theorem and the Lyapunov functional method. Moreover, a numerical example is given to show the effectiveness of the main results.

1 Introduction

The concept of pseudo almost automorphy was first introduced by Xiao et al. [1], which is a natural generalization of almost periodicity and almost automorphy. Meanwhile, the pseudo almost automorphic functions are more general and complicated than pseudo almost periodic functions and almost automorphic functions. The existence and stability of almost automorphic and pseudo almost automorphic solutions are the most attractive topics in qualitative theory of differential equations due to their significance and applications in physics, mechanics and mathematical biology. In recent years, the existence and stability of almost automorphic and pseudo almost automorphic solutions on different kinds of differential equations have been widely studied; for instance, see [2–6] and the references therein.

On the other hand, there have been extensive results on the problem of the existence and uniqueness of solutions or their dynamic analysis for Cohen-Grossberg type neural networks; see [7–12] among others. However, there have been few results for pseudo almost automorphic functions since they are more general and complicated than both pseudo almost periodic functions and almost automorphic functions. To the best of our knowledge, the existence of pseudo almost automorphic solution to Cohen-Grossberg neural networks (CGNNs) with variable coefficients and mixed delays has not been studied.

Motivated by the above discussion, in this paper we study the existence, uniqueness, and exponential stability of pseudo almost automorphic solutions for the following CGNNs:

$$\begin{aligned} \textstyle\begin{cases} x_{i}^{\prime}(t)=-a_{i}( x_{i}(t))[b_{i}(x_{i}(t)) -\sum_{j=1}^{m}c_{ij}(t)f_{j}(x_{j}(t))-\sum_{j=1}^{m}d_{ij}(t)g_{j}(x_{j}(t-\tau_{ij}(t))) \\ \hphantom{x_{i}^{\prime}(t)=}{}-\sum_{j=1}^{m}p_{ij}(t)\int_{-\infty }^{t}G_{ij}(t-s)h_{j}(x_{j}(s))\,ds-I_{i}(t)],\quad t\geq0, \\ x_{i}(t)=\Phi_{i}(t),\quad t< 0. \end{cases}\displaystyle \end{aligned}$$

(1)

By using the Banach fixed point theorem and the Lyapunov functional method, we prove the existence, uniqueness, and exponential stability of pseudo almost automorphic solutions to system (1).

The organization of this paper is as follows. In Section 2, we introduce some basic definitions, assumptions and preliminary lemmas. In Section 3, we establish the existence and uniqueness of pseudo almost automorphic solution of system (1) by applying the Banach fixed point theorem. In Section 4, the exponential stability result is shown. In Section 5, an example is provided to demonstrate the effectiveness of the main results. In Section 6, we conclude the paper with some general remarks.

2 Preliminaries

In this section, we introduce some basic definitions, assumptions and preliminary lemmas. Throughout this paper, unless otherwise specified, $\mathbb{R}$ denotes the set of real numbers, $\mathbb{R}^{+}$ denotes the set of non-negative real numbers, $\mathbb{R}^{m}$ denotes the real m-dimensional space.

Definition 2.1

[5]

A continuous function $f:\mathbb{R} \rightarrow\mathbb{R}^{m}$ is said to be almost automorphic if for every sequence of $(s_{n}^{\prime})_{n\in N}$, there exists a subsequence $(s_{n})_{n\in N}\subset(s_{n}^{\prime})_{n\in N}$ such that

$$\begin{aligned} g(t)= \lim_{n\rightarrow\infty}f(t+s_{n}) \end{aligned}$$

is well defined for each $t\in\mathbb{R}$, and

$$\begin{aligned} \lim_{n\rightarrow\infty}g(t-s_{n})=f(t) \end{aligned}$$

for each $t\in\mathbb{R}$. The collection of all almost automorphic functions is denoted by $\operatorname {AA}(\mathbb{R},\mathbb{R}^{m})$. It is well known that the set $\operatorname {AA}(\mathbb{R},\mathbb{R}^{m})$ is a Banach space with supremum norm.

Remark 2.1

The function g in Definition 2.1 is measurable but not necessarily continuous. Moreover, if g is continuous, then f is uniformly continuous. Besides, if the convergence in Definition 2.1 is uniform in $t\in\mathbb{R}$, then f is almost periodic. For example, Bocher [13] gave an almost automorphic but not almost periodic function defined in the integer set

$$\varphi(n)=\operatorname {signum}(\cos2\pi n \theta), \quad -\infty< n< \infty, $$

where θ is a non-rational number.

Definition 2.2

[5]

A continuous function $f:\mathbb{R} \times\mathbb{R}^{m}\rightarrow\mathbb{R}^{m}$ is said to be almost automorphic if for every sequence of $(s_{n}^{\prime})_{n\in N}$, there exists a subsequence $(s_{n})_{n\in N}\subset(s_{n}^{\prime})_{n\in N}$ such that

$$\begin{aligned} g(t,x)= \lim_{n\rightarrow\infty}f(t+s_{n},x) \end{aligned}$$

is well defined for each $t\in\mathbb{R}$, $x\in\mathbb{R}^{m}$, and

$$\begin{aligned} \lim_{n\rightarrow\infty}g(t-s_{n},x)=f(t,x) \end{aligned}$$

for each $t\in\mathbb{R}$, $x\in\mathbb{R}^{m}$. The collection of all almost automorphic functions is denoted by $\operatorname {AA}(\mathbb{R}\times \mathbb{R}^{m},\mathbb{R}^{m})$.

Define the class of functions $\operatorname {PAA}_{0}(\mathbb{R}, \mathbb{R}^{m})$ and $\operatorname {PAA}_{0}(\mathbb{R}\times\mathbb{R}^{m}, \mathbb{R}^{m})$ as follows:

$$\begin{aligned}& \operatorname {PAA}_{0} \bigl(\mathbb{R},\mathbb{R}^{m} \bigr)= \biggl\{ f \in \operatorname {BC}\bigl(\mathbb{R}, \mathbb{R}^{m} \bigr)\Bigm| \lim _{T\rightarrow+\infty} \frac{1}{2T} \int _{-T}^{T} \bigl\Vert f(t) \bigr\Vert \,dt=0 \biggr\} , \\& \operatorname {PAA}_{0} \bigl(\mathbb{R}\times\mathbb{R}^{m}, \mathbb{R}^{m} \bigr) \\& \quad = \biggl\{ f\in \operatorname {BC}\bigl(\mathbb{R}\times \mathbb{R}^{m}, \mathbb{R}^{m} \bigr)\Bigm| \lim _{T\rightarrow+\infty}\frac{1}{2T} \int _{-T}^{T} \bigl\Vert f(t, x) \bigr\Vert \,dt=0, \forall x\in\mathbb{R}^{m} \biggr\} , \end{aligned}$$

where $\operatorname {BC}(\mathbb{R},\mathbb{R}^{m})$ (or $\operatorname {BC}(\mathbb{R}\times \mathbb{R}^{m}, \mathbb{R}^{m})$) is the collection of the set of bounded continuous functions from $\mathbb{R}$ (or $\mathbb{R}\times\mathbb{R}^{m}$) to $\mathbb{R}^{m}$.

Definition 2.3

[4, 6]

A function $f\in \operatorname {BC}(\mathbb{R}, \mathbb{R}^{m})$ (or $\operatorname {BC}(\mathbb{R}\times \mathbb{R}^{m}, \mathbb{R}^{m})$) is called pseudo almost automorphic if it can be expressed as

$$f=f_{1}+f_{0}, $$

where $f_{1}\in \operatorname {AA}(\mathbb{R},\mathbb{R}^{m})$ (or $\operatorname {AA}(\mathbb{R}\times\mathbb{R}^{m}, \mathbb{R}^{m})$) and $f_{0}\in \operatorname {PAA}_{0}(\mathbb{R},\mathbb{R}^{m})$ (or $\operatorname {PAA}_{0}(\mathbb{R}\times\mathbb{R}^{m}, \mathbb{R}^{m})$). The collection of such functions will be denoted by $\operatorname {PAA}(\mathbb{R},\mathbb{R}^{m})$ or $\operatorname {PAA}(\mathbb{R}\times \mathbb{R}^{m}, \mathbb{R}^{m})$).

Remark 2.2

Obviously, we have

$$\operatorname {AP}\bigl(\mathbb{R},\mathbb{R}^{m} \bigr)\subset \operatorname {AA}\bigl(\mathbb{R}, \mathbb{R}^{m} \bigr)\subset \operatorname {PAA}\bigl(\mathbb{R},\mathbb{R}^{m} \bigr)\subset \operatorname {BC}\bigl(\mathbb{R},\mathbb{R}^{m} \bigr), $$

where $\operatorname {AP}(\mathbb{R},\mathbb{R}^{m})$ is the collection of all almost periodic functions from $\mathbb{R}$ to $\mathbb{R}^{m}$.

Lemma 2.1

[4, 6]

Suppose $f,g\in \operatorname {PAA}(\mathbb{R},\mathbb{R}^{m})$ and for all $\tau\in\mathbb{R}$, then the following holds true:

• (1) $f+g, \tau f, f_{\tau}(t,x):=f(t+\tau,x)\textit{ and }f(-t,x)\in \operatorname {PAA}(\mathbb{R},\mathbb{R}^{m})$.

• (2) f is bounded for each $x\in\mathbb{R}^{m}$.

Lemma 2.2

[4, 6]

Let $f=f_{1}+f_{0}\in \operatorname {PAA}(\mathbb{R} \times\mathbb{R}^{m}, \mathbb{R}^{m})$, where $f_{1}(t,\varphi)\in \operatorname {AA}(\mathbb{R}\times\mathbb{R}^{m}, \mathbb{R}^{m})$, $f_{0}(t,\varphi)\in \operatorname {PAA}_{0}(\mathbb{R}\times \mathbb{R}^{m}, \mathbb{R}^{m})$. Moreover, assume that the following conditions are satisfied:

• (a) $f_{1}(t,\varphi)$ is uniformly continuous for any bounded subset $K\subset\mathbb{R}^{m}$ and $t\in\mathbb{R}$.

• (b) $f(t,\varphi)$ is uniformly continuous (or satisfies the Lipschitz condition) for every bounded subset $K\subset \mathbb{R}^{m}$ and $t\in\mathbb{R}$.

Then the function $\zeta: t\rightarrow\zeta(t)=f(t,\varphi(t))$ is pseudo almost automorphic for all $\varphi\in \operatorname {PAA}(\mathbb{R},\mathbb{R}^{m})$.

Lemma 2.3

[4, 6]

Assume that $f\in \operatorname {AA}(\mathbb{R},\mathbb{R}^{m})$ and $\phi\in C(\mathbb{R}^{m},\mathbb{R}^{n})$, then $\phi(f(t))\in \operatorname {AA}(\mathbb{R},\mathbb{R}^{n})$.

Lemma 2.4

(Lebesgue’s dominated convergence theorem)

Let $\{f_{n}\}$ be a sequence of real-valued measurable functions on a measurable set E. Suppose that the sequence converges pointwise to a function f and is dominated by some integrable function F in the sense that $\vert f_{n}(x)\vert \leq F(x)$ for all numbers n in the index set of the sequence and all points $x \in E$. Then f is integrable and $\lim_{n\to\infty} \int_{E} f_{n}(x)\,dx =\int_{E} f(x) \,dx$.

Throughout this paper, we make the following assumptions.

$(H_{1})$::

$a_{i}(u)$ are uniformly continuous functions and there are positive constants $a_{i}^{+}$, $a_{i}^{-}$ such that

$$0 < a_{i}^{-}\leq a_{i}(u)\leq a_{i}^{+}, \quad \forall u\in\mathbb{R}, i = 1, 2, \ldots, m. $$

$(H_{2})$::

$b_{i}(u)$, $i = 1, 2, \ldots, m$, are uniformly continuous functions and there exist positive constants $b_{i}^{-}$, $b_{i}^{+}$ such that

$$b_{i}^{-} \leq\frac{b_{i}(u)-b_{i}(v)}{u-v}\leq b_{i}^{+},\quad\forall u, v\in\mathbb{R}, u\neq v, b_{i}(0)=0. $$

$(H_{3})$::

$c_{ij}(t), d_{ij}(t), p_{ij}(t), I_{i}(t) \in C(\mathbb{R},\mathbb{R})$, $\tau_{ij}(t)\in C(\mathbb{R},\mathbb{R}^{+})$ are pseudo almost automorphic functions, where $i,j= 1, 2, \ldots, m$.

$(H_{4})$::

The delay kernel function $G_{ij}: [0,+\infty)\rightarrow [0,+\infty)$ is piecewise continuous and integrable, and there exists a real number $\varepsilon_{0}$ such that

$$\int_{0}^{+\infty}G_{ij}(u)\,du=1,\quad\quad \int_{0}^{\infty}e^{\varepsilon_{0} u}G_{ij}(u)\,du< + \infty ,\quad i,j= 1, 2, \ldots, m. $$

$(H_{5})$::

The functions $f_{j}(u), g_{j}(u), h_{j}(u) \in C(\mathbb{R},\mathbb{R})$ satisfy the Lipschitz condition, i.e., there are nonnegative constants $L_{j}^{f}$, $L_{j}^{g}$, and $L_{j}^{h}$ such that

$$\begin{aligned}& \bigl\vert f_{j}(u)-f_{j}(v) \bigr\vert \leq L_{j}^{f}\vert u-v\vert ,\quad \forall u, v\in\mathbb{R}, j = 1, 2, \ldots, m, \\& \bigl\vert g_{j}(u)-g_{j}(v) \bigr\vert \leq L_{j}^{g}\vert u-v\vert , \quad \forall u, v\in\mathbb{R}, j = 1, 2, \ldots, m, \\& \bigl\vert h_{j}(u)-h_{j}(v) \bigr\vert \leq L_{j}^{h}\vert u-v\vert , \quad \forall u, v\in\mathbb{R}, j = 1, 2, \ldots, m. \end{aligned}$$

Constants $c_{ij}^{+}$, $d_{ij}^{+}$, $p_{ij}^{+}$, $I_{i}^{+}$ ($i=1,2,\ldots,m$) are denoted as follows:

$$\begin{aligned}& \sup_{t\in\mathbb{R}}c_{ij}(t)=c_{ij}^{+}>0,\quad\quad \sup_{t\in\mathbb{R}}d_{ij}(t)=d_{ij}^{+}>0, \\& \sup_{t\in \mathbb{R}}p_{ij}(t)=p_{ij}^{+}>0,\quad\quad \sup_{t\in\mathbb{R}}I_{i}(t)=I_{i}^{+}>0. \end{aligned}$$

3 The existence and uniqueness of pseudo almost automorphic solutions

In this section, we study the existence and uniqueness of pseudo almost automorphic solutions of system (1).

By the assumption $(H_{1})$, we know that the antiderivative of $\frac {1}{a_{i}(x_{i}(t))}$ exists. Then we choose an antiderivative $F_{i}(x_{i})$ of $\frac{1}{a_{i}(x_{i}(t))}$ with $F_{i}(0)=0$. It is clear that $F_{i}^{\prime}(x_{i})=\frac{1}{a_{i}(x_{i}(t))}$. Since $a_{i}(x_{i}(t))>0$, we see that $F_{i}(x_{i})$ is increasing on $x_{i}$ and there exists an inverse function $F_{i}^{-1}(x_{i})$ of $F_{i}(x_{i})$, which is continuous and differential. Moreover, we have $(F_{i}^{-1}(x_{i}))^{\prime}=a_{i}(x_{i}(t))$. Denoting $F_{i}^{\prime}(x_{i})x_{i}^{\prime}(t)=\frac{x_{i}^{\prime}(t)}{a_{i}(x_{i}(t))}:= u_{i}^{\prime}(t)$, we get $x_{i}(t)=F_{i}^{-1}(u_{i}(t))$. Then it follows from (1) that

$$\begin{aligned} \textstyle\begin{cases} u_{i}^{\prime}(t)=-b_{i}(F_{i}^{-1}(u_{i}(t)))+\sum_{j=1}^{m}c_{ij}(t)f_{j}(F_{j}^{-1}(u_{j}(t))) \\ \hphantom{u_{i}^{\prime}(t)=}{}+\sum_{j=1}^{m}d_{ij}(t)g_{j}(F_{j}^{-1}(u_{j}(t-\tau_{ij}(t)))) \\ \hphantom{u_{i}^{\prime}(t)=}{}+\sum_{j=1}^{m}p_{ij}(t)\int_{-\infty }^{t}G_{ij}(t-s)h_{j}(F_{j}^{-1}(u_{j}(s)))\,ds+I_{i}(t),\quad t\geq0, \\ u_{i}(t)=F_{i}(\Phi_{i}(t)),\quad t< 0. \end{cases}\displaystyle \end{aligned}$$

(2)

By the assumption $(H_{2})$ and the mean value theorem, we obtain

$$b_{i} \bigl(F_{i}^{-1} \bigl(u_{i}(t) \bigr) \bigr)= \bigl[b_{i} \bigl(F_{i}^{-1} \bigl( \theta_{i} u_{i}(t) \bigr) \bigr) \bigr]^{\prime}u_{i}(t):= b_{i}^{\sim} \bigl(u_{i}(t) \bigr)u_{i}(t), $$

where $\theta_{i}$ is a constant such that $0\leq\theta_{i} \leq 1$. Substituting this into (2) yields,

$$ \textstyle\begin{cases} u_{i}^{\prime}(t)=-b_{i}^{\sim}(u_{i}(t))u_{i}(t)+\sum_{j=1}^{m}c_{ij}(t)f_{j}(F_{j}^{-1}(u_{j}(t))) \\ \hphantom{u_{i}^{\prime}(t)=}{}+\sum_{j=1}^{m}d_{ij}(t)g_{j}(F_{j}^{-1}(u_{j}(t-\tau_{ij}(t)))) \\ \hphantom{u_{i}^{\prime}(t)=}{}+\sum_{j=1}^{m}p_{ij}(t)\int_{-\infty }^{t}G_{ij}(t-s)h_{j}(F_{j}^{-1}(u_{j}(s)))\,ds+I_{i}(t), \quad t\geq0, \\ u_{i}(t)=F_{i}(\Phi_{i}(t)), \quad t< 0. \end{cases} $$

(3)

Obviously, system (1) has a unique pseudo almost automorphic solution, if and only if system (3) has a unique pseudo almost automorphic solution. So we only need to consider the pseudo almost automorphic solution of system (3). It follows from the Lagrange theorem that

$$\bigl\vert F_{i}^{-1}(u)-F_{i}^{-1}(v) \bigr\vert = \bigl\vert \bigl[F_{i}^{-1} \bigl(v+ \theta_{i}(u-v) \bigr) \bigr]^{\prime}(u-v) \bigr\vert = \bigl\vert a_{i} \bigl(v+\theta_{i} (u-v) \bigr) \bigr\vert \vert u-v\vert . $$

By $(H_{1})$ again, we get

$$a_{i}^{-}\vert u-v\vert \leq \bigl\vert F_{i}^{-1}(u)-F_{i}^{-1}(v) \bigr\vert \leq a_{i}^{+}\vert u-v\vert . $$

Combined with $(H_{2})$, we have

$$b_{i}^{-} a_{i}^{-}\leq \bigl[b_{i} \bigl(F_{i}^{-1}(\cdot) \bigr) \bigr]^{\prime}\leq b_{i}^{+} a_{i}^{+}. $$

In order to prove our main result, we present the following lemma.

Lemma 3.1

Assume that the assumption $(H_{4})$ holds and $\varphi_{j} (\cdot)\in \operatorname {PAA}(\mathbb{R},\mathbb{R})$. Then

$$\Psi_{ij}: t\rightarrow \int_{-\infty}^{t}G_{ij}(t-s) \varphi_{j}(s)\,ds $$

belongs to $\operatorname {PAA}(\mathbb{R},\mathbb{R})$.

Proof

Noting that $\varphi_{j} (\cdot)\in \operatorname {PAA}(\mathbb{R},\mathbb{R})$, then it follows from Definition 2.3 that

$$\varphi_{j}=\varphi_{j1}+\varphi_{j0}, $$

and so

$$\begin{aligned} \Psi_{ij} =& \int_{-\infty}^{t}G_{ij}(t-s) \varphi_{j1}(s)\,ds+ \int_{-\infty }^{t}G_{ij}(t-s) \varphi_{j0}(s)\,ds \\ =&\Psi_{ij1}+\Psi_{ij0}. \end{aligned}$$

The rest of the proof is divided into two steps.

Step 1: We first prove $\Psi_{ij1}\in \operatorname {AA}(\mathbb{R},\mathbb{R})$.

Let $(s_{n}^{\prime})$ be a sequence of real numbers. By Definition 2.1, there exists a subsequence $(s_{n})$ of $(s_{n}^{\prime})$ such that for all $t,s\in\mathbb{R}$,

$$\begin{aligned} \lim_{n\rightarrow \infty}\varphi_{j1}(t+s_{n})= \overline{\varphi}_{j1}(t),\quad\quad \lim_{n\rightarrow\infty} \overline{ \varphi}_{j1} (t-s_{n})= \varphi_{j1}(t). \end{aligned}$$

Define

$$\overline{\Psi}_{ij1}: t\rightarrow \int_{-\infty}^{t}G_{ij}(t-s)\overline{ \varphi}_{j1}(s)\,ds. $$

Then we have

$$\begin{aligned}& \bigl\vert \Psi_{ij1}(t+s_{n})-\overline{ \Psi}_{ij1}(t) \bigr\vert \\& \quad = \biggl\vert \int_{-\infty}^{t+s_{n}}G_{ij}(t+s_{n}-s) \varphi_{j1}(s)\,ds- \int _{-\infty}^{t}G_{ij}(t-s)\overline{ \varphi}_{j1}(s)\,ds \biggr\vert \\& \quad = \biggl\vert \int_{-\infty}^{t}G_{ij}(t-v) \varphi_{j1}(v+s_{n})\,dv- \int_{-\infty }^{t}G_{ij}(t-s)\overline{ \varphi}_{j1}(s)\,ds \biggr\vert \\& \quad \leq \int_{-\infty}^{t}G_{ij}(t-s) \bigl\vert \varphi_{j1}(s+s_{n})-\overline {\varphi}_{j1}(s) \bigr\vert \,ds. \end{aligned}$$

By the Lebesgue dominated convergence theorem and $(H_{4})$, we obtain

$$\lim_{n\rightarrow \infty}\Psi_{ij1}(t+s_{n})=\overline{ \Psi}_{ij1}(t). $$

Similarly, we have

$$\lim_{n\rightarrow\infty} \overline{\Psi}_{ij1}(t-s_{n})= \Psi_{ij1}(t), $$

which implies that $\Psi_{ij1}: t\rightarrow \int_{-\infty}^{t}G_{ij}(t-s)\varphi_{j1}(s)\,ds$ belongs to $\operatorname {AA}(\mathbb{R},\mathbb{R})$.

Step 2: Next, we prove that $\Psi_{ij0}\in \operatorname {PAA}_{0}(\mathbb{R},\mathbb{R})$. In fact,

$$\begin{aligned} \lim_{T\rightarrow+\infty}\frac{1}{2T} \int_{-T}^{T}\vert \Psi_{ij0}\vert \,dt =& \sup_{t\in R} \lim_{T\rightarrow +\infty}\frac{1}{2T} \int_{-T}^{T} \biggl\vert \int_{-\infty}^{t}G_{ij}(t-s) \varphi_{j0}(s)\,ds \biggr\vert \,dt \\ \leq& \sup_{t\in R} \lim_{T\rightarrow +\infty} \frac{1}{2T} \int_{0}^{+\infty} \bigl\vert G_{ij}(u) \bigr\vert \int_{-T+u}^{T+u} \bigl\vert \varphi_{j0}(v) \bigr\vert \,dv\,du =0, \end{aligned}$$

which implies that $\Psi_{ij0}\in \operatorname {PAA}_{0}(\mathbb{R},\mathbb{R})$.

Therefore, we see that $\Psi_{ij}: t\rightarrow \int_{-\infty}^{t}G_{ij}(t-s)\varphi_{j}(s)\,ds$ belongs to $\operatorname {PAA}(\mathbb{R},\mathbb{R})$. □

Theorem 3.1

Suppose that assumptions $(H_{1})$-$(H_{5})$ hold, and $f_{j}$, $g_{j}$, $h_{j}$ are as in Lemma  2.2. Then system (1) has a unique pseudo almost automorphic solution in the region $\Vert z-z_{0}\Vert \leq\frac{\delta I }{1-\delta}$, if $\delta<1$, where

$$\begin{aligned}& \delta= \max_{1\leq i\leq m} \Biggl\{ \frac{1}{b_{i}^{-}a_{i}^{-}}\sum _{j=1}^{m} \bigl(L_{j}^{f}c_{ij}^{+}+L_{j}^{g}d_{ij}^{+}+L_{j}^{h}p_{ij}^{+} \bigr)a_{j}^{+} \Biggr\} < 1, \\& I= \max_{1\leq i\leq m} \biggl\{ \frac{I_{i}^{+}}{b_{i}^{-}a_{i}^{-}} \biggr\} , \\& z_{0}= \biggl( \int_{-\infty}^{t}I_{1}(s)e^{-\int_{s}^{t}b_{1}^{\sim}(\phi_{1}(\tau ))\,d\tau}\,ds, \ldots, \int_{-\infty}^{t}I_{m}(s)e^{-\int_{s}^{t}b_{m}^{\sim }(\phi_{m}(\tau))\,d\tau}\,ds \biggr). \end{aligned}$$

Proof

For all $z(t)=\phi(t)^{T}=(\phi_{1}(t),\ldots,\phi_{m}(t))^{T}\in \operatorname {PAA}(\mathbb{R},\mathbb{R}^{m})$, and for any given function $u_{i}(t)\in \operatorname {PAA}(\mathbb{R},\mathbb{R}^{m})$, we define the nonlinear operator

$$\begin{aligned} T: z(t)\rightarrow T(z) (t)= \bigl(x_{\phi}(t) \bigr)^{T}, \end{aligned}$$

(4)

where

$$\begin{aligned} x_{\phi_{i}}(t) =& \int_{-\infty}^{t}e^{-\int_{s}^{t}b_{i}^{\sim }(u_{i}(\tau))\,d\tau} \Biggl[\sum _{j=1}^{m}c_{ij}(s)f_{j} \bigl(F_{j}^{-1} \bigl(\phi _{j}(s) \bigr) \bigr) \\ &{} +\sum_{j=1}^{m}d_{ij}(s)g_{j}\bigl(F_{j}^{-1} \bigl(\phi _{j} \bigl(s-\tau_{ij}(s) \bigr) \bigr)\bigr) \\ &{} +\sum_{j=1}^{m}p_{ij}(s) \int_{-\infty }^{s}G_{ij}(s-v)h_{j} \bigl(F_{j}^{-1} \bigl(\phi_{j}(v) \bigr) \bigr)\,dv+I_{i}(s) \Biggr]\,ds. \end{aligned}$$

Now, we prove that

$$T:\operatorname {PAA}\bigl(\mathbb{R},\mathbb{R}^{m} \bigr)\rightarrow \operatorname {PAA}\bigl( \mathbb{R},\mathbb{R}^{m} \bigr). $$

For $z(t)\in \operatorname {PAA}(\mathbb{R},\mathbb{R}^{m})$, it follows from Lemmas 2.1, 2.2, 3.1 that the function

$$\begin{aligned} E_{ij}: s \rightarrow&\sum_{j=1}^{m}c_{ij}(s)f_{j} \bigl(F_{j}^{-1} \bigl(\phi _{j}(s) \bigr) \bigr)+ \sum_{j=1}^{m}d_{ij}(s)g_{j}\bigl(F_{j}^{-1} \bigl(\phi_{j} \bigl(s-\tau _{ij}(s) \bigr) \bigr)\bigr) \\ &{}+\sum_{j=1}^{m}p_{ij}(s) \int_{-\infty }^{s}G_{ij}(s-v)h_{j} \bigl(F_{j}^{-1} \bigl(\phi_{j}(v) \bigr) \bigr)\,dv+I_{i}(s) \end{aligned}$$

belongs to $\operatorname {PAA}(\mathbb{R},\mathbb{R})$. Therefore, we can write

$$x_{\phi_{i}}(t)= \int_{-\infty}^{t}e^{-\int_{s}^{t}b_{i}^{\sim }(u_{i}(\tau))\,d\tau}E_{ij}(s)\,ds. $$

From Definition 2.3, we have $E_{ij}=E_{ij1}+E_{ij0}$, where $E_{ij1}\in \operatorname {AA}(\mathbb{R},\mathbb{R})$, $E_{ij0}\in \operatorname {PAA}_{0}(\mathbb{R},\mathbb{R})$. Then

$$\begin{aligned} x_{\phi_{i}}(t) =& \int_{-\infty}^{t}e^{-\int_{s}^{t}b_{i}^{\sim }(u_{i}(\tau))\,d\tau}E_{ij1}(s)\,ds+ \int_{-\infty}^{t}e^{-\int _{s}^{t}b_{i}^{\sim}(u_{i}(\tau))\,d\tau}E_{ij0}(s)\,ds \\ =&T_{ij1}+T_{ij0}, \end{aligned}$$

where $T_{ij1}=\int_{-\infty}^{t}e^{-\int_{s}^{t}b_{i}^{\sim}(u_{i}(\tau ))\,d\tau}E_{ij1}(s)\,ds$, $T_{ij0}=\int_{-\infty}^{t}e^{-\int_{s}^{t}b_{i}^{\sim}(u_{i}(\tau ))\,d\tau}E_{ij0}(s)\,ds$.

From the assumptions $(H_{1})$ and $(H_{2})$ and Lemma 2.3, the function $\rho_{i}: \tau\rightarrow b_{i}^{\sim}(u_{i}(\tau))$ belongs to $\operatorname {AA}(\mathbb{R},\mathbb{R})$.

Let $(s_{n}^{\prime})$ be a sequence of real numbers. Then it follows from Definition 2.1 that there exists a subsequence $(s_{n})$ of $(s_{n}^{\prime})$ such that for all $t,s\in\mathbb{R}$

$$\lim_{n\rightarrow\infty}\rho_{i}(t+s_{n})= \overline{ \rho}_{i}(t), \quad\quad \lim_{n\rightarrow \infty} \overline{\rho} _{i}(t-s_{n})= \rho_{i}(t), $$

and

$$\lim_{n\rightarrow \infty}E_{ij1}(t+s_{n})= \overline{E}_{ij}(t), \quad\quad \lim_{n\rightarrow\infty} \overline{E}_{ij} (t-s_{n})= E_{ij1}(t). $$

Taking

$$\overline{T}_{ij1}(t)= \int_{-\infty}^{t}e^{-\int_{s}^{t}\overline{\rho }_{i}(\tau)\,d\tau}\overline{E}_{ij1}(s)\,ds, $$

then we have

$$\begin{aligned} T_{ij1}(t)-\overline{T}_{ij1}(t) =& \int_{-\infty}^{t+s_{n}}e^{-\int _{s}^{t+s_{n}}\rho_{i}(\tau)\,d\tau}E_{ij1}(s)\,ds- \int_{-\infty}^{t}e^{-\int_{s}^{t}\overline{\rho}_{i}(\tau)\,d\tau }\overline{E}_{ij1}(s)\,ds \\ =& \int_{-\infty}^{t+s_{n}}e^{-\int_{s-s_{n}}^{t}\rho _{i}(\sigma+s_{n})\,d\sigma}E_{ij1}(s)\,ds- \int_{-\infty}^{t}e^{-\int_{s}^{t}\overline{\rho}_{i}(\tau)\,d\tau }\overline{E}_{ij1}(s)\,ds \\ =& \int_{-\infty}^{t}e^{-\int_{u}^{t}\rho_{i}(\sigma +s_{n})\,d\sigma}E_{ij1}(u+s_{n})\,du- \int_{-\infty}^{t}e^{-\int_{s}^{t}\overline{\rho}_{i}(\tau)\,d\tau }\overline{E}_{ij1}(s)\,ds \\ =& \int_{-\infty}^{t}e^{-\int_{u}^{t}\rho_{i}(\sigma +s_{n})\,d\sigma}E_{ij1}(u+s_{n})\,du- \int_{-\infty}^{t}e^{-\int_{u}^{t}\rho_{i}(\sigma+s_{n})\,d\sigma }\overline{E}_{ij1}(u)\,du \\ &{} + \int_{-\infty}^{t}e^{-\int_{u}^{t}\rho_{i}(\sigma +s_{n})\,d\sigma}\overline{E}_{ij1}(u)\,du- \int_{-\infty}^{t}e^{-\int_{s}^{t}\overline{\rho}_{i}(\sigma)\,d\sigma }\overline{E}_{ij1}(u)\,du \\ =& \int_{-\infty}^{t}e^{-\int_{u}^{t}\rho_{i}(\sigma +s_{n})\,d\sigma} \bigl[E_{ij1}(u+s_{n})- \overline{E}_{ij1}(u) \bigr]\,du \\ &{} + \int_{-\infty}^{t} \bigl[e^{-\int_{u}^{t}\rho_{i}(\sigma +s_{n})\,d\sigma}-e^{-\int_{s}^{t}\overline{\rho}_{i}(\sigma)\,d\sigma } \bigr]\overline{E}_{ij1}(u)\,du. \end{aligned}$$

By the Lebesgue dominated convergence theorem, we get

$$\lim_{n\rightarrow \infty}T_{ij1}(t+s_{n})= \overline{T}_{ij1}(t). $$

Similarly, we can prove that

$$\lim_{n\rightarrow\infty} \overline{T}_{ij1}(t-s_{n})= T_{ij1}(t), $$

which implies that the function $T_{ij1}(t)$ belongs to $\operatorname {AA}(\mathbb{R},\mathbb{R})$.

On the other hand, we have

$$\begin{aligned}& \lim_{T\rightarrow+\infty}\frac{1}{2T} \int_{-T}^{T} \biggl\vert \int _{-\infty}^{t}e^{-\int_{s}^{t}b_{i}^{\sim}(u_{i}(\tau))\,d\tau }E_{ij0}(s)\,ds \biggr\vert \,dt \\& \quad \leq \lim_{T\rightarrow+\infty}\frac{1}{2T} \int_{-T}^{T} \biggl\vert \int _{-T}^{t}e^{-\int_{s}^{t}b_{i}^{\sim}(u_{i}(\tau))\,d\tau }E_{ij0}(s)\,ds \biggr\vert \,dt \\& \quad\quad{} + \lim_{T\rightarrow+\infty}\frac{1}{2T} \int_{-T}^{T} \biggl\vert \int _{-\infty}^{-T}e^{-\int_{s}^{t}b_{i}^{\sim}(u_{i}(\tau))\,d\tau }E_{ij0}(s)\,ds \biggr\vert \,dt \\& \quad \leq \lim_{T\rightarrow+\infty}\frac{1}{2T} \int_{-T}^{T} \bigl\Vert E_{ij0}(t) \bigr\Vert \,dt \int_{-T}^{t}e^{-b_{i}^{-}a_{i}^{-}(t-s) }\,ds \\& \quad\quad{} + \lim_{T\rightarrow+\infty}\frac{ \sup_{t\in R}\vert E_{ij0}(t)\vert }{2T} \int_{-T}^{T}\,dt \biggl( \int_{-\infty }^{-T} \bigl\vert e^{-b_{i}^{-}a_{i}^{-}(t-s)} \bigr\vert \,ds \biggr) \\& \quad \leq \lim_{T\rightarrow+\infty}\frac {1}{2Tb_{i}^{-}a_{i}^{-}} \int_{-T}^{T} \bigl\Vert E_{ij0}(t) \bigr\Vert \,dt+ \lim_{T\rightarrow+\infty}\frac{ \sup_{t\in R}\vert E_{ij0}(t)\vert }{2T(b_{i}^{-}a_{i}^{-})^{2}} \bigl(1-e^{-b_{i}^{-}a_{i}^{-}(2T)} \bigr) \\& \quad = 0+ \lim_{T\rightarrow+\infty}\frac{ \sup_{t\in R}\vert E_{ij0}(t)\vert }{2T(b_{i}^{-}a_{i}^{-})^{2}} \bigl(1-e^{-b_{i}^{-}a_{i}^{-}(2T)} \bigr) \\& \quad =0. \end{aligned}$$

Thus, $T_{ij0}\in \operatorname {PAA}_{0}(\mathbb{R},\mathbb{R})$. Then $x_{\phi_{i}}(t)\in \operatorname {PAA}(\mathbb{R},\mathbb{R})$. Therefore $z_{(\phi)^{T}}(t)\in \operatorname {PAA}(\mathbb{R},\mathbb{R}^{m})$.

Setting $B^{\ast}=\{z\mid z\in \operatorname {PAA}(\mathbb{R},\mathbb{R}^{m}), \Vert z-z_{0}\Vert \leq\frac{\delta I }{1-\delta}\}$, then we obtain

$$\begin{aligned} \Vert z_{0}\Vert =& \sup_{t\in \mathbb{R}} \max _{1\leq i\leq m} \biggl\vert \int_{-\infty}^{t}I_{i}(s)e^{-\int_{s}^{t}b_{i}^{\sim}(u_{i}(\tau ))\,d\tau}\,ds \biggr\vert \\ \leq& \sup_{t\in\mathbb{R}} \max_{1\leq i\leq m} \biggl\vert \int_{-\infty}^{t}I_{i}(s)e^{- b_{i}^{-}a_{i}^{-}(t-s)}\,ds \biggr\vert \\ \leq& \max_{1\leq i\leq m} \biggl(\frac{I_{i}^{+}}{ b_{i}^{-}a_{i}^{-}} \biggr) \\ =&I. \end{aligned}$$

For every $z\in B^{\ast}$, we get

$$\Vert z\Vert \leq \Vert z-z_{0}\Vert +\Vert z_{0} \Vert \leq\frac{\delta I }{1-\delta}+I=\frac{ I }{1-\delta}. $$

Second, we will prove that the mapping T is a self-mapping from $B^{\ast}$ to $B^{\ast}$. Actually, for every $z\in B^{\ast}$, noting that $F_{j}^{-1}(0)=0$ and $\vert F_{j}^{-1}(u)-F_{j}^{-1}(v)\vert \leq a_{j}^{+}\vert u-v\vert$, we have

$$\begin{aligned} \bigl\Vert T(z)-z_{0} \bigr\Vert =& \sup_{t\in R} \max_{1\leq i\leq m} \Biggl\vert \int_{-\infty}^{t}e^{-\int_{s}^{t}b_{i}^{\sim}(u_{i}(\tau))\,d\tau } \Biggl[ \sum _{j=1}^{m}c_{ij}(s)f_{j} \bigl(F_{j}^{-1} \bigl(\phi_{j}(s) \bigr) \bigr) \\ &{}+ \sum_{j=1}^{m}d_{ij}(s)g_{j} \bigl(F_{j}^{-1} \bigl(\phi _{j} \bigl(s- \tau_{ij}(s) \bigr) \bigr) \bigr) \\ &{} +\sum_{j=1}^{m}p_{ij}(s) \int_{-\infty }^{s}G_{ij}(s-v)h_{j} \bigl(F_{j}^{-1} \bigl(\phi_{j}(v) \bigr) \bigr)\,dv \Biggr]\,ds \Biggr\vert \\ \leq& \max_{1\leq i\leq m} \Biggl\{ \frac{1}{b_{i}^{-}a_{i}^{-}}\sum _{j=1}^{m} \bigl(L_{j}^{f}c_{ij}^{+}+L_{j}^{g}d_{ij}^{+}+L_{j}^{h}p_{ij}^{+} \bigr)a_{j}^{+} \Biggr\} \Vert z\Vert \\ =&\delta \Vert z\Vert \\ \leq&\frac{\delta I }{1-\delta}, \end{aligned}$$

which implies that $T(z)(t)\in B^{\ast}$, and therefore T is a self-mapping from $B^{\ast}$ to $B^{\ast}$.

Finally, we will prove that the mapping T is a contraction mapping.

In view of $(H_{1})$-$(H_{5})$, we have, for any $z, z^{\ast}\in B^{\ast}$, where $z=(\phi_{1},\ldots,\phi_{m})^{T}$, $z^{\ast}=(\phi_{1}^{\ast}, \ldots,\phi_{m}^{\ast})^{T}$,

$$\begin{aligned}& \bigl\Vert T(z)-T \bigl(z^{\ast}\bigr) \bigr\Vert \\& \quad = \sup_{t\in\mathbb{R}} \max_{1\leq i\leq m} \Biggl\vert \int_{-\infty}^{t}e^{-\int_{s}^{t}b_{i}^{\sim}(u_{i}(\tau))\,d\tau }\Biggl\{ \sum _{j=1}^{n}c_{ij}(s) \bigl[f_{j} \bigl(F_{j}^{-1} \bigl(\phi_{j}(s) \bigr) \bigr)-f_{j} \bigl(F_{j}^{-1} \bigl( \phi_{j}^{\ast}(s) \bigr) \bigr) \bigr] \\& \quad\quad{} +\sum _{j=1}^{n}d_{ij}(s) \bigl[g_{j}(F_{j}^{-1} \bigl(\phi _{j} \bigl(s-\tau_{ij}(s) \bigr) \bigr)-g_{j}\bigl(F_{j}^{-1} \bigl(\phi_{j}^{\ast}\bigl(s-\tau_{ij}(s) \bigr) \bigr)\bigr) \bigr] \\& \quad\quad{} +\sum_{j=1}^{n}p_{ij}(s) \int_{-\infty }^{s}G_{ij}(s-v) \bigl[h_{j} \bigl(F_{j}^{-1} \bigl( \phi_{j}(v) \bigr) \bigr)-h_{j} \bigl(F_{j}^{-1} \bigl(\phi _{j}^{\ast}(v) \bigr) \bigr)\bigr]\,dv \Biggr\} \,ds \Biggr\vert \\& \quad \leq \max_{1\leq i\leq m} \Biggl\{ \frac{1}{b_{i}^{-}a_{i}^{-}}\sum _{j=1}^{m} \bigl(L_{j}^{f}c_{ij}^{+}+L_{j}^{g}d_{ij}^{+}+L_{j}^{h}p_{ij}^{+} \bigr)a_{j}^{+} \Biggr\} \bigl\Vert z-z^{\ast}\bigr\Vert \\& \quad =\delta \bigl\Vert z-z^{\ast}\bigr\Vert . \end{aligned}$$

Noting that $\delta<1$, we see that the mapping T is a contraction mapping. Hence, there exists a unique fixed point $\varphi^{\ast}\in B^{\ast}$ such that $T\varphi^{\ast}= \varphi^{\ast}$. Take $u_{i}(t)=\varphi_{i}(t)$ in (4). Thus $(\varphi^{\ast})^{T}$ is a pseudo almost automorphic solution of system (3) in $B^{\ast}$. This completes the proof. □

Corollary 3.1

In (1), assume that $c_{ij}(t), d_{ij}(t), p_{ij}(t), I_{i}(t) \in C(\mathbb{R},\mathbb{R})$, $\tau_{ij}(t)\in C(\mathbb{R},\mathbb {R}^{+})$ are all almost automorphic functions. $a_{i}(u)\in C(\mathbb {R},\mathbb{R})$, $b_{i}(u)\in \operatorname {BC}(\mathbb{R},\mathbb{R})$ and there are positive constants $a_{i}^{+}$, $a_{i}^{-}$, $b_{i}^{-}$, $b_{i}^{+}$ such that

$$\begin{aligned}& 0 < a_{i}^{-}\leq a_{i}(u)\leq a_{i}^{+},\quad \forall u\in\mathbb{R}, \\& b_{i}^{-} \leq\frac{b_{i}(u)-b_{i}(v)}{u-v}\leq b_{i}^{+},\quad u\neq v, \forall u, v\in\mathbb{R} ,b_{i}(0)=0. \end{aligned}$$

where $i,j= 1, 2, \ldots, m$. If the conditions $(H_{4})$-$(H_{5})$ hold, and then system (1) has a unique almost automorphic solution.

Remark 3.1

Recently, there have been some results on the existence and uniqueness of almost automorphic solutions to cellular neural networks; for instance see [2] and [3]. However, to the best of our knowledge, there is not any paper to consider the existence and uniqueness of pseudo almost automorphic solution to Cohen-Grossberg type neural networks (1). Actually in CGNNs (1), taking $a_{i}(u)\equiv1$, $b_{i}(x_{i}(t))=d_{i}(t)x_{i}(t)$, $a_{ij}(t)=c_{ij}(t)$, $d_{ij}(t)=b_{ij}(t)$, $p_{ij}(t)=c_{ij}(t)$, we can get the corresponding recurrent neural networks of [3]:

$$\begin{aligned} \textstyle\begin{cases} x_{i}^{\prime}(t)=-d_{i}(t)x_{i}(t)+\sum_{j=1}^{m}a_{ij}(t)f_{j}(x_{j}(t))+\sum_{j=1}^{m}b_{ij}(t)g_{j}(x_{j}(t-\tau_{ij}(t))) \\ \hphantom{x_{i}^{\prime}(t)=}{} +\sum_{j=1}^{m}c_{ij}(t)\int_{-\infty }^{t}G_{ij}(t-s)h_{j}(x_{j}(s))\,ds+J_{i}(t), \quad t\geq0,\\ x_{i}(t)=\hat{x}_{i}(t),\quad t< 0. \end{cases}\displaystyle \end{aligned}$$

(5)

It should be mentioned that only the almost automorphic solution was studied in [3], and pseudo almost automorphic solution was not discussed in [3]. So, our result can be regarded as a generalization and improvement of that obtained in [3].

Remark 3.2

In [2], the authors studied the existence of k-almost automorphic sequence solution to the discrete analog of the cellular neural networks,

$$\begin{aligned} \textstyle\begin{cases} x_{i}^{\prime}(t)=-a_{i}(t)x_{i}(t)+\sum_{j=1}^{m}b_{ij}(t)f_{j}(x_{j}([\frac{t}{k}]k-[\frac{\alpha _{ij}}{k}]k))+I_{i}(t),\\ x_{i}(t)=\phi_{i}(t), \quad t\in[-\alpha_{ij},0]. \end{cases}\displaystyle \end{aligned}$$

It should be mentioned that the activity function $f_{j}$ in [2] was required to be global Lipschitz continuous and boundedness. However, in this paper we remove the condition of boundedness imposed on the activity functions $f_{j}$, $g_{j}$, $h_{j}$ of (1).

4 The exponential stability of pseudo almost automorphic solution

In this section, we study the exponential stability of the unique pseudo almost automorphic solution of the system (1).

Theorem 4.1

Suppose that assumptions $(H_{1})$-$(H_{5})$ hold. Let $z^{*}(t)=(x_{1}^{*}(t),\ldots, x_{m}^{*}(t))$ be a unique pseudo almost automorphic solution to system (1) in $B^{*}$. If $\dot{\tau}_{ij}(t)\leq\tau^{*}<1$, $\tau_{ij}(t)\leq\tau$, and

$$(H_{6}):\quad -\overline{b}_{i}+\sum _{j=1}^{m}c_{ji}^{+}L_{i}^{f}+ \sum_{j=1}^{m}\frac{d_{ji}^{+}L_{i}^{g}}{1-\tau^{*}} +\sum _{j=1}^{m}p_{ji}^{+}L_{i}^{h}< 0, $$

then there exist constants $\varepsilon_{0}>0$ and $k>0$ such that for any solution $x(t)$ of system (1), we have $\sum_{i=1}^{m}\vert x_{i}(t)-x_{i}^{*}(t)\vert \leq k e^{-\varepsilon_{0} t }$, $t>0$.

Proof

Let $z^{*}(t)=(x_{1}^{*}(t),\ldots, x_{m}^{*}(t))$ be a unique pseudo almost automorphic solution to system (1) in $B^{*}$. $z(t)=(x_{1}(t),\ldots, x_{m}(t))$ is any solution of system (1). Consider the Lyapunov functional $V(t)=V_{1}(t)+V_{2}(t)$, where

$$\begin{aligned}& V_{1}(t) = e^{\varepsilon t}\sum_{i=1}^{m} \biggl\vert \int_{\overline{x}_{i}(t)}^{x_{i}(t)}\frac {1}{a_{i}(s)}\,ds \biggr\vert , \\& V_{2}(t) = \sum_{i=1}^{m}\sum _{j=1}^{m} \biggl\{ \frac {d_{ij}^{+}L_{j}^{g}}{1-\tau^{*}} \int_{t-\tau_{ij}(t)}^{t} \bigl\vert x_{j}(s)-x_{j}^{*}(s) \bigr\vert e^{\varepsilon(s+\tau) }\,ds \\& \hphantom{V_{2}(t) =}{} +p_{ij}^{+}L_{j}^{h} \int_{0}^{\infty}G_{ij}(u) \int_{t-u}^{t} \bigl\vert x_{j}(s)-x_{j}^{*}(s) \bigr\vert e^{\varepsilon(s+u)}\,ds\,du \biggr\} . \end{aligned}$$

Calculating the Dini derivative $D^{+}V_{i}(t)$, $i=1,2$, we have

$$\begin{aligned}& D^{+}V_{1}(t) \\ & \quad \leq \varepsilon e^{\varepsilon t}\sum_{i=1}^{m} \biggl\vert \int_{x_{i}^{*}(t)}^{x_{i}(t)}\frac {1}{a_{i}(s)}\,ds \biggr\vert +e^{\varepsilon t}\sum_{i=1}^{m} \operatorname {Sgn}\bigl(x_{i}(t)-x_{i}^{*}(t) \bigr) \biggl[ \frac{\dot {x}_{i}(t)}{a_{i}(x_{i}(t))}-\frac{\dot{x}_{i}^{*}(t)}{a_{i}(x_{i}^{*}(t))} \biggr] \\ & \quad \leq \varepsilon e^{\varepsilon t}\sum_{i=1}^{m} \frac{1}{\overline{a}_{i}} \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert +e^{\varepsilon t}\sum_{i=1}^{m} \operatorname {Sgn}\bigl(x_{i}(t)-x_{i}^{*}(t) \bigr) \\ & \quad\quad{} \times \Biggl\{ - \bigl[b_{i} \bigl(x_{i}(t) \bigr)-b_{i} \bigl(x_{i}^{*}(t) \bigr) \bigr]+ \sum_{j=1}^{m}c_{ij}(t) \bigl[f_{j} \bigl(x_{j}(t) \bigr)-f_{j} \bigl(x_{j}^{*}(t) \bigr) \bigr] \\ & \quad\quad{} +\sum_{j=1}^{m}d_{ij}(t) \bigl[g_{j} \bigl(x_{j} \bigl(t-\tau _{ij}(t) \bigr) \bigr)-g_{j} \bigl(x_{j}^{*} \bigl(t- \tau_{ij}(t) \bigr) \bigr) \bigr] \\ & \quad\quad{} +\sum_{j=1}^{m}p_{ij}(t) \int_{-\infty }^{t}G_{ij}(t-s) \bigl[h_{j} \bigl(x_{j}(s) \bigr)-h_{j} \bigl(x_{j}^{*}(s) \bigr) \bigr]\,ds \Biggr\} \\ & \quad = \varepsilon e^{\varepsilon t}\sum_{i=1}^{m} \frac{1}{\overline{a}_{i}} \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert +e^{\varepsilon t}\sum_{i=1}^{m} \operatorname {Sgn}\bigl(x_{i}(t)-x_{i}^{*}(t) \bigr) \\ & \quad\quad{} \times \Biggl\{ -\frac {[b_{i}(x_{i}(t))-b_{i}(x_{i}^{*}(t))]}{x_{i}(t)-x_{i}^{*}(t)}\cdot \bigl(x_{i}(t)-x_{i}^{*}(t) \bigr)+\sum_{j=1}^{m}c_{ij}(t) \bigl[f_{j} \bigl(x_{j}(t) \bigr)-f_{j} \bigl(x_{j}^{*}(t) \bigr) \bigr] \\ & \quad\quad{} +\sum_{j=1}^{m}d_{ij}(t) \bigl[g_{j} \bigl(x_{j} \bigl(t-\tau _{ij}(t) \bigr) \bigr)-g_{j} \bigl(x_{j}^{*} \bigl(t- \tau_{ij}(t) \bigr) \bigr) \bigr] \\ & \quad\quad{} +\sum_{j=1}^{m}p_{ij}(t) \int_{0}^{\infty }G_{ij}(u) \bigl[h_{j} \bigl(x_{j}(t-u) \bigr)-h_{j} \bigl(x_{j}^{*}(t-u) \bigr) \bigr]\,du \Biggr\} \\ & \quad \leq e^{\varepsilon t}\sum_{i=1}^{m} \biggl(\frac{\varepsilon}{\overline{a}_{i}}-\overline {b}_{i} \biggr) \bigl\vert x_{i}(t)-x^{*}_{i}(t) \bigr\vert +e^{\varepsilon t}\sum _{i=1}^{m}\sum_{j=1}^{m}c_{ij}^{+}L_{j}^{f} \bigl\vert x_{j}(t)-x^{*}_{j}(t) \bigr\vert \\ & \quad\quad{} + e^{\varepsilon t}\sum_{i=1}^{m}\sum _{j=1}^{m}d_{ij}^{+}L_{j}^{g} \bigl\vert x_{j} \bigl(t-\tau _{ij}(t) \bigr)-x_{j}^{*} \bigl(t-\tau_{ij}(t) \bigr) \bigr\vert \\ & \quad\quad{} + e^{\varepsilon t}\sum_{i=1}^{m}\sum _{j=1}^{m}p_{ij}^{+}L_{j}^{h} \int_{0}^{\infty}G_{ij}(u) \bigl\vert x_{j}(t-u)-x_{j}^{*}(t-u) \bigr\vert \,du \\ & \quad = e^{\varepsilon t}\sum_{i=1}^{m} \Biggl( \frac{\varepsilon}{\overline{a}_{i}}-\overline {b}_{i}+\sum _{j=1}^{m}c_{ji}^{+}L_{i}^{f} \Biggr) \bigl\vert x_{i}(t)-x^{*}_{i}(t) \bigr\vert \\ & \quad\quad{} + e^{\varepsilon t}\sum_{i=1}^{m}\sum _{j=1}^{m}d_{ij}^{+}L_{j}^{g} \bigl\vert x_{j} \bigl(t-\tau _{ij}(t) \bigr)-x_{j}^{*} \bigl(t-\tau_{ij}(t) \bigr) \bigr\vert \\ & \quad\quad{} + e^{\varepsilon t}\sum_{i=1}^{m}\sum _{j=1}^{m}p_{ij}^{+}L_{j}^{h} \int_{0}^{\infty}G_{ij}(u) \bigl\vert x_{j}(t-u)-x_{j}^{*}(t-u) \bigr\vert \,du. \end{aligned}$$

Noting that $\frac{1-\dot{\tau}_{ij}(t)}{1-\tau^{*}}>1$ and $e^{\tau-\tau _{ij}(t)}>1$, we have

$$\begin{aligned} D^{+}V_{2}(t) =&\sum_{i=1}^{m} \sum_{j=1}^{m}\frac {d_{ij}^{+}L_{j}^{g}}{1-\tau^{*}} \bigl\vert x_{j}(t)-x_{j}^{*}(t) \bigr\vert e^{\varepsilon(t+\tau)} \\ &{}-\sum_{i=1}^{m}\sum _{j=1}^{m}\frac {d_{ij}^{+}L_{j}^{g}}{1-\tau^{*}} \bigl\vert x_{j} \bigl(t-\tau_{ij}(t) \bigr)-x_{j}^{*} \bigl(t- \tau_{ij}(t) \bigr) \bigr\vert e^{\varepsilon (t-\tau_{ij}(t)+\tau)} \bigl(1-\dot{ \tau}_{ij}(t) \bigr) \\ &{}+\sum_{i=1}^{m}\sum _{j=1}^{m}p_{ij}^{+}L_{j}^{h} \int _{0}^{\infty}G_{ij}(u) \bigl\vert x_{j}(t)-x_{j}^{*}(t) \bigr\vert e^{\varepsilon(t+u)}\,du \\ &{}-\sum_{i=1}^{m}\sum _{j=1}^{m}p_{ij}^{+}L_{j}^{h} \int _{0}^{\infty}G_{ij}(u) \bigl\vert x_{j}(t-u)-x_{j}^{*}(t-u) \bigr\vert e^{\varepsilon t}\,du \\ \leq& e^{\varepsilon t }\sum_{i=1}^{m}\sum _{j=1}^{m}\frac {d_{ij}^{+}L_{j}^{g}}{1-\tau^{*}}e^{\varepsilon\tau} \bigl\vert x_{j}(t)-x_{j}^{*}(t) \bigr\vert \\ &{}-e^{\varepsilon t }\sum_{i=1}^{m}\sum _{j=1}^{m}d_{ij}^{+}L_{j}^{g} \bigl\vert x_{j} \bigl(t-\tau_{ij}(t) \bigr)-x_{j}^{*} \bigl(t-\tau_{ij}(t) \bigr) \bigr\vert \\ &{}+e^{\varepsilon t }\sum_{i=1}^{m}\sum _{j=1}^{m}p_{ij}^{+}L_{j}^{h} \int_{0}^{\infty}G_{ij}(u)e^{\varepsilon u }\,du \bigl\vert x_{j}(t)-x_{j}^{*}(t) \bigr\vert \\ &{}-e^{\varepsilon t }\sum_{i=1}^{m}\sum _{j=1}^{m}p_{ij}^{+}L_{j}^{h} \int_{0}^{\infty }G_{ij}(u) \bigl\vert x_{j}(t-u)-x_{j}^{*}(t-u) \bigr\vert \,du. \end{aligned}$$

So it follows that

$$\begin{aligned} D^{+} \bigl(V_{1}(t)+V_{2}(t) \bigr) \leq& e^{\varepsilon t}\sum_{i=1}^{m} \Biggl( \frac{\varepsilon}{\overline{a}_{i}}-\overline {b}_{i}+\sum_{j=1}^{m}c_{ji}^{+}L_{i}^{f} \Biggr) \bigl\vert x_{i}(t)-x^{*}_{i}(t) \bigr\vert \\ &{}+e^{\varepsilon t }\sum_{i=1}^{m}\sum _{j=1}^{m}\frac {d_{ij}^{+}L_{j}^{g}}{1-\tau^{*}}e^{\varepsilon\tau} \bigl\vert x_{j}(t)-x_{j}^{*}(t) \bigr\vert \\ &{}+e^{\varepsilon t }\sum_{i=1}^{m}\sum _{j=1}^{m}p_{ij}^{+}L_{j}^{h} \int_{0}^{\infty}G_{ij}(u)e^{\varepsilon u }\,du \bigl\vert x_{j}(t)-x_{j}^{*}(t) \bigr\vert \\ =& e^{\varepsilon t}\sum_{i=1}^{m} \Biggl( \frac{\varepsilon}{\overline{a}_{i}}-\overline {b}_{i}+\sum _{j=1}^{m}c_{ji}^{+}L_{i}^{f} \Biggr) \bigl\vert x_{i}(t)-x^{*}_{i}(t) \bigr\vert \\ &{}+e^{\varepsilon t }\sum_{i=1}^{m}\sum _{j=1}^{m}\frac {d_{ji}^{+}L_{i}^{g}}{1-\tau^{*}}e^{\varepsilon\tau} \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert \\ &{}+e^{\varepsilon t }\sum_{i=1}^{m}\sum _{j=1}^{m}p_{ji}^{+}L_{i}^{h} \int_{0}^{\infty}G_{ji}(u)e^{\varepsilon u }\,du \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert . \end{aligned}$$

Namely,

$$\begin{aligned} D^{+}V(t) \leq& e^{\varepsilon t}\sum_{i=1}^{m} \Biggl[\frac{\varepsilon}{\overline {a}_{i}}-\overline{b}_{i}+\sum _{j=1}^{m}c_{ji}^{+}L_{i}^{f}+ \sum_{j=1}^{m}\frac{d_{ji}^{+}L_{i}^{g}}{1-\tau^{*}}e^{\varepsilon\tau} +\sum_{j=1}^{m}p_{ji}^{+}L_{i}^{h} \int_{0}^{\infty }G_{ji}(u)e^{\varepsilon u }\,du \Biggr] \\ &{} \times \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert . \end{aligned}$$

Define the function

$$H(\varepsilon):=\frac{\varepsilon}{\overline{a}_{i}}-\overline{b}_{i}+\sum _{j=1}^{m}c_{ji}^{+}L_{i}^{f}+ \sum_{j=1}^{m}\frac {d_{ji}^{+}L_{i}^{g}}{1-\tau^{*}}e^{\varepsilon\tau} +\sum_{j=1}^{m}p_{ji}^{+}L_{i}^{h} \int_{0}^{\infty }G_{ji}(u)e^{\varepsilon u }\,du,\quad \varepsilon\in[0,+\infty]. $$

By $(H_{6})$, we have

$$H(0)=-\overline{b}_{i}+\sum_{j=1}^{m}c_{ji}^{+}L_{i}^{f}+ \sum_{j=1}^{m}\frac{d_{ji}^{+}L_{i}^{g}}{1-\tau^{*}} +\sum _{j=1}^{m}p_{ji}^{+}L_{i}^{h}< 0. $$

Utilizing the continuity of the function $H(\cdot)$, there exists a real number $\varepsilon_{0}$ such that

$$H(\varepsilon_{0})= \frac{\varepsilon_{0}}{\overline{a}_{i}}-\overline {b}_{i}+ \sum_{j=1}^{m}c_{ji}^{+}L_{i}^{f}+ \sum_{j=1}^{m}\frac {d_{ji}^{+}L_{i}^{g}}{1-\tau^{*}}e^{\varepsilon_{0} \tau} +\sum_{j=1}^{m}p_{ji}^{+}L_{i}^{h} \int_{0}^{\infty }G_{ji}(u)e^{\varepsilon_{0} u }\,du< 0. $$

It means that $D^{+}V(t)<0$. Hence $V(t)< V(0)$, $t>0$. On the other hand,

$$V(t)\geq e^{\varepsilon_{0} t}\sum_{i=1}^{m} \biggl\vert \int_{\overline{x}_{i}(t)}^{x_{i}(t)}\frac {1}{a_{i}(s)}\,ds \biggr\vert \geq e^{\varepsilon_{0} t}\min_{1\leq i \leq m} \biggl\{ \frac{1}{a_{i}^{+}} \biggr\} \sum_{i=1}^{m} \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert . $$

So

$$\sum_{i=1}^{m} \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert \leq \frac{V(0)}{\min_{1\leq i \leq m} \{{a_{i}^{+}}^{-1} \}} e^{-\varepsilon_{0} t},\quad t>0. $$

It follows from the definition of $V(t)$ that

$$\begin{aligned} V(0) =&\sum_{i=1}^{m} \biggl\vert \int_{x_{i}^{*}(0)}^{x_{i}(0)}\frac {1}{a_{i}(s)}\,ds \biggr\vert + \sum_{i=1}^{m}\sum _{j=1}^{m} \biggl\{ \frac {d_{ji}^{+}L_{j}^{g}}{1-\tau^{*}} \int_{-\tau_{ij}(0)}^{0} \bigl\vert x_{j}(s)-x_{j}^{*}(s) \bigr\vert e^{\varepsilon_{0}(s+\tau) }\,ds \\ &{}+p_{ij}^{+}L_{j}^{h} \int_{0}^{\infty}G_{ij}(u) \int_{-u}^{0} \bigl\vert x_{j}^{*}(s)-x_{j}^{*}(s) \bigr\vert e^{\varepsilon_{0}(s+u)}\,ds\,du \biggr\} \\ \leq&\sum_{i=1}^{m}{\frac{\vert x_{i}(0)-x_{i}^{*}(0)\vert }{\overline {a}_{i}}}+ \sum_{i=1}^{m}\sum _{j=1}^{m} \biggl\{ \frac {d_{ij}^{+}L_{j}^{g}}{1-\tau^{*}} \int_{-\tau}^{0} e^{\varepsilon_{0}(s+\tau) }\,ds\sup _{(-\infty,0]} \bigl\{ \bigl\vert x_{j}(s)-x_{j}^{*}(s) \bigr\vert \bigr\} \\ &{}+p_{ij}^{+}L_{j}^{h} \int_{0}^{\infty}G_{ij}(u) \int_{-u}^{0} e^{\varepsilon_{0}(s+u)}\,ds\,du\sup _{(-\infty,0]} \bigl\{ \bigl\vert x_{j}(s)-x_{j}^{*}(s) \bigr\vert \bigr\} \biggr\} \\ \leq&\sum_{i=1}^{m} \Biggl[{ \frac{1}{\overline{a}_{i}}}+\sum_{j=1}^{m} \frac{d_{ji}^{+}L_{i}^{g}(e^{\varepsilon_{0}\tau}-1)}{\varepsilon _{0}(1-\tau^{*})} +p_{ji}^{+}L_{i}^{h} \int_{0}^{\infty}e^{\varepsilon_{0}u}G_{ji}(u)\,du- \frac {p_{ji}L_{i}^{h}}{\varepsilon_{0}} \Biggr] \\ &{}\times \max_{1\leq i \leq m}\sup_{(-\infty,0]} \bigl\{ \bigl\vert x_{i}(s)-x_{i}^{*}(s) \bigr\vert \bigr\} \\ :=&\alpha. \end{aligned}$$

So,

$$\sum_{i=1}^{m} \bigl\vert x_{i}(t)-x_{i}^{*}(t) \bigr\vert \leq \frac{\alpha}{\min_{1\leq i \leq m} \{{a_{i}^{+}}^{-1} \}} e^{-\varepsilon_{0} t}:=ke^{-\varepsilon_{0} t}, \quad t>0. $$

This completes the proof. □

Remark 4.1

In [3], sufficient conditions were obtained to ensure the existence and stability of an almost automorphic solution to recurrent neural networks (5) by using the Lebesgue dominated convergence theorem and Banach fixed theorem. It is worth pointing out that the authors in [3] assumed that the kernel $K_{ij}(\cdot)$ is almost automorphic and there exist $M > 0$ and $w > 0$ such that $K_{ij} (t)\leq M e^{-t \omega}$. However, in this paper we only assume that the kernel functions $G_{ij}(\cdot)$ are piecewise continuous, integrable, and satisfying $\int_{0}^{+\infty}G_{ij}(u)\,du=1$, $\int_{0}^{\infty }e^{\varepsilon_{0} u}G_{ij}(u)\,du<+\infty$, $i,j= 1, 2, \ldots, m$. Therefore, our result has some significance in theories as well as in applications of pseudo almost automorphic solutions.

5 An example

In this section, an example is given to illustrate the feasibility of our result.

Let us consider the following simple neural network:

$$\begin{aligned} x_{i}^{\prime}(t) =&-a_{i} \bigl(x_{i}(t) \bigr) \Biggl[b_{i} \bigl(x_{i}(t) \bigr)-\sum _{j=1}^{2}c_{ij}(t)f_{j} \bigl(x_{j}(t) \bigr) \\ &{}-\sum_{j=1}^{2}d_{ij}(t)g_{j} \bigl(x_{j} \bigl(t-\tau _{ij}(t) \bigr) \bigr) \\ &{}-\sum_{j=1}^{2}p_{ij}(t) \int_{-\infty }^{t}G_{ij}(t-s)h_{j} \bigl(x_{j}(s) \bigr)\,ds-I_{i}(t) \Biggr],\quad i=1,2, \end{aligned}$$

(6)

where the initial functions

$$\begin{aligned}& \Phi_{1}(t)=\sin\frac{1}{2+\cos t+\cos (\pi t )}+e^{-t^{4}{\cos}^{2} t},\quad t< 0, \\& \Phi_{2}(t)=\cos \frac{1}{2+\sin t+\sin(\sqrt{3} t) }+e^{-t^{2}{\sin}^{4} t},\quad t< 0, \end{aligned}$$

and $\tau_{ij}(t)=5$, $i=1,2$, $j=1,2$,

$$\begin{aligned}& a_{i} \bigl( x_{i}(t) \bigr)=7+\sin\frac{1}{2+\cos x_{i}(t)+\cos(\pi x_{i}(t)) }-e^{-\vert x_{i}(t)\vert }, \\& b_{i} \bigl(x_{i}(t) \bigr)=4+\cos\frac{1}{2+\sin x_{i}(t)+\sin(\sqrt{2} x_{i}(t))}-e^{-\vert x_{i}(t)\vert },\quad i=1,2. \end{aligned}$$

Let

$$\begin{aligned}& \left( \begin{matrix} c_{11}(t) & c_{12}(t) \\ c_{21}(t) & c_{22}(t) \end{matrix} \right)=\frac{1}{12} \left( \begin{matrix} \sin\frac{1}{2+\cos t+\cos(\pi t )}+e^{-t^{4}{\cos}^{2} t} & \sin \frac{1}{2+\sin t+\sin(\sqrt{3} t )}+e^{-t^{4}{\sin}^{2} t} \\ \cos\frac{1}{2+\sin t+\sin(\sqrt{3} t) }+e^{-t^{2}{\sin}^{4} t} & \sin\frac{1}{2+\sin t+\sin(\sqrt{5} t) }+e^{-t^{4}{\cos}^{4} t} \end{matrix} \right), \\& \left( \begin{matrix} d_{11}(t) & d_{12}(t) \\ d_{21}(t) & d_{22}(t) \end{matrix} \right )=\frac{1}{12} \left( \begin{matrix} \sin\frac{1}{2+\sin t+\sin(\sqrt{3} t) }+e^{-t^{2}{\cos}^{2} t} & \cos \frac{1}{2+\sin t+\sin(\pi t)} +e^{-t^{4}{\sin}^{2} t} \\ \sin\frac{1}{2+\sin t+\sin(\sqrt{5} t )}+e^{-t^{2}{\cos}^{2} t} & \cos\frac{1}{2+\cos t+\cos(\sqrt{5} t)}+e^{-t^{2}{\cos}^{4} t} \end{matrix} \right), \\& \left( \begin{matrix} p_{11}(t) & p_{12}(t) \\ p_{21}(t) & p_{22}(t) \end{matrix} \right)=\frac{1}{12} \left( \begin{matrix} \sin\frac{1}{2+\sin t+\sin(\sqrt{2} t) }+\frac{1}{1+t^{2}} & \cos\frac {1}{2+\cos t+\cos(\sqrt{5} t)}+\frac{1}{1+t^{4}} \\ \sin\frac{1}{2+\cos t+\cos(\sqrt{3} t) }+\frac{1}{1+t^{4}} & \sin \frac{1}{2+\sin t+\sin(\sqrt{2} t) }+\frac{1}{1+t^{2}} \end{matrix} \right ), \\& I_{1}(t)=I_{2}(t)=\sin\frac{1}{2+\cos t+\cos(\sqrt{2} t )}+ \frac{1}{1+t^{4}}, \\& f_{j}(x_{j})=g_{j}(x_{j})=h_{j}(x_{j})= \frac{\vert x+1\vert -\vert x-1\vert }{2},\quad \quad G_{ij}(u)=e^{-u}. \end{aligned}$$

Then we have $a_{i}^{+}=8$, $a_{i}^{-}=5$, $b_{i}^{-}=2$, $c_{ij}^{+}=d_{ij}^{+}=p_{ij}^{+}=\frac{1}{6}$, $L_{j}^{f}=L_{j}^{g}=L_{j}^{h}=1$, where $i,j=1,2$. Moreover,

$$\delta= \max_{1\leq i\leq 2} \Biggl\{ \frac{1}{b_{i}^{-}a_{i}^{-}}\sum _{j=1}^{2}L_{j}^{f} \bigl(c_{ij}^{+}+d_{ij}^{+}+p_{ij}^{+} \bigr)a_{j}^{+} \Biggr\} =\frac {4}{5}< 1. $$

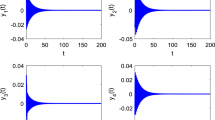
Therefore, by Theorem 3.1, we see that system (6) has a unique pseudo almost automorphic solution. The corresponding simulation result of the solution is seen in Figure 1. Moreover, we verify the condition of Theorem 4.1:

$$(H_{6}):\quad -\overline{b}_{i}+\sum _{j=1}^{2}c_{ji}^{+}L_{i}^{f}+ \sum_{j=1}^{2}\frac{d_{ji}^{+}L_{i}^{g}}{1-\tau^{*}} +\sum _{j=1}^{m}p_{ji}^{+}L_{i}^{h}=- \frac{4}{3}< 0,\quad i=1,2. $$

Therefore, the pseudo almost automorphic solutions of system (6) is exponential stable.

Figure 1

Simulation result of the solution.

6 Conclusions

In this paper, we have studied the existence, uniqueness, and exponential stability of pseudo almost automorphic solutions of system (1). By applying the Banach fixed point theorem and the Lyapunov functional method, some novel sufficient conditions are obtained to ensure the existence, uniqueness, and exponential stability of pseudo almost automorphic solutions of system (1). The results have an important role in the design and applications of CGNNs. Moreover, an example is given to demonstrate the effectiveness of the obtained results. In the future, we will study the other dynamic behaviors of system (1).