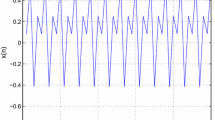
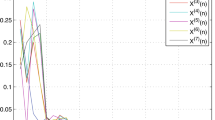
Abstract
Closed form formulas of the solutions to the following system of difference equations:
where \(a_{n}\), \(b_{n}\), \(\alpha _{n}\), \(\beta _{n}\), \(n\in \mathbb {N}_{0}\), and initial values \(x_{-i}\), \(y_{-i}\), \(i\in\{1,2\}\) are real numbers, are found. The domain of undefinable solutions to the system is described. The long-term behavior of its solutions is studied in detail for the case of constant \(a_{n}\), \(b_{n}\), \(\alpha _{n}\) and \(\beta _{n}\), \(n\in \mathbb {N}_{0}\).
Similar content being viewed by others
1 Introduction
Studying concrete nonlinear difference equations and systems is a topic of a great recent interest (see, e.g., [1–46] and the references therein). Studying systems of difference equations, especially symmetric and close to symmetric ones, is a topic of considerable interest (see, e.g., [2, 6, 7, 10, 12–16, 18, 19, 23, 24, 26–29, 31–38, 40, 41, 44, 46]). Another topic of interest is solvable difference equations and systems and their applications (see, e.g., [1–5, 7, 17, 20, 21, 23–27, 29–37, 39–46]). Renewed interest in the area started after the publication of [20] where a formula for a solution of a difference equation was theoretically explained. The most interesting thing in [20] was a change of variables which reduced the equation to a linear one with constant coefficients. Related ideas were later used, e.g., in [1, 4, 7, 17, 21, 23–27, 29–37, 39–45].
Quite recently in [2] the following systems of difference equations were presented:
where \(x_{-i}\), \(y_{-i}\), \(i\in\{1,2\}\) are real numbers, and some formulas for their solutions are given, some of which are proved by induction.
The next system of difference equations
where \(a_{n}\), \(b_{n}\), \(\alpha _{n}\), \(\beta _{n}\), \(n\in \mathbb {N}_{0}\), and initial values \(x_{-i}\), \(y_{-i}\), \(i\in\{1,2\}\), are real numbers, is a generalization of the system in (1). Our aim is to show that more general system (2) is solvable by giving a natural method for getting its solutions. The domain of undefinable solutions to the system is also described. For the case when \(a_{n}\), \(b_{n}\), \(\alpha _{n}\), \(\beta _{n}\), \(n\in \mathbb {N}_{0}\), are constant, the long-term behavior of its solutions is investigated in detail.
A solution \((x_{n}, y_{n})_{n\ge-2}\) of system (2) is called periodic, or eventually periodic, with period p if there is \(n_{0}\ge-2\) such that
For some results in the area, see, e.g., [6, 9–11, 19, 21, 22, 28].
2 Solutions to system (2) in closed form
Assume first that \(x_{-i}\ne0\), \(y_{-i}\ne0\), \(i\in\{1,2\}\). Then, by the method of induction and the equations in (2), it follows that for every well-defined solution to system (2), \(x_{n}\ne0\) and \(y_{n}\ne0\), for every \(n\in \mathbb {N}_{0}\). On the other hand, if \(x_{n_{0}}=0\) for some \(n_{0}\in \mathbb {N}\), then the first equation in (2) implies that \(y_{n_{0}-1}=0\) or \(y_{n_{0}-2}=0\). If \(y_{n_{0}-1}=0\), then \(x_{n_{0}-2}=0\) or \(x_{n_{0}-3}=0\), while if \(y_{n_{0}-2}=0\), then \(x_{n_{0}-3}=0\) or \(x_{n_{0}-4}=0\). Repeating this procedure, we get that \(x_{-i}=0\) or \(y_{-i}=0\) for some \(i\in\{1,2\}\). Similarly, if \(y_{n_{1}}=0\) for some \(n_{1}\in \mathbb {N}\), we get \(x_{-i}=0\) or \(y_{-i}=0\) for some \(i\in\{1,2\}\). Hence, for a well-defined solution \((x_{n},y_{n})_{n\ge-2}\) of system (2), we have that
if and only if \(x_{-i}y_{-i}\ne0\), \(i\in\{1,2\}\).
Assume now that \((x_{n},y_{n})_{n\ge-2}\) is a solution to system (2) such that (3) holds. Then, by multiplying the first equation in (2) by \(x_{n-1}\) and the second one by \(y_{n-1}\), and using the following changes of variables
\(n\ge-1\), system (2) is transformed in the following one:
From (5) it follows that
This means that \((u_{2n})_{n\in \mathbb {N}_{0}}\), \((u_{2n-1})_{n\in \mathbb {N}_{0}}\), \((v_{2n})_{n\in \mathbb {N}_{0}}\), and \((v_{2n-1})_{n\in \mathbb {N}_{0}}\) are solutions to two linear first-order difference equations, which are solvable.
Solving these equations, we get
Using (4) we obtain
and
for \(2n+i\ge0\), from which it follows that
for every \(m\in \mathbb {N}_{0}\), \(i\in\{0,1\}\).
3 Case of constant coefficients
In this section we consider the case when all the coefficients in system (2) are constant, that is, when
Then (2) is
Assume that \((x_{n},y_{n})_{n\ge-2}\) is a solution to system (2) such that (3) holds. Then we have
and
for \(n\in \mathbb {N}_{0}\), \(l\in\{0,1\}\) when \(a\alpha \ne 1\), while if \(a\alpha =1\), we have
and we also have
\(n\in \mathbb {N}_{0}\), \(l\in\{0,1\}\) if \(a\alpha \ne1\), while if \(a\alpha =1\), we have
Now we present formulae for solutions to system (14).
Case \(a\alpha \ne1\). We have
for every \(m\in \mathbb {N}_{0}\).
Case \(a\alpha =1\). We have
for every \(m\in \mathbb {N}_{0}\).
4 Long-term behavior of solutions to system (14)
Before we formulate and prove the main results regarding the long-term behavior of well-defined solutions to system (14), we quote the following well-known asymptotic formula which will be used in the proofs of the main results:
We also define the following quantities:
Finally, we give another auxiliary result.
Lemma 1
If \(a\alpha \ne1\), \(a\beta +b\ne0\ne \alpha b+\beta \). Then system (14) has two-periodic solutions.
Proof
The equilibrium solution to system (15) is
From (4) and (31) it follows that
and
as desired. □
The next three results are devoted to the long-term behavior of well-defined solutions to system (14).
Theorem 1
Assume that \(\vert a\alpha \vert \ne1\) and \((x_{n}, y_{n})_{n\ge-2}\) is a well-defined solution to system (14). Then the following statements are true.
-
(a)
If \(a\beta +b\ne0\ne \alpha b+\beta \) and \(\vert a\alpha \vert <1\), then \((x_{n},y_{n})\) converges to a, not necessarily prime, two-periodic solution.
-
(b)
If \(u_{-1}=u_{0}=(a\beta +b)/(1-a\alpha )\), then the sequences \((x_{2m})_{m\ge-1}\) and \((x_{2m+1})_{m\ge-1}\) are constant.
-
(c)
If \(v_{-1}=v_{0}=(\alpha b+\beta )/(1-a\alpha )\), then the sequences \((y_{2m})_{m\ge-1}\) and \((y_{2m+1})_{m\ge-1}\) are constant.
-
(d)
If \(\vert a\alpha \vert >1\) and \(u_{-1}=(a\beta +b)/(1-a\alpha )\ne u_{0}\), then \(x_{2m}\to0\) and \(\vert x_{2m+1}\vert \to\infty\), as \(m\to\infty\).
-
(e)
If \(\vert a\alpha \vert >1\) and \(u_{-1}\ne(a\beta +b)/(1-a\alpha )=u_{0}\), then \(x_{2m+1}\to0\) and \(\vert x_{2m}\vert \to\infty\), as \(m\to\infty\).
-
(f)
If \(\vert a\alpha \vert >1\) and \(v_{-1}=(a\beta +b)/(1-a\alpha )\ne v_{0}\), then \(y_{2m}\to0\) and \(\vert y_{2m+1}\vert \to\infty\), as \(m\to\infty\).
-
(g)
If \(\vert a\alpha \vert >1\) and \(v_{-1}\ne(a\beta +b)/(1-a\alpha )=v_{0}\), then \(y_{2m+1}\to0\) and \(\vert y_{2m}\vert \to\infty\), as \(m\to\infty\).
-
(h)
If \(\vert a\alpha \vert >1\), \(u_{-1}\ne(a\beta +b)/(1-a\alpha )\ne u_{0}\) and \(\vert L_{1}\vert <1\), then \(x_{2m}\to0\), as \(m\to\infty\).
-
(i)
If \(\vert a\alpha \vert >1\), \(u_{-1}\ne(a\beta +b)/(1-a\alpha )\ne u_{0}\) and \(\vert L_{1}\vert >1\), then \(\vert x_{2m}\vert \to\infty\), as \(m\to\infty\).
-
(j)
If \(\vert a\alpha \vert >1\), \(u_{-1}\ne(a\beta +b)/(1-a\alpha )\ne u_{0}\) and \(L_{1}=1\), then \((x_{2m})_{m\ge-1}\) is constant.
-
(k)
If \(\vert a\alpha \vert >1\), \(u_{-1}\ne(a\beta +b)/(1-a\alpha )\ne u_{0}\) and \(L_{1}=-1\), then \((x_{4m})_{m\ge-1}\) and \((x_{4m+2})_{m\ge-1}\) are convergent.
-
(l)
If \(\vert a\alpha \vert >1\), \(u_{-1}\ne(a\beta +b)/(1-a\alpha )\ne u_{0}\) and \(\vert L_{2}\vert <1\), then \(x_{2m+1}\to0\), as \(m\to\infty\).
-
(m)
If \(\vert a\alpha \vert >1\), \(u_{-1}\ne(a\beta +b)/(1-a\alpha )\ne u_{0}\) and \(\vert L_{2}\vert >1\), then \(\vert x_{2m+1}\vert \to\infty\), as \(m\to\infty\).
-
(n)
If \(\vert a\alpha \vert >1\), \(u_{-1}\ne(a\beta +b)/(1-a\alpha )\ne u_{0}\) and \(L_{2}=1\), then \((x_{2m+1})_{m\ge-1}\) is constant.
-
(o)
If \(\vert a\alpha \vert >1\), \(u_{-1}\ne(a\beta +b)/(1-a\alpha )\ne u_{0}\) and \(L_{2}=-1\), then \((x_{4m+1})_{m\ge-1}\) and \((x_{4m+3})_{m\ge-1}\) are convergent.
-
(p)
If \(\vert a\alpha \vert >1\), \(v_{-1}\ne(\alpha b+\beta )/(1-a\alpha )\ne v_{0}\) and \(\vert L_{3}\vert <1\), then \(y_{2m}\to0\), as \(m\to\infty\).
-
(q)
If \(\vert a\alpha \vert >1\), \(v_{-1}\ne(\alpha b+\beta )/(1-a\alpha )\ne v_{0}\) and \(\vert L_{3}\vert >1\), then \(\vert y_{2m}\vert \to\infty\), as \(m\to\infty\).
-
(r)
If \(\vert a\alpha \vert >1\), \(v_{-1}\ne(\alpha b+\beta )/(1-a\alpha )\ne v_{0}\) and \(L_{3}=1\), then \((y_{2m})_{m\ge-1}\) is constant.
-
(s)
If \(\vert a\alpha \vert >1\), \(v_{-1}\ne(\alpha b+\beta )/(1-a\alpha )\ne v_{0}\) and \(L_{3}=-1\), then \((y_{4m})_{m\ge-1}\) and \((y_{4m+2})_{m\ge-1}\) are convergent.
-
(t)
If \(\vert a\alpha \vert >1\), \(v_{-1}\ne(\alpha b+\beta )/(1-a\alpha )\ne v_{0}\) and \(\vert L_{4}\vert <1\), then \(y_{2m+1}\to0\), as \(m\to\infty\).
-
(u)
If \(\vert a\alpha \vert >1\), \(v_{-1}\ne(\alpha b+\beta )/(1-a\alpha )\ne v_{0}\) and \(\vert L_{4}\vert >1\), then \(\vert y_{2m+1}\vert \to\infty\), as \(m\to\infty\).
-
(v)
If \(\vert a\alpha \vert >1\), \(v_{-1}\ne(\alpha b+\beta )/(1-a\alpha )\ne v_{0}\) and \(L_{4}=1\), then \((y_{2m+1})_{m\ge-1}\) is constant.
-
(w)
If \(\vert a\alpha \vert >1\), \(v_{-1}\ne(\alpha b+\beta )/(1-a\alpha )\ne v_{0}\) and \(L_{4}=-1\), then \((y_{4m+1})_{m\ge-1}\) and \((y_{4m+3})_{m\ge-1}\) are convergent.
Proof
Let
for \(m\in \mathbb {N}_{0}\).
(a) By using (30) we have
for sufficiently large m.
From (34)-(37), by using the condition \(\vert a\alpha \vert <1\) and a well-known criterion for the convergence of products, the statement easily follows.
(b) By using the condition \(u_{-1}=u_{0}=(a\beta +b)/(1-a\alpha )\) in (22) and (23), the statement immediately follows.
(c) By using the condition \(v_{-1}=v_{0}=(\alpha b+\beta )/(1-a\alpha )\) in (24) and (25), the statement immediately follows.
(d) By using the condition \(u_{-1}=(a\beta +b)/(1-a\alpha )\ne u_{0}\), we get
Letting \(m\to\infty\) in (38) and (39) and using the condition \(\vert a\alpha \vert >1\), we have \(p_{m}\to0\) and \(\vert \hat{p}_{m}\vert \to\infty\), from which along with (22) and (23) the statement easily follows.
(e) By using the condition \(u_{-1}\ne(a\beta +b)/(1-a\alpha )=u_{0}\), we get
Letting \(m\to\infty\) in (40) and (41) and using the condition \(\vert a\alpha \vert >1\), we have \(\vert p_{m}\vert \to\infty\) and \(\hat{p}_{m}\to0\), from which along with (22) and (23) the statement easily follows.
(f) By using the condition \(v_{-1}=(a\beta +b)/(1-a\alpha )\ne v_{0}\), we get
Letting \(m\to\infty\) in (42) and (43) and using the condition \(\vert a\alpha \vert >1\), we have \(q_{m}\to0\) and \(\vert \hat{q}_{m}\vert \to\infty\), from which along with (24) and (25) the statement easily follows.
(g) By using the condition \(v_{-1}\ne(a\beta +b)/(1-a\alpha )= v_{0}\), we get
Letting \(m\to\infty\) in (44) and (45) and using the condition \(\vert a\alpha \vert >1\), we have \(\vert q_{m}\vert \to\infty\) and \(\hat{q}_{m}\to0\), from which along with (24) and (25) the statement easily follows.
(h), (i) Note that \(\lim_{m\to\infty}p_{m}=L_{1}\). Hence, from the assumptions \(\vert L_{1}\vert <1\), that is, \(\vert L_{1}\vert >1\) along with (22), the statements easily follow.
(j) The statement immediately follows by using the condition \(L_{1}=1\) in (22).
(k) Since \(L_{1}=-1\) and by using (30), we have that
From (46), by using the condition \(\vert a\alpha \vert >1\) and a well-known criterion for the convergence of products, the statement easily follows.
(l), (m) Note that \(\lim_{m\to\infty}\hat{p}_{m}=L_{2}\). Hence, from the assumptions \(\vert L_{2}\vert <1\), that is, \(\vert L_{2}\vert >1\) along with (23), the statements easily follow.
(n) The statement immediately follows by using the condition \(L_{2}=1\) in (23).
(o) Since \(L_{2}=-1\) and by using (30), we have that
From (47), by using the condition \(\vert a\alpha \vert >1\) and a well-known criterion for the convergence of products, the statement easily follows.
(p), (q) Note that \(\lim_{m\to\infty}q_{m}=L_{3}\). Hence, from the assumptions \(\vert L_{3}\vert <1\), that is, \(\vert L_{3}\vert >1\) along with (24), the statements easily follow.
(r) The statement immediately follows by using the condition \(L_{3}=1\) in (24).
(s) Since \(L_{3}=-1\) and by using (30), we have that
From (48), by using the condition \(\vert a\alpha \vert >1\) and a well-known criterion for the convergence of products, the statement easily follows.
(t), (u) Note that \(\lim_{m\to\infty}\hat{q}_{m}=L_{4}\). Hence, from the assumptions \(\vert L_{4}\vert <1\), that is, \(\vert L_{4}\vert >1\) along with (25), the statements easily follow.
(v) The statement immediately follows by using the condition \(L_{4}=1\) in (25).
(w) Since \(L_{4}=-1\) and by using (30), we have that
From (49), by using the condition \(\vert a\alpha \vert >1\) and a well-known criterion for the convergence of products, the statement easily follows. □
Let
Theorem 2
Assume that \(a\alpha =-1\) and \((x_{n}, y_{n})_{n\ge-2}\) is a well-defined solution to system (14). Then the following statements are true.
-
(a)
If \(\vert M_{1}\vert <1\), then \(x_{2m}\to0\) and \(\vert x_{2m+1}\vert \to\infty\), as \(m\to\infty\).
-
(b)
If \(\vert M_{1}\vert >1\), then \(x_{2m+1}\to0\) and \(\vert x_{2m}\vert \to\infty\), as \(m\to\infty\).
-
(c)
If \(M_{1}=1\), then \((x_{n})_{n\ge-2}\) is four-periodic.
-
(d)
If \(M_{1}=-1\), then \((x_{n})_{n\ge-2}\) is eight-periodic.
-
(e)
If \(\vert M_{2}\vert <1\), then \(y_{2m}\to0\) and \(\vert y_{2m+1}\vert \to\infty\), as \(m\to\infty\).
-
(f)
If \(\vert M_{2}\vert >1\), then \(y_{2m+1}\to0\) and \(\vert y_{2m}\vert \to\infty\), as \(m\to\infty\).
-
(g)
If \(M_{2}=1\), then \((y_{n})_{n\ge-2}\) is four-periodic.
-
(h)
If \(M_{2}=-1\), then \((y_{n})_{n\ge-2}\) is eight-periodic.
Proof
First, note that since \(a\alpha =-1\), from (22)-(25) we have
for \(m\in \mathbb {N}_{0}\). From (50) and (51) all the statements easily follow. □
Let
Theorem 3
Assume that \(a\alpha =1\) and \((x_{n}, y_{n})_{n\ge-2}\) is a well-defined solution to system (14). Then the following statements hold true.
-
(a)
If \(a\beta +b=0\) and \(\vert N_{1}\vert <1\), then \(x_{2m}\to0\) and \(\vert x_{2m+1}\vert \to\infty\), as \(m\to\infty\);
-
(b)
If \(a\beta +b=0\) and \(\vert N_{1}\vert >1\), then \(\vert x_{2m}\vert \to\infty\) and \(x_{2m+1}\to0\), as \(m\to\infty\);
-
(c)
If \(a\beta +b=0\) and \(N_{1}=1\), then \((x_{2m})_{m\ge-1}\) and \((x_{2m+1})_{m\ge-1}\) are constant;
-
(d)
If \(a\beta +b=0\) and \(N_{1}=-1\), then \((x_{4m+i})_{m\ge-1}\), \(i=\overline {0,3}\), are constant.
-
(e)
If \(a\beta +b\ne0\) and \((u_{-1}-u_{0})/(a\beta +b)>0\), then \(\vert x_{2m}\vert \to\infty\), as \(m\to\infty\);
-
(f)
If \(a\beta +b\ne0\) and \((u_{-1}-u_{0})/(a\beta +b)<0\), then \(x_{2m}\to0\), as \(m\to\infty\);
-
(g)
If \(a\beta +b\ne0\) and \(u_{-1}=u_{0}\), then \((x_{2m})_{m\ge-1}\) is constant;
-
(h)
If \(a\beta +b\ne0\) and \((u_{0}-u_{-1})/(a\beta +b)>1\), then \(\vert x_{2m+1}\vert \to\infty\), as \(m\to\infty\);
-
(i)
If \(a\beta +b\ne0\) and \((u_{0}-u_{-1})/(a\beta +b)<1\), then \(x_{2m+1}\to0\), as \(m\to\infty\);
-
(j)
If \(a\beta +b\ne0\) and \(u_{-1}-u_{0}=a\beta +b\), then \((x_{2m+1})_{m\ge-1}\) is constant;
-
(k)
If \(\alpha b+\beta =0\) and \(\vert N_{2}\vert <1\), then \(y_{2m}\to0\) and \(\vert y_{2m+1}\vert \to\infty\), as \(m\to\infty\);
-
(l)
If \(\alpha b+\beta =0\) and \(\vert N_{2}\vert >1\), then \(\vert y_{2m}\vert \to\infty\) and \(y_{2m+1}\to0\), as \(m\to\infty\);
-
(m)
If \(\alpha b+\beta =0\) and \(N_{2}=1\), then \((y_{2m})_{m\ge-1}\) and \((y_{2m+1})_{m\ge-1}\) are constant;
-
(n)
If \(\alpha b+\beta =0\) and \(N_{2}=-1\), then \((y_{4m+i})_{m\ge-1}\), \(i=\overline {0,3}\), are constant.
-
(o)
If \(\alpha b+\beta \ne0\) and \((v_{-1}-v_{0})/(\alpha b+\beta )>0\), then \(\vert y_{2m}\vert \to\infty\), as \(m\to\infty\);
-
(p)
If \(\alpha b+\beta \ne0\) and \((v_{-1}-v_{0})/(\alpha b+\beta )<0\), then \(y_{2m}\to0\), as \(m\to\infty\);
-
(q)
If \(\alpha b+\beta \ne0\) and \(v_{-1}=v_{0}\), then \((y_{2m})_{m\ge -1}\) is constant.
-
(r)
If \(\alpha b+\beta \ne0\) and \((v_{0}-v_{-1})/(\alpha b+\beta )<1\), then \(y_{2m+1}\to0\), as \(m\to\infty\);
-
(s)
If \(\alpha b+\beta \ne0\) and \((v_{0}-v_{-1})/(\alpha b+\beta )>1\), then \(\vert y_{2m+1}\vert \to\infty\), as \(m\to\infty\);
-
(t)
If \(\alpha b+\beta \ne0\) and \(v_{-1}-v_{0}=\alpha b+\beta \), then \((y_{2m+1})_{m\ge-1}\) is constant.
Proof
Let
(a)-(d) Since in this case we have
these statements easily follow.
(e), (f) By using (30) we have
for sufficiently large m.
From (52), by using the fact that for every \(k\in \mathbb {N}\)
and a known criterion for convergence of products, the statements easily follow.
(g) Using the condition \(u_{-1}=u_{0}\) in (26), the statement immediately follows.
(h), (i) By using (30) we have
for sufficiently large m.
From (54), (53), (27) and a known criterion for convergence of products, the statements easily follow.
(j) Using the condition \(u_{0}=u_{-1}+a\beta +b\) in (27), the statement immediately follows.
(k)-(n) Since in this case we have
these statements easily follow.
(o), (p) By using (30) we have
for sufficiently large m.
From (55), (53), (28) and a known criterion for convergence of products, the statements easily follow.
(q) Using the condition \(v_{0}=v_{-1}\) in (28), the statement immediately follows.
(r), (s) By using (30) we have
for sufficiently large m.
From (56), (53), (29) and a known criterion for convergence of products, the statements easily follow.
(t) Using the condition \(v_{0}=v_{-1}+\alpha b+\beta \) in (29), the statement immediately follows. □
5 Domain of undefinable solutions to system (2)
In Section 2 we proved that solutions to system (2), for which \(x_{-j}=0\) or \(y_{-j}=0\) for some \(j\in\{1,2\}\), are not defined. The set of all such initial values is characterized here.
Definition 1
Consider the system of difference equations
where \(s\in \mathbb {N}\), and \(x_{-i},y_{-i}\in \mathbb {R}\), \(i=\overline {1,s}\). The string of vectors
where \(n_{0}\ge-1\), is called an undefined solution of system (57) if
and
for \(0\le j< n_{0}+1\), and \(x_{n_{0}+1}\) or \(y_{n_{0}+1}\) is not a defined number, that is, the quantity
or
is not defined.
The set of all initial values \((x_{-s},y_{-s}),\ldots,(x_{-1},y_{-1})\) which generate undefined solutions to system (57) is called domain of undefinable solutions of the system.
The next result characterizes the domain of undefinable solutions to system (2) when \(a_{n}b_{n}\alpha _{n}\beta _{n}\ne0\), \(n\in \mathbb {N}_{0}\).
Theorem 4
Assume that \(a_{n}b_{n}\alpha _{n}\beta _{n}\ne0\), \(n\in \mathbb {N}_{0}\). Then the domain of undefinable solutions to system (2) is the following set:
where
Proof
We have already proved that the set
belongs to the domain of undefinable solutions to system (2).
If \(x_{-j}\ne0\ne y_{-j}\), \(j=\overline {1,2}\) (i.e., \(x_{n}\ne0\ne y_{n}\) for every \(n\ge-2\)), then such a solution \((x_{n},y_{n})_{n\ge-2}\) is not defined if and only if
for some \(n\in \mathbb {N}_{0}\), which is equivalent to
for some \(n\in \mathbb {N}_{0}\).
Note that
We have
for \(m\in \mathbb {N}_{0}\).
From (61) and (62) we have that
for some \(m\in \mathbb {N}_{0}\) if and only if
From (61) and (63) we have that
for some \(m\in \mathbb {N}_{0}\) if and only if
From (61) and (64) we have that
for some \(m\in \mathbb {N}_{0}\) if and only if
From (61) and (65) we have that
for some \(m\in \mathbb {N}_{0}\) if and only if
From (66)-(69) we see that the first union in (58) also belongs to the domain of undefinable solutions, finishing the proof of the theorem. □
Remark 1
Quantities
can be calculated for every \(m\in \mathbb {N}_{0}\).
Indeed, note that
and also that
and
On the other hand, if
it is easy to see that
From (74)-(80) explicit formulas for the quantities in (70)-(73) are easily obtained.
References
Aloqeili, M: Dynamics of a kth order rational difference equation. Appl. Math. Comput. 181, 1328-1335 (2006)
Alzahrani, EO, El-Dessoky, MM, Elsayed, EM, Kuang, Y: Solutions and properties of some degenerate systems of difference equations. J. Comput. Anal. Appl. 18(2), 321-333 (2015)
Andruch-Sobilo, A, Migda, M: On the rational recursive sequence \(x_{n+1}=ax_{n-1}/(b+cx_{n}x_{n-1})\). Tatra Mt. Math. Publ. 43, 1-9 (2009)
Bajo, I, Liz, E: Global behaviour of a second-order nonlinear difference equation. J. Differ. Equ. Appl. 17(10), 1471-1486 (2011)
Berezansky, L, Braverman, E: On impulsive Beverton-Holt difference equations and their applications. J. Differ. Equ. Appl. 10(9), 851-868 (2004)
Berg, L, Stević, S: Periodicity of some classes of holomorphic difference equations. J. Differ. Equ. Appl. 12(8), 827-835 (2006)
Berg, L, Stević, S: On some systems of difference equations. Appl. Math. Comput. 218, 1713-1718 (2011)
Berg, L, Stević, S: On the asymptotics of the difference equation \(y_{n}(1+y_{n-1}\cdots y_{n-k+1})=y_{n-k}\). J. Differ. Equ. Appl. 17(4), 577-586 (2011)
Grove, EA, Ladas, G: Periodicities in Nonlinear Difference Equations. Chapman & Hall/CRC Press, Boca Raton (2005)
Iričanin, B, Stević, S: Some systems of nonlinear difference equations of higher order with periodic solutions. Dyn. Contin. Discrete Impuls. Syst. 13a(3-4), 499-508 (2006)
Iričanin, B, Stević, S: Eventually constant solutions of a rational difference equation. Appl. Math. Comput. 215, 854-856 (2009)
Papaschinopoulos, G, Schinas, CJ: On a system of two nonlinear difference equations. J. Math. Anal. Appl. 219(2), 415-426 (1998)
Papaschinopoulos, G, Schinas, CJ: On the behavior of the solutions of a system of two nonlinear difference equations. Commun. Appl. Nonlinear Anal. 5(2), 47-59 (1998)
Papaschinopoulos, G, Schinas, CJ: Invariants for systems of two nonlinear difference equations. Differ. Equ. Dyn. Syst. 7(2), 181-196 (1999)
Papaschinopoulos, G, Schinas, CJ: Invariants and oscillation for systems of two nonlinear difference equations. Nonlinear Anal. TMA 46(7), 967-978 (2001)
Papaschinopoulos, G, Schinas, CJ: On the dynamics of two exponential type systems of difference equations. Comput. Math. Appl. 64(7), 2326-2334 (2012)
Papaschinopoulos, G, Stefanidou, G: Asymptotic behavior of the solutions of a class of rational difference equations. Int. J. Difference Equ. 5(2), 233-249 (2010)
Stefanidou, G, Papaschinopoulos, G, Schinas, CJ: On a system of two exponential type difference equations. Commun. Appl. Nonlinear Anal. 17(2), 1-13 (2010)
Stević, S: A global convergence results with applications to periodic solutions. Indian J. Pure Appl. Math. 33(1), 45-53 (2002)
Stević, S: More on a rational recurrence relation. Appl. Math. E-Notes 4, 80-85 (2004)
Stević, S: A short proof of the Cushing-Henson conjecture. Discrete Dyn. Nat. Soc. 2006, Article ID 37264 (2006)
Stević, S: Periodicity of max difference equations. Util. Math. 83, 69-71 (2010)
Stević, S: On a system of difference equations. Appl. Math. Comput. 218, 3372-3378 (2011)
Stević, S: On a system of difference equations with period two coefficients. Appl. Math. Comput. 218, 4317-4324 (2011)
Stević, S: On the difference equation \(x_{n}=x_{n-2}/(b_{n}+c_{n}x_{n-1}x_{n-2})\). Appl. Math. Comput. 218, 4507-4513 (2011)
Stević, S: On a solvable rational system of difference equations. Appl. Math. Comput. 219, 2896-2908 (2012)
Stević, S: On a third-order system of difference equations. Appl. Math. Comput. 218, 7649-7654 (2012)
Stević, S: On some periodic systems of max-type difference equations. Appl. Math. Comput. 218, 11483-11487 (2012)
Stević, S: On some solvable systems of difference equations. Appl. Math. Comput. 218, 5010-5018 (2012)
Stević, S: On the difference equation \(x_{n}=x_{n-k}/(b+cx_{n-1}\cdots x_{n-k})\). Appl. Math. Comput. 218, 6291-6296 (2012)
Stević, S: Solutions of a max-type system of difference equations. Appl. Math. Comput. 218, 9825-9830 (2012)
Stević, S: Domains of undefinable solutions of some equations and systems of difference equations. Appl. Math. Comput. 219, 11206-11213 (2013)
Stević, S: On a system of difference equations which can be solved in closed form. Appl. Math. Comput. 219, 9223-9228 (2013)
Stević, S: On a system of difference equations of odd order solvable in closed form. Appl. Math. Comput. 219, 8222-8230 (2013)
Stević, S: On the system \(x_{n+1}=y_{n}x_{n-k}/(y_{n-k+1}(a_{n}+b_{n}y_{n}x_{n-k}))\), \(y_{n+1}=x_{n}y_{n-k}/(x_{n-k+1}(c_{n}+d_{n}x_{n}y_{n-k}))\). Appl. Math. Comput. 219, 4526-4534 (2013)
Stević, S: Representation of solutions of bilinear difference equations in terms of generalized Fibonacci sequences. Electron. J. Qual. Theory Differ. Equ. 2014, Article ID 67 (2014)
Stević, S, Alghamdi, MA, Alotaibi, A, Shahzad, N: On a higher-order system of difference equations. Electron. J. Qual. Theory Differ. Equ. 2013, Article ID 47 (2013)
Stević, S, Alghamdi, MA, Alotaibi, A, Shahzad, N: Boundedness character of a max-type system of difference equations of second order. Electron. J. Qual. Theory Differ. Equ. 2014, Article ID 45 (2014)
Stević, S, Alghamdi, MA, Maturi, DA, Shahzad, N: On a class of solvable difference equations. Abstr. Appl. Anal. 2013, Article ID 157943 (2013)
Stević, S, Diblik, J, Iričanin, B, Šmarda, Z: On a third-order system of difference equations with variable coefficients. Abstr. Appl. Anal. 2012, Article ID 508523 (2012)
Stević, S, Diblik, J, Iričanin, B, Šmarda, Z: On some solvable difference equations and systems of difference equations. Abstr. Appl. Anal. 2012, Article ID 541761 (2012)
Stević, S, Diblik, J, Iričanin, B, Šmarda, Z: On the difference equation \(x_{n+1}=x_{n}x_{n-k}/(x_{n-k+1}(a+bx_{n}x_{n-k}))\). Abstr. Appl. Anal. 2012, Article ID 108047 (2012)
Stević, S, Diblik, J, Iričanin, B, Šmarda, Z: On the difference equation \(x_{n}=a_{n}x_{n-k}/(b_{n}+c_{n}x_{n-1}\cdots x_{n-k})\). Abstr. Appl. Anal. 2012, Article ID 409237 (2012)
Stević, S, Diblik, J, Iričanin, B, Šmarda, Z: On a solvable system of rational difference equations. J. Differ. Equ. Appl. 20(5-6), 811-825 (2014)
Stević, S, Diblik, J, Iričanin, B, Šmarda, Z: Solvability of nonlinear difference equations of fourth order. Electron. J. Differ. Equ. 2014, Article ID 264 (2014)
Tollu, DT, Yazlik, Y, Taskara, N: On fourteen solvable systems of difference equations. Appl. Math. Comput. 233, 310-319 (2014)
Acknowledgements
The work of the first and the second authors was supported by the Serbian Ministry of Education and Science, project III 41025. The work of the first author was also supported by the Serbian Ministry of Education and Science, project III 44006. The work of the second author was also supported by the Serbian Ministry of Education and Science, project OI 171007. The work of the third author was realized in CEITEC - Central European Institute of Technology with research infrastructure supported by project CZ.1.05/1.1.00/02.0068 financed from the European Regional Development Fund. The third author was also supported by the project FEKT-S-14-2200 of Brno University of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Stević, S., Iričanin, B. & Šmarda, Z. On a close to symmetric system of difference equations of second order. Adv Differ Equ 2015, 264 (2015). https://doi.org/10.1186/s13662-015-0591-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-015-0591-7