1 Introduction

Consider the initial value problem

$$ u^{(m)}(x)+\sum_{i=0}^{m-1} a_{i}(x)u^{(i)}(x)=f(x),\quad x \in [0,\infty[, $$
(1)

with initial conditions

$$ u^{(i)}(0)=\alpha_{i},\quad i=0,1, \ldots, m-1, $$
(2)

where the functions \(a_{0}(x),a_{1}(x), \ldots, a_{m-1}(x)\) are continuous on the half line \([0,\infty[\) and \(\alpha_{0},\alpha_{1},\ldots, \alpha_{m-1}\) are constants. Eq. (1) was investigated to a wide class of deterministic and stochastic problems. This problem describes several phenomena in engineering, physics and chemical reaction, and so on. Many numerical methods are applied by many authors to study high-order differential equations. Some of more recent methods are collocation method [1–3], multiple iterative splitting method [4], modified Adomian decomposition method [5–7], spectral-Galerkin method [8–11], wavelets method [12, 13], homotopy method [14, 15], variational iteration method [16, 17], elegant harmonic numbers operational matrix of derivatives [18] and others [19–24].

In this article, we derive the operational matrix of differentiation of exponential Jacobi functions, and then we implement a new exponential Jacobi pseudospectral method in conjunction with the operational matrix of differentiation of exponential Jacobi functions to obtain numerical solutions of high-order ordinary differential equations on a semi-infinite interval. Spectral methods (see, for instance, [25–29]), based on using operational matrices, have been implemented in various problems such as fractional differential equations [30, 31], fractional optimal control problems [32], Lane-Emden equation [33, 34], and various integral equations [35]. This equation is collocated at the exponential Jacobi-Gauss quadrature nodes. Doing so, we find that we can obtain very accurate results with minimal computation. Hence, the method is rather computationally efficient compared with other numerical or analytical approaches. Finally, numerical experiments of high-order ODEs are implemented to demonstrate the validity and efficiency of the proposed algorithm. In particular, in Section 2 we design the exponential Jacobi pseudospectral method technique for solving high-order ODEs. In Section 3, several numerical examples are presented to demonstrate the efficiency of present numerical algorithm. Finally, in Section 4, a few concluding remarks and future work are included.

2 Exponential Jacobi pseudospectral method

This section presents technical details of the new exponential Jacobi functions and the exponential Jacobi pseudospectral method (EJPM). First, we outline some useful mathematical properties that we shall make use of. Then, the derivative operational matrix of exponential Jacobi functions is derived and proved. Finally, we derive the EJPM.

2.1 Mathematical preliminaries

Here we list some useful mathematical relations and identities useful in the construction of the exponential Jacobi operational matrix (EJOM). Consider the classical Jacobi polynomials \(J^{(\theta,\vartheta)}_{k}(z)\) on the interval \([-1,1]\) with the weight function \(\omega^{(\theta,\vartheta)}(x)=(1-x)^{\theta}(1+x)^{\vartheta}\), \(\theta ,\vartheta>-1\),

$$J^{(\theta,\vartheta)}_{0}(z)=1,\qquad J^{(\theta,\vartheta)}_{1}(z)= \frac{1}{2} \bigl(\theta-\vartheta+z (\theta+\vartheta+2) \bigr), $$

the set \(\{J^{(\theta,\vartheta)}_{k}(z):k=0,1,\ldots\}\) forms a complete orthogonal system in the weighted Hilbert space \(L_{\omega^{\theta,\vartheta}(x)}^{2}[-1,1]\) with the inner product

$$(u,v)_{\omega^{(\theta,\vartheta)}(x)}:=\int_{-1}^{1}u(x)v(x)\omega ^{(\theta,\vartheta)}(x)\,dx $$

and the norm

$$\|u\|_{\omega^{(\theta,\vartheta)}(x)}=(u,u)_{\omega^{(\theta,\vartheta )}(x)}^{\frac{1}{2}}. $$

Let us define the exponential Jacobi functions by replacing z by \(1-2 \exp(-x/L)\). Denoting the exponential Jacobi functions \(J^{(\theta ,\vartheta)}_{i} (1-2 \exp(-x/L))\) by \(EJ^{(\theta,\vartheta)}_{i}(x)\), \(x\in[0,\infty)\). Therefore, \(EJ^{(\theta,\vartheta)}_{i}(x)\) may be created by the following recurrence relation:

$$\begin{aligned} &EJ^{(\theta,\vartheta)}_{k+1}(x) \\ &\quad=\frac{(2 k+\theta+\vartheta+1) (2 k+\theta+\vartheta+2)}{(k+1) (k+\theta+\vartheta+1)} \biggl[ \biggl( \frac{((\theta+1) (\theta+\vartheta) +2 k^{2}+2 k (\theta +\vartheta+1))}{(2 k+\theta+\vartheta) (2 k+\theta+\vartheta+2)} \\ &\qquad{}-\exp(-x/L) \biggr)EJ^{(\theta,\vartheta)}_{k}(x)- \frac{(k+\theta) ( k+\vartheta)}{ (2 k+\theta+\vartheta) (2 k+\theta+\vartheta+1)}EJ^{(\theta ,\vartheta)}_{k-1}(x) \biggr],\quad k\geq1, \end{aligned}$$
(3)

where

$$EJ^{(\theta,\vartheta)}_{0}(x)=1,\qquad EJ^{(\theta,\vartheta)}_{1}(x) = ( \theta+1)-(\theta+\vartheta+2) \exp(-x/L), $$

and

$$ (k+\theta+\vartheta)EJ_{i}^{(\theta,\vartheta)}(x)=(k+\vartheta) EJ_{i}^{(\theta,\vartheta-1)}(x) +(k+\theta)EJ_{i}^{(\theta-1,\vartheta)}(x). $$

The exponential Jacobi functions \(EJ^{(\theta,\vartheta)}_{i}(x)\) of degree i can be written as

$$EJ^{(\theta,\vartheta)}_{i}(x)=\sum_{k=0}^{i}(-1)^{k} \frac{\Gamma (i+\theta+1)\Gamma (i+k+\theta+\vartheta+1)}{ \Gamma (\theta+k+1)\Gamma (i+\theta+\vartheta+1)(i-k)!k!}\exp(-k x/L), $$

where

$$\begin{aligned}& EJ_{i}^{(\theta,\vartheta)}(0)=\sum_{k=0}^{i}(-1)^{k} \frac{\Gamma (i+\theta+1)\Gamma (i+k+\theta+\vartheta+1)}{ \Gamma (\theta+k+1)\Gamma (i+\theta+\vartheta+1)(i-k)!k!}, \end{aligned}$$
(4)
$$\begin{aligned}& D^{q}EJ_{i}^{(\theta,\vartheta)}(0)=\sum _{k=0}^{i}(-1)^{k+q}\frac {k^{q}\Gamma (i+\theta+1)\Gamma (i+k+\theta+\vartheta+1)}{ L^{q}\Gamma (\theta+k+1)\Gamma (i+\theta+\vartheta+1)(i-k)!k!}. \end{aligned}$$
(5)

Let \(\chi_{R}^{(\theta,\vartheta)}(x) =1/L \exp(-x(\theta+1)/L) (1-\exp(-x/L))^{\vartheta}\), \(\theta, \vartheta> -1\). The orthogonality condition of exponential Jacobi functions is

$$ \int_{0}^{\infty} EJ_{i}^{(\theta,\vartheta)}(x)EJ_{j}^{(\theta ,\vartheta)}(x) \chi_{R}^{(\theta,\vartheta)}(x)\,dx= \begin{cases} \gamma_{i}^{(\theta,\vartheta)}, & i=j,\\ 0, & i\neq j, \end{cases} $$
(6)

where

$$ \gamma_{i}^{(\theta,\vartheta)}=\frac{\Gamma (i+\theta+1)\Gamma (i+\vartheta+1)}{ (2i+\theta+\vartheta+1)\Gamma (i+1)\Gamma (i+\theta+\vartheta+1)}. $$

Any function \(u(x)\in L_{\chi_{R}^{(\theta,\vartheta)}(x)}^{2}[0,\infty)\) can be expanded in terms of exponential Jacobi functions as

$$u(x)=\sum_{j=0}^{\infty} c_{j} EJ^{(\theta,\vartheta)}_{j}(x), $$

where the coefficients \(c_{j}\) are given by

$$c_{j}=\frac{1}{\gamma_{j}^{(\theta,\vartheta)}}\int_{0}^{\infty} u(x)EJ_{j}^{(\theta,\vartheta)}(x) \chi_{R}^{(\theta,\vartheta)}(x)\,dx, \quad j=0,1,\ldots. $$

Here, we outline the exponential Jacobi-Gauss quadrature. Assume that \(x^{(\theta,\vartheta)}_{N,j}\), \(0\leqslant j\leqslant N\), are the zeros of the Jacobi-Gauss interpolation on the interval \((-1, 1)\) and \(\varpi^{(\theta,\vartheta)}_{N,j}\), \(0\leqslant j\leqslant N\), are the corresponding weights of this interpolation. The nodes of the exponential Jacobi-Gauss interpolation on the interval \((0,\infty)\) are the zeros of \(EJ_{N+1}^{(\theta, \vartheta)}(x)\), which are denoted by \(x^{(\theta,\vartheta)}_{R,N,j}\), \(0\leqslant j\leqslant N\). Clearly \(x^{(\theta,\vartheta)}_{R,N,j} =-L \ln(\frac{1-x^{(\theta,\vartheta)}_{N,j}}{2})\), and weights are \(\varpi^{(\theta,\vartheta)}_{R,N,j} =\frac{1}{2^{\theta+\vartheta+1}} \varpi^{(\theta,\vartheta)}_{N,j}\), \(0\leqslant j\leqslant N\). Let \(S_{N}(0,\infty)\) be the set of all polynomials of degree at most N.

Let N be any positive integer, and

$$ S_{N}(0,\infty)=\textrm{span} \bigl\{ EJ^{(\theta, \vartheta)}_{0}(x),EJ^{(\theta, \vartheta)}_{1}(x), \ldots,EJ^{(\theta, \vartheta)}_{N}(x) \bigr\} . $$
(7)

Then, for any \(\phi\in S_{2N+1}(0,\infty)\), we obtain

$$\begin{aligned} &\int_{0}^{\infty} \frac{1}{L} \exp \biggl(\frac{-x(\theta+1)}{L} \biggr) \biggl(1-\exp \biggl( \frac{-x}{L} \biggr) \biggr)^{\vartheta}\phi(x)\,dx \\ &\quad = \frac{1}{2^{\theta+\vartheta+1}} \int_{-1}^{1}(1-x)^{\theta}(1+x)^{\vartheta}\phi \biggl(-L \ln \biggl(\frac{1-x}{2} \biggr) \biggr)\,dx \\ &\quad=\frac{1}{2^{\theta+\vartheta+1}}\sum_{j=0}^{N} \varpi^{(\theta ,\vartheta)}_{N,j} \phi \biggl(-L \ln \biggl(\frac{1-x^{(\theta,\vartheta)}_{N,j}}{2} \biggr) \biggr) \\ &\quad=\sum_{j=0}^{N}\varpi^{(\theta,\vartheta)}_{R,N,j} \phi \bigl(x^{(\theta,\vartheta)}_{R,N,j} \bigr). \end{aligned}$$
(8)

Now, approximating \(u(x)\) by \(N+1\) terms of exponential Jacobi functions yields

$$ u(x)\simeq\sum_{j=0}^{N} c_{j} EJ^{(\theta,\vartheta)}_{j}(x)=C^{T}\phi(x) , $$
(9)

where C and \(\phi(x)\) are the unknown coefficients vector and the exponential Jacobi function vector, respectively, and they are given by:

$$\begin{aligned}& C=[c_{0},c_{1},\ldots,c_{N}]^{T}, \end{aligned}$$
(10)
$$\begin{aligned}& \phi(x)= \bigl[EJ_{0}^{(\theta,\vartheta)}(x),EJ_{1}^{(\theta,\vartheta )}(x), \ldots,EJ_{N}^{(\theta,\vartheta)}(x) \bigr]^{T}. \end{aligned}$$
(11)

2.2 The derivative operational matrix of exponential Jacobi function

Here we shall give the derivation of a new operational matrix of derivative of the exponential Jacobi functions, which is essential to our numerical method.

Theorem 2.1

Let \(\phi(x)\) be the exponential Jacobi vector defined in (11). The derivative of the vector \(\phi(x)\) can be expressed by

$$ \phi^{\prime}(x)=\frac{d\phi(x)}{dx}\simeq\mathbf{D}\phi(x), $$
(12)

where D is the \((N+1)\times(N+ 1)\) operational matrix of the derivative. Then the nonzero elements \(d_{ij}\) for \(0\leq i,j\leq N\) are given as follows:

$$\begin{aligned}& d_{i+1,i}=\frac{(\theta+i+1)(\theta+\vartheta+2i+1)}{L(\theta+\vartheta +i+1)},\qquad d_{ii}=-\frac{i}{L}, \\& d_{ij}=\frac{(-1)^{i+j+1}(2j+\theta+\vartheta+1)}{L}\prod_{k=1}^{i-j} \frac{(\theta+i-k+1)}{(\theta+\vartheta+i-k+1)},\quad j< i-1. \end{aligned}$$

It is noticed that D is a lower-Heisenberg matrix.

Proof

By differentiation with respect to x in (3) we get

$$\begin{aligned} \frac{d}{dx}{EJ_{k+1}^{(\theta,\vartheta)}}(x)={}& \frac{(2 k+\theta +\vartheta+1) (2 k+\theta+\vartheta+2)}{(k+1) (k+\theta +\vartheta+1)} \\ &{} \times \biggl[ \biggl( \frac{((\theta+1) (\theta +\vartheta)+2 k^{2}+2 k (\theta+\vartheta+1))}{(2 k+\theta +\vartheta) (2 k+\theta+\vartheta+2)} \\ &{}-\exp \biggl(\frac{-x}{L} \biggr) \biggr)\frac{d}{dx}{EJ_{k}^{(\theta,\vartheta)}}(x) +\frac{1}{L} \exp \biggl(\frac{-x}{L} \biggr) EJ^{(\theta,\vartheta)}_{k}(x) \\ &{} -\frac{(k+\theta) ( k+\vartheta)}{ (2 k+\theta+\vartheta) (2 k+\theta+\vartheta+1)} \frac{d}{dx}{EJ_{k-1}^{(\theta,\vartheta)}}(x) \biggr],\quad k\geq1. \end{aligned}$$

According to

$$ (\theta+\vartheta+2)\exp \biggl( \frac{-x}{L} \biggr)=( \theta+1) EJ^{(\theta,\vartheta)}_{0} (x)-EJ^{(\theta,\vartheta)}_{1}(x) = \frac{d}{dx}{EJ_{1}^{(\theta,\vartheta)}}(x), $$
(13)

the elements \(d_{ij}\) of the matrix D may be achieved from

$$\begin{aligned}& \begin{aligned}[b] \frac{d}{dx}{EJ_{k+1}^{(\theta,\vartheta)}}(x)={}& \frac{(2 k+\theta +\vartheta+1) (2 k+\theta+\vartheta+2)}{(k+1) (k+\theta +\vartheta+1)} \\ &{} \times \biggl[ \biggl(\frac{((\theta+1) (\theta +\vartheta)+2 k^{2}+2 k (\theta+\vartheta+1))}{(2 k+\theta +\vartheta) (2 k+\theta+\vartheta+2)} \\ &{}-\exp \biggl(\frac{-x}{L} \biggr) \biggr)\frac{d}{dx}{EJ_{k}^{(\theta,\vartheta)}}(x) +\frac{1}{(\theta+\vartheta+2) L} \frac{d}{dx}{EJ_{1}^{(\theta,\vartheta )}}(x) EJ^{(\theta,\vartheta)}_{k}(x) \\ &{} -\frac{(k+\theta) ( k+\vartheta)}{ (2 k+\theta+\vartheta) (2 k+\theta+\vartheta+1)} \frac{d}{dx}{EJ_{k-1}^{(\theta,\vartheta)}}(x) \biggr],\quad k\geq1, \end{aligned} \end{aligned}$$
(14)
$$\begin{aligned}& \frac{d}{dx}{EJ_{1}^{(\theta,\vartheta)}}(x)=(\theta+1) EJ^{(\theta,\vartheta)}_{0}(x)-EJ^{(\theta,\vartheta)}_{1}(x), \end{aligned}$$
(15)
$$\begin{aligned}& \frac{d}{dx}{EJ_{0}^{(\theta,\vartheta)}}(x)=0. \end{aligned}$$
(16)

A combination of Eqs. (14), (15) and (16) leads to the desired result. □

The main advantages of studying the general class of exponential Jacobi functions is that the exponential Legendre functions, exponential Chebyshev functions of all kinds, and the exponential Gegenbauer functions can be obtained as immediately special cases of the exponential Jacobi functions. Accordingly, in this article we cover all the previous mentioned functions. More specifically, exponential Legendre, exponential Chebyshev and exponential Gegenbauer operational matrices can be obtained as special cases from the derived exponential Jacobi functions. These cases are summarized in the following corollaries.

Corollary 2.2

If \(\theta= \vartheta= 0\), we obtain the exponential Legendre functions, then the nonzero elements of the operational matrix of the exponential Legendre functions \(d_{ij}\) for \(0\leq i,j\leq N\) are given as follows:

$$\begin{aligned}& d_{i+1,i}=\frac{2i+1}{L},\qquad d_{ii}=-\frac{i}{L}, \\& d_{ij}=(-1)^{i+j+1}\frac{(2 j+1)}{L} ,\quad j< i-1. \end{aligned}$$

Corollary 2.3

If \(\theta= \vartheta=- \frac{1}{2}\), we have the exponential Chebyshev functions of the first kind, then the nonzero elements of the operational matrix of the exponential Chebyshev functions of the first kind \(d_{ij}\) for \(0\leq i,j\leq N\) are given as follows:

$$\begin{aligned}& d_{i+1,i}= \frac{(2 i+1)}{L},\qquad d_{ii}=- \frac{i}{L}, \\& d_{ij}=\frac{2(-1)^{i+j+1}j(i-\frac{1}{2})_{i-j}}{L(1-i)_{i-j}} ,\quad j< i-1. \end{aligned}$$

Corollary 2.4

If \(\theta= \vartheta= \frac{1}{2}\), we have the exponential Chebyshev functions of the second kind, then the nonzero elements of the operational matrix of the exponential Chebyshev functions of the second kind \(d_{ij}\) for \(0\leq i,j\leq N\) are given as follows:

$$\begin{aligned}& d_{i+1,i}=\frac{(2i+3)(i+1)}{L(i+2)} ,\qquad d_{ii}=- \frac{i}{L}, \\& d_{ij}=\frac{2(-1)^{i+j+1}(j+1)(i-\frac{1}{2})_{i-j}}{L(-i-1)_{i-j}},\quad j< i-1. \end{aligned}$$

Corollary 2.5

If \(\theta= -\frac{1}{2}\), \(\vartheta= \frac{1}{2}\), we have the exponential Chebyshev functions of the third kind, then the nonzero elements \(d_{ij}\) for \(0\leq i,j\leq N\) are given as follows:

$$\begin{aligned}& d_{i+1,i}=\frac{(2 i+1)^{2} }{ 2L(i+1)},\qquad d_{ii}=-\frac{i}{L}, \\& d_{ij}=\frac{(2 j+1) (-1)^{i+j+1} \Gamma(-i) (\frac {1}{2}-i )_{i-j}}{L\Gamma(-j)},\quad j< i-1. \end{aligned}$$

Corollary 2.6

If \(\theta= \frac{1}{2}\), \(\vartheta=- \frac{1}{2}\), we have the exponential Chebyshev functions of the fourth kind, then the nonzero elements \(d_{ij}\) for \(0\leq i,j\leq N\) are given as follows:

$$\begin{aligned}& d_{i+1,i}=\frac{(2 i+3) (2 i+1)}{2L (i+1)},\qquad d_{ii}=-\frac{i}{L}, \\& d_{ij}=\frac{2 (-1)^{i+j} \Gamma(-i) \Gamma (\frac {1}{2}-j )}{L\Gamma (-i-\frac{1}{2} ) \Gamma(-j)} , \quad j< i-1. \end{aligned}$$

Remark 2.7

The operational matrix for the nth derivative can be derived as

$$ \frac{d^{n} \phi(x)}{dx^{n}}= \bigl(\mathbf{D}^{(1)} \bigr)^{n} \phi(x), $$
(17)

where \(n \in N\) and the superscript in \({\mathbf{D}}^{(1)}\) denotes matrix powers. Thus

$$ {\mathbf{D}}^{(n)}= \bigl({\mathbf{D}}^{(1)} \bigr)^{n},\quad n=1,2,\ldots. $$
(18)

2.3 Derivation of the pseudospectral method

The purpose of this section is to derive a numerical algorithm for the exponential Jacobi spectral collocation method based on the operational matrix of derivative of exponential Jacobi function to solve high-order ordinary differential equations on the half line. Let us consider the high-order ordinary differential equations of the form

$$ u^{(m)}(x)+\sum_{i=0}^{m-1} a_{i}(x)u^{(i)}(x)=f(x),\quad x\in[0,\infty[, $$
(19)

with initial conditions

$$ u^{(i)}(0)=\alpha_{i}, \quad\mbox{for }i=0,1, \ldots,m-1. $$
(20)

We give some needed properties of exponential Jacobi functions in the preceding subsections, along with the derivation of the operational matrix of derivatives of exponential Jacobi functions.

We will obtain a system of \(N+1\) algebraic equations from: (i) applying the operational matrix of an exponential Jacobi function; (ii) collocation of the high-order ordinary differential equations at \((N -m- 1)\) exponential Jacobi-Gauss points; (iii) imposition of m initial conditions.

In order to use the exponential Jacobi operator matrix for this problem, we first approximate \(u(x)\), \(u^{(i)}(x)\) and \(u^{(m)}(x)\) by the exponential Jacobi functions as

$$\begin{aligned}& u_{N}(x)\simeq\sum_{j=0}^{N}c_{j} R^{(\theta,\vartheta )}_{j}(x)=C^{T}\phi(x), \end{aligned}$$
(21)
$$\begin{aligned}& u^{(i)}_{N}(x)\simeq\sum_{j=0}^{N}c_{j} \frac{d^{i}}{dx^{i}} R^{(\theta,\vartheta)}_{j}(x)=C^{T} \mathbf{D}^{(i)}\phi(x), \end{aligned}$$
(22)

and

$$ u^{(m)}_{N}(x)\simeq\sum _{j=0}^{N}c_{j} \frac{d^{m}}{dx^{m}} R^{(\theta,\vartheta)}_{j}(x)=C^{T} \mathbf{D}^{(m)} \phi(x). $$
(23)

By substituting Eqs. (21), (22) and (23) in Eq. (19), we get

$$ C^{T}\mathbf{D}^{(m)}\phi(x)+\sum _{i=0}^{m-1}a_{i}(x)C^{T}\mathbf {D}^{(i)}\phi(x)=f(x). $$
(24)

Now, we satisfy (24) exactly at the collocation points of Jacobi rational Gauss quadrature. In other words, we have to collocate this operational matrix relation at the \((N -m-1)\) exponential Jacobi roots; \(x^{(\theta,\vartheta )}_{R,N-m,k}\), \(k=0,1,\ldots,N-m\),

$$\begin{aligned} &C^{T}\mathbf{D}^{(m)} \phi \bigl(x^{(\theta,\vartheta)}_{R,N-2,k} \bigr) +\sum_{i=0}^{m-1}a_{i} \bigl(x^{(\theta,\vartheta)}_{R,N-2,k} \bigr)C^{T}\mathbf {D}^{(i)}\phi \bigl(x^{(\theta,\vartheta)}_{R,N-2,k} \bigr) =f \bigl(x^{(\theta,\vartheta)}_{R,N-2,k} \bigr), \\ &\quad k=0,1,\ldots,N-m. \end{aligned}$$
(25)

Furthermore, for imposing of m initial conditions, substituting Eq. (21) in Eq. (20) gives

$$ u^{(i)}(0)=C^{T}\mathbf{D}^{(i)} \phi(0)=\alpha_{i}. $$
(26)

Finally, the relations (25)-(26) constitute a system of \((N +1)\) algebraic equations, which can be solved using any iterative technique. Consequently, the approximate solution \(u_{N}(x)\) can be obtained (for more details, see [3, 36, 37]).

3 Numerical results

This section presents several numerical examples to demonstrate the high accuracy and applicability of the present method, and all of them were performed on the computer using a program written in Mathematica 8.0. The absolute errors in the given tables are the values of \(|u(x)-u_{N}(x)|\) at selected points. Moreover, the obtained results are compared with those obtained using other techniques. We consider the following examples.

Example 1

Consider the nonlinear Emden-Fowler equation

$$ u^{(2)}(x)+ \frac{6}{(x)}u^{(1)}(x)+14 u(x)=-4u \ln u,\quad x\geq0, $$
(27)

subject to

$$u(0)=1,\qquad u^{(1)}(0)=0. $$

The analytical solution is \(u(x)=e^{-x^{2}}\).

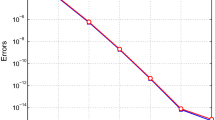
In this example, ten node points in \([0,1]\) and six corresponding weights with respect to first six exponential Jacobi functions are considered. Table 1 shows the analytical and approximation solutions of \(u(x)\) obtained by Chebyshev neural network (ChNN) [38] and exponential Jacobi operational matrix (EJOM) with \(\theta=\vartheta= -\frac{1}{2}\) (first kind exponential Chebyshev functions), \(\theta=\vartheta= 0\) (exponential Legendre functions) and \(\theta=\vartheta= \frac{1}{2}\) (second kind exponential Chebyshev functions), respectively. Absolute errors obtained by EJOM with \(\theta= \frac{1}{2}\), \(\vartheta=-\frac{1}{2}\), \(N=20\) and \(L=1\) for Example 1 are plotted in Figure 1. The graph of analytical solution and approximate solution for \(\theta= \frac{1}{2}\), \(\vartheta=-\frac{1}{2}\), \(N=20\) and \(L=1\) is displayed in Figure 2 to make it easer to compare with analytical solution. Moreover the resulting graph of Eq. (27) for the presented method and the analytic solution are shown in Figure 3.

Figure 1
figure 1

Absolute residual error functions with \(\pmb{\theta = \frac{1}{2}}\) , \(\pmb{\vartheta=-\frac{1}{2}}\) , \(\pmb{N=20}\) and \(\pmb{L=1}\) for Example 1 .

Full size image
Figure 2
figure 2

Exact solution and approximate solution at \(\pmb{\theta = \frac{1}{2}}\) , \(\pmb{\vartheta=-\frac{1}{2}}\) , \(\pmb{N=20}\) and \(\pmb{L=1}\) for Example 1 .

Full size image
Figure 3
figure 3

Exact solution and approximate solution with \(\pmb{\theta = \frac{1}{2}}\) , \(\pmb{\vartheta=-\frac{1}{2}}\) , \(\pmb{N=20}\) and \(\pmb{L=1}\) for Example 1 .

Full size image
Table 1 Comparison of the absolute errors for Example 1
Full size table

Example 2

Consider the second-order nonlinear differential equation

$$ u^{(2)}(x)+ \frac{8}{(x)}u^{(1)}(x)+ u^{2}(x)=\operatorname{erf}(x)^{2}- \frac{4 e^{-x^{2}} (x^{2}-4 )}{\sqrt{\pi} x} , \quad x\geq0, $$
(28)

subject to

$$u(0)=0,\qquad u^{(1)}(0)=\frac{2}{\sqrt{\pi}}. $$

The analytical solution is \(u(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x}e^{-t^{2}}\,dt\).

In Table 2, we introduce the absolute errors with different values of θ, ϑ, \(N = 24\) and \(L=1\). In Figure 4, we plot the absolute errors obtained by EJOM with \(\theta=- \frac{1}{2}\), \(\vartheta=\frac{1}{2}\), \(N=24\) and \(L=1\), while Figure 5 presents the analytic solution with the approximate solution with \(\theta=- \frac{1}{2}\), \(\vartheta=\frac{1}{2}\), \(N=24\) and \(L=1\).

Figure 4
figure 4

Absolute residual error functions with \(\pmb{\theta = -\frac{1}{2}}\) , \(\pmb{\vartheta=\frac{1}{2}}\) , \(\pmb{N=24}\) and \(\pmb{L=1}\) for Example 2 .

Full size image
Figure 5
figure 5

Exact solution and approximate solution with \(\pmb{\theta = -\frac{1}{2}}\) , \(\pmb{\vartheta=\frac{1}{2}}\) , \(\pmb{N=24}\) and \(\pmb{L=1}\) for Example 2 .

Full size image
Table 2 Comparison of the absolute errors for Example 2
Full size table

Example 3

Consider the linear third-order problem

$$ u^{(3)}(x)+\frac{1}{(x+1)}u^{(2)}(x)- \frac{1}{(x+1)^{2}}u^{(1)}(x) +\frac{x}{x+1}u(x)=\frac{x \ln(x+1)}{ x+1},\quad x\in[0,1], $$
(29)

subject to the conditions

$$u(0)=0,\qquad u^{(1)}(0)=1,\qquad u^{(2)}(0)=-1, $$

and the analytical solution \(u(x)=\ln(x+1)\). We apply the proposed exponential Jacobi operational matrix (EJOM) with three choices of θ and ϑ; \(\theta= \vartheta= -1/2\) (first kind exponential Chebyshev functions), \(\theta= \vartheta = 0\) (exponential Legendre functions), \(\theta= \vartheta = 1/2\) (second kind exponential Chebyshev functions) and the numerical results are tabulated in Table 3. In this table we compare our results with those obtained by the rational Chebyshev collocation (RCC) method [36]. Numerical results of this problem show that (EJOM) is more accurate than the presented method in [36]. The graph of analytical solution and approximate solution for \(\theta= \frac{1}{2}\), \(\vartheta=-\frac{1}{2}\) at \(N=16\) and \(L=10\) is displayed in Figure 6 to make it easer to compare with analytical solution. Figure 7 shows the absolute residual error functions for \(\theta= \frac{1}{2}\), \(\vartheta=-\frac{1}{2}\) at \(N=20\) and \(L=10\).

Figure 6
figure 6

Exact solution and approximate solution with \(\pmb{\theta = \frac{1}{2}}\) , \(\pmb{\vartheta=-\frac{1}{2}}\) , \(\pmb{N=16}\) and \(\pmb{L=10}\) for Example 3 .

Full size image
Figure 7
figure 7

Absolute residual error functions with \(\pmb{\theta = \frac{1}{2}}\) , \(\pmb{\vartheta=-\frac{1}{2}}\) , \(\pmb{N=20}\) and \(\pmb{L=10}\) for Example 3 .

Full size image
Table 3 Comparison of the absolute errors for Example 3
Full size table

Example 4

Consider the linear fourth-order problem

$$\begin{aligned} &u^{(4)}(x)+ \cos x u^{(3)}(x)+ \sin x u^{(2)}(x) \\ &\quad{}-2 \cos x u^{(1)}(x) -2 \sin x u(x)=f(x),\quad x \in[0,100], \end{aligned}$$
(30)

subject to the conditions

$$u(0)=0, \qquad u^{(1)}(0)=1,\qquad u^{(2)}(0)=-2,\qquad u^{(3)}(0)=2, $$

where f is selected such that exact solution is \(u(x)=e^{-x} \sin x\). In Table 4, we list the absolute errors obtained by EJOM with different values of θ, ϑ at \(N = 24\) and \(L=24\). Figure 8 is plotted to compare the analytic solution with the approximate solution with \(\theta=\vartheta=-\frac {1}{2}\) at \(N=24\) and \(L=6\).

Figure 8
figure 8

Exact solution and approximate solution with \(\pmb{\theta =\vartheta=-\frac{1}{2}}\) , \(\pmb{N=24}\) and \(\pmb{L=6}\) for Example 4 .

Full size image
Table 4 Comparison of the absolute errors for Example 4
Full size table

4 Conclusions

In this paper, we derived the operational matrix of derivative of exponential Jacobi functions. This operational matrix in conjunction with the exponential Jacobi spectral collocation method is utilized for reducing the solution of high-order ordinary differential equations on the semi-infinite interval to that of a system of algebraic equations, which may then be solved much more easily. The operational matrices of derivatives of exponential Legendre and exponential Chebyshev functions of the first and second kinds, which often appear in conjunction with such spectral methods in the literature, may be obtained as special cases of the operational matrix of exponential Jacobi functions by taking the corresponding spacial cases of the exponential Jacobi functions parameters θ and ϑ.

Illustrative numerical examples with the satisfactory approximate solutions are achieved to demonstrate the applicability and high accuracy of the present technique. The obtained approximations of the exact solutions for the test problems make this technique very attractive and contributed to the good agreement between approximate and exact values in the numerical example. In addition, the present method could prove fruitful for those investigating not only high-order ordinary differential equations, but more broadly equations with (i) strong nonlinearity and (ii) singularities.

It can be expected that the new exponential Jacobi pseudospectral scheme coupled with a spectral element method will be an effective tool for the numerical solution of time-dependent differential equations [39]. It also may be extended to solve nonlocal boundary value problems with more complicated conditions, meanwhile its extension to the two-dimensional problems is straightforward. We assert that the proposed technique can be applied to a much larger class of fixed-order and variable-order fractional differential equations (see, for instance, [40, 41]).