1 Introduction

It is well known that a real system inevitably contains some uncertain parameters because of work environment change, measure error, model approximation and so on. The uncertain parameters perhaps change the system structure and even destroy the system. For a practical system, the uncertain parameters should be considered, otherwise, one cannot obtain their desired goals. Recently, robust \(H_{\infty}\) (sub) optimal control has become one of the most important notions in the field of automatic control theory, it has drawn considerable attention from many researchers. Although robust \(H_{\infty}\) control theory has been perfectly developed over the last decade, most of the results were developed based on uncertain linear systems [1–4]. Besides, some physical phenomena, like impulse and hysterics, which are important in circuit theory, cannot be treated in the linear system models. It is well known that time delay is frequently encountered in a variety of industrial and engineering systems, and it has become one of the main sources for causing instability and poor performance of the network system [5, 6].

Singular systems are also referred to as generalized systems, descriptor systems, differential-algebraic systems, or implicit systems, which are also a natural representation of dynamic systems and describe a larger family of systems than the normal linear systems [7]. A singular system provides a suitable way to handle such problems, the robust control theory based on singular system models has been widely developed for many years. Dai first gave some notions of controllability, observability and duality in singular systems [8], some excellent results on disk pole constraints [9] and robust control [10, 11]. Problem of control and stabilization for uncertain dynamical systems with deviating argument is modern now. For example, robust stability and \(H_{\infty}\) were studied for uncertain systems with impulsive perturbations [12]. Moreover, robust \(H_{\infty}\) synchronization was studied for chaotic systems with input saturation and time varying delay [13]. In [14, 15], stabilization and perturbation estimation were studied in neutral type direct control systems. In [16], stabilization was studied for Lur’e-type nonlinear control systems by using Lyapunov-Krasovskii functionals. In addition, dissipativity was studied for singular systems with Markovian jump parameters and mode-dependent mixed time-delays [7]. However, for the singular system, robust \(H_{\infty}\) control problem has been little considered with uncertainties and time-delay recently.

In this paper, by means of linear matrix inequalities (LMIs), we present sufficient conditions for the existence of memory-less and memorial linear state feedback controllers such that the closed-loop system not only has \(H_{\infty}\) performance, but it also is generalized quadratically stable; moreover, the design methods for such controllers are also provided.

2 System description and preliminaries

Consider a linear singular system with state delay and parameter uncertainties described by

$$\begin{aligned}& E\dot{x}(t)= (A+\Delta A)x(t)+(A_{d}+\Delta A_{d})x(t-d) \\& \hphantom{E\dot{x}(t)=}{}+(B_{1}+\Delta B_{1})\omega(t)+ (B_{2}+\Delta B_{2})u(t), \\& z(t)= (C_{1}+\Delta C_{1})x(t)+(C_{1d}+\Delta C_{1d})x(t-d) \\& \hphantom{z(t)=}{}+(D_{11}+\Delta D_{11})\omega(t)+ (D_{12}+\Delta D_{12})u(t), \\& x(t)= \phi(t),\quad t\in[-d,0], \end{aligned}$$
(1)

where \(x(t)\in R^{n}\) is the state, \(\omega(t)\in R^{m}\) is the exogenous input with \(\omega(t)\in L_{2}[0,\infty)\), \(z(t)\in R^{p}\) is the controlled output, \(u(t)\in R^{q}\) is the control input. E, A, \(A_{d}\), \(B_{1}\), \(B_{2}\), \(C_{1}\), \(C_{1d}\), \(D_{11}\) and \(D_{12}\) are known real constant matrices with appropriate dimensions, \(\operatorname{rank}E=r< n\). \(d>0\) is a constant time delay, \(\phi(t)\) is a compatible vector-valued continuous function. ΔA, \(\Delta A_{d}\), \(\Delta B_{1}\), \(\Delta B_{2}\), \(\Delta C_{1}\), \(\Delta C_{1d}\), \(\Delta D_{11}\) and \(\Delta D_{12}\) are time-invariant matrices representing norm-bounded parameter uncertainties and are assumed to be of the following form:

$$ \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} \Delta A& \Delta A_{d}& \Delta B_{1}& \Delta B_{2} \\ \Delta C_{1}& \Delta C_{1d}& \Delta D_{11}& \Delta D_{12} \end{array} \right ]= \left [ \begin{array}{@{}c@{}} H_{1} \\ H_{2} \end{array} \right ] F(\sigma)[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} E_{1}&E_{2}&E_{3}&E_{4} \end{array} ], $$
(2)

where \(H_{1}\), \(H_{2}\), \(E_{1}\), \(E_{2}\), \(E_{3}\) and \(E_{4}\) are known real constant matrices with appropriate dimensions. The uncertain matrix \(F(\sigma)\)satisfies

$$ F^{T}(\sigma)F(\sigma)\leq I $$
(3)

and \(\sigma\in\Theta\), where Θ is a compact set in R. Furthermore, it is assumed that given any matrix F: \(F^{T}F\leq I\), there exists \(\sigma\in\Theta\) such that \(F=F(\sigma)\).

ΔA, \(\Delta A_{d}\), \(\Delta B_{1}\), \(\Delta B_{2}\), \(\Delta C_{1}\), \(\Delta C_{1d}\), \(\Delta D_{11}\) and \(\Delta D_{12}\) are said to be admissible if both (2) and (3) hold.

The nominal unforced system of (1) can be written as

$$ E\dot{x}(t)=Ax(t)+A_{d}x(t-d). $$
(4)

Lemma 1

[11]

Suppose that the pair \((E,A)\) is regular and impulse free, then the solution to (4) exists and is impulse free and unique on \([0, \infty)\).

Definition 1

[11, 17]

  1. (1)

    The singular delay system (4) is said to be regular and impulse free if the pair \((E,A)\) is regular and impulse free.

  2. (2)

    The singular delay system (4) is said to be asymptotically stable if for any \(\epsilon>0\), there exists a scalar \(\delta(\epsilon)>0\) such that, for any compatible initial conditions \(\phi(t)\) satisfying \(\sup_{-d\leq t\leq0}\|\phi(t)\|\leq\delta(\epsilon)\), the solution \(x(t)\) of system (4) satisfies \(\|x(t)\|\leq\epsilon\) for \(t\geq 0\). Furthermore, \(x(t)\rightarrow0\), \(t\rightarrow\infty\).

Definition 2

[17]

The uncertain singular delay system (1) is said to be robust stable if system (1) with \(u(t)\equiv0\) and \(\omega(t)\equiv0\) is regular, impulse free and asymptotically stable for all admissible uncertainties ΔA, \(\Delta A_{d}\).

Definition 3

[11]

The uncertain singular delay system (1) is said to be generalized quadratically stable if there exists a matrix \(X>0\) such that

$$ \left [ \begin{array}{@{}c@{\quad}c@{}} (A+\Delta A)^{T}XE+E^{T}X(A+\Delta A)+X& E^{T}X(A_{d}+\Delta A_{d}) \\ (A_{d}+\Delta A_{d})^{T}XE& -X \end{array} \right ]< 0 $$
(5)

for all admissible uncertainties ΔA, \(\Delta A_{d}\).

Lemma 2

[11]

If the uncertain singular delay system (1) is generalized quadratically stable, then it is robustly stable.

Lemma 3

[18]

Given matrices Ω, Γ, Ξ of appropriate dimensions and with Ω symmetrical, then

$$\Omega+\Gamma F(\sigma)\Xi+\bigl(\Gamma F(\sigma) \Xi\bigr)^{T}< 0 $$

for all \(F(\sigma)\) satisfying (3), if and only if there exists a scalar \(\epsilon> 0\) such that

$$\Omega+\epsilon\Gamma\Gamma^{T}+\epsilon^{-1} \Xi^{T}\Xi< 0. $$

The robust \(H_{\infty}\) problem we consider in this paper is, for an uncertain singular delay system and a given constant \(\gamma> 0\), under zero initial state if

$$\bigl\Vert z(t)\bigr\Vert _{2}\leq\gamma\bigl\Vert \omega(t) \bigr\Vert _{2},\quad \forall\omega(t)\in L_{2}[0,\infty) $$

for all admissible uncertainties, then we say the system has \(H_{\infty}\) performance γ.

3 Main results

Theorem 1

For the unforced uncertain singular delay system of (1) (i.e., \(u(t)\equiv0\)) and a given constant \(\gamma> 0\), if there exist a matrix \(P>0\) and a scalar \(\epsilon>0\) satisfying the following LMI:

$$ \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} A^{T}PE+E^{T}PA+P& E^{T}PA_{d}& E^{T}PB_{1}& C_{1}^{T}&E_{1}^{T}&\epsilon E^{T}PH_{1} \\ A_{d}^{T}PE& -P&0& C_{1d}^{T}& E_{2}^{T}& 0 \\ B_{1}^{T}PE&0&-\gamma^{2}I&D_{11}^{T}&E_{3}^{T}&0 \\ C_{1}&C_{1d}&D_{11}&-I&0 &\epsilon H_{2} \\ E_{1}&E_{2}&E_{3}&0&-\epsilon I&0 \\ \epsilon H_{1}^{T}PE&0&0&\epsilon H_{2}^{T}&0&-\epsilon I \end{array} \right ]< 0, $$
(6)

then the system is generalized quadratically stable with \(H_{\infty}\) performance γ.

Proof

For simplicity, we introduce

$$ \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} \widetilde{A}& \widetilde{A}_{d}& \widetilde{B}_{1} \\ \widetilde{C}_{1}& \widetilde{C}_{1d}&\widetilde{D}_{11} \end{array} \right ]=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} A+\Delta A& A_{d}+\Delta A_{d}&B_{1}+\Delta B_{1} \\ C_{1}+\Delta C_{1}&C_{1d}+\Delta C_{1d}&D_{11}+\Delta D_{11} \end{array} \right ]. $$

Let \(X=P\), then (5) is the same as

$$ \left [ \begin{array}{@{}c@{\quad}c@{}} \widetilde{A}^{T}PE+E^{T}P\widetilde{A}+P& E^{T}P\widetilde{A}_{d} \\ \widetilde{A}_{d}^{T}PE& -P \end{array} \right ]< 0. $$
(7)

Combing (2), (3) and Lemma 3, (7) is equivalent to

$$ \left [ \begin{array}{@{}c@{\quad}c@{}} A^{T}PE+E^{T}PA+P& E^{T}PA_{d} \\ A_{d}^{T}PE& -P \end{array} \right ] + \epsilon \left [ \begin{array}{@{}c@{}} E^{T}PH_{1} \\ 0 \end{array} \right ] \bigl[ \begin{array}{@{}c@{\quad}c@{}} H_{1}^{T}PE &0 \end{array} \bigr] +\epsilon^{-1}\left [ \begin{array}{@{}c@{}} E_{1}^{T} \\ E_{2}^{T} \end{array} \right ] [ \begin{array}{@{}c@{\quad}c@{}} E_{1}&E_{2} \end{array} ]< 0 $$

for a scalar \(\epsilon> 0\), which is equivalent to

$$ \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} A^{T}PE+E^{T}PA+P& E^{T}PA_{d}&E_{1}^{T}&\epsilon E^{T}PH_{1} \\ A_{d}^{T}PE& -P&E_{2}^{T}&0 \\ E_{1}&E_{2}&-\epsilon I&0 \\ \epsilon H_{1}^{T}PE&0&0&-\epsilon I \end{array} \right ]< 0 $$
(8)

by invoking again a Schur complement argument and (8) is already by (6). Hence, the unforced uncertain singular delay system of (1) is generalized quadratically stable.

Then we prove that the system has \(H_{\infty}\) performance γ.

Let the candidate on Lyapunov-Krasovskii functional [19] be as follows:

$$V(x_{t})=x(t)^{T}E^{T}PEx(t)+\int _{t-d}^{t}x(\tau)^{T}Px(\tau)\, d\tau. $$

Obviously, \(V(x_{t})\geq0\) and

$$\begin{aligned} \begin{aligned} &\dot{V}(x_{t})-\gamma^{2}\omega(t)^{T} \omega(t)+z(t)^{T}z(t) \\ &\quad=\bigl[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} x(t)^{T}&x(t-d)^{T}&\omega(t)^{T} \end{array} \bigr] L \bigl[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} x(t)^{T}&x(t-d)^{T}&\omega(t)^{T} \end{array} \bigr]^{T}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} L =&\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} \widetilde{A}^{T}PE+E^{T}P\widetilde{A}+P& E^{T}P\widetilde{A}_{d} &E^{T}P\widetilde{B}_{1} \\ \widetilde{A}_{d}^{T}PE& -P&0 \\ \widetilde{B}_{1}^{T}&0&-\gamma^{2}I \end{array} \right ] \\ &{}+[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} \widetilde{C}_{1}& \widetilde{C}_{1d}&\widetilde{D}_{11} \end{array} ]^{T}[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}}\widetilde{C}_{1}& \widetilde{C}_{1d}&\widetilde{D}_{11} \end{array} ]. \end{aligned}$$

Now we consider the condition of \(L<0\). By using a Schur complement argument, it follows that \(L<0\) is equivalent to

$$ \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} \widetilde{A}^{T}PE+E^{T}P\widetilde{A}+P& E^{T}P\widetilde{A}_{d} &E^{T}P\widetilde{B}_{1}&\widetilde{C}_{1}^{T} \\ \widetilde{A}_{d}^{T}PE& -P&0&\widetilde{C}_{1d}^{T} \\ \widetilde{B}_{1}^{T}&0&-\gamma^{2}I&\widetilde{D}_{11}^{T} \\ \widetilde{C}_{1}& \widetilde{C}_{1d}&\widetilde{D}_{11}&-I \end{array} \right ]< 0. $$
(9)

By (2) and Lemma 3, (9) holds if and only if

$$ \Omega+\epsilon\Gamma\Gamma^{T}+\varepsilon^{-1} \Xi^{T}\Xi< 0 $$
(10)

for a scalar \(\epsilon>0\), where

$$\begin{aligned}& \Omega= \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} A^{T}PE+E^{T}PA+P& E^{T}PA_{d} &E^{T}PB_{1}&C_{1}^{T} \\ A_{d}^{T}PE& -P&0&C_{1d}^{T} \\ B_{1}^{T}&0&-\gamma^{2}I&D_{11}^{T} \\ C_{1}& C_{1d}&D_{11}&-I \end{array} \right ], \\& \Gamma= \bigl[ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} H_{1}^{T}PE&0&0&H_{2}^{T} \end{array} \bigr]^{T} ,\qquad\Xi= [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} E_{1}&E_{2}&E_{3}&0 \end{array} ], \end{aligned}$$

and (10) is equivalent to (6) by a Schur complement argument, then we have

$$\dot{V}(x_{t})\leq\gamma^{2}\omega(t)^{T} \omega(t)-z(t)^{T}z(t). $$

Therefore the system has \(H_{\infty}\) performance γ from dissipative theory. □

Based on Theorem 1, we will further discuss the robust \(H_{\infty}\) control problem via state feedback for system (1).

Consider a memory-less state feedback controller as follows:

$$ u(t)=Kx(t). $$
(11)

Then the resulting closed-loop system is

$$ \begin{aligned} &E\dot{x}(t)= \widetilde{A}_{c1}x(t)+ \widetilde{A}_{d}x(t-d)+\widetilde {B}_{1}\omega(t), \\ &z(t)= \widetilde{C}_{c1}x(t)+\widetilde{C}_{1d}x(t-d)+ \widetilde {D}_{11}\omega(t), \end{aligned} $$
(12)

where

$$ \left [ \begin{array}{@{}c@{}} \widetilde{A}_{c1} \\ \widetilde{C}_{c1} \end{array} \right ]=\left [ \begin{array}{@{}c@{}} A+B_{2}K \\ C_{1}+D_{12}K \end{array} \right ]+\left [ \begin{array}{@{}c@{}} H_{1} \\ H_{2} \end{array} \right ]F(\sigma) (E_{1}+E_{4}K). $$

From Theorem 1, we can easily obtain the following theorem.

Theorem 2

For system (1) and a given constant \(\gamma>0\), if there exist matrices \(P>0\), K and a scalar \(\epsilon>0\) satisfying the following matrix inequality:

$$ \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \Sigma_{1}& E^{T}PA_{d}& E^{T}PB_{1}& \Sigma_{2}^{T}&\Sigma_{3}^{T}&\epsilon E^{T}PH_{1} \\ A_{d}^{T}PE& -P&0& C_{1d}^{T}& E_{2}^{T}& 0 \\ B_{1}^{T}PE&0&-\gamma^{2}I&D_{11}^{T}&E_{3}^{T}&0 \\ \Sigma_{2}&C_{1d}&D_{11}&-I&0 &\epsilon H_{2} \\ \Sigma_{3}&E_{2}&E_{3}&0&-\epsilon I&0 \\ \epsilon H_{1}^{T}PE&0&0&\epsilon H_{2}^{T}&0&-\varepsilon I \end{array} \right ]< 0, $$
(13)

where

$$\begin{aligned}& \Sigma_{1}= A^{T}PE+E^{T}PA+E^{T}PB_{2}K+K^{T}B_{2}^{T}PE+P, \\& \Sigma_{2}= C_{1}+D_{12}K, \\& \Sigma_{3}= E_{1}+E_{4}K, \end{aligned}$$

then there exists a memory-less state feedback controller such that the closed-loop uncertain delay singular system is generalized quadratically stable with \(H_{\infty}\) performance γ; moreover, the controller can be of the form (11).

Remark 1

According to Theorem 2, a controller can be obtained by solving the matrix inequality (13). However, it is worth pointing out that (13) is not a linear matrix inequality, so it cannot be solved using the LMI Toolbox of Matlab. However, using the method dealing with inequalities which was developed in [20], note that a necessary condition of (13) is

$$ \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{}} -P&C_{1d}^{T}&E_{2}^{T}&0 \\ C_{1d}&-I&0&\epsilon H_{2} \\ E_{2}&0&-\epsilon I&0 \\ 0&\epsilon H_{2}^{T}&0&-\epsilon I \end{array} \right ]< 0. $$
(14)

Obviously, (14) is a strict LMI about matrix P and a scalar \(\epsilon>0\), which can be solved numerically very efficiently by using the LMI Toolbox of Matlab.

Substituting the matrix P and the scalar \(\varepsilon>0\) obtained by solving (14) into (13), we can get the strict LMI about K, so the gain matrix can be obtained.

Since a memory-less state feedback controller does not sufficiently use the information of delay state, we want to consider a memorial state feedback controller as follows:

$$ u(t)=K_{1}x(t)+K_{2}x(t-d), $$
(15)

where \(K_{2}\neq0\), then the closed-loop system is

$$ \begin{aligned} &E\dot{x}(t)= \widetilde{A}_{c2}x(t)+ \widetilde {A}_{d1}x(t-d)+\widetilde{B}_{1}\omega(t), \\ &z(t)=\widetilde{C}_{c2}x(t)+\widetilde{C}_{d1}x(t-d)+ \widetilde {D}_{11}\omega(t), \end{aligned} $$
(16)

where

$$\begin{aligned} \left [ \begin{array}{@{}c@{\quad}c@{}} \widetilde{A}_{c2}&\widetilde{A}_{d1} \\ \widetilde{C}_{c2}&\widetilde{C}_{d1} \end{array} \right ] =&\left [ \begin{array}{@{}c@{\quad}c@{}} A+B_{2}K_{1}&A_{d}+B_{2}K_{2} \\ C_{1}+D_{12}K1&C_{1d}+D_{12}K2 \end{array} \right ] \\ &{}+\left [ \begin{array}{@{}c@{}} H_{1} \\ H_{2} \end{array} \right ]F(\sigma)[ \begin{array}{@{}c@{\quad}c@{}} E_{1}+E_{4}K_{1}&E_{2}+E_{4}K_{2} \end{array} ]. \end{aligned}$$

Similar to Theorem 2, we have the following conclusion.

Theorem 3

For system (1) and a given constant \(\gamma>0\), if there exist matrices \(P>0\), \(K_{1}\), \(K_{2}\) and a scalar \(\epsilon >0\) satisfying the following matrix inequality:

$$ \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} \Pi_{1}& \Pi_{2}^{T}& E^{T}PB_{1}& \Pi_{3}^{T}&\Pi_{4}^{T}&\epsilon E^{T}PH_{1} \\ \Pi_{2}& -P&0& \Pi_{5}^{T}& \Pi_{6}^{T}& 0 \\ B_{1}^{T}PE&0&-\gamma^{2}I&D_{11}^{T}&E_{3}^{T}&0 \\ \Pi{3}&\Pi_{5}&D_{11}&-I&0 &\epsilon H_{2} \\ \Pi_{4}&\Pi_{6}&E_{3}&0&-\epsilon I&0 \\ \epsilon H_{1}^{T}PE&0&0&\epsilon H_{2}^{T}&0&-\epsilon I \end{array} \right ]< 0, $$
(17)

where

$$\begin{aligned}& \Pi_{1}= A^{T}PE+E^{T}PA+E^{T}PB_{2}K_{1}+K^{T}_{1}B_{2}^{T}PE+P, \\& \Pi_{2}= E^{T}PA_{d}+A^{T}_{d}PE+E^{T}PB_{2}K_{2}+K_{2}^{T}B_{2}^{T}PE, \\& \Pi_{3}= C_{1}+D_{12}K_{1}, \\& \Pi_{4}= E_{1}+E_{4}K_{1}, \\& \Pi_{5}= C_{1d}+D_{12}K_{2}, \\& \Pi_{6}= E_{2}+E_{4}K_{2}, \end{aligned}$$

then there exists a memorial state feedback controller such that the closed-loop uncertain delay singular system is generalized quadratically stable with \(H_{\infty}\) performance γ; moreover, the controller can be of the form (15).

Remark 2

According to Theorem 3, a memorial controller can be obtained by solving the matrix inequality (17). However, it is worth pointing out that (17) is not a linear matrix inequality. Similarly, note that a necessary condition of (17) is

$$ \left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} -P&\Pi_{5}^{T}&\Pi_{6}^{T} \\ \Pi_{5}&-I&0 \\ \Pi_{6}&0&-\epsilon I \end{array} \right ]< 0. $$
(18)

Obviously, (18) is a strict LMI about matrix P, \(K_{2}\) and a scalar \(\varepsilon>0\).

Substituting the matrix P, \(K_{2}\) and the scalar \(\varepsilon>0\) obtained by solving (18) into (17), we can get the strict LMI about \(K_{1}\), so the two gain matrices can be obtained.

The robust \(H_{\infty}\) control problem for singular time delay system with norm-bounded parametric uncertainties is considered in this paper. All the coefficient matrices except the matrix E include uncertainties. The authors derive sufficient conditions about the generalized quadratic stability and \(H_{\infty}\) performance of the closed-loop systems. The control laws proposed by using strict LMI approaches can guarantee that the resultant closed-loop systems are generalized quadratic stable for all admissible uncertainties.

4 Numerical examples

In this section, we present an example to illustrate the application of the proposed theoretical method given in this paper.

Example

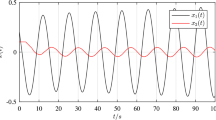
Consider the parameter uncertain singular systems with state delay

$$\begin{aligned}& E=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} -2&0&1 \\ -2&0&1 \\ 0&-1&1 \end{array} \right ],\qquad A=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 3&0&-1 \\ 0.2&-2&0 \\ 0&4&-4 \end{array} \right ],\qquad A_{d}=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 0.1&0&0.1 \\ 0&0.1&0 \\ 0.1&0&-0.1 \end{array} \right ], \\& E_{3}=\left [ \begin{array}{@{}c@{}} -1 \\ -2 \\ 0 \end{array} \right ],\qquad D_{11}=\left [ \begin{array}{@{}c@{}} -1 \\ 0 \\ -1 \end{array} \right ],\qquad C_{1}=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} -2&0&0.2 \\ 0&0.1&-0.1 \\ 1&0.1&0 \end{array} \right ], \\& E_{1}=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} -0.1&-0.2&0 \\ 2&1&0 \\ 1&0&0.2 \end{array} \right ],\qquad E_{2}=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1&0&1 \\ -1&2&0.1 \\ 0.1&-1&-0.2 \end{array} \right ], \\& H_{2}=\left [ \begin{array}{@{}c@{}} -2 \\ 1 \\ 0 \end{array} \right ],\qquad B_{1}=\left [ \begin{array}{@{}c@{}} -2 \\ 0 \\ -2 \end{array} \right ],\qquad B_{2}=\left [ \begin{array}{@{}c@{}} 1 \\ 0 \\ 2 \end{array} \right ],\qquad D= \left [ \begin{array}{@{}c@{}} -1 \\ 0 \\ -2 \end{array} \right ], \\& C_{1d}=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} -1&-2&0 \\ 1&1&1 \\ 2&0&-1 \end{array} \right ],\qquad D_{11}=\left [ \begin{array}{@{}c@{}} -1 \\ 0 \\ -1 \end{array} \right ]. \end{aligned}$$

Applying Theorem 3, choose \(\gamma=1\). We use the software package LMI Lab to solve the LMI problem (17) of the parameter uncertain singular systems with state delay. The solution is as follows:

$$\begin{aligned}& P=\left [ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 19.0497&0.2132&-0.0725 \\ 0.2132&18.7966&0.0837 \\ -0.0725&0.0837&17.4624 \end{array} \right ]>0,\qquad K_{1}=[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1.9299&0.5050&-1.3109 \end{array} ], \\& K_{2}=[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} -0.2191&-1.2652&-0.4616 \end{array} ]\neq0,\qquad \epsilon=0.0803. \end{aligned}$$

A memorial state feedback controller is as follows:

$$\begin{aligned} u(t) =&[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} 1.9299&0.5050&-1.3109 \end{array} ]x(t) \\ &{}+[ \begin{array}{@{}c@{\quad}c@{\quad}c@{}} -0.2191&-1.2652&-0.4616 \end{array} ]x(t-d). \end{aligned}$$

5 Conclusions

A positive solution matrix was proposed for the problem of robust \(H_{\infty}\) control via state feedback for a class of uncertain continuous-time singular systems with state delay. The solution provides sufficient conditions in the form of linear matrix inequalities. It was shown by the numerical example that the proposed method can solve generalized quadratic stability with \(H_{\infty}\) performance for the parameter uncertain continuous-time singular systems with state delay.