Enhanced shifted Jacobi operational matrices of derivatives: spectral algorithm for solving multiterm variable-order fractional differential equations

Abstract

This paper presents a new way to solve numerically multiterm variable-order fractional differential equations (MTVOFDEs) with initial conditions by using a class of modified shifted Jacobi polynomials (MSJPs). As their defining feature, MSJPs satisfy the given initial conditions. A key aspect of our methodology involves the construction of operational matrices (OMs) for ordinary derivatives (ODs) and variable-order fractional derivatives (VOFDs) of MSJPs and the application of the spectral collocation method (SCM). These constructions enable efficient and accurate numerical computation. We establish the error analysis and the convergence of the proposed algorithm, providing theoretical guarantees for its effectiveness. To demonstrate the applicability and accuracy of our method, we present five numerical examples. Through these examples, we compare the results obtained with other published results, confirming the superiority of our method in terms of accuracy and efficiency. The suggested algorithm yields very accurate agreement between the approximate and exact solutions, which are shown in tables and graphs.

1 Introduction

Fractional calculus has gained significant interest from researchers across various disciplines over the past few decades. This interest stems from the fact that fractional operators offer a universal perspective on system evolution. As a result, fractional derivatives provide a more accurate description of certain physical phenomena [1–4]. In the literature, numerous definitions of fractional differentiation (for more information, we refer to [5–7]).

A recent advancement in the field of fractional calculus involves extending the theory to accommodate VOFDs. This enables a more flexible and dynamic characterization of systems. In a specific study conducted by the authors [8], they explored the properties of VOFD operators [9, 10].

Variable-order fractional calculus (VOFC) provides a powerful framework for capturing the nonlocal characteristics exhibited by various systems, and it has been widely applied in physics, mechanics, control, and signal processing to describe real-world phenomena [11–15]. In the field of engineering mechanics, VOFC has found numerous applications. For instance, in [16], VOFD operators were utilized to model the microscopic structure of materials. The Riesz–Caputo fractional derivative of space-dependent order was employed in continuum elasticity, as demonstrated in [17]. The nonlinear viscoelastic behavior of fractional systems of time-dependent fractional order was investigated in [18, 19]. These examples highlight the diverse applications of VOFC in engineering mechanics, illustrating its ability to capture complex behaviors and phenomena.

Finding analytical solutions for fractional differential equations (FDEs) is a challenging task, leading researchers to rely on numerical approximations in most cases. Consequently, numerous numerical methods have been introduced and developed to obtain approximated solutions for this class of equations. In previous works, researchers have employed various techniques to construct numerical solutions for FDEs using orthogonal and non-orthogonal polynomials (see, for instance, [20–29]), whereas the Bernstein polynomials were employed in [30, 31]. In [32] a numerical scheme based on Fourier analysis was proposed. In [33], proposed schemes were discussed based on finite difference approximations. These references highlight the diverse range of numerical methods employed in approximating solutions for FDEs, showcasing the utilization of Jacobi polynomials (JPs), Legendre polynomials, Legendre wavelets, operational matrices, Chebyshev polynomials, and Bernstein polynomials.

Orthogonal JPs [34–37] possess numerous advantageous properties that render them highly valuable in the numerical solution of various types of DEs, particularly through spectral methods. The key characteristics of JPs include orthogonality, exponential accuracy, and the presence of two parameters that offer flexibility in shaping the approximate solutions. These properties make JPs well suited for solving diverse problems. In the current research, we leverage the MSJPs that satisfy the given initial conditions to develop an SCM capable of addressing linear and nonlinear FDEs of variable order. By utilizing these polynomials we can effectively construct an accurate numerical approach for solving FDEs, taking advantage of the SCM and the desirable properties of JPs. This algorithm is based on building two types of OMs for the ODs and the VOFDs of MSJPs. Another advantage of the presented method is that it does not require the uniqueness of the suggested solution. This is important because many differential equations have multiple solutions, and the collocation method can still be used to approximate these solutions. For more explanation, the collocation method approximates the solution by interpolating it at a set of collocation points. Even if the solution is not unique, the collocation method will still produce an approximation that is accurate at the collocation points. As the number of collocation points increases, the approximation will become more accurate and converge to the exact solution.

Here we examine the following general form of an MTVOFDE:

$$ D^{\nu (t)}y(t)=F\bigl(t,y(t),D^{\nu _{1}(t)}y(t),D^{\nu _{2}(t)}y(t), \dots,D^{\nu _{m}(t)}y(t)\bigr),\quad 0 < t\leq \ell, $$

(1.1)

subject to the initial conditions

$$ y^{(j)}(0)=\beta _{j},\quad j=0,1,\dots,n-1, $$

(1.2)

where n is the smallest positive integer number such that $0<\nu _{1}(t)<\nu _{2}(t)<\cdots <\nu _{m}(t)<\nu (t)\le n$ for all $t\in [0,\ell ]$, and $D^{\nu (t)}y(t)$, $D^{\nu _{i}(t)}y(t)$ $(i=1,2,\dots,m)$ are the VOFDs defined in the Caputo sense. Equations of the form (1.1) and (1.2) hold significant practical relevance, as they find applications in various domains. Specifically, these equations have been employed in noise reduction and signal processing [38, 39], geographical data processing [40], and signature verification [41]. These applications highlight the broad range of fields where these equations play a crucial role in addressing real-world challenges.

We have come up with a novel way to deal with problem (1.1)–(1.2) by making a new Galerkin operational matrix (OM) of ODs and a new operational matrix of VOFDs in the Caputo sense that are both designed for the MSJPs’ basis vector. These OMs serve as a powerful tool for achieving accurate numerical solutions through the utilization of the SCM. To the best of our knowledge, this is the first instance in the existing literature where a method for solving a broad class of MTVOFDEs, based on the Caputo derivative of the proposed basis vector, has been introduced. This novel methodology opens up new avenues for effectively addressing and obtaining numerical solutions for this class of FDEs.

This paper is structured as follows. In Sect. 2, we provide a review of the fundamental notiond and principles of VOFC. In Sect. 3, we present certain characteristics of the shifted JPs and MSJPs. In Sect. 4, we focus on making new OMs for the ODs and VOFDs of MSJPs. This is done to solve the problem shown in equations (1.1) and (1.2). In Sect. 5, we explore the application of constructed new OMs with the SCM as a numerical approach to solve this problem. The evaluation of the error estimate for the numerical solution obtained through this new scheme is presented in Sect. 6. To illustrate the effectiveness of the proposed method, Sect. 7 includes six examples and comparisons with various other methods available in the literature. Finally, in Sect. 8, we summarize the main findings and draw conclusions based on our study.

2 Basic definition of Caputo variable-order fractional derivatives

In this section, we present the essential notions and fundamental tools necessary for developing the proposed technique. These notions and tools form the foundation upon which our approach is built, enabling us to effectively address the problem at hand.

Definition 2.1

[23, 31, 42] The Caputo VOFDs for $h(t) \in C^{m}[0,\ell ]$ are defined as

$$ D^{\mu (t)}h(t)=\frac {1}{\Gamma (1-\mu (t))} \int _{0+}^{t}(t- \tau )^{-\mu (t)}h^{\prime}( \tau ) \,d\tau + \frac{h(0^{+})-h(0^{-})}{\Gamma (1-\mu (t))} t^{-\mu (t)}. $$

(2.1)

In the context of a perfect beginning time and $0< \mu (t)< 1$, we get the following:

Definition 2.2

[23, 31, 42]At the beginning time, we have

$$ D^{\mu (t)}h(t)=\frac {1}{\Gamma (1-\mu (t))} \int _{0+}^{t}(t- \tau )^{-\mu (t)}h^{\prime}( \tau ) \,d\tau \quad \bigl(0< \mu (t)< 1\bigr). $$

(2.2)

The Caputo VOFD operator has the following properties:

$$\begin{aligned} &D^{\mu (t)}\bigl(\lambda _{1} h_{1}(t)+\lambda _{2} h_{2}(t)\bigr)=\lambda _{1} D^{\mu (t)}h_{1}(t)+\lambda _{2} D^{\mu (t)}h_{2}(t), \end{aligned}$$

(2.3a)

$$D^{\mu (t)}f(t)=\frac{d^{n}f(t)}{d{t}^n},\mu (t)=n,n\in \mathbb{N}$$

(2.3b)

As shown in [23, 31], equation (2.1) yields

$$\begin{aligned} &D^{\mu (t)}(C)=0\quad \text{($C$ is a constant)}, \end{aligned}$$

(2.4a)

$$\begin{aligned} &D^{\mu (t)}t^{k}= \textstyle\begin{cases} 0,& k=0, \\ \frac {\Gamma (k+1)}{\Gamma (k+1-\mu (t))}t^{k-\mu (t)},& k=1,2, \dots. \end{cases}\displaystyle \end{aligned}$$

(2.4b)

Remark 2.1

The interested reader can refer to [4, pp.35–42] for numerous definitions and more properties related to the VOFDs.

3 An overview on the shifted JPs and their modified ones

This section concentrates on presenting some elementary properties of the JPs and their shifted ones. Furthermore, we will introduce a new kind of orthogonal polynomials, which we call MSJPs.

3.1 An overview on the shifted JPs

The orthogonal JPs, $P^{(\alpha,\beta )}_{n}(x), \alpha, \beta >-1$, satisfy the orthogonality relation [43]

$$ \int _{-1}^{1}w^{\alpha,\beta}(x) P^{(\alpha,\beta )}_{n}(x) P^{( \alpha,\beta )}_{m}(x) \,dx = \textstyle\begin{cases} 0,& m\neq n, \\ h^{(\alpha,\beta )}_{n},& m=n,\end{cases} $$

where $w^{\alpha,\beta}(x)=(1-x)^{\alpha}(1+x)^{\beta}$ and $h^{(\alpha,\beta )}_{n}= \frac {2^{\lambda}\Gamma (n+\alpha +1)\Gamma (n+\beta +1)}{n!(2n+\lambda )\Gamma (n+\lambda )}, \lambda =\alpha +\beta +1$.

The so-called shifted JPs, $P^{(\alpha,\beta )}_{\ell,n}(t)=P^{(\alpha,\beta )}_{n}(2t/\ell -1)$, satisfy the relation

$$ \int _{0}^{\ell}w^{\alpha,\beta}_{\ell}(t) P^{(\alpha,\beta )}_{ \ell,n}(t) P^{(\alpha,\beta )}_{\ell,m}(t) \,dt = \textstyle\begin{cases} 0,& m\neq n, \\ (\frac{\ell}{2} )^{\lambda}h^{(\alpha,\beta )}_{n},& m=n,\end{cases} $$

where $w^{\alpha,\beta}_{\ell}(t)=(\ell -t)^{\alpha} t^{\beta}$.

The power-form representation of $P^{(\alpha,\beta )}_{\ell,n}(t)$ is as follows:

$$ P^{(\alpha,\beta )}_{\ell,i}(t)=\sum _{k=0}^{i} c^{(i)}_{k} t^{k}, $$

(3.1)

where

$$ c^{(i)}_{k}= \frac{(-1)^{i-k} \Gamma (i+\beta +1) \Gamma (i+k+\lambda )}{\ell ^{k} k! (i-k)! \Gamma (k+\beta +1) \Gamma (i+\lambda )}. $$

(3.2)

Alternatively, the expression for $t^{k}$ in relation to $P^{(\alpha,\beta )}_{\ell,r}(t)$ has the form

$$ t^{k}=\sum_{r=0}^{k}b^{(k)}_{r} P^{(\alpha,\beta )}_{\ell,r}(t), $$

(3.3)

where

$$ b^{(k)}_{r}= \frac{\ell ^{k} k! (\lambda +2 r) \Gamma (k+\beta +1) \Gamma (r+\lambda )}{(k-r)! \Gamma (r+\beta +1) \Gamma (k+r+\lambda +1)}. $$

(3.4)

3.2 Introducing MSJPs

In this section, it is advantageous to introduce a definition for the polynomials $\{\phi ^{(\alpha,\beta )}_{n,j}(t)\}_{j \ge 0}$ to satisfy the given form of homogeneous initial conditions:

$$ \phi ^{(\alpha,\beta )}_{n,j}(t)=t^{n}P^{(\alpha,\beta )}_{\ell,j}(t). $$

(3.5)

Subsequently, the polynomials $\phi ^{(\alpha,\beta )}_{n,j}(t)$ satisfy the orthogonality relation, as follows:

$$ \int _{0}^{\ell}w^{\alpha,\beta}_{n,\ell}(t) \phi ^{(\alpha,\beta )}_{n,i}(t) \phi ^{(\alpha,\beta )}_{n,j}(t) \,dt = \textstyle\begin{cases} 0,& i\neq j, \\ (\frac{\ell}{2} )^{\lambda}h^{(\alpha,\beta )}_{i},& i=j,\end{cases} $$

(3.6)

where $w^{\alpha,\beta}_{n,\ell}(t)=\frac {1}{t^{2n}}(\ell -t)^{\alpha} t^{ \beta}$.

Remark 3.1

For $n=0$, we have

$$ \phi ^{(\alpha,\beta )}_{0,i}(t)=P^{(\alpha,\beta )}_{\ell,i}(t), $$

and thus $\phi ^{(\alpha,\beta )}_{n,i}(t)$ are generalizations of $P^{(\alpha,\beta )}_{\ell,i}(t)$.

4 Two OMs for ODs and VOFDs of $\phi ^{(\alpha,\beta )}_{n,i}(t)$

In this section, we present two OMs for ODs and VOFDs of $\phi ^{(\alpha,\beta )}_{n,i}(t)$, with $n=0,1,2,\dots$. To accomplish this, we first start with the following theorem.

Theorem 4.1

The first derivative of $\phi ^{(\alpha,\beta )}_{n,i}(t)$ for all $i\ge 0$ can be written in the form

$$ D\phi ^{(\alpha,\beta )}_{n,i}(t)=\sum _{j=0}^{i-1}\theta ^{\alpha, \beta}_{i,j}(n) \phi ^{(\alpha,\beta )}_{n,j}(t)+ \epsilon _{n,i}(t), $$

(4.1)

where $\epsilon _{n,i}(t)=\frac {1}{i!}(-1)^{i} n (\beta +1)_{i} t^{n-1}$, and

$$ \theta ^{\alpha,\beta}_{i,j}(n)=C^{\alpha,\beta}_{i,j} \sum_{r=0}^{i-j-1} \frac{(-1)^{r} (j+n+r+1) (i+j+\lambda +1)_{r}}{r! (j+r+1) (j+r+\beta +1)\Gamma (i-j-r) \Gamma (2 j+r+\lambda +1)}, $$

(4.2)

where

$$ C^{\alpha,\beta}_{i,j}= \frac{(-1)^{i+j-1} (\lambda +i) (\beta +1)_{i} (\lambda +2 j) \Gamma (j+\lambda ) (i+\lambda +1)_{j}}{\ell (\beta +1)_{j}}. $$

Proof

In view of relations (3.1) and (3.3), following the same procedures as in [44, Theorem 1], formula (4.1) can be proved. □

Now we have reached the main desired two results in this section, which are the two mentioned OMs of

$$ {\boldsymbol{\Phi}^{(\alpha,\beta )}_{n,N}}(t)=\bigl[\phi ^{(\alpha,\beta )}_{n,0}(t), \phi ^{(\alpha,\beta )}_{n,1}(t),\dots, \phi ^{(\alpha,\beta )}_{n,N}(t) \bigr]^{T}. $$

(4.3)

The first result is given in Corollary 4.1, which is a direct consequence of Theorem 4.1, and the second one is proved in Theorem 4.2 as follows.

Corollary 4.1

The mth derivative of the vector $\boldsymbol{\Phi}^{(\alpha,\beta )}_{n,N}(t)$ has the form

$$ \frac{d^{m}\boldsymbol{\Phi}^{(\alpha,\beta )}_{n,N}(t)}{dt^{m}}= G^{m}_{n}\boldsymbol{ \Phi}^{(\alpha,\beta )}_{n,N}(t)+\boldsymbol{\eta}^{(m)}_{n,N}(t) $$

(4.4)

with $\boldsymbol{\eta}^{(m)}_{n,N}(t)=\sum_{k=0}^{m-1}G^{k}_{n} \boldsymbol{\epsilon}^{(m-k-1)}_{n,N}(t)$, where ${\boldsymbol{\epsilon}_{n,N}}(t)= [\epsilon _{n,0}(t),\epsilon _{n,1}(t), \dots,\epsilon _{n,N}(t) ]^{T}\textit{ and } G_{n}= (g_{i,j}(n) )_{0\le i,j\le N}$,

$$ g_{i,j}(n)= \textstyle\begin{cases} \theta ^{\alpha,\beta}_{i,j}(n),& i> j, \\ 0& \textit{otherwise.} \end{cases} $$

Theorem 4.2

$D^{\mu (t)}\phi ^{(\alpha,\beta )}_{n,i}(t)$ for all $i\ge 0$ can be written in the form

$$ D^{\mu (t)}\phi ^{(\alpha,\beta )}_{n,i}(t)=t^{-\mu (t)} \sum_{j=0}^{i} \Theta _{i,j}^{(n)} \bigl(\mu (t)\bigr)\phi ^{(\alpha,\beta )}_{n,j}(t), $$

(4.5)

and, consequently, the VOFD of $\boldsymbol{\Phi}^{(\alpha,\beta )}_{n,N}(t)$ has the form

$$ D^{\mu (t)}\boldsymbol{\Phi}^{(\alpha,\beta )}_{n,N}(t)=t^{-\mu (t)}{ \mathbf{D}}_{n}^{( \mu (t))}\boldsymbol{\Phi}^{(\alpha,\beta )}_{n,N}(t), $$

(4.6)

where ${\mathbf{D}}_{n}^{(\mu (t))}=(d_{i,j}^{(n)}(\mu (t)))$ is the matrix of order $(N+1)\times (N+1)$ explicitly expressed as

$$ \begin{pmatrix} \Theta _{0,0}^{(n)}(\mu (t)) & 0 & \cdots & \cdots & \cdots & 0 \\ \Theta _{1,0}^{(n)}(\mu (t)) & \Theta _{1,1}^{(n)}(\mu (t)) & 0 & \cdots & \cdots & 0 \\ \vdots & & \ddots & & & \vdots \\ \Theta _{i,0}^{(n)}(\mu (t)) & \cdots & \Theta _{i,i}^{(n)}(\mu (t)) &0 &\cdots &0 \\ \vdots & & & \ddots & & \vdots \\ \vdots & & & & \ddots & 0 \\ \Theta _{N,0}^{(n)}(\mu (t)) &\cdots & \cdots & \cdots &\cdots & \Theta _{N,N}^{(n)}(\mu (t)) \end{pmatrix}, $$

(4.7)

where

$$ d_{i,j}^{(n)}\bigl(\mu (t)\bigr)= \textstyle\begin{cases} \Theta _{i,j}^{(n)}(\mu (t)),& i\ge j, \\ 0&\textit{otherwise,} \end{cases} $$

(4.8)

and

$$\begin{aligned} \Theta _{i,j}^{(n)}\bigl(\mu (t)\bigr)= {}&\frac{(-1)^{i-j} (n+j)! \Gamma (i+\beta +1) \Gamma (j+\lambda ) \Gamma (i+j+\lambda )}{(i-j)! \Gamma (j+\beta +1) \Gamma (2 j+\lambda ) \Gamma (i+\lambda ) \Gamma (n+j-\mu (t) +1)} \\ &{}\times _{3}F_{2}\left ( \textstyle\begin{array}{l} j-i,n+j+1,i+j+\lambda \\ 2 j+\lambda +1,n+j-\mu (t) +1 \end{array}\displaystyle ;1 \right ). \end{aligned}$$

(4.9)

Proof

In view of (3.1), using (2.4b), we have

$$ D^{\mu (t)}\phi ^{(\alpha,\beta )}_{n,i}(t)=t^{n-\mu (t)} \sum_{k=0}^{i} c^{(i)}_{k} \frac{\Gamma (k+n+1)}{\Gamma (k+n-\mu (t) +1)}t^{k}. $$

(4.10)

Employing relation (3.3), (4.10) can be expressed in the form (4.5), which can be written as follows:

$$ D^{\mu (t)}\phi ^{(\alpha,\beta )}_{n,i}(t)=t^{-\mu (t)}\bigl[ \Theta _{i,0}^{(n)}\bigl( \mu (t)\bigr),\Theta _{i,1}^{(n)}\bigl(\mu (t)\bigr),\dots,\Theta _{i,i}^{(n)}\bigl(\mu (t)\bigr),0, \dots,0\bigr]\boldsymbol{ \Phi}^{(\alpha,\beta )}_{n,N}(t), $$

(4.11)

and this expression leads to the proof of (4.6). □

For instance, if $N=4, \alpha =\beta =0$, and $\mu (t)=t$, then we get

$$ G_{n}=\frac{1}{\ell} \begin{pmatrix} 0 & 0 & 0 & 0 & 0 \\ 2 (n+1) & 0 & 0 & 0 & 0 \\ -3 n & 3 (n+2) & 0 & 0 & 0 \\ \frac{11 n}{3}+2 & -5 n & \frac{10 (n+3)}{3} & 0 & 0 \\ -\frac{1}{6} (25 n) & \frac{13 n}{2}+6 & -\frac{1}{6} (35 n) & \frac{7 (n+4)}{2} & 0 \end{pmatrix} _{5\times 5} $$

(4.12)

and

$$ {\mathbf{D}}_{n}^{(\mu (t))}= \begin{pmatrix} \frac{n!}{\Gamma (n-t+1)} & 0 & 0 & 0 & 0 \\ \frac{t n!}{\Gamma (n-t+2)} & \frac{\Gamma (n+2)}{\Gamma (n-t+2)} & 0 & 0 & 0 \\ \frac{t n! (n+t)}{\Gamma (n-t+3)} & \frac{3 t \Gamma (n+2)}{\Gamma (n-t+3)} & \frac{\Gamma (n+3)}{\Gamma (n-t+3)} & 0 & 0 \\ \frac{t n! (n^{2}+3 n t+t^{2}+1 )}{\Gamma (n-t+4)} & \frac{3 t (n+2 t) \Gamma (n+2)}{\Gamma (n-t+4)} & \frac{5 t \Gamma (n+3)}{\Gamma (n-t+4)} & \frac{\Gamma (n+4)}{\Gamma (n-t+4)} & 0 \\ \frac{t n! (n+t) (n^{2}+5 n t+t^{2}+5 )}{\Gamma (n-t+5)} & \frac{t (3 n^{2}+15 n t+10 t^{2}+8 ) \Gamma (n+2)}{\Gamma (n-t+5)} & \frac{5 t (n+3 t) \Gamma (n+3)}{\Gamma (n-t+5)} & \frac{7 t \Gamma (n+4)}{\Gamma (n-t+5)} & \frac{\Gamma (n+5)}{\Gamma (n-t+5)} \end{pmatrix}_{5\times 5}. $$

(4.13)

5 Numerical handling for MTVOFDE subject to initial conditions

In this section, we utilize the OMs derived in Corollary 4.1 and Theorem 4.2 to get numerical solutions for MTVOFDE (1.1) subject to initial conditions (1.2).

5.1 Homogeneous initial conditions

Suppose that the initial conditions (1.2) are homogeneous, that is, $\beta _{j}=0, j=0,1,2,\dots,n-1$. We can consider an approximate solution to $y(t)$ in the form

$$ y(t)\simeq y_{N}(t)=\sum_{i=0}^{N}c_{i} \phi ^{( \alpha,\beta )}_{n,i}(t)={\mathbf{A}}^{T} \boldsymbol{\Phi}^{(\alpha,\beta )}_{n,N}(t), $$

(5.1)

where ${\mathbf{A}}= [c_{0}, c_{1},\dots,c_{N} ]^{T}$.

Corollary 4.1 and Theorem 4.2 enable us to approximate the derivatives $y^{(\mu (t))}(t)$ in matrix form:

$$ D^{\mu (t) }y_{N}(t)=\textstyle\begin{cases} {\mathbf{A}}^{T} G^{m}_{n} \boldsymbol{\Phi}^{(\alpha,\beta )}_{n,N}(t)+ \boldsymbol{\eta}^{(m)}_{n,N}(t), & \mu (t)=m,\, m \text{ is an integer,} \\ t^{-\mu (t)} {\mathbf{A}}^{T} {\mathbf{D}}_{n}^{(\mu (t))}\boldsymbol{\Phi}^{( \alpha,\beta )}_{n,N}(t), &\mu (t) \text{ is a fraction number or function.} \end{cases} $$

(5.2)

In this method, approximations (5.2) allow us to write the residual of equation (1.1) as

$$\begin{aligned} R_{n,N}(t)={}&t^{-\nu (t)} {\mathbf{A}}^{T} { \mathbf{D}}_{n}^{(\nu (t))} \boldsymbol{\Phi}^{(\alpha,\beta )}_{n,N}(t) \\ &{}-F \bigl(t,{\mathbf{A}}^{T} \boldsymbol{\Phi}^{( \alpha,\beta )}_{n,N}(t),t^{-\nu _{1}(t)} {\mathbf{A}}^{T} {\mathbf{D}}_{n}^{( \nu _{1})}\boldsymbol{ \Phi}^{(\alpha,\beta )}_{n,N}(t),\dots,t^{-\nu _{m}(t)} { \mathbf{A}}^{T} {\mathbf{D}}_{n}^{(\nu _{m})}\boldsymbol{ \Phi}^{(\alpha,\beta )}_{n,N}(t)\bigr). \end{aligned}$$

(5.3)

In this section, we propose a spectral approach, referred to as the modified shifted Jacobi collocation operational matrix method (MSJCOPMM), to obtain the numerical solution of equation (1.1) under the initial conditions specified in (1.2) (with $\beta _{j}=0, j=0,1,\dots,n-1$). The collocation points for this method are chosen as the $N+1$ zeros of $P^{(\alpha,\beta )}_{\ell,N+1}(t)$ or, alternatively, as the points $t_{i}=\frac{\ell (i+1)}{N+2}$, $i=0,1,\dots,N$. These points serve as the basis for performing the spectral approximation in our proposed numerical approach. So we have

$$ R_{n,N}(t_{i})=0,\quad i=0,1,\dots,N. $$

(5.4)

By solving a set of $N+1$ linear or nonlinear algebraic equations (5.4) using an appropriate solver, the unknown coefficients $c_{i}$ (where $i=0,1,\dots,N$) can be determined. These coefficients play a crucial role in obtaining the desired numerical solution (5.1).

5.2 Nonhomogeneous initial conditions

A crucial aspect of developing the proposed algorithm involves transforming equation (1.1) together with the nonhomogeneous conditions (1.2) into an equivalent form with homogeneous conditions. This transformation is achieved through the following conversion:

$$ \bar{y}(t)=y(t)-q_{n}(t),\quad q_{n}(t)=\sum _{i=0}^{n-1} \frac{\beta _{i}}{i!} t^{i}. $$

(5.5)

Thus it is sufficient to solve the following modified equation, simplifying the problem at hand:

$$\begin{aligned} D^{\nu (t)}\bar{y}(t)={}&-D^{\nu (t)}q_{n}(t)+F \bigl(t,\bar{y}(t)+q_{n}(t),D^{ \nu _{1}(t)}\bigl(\bar{y}(t)+q_{n}(t) \bigr), \\ &{}D^{\nu _{2}(t)}\bigl(\bar{y}(t)+q_{n}(t)\bigr), \dots,D^{\nu _{m}(t)}\bigl(\bar{y}(t)+q_{n}(t)\bigr)\bigr), \quad 0\leq t\leq \ell, \end{aligned}$$

(5.6)

subject to the homogeneous conditions

$$ \bar{y}^{(j)}(0)=0, \quad j=0,1,\dots,n-1. $$

(5.7)

Then

$$ y_{N}(t)=\bar{y}_{N}(t)+q_{n}(t). $$

(5.8)

Remark 5.1

We present an algorithm to solve multiple numerical examples in Sect. 7. The computations were performed using Mathematica 13.3 on a computer system equipped with an Intel(R) Core(TM) i9-10850 CPU operating at 3.60 GHz, featuring 10 cores and 20 logical processors. The algorithmic steps for solving the MTVOFDE using MSJCOPMM are expressed as follows:

Algorithm

MSJCOPMM algorithm

6 Convergence and error analysis

Within this section, we investigate the convergence and error estimates of the proposed approach. We focus on the space $S_{n,N}$ defined as follows:

$$ S_{n,N}=\operatorname{Span}\bigl\{ \phi ^{(\alpha,\beta )}_{n,0}(t), \phi ^{(\alpha, \beta )}_{n,1}(t),\dots,\phi ^{(\alpha,\beta )}_{n,N}(t) \bigr\} . $$

Additionally, the error between $y(t)$ and its approximation $y_{N}(t)$ can be defined by

$$ E_{N}(t)= \bigl\vert y(t)-y_{N}(t) \bigr\vert . $$

(6.1)

In the paper, we analyze the error of the numerical scheme by using the $L_{2}$ norm error estimate

$$ \Vert E_{N} \Vert _{2}= \Vert y-y_{N} \Vert _{2}= \biggl( \int _{0}^{\ell} \bigl\vert y(t)-y_{N}(t) \bigr\vert ^{2} \,dt \biggr)^{1/2} $$

(6.2)

and the $L_{\infty}$ norm error estimate

$$ \Vert E_{N} \Vert _{\infty}= \Vert y-y_{N} \Vert _{\infty}= \max_{0\le t \le \ell} \bigl\vert y(t)-y_{N}(t) \bigr\vert . $$

(6.3)

Theorem 6.1

Assume that $y(t)=t^{n} u(t)$ and suppose that $y_{N}(t)$ has the form (5.1) and represents the best possible approximation for $y(t)$ out of $S_{n,N}$. Then there is a constant K such that

$$ \Vert E_{N} \Vert _{\infty}\leq \frac{K \ell ^{n+1}}{2^{\lambda}} \biggl( \frac{e \ell}{4} \biggr)^{N}(N+1)^{q-N-1} $$

(6.4)

and

$$ \Vert E_{N} \Vert _{2}\leq \frac{K \ell ^{2n+3/2}}{2^{\lambda}} \biggl( \frac{e \ell}{4} \biggr)^{N}(N+1)^{q-N-1}, $$

(6.5)

where $q=\max \{\alpha,\beta,-1/2\}< N+1$ and $K=\max_{t\in [0,\ell ]} | \frac {d^{N+1} u(\eta )}{d t^{N+1}} |, \eta \in [0,\ell ]$.

Proof

Using Theorem 3.3 in [45, p. 109], we can write the function $u(t)$ as

$$ u(t)=u_{N}(t)+\frac{K}{(N+1)!}\prod^{N}_{k=0}(t-t_{k}), $$

(6.6)

where $u_{N}(t)$ is the interpolating polynomial for $u(t)$ at the points $t_{k}, k=0,1,\dots,N$, which are the roots of $P^{(\alpha,\beta )}_{\ell,N+1}(t)$ such that $N>q-1$. Then we get

$$ \Vert u-u_{N} \Vert _{\infty}\le \frac{K}{(N+1)!} \Biggl\Vert \prod^{N}_{k=0}(t-t_{k}) \Biggr\Vert _{\infty}=\frac{K}{(N+1)!c^{N+1}_{N+1}} \bigl\Vert P^{(\alpha,\beta )}_{ \ell,N+1}(t) \bigr\Vert _{\infty}, $$

(6.7)

where $c^{N+1}_{N+1}= \frac {\Gamma (2N+\lambda +2)}{\ell ^{N+1} (N+1)! \Gamma (N+\lambda +1)}$.

In view of formula [43, formula (7.32.2)], we obtain

$$ \bigl\Vert P^{(\alpha,\beta )}_{\ell,N+1} \bigr\Vert _{\infty} \simeq (N+1)^{q}, $$

(6.8)

and hence

$$ \Vert u-u_{N} \Vert _{\infty}\le K \frac{\ell ^{N+1} \Gamma (N+\lambda +1) (N+1)^{q} }{\Gamma (2 N+\lambda +2)}, $$

(6.9)

By using the asymptotic result (see [46, pp. 232–233])

$$ \begin{aligned}& \Gamma (m+\lambda )=\mathcal{O} \bigl(m^{\lambda -1} m!\bigr),\qquad (2m)!= \frac {1}{\sqrt{\pi}} 4^{m} m! \Gamma (m+1/2),\\ & m!=\mathcal{O} \biggl(\sqrt{2\pi m} \biggl(\frac {m}{e} \biggr)^{m} \biggr), \end{aligned}$$

(6.10)

inequality (6.9) takes the form

$$ \Vert u-u_{N} \Vert _{\infty}\le \frac{K \ell}{2^{\lambda}} \biggl( \frac{e \ell}{4} \biggr)^{N}(N+1)^{q-N-1}. $$

(6.11)

Now consider the approximation $y(t)\simeq Y_{N}(t)=t^{n}u_{N}(t)$. Then

$$ \Vert y-Y_{N} \Vert _{\infty}\le \ell ^{n} \Vert u-u_{N} \Vert _{\infty}\le \frac{K \ell ^{n+1}}{2^{\lambda}} \biggl( \frac{e \ell}{4} \biggr)^{N}(N+1)^{q-N-1}. $$

(6.12)

Since the approximate solution $y_{N}(t)\in S_{n,N}$ represents the best possible approximation to $y(t)$, we get

$$ \Vert y-y_{N} \Vert _{\infty}\le \Vert y-h \Vert _{\infty}\quad \forall h\in S_{n,N}, $$

(6.13)

and

$$ \Vert y-y_{N} \Vert _{2}\le \Vert y-h \Vert _{2} \quad\forall h\in S_{n,N}. $$

(6.14)

Therefore

$$ \Vert y-y_{N} \Vert _{\infty}\le \Vert y-Y_{N} \Vert _{\infty}\le \frac{K \ell ^{n+1}}{2^{\lambda}} \biggl( \frac{e \ell}{4} \biggr)^{N}(N+1)^{q-N-1}, $$

(6.15)

and

$$\begin{aligned} \Vert y-y_{N} \Vert _{2}&\le \Vert y-Y_{N} \Vert _{2}\le \ell ^{n} \Vert u-u_{N} \Vert _{2}= \ell ^{n} \biggl( \int _{0}^{\ell} \bigl\vert u(t)-u_{N}(t) \bigr\vert ^{2} \,dt \biggr)^{1/2} \\ &\le \frac{K \ell ^{2n+3/2}}{2^{\lambda}} \biggl(\frac{e \ell}{4} \biggr)^{N}(N+1)^{q-N-1}. \end{aligned}$$

(6.16)

 □

The following corollary shows that the obtained error has a very rapid rate of convergence.

Corollary 6.1

For all $N> q-1$, we have the following two estimates:

$$ \Vert E_{N} \Vert _{\infty}=\mathcal{O} \bigl((e \ell /4)^{N} N^{q-N-1}\bigr), $$

(6.17)

and

$$ \Vert E_{N} \Vert _{2}=\mathcal{O} \bigl((e \ell /4)^{N} N^{q-N-1}\bigr). $$

(6.18)

The next theorem emphasizes the stability of error by making an estimate of error propagation.

Theorem 6.2

For any two successive approximations of $y(t)$, we have

$$ \vert y_{N+1}-y_{N} \vert \lesssim \mathcal{O}\bigl((e \ell /4)^{N} N^{q-N-1}\bigr),\quad N> q-1, $$

(6.19)

where ≲ means that there exists a generic constant d such that $|y_{N+1}-y_{N}|\le d (e \ell /4)^{N} N^{q-N-1}$.

Proof

In view of Theorem 6.1, it is not difficult to obtain (6.19). □

7 Numerical simulations

In this section, we give five examples to demonstrate the applicability and high efficiency of the proposed method established in Sect. 5. The maximum absolute error (MAE) between exact and approximate solutions is presented for evaluation. In the provided numerical problems, we explain that MSJCOPMM gives the exact solution if the given problem has a polynomial solution of degree N, as shown in Examples 7.1–7.3. This solution can be found by combining $\phi ^{(\alpha,\beta )}_{0,i}(t), \dots,\phi ^{(\alpha,\beta )}_{N-2,i}(t)$.

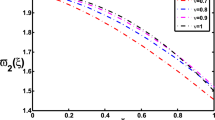
Furthermore, the computed errors to obtain some numerical solutions $y_{N}(t)$ using MSJCOPMM for $N = 1,\dots,12$ are presented in two Tables 3 and 5. In these tables, we see excellent computational results. The comparisons of MSJCOPMM and other techniques in [23–25, 28, 47, 48] are presented in Tables 1, 2, 4, and 6. These tables confirm that MSJCOPMM provides more precise results than the other techniques. In addition, as we can see in Figs. 1 and 3, the exact and approximate solutions in Examples 7.4 and 7.5 are in excellent agreement. Besides, Figs. 2(a), 4(a) and Figs. 2(b), 4(b) display absolute and log-errors for various N values and different values of $\alpha, \beta$ as a way of demonstrating the convergence and stability of the solutions, respectively, to Problems 7.4 and 7.5 when MSJCOPMM is applied. As well, Example 7.6 illuminates a valuable technique for assessing accuracy in cases where the exact solution remains elusive. Along with the insightful results shown in Table 7, Figs. 5 and 6 also clearly demonstrate that MSJCOPMM produces extremely accurate solutions.

Figure 1

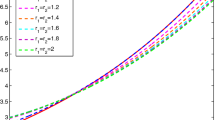
Approximate and exact solutions plots for Example 7.4 using $\alpha =\beta =0$

Figure 2

Figures of obtained errors $E_{N}$ using various N and $\alpha =\beta =0$ for Example 7.4

Figure 3

Approximate and exact solutions plots for Example 7.5 using $\alpha =0$ and $\beta =1$

Figure 4

Figures of obtained errors $E_{N}$ using various N, $\alpha =0$, and $\beta =1$ for Example 7.5

Figure 5

Error plot for Example 7.6 using $N=14, \alpha =0$, and $\beta =0$

Figure 6

Approximate solutions plots for Example 7.6 using $N=0,3,5$ and $\alpha =\beta =0$

Table 1 Comparison of $\| E_{N}\| _{\infty }$ between the two methods [23, 24] and $SJCOPMM$ for Example 7.1 using $\alpha = \beta =0$

Table 2 Comparison of the methods in [24, 25, 28] and $MSJCOPMM$ for Example 7.3 using $\alpha =\beta =1$

Problem 7.1

Consider the differential equation [23, 24]

$$ \left.\textstyle\begin{array}{l@{\quad}l} D^{2t}y(t)+t^{1/2} D^{t/3}y(t)+t^{1/3} D^{t/4}y(t)+t^{1/4} D^{t/5}y(t)+t^{1/5} y(t)=g(t), & 0\leq t\leq \ell, \\ y(0)=2, \quad \textit{and}\quad y^{\prime}(0)=0,& \end{array}\displaystyle \right\} $$

(7.1)

where $g(t)$ is chosen such that the exact solution is $y(t)=2-\frac{t^{2}}{2}$.

The application of proposed method $SJCOPMM$ gives the exact solution in the form

$$ y(t)=y_{N}(t)=\sum_{i=0}^{N}c_{i} \phi ^{(\alpha, \beta )}_{2,i}(t)+2,\quad N=0,1,2,\dots,6, $$

where $c_{0}=-1/2$ and $c_{i}=0, i=1,2,\dots,N$.

Problem 7.2

Consider Bagley–Torvik equation [24, 49]

$$ \left.\textstyle\begin{array}{l@{\quad}l} D^{2} y(t)+D^{3/2}y(t)+ y(t)=t^{2}+ 4 \sqrt{t/\pi}+2, & 0 \leq t\leq \ell, \\ y(0)=y^{\prime}(0)=0, \end{array}\displaystyle \right\} $$

(7.2)

where the exact solution is $y(t)=t^{2}$.

The application of proposed method $SJCOPMM$ gives the exact solution in the form

$$ y(t)=y_{N}(t)=\sum_{i=0}^{N}c_{i} \phi ^{(\alpha, \beta )}_{2,i}(t),\quad N=0,1,2,\dots,6, $$

where $c_{0}=1$ and $c_{i}=0, i=1,2,\dots,N$.

Remark 7.1

It is worth noting that the exact solution of (7.2) is obtained using $N=0, \alpha,\beta >-1$, whereas the authors in [24] presented the exact solution using $N=2$. Moreover, the authors in [49] show that the exact solution is obtained as $N\rightarrow \infty$, and the best error obtained was $2\times 10^{-10}$.

Problem 7.3

Consider the differential equation [24, 25, 28]

$$ \left.\textstyle\begin{array}{l} D^{\mu (t)}y(t)-10 Dy(t)+ y(t)=10 ( \frac {t^{2-\mu{(t)}}}{\Gamma (3-\mu (t))}+ \frac {t^{1-\mu{(t)}}}{\Gamma (2-\mu (t))} )+5 t^{2}-90 -t-95,\\ \quad 0\leq t\leq 1, \\ y(0)=5, \quad \textit{and}\quad y^{\prime}(0)=10, \end{array}\displaystyle \right\} $$

(7.3)

where $\mu (t)=\frac {t+2e^{t}}{7}$. The exact solution is $y(t)=5(1+t)^{2}$.

The application of proposed method $MSJCOPMM$ gives the exact solution in the form

$$ y(t)=y_{N}(t)=\sum_{i=0}^{N}c_{i} \phi ^{(\alpha, \beta )}_{2,i}(t)+5+10 t,\quad N=0,1,2,\dots,6, $$

where $c_{0}=5$ and $c_{i}=0, i=1,2,\dots,N$.

Problem 7.4

Consider the nonlinear initial value problem, [47, 50]

$$ \left.\textstyle\begin{array}{l@{\quad}l} D^{\mu (t)}y(t)+\sin (t) (y(t))^{2}= \frac {\Gamma (9/2) t^{7/2-\mu (t)}}{\Gamma (9/2-\mu (t))}+ \sin (t) t^{7},& 0 < \mu (t)\leq 1, 0\leq t\leq 1, \\ y(0)=0, \qquad \mu (t)=1-0.5 e^{-t}, \end{array}\displaystyle \right\} $$

(7.4)

where the exact solution is $y(t)=t^{7/2}$. This solution agrees perfectly with the numerical solutions of accuracy 10⁻⁸ at $N=12$, as shown in Table 3.

Table 3 Errors obtained for Example 7.4 using various values for $\alpha, \beta$ at different N

Table 4 Comparison of MAE between the method [47] and $MSJCOPMM$ for Example 7.4

Problem 7.5

Consider the initial value problem, [47, 48]

$$ \left.\textstyle\begin{array}{l@{\quad}l} D^{\mu (t)}y(t)+ 3 y^{\prime}(t)- y(t)=g(t), & 0 < t\leq 1, \\ y(0)=1,\quad \mu (t)=0.25(1+\cos ^{2}(t)), \end{array}\displaystyle \right\} $$

(7.5)

where g(t) is chosen such that the exact solution is $y(t)=e^{t}$. This solution agrees perfectly with the numerical solutions of accuracy 10⁻¹⁶ at $N=11$, as shown in Table 5.

Table 5 Errors obtained and CPU time (seconds) for Example 7.5 using various values for $\alpha, \beta$ at different N

Table 6 Comparison of MAE between the methods [47, 48] and $MSJCOPMM$ for Example 7.5

Problem 7.6

Consider the fractional-order nonlinear equation

$$ \left.\textstyle\begin{array}{l@{\quad}l} D^{2}y(t)+\frac {2}{t^{\mu -\nu}}D^{t/4}y(t)-e^{-y(t)}=0, & 0< t \leq 1, \\ y(0)=y^{\prime}(0)=0, \end{array}\displaystyle \right\} $$

(7.6)

where the explicit exact solution is not available, so the following error norm is used to check the accuracy in this case:

$$ \Vert E_{N} \Vert _{\infty}=\max _{t\in [0,1]} \bigl\vert t D^{2}y_{N}(t)+2 t^{t/4-1} D^{t/4}y_{N}(t)-t e^{-y_{N}(t)} \bigr\vert . $$

(7.7)

The application of MSJCOPMM with different choices of α and β and $N=0,3,6,9,12,14$ gives the numerical results shown in Table 7.

Table 7 MAE for Example 7.6 using various values for $\alpha, \beta$ at different N

8 Conclusions

In this work, we have introduced a modified version of shifted JPs that satisfy homogeneous initial conditions. Moreover, by utilizing the OMs derived in Sect. 4 along with the CSM, we have developed an approximation technique for the given MTVOFDEs. The proposed method, known as MSJCOPMM, has been applied and tested on five different examples demonstrating its high accuracy and efficiency. We recognize the potential for extending our results to boundary value problems (BVPs), where the investigation of the system behavior at boundary conditions would provide valuable insights and further enhance the applicability of our findings. Additionally, we believe that the theoretical findings presented in this paper can be further employed to address other types of FDEs.