1 Introduction

The theory of impulsive equations has been considered to be one of the significant research topics from both the theoretical as well as application points of view. Impulsive equations have been widely utilized for modeling the dynamics of processes in which discontinuous jumps occur unexpectedly during their evolution. Such types of equations have received appreciable consideration from researchers around the globe. Researchers have investigated impulsive differential equations for the past several years and the theory for these equations has been developed extensively, readers can refer to the popular books and interesting papers [1–8], and references therein. However, surprisingly, its discrete version, impulsive difference equations, has been less acknowledged and relatively few works are available for impulsive difference equations.

The topic of ‘calculus and dynamic equations on time scales’emerged into the mathematics literature about 35 years ago. It provides a unified mathematical framework for difference equations and differential equations and found applicable in modeling the continuous-discrete hybrid time phenomena. This topic has now grown profoundly. In recent years, considerable progress has been made in the theory and applications of impulsive dynamic equations on time scales, we refer to [9–13], and references therein. In the study of dynamic equations time scales, the stability problem is substantial and of great interest for researchers working in the field. Although there are several types of stability, the Ulam stability is interesting and worthy of attention because it provides a relation between the exact solution and an approximate solution of the equation under consideration. To investigate the Ulam stability, there are several approaches available, one of which is by employing inequality. The main advantage of this approach is that it requires less restriction and is much simpler than any other approach.

It is worth noting that over the period the Ulam stability of various differential and integral equations has been investigated by researchers [14–20], to mention a few. In addition, there are some of the earliest investigations on the Ulam stability of difference equations [21–27]. Further, along with the development of dynamic equations on time scales, much work pertaining to the investigation of the Ulam stability for dynamic equations on time scales is also available, see [28–37].

Motivated by the work mentioned above, we assert that studying the Ulam stability of impulsive dynamic equations is worthwhile. In this paper, we introduce the Ulam stability for first-order nonlinear impulsive dynamic equations of the form

$$\begin{aligned} \begin{aligned}& x^{\Delta}(t)+p(t)x^{\sigma}(t)=f \bigl(t,x(t)\bigr),\quad t\in \mathbb{J}^{\kappa}\setminus \{t_{i}\}, i \in \mathcal{N}, \\ &x\bigl(t^{+}_{i}\bigr)-x\bigl(t^{-}_{i} \bigr)=I_{i}\bigl(x\bigl(t^{-}_{i}\bigr)\bigr),\quad i \in \mathcal{N}, \\ &x(t_{0})=A\in \mathbb{R}, \end{aligned} \end{aligned}$$
(1)

where \(\mathbb{J}:=[t_{0}, T]_{\mathbb{T}}\), \(t_{0},T\in \mathbb{T}\) with \(0\le t_{0}< T<\infty \), \(x\colon \mathbb{J}\to \mathbb{R}\) is an unknown function to be determined, \(x^{\sigma}=x\circ \sigma \), \(x^{\Delta}\) is the delta derivative of x, \(p\colon \mathbb{T} \to \mathbb{R}\) is positively regressive and rd-continuous, \(f\colon \mathbb{J}\times \mathbb{R}\to \mathbb{R}\) is rd-continuous in the first variable and continuous in the second variable, each \(t_{i}\) represents a priori known moments of impulse and satisfies \(t_{0}< t_{i}< t_{i+1}< T\), \(\{t_{i}\}_{i\in \mathcal{N}}\subset \mathbb{J}\), where \(\mathcal{N}=\{1,2,\ldots,m\}\subset \mathbb{N}\), \(I_{i}\colon \mathbb{R}\to \mathbb{R}\) describes the discontinuity of x at each \(t_{i}\).

For results concerning the existence and uniqueness of the solution to the impulsive dynamic problem (IDP) (1), readers can refer to [38–43]. The existence results for problem (1) without impulses (i.e., for \(I_{i}\equiv 0\), \(i\in \mathcal{N}\)) have been studied in [44–46]. We note that the qualitative and asymptotic analysis of solutions to nonlinear dynamical systems involving double-phase problems was recently studied in [47–49].

The rest of the paper is structured as follows. Section 2 covers some essential materials for the readership of this paper. An extended integral inequality on time scales is established in Sect. 3. In Sect. 4, we investigate Ulam stability of (1) on finite time scale intervals by means of the extended inequality. An illustrative example is given in Sect. 5. Finally, conclusions and future research directions are mentioned in Sect. 6.

2 Preliminaries

In this section, we shall provide some essential materials from time scales calculus that are pertinent to the present paper. The reader can find more details on the topic in [50, 51]. A nonempty, closed subset of the real line \(\mathbb{R}\) is a time scale \(\mathbb{T}\). We usually write \(\mathbb{T}^{\kappa}=\mathbb{T}\setminus \{\max \mathbb{T}\}\) if \(\max \mathbb{T}<\infty \), otherwise \(\mathbb{T}^{\kappa}=\mathbb{T}\).

Definition 2.1

A function \(f\colon \mathbb{T}\to \mathbb{R}\) is said to be delta differentiable at \(t\in \mathbb{T}^{\kappa}\) if there exists \(f^{\Delta}(t)\in \mathbb{R}\), a so-called delta derivative of f at t, with the following property: For any \(\varepsilon >0\) there is a neighborhood N of t such that

$$\begin{aligned} \bigl\vert f\bigl(\sigma (t)\bigr)-f(s)-f^{\Delta}(t) \bigl(\sigma (t)-s \bigr) \bigr\vert \leq \varepsilon \bigl\vert \sigma (t)-s \bigr\vert \quad\text{for all } s\in N. \end{aligned}$$

Definition 2.2

A function \(f\colon \mathbb{T} \rightarrow \mathbb{R}\) is rd-continuous if it is continuous at every right-dense point or maximal point in \(\mathbb{T}\) and its left-sided limits exist at left-dense points in \(\mathbb{T}\). The symbol \(\mathrm{C}_{rd}(\mathbb{T}, \mathbb{R})\) will be used for the set of all such functions.

If a function \(f\colon \mathbb{T}\times \mathbb{R}\to \mathbb{R}\) is rd-continuous in the first variable and continuous in the second variable, then we write \(f\in{ \mathrm{C}_{rd}}(\mathbb{T}\times \mathbb{R}, \mathbb{R})\).

Note 2.1

The family, \({ \mathrm{C}_{rd}}(\mathbb{J}, \mathbb{R})\), of all rd-continuous functions from \(\mathbb{J}\) into \(\mathbb{R}\) forms a Banach space coupled with the norm \(\|\cdot \|\) defined as \(\|x\|:= \sup_{t\in \mathbb{J}}|x(t)|\).

Definition 2.3

A function \(p\colon \mathbb{T}\to \mathbb{R}\) is regressive if \(1+\mu (t)p(t)\neq 0\) for all \(t\in \mathbb{T}\). The symbol \(\mathcal{R}(\mathbb{T}, \mathbb{R})\) will be used for the set of all rd-continuous regressive functions.

If \(1+\mu (t)p(t)> 0\) for all \(t\in \mathbb{T}\), then p is said to be positively regressive and \(\mathcal{R}^{+}(\mathbb{T}, \mathbb{R})\) denotes the set of all rd-continuous positively regressive functions.

Definition 2.4

For \(p\in \mathcal{R}(\mathbb{T}, \mathbb{R})\), the exponential function \(e_{p} (t, s)\) on the time scale \(\mathbb{T}\) is defined as

$$\begin{aligned} e_{p} (t, s):= \textstyle\begin{cases} \exp ( \int _{s}^{t} ( \frac{\operatorname{Log}(1+\mu (r)p(r))}{\mu (r)} )\Delta r ) &\text{if } \mu (r)\neq 0, \\ \exp ( \int _{s}^{t} p(r)\Delta r ) & \text{if } \mu (r)= 0. \end{cases}\displaystyle \end{aligned}$$

For \(p,q\in \mathcal{R}(\mathbb{T}, \mathbb{R})\), we define the following.

$$\begin{aligned} p\oplus q:=p+q+\mu p q, \qquad\ominus p:=\frac{-p}{1+\mu p},\qquad p \ominus q:=p\oplus ( \ominus q). \end{aligned}$$

We let

$$\begin{aligned} 0< E_{p}:=\sup_{s, t\in \mathbb{J}} \bigl\vert e_{\ominus p}(t,s) \bigr\vert < \infty. \end{aligned}$$

Lemma 2.1

(See [44, Lemma 3.1])

Let \(p\in (\mathbb{J},\mathbb{R})\), \(t_{0}\in \mathbb{T}\), and \(f\in { \mathrm{C}_{rd}}(\mathbb{J}\times \mathbb{R}, \mathbb{R})\). Then, \(x\in{\mathrm{ C}_{rd}}(\mathbb{J}, \mathbb{R})\) is a solution of (1) without any impulse, if and only if

$$\begin{aligned} x(t)=e_{\ominus p}(t, t_{0}) A+ \int _{t_{0}}^{t} e_{\ominus p}(t, s) f\bigl(s,x(s) \bigr) \Delta s \quad\textit{for all } t\in \mathbb{J}. \end{aligned}$$

Remark 2.1

From Lemma 2.1, it is clear that \(x\in{ \mathrm{PC}^{1}}(\mathbb{J}, \mathbb{R})\) is a solution of (1) if and only if

$$\begin{aligned} x(t)=e_{\ominus p}(t, t_{0}) A+ \int _{t_{0}}^{t} e_{\ominus p}(t, s) f\bigl(s,x(s) \bigr) \Delta s+\sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(x\bigl(t^{-}_{i} \bigr)\bigr) \quad\text{for all } t\in \mathbb{J}. \end{aligned}$$
(2)

Let \(\mathcal{C} (\mathbb{J}, \mathbb{R} )\) be the Banach space of all continuous functions x with domain \(\mathbb{J}\) and taking values in \(\mathbb{R}\) with the norm \(\|x\|:= \sup_{t\in \mathbb{J}}|x(t)|\). We write \(J_{0}:=[t_{0}, t_{1}]\) and for each \(i\in \mathcal{N}\), \(J_{i}:=(t_{i}, t_{i+1}]\).

Define

$$\begin{aligned} \mathcal{PC}(\mathbb{J}, \mathbb{R}):= \bigl\{ x\colon \mathbb{J} \to \mathbb{R}: & x\in \mathcal{C}(J_{i}, \mathbb{R})\text{ and } x \bigl(t_{i}^{+}\bigr), x\bigl(t_{i}^{-} \bigr) \text{ exist with } x\bigl(t_{i}^{-} \bigr)=x(t_{i}), i\in \mathcal{N} \bigr\} \end{aligned}$$

and

$$\begin{aligned} \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R}):= \bigl\{ x\in \mathcal{PC}( \mathbb{J}, \mathbb{R}) \colon x^{\Delta}\in \mathcal{PC}(\mathbb{J}, \mathbb{R})\bigr\} . \end{aligned}$$

It can be readily seen that the set \(\mathcal{PC}\) is a Banach space coupled with the norm \(\|x\|_{\mathcal{PC}}:= \max_{ i\in \mathcal{N}} \{ \|x\|_{i} \}\), where \(\|x\|_{i}= \sup_{t\in J_{i}} |x(t)|\), and the set \(\mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) is also a Banach space coupled with the norm \(\|x\|_{\mathcal{PC}^{1}}:= \max \{\|x\|_{\mathcal{PC}}, \|x^{\Delta}\|_{\mathcal{PC}}\}\).

Definition 2.5

A function \(x\in \mathcal{PC}^{1}\) is said to be a solution of the IDP (1), if x satisfies the dynamic equation \(x^{\Delta}(t)+p(t)x^{\sigma}(t)=f(t, x(t))\) everywhere on \(\mathbb{J}^{\kappa} \setminus \{t_{i}\}\), \(i\in \mathcal{N}\), and the conditions \(x(t_{i}^{+})-x(t_{i}^{-})=I_{i}(x(t^{-}_{i})), i\in \mathcal{N}\); \(x(t_{0})=A\).

Now, we introduce stability definitions that will be used in this paper.

Definition 2.6

The IDP (1) is Hyers–Ulam stable if there exists a constant \(K_{f, \mathcal{N}}>0\) with the following property: For any \(\varepsilon >0\), if \(y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) is such that

$$\begin{aligned} \begin{aligned} &\bigl\vert y^{\Delta}(t)+p(t)y^{\sigma}(t)-f \bigl(t,y(t)\bigr) \bigr\vert \le \varepsilon,\quad t\in \mathbb{J}^{\kappa} \setminus \{t_{i}\}, \\ &\bigl\vert y\bigl(t_{i}^{+}\bigr)-y\bigl(t_{i}^{-} \bigr)-I_{i}\bigl(y\bigl(t^{-}_{i}\bigr)\bigr) \bigr\vert \le \varepsilon,\quad i\in \mathcal{N}, \end{aligned} \end{aligned}$$
(3)

then there exists \(x\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) satisfying (1) such that

$$\begin{aligned} \bigl\vert y(t)-x(t) \bigr\vert \le K_{f, \mathcal{N}} \varepsilon,\quad t\in \mathbb{J}. \end{aligned}$$
(4)

The constant \(K_{f, \mathcal{N}}>0\) is known as the HUS constant.

Definition 2.7

The IDP (1) is generalized Hyers–Ulam stable if there exists \(\theta _{f, \mathcal{N}}\in \mathcal{C}(\mathbb{R}^{+}, \mathbb{R}^{+})\), \(\theta _{f}(0)=0\) with the following property: For any \(\varepsilon >0\), if \(y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) is such that

$$\begin{aligned} \begin{aligned}& \bigl\vert y^{\Delta}(t)+p(t)y^{\sigma}(t)-f \bigl(t,y(t)\bigr) \bigr\vert \le \varepsilon,\quad t\in \mathbb{J}^{\kappa} \setminus \{t_{i}\}, \\ &\bigl\vert y\bigl(t_{i}^{+}\bigr)-y\bigl(t_{i}^{-} \bigr)-I_{i}\bigl(y\bigl(t^{-}_{i}\bigr)\bigr) \bigr\vert \le \varepsilon,\quad i\in \mathcal{N}, \end{aligned} \end{aligned}$$
(5)

then there exists \(x\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) satisfying (1) such that

$$\begin{aligned} \bigl\vert y(t)-x(t) \bigr\vert \le \theta _{f, \mathcal{N}}( \varepsilon ),\quad t\in \mathbb{J}. \end{aligned}$$
(6)

Definition 2.8

The IDP (1) is Hyers–Ulam–Rassias stable with respect to \((\phi, \psi )\) if there exists \(K_{f,\mathcal{N},\phi}>0\) with the following property: For any nondecreasing \(\phi \in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R}^{+})\), \(\varepsilon >0\), and \(\psi \ge 0\), if \(y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) is such that

$$\begin{aligned} \begin{aligned} &\bigl\vert y^{\Delta}(t)+p(t)y^{\sigma}(t)-f \bigl(t,y(t)\bigr) \bigr\vert \le \varepsilon \phi (t),\quad t\in \mathbb{J}^{\kappa}\setminus \{t_{i}\}, \\ &\bigl\vert y\bigl(t_{i}^{+}\bigr)-y\bigl(t_{i}^{-} \bigr)-I_{i}\bigl(y\bigl(t^{-}_{i}\bigr)\bigr) \bigr\vert \le \varepsilon \psi,\quad i\in \mathcal{N}, \end{aligned} \end{aligned}$$
(7)

then there exists \(x\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) satisfying (1) such that

$$\begin{aligned} \bigl\vert y(t)-x(t) \bigr\vert \le K_{f,\mathcal{N},\phi} \varepsilon \bigl(\phi (t)+\psi \bigr),\quad t\in \mathbb{J}. \end{aligned}$$
(8)

The constant \(K_{f,\mathcal{N},\phi}>0\) is known as the HURS constant.

Definition 2.9

The IDP (1) is generalized Hyers–Ulam–Rassias stable with respect to \((\phi, \psi )\) if there exists \(K_{f,\mathcal{N},\phi}>0\) with the following property: For any nondecreasing \(\phi \in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R}^{+})\) and \(\psi \ge 0\), if \(y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) is such that

$$\begin{aligned} \begin{aligned} &\bigl\vert y^{\Delta}(t)+p(t)y^{\sigma}(t)-f \bigl(t,y(t)\bigr) \bigr\vert \le \phi (t),\quad t\in \mathbb{J}^{\kappa} \setminus \{t_{i}\}, \\ &\bigl\vert y\bigl(t_{i}^{+}\bigr)-y\bigl(t_{i}^{-} \bigr)-I_{i}\bigl(y\bigl(t^{-}_{i}\bigr)\bigr) \bigr\vert \le \psi,\quad i\in \mathcal{N}, \end{aligned} \end{aligned}$$
(9)

then there exists \(x\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) satisfying (1) such that

$$\begin{aligned} \bigl\vert y(t)-x(t) \bigr\vert \le K_{f,\mathcal{N},\phi}\bigl( \phi (t)+\psi \bigr),\quad t\in \mathbb{J}. \end{aligned}$$
(10)

The constant \(K_{f,\mathcal{N},\phi}>0\) is known as the GHURS constant.

Remark 2.2

A function \(y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) satisfies (7) if and only if there exists a function \(g\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) and a sequence \(\{g_{i}\}_{i\in \mathcal{N}}\) (which depends on y) with the following properties:

  1. (i)

    \(|g(t)|\le \varepsilon \phi (t)\), \(t\in \mathbb{J}\) and \(|g_{i}|\le \varepsilon \psi \);

  2. (ii)

    \(y^{\Delta}(t)+p(t)y^{\sigma}(t)=f(t,y(t))+g(t)\), \(t\in \mathbb{J}^{\kappa}\setminus \{t_{i}\}\);

  3. (iii)

    \(y(t_{i}^{+})-y(t_{i}^{-})=I_{i}(y(t^{-}_{i}))+g_{i}\), \(i\in \mathcal{N}\).

Similar arguments hold for the inequalities (5) and (9).

Lemma 2.2

(See [12, Lemma 2.1])

Let \(t_{0}, t\in \mathbb{T}\) with \(t\ge t_{0}>0\), \(y\in{ \mathrm{C}_{rd}}(\mathbb{T}, \mathbb{R})\), \(p\in \mathcal{R}^{+}(\mathbb{T},\mathbb{R})\), and \(c, b_{i}\in \mathbb{R}^{+}\), \(i\in \mathcal{N}\). Then,

$$\begin{aligned} y(t)\le c+ \int _{t_{0}}^{t} p(s)y(s)\Delta s +\sum _{t_{0}< t_{i}< t} b_{i}y(t_{i}),\quad t\ge t_{0} \end{aligned}$$

implies

$$\begin{aligned} y(t)\le c \prod_{t_{0}< t_{i}< t} (1+b_{i})e_{p}(t, t_{0}),\quad t\ge t_{0}. \end{aligned}$$

3 Extended integral inequality on time scales

In this section, we establish the timescale analog of the integral inequality for the piecewise-continuous functions studied by Samoilenko and Perestyuk [6].

Theorem 3.1

Let \(t_{0}, t\in \mathbb{T}\), \(t\ge t_{0}\), and the following inequality hold:

$$\begin{aligned} y(t)\le a(t)+ \int _{t_{0}}^{t} p(s)y(s)\Delta s +\sum _{t_{0}< t_{i}< t} b_{i} y(t_{i}),\quad t\ge t_{0}, \end{aligned}$$
(11)

where \(b_{k}\in \mathbb{R}_{+}\), \(i\in \mathcal{N}\), \(y\in \mathcal{PC}(\mathbb{T}, \mathbb{R})\), \(p\in \mathcal{R}^{+}(\mathbb{T},\mathbb{R})\), and \(a\in \mathcal{PC}(\mathbb{T}, \mathbb{R}^{+})\) is a nondecreasing function. Then, the following inequality is valid:

$$\begin{aligned} y(t)\le a(t) \prod_{t_{0}< t_{i}< t} (1+b_{i})e_{p}(t, t_{0}), \quad t \ge t_{0}. \end{aligned}$$

Proof

We rewrite (11) as

$$\begin{aligned} y(t)\le a(t)+ \int _{t_{0}}^{t} p(s)\frac{y(s)}{a(s)}a(s)\Delta s + \sum_{t_{0}< t_{i}< t} b_{i}\frac{y(t_{i})}{a(t_{i})}a(t_{i}). \end{aligned}$$

Since a is nondecreasing and \(a(t)>0\), \(t\ge t_{0}\), we obtain

$$\begin{aligned} y(t)\le a(t)+ \int _{t_{0}}^{t} p(s)\frac{y(s)}{a(s)}a(t)\Delta s + \sum_{t_{0}< t_{i}< t} b_{i}\frac{y(t_{i})}{a(t_{i})}a(t), \end{aligned}$$

i.e.,

$$\begin{aligned} \frac{y(t)}{a(t)}\le 1+ \int _{t_{0}}^{t} p(s)\frac{y(s)}{a(s)}\Delta s +\sum _{t_{0}< t_{i}< t} b_{i}\frac{y(t_{i})}{a(t_{i})}. \end{aligned}$$

Now, application of Lemma 2.2 yields,

$$\begin{aligned} \frac{y(t)}{a(t)}\le 1\prod_{t_{0}< t_{i}< t} (1+b_{i})e_{p}(t, t_{0}),\quad t\ge t_{0}. \end{aligned}$$

That is,

$$\begin{aligned} y(t)\le a(t) \prod_{t_{0}< t_{i}< t} (1+b_{i})e_{p}(t, t_{0}),\quad t \ge t_{0}. \end{aligned}$$

This completes the proof. □

4 Main results

In this section, we investigate the Ulam stability for first-order nonlinear impulsive dynamic equations on time scales (1), by means of the impulsive integral inequality given in Theorem 3.1. For this, below we list some essential conditions:

(C1):

Let \(p\in \mathcal{R}^{+}(\mathbb{J}, \mathbb{R})\).

(C2):

For \(f\in{ \mathrm{C}_{rd}(\mathbb{J}\times \mathbb{R}, \mathbb{R})}\), there exists a function \(L_{f}\in \mathcal{C}(\mathbb{J}, \mathbb{R}^{+})\) such that

$$\begin{aligned} \bigl\vert f(t, u)-f(t, v) \bigr\vert \le L_{f}(t) \vert u-v \vert \quad \text{for all }t\in \mathbb{J} \text{ and }u,v\in \mathbb{R}. \end{aligned}$$
(12)

Also, set \(L^{*}_{f}:= \sup_{t\in \mathbb{J}}L_{f}(t)\).

(C3):

For \(I\colon \mathbb{R}\to \mathbb{R}\), there exists a constant \(L_{I_{i}}>0\) such that

$$\begin{aligned} \bigl\vert I_{i}\bigl(u\bigl(t^{-}_{i} \bigr)\bigr)-I_{i}\bigl(v\bigl(t^{-}_{i}\bigr) \bigr) \bigr\vert \le L_{I_{i}} \vert u-v \vert \quad\text{for all }u,v\in \mathbb{R} \text{ and } i\in \mathcal{N}. \end{aligned}$$
(13)
(C4):

For a nondecreasing function \(\phi \in \mathcal{PC}(\mathbb{J}, \mathbb{R})\), there exists a constant \(L_{\phi}\) such that

$$\begin{aligned} \int _{t_{0}}^{t}\phi (s)\Delta s\le L_{\phi} \phi (t) \quad\text{for all }t\in \mathbb{J}. \end{aligned}$$
(14)

Theorem 4.1

Consider the IDP (1). Under the conditions (C1)–(C4), the following assertions hold:

  1. (i)

    If \(( E_{p} L^{*}_{f}(T-t_{0})+ \sum_{i=1}^{m}|e_{ \ominus p}(T, t_{i})|L_{I_{i}} )<1\), then the IDP (1) has a unique solution \(x\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) satisfying initial condition \(x(t_{0})=A\) for any initial value \(A\in \mathbb{R}\).

  2. (ii)

    The IDP (1) is Hyers–Ulam–Rassias stable with respect to \((\phi, \psi )\) and the HURS constant is \(E_{p}\varepsilon (L_{\phi}+m) \prod_{i\in \mathcal{N}}(1+E_{p}L_{I_{i}})e_{E_{p} L^{*}_{f}}(T, t_{0})\).

Proof

(i) First, fix \(A\in \mathbb{R}\) and define the mapping \(F\colon \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\to \mathcal{PC}^{1}( \mathbb{J}, \mathbb{R})\) by

$$\begin{aligned} F[x](t):=e_{\ominus p}(t, t_{0}) A+ \int _{t_{0}}^{t} e_{\ominus p}(t, s) f\bigl(s,x(s) \bigr) \Delta s+\sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(x\bigl(t^{-}_{i} \bigr)\bigr). \end{aligned}$$
(15)

In view of Remark 2.1, it is clear that the fixed points of F are the solutions of (1). Hence, we show that F has a fixed point and for this we use the contraction mapping principle. For any \(x,y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\), we can write

$$\begin{aligned} &\bigl\vert F[x](t)-F[y](t) \bigr\vert \\ &\quad\le \bigl\vert e_{\ominus p}(t, t_{0}) \bigr\vert \vert A-A \vert + \int _{t_{0}}^{t} \bigl\vert e_{ \ominus p}(t, s) \bigr\vert \bigl\vert f\bigl(s, x(s)\bigr)-f\bigl(s, y(s)\bigr) \bigr\vert \Delta s \\ &\qquad{} +\sum_{t_{0}< t_{i}< t} \bigl\vert e_{\ominus p}(t, t_{i}) \bigr\vert \bigl\vert I_{i}\bigl(x \bigl(t^{-}_{i}\bigr)\bigr)-I_{i}\bigl(y \bigl(t^{-}_{i}\bigr)\bigr) \bigr\vert \\ &\quad\stackrel{\text{\textup {(}C$_{2}$\textup {)},\textup {(}C$_{3}$\textup {)}}}{\le} E_{p} \int _{t_{0}}^{t} L_{f}(t) \bigl\vert x(s)-y(s) \bigr\vert \Delta s+\sum_{t_{0}< t_{i}< t} \bigl\vert e_{\ominus p}(t, t_{i}) \bigr\vert L_{I_{i}} \bigl\vert x\bigl(t^{-}_{i}\bigr)-y\bigl(t^{-}_{i} \bigr) \bigr\vert \\ &\quad\le \biggl( E_{p} L_{f}(t) (T-t_{0})+\sum _{t_{0}< t_{i}< t} L_{I_{i}} \bigl\vert e_{ \ominus p}(t, t_{i}) \bigr\vert \biggr) \Vert x-y \Vert _{\mathcal{PC}^{1}}. \end{aligned}$$

Thus, for all \(x,y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\)

$$\begin{aligned} \bigl\Vert F[x]-F[y] \bigr\Vert _{\mathcal{PC}^{1}}\le \Biggl( E_{p} L^{*}_{f}(T-t_{0})+ \sum _{i=1}^{m} L_{I_{i}} \bigl\vert e_{\ominus p}(T, t_{i}) \bigr\vert \Biggr) \Vert x-y \Vert _{ \mathcal{PC}^{1}}. \end{aligned}$$

Since \(( E_{p} L^{*}_{f}(T-t_{0})+ \sum_{i=1}^{m}|e_{ \ominus p}(T, t_{i})|L_{I_{i}} )<1\), the above inequality implies that the mapping F is contraction on \(\mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\). Therefore, F has a unique fixed point \(x^{*}\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\), which is the unique solution of the IDP (1) satisfying \(x^{*}(t_{0})=A\).

(ii) Let \(y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) satisfy (7) and let \(x\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) be the unique solution of (1) satisfying initial condition \(x(t_{0})=y(t_{0})\). Then, in view of (C1), Remark 2.1 allows us to write

$$\begin{aligned} &x(t)=e_{\ominus p}(t, t_{0})y(t_{0})+ \int _{t_{0}}^{t} e_{\ominus p}(t, s) f\bigl(s, x(s) \bigr)\Delta s+\sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(x\bigl(t^{-}_{i} \bigr)\bigr)\\ &\quad \text{for all } t\in \mathbb{J}. \end{aligned}$$

Now, since \(y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) satisfies (7), by Remark 2.2, we can write

$$\begin{aligned} y^{\Delta}(t)+p(t)y^{\sigma}(t)=f\bigl(t,y(t)\bigr)+g(t) \quad\text{for all } t \in \mathbb{J}^{\kappa}\setminus \{t_{i}\} \end{aligned}$$

and

$$\begin{aligned} y\bigl(t^{+}_{i}\bigr)-y\bigl(t^{-}_{i} \bigr)=I_{i}\bigl(y\bigl(t^{-}_{i}\bigr) \bigr)+g_{i},\quad i\in \mathcal{N}, \end{aligned}$$

where \(|g(t)|\le \varepsilon \phi (t)\) for all \(t\in \mathbb{J}\) and \(|g_{i}|\le \varepsilon \psi \), \(i\in \mathcal{N}\). Thus,

$$\begin{aligned} y(t)={}&e_{\ominus p}(t, t_{0})y(t_{0})+ \int _{t_{0}}^{t} e_{\ominus p}(t, s) \bigl[f\bigl(s, y(s)\bigr)+g(s)\bigr]\Delta s \\ &{}+\sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i}) \bigl(I_{i}\bigl(y\bigl(t^{-}_{i}\bigr) \bigr)+g_{i} \bigr) \\ ={}&e_{\ominus p}(t, t_{0})y(t_{0})+ \int _{t_{0}}^{t} e_{\ominus p}(t, s) f\bigl(s, y(s) \bigr)\Delta s + \int _{t_{0}}^{t} e_{\ominus p}(t, s) g(s) \Delta s \\ &{}+\sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(y\bigl(t^{-}_{i} \bigr)\bigr)+ \sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})g_{i}. \end{aligned}$$

This gives

$$\begin{aligned} & \biggl\vert y(t)-e_{\ominus p}(t, t_{0})y(t_{0})- \int _{t_{0}}^{t} e_{ \ominus p}(t, s) f\bigl(s, y(s) \bigr)\Delta s-\sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(y\bigl(t^{-}_{i} \bigr)\bigr) \biggr\vert \\ &\quad\le \int _{t_{0}}^{t} \bigl\vert e_{\ominus p}(t, s) \bigr\vert \bigl\vert g(s) \bigr\vert \Delta s+ \sum _{t_{0}< t_{i}< t} \bigl\vert e_{ \ominus p}(t, t_{i}) \bigr\vert \vert g_{i} \vert \\ &\quad\le E_{p} \varepsilon \int _{t_{0}}^{t}\phi (s)\Delta s+E_{p} \sum _{t_{0}< t_{i}< t} \varepsilon \psi \\ &\quad\stackrel{\text{\textup {(}C$_{4}$\textup {)}}}{\le} E_{p}\varepsilon L_{\phi} \phi (t)+mE_{p} \varepsilon \psi \\ &\quad=E_{p}\varepsilon \bigl(L_{\phi}\phi (t)+m \psi \bigr)\quad \text{for all }t\in \mathbb{J}. \end{aligned}$$
(16)

Now, for \(t\in \mathbb{J}\), we can write

$$\begin{aligned} & \bigl\vert y(t)-x(t) \bigr\vert \\ &\quad= \biggl\vert y(t)-e_{\ominus p}(t, t_{0})y(t_{0})- \int _{t_{0}}^{t} e_{\ominus p}(t, s) f\bigl(s, x(s) \bigr)\Delta s+ \int _{t_{0}}^{t} e_{\ominus p}(t, s) f\bigl(s, y(s) \bigr)\Delta s \\ &\qquad{} - \int _{t_{0}}^{t} e_{\ominus p}(t, s) f\bigl(s, y(s) \bigr)\Delta s- \sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(x\bigl(t^{-}_{i} \bigr)\bigr) \\ &\qquad{} -\sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(y\bigl(t^{-}_{i} \bigr)\bigr)+ \sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(y\bigl(t^{-}_{i} \bigr)\bigr) \biggr\vert \\ &\quad\le \biggl\vert y(t)-e_{\ominus p}(t, t_{0})y(t_{0})- \int _{t_{0}}^{t} e_{ \ominus p}(t, s) f\bigl(s, y(s) \bigr)\Delta s- \sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(y\bigl(t^{-}_{i} \bigr)\bigr) \biggr\vert \\ &\qquad{} + \biggl\vert \sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(x\bigl(t^{-}_{i} \bigr)\bigr)- \sum_{t_{0}< t_{i}< t}e_{\ominus p}(t, t_{i})I_{i}\bigl(y\bigl(t^{-}_{i} \bigr)\bigr) \biggr\vert \\ &\qquad{} + \biggl\vert \int _{t_{0}}^{t} e_{\ominus p}(t, s) f\bigl(s, y(s) \bigr) \Delta s- \int _{t_{0}}^{t} e_{\ominus p}(t, s)f\bigl(s, x(s) \bigr)\Delta s \biggr\vert \\ &\quad \stackrel{\text{(16)}}{\leq} E_{p}\varepsilon \bigl(L_{\phi} \phi (t)+m \psi \bigr)+ \int _{t_{0}}^{t} \bigl\vert e_{\ominus p}(t, s) \bigr\vert \bigl\vert f\bigl(s, y(s)\bigr)-f\bigl(s, x(s)\bigr) \bigr\vert \Delta s \\ &\qquad{} + \sum_{t_{0}< t_{i}< t} \bigl\vert e_{\ominus p}(t, t_{i}) \bigr\vert \bigl\vert I_{i}\bigl(x \bigl(t^{-}_{i}\bigr)\bigr)-I_{i}\bigl(y \bigl(t^{-}_{i}\bigr)\bigr) \bigr\vert \\ &\quad\stackrel{\text{\textup {(}C$_{2}$\textup {)}, \textup {(}C$_{3}$\textup {)}}}{\leq} E_{p}\varepsilon \bigl(L_{\phi} \phi (t)+m \psi \bigr)+ \int _{t_{0}}^{t} L_{f}(s) \bigl\vert e_{\ominus p}(t, s) \bigr\vert \bigl\vert y(s)-x(s) \bigr\vert \Delta s \\ &\qquad{}+ \sum_{t_{0}< t_{i}< t} \bigl\vert e_{\ominus p}(t, t_{i}) \bigr\vert L_{I_{i}} \bigl\vert x \bigl(t^{-}_{i}\bigr)-y\bigl(t^{-}_{i} \bigr) \bigr\vert \\ &\quad\le E_{p}\varepsilon \bigl(L_{\phi}\phi (t)+m \psi \bigr)+ \int _{t_{0}}^{t}E_{p} L_{f}(s) \bigl\vert x(s)-y(s) \bigr\vert \Delta s+ \sum_{t_{0}< t_{i}< t} E_{p}L_{I_{i}} \bigl\vert x\bigl(t^{-}_{i} \bigr)-y\bigl(t^{-}_{i}\bigr) \bigr\vert . \end{aligned}$$

According to Theorem 3.1, we can write for all \(t\ge t_{0}\)

$$\begin{aligned} \bigl\vert y(t)-x(t) \bigr\vert &\le E_{p}\varepsilon \bigl(L_{\phi}\phi (t)+m \psi \bigr) \prod_{t_{0}< t_{i}< t}(1+E_{p}L_{I_{i}})e_{E_{p} L_{f}}(t, t_{0}) \\ &\le E_{p} (L_{\phi}+m)\varepsilon \bigl(\phi (t)+\psi \bigr) \prod_{i\in \mathcal{N}}(1+E_{p}L_{I_{i}})e_{E_{p} L^{*}_{f}}(T, t_{0}), \end{aligned}$$

i.e.,

$$\begin{aligned} \bigl\vert y(t)-x(t) \bigr\vert \le K_{f, \mathcal{N}, \phi} \varepsilon \bigl(\phi (t)+ \psi \bigr), \end{aligned}$$

where \(K_{f, \mathcal{N}, \phi}:=E_{p} (L_{\phi}+m) \prod_{i \in \mathcal{N}}(1+E_{p}L_{I_{i}})e_{E_{p} L^{*}_{f}}(T, t_{0})\). Thus, the IDP (1) is Hyers–Ulam–Rassias stable with respect to \((\phi, \psi )\). □

Corollary 4.1

Consider the IDP (1). Under the conditions (C1)–(C4), the IDP (1) is generalized Hyers–Ulam–Rassias stable with respect to \((\phi, \psi )\) and the GHURS constant is \(E_{p}(L_{\phi}+m) \prod_{i\in \mathcal{N}}(1+E_{p}L_{I_{i}})e_{E_{p} L^{*}_{f}}(T, t_{0})\).

Proof

In the proof of Theorem 4.1, we take \(\varepsilon =1\) and the proof follows. □

Corollary 4.2

Consider the IDP (1). Under the conditions (C1)–(C4), IDP (1) is Hyers–Ulam stable and the HUS constant is \(2E_{p}\varepsilon (T-t_{0}+m) \prod_{i\in \mathcal{N}}(1+E_{p}L_{I_{i}})e_{E_{p} L^{*}_{f}}(T, t_{0})\).

Proof

In the proof of Theorem 4.1, we take \(\phi (t)\equiv 1\) and \(\psi =1\) and the proof follows easily. □

Corollary 4.3

Consider the IDP (1). Under the conditions (C1)–(C4), IDP (1) is generalized Hyers–Ulam stable.

Proof

Taking \(\theta _{f, \mathcal{N}}(\varepsilon ):=E_{p}\varepsilon (T-t_{0}+m) \prod_{i\in \mathcal{N}}(1+E_{p}L_{I_{i}})e_{E_{p} L^{*}_{f}}(T, t_{0})\) the result follows from Corollary 4.2. □

Remark 4.1

In the absence of impulses (i.e., for \(I_{i}\equiv 0\), \(i\in \mathcal{N}\)), Theorem 4.1 and its corollaries are reduced to the results of [33].

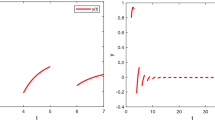
5 Illustrative example

In this section, we give an illustrative example to show the validity of our result obtained in Sect. 5 concerning the Ulam stability of IDP (1) in the finite time scale domain.

Example 5.1

Let \(\mathbb{T}=[0,1]\cup [2,3]\) and \(t_{0}=0\), \(T=3\), \(t_{1}=\frac{1}{2}\), and \(t_{2}=\frac{3}{2}\). Then, take \(\mathbb{J}:=[0,3]_{\mathbb{T}}\). Consider the impulsive dynamic problem

$$\begin{aligned} \begin{aligned} &x^{\Delta}(t)+x^{\sigma}(t)= \frac{1}{10e^{2}}\bigl(x^{2}(t)+2\bigr)^{ \frac{1}{2}}+t,\quad t\in [0,3]^{\kappa}_{\mathbb{T}}\setminus \{t_{1}, t_{2} \}, \\ &x\bigl(t^{+}_{k}\bigr)-x\bigl(t^{-}_{k} \bigr)=\frac{x(t^{-}_{k})}{1+x(t^{-}_{k})},\quad k=1,2, \\ &x(0)=0 \end{aligned} \end{aligned}$$
(17)

and its associated inequality

$$\begin{aligned} \begin{aligned}& \biggl\vert y^{\Delta}(t)+y^{\sigma}(t)- \frac{1}{10e^{2}}\bigl(y^{2}(t)+2\bigr)^{ \frac{1}{2}}-t \biggr\vert \le \varepsilon,\quad t\in [0,3]^{\kappa}_{ \mathbb{T}}\setminus \{t_{1}, t_{2}\}, \\ &\biggl\vert y\bigl(t^{+}_{k}\bigr)-y\bigl(t^{-}_{k} \bigr)-\frac{y(t^{-}_{k})}{1+y(t^{-}_{k})} \biggr\vert \le \varepsilon,\quad k=1,2. \end{aligned} \end{aligned}$$
(18)

Here, \(p(t)\equiv 1\) for which \(1+\mu (t)p(t)> 0\), \(f(t, x(t))=\frac{1}{10e^{2}}(x^{2}(t)+5)^{\frac{1}{2}}+t\) that verifies (C2) with \(L^{*}_{f}=\frac{1}{10e^{2}}\), and \(I_{k}(x(t^{-}_{k}))=\frac{x(t^{-}_{k})}{1+x(t^{-}_{k})}\) that verifies (C3) with \(L_{I_{k}}=1\). With these values, we obtain

$$\begin{aligned} E_{p}=\sup_{s,t\in [0,3]_{\mathbb{T}}} \bigl\vert e_{\ominus p}(t,s) \bigr\vert =2e^{2}, \end{aligned}$$

\(e_{\ominus p}(T, t_{1})=e_{\ominus 1}(3, \frac{1}{2})= \frac{1}{e^{2}\sqrt{e}}\) and \(e_{\ominus p}(T, t_{2})=e_{\ominus 1}(3, \frac{3}{2})= \frac{1}{e\sqrt{e}}\). This leads to

$$\begin{aligned} E_{p}L^{*}_{f}(T-t_{0})+ \bigl\vert e_{\ominus p}(T, t_{1}) \bigr\vert L_{I_{1}}+ \bigl\vert e_{ \ominus p}(T, t_{2}) \bigr\vert L_{I_{2}}& =2e^{2}\frac{1}{10e^{2}}(3-0)+ \frac{1}{e^{2}\sqrt{e}}(1)+ \frac{1}{e\sqrt{e}}(1) \\ &=\frac{3}{5}+\frac{1}{e^{2}\sqrt{e}}+\frac{1}{e\sqrt{e}} \\ &< 1. \end{aligned}$$

Thus, all conditions in Corollary 4.2 are satisfied. Hence, the impulsive dynamic problem (17) has a unique solution. This unique solution is given by

$$\begin{aligned} x(t)={}& \int _{0}^{t} e_{\ominus 1}(t, s) \biggl( \frac{1}{10e^{2}}\bigl(x^{2}(s)+5\bigr)^{ \frac{1}{2}}+s \biggr)\Delta s+e_{\ominus p}(t, 1/2) \frac{x(\frac{1}{2}^{-})}{1+x(\frac{1}{2}^{-})} \\ &{} +e_{\ominus p}(t, 3/2) \frac{x(\frac{3}{2}^{-})}{1+x(\frac{3}{2}^{-})},\quad t\in [0,3]^{ \kappa}_{\mathbb{T}}. \end{aligned}$$
(19)

Next, let \(y\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) be a solution of (18). Then, by Remark 2.2, there exists \(g\in \mathcal{PC}^{1}(\mathbb{J}, \mathbb{R})\) and \(g_{1}, g_{2}\in \mathbb{R}\) with \(|g(t)|\le \varepsilon \) and \(|g_{1}|\le \varepsilon \), \(|g_{2}|\le \varepsilon \) such that

$$\begin{aligned} \begin{aligned}& y^{\Delta}(t)+y^{\sigma}(t)= \frac{1}{10e^{2}}\bigl(y^{2}(t)+2\bigr)^{ \frac{1}{2}}+t+g(t), \quad t\in [0,3]^{\kappa}_{\mathbb{T}}\setminus \{t_{1}, t_{2} \}, \\ &y\bigl(t^{+}_{k}\bigr)-y\bigl(t^{-}_{k} \bigr)=\frac{y(t^{-}_{k})}{1+y(t^{-}_{k})}+g_{k},\quad k=1,2. \end{aligned} \end{aligned}$$
(20)

By Remark 2.1, the unique solution of (20) is given by

$$\begin{aligned} y(t)={}& \int _{0}^{t} e_{\ominus 1}(t, s) \biggl( \frac{1}{10e^{2}}\bigl(y^{2}(s)+5\bigr)^{ \frac{1}{2}}+s+ g(s) \biggr) \Delta s+e_{\ominus 1}(t, 1/2) \biggl( \frac{y(\frac{1}{2}^{-})}{1+y(\frac{1}{2}^{-})}+g_{1} \biggr) \\ &{} +e_{\ominus p}(t, 3/2) \biggl( \frac{y(\frac{3}{2}^{-})}{1+y(\frac{3}{2}^{-})}+g_{2} \biggr),\quad t \in [0,3]^{\kappa}_{\mathbb{T}}. \end{aligned}$$
(21)

Now, from (19) and (21), we can write for \(t\in [0,3]^{\kappa}_{\mathbb{T}}\)

$$\begin{aligned} & \bigl\vert y(t)-x(t) \bigr\vert \\ &\quad= \biggl\vert \int _{0}^{t} e_{\ominus 1}(t, s) \biggl[ \biggl( \frac{1}{10e^{2}}\bigl(y^{2}(s)+5\bigr)^{\frac{1}{2}}+s \biggr)- \biggl(\frac{1}{10e^{2}}\bigl(x^{2}(s)+5\bigr)^{\frac{1}{2}}+s \biggr) \biggr] \Delta s \\ &\qquad{} +e_{\ominus 1}(t, 1/2) \biggl[ \frac{y(\frac{1}{2}^{-})}{1+y(\frac{1}{2}^{-})}- \frac{x(\frac{1}{2}^{-})}{1+x(\frac{1}{2}^{-})}+g_{1} \biggr] \\ &\qquad{} +e_{\ominus 1}(t, 3/2) \biggl[ \frac{y(\frac{3}{2}^{-})}{1+y(\frac{3}{2}^{-})}- \frac{x(\frac{3}{2}^{-})}{1+x(\frac{3}{2}^{-})}+g_{2} \biggr]+ \int _{0}^{t} e_{\ominus 1}(t, s)g(s)\Delta s \biggr\vert \\ &\quad\le \int _{0}^{t} \bigl\vert e_{\ominus 1}(t, s) \bigr\vert \frac{1}{10e^{2}} \bigl\vert y(s)-x(s) \bigr\vert \Delta s+ \bigl\vert e_{\ominus 1}(t, 1/2) \bigr\vert \biggl\vert y \biggl( \frac{1}{2}^{-} \biggr)-x \biggl(\frac{1}{2}^{-} \biggr) \biggr\vert \\ &\qquad{} + \bigl\vert e_{\ominus 1}(t, 3/2) \bigr\vert \biggl\vert y \biggl( \frac{3}{2}^{-} \biggr)-x \biggl(\frac{3}{2}^{-} \biggr) \biggr\vert + \bigl\vert e_{\ominus 1}(t, 1/2) \bigr\vert \vert g_{1} \vert + \bigl\vert e_{ \ominus 1}(t, 3/2) \bigr\vert \vert g_{2} \vert \\ & \qquad{}+ \int _{0}^{t} \bigl\vert e_{\ominus 1}(t, s) \bigr\vert \bigl\vert g(s) \bigr\vert \Delta s \\ &\quad\le \int _{0}^{t} \frac{1}{10e} \bigl\vert y(s)-x(s) \bigr\vert \Delta s+\sqrt{e} \biggl\vert y \biggl( \frac{1}{2}^{-} \biggr)-x \biggl(\frac{1}{2}^{-} \biggr) \biggr\vert \\ &\qquad{} +e\sqrt{e} \biggl\vert y \biggl(\frac{3}{2}^{-} \biggr)-x \biggl( \frac{3}{2}^{-} \biggr) \biggr\vert +\varepsilon \sqrt{e}+\varepsilon e \sqrt{e}+ \varepsilon \int _{0}^{t} \bigl\vert e_{\ominus 1}(t, s) \bigr\vert \Delta s \\ &\quad\le \varepsilon \sqrt{e}+\varepsilon e\sqrt{e}+ \varepsilon et + \int _{0}^{t} \frac{1}{10e} \bigl\vert y(s)-x(s) \bigr\vert \Delta s +\sqrt{e} \biggl\vert y \biggl( \frac{1}{2}^{-} \biggr)-x \biggl(\frac{1}{2}^{-} \biggr) \biggr\vert \\ &\qquad{} +e\sqrt{e} \biggl\vert y \biggl(\frac{3}{2}^{-} \biggr)-x \biggl( \frac{3}{2}^{-} \biggr) \biggr\vert \\ &\quad= (\sqrt{e}+e\sqrt{e} + et)\varepsilon + \int _{0}^{t} \frac{1}{10e} \bigl\vert y(s)-x(s) \bigr\vert \Delta s +\sqrt{e} \biggl\vert y \biggl( \frac{1}{2}^{-} \biggr)-x \biggl( \frac{1}{2}^{-} \biggr) \biggr\vert \\ &\qquad{} +e\sqrt{e} \biggl\vert y \biggl(\frac{3}{2}^{-} \biggr)-x \biggl( \frac{3}{2}^{-} \biggr) \biggr\vert . \end{aligned}$$

Employing Theorem 3.1 with \(a(t)=(\sqrt{e}+e\sqrt{e} + et)\varepsilon \), \(p(s)=\frac{1}{10e}\), and \(b_{i}=e^{i-1}\sqrt{e}\); \(i=1,2\), we obtain

$$\begin{aligned} \bigl\vert y(t)-x(t) \bigr\vert \le \varepsilon (\sqrt{e}+e\sqrt{e} + et) (1+\sqrt{e}) (1+e \sqrt{e}) e_{\frac{1}{10e}}(t, 0),\quad t\ge 0. \end{aligned}$$

Thus, \(|y(t)-x(t)|\le \varepsilon e(3+2\sqrt{e})(1+\sqrt{e})(1+e\sqrt{e}) e_{ \frac{1}{10e}}(3, 0)\), \(t\in [0,3]_{\mathbb{T}}\), which yields that (17) has Hyers–Ulam stability with HUS constant \(e (3+2\sqrt{e})(1+\sqrt{e})(1+e\sqrt{e}) e_{\frac{1}{10e}}(3, 0)\).

6 Conclusion

We have investigated the Ulam stability for first-order nonlinear impulsive dynamic equations on bounded timescale intervals. We have achieved our results by effectively employing an extended integral inequality on time scales. The Ulam stability is an essential and reliable tool in solving the considered problem approximately, when it is not easy to find the exact solution. Also, impulsive dynamic equations are committed to model the continuous-discrete hybrid phenomena that unexpectedly undergo some discontinuous jumps during their evolution. Thus, we are confident that the results of the present paper are valuable and find their place in approximation theory, control theory, optimization, and other related fields. We believe that the results obtained in this paper can be easily extended to systems of impulsive dynamic equations and to Banach spaces. Further, it would be an exciting topic to study impulsive problems (1) with suitable delays.