Abstract
The Cauchy problem of the Laplace equation is investigated for both exact and perturbed data on a doubly connected domain, i.e., the numerical reconstruction of the function value and the normal derivative value on a part of the boundary from the knowledge of exact or noisy Cauchy data on the remaining and accessible boundary, which is completely different from the Cauchy problem on a simply connected bounded region. We first establish the existence of a solution through the potential theory. By expressing the solution as a sum of single-layer potentials using boundary value condition, we get the integral equation systems about the density function on the boundary, and by applying local regularization scheme to the obtained integral equation systems, we get the regularization solution of the original problem. Some numerical results are presented to validate the applicability and effectiveness of the proposed method.
Similar content being viewed by others
1 Introduction
The Laplace equation arises in many areas of science and engineering, especially in practical physical applications such as electrical, magnetic, and gravitational potentials, steady-state temperatures, and so on. The direct problems for the Laplace equation, i.e., the Laplace equation with Dirichlet [1, 2], Neumann [3], oblique derivative [4], generalized impedance [5], or transmission boundary conditions [6] specified on the whole boundary of the solution domain, have been studied extensively in the past century. Unfortunately, in some practical engineering problems, the boundary data on the whole boundary cannot be obtained. We only have the noisy data on a part of the boundary or at some interior points of the concerned domain, which will lead to some inverse problems.
In this paper, we consider the inverse problem of reconstructing the stationary radiation field from a pair of measured data given on the accessible part boundary of a bounded domain. The mathematical model is described by a Cauchy problem for the Laplace equation. It is well known that the Cauchy problem for the Laplace equation is severely ill-posed in the sense that the solution, if it exists, does not depend continuously on the given Cauchy data. That is, a small perturbation in the given Cauchy data may cause large change to the solution, see [7]. To overcome such difficulties, some special skills, such as the regularization scheme, are needed.
In the past years, some numerical methods, such as the iterative boundary element method [8], the Tikhonov regularization approach [9], including the alternating iterative method [10–12], the conjugate gradient method [13], energy regularization method [14], some other regularization method [15], have been proposed to deal with the Cauchy problem for the Laplace equation [8, 16]. Although many regularization methods have been applied to solve the Cauchy problem for the Laplace equation in annulus domain [14, 16], we note that there are much fewer works devoted to the Cauchy problem of the Laplace equation in a general doubly connected planar domain [10, 17, 18] instead of an annular domain between concentric circles, but such a problem has important physical applications in the engineering field.
In this paper, we propose a local regularization method to solve the Cauchy problem for the Laplace equation in a doubly connected planar domain. Compared with the whole regularization method used in [9, 10], the primary benefits of this method are that it can greatly reduce the amount of calculation and obtain more reliable numerical results with lower computational cost, which is particularly important for the Cauchy problem of the second-order elliptic equations with variable coefficients.
To precisely describe the topic considered in this paper, let be a simply connected sufficiently smooth bounded domain with boundary \(\Gamma _{2}\), and let \(D_{1}\) be a simply connected (smooth) bounded domain with boundary \(\Gamma _{1}\) such that \(\overline{D}_{1}\subset D_{2}\) and \(\Gamma _{1} \cap \Gamma _{2}=\emptyset \) (see Fig. 1). We define \(D:=D_{2} \backslash \overline{D}_{1}\), we shall denote by \(\nu _{1}\) the unit normal to \(\Gamma _{1}\) directed into the interior of D and by \(\nu _{2}\) the unit normal to \(\Gamma _{2}\) directed into the exterior of D.
Given the sufficiently smooth continuous functions \(f_{2}\in H^{1/2}(\Gamma _{2})\) and \(g_{2}\in H^{-1/2}(\Gamma _{2})\) on \(\Gamma _{2}\), we consider the following Cauchy problem of finding a function \(u\in {C}^{2}(D)\cap {C}^{1}(\overline{D})\) that satisfies the Laplace equation
with the boundary conditions
To ensure that the above Cauchy problem is uniquely solvable, we always require that the boundary data \(f_{2}\) and \(g_{2}\) are compatible, which means that this pair \((f_{2},g_{2})\) is indeed the trace of a single harmonic function in D, such an attempt seems reasonable.
The plan of the paper is as follows. In Sect. 2, the existence of a solution to the Cauchy problem is established by adopting potential theory. Then, in Sect. 3, we propose a local regularization scheme for solving the resulting ill-posed integral equation systems. In Sect. 4, numerical results are carried out to test the feasibility of the proposed method. In the final section, conclusions are given.
2 Boundary integral equation
We establish the existence of a solution to the Cauchy problem by adopting a potential approach to transform the original problem into a system of boundary integral equations. To this end, we introduce the fundamental solutions for the two-dimensional Laplace equation by
For \(j,k=1,2\), we define single- and double-layer operators \(S_{jk},K_{jk}:C(\Gamma _{j})\rightarrow C(\Gamma _{k})\),
and
and the corresponding normal derivative operators \(K'_{jk}:C(\Gamma _{j})\rightarrow C(\Gamma _{k})\),
The operators \(S_{jk}\), \(K_{jk}\), and \(K'_{jk}\) are compact since they represent integral operators with weakly singular kernels for \(j=k\) and continuous kernels for \(j \neq k\).
To prove the solvability of the Cauchy problem, we represent the solution u of (1.1)–(1.2) in the form of a sum of single-layer potentials
with unknown densities \(\varphi _{1}\in {C} (\Gamma _{1})\) and \(\varphi _{2}\in {C} (\Gamma _{2})\).
Clearly, the function u in (2.5) satisfies the Laplace equation (1.1). Matching this representation with the given Cauchy data in (1.2) using well-known properties for the restriction of these single-layer potentials and their derivatives on the boundary of the domain D, we get the following system of integral equations:
to be solved for the unknown densities \(\varphi _{1}\) and \(\varphi _{2}\), then we can rewrite (2.6) in the operator form

Taking the trace on \(\Gamma _{1}\) of the solution represented by (2.5) and its normal derivative, using jump relations of the layer potentials, gives
and
Having found \(\varphi _{1}\) and \(\varphi _{2}\) from (2.7a) and (2.7b), using (2.8) and (2.9), we can get Cauchy data on \(\Gamma _{1}\) for the sake of convenience. We rewrite it as the following operator form:
Define the operator \(A: L^{2}(\Gamma _{1}) \times L^{2}(\Gamma _{2}) \rightarrow L^{2}( \Gamma _{2}) \times L^{2}(\Gamma _{2})\),
Let \(\varphi =(\varphi _{1},\varphi _{2})^{T}\), \(h=2(f_{2},g_{2})^{T}\), we can write it as the following operator form:
Theorem 2.1
The operator A defined in (2.12) is injective and has a dense range.
Proof
From now on, without loss of generality, we assume that there exists a point \(x_{i} \in D_{i}\), (\(i=1,2\)). such that \(|x-x_{i}|\neq 1\) for all \(x\in \Gamma _{i}\). Then Theorem 3.16 in [12] guarantees that the corresponding single-layer boundary integral operator \(S_{ii} \varphi _{i}\) is injective.
Consider the following homogeneous problem:

where \(\varphi =(\varphi _{1},\varphi _{2})\in L^{2}(\Gamma _{1}) \times L^{2}( \Gamma _{2})\), we first note that from equation (2.13b), \(\varphi _{2}\) is continuous. We note the solution to the following definition:
The function \(u(x)\) also satisfies the harmonic equation \(\Delta u=0\) in both region \(D_{1}\) and region , \(u(x)\) defined by (2.14) satisfies \(u=0\), \(\frac{\partial u}{\partial \nu}=0\) on \(\Gamma _{2}\). Holmgren’s uniqueness theorem implies \(u=0\) in D. Since the single-layer potential defined by (2.14) with \(L^{2}\) density \(u(x)\) is continuous across \(\Gamma _{1}\), then \(u(x)=0\) on \(\Gamma _{1}\), and the solution \(u(x)\) defined by (2.14) also satisfies the harmonic equation in the region \(D^{+}\), while the Cauchy data on \(\Gamma _{2}\) is zero. From the unique solvability of the exterior Dirichlet problem in \(D^{+}\), we know that \(u(x)=0\) in \(D^{+}\). Take normal derivative on the boundary \(\Gamma _{2}\) for (2.14), let x tend to the boundary \(\Gamma _{2}\) from both sides of \(\Gamma _{2}\). Combining with the jump relationship of the normal derivative of the single-layer potential, we can see that \(\varphi _{2}=0\). Let x tend to the boundary \(\Gamma _{1}\) in (2.14). Combining with the conclusions already obtained, we get \(S_{11} \varphi _{1}=0\). From the previous assumptions about the domain \(D_{1}\), we can see that \(\varphi _{1}=0\), so the operator A is injective.
Next we want to show that \(A^{*}\) is injective, which implies that A has a dense range. For a solution to the homogeneous equation

we define
Then the second equation of (2.15b) implies that \(v(x)\) solves the exterior Dirichlet problem in \(D^{+}\) with homogeneous boundary condition, and consequently \(v(x)=0\) in \(D^{+}\).
The first equation of (2.15a) implies that \(v(x)\) solves the interior Dirichlet problem in the \(D_{1}\) with homogeneous boundary condition \(v(x)=0\) on \(\Gamma _{1}\), thus \(v(x)=0\) in \(D_{1}\) since \(v(x)\) defined by (2.16) is smooth across \(\Gamma _{1}\). \(v(x)=0\) also in D by analytic continuation, thus \(v(x)=0\) on the entire . Let x tend to the boundary \(\Gamma _{2}\) from both sides of \(\Gamma _{2}\) in (2.16). Combining with the jump relation, we have \(\phi _{2}=0\). We get \(S_{22} \phi _{1}=0\) from (2.15b). From the previous assumptions about the domain \(D_{2}\), we can see that \(\phi _{1}=0\), so the operator \(A^{*}\) is injective, thus A has a dense range. □
Due to the severe ill-posedness of the Cauchy problem itself, it is very dangerous to directly solve the systems. To restore stability, we need to adopt some regularization method, so the author in [9] considers the solution of the following Tikhonov regularization form:
where \(A^{*}\) is the adjoint operator to A and α is a regularization parameter to be chosen appropriately.
If you have written the program yourself, then you will notice that the numerical computation overhead of doing this is very large, so we propose the following local regularization idea.
3 Local regularization scheme
Since the second equation in the above system (2.7a)–(2.7b) is already an integral equation of the second type with respect to density \(\varphi _{2}\), we only implement regularization for the first equation with respect to density \(\varphi _{1}\):

Here we use \(\varphi _{i}^{\alpha}\) (\(i=1,2\)) to indicate that the density \(\varphi _{i}\) depends on the regularization parameter α. In this way, (3.1a) is an integral equation of the second kind about the density \(\varphi _{1}\), and (3.1b) is also of the second kind about the density \(\varphi _{2}\), and the whole is well posed. Let \(\varphi ^{\alpha}=(\varphi _{1}^{\alpha},\varphi _{2}^{\alpha})^{T}\), \(h=2(S_{12}^{*} f_{2},g_{2})^{T}\),
define the operator
B obviously is compact since all its components are compact, we get
Clearly, E has a bounded inverse for \(\alpha >0\). By the Riesz theory, it suffices to show that \((B+E)\) is injective to ensure that it has bounded inverse.
Theorem 3.1
For any \(\alpha >0\), there exists a unique solution to (3.1a) and (3.1b).
Proof
We only need to prove that the corresponding homogeneous equation has only the trivial solution by the Fredholm alternative:

The existence of the solution of equation (3.3a) and (3.3b) is obvious. Next, we prove its uniqueness. It can be seen from equation (3.3b)
Substituting it into formula (3.3a), we get
We define the following minimization functional:
We note that the Euler equation of the above minimization functional is (3.5). Obviously, the functional defined by formula (3.6) has a unique minimal element \(\varphi _{1}=0\). □
It can be seen from equation (3.1a) that
Let \(R_{\alpha}:= ( \alpha I+ S_{12}^{*}S_{12} )^{-1}S_{12}^{*}\), thus \(\varphi _{1}^{\alpha}=R_{\alpha} ( 2f_{2}- S_{22}\varphi _{2}^{ \alpha} )\), take the norm on both sides and use \(\|R_{\alpha}\| \leq \frac{1}{2 \sqrt{\alpha}}\). Let \(\alpha \rightarrow \infty \), we get \(\|\varphi _{1}^{\alpha}\|\leq 0\). It can be seen from the continuity of \(\varphi _{1}^{\alpha}\), we get \(\varphi _{1}^{\alpha} \rightarrow 0\) as \(\alpha \rightarrow \infty \).
From (3.1b) we know
when \(\alpha \rightarrow \infty \), we can get the following result.
Lemma 3.1
When \(\alpha \rightarrow \infty \) in (3.1a) and (3.1b), we get \(\varphi _{1}^{\alpha} \rightarrow 0\), \(\varphi _{2}^{\alpha} \rightarrow 2 (I+K'_{22} )^{-1} g_{2}\) for accurate Cauchy data on \(\Gamma _{2}\).
For the regularization solution defined by
when \(\alpha \rightarrow \infty \), which degenerates into an integral defined only on the boundary \(\Gamma _{2}\), independent of the closed curve \(\Gamma _{1}\) contained in it. Let \(u^{*}(x):=\lim_{\alpha \to \infty} u^{\alpha}(x)\),thus
When \(\alpha \rightarrow \infty \), the above formula shows that the function \(u^{\alpha}(x)\) defined on the region D only depends on the normal derivative value \(g_{2}\) on the outer boundary \(\Gamma _{2}\) and has nothing to do with \(f_{2}\) in form.
Obviously, the function \(u^{*}(x)\) defined above satisfies the Laplace equation over the entire region \(D_{2}\), namely, \(\Delta u^{*}(x)=0\), and always satisfies the Neumann boundary condition on \(\Gamma _{2}\). In other words,
So far we have come to the following conclusions:when \(\alpha \rightarrow \infty \) in (3.1a) and (3.1b), the Cauchy problem in the domain \(D:=D_{2} \backslash \overline{D}_{1}\) is replaced with the Neumann problem in region \(D_{2}\) since (3.10) is only defined on the boundary \(\Gamma _{2}\), but the boundary \(\Gamma _{1}\) is contained within the boundary \(\Gamma _{2}\) for any harmonic function \(v(x)\) on the domain \(D_{2}\). Of course, the harmonic equation is also satisfied on the inner curve \(\Gamma _{1}\) of \(D_{2}\), but at this time, it is unknown whether it meets the requirements on the inner boundary \(\Gamma _{1}\) of the doubly connected bounded domain D.
In addition, we know from the maximum and minimum principle (Theorem 6.9, [19]) of the harmonic equation that for doubly connected bounded domain D, it can be achieved on the inner boundary \(\Gamma _{1}\) and the outer boundary \(\Gamma _{2}\), but for region \(D_{2}\), it can be reached on only \(\Gamma _{2}\). Therefore, we cannot infer the information on the doubly connected bounded domain D from the information that satisfies the Laplace equation on the area \(D_{2}\).
For the selection of the regularization parameter α, if it is chosen too small, then the regularized solution remains unstable and, conversely, if too large, then the original Cauchy problem will be replaced with the Neumann problem. So we must choose an appropriate regularization parameter to obtain a more reasonable approximate solution. Generally speaking, a reasonable selection of regularization parameters is not an easy task. Although there are optimal choices for the regularization parameter (the discrepancy principle), it is often simpler and faster to use a heuristic choice such as the L-curve rule [20]. For more details on the choice of regularization parameters, refer to [21].
To solve equation (3.1a) and (3.1b) numerically efficiently, we need to parameterize it, so below we describe how to parameterize it.
4 Numerical examples
We assume that the inner and outer boundary curves \(\Gamma _{1}\) and \(\Gamma _{2}\) have the following parametric forms:
where are 2π-periodic and twice continuously differentiable functions such that the orientation of \(\Gamma _{j}\) is counter-clockwise. Then the normal vectors are given by
Here, for any vector \(a=(a_{1},a_{2})\), the normal vector is defined by \(a^{\perp}=(a_{2},-a_{1})\), we obtain for the single-layer operator
and its normal derivative
where \(\psi (\tau ):=\varphi (x(\tau ))\).
To handle the logarithmic singularity in the kernel of \(S_{jj}\), we split it in the following form:
where \(A(t, \tau )\) is a smooth function.
For the numerical calculation of operators \(S_{jk}\) and \(K'_{jk}\), we use the Nyström method based on trigonometric interpolation polynomial; for more details, we refer to [10, 22]. Here we omit some repetitive work. For the related error and convergence analysis of the above methods, we refer to [22]. If the region boundary is sufficiently smooth, then exponential convergence rate can be obtained.
In the last part, we illustrate by numerical examples the robustness of the proposed method based on integral equations and aimed at the reconstruction of the Cauchy data on interior boundary \(\Gamma _{1}\) for both exact and noisy data. In the case of noisy data, random pointwise errors are added to the values of the functions \(f_{2}\) and \(g_{2}\) on the outer boundary with percentage, which are always generated by
where ε denotes relative noise level, “rand( )” returns a pseudorandom number uniformly distributed in the interval \((0,1)\).
We use the following Example 4.1 to test the correctness of our computer code. Taking a function \(u(x)\) that satisfies the harmonic equation in the region \(D_{2}\), we calculate the function value and normal derivative value on the outer boundary \(\Gamma _{2}\) as our input data to solve Problem (1.1)–(1.2) and then compare the calculated data and exact value of \(u(x)\) on \(\Gamma _{1}\).
Example 4.1
Consider a solution domain D whose outer boundary \(\Gamma _{2}\) (see Fig. 1) is a rounded triangle
with radial function \(\rho (t)=2+0.3 \cos 3t\), and the interior boundary is a circle centered at the origin of radius 1,
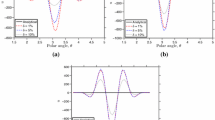
We choose the exact solution of Laplace’s equation to generate the required input data on \(\Gamma _{2}\), taking \(u_{\mathrm{ex}}(x)=x_{1}^{3}+3x_{1}^{2} x_{2}-3x_{2}^{2} x_{1}-x_{2}^{3}\), thus \(f_{2}=u_{\mathrm{ex}}(x)\) and \(g_{2}=\frac{\partial u_{\mathrm{ex}}}{\partial \nu _{2}}(x)\), \(x\in \Gamma _{2}\). We compute the approximate \(u_{\mathrm{app}}(x)\) and \(\frac{\partial u_{\mathrm{app}}}{\partial \nu _{1}}\) with different relative noise level and plot the graph (Fig. 2). For the exact data, the Tikhonov parameters are \(\alpha =1E-11\), and for the noisy case, \(\alpha =\varepsilon \) is chosen.
It should be pointed out here that we mainly use Example 4.1 to test the correctness of our computer code. Since the \(u(x)\) we take is a harmonic function on the entire , the corresponding Cauchy data is only the restriction of harmonic function to the boundary of its domain. Therefore, the numerical performance is quite good. In fact, a bit more noise can be added, but this does not mean that the anti-noise ability of our algorithm is particularly excellent. From [7], we can see that the Cauchy problem is seriously ill-posed; in other words, it is exponentially ill-posed. This means that the noise cannot be added too much, so the following example can really reflect the serious ill-posedness of the Cauchy problem. To illustrate the superiority of our proposed method, the same numerical example as in [10] is taken to test.
Example 4.2
We consider the case where the two boundary curves are described by the parametrizations
and
To generate compatible Cauchy data \((f_{2},g_{2})\) on outer boundary \(\Gamma _{2}\), we first solve the mixed boundary value problem as follows and then calculate the Dirichlet data on the outer boundary \(\Gamma _{2}\) as \(f_{2}\) in the original Cauchy problem. For the sake of comparison, we also calculate the normal derivative on the inner boundary \(\Gamma _{1}\)
we take \(f_{1}=\exp (-z_{11})z_{12}\) on \(\Gamma _{1}\) and \(g_{2}=z_{21} \) on \(\Gamma _{2}\). Figure 3 shows the comparisons of the exact solution \(u_{\mathrm{ex}}(x)\) and the approximation \(u_{\mathrm{app}}(x)\) at the same points and for different noise levels ε. The parameter \(\alpha =1E-11\) is chosen for the noiseless case and \(\alpha =0.1 \varepsilon \) for the noisy case. For each figure, we can find that the smaller the ε is, the better the computed approximation is. And the bigger the ε is, the worse the computed approximation is.
It is not difficult to see from Fig. 3 that our numerical results are better than those in [10]. It is well known that Tikhonov regularization has the disadvantage of over-smoothing. If the whole regularization method is adopted, it not only smooths the boundary data in the first equation, but also smooths the boundary data in the second equation, which leads to over-smoothing. In the local regularization scheme proposed by us, to restore the stability of the solution, only necessary regularization is carried out on the first equation, and the second equation remains unchanged, thus half of the original boundary data is retained, so our numerical performance is better.
The programs involved in this article are written by the author using Fortran 95 language with the Mingw-w64 compiler on Windows 10 64bit platform. All images are drawn by using Matlab 2009a.
5 Conclusions
In this paper, a Cauchy problem for the Laplace equation on a doubly connected domain has been investigated. Finally, we expect that similar results can be obtained for Helmholtz-type equation, and the proposed method can be extended to second-order elliptic equations with variable coefficients. The detailed comparison with the other regularization method available in the literature will be investigated in our future work.
Availability of data and materials
Not applicable.
References
Murota, K.: Comparison of conventional and “invariant” schemes of fundamental solutions method for annular domains. Jpn. J. Ind. Appl. Math. 12(1), 61–85 (1995)
El-shenawy, A., Shirokova, E.A.: The approximate solution of 2D Dirichlet problem in doubly connected domains. Adv. Math. Phys. 2018, Article ID 6951513 (2018)
El-Shenawy, A., Shirokova, E.A.: A Cauchy integral method to solve the 2D Dirichlet and Neumann problems for irregular simply-connected domains. Uch. Zap. Kazan. Univ. Ser. Fiz.-Mat. Nauki 160(4), 778–787 (2018)
Lesnic, D.: The boundary element method for solving the Laplace equation in two-dimensions with oblique derivative boundary conditions. Commun. Numer. Methods Eng. 23(12), 1071–1080 (2007)
Cakoni, F., Kress, R.: Integral equation methods for the inverse obstacle problem with generalized impedance boundary condition. Inverse Probl. 29(1), 015005 (2013)
Medková, D.: Transmission problem for the Laplace equation and the integral equation method. J. Math. Anal. Appl. 387(2), 837–843 (2012)
Belgacem, F.B.: Why is the Cauchy problem severely ill-posed? Inverse Probl. 23(2), 823–836 (2007)
Lesnic, D., Elliott, L., Ingham, D.: An iterative boundary element method for solving numerically the Cauchy problem for the Laplace equation. Eng. Anal. Bound. Elem. 20(2), 123–133 (1997)
Chapko, R., Johansson, B.: Boundary-integral approach for the numerical solution of the Cauchy problem for the Laplace equation. Ukr. Mat. Zh. 68(12), 1665–1682 (2016)
Chapko, R., Johansson, B.T., Savka, Y.: On the use of an integral equation approach for the numerical solution of a Cauchy problem for Laplace equation in a doubly connected planar domain. Inverse Probl. Sci. Eng. 22(1), 130–149 (2014)
Helsing, J., Johansson, B.T.: Fast reconstruction of harmonic functions from Cauchy data using integral equation techniques. Inverse Probl. Sci. Eng. 18(3), 381–399 (2010)
Kozlov, V.A., Maz’ya, V.G.: Iterative procedures for solving ill-posed boundary value problems that preserve the differential equations. Algebra Anal. 1(5), 144–170 (1989)
Hào, D.N., Lesnic, D.: The Cauchy problem for Laplace’s equation via the conjugate gradient method. IMA J. Appl. Math. 65(2), 199–217 (2000)
Han, H., Ling, L., Takeuchi, T.: An energy regularization for Cauchy problems of Laplace equation in annulus domain. Commun. Comput. Phys. 9(4), 878–896 (2011)
Qian, Z., Fu, C.-L., Li, Z.-P.: Two regularization methods for a Cauchy problem for the Laplace equation. J. Math. Anal. Appl. 338(1), 479–489 (2008)
Tadi, M., Radenkovic, M.: Non-iterative solution methods for Cauchy problems for Laplace and Helmholtz equation in annulus domain. Mathematics 9(3), 268 (2021)
Liu, C.-S.: A highly accurate MCTM for inverse Cauchy problems of Laplace equation in arbitrary plane domains. Comput. Model. Eng. Sci. 35(2), 91–111 (2008)
Liu, J.-C., Zhang, Q.-G.: Cauchy problem for the Laplace equation in 2D and 3D doubly connected domains. Comput. Model. Eng. Sci. 93(3), 203–219 (2013)
Kress, R.: Linear Integral Equations, 3rd edn. Applied Mathematical Sciences, vol. 82. Springer, New York (2014)
Hansen, P.C.: The L-curve and its use in the numerical treatment of inverse problems (1999)
Reichel, L., Rodriguez, G.: Old and new parameter choice rules for discrete ill-posed problems. Numer. Algorithms 63(1), 65–87 (2013)
Kress, R., Yaman, F., Yapar, A., Akduman, I.: Inverse scattering for an impedance cylinder buried in a dielectric cylinder. Inverse Probl. Sci. Eng. 17(4), 473–488 (2009)
Acknowledgements
The authors are grateful to the anonymous reviewers for their helpful, valuable comments and suggestions for the improvement of this manuscript.
Funding
Innovation Fund for Higher Education of Gansu Province (2023B-403).
Author information
Authors and Affiliations
Contributions
All authors participated in the preparation of all stages of the article and have the same contribution and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gong, X., Yang, S. A local regularization scheme of Cauchy problem for the Laplace equation on a doubly connected domain. Bound Value Probl 2023, 30 (2023). https://doi.org/10.1186/s13661-023-01717-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-023-01717-2