1 Introduction

Recently, numerous and improved applications of fractional calculus have given rise to this issue (see [1–11] and references therein). In 2014, Khalil et al. introduced a new definition of local type for the fractional derivative using “conformable derivative” \((\mathbb{C}_{\mathcal{D}})\) [3]. The fact that this derivative satisfies a huge portion of the well-known characteristics of integer order derivatives is described as a main reason for its adoption [10]. Later, Abdeljawad [8] used this newly defined terminology to describe the fundamental features and results of fractional calculus.

In [12, 13], the authors discussed the physical and geometric interpretation of the conformable derivatives, respectively. In [14], the authors proposed Euler’s and modified Euler’s method utilizing \(\mathbb{C}_{\mathcal{D}}\). Moreover, they have discussed the validity of the proposed method briefly. Since with the rapid development of non-linear science over the last two decades, scientists and engineers have become increasingly interested in analytical tools for non-linear problems.

Perturbation methods \((\mathrm{P}\mathbb{M})\) are frequently used techniques. However, perturbation methods, like other nonlinear analytical techniques, have their own set of restrictions. Almost all perturbation methods start with the assumption that the equation must have a small parameter. The applicability of perturbation techniques is severely limited by this so-called small parameter assumption [15]. The Homotopy Perturbation Method \((\mathrm{HP}\mathbb{M})\) was first proposed by Ji Huan He [15, 16]. The \(\mathrm{HP}\mathbb{M}\) has been used by many researchers in recent years to solve different types of linear and non-linear differential equations, see, for example, [17–19] and references therein. In [20], the author applied the \(\mathrm{HP}\mathbb{M}\) along with Elzaki transformation \((\mathrm{E}\mathbb{T})\) to provide the solution of some non-linear partial differential equation \((\mathbb{N}\mathbbm{-}\mathbb{PDE}s)\). Furthermore, they discussed that the developed algorithm can solve \(\mathbb{N}\mathbbm{-}\mathbb{PDE}s\) without “Adomian’s polynomials”, which is considered a clear advantage of this technique over the decomposition method. In 2022, Anaç presented the applications of the Homotopy perturbation Elzaki transform method to obtain the numerical solutions of Gas-dynamics and Klein-Gordon equations and showed that numerical solutions of fractional partial differential equations obtain both quickly and efficiently via a current method [21]. They studied random non-linear partial differential equations to acquire the approximate solutions of these equations by the Homotopy perturbation Elzaki Transform method [22].

The Homotopy Perturbation Method using \(\mathrm{E}\mathbb{T}\) is presented by Elzaki et al. in [20]. In this research paper, we successfully apply this technique to solve non-linear homogeneous and non-homogeneous \(\mathbb{PDE}s\). The efficiency of \(\mathrm{E}\mathbb{T}-\mathrm{HP}\mathbb{M}\) to solve this type of problem is also shown in [23, 24]. We are now going to formulate a Con-version of \(\mathrm{HP}\mathbb{M}\) using \(\mathrm{E}\mathbb{T}\) \((\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\mathrm{HP}\mathbb{M})\) to solve non-linear time-fractional partial differential equations \((\mathbb{N}\mathbbm{-}\mathbb{TFPDE}s)\). Thus, given a \(\mathbb{N}\mathbbm{-}\mathbb{TFPDE}s\) as follows

$$ L_{\mathbb{C}}^{ \upalpha} \mathrm{y}(u,\nu ) + \mathcal{N}_{1} \bigl(\mathrm{y}(u,\nu ) \bigr) + \mathcal{N}_{2} \bigl(\mathrm{y}(u, \nu ) \bigr)= \mathcal{H}(u,\nu ), $$
(1)

subject to the initial condition \((\mathbb{I}\mathbbm{.}\mathbb{C}\mathbbm{.})\)

$$ \mathrm{y}(u,0)=\mathrm{y}(u), $$
(2)

where y is a function of two variables, \(L_{\mathbb{C}}^{ \upalpha} = \frac{\partial ^{\upalpha}}{ \partial \nu ^{\upalpha}}\) is a linear operator with \(\mathbb{C}_{\mathcal{D}}\) of order \(0 < \upalpha \leq 1\), \(\mathcal{N}_{1} \) and \(\mathcal{N}_{2}\) are a non-linear operator and the second part of linear operator, respectively, and \(\mathcal{H}(u,\nu )\) is a non-homogeneous term.

The article is outlined as follows: Sect. 2 introduces some key concepts in the conformable calculus. Section 3 outlines the essential features of the \(\mathrm{E}\mathbb{T}\) by proposing a new definition based on \(\mathbb{C}_{\mathcal{D}}\) and integrals. Following that, Sect. 4 is built using conformable-Elzaki transform \((\mathbb{C}_{\mathcal{D}} \mathrm{E}\mathbb{T})\). This section also includes results on the uniqueness and convergence of the solution found using the suggested approach. We applied the approach to several types of \(\mathbb{N}\mathbbm{-}\mathbb{TFPDE}s\) and discussed their numerical solutions in Sect. 5. Finally, Sect. 6 addresses the conclusion of the work.

2 Fundamental properties of conformable calculus

In this section, we will highlight some of the basic properties of \(\mathbb{C}_{\mathcal{D}}\) and \(\mathrm{E}\mathbb{T}\).

Definition 2.1

Given \(\mathrm{y}: [0,\infty )\to \mathbb{R}\) as a function. Then, the αth order \(\mathbb{C}_{\mathcal{D}}\) is expressed as [3],

$$ \bigl( \mathbb{C}_{\mathcal{D}}^{\upalpha } \mathrm{y} \bigr) ( \nu ) = \lim_{ \epsilon \to 0} \frac { \mathrm{y} ( \nu + \epsilon \nu ^{1- \upalpha} ) - \mathrm{y}(\nu )}{ \epsilon}, \quad \forall \nu >0, \upalpha \in (0,1]. $$
(3)

If y is α-differentiable (α-Diff) in some \((0,\tau _{\circ}), \tau _{\circ }>0 \), and \(( \mathbb{C}_{\mathcal{D}}^{\upalpha } \mathrm{y} )( \nu )\) exists, then it is expressed as

$$ \bigl( \mathbb{C}_{\mathcal{D}}^{\upalpha } \mathrm{y} \bigr) (0) = \bigl( \mathbb{C}_{\mathcal{D}}^{\upalpha } \mathrm{y} \bigr) ( \nu ).$$

Remark 2.1

From definition 2.1, the basic properties of the \(\mathbb{C}_{\mathcal{D}}\) can be easily established (see [3]). In addition, by the direct application of the same definition, the values of the main elementary functions using \(\mathbb{C}_{\mathcal{D}}\) can be easily obtained (see [3]). We will only highlight the following result that relates the \(\mathbb{C}_{\mathcal{D}}\) with the ordinary derivatives

Let y is α-Diff at a point \(\nu > 0\). If y is Diff then

$$ \bigl( \mathbb{C}_{\mathcal{D}}^{\upalpha } \mathrm{y} \bigr) ( \nu ) = \nu ^{1-\upalpha} \,\frac {{\mathrm {d}}\mathrm{y}}{ {\mathrm {d}} \nu}(\nu ).$$

Remark 2.2

Another important result of the mathematical analysis of functions of a real variable, the chain rule, has also been formulated in a conformable sense in [8].

The Con-laplace transform of order α is expressed as [8, 25]

$$ L_{\mathbb{C}}^{ \upalpha} \bigl[ \mathrm{y}(\nu )\bigr](\mathrm{s}) = \int _{0}^{\infty} e^{ ( -\mathrm{s} \frac{\nu ^{\upalpha}}{ \upalpha} )} \mathrm{y}(\nu ) \,\frac{{\mathrm {d}} \nu}{\nu ^{1- \upalpha}}. $$
(4)

The function y is considered as conformable exponentially bounded if there are constants \(\breve{M}>0\), \(\gamma \in \mathbb{R}\) and \(\tau _{\circ}>0\), such that

$$ \bigl\vert \mathrm{y}(\nu ) \bigr\vert \leq \breve{M}e^{ \gamma \frac{ \nu ^{\upalpha}}{\upalpha}}, \quad \forall \nu \geq \tau _{ \circ}. $$
(5)

Finally, for a real valued function of several variable, the conformable partial derivative can be stated as follows. Consider the real-valued function of n variables with \(\textbf{b} = (b_{1},\dots , b_{n} )\in \mathbb{R}^{n}\) being a point whose ith component is positive. Then, the limit can be defined as follows

$$ \lim_{ \epsilon \to 0} \frac { ( \mathrm{y}( b_{1}, \dots , b_{i} + \epsilon b^{1- \upalpha}_{i}, \dots , b_{n}) - \mathrm{y}( b_{1}, \dots , b_{n}) ) }{ \epsilon}. $$
(6)

If the above limit exists, then we have the \(\upalpha \in (0,1]\) order ith con-partial derivative of y at b, denoted by \(\frac{ \partial ^{\upalpha}}{ \partial b_{i}^{\upalpha }} \mathrm{y}( \textbf{b})\). The α-conformable integral of a function y beginning from \(\tau _{\circ}\ge 0\) is defined as [1],

$$ \mathcal{I}_{\mathcal{D}, \tau _{\circ}}^{ \upalpha} (\mathrm{y}) ( \nu ) = \int _{\tau _{\circ}}^{\nu} \frac{ \mathrm{y}(\xi ) }{ \xi ^{1- \upalpha}} \,{\mathrm {d}} \xi , $$
(7)

whereas, this is a usual Riemann improper integral for \(\upalpha \in (0,1]\). As a result, we have

$$ \mathbb{C}_{\mathcal{D},\tau _{\circ}}^{ \upalpha} \mathcal{I}_{ \mathcal{D}, \tau _{\circ}}^{ \upalpha} (\mathrm{y}) (\nu ) = \mathrm{y}(\nu ), \quad \forall \nu \ge \tau _{\circ},$$

where y is any continuous function. Also,

$$ \mathcal{I}_{\mathcal{D}, \tau _{\circ}}^{ \upalpha} \mathbb{C}_{ \mathcal{D}, \tau _{\circ}}^{ \upalpha} (\mathrm{y}) (\nu ) = \mathrm{y}(\nu ) - \mathrm{y}(\tau _{\circ}), \quad \forall \tau _{ \circ }>0 $$
(8)

whenever the real-valued function y is α-Diff with \(0 < \upalpha \leq 1\) [26].

3 The conformable Elzaki transform

Elzaki introduces a new integral transform, namely the Elzaki transform, and its main properties are established in [27]. Subsequent research works show the applicability of this transform to solve important problems related to ordinary and partial differential equations [28]. Next, we will define the \(\mathrm{E}\mathbb{T}\) in Con-sense and derive its properties.

Definition 3.1

Suppose that \(\upalpha \in (0,1]\) and \(\mathrm{y}:[0,\infty )\to \mathbb{R}\) are real-valued functions. Then, the \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) of order α is expressed as

$$ E_{\upalpha }\bigl[\mathrm{y}(\nu )\bigr](\mathrm{s}) = \mathrm{s} \int _{0}^{ \infty} e^{ \frac{-\nu ^{\upalpha}}{\upalpha \mathrm{s}}} \mathrm{y}( \nu ) \,\frac{{\mathrm {d}} \nu}{\nu ^{1 - \upalpha}},\quad \mathrm{s} \neq 0. $$
(9)

Theorem 3.2

If y is a piece-wise continuous function on \([0,\infty )\) and Con-exponentially bounded, then \(E_{\upalpha }[\mathrm{y}(\nu )](\mathrm{s})\) exists for \(\frac{1}{\mathrm{s}} > \gamma \), \(\mathrm{s}\neq 0\).

Proof

Since y is Con-exponentially bounded, there exist constants \(\breve{M}_{1}>0\), \(\gamma \in \mathbb{R}\) and \(\tau _{\circ}>0\) such that

$$ \bigl\vert \mathrm{y}(\nu ) \bigr\vert \leq \breve{M}_{1} e^{ \gamma \frac{\nu ^{\upalpha}}{\upalpha}},\quad \forall \nu \geq \tau _{ \circ}. $$
(10)

Furthermore, y is piece-wise continuous on \([0,\tau _{\circ}]\) and hence bounded there, say

$$ \bigl\vert \mathrm{y}(\nu ) \bigr\vert \leq \breve{M}_{2}, \quad \forall \nu \in [0,\tau _{ \circ}].$$

This mean that, a constant M̆ can be chosen sufficiently large so that the inequality (10) holds. Therefore,

$$\begin{aligned} \biggl\vert \mathrm{s} \int _{0}^{\tau} e^{ - \frac{\nu ^{\upalpha}}{ \upalpha \mathrm{s}}} \mathrm{y}(\nu ) \,\frac{{\mathrm {d}} \nu}{ \nu ^{1 - \upalpha}} \biggr\vert & \leq \mathrm{s} \int _{0}^{\tau} \bigl\vert e^{ \frac{-\nu ^{\upalpha}}{ \upalpha \mathrm{s}}} \mathrm{y}(\nu ) \bigr\vert \,\frac{{\mathrm {d}} \nu}{\nu ^{1 - \upalpha}} \\ & \leq \breve{M} \mathrm{s} \int _{0}^{\tau} e^{- ( \frac{1}{\mathrm{s}} - \gamma ) \frac{\nu ^{\upalpha}}{ \upalpha}} \,\frac{{\mathrm {d}} \nu}{\nu ^{ 1 -\upalpha}} \\ & = - \frac{\breve{M} \mathrm{s}^{2}}{1 - \gamma \mathrm{s}} \bigl( e^{- ( \frac{1}{\mathrm{s}} - \gamma ) \frac{\nu ^{\upalpha}}{ \upalpha}}-1 \bigr). \end{aligned}$$

Letting \(\tau \to \infty \), we see that

$$ \mathrm{s} \int _{0}^{\infty} \bigl\vert e^{ \frac{-\nu ^{\upalpha}}{ \upalpha \mathrm{s}}} \mathrm{y}(\nu ) \bigr\vert \,\frac{{\mathrm {d}}\nu}{\nu ^{ 1 - \upalpha}} \leq \frac{ \breve{M} \mathrm{s}^{2}}{ 1 - \gamma \mathrm{s}}, \quad \frac{1}{\mathrm{s}} > \gamma , (\mathrm{s} \neq 0).$$

 □

Theorem 3.3

Let \(\upalpha \in (0,1]\), \(\mathrm{y}, \acute{\mathrm{y}} : [0,\infty )\to \mathbb{R}\) be real-valued functions, and \(\lambda _{i} \in \mathbb{R}\), \(i = 1,2\). If \(E_{\upalpha}[\mathrm{y}(\nu )](\mathrm{s}) \) and \(E_{\upalpha}[\acute{\mathrm{y}}(\nu )](\mathrm{s})\) exists, then

$$ E_{\upalpha } \bigl[ \lambda _{1} \mathrm{y}(\nu ) + \lambda _{2} \acute{\mathrm{y}}(\nu ) \bigr] (\mathrm{s}) =\lambda _{1} E_{ \upalpha }\bigl[\mathrm{y}(\nu )\bigr]\bigl(\mathrm{y}( \nu )\bigr) + \lambda _{2} E_{ \upalpha }\bigl[\acute{ \mathrm{y}}(\nu )\bigr](\mathrm{s}).$$

Proof

This result follows directly from the linearity of the integral. □

Theorem 3.4

Let \(\upalpha \in (0,1]\). So, we have

  1. 1)

    \(E_{\upalpha }[c](\mathrm{s}) =c \mathrm{s}^{2}\), for any \(c \in \mathbb{R}\) and \(\mathrm{s}>0\);

  2. 2)

    \(E_{\upalpha }[\nu ^{b} ](\mathrm{s}) = \upalpha ^{\frac{b}{\upalpha}} \Gamma ( 1 + \frac{b}{ \upalpha}) \mathrm{s}^{ ( 2+ \frac{b}{ \upalpha} )}\), \(b>-1\) and \(\mathrm{s}>0\);

  3. 3)

    \(E_{\upalpha }[e^{c\frac{\nu ^{\upalpha}}{\upalpha} }]( \mathrm{s}) = \frac{\mathrm{s}^{2}}{ 1 - c\mathrm{s}}\), c is any real number and \(\mathrm{s}> \frac{1}{c}\);

  4. 4)

    \(E_{\upalpha } [ \sin c \frac{\nu ^{\upalpha }}{ \upalpha} ] (\mathrm{s}) = \frac{c \mathrm{s}^{3}}{1 + c^{2} \mathrm{s}^{2} }\), c is any real number and \(\mathrm{s}>0\);

  5. 5)

    \(E_{\upalpha } [ \cos c \frac{ \nu ^{\upalpha}}{ \upalpha} ] (\mathrm{s}) = \frac{\mathrm{s}^{2}}{1+c^{2} \mathrm{s}^{2} }\), c is any real number and \(\mathrm{s}>0\);

  6. 6)

    \(E_{\upalpha } [ \sinh c \frac{\nu ^{\upalpha}}{ \upalpha} ] ( \mathrm{s}) = \frac{c \mathrm{s}^{3}}{1 - c^{2} \mathrm{s}^{2} }\), c is any real number and \(0<\mathrm{s} < \frac{1}{| \mathrm{s}| }\);

  7. 7)

    \(E_{\upalpha } [ \cosh c \frac{\nu ^{\upalpha}}{\upalpha} ]( \mathrm{s}) = \frac{\mathrm{s}^{2}}{ 1 - c^{2} \mathrm{s}^{2} }\), c is any real number and \(0<\mathrm{s} <\frac{1}{| c| }\).

Proof

  1. 1)

    Follows from the definition directly.

  2. 2)

    Through a change of variables, we have

    $$ \mathrm{s} \int _{0}^{\infty} e^{ \frac{-\nu ^{\upalpha}}{ \upalpha \mathrm{s}}} \nu ^{b}\, \frac{{\mathrm {d}} \nu}{\nu ^{1 - \upalpha}} = \upalpha ^{ \frac{b}{\upalpha}} \mathrm{s}^{ ( 2 + \frac{b}{\upalpha} )} \int _{0}^{\infty} \xi ^{\frac{b}{\upalpha}} e^{-\xi} \,{ \mathrm {d}} \xi = \upalpha ^{\frac{b}{ \upalpha}} \Gamma \biggl( 1 + \frac{b}{\upalpha} \biggr) \mathrm{s}^{ ( 2+\frac{b}{\upalpha} )}.$$
  3. 3)

    Since,

    $$ \mathrm{s} \int _{o}^{\infty} e^{ \frac{-\nu ^{\upalpha}}{\upalpha \mathrm{s}}} e^{ c \frac{ \nu ^{\upalpha}}{\upalpha}} \,\frac{ {\mathrm {d}} \nu}{\nu ^{1 - \upalpha}} = \mathrm{s} \int _{0}^{ \infty} e^{\frac{ - \nu ^{\upalpha}}{ \upalpha} ( \frac{1}{ \mathrm{s}}-c ) } \,\frac{ {\mathrm {d}}\nu}{\nu ^{1 - \upalpha}} = \frac{ \mathrm{s}^{2}}{1 - c\mathrm{s}}.$$
  4. 4)

    Using the fact that

    $$ \int _{0}^{\infty} e^{-\nu ^{\frac{ \upalpha}{\upalpha \mathrm{s}}}} \sin \bigl(c \nu ^{\frac{ \upalpha}{\upalpha}} \bigr)\, \frac{ {\mathrm {d}} \nu}{\nu ^{1 - \upalpha}} = - \frac{c\mathrm{s}^{2}}{ 1+ c^{2} \mathrm{s}^{2} } e^{-\nu ^{ \frac{ \upalpha}{ \upalpha \mathrm{s}}}} \biggl( \cos \biggl( c \frac{\nu ^{\upalpha}}{ \upalpha} \biggr) + \frac{1}{c \mathrm{s}} \sin \biggl( c { \frac{\nu ^{\upalpha}}{ \upalpha }} \biggr) \biggr),$$

    we can get the required result.

  5. 5)

    Similarly, we have

    $$ \int _{0}^{ \infty} e^{-\nu ^{\frac{\upalpha}{ \upalpha \mathrm{s}}}} \cos \bigl( c \nu ^{\frac{ \upalpha}{ \upalpha}} \bigr)\, \frac{{\mathrm {d}} \nu }{ \nu ^{ 1 - \upalpha}} = - \frac{ c \mathrm{s}^{3}}{1 + c^{2} \mathrm{s}^{2}} e^{ - \nu ^{ \frac{ \upalpha}{ \upalpha \mathrm{s}}}} \biggl( \sin \biggl( c \frac { \nu ^{\upalpha}}{\upalpha} \biggr) - \frac{1}{c\nu} \cos \biggl( c { \frac{\nu ^{\upalpha}}{\upalpha }} \biggr) \biggr).$$
  6. 6)

    As

    $$ E_{\upalpha } \biggl[ \sinh \biggl( c \frac{\nu ^{\upalpha}}{\upalpha} \biggr) \biggr]( \mathrm{s}) = \frac{1}{2} \bigl( E_{\upalpha } \bigl[ e^{c \frac{\nu ^{\upalpha}}{ \upalpha}} \bigr](\mathrm{s}) - E_{ \upalpha } \bigl[e^{-c \frac{\nu ^{\upalpha}}{ \upalpha}} \bigr]( \mathrm{s}) \bigr),$$

    it is easy to get the required result.

  7. 7)

    Similarly, as

    $$ E_{\upalpha } \biggl[ \cosh \biggl( c \frac{\nu ^{\upalpha}}{ \upalpha} \biggr) \biggr]( \mathrm{s}) = \frac{1}{2} \bigl( E_{\upalpha } \bigl[ e^{c \frac{\nu ^{\upalpha}}{\upalpha}} \bigr]( \mathrm{s}) + E_{ \upalpha } \bigl[ e^{- \frac{\nu ^{\upalpha}}{\upalpha}} \bigr]( \mathrm{s}) \bigr),$$

    it is easy to get the required result.

 □

Theorem 3.5

Suppose that \(\mathrm{y}(\nu )\) is continuous, and \(( \mathbb{C}_{\mathcal{D}}^{\upalpha } \mathrm{y} )( \nu )\) is piece-wise continuous for all \(\nu \geq 0\). Suppose further that \(\mathrm{y}(\nu )\) is Con-exponentially bounded. Then

$$ E_{\upalpha } \bigl[ \bigl( \mathbb{C}_{\mathcal{D}}^{\upalpha } \mathrm{y} \bigr) (\nu ) \bigr](\mathrm{s}),\quad \biggl( \frac{1}{\mathrm{s}} > \gamma \biggr),$$

exists and, moreover,

$$ E_{\upalpha } \bigl[ \bigl( \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y} \bigr) (\nu ) \bigr] (\mathrm{s}) = \frac{1}{\mathrm{s}} E_{ \upalpha } \bigl[ \mathrm{y}(\nu ) \bigr]( \mathrm{s}) - \mathrm{s} \mathrm{y}(0).$$

Proof

Using definition 3.1, we have

$$ E_{\upalpha } \bigl[ \bigl( \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y} \bigr) (\nu ) \bigr] (\mathrm{s}) = \mathrm{s} \int _{0}^{ \infty} e^{ \frac{- \nu ^{\upalpha}}{\upalpha \mathrm{s}}} \bigl( \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y} \bigr) (\nu ) \,\frac{{\mathrm {d}}\nu}{\nu ^{1-\upalpha}}.$$

Now, using integration by parts [8], we get

$$\begin{aligned} E_{\upalpha } \bigl[ \bigl( \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y} \bigr) (\nu ) \bigr](\mathrm{s}) & = \mathrm{s} \bigl[ e^{- \frac{\nu ^{\upalpha}}{\upalpha \mathrm{s}}} \mathrm{y}(\nu ) \bigr]_{0}^{ \tau} + \frac{1}{\mathrm{s}} \int _{0}^{\infty} e^{- \frac{\nu ^{\upalpha}}{\upalpha \mathrm{s}}} \mathrm{y}(\nu ) \,\frac{{\mathrm {d}}\nu}{\nu ^{1-\upalpha}} \\ & = \mathrm{s} \Bigl[\lim_{\tau \to \infty} e^{- \frac{\tau ^{\upalpha}}{\upalpha \mathrm{s}}} \mathrm{y}(\tau ) - \mathrm{y}(0) \Bigr] + \frac{1}{\mathrm{y}} E_{\upalpha } \bigl[\mathrm{y}( \nu )\bigr](\mathrm{y}). \end{aligned}$$

Since \(\mathrm{y}(\nu )\) is Con-exponentially bounded, \(\lim_{\tau \to \infty} e^{- \frac{\tau ^{\upalpha}}{\upalpha \mathrm{s}}} \mathrm{y}(\tau )=0\), whenever \(\frac{1}{ \mathrm{s}} > \gamma \). Hence,

$$ E_{\upalpha } \bigl[ \bigl( \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y} \bigr) (\nu ) \bigr]( \mathrm{s}) = \frac{1}{\mathrm{s}} E_{\upalpha }\bigl[\mathrm{y}(\nu )\bigr](\mathrm{s}) - \mathrm{s} \mathrm{y}(0),$$

for \(\frac{1}{\mathrm{s}} > \gamma \). □

Indeed, provided that the function y and its \(\mathbb{C}_{\mathcal{D}}\) satisfy the appropriate conditions, an expression for the \(\mathbb{C}_{\mathcal{D}}\mathrm{ET}\) of the derivative \((n) \mathbb{C}_{\mathcal{D}}^{ \upalpha}\) can be derived by successive applications of the previous theorem. This result is given in the following corollary.

Corollary 3.1

Suppose that \(\mathrm{y}, \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y}, \dots , (n-1)\mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y}\) are continuous, and \((n) \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y}\) is piecewise continuous for all \(\nu \geq 0\). Suppose further that \(\mathrm{y}, \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y}, \dots , (n-1) \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y}\) are con-exponentially bounded. Then \(E_{\upalpha } [ (n) ( \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y} )(\nu ) ](\mathrm{s})\) exists for \(\frac{1}{\mathrm{s}}> \gamma \) and is given by

$$ E_{\upalpha } \bigl[ (n) \bigl( \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y} \bigr) (\nu ) \bigr]( \mathrm{s} ) = \frac{1}{\mathrm{s}^{n}} E_{\upalpha }\bigl[\mathrm{y}(\nu )\bigr](\mathrm{s}) - \sum _{k=0}^{n-1} \mathrm{s}^{2-n+k}(k) \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y}(0).$$

Remark 3.1

Here, \((n) ( \mathbb{C}_{\mathcal{D}}^{ \upalpha} \mathrm{y} )(\nu )\) means the application of the \(\mathbb{C}_{\mathcal{D}}\), n times.

Remark 3.2

If we assume that \(\mathrm{y}(x,\nu )\) is piece-wise continuous and Con-exponentially bounded, the following results are easily obtained

  1. 1

    Using Leibniz’s rule, we can find

    $$\begin{aligned} E_{\upalpha } \biggl[ \frac{\partial \mathrm{y}(x,\nu )}{ \partial x} \biggr]( \mathrm{s}) & = \mathrm{s} \int _{0}^{\infty} e^{- \frac{\nu ^{\upalpha}}{\upalpha \mathrm{s}}} \frac{\partial \mathrm{y}(x,\nu ) }{\partial x} \,\frac {{\mathrm {d}}\nu}{\nu ^{1-\upalpha}} \\ & = \frac{\partial}{\partial x} \biggl[ \int _{0}^{\infty} \mathrm{s} e^{-\frac{t^{\upalpha}}{\upalpha \mathrm{s}}} \mathrm{y}(x,\nu ) \,\frac {{\mathrm {d}} \nu}{\nu ^{1-\upalpha}} \biggr] = \frac{\partial}{\partial x} \bigl[ \mathbb{C}_{\mathcal{D}}^{ \upalpha}(x,\mathrm{s}) \bigr]. \end{aligned}$$

    Also,

    $$ E_{\upalpha } \biggl[ \frac{\partial ^{2} \mathrm{y}(x,\nu )}{ \partial x^{2}} \biggr]( \mathrm{s}) = \frac{\partial ^{2}}{\partial x^{2}} \bigl[ \mathbb{C}_{ \mathcal{D}}^{ \upalpha}(x, \mathrm{s}) \bigr].$$
  2. 2

    From Theorem 2.4, we have

    $$ E_{\upalpha } \biggl[ \frac{\partial ^{\upalpha }\mathrm{y}(x,\nu )}{ \partial \nu ^{\upalpha }} \biggr](\mathrm{s}) = \frac{1}{\mathrm{s}} E_{\upalpha } \bigl[ \mathrm{y}(x,\nu ) \bigr]( \mathrm{s})-\mathrm{s} \mathrm{y} (x,0).$$

Another important property of the \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) is the convolution theorem, which is stated below.

Theorem 3.6

Consider two real-valued functions, i.e., \(\mathrm{y}, \acute{\mathrm{y}}:[0,\infty )\to \mathbb{R}\), if the convolution of y and ý of order \(0 < \upalpha \leq 1\), expressed as

$$ (\mathrm{y}*\acute{\mathrm{y}}) = \int _{0}^{\nu} \mathrm{y} \biggl( \frac{\nu ^{\upalpha}}{\upalpha} - \frac{\xi ^{\upalpha}}{ \upalpha} \biggr) \acute{\mathrm{y}} \biggl( \frac{ \xi ^{\upalpha}}{ \upalpha} \biggr) \,\frac{ {\mathrm {d}} \xi}{\xi ^{1-\upalpha}}. $$
(11)

Then, one can obtain the \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) as

$$ E_{\upalpha } \bigl[( \mathrm{y} * \acute{\mathrm{y}}) \bigr]( \mathrm{s}) = \frac{1}{\mathrm{s}} E_{\upalpha}[\mathrm{y}]( \mathrm{s}) E_{\upalpha}[\acute{\mathrm{y}}](\mathrm{s}).$$

Proof

Applying \(\mathbb{C}_{\mathcal{D}}\mathrm{ET}\) on Eq. (8), we have

$$ E_{\upalpha } \bigl[( \mathrm{y} * \acute{\mathrm{y}}) \bigr]( \mathrm{s}) = \mathrm{s} \int _{0}^{ \infty} e^{- \frac{ \nu ^{\upalpha}}{\upalpha \mathrm{s}}} \biggl( \int _{0}^{\nu} \mathrm{y} \biggl( \frac{\nu ^{\upalpha}}{ \upalpha} - \frac{\xi ^{\upalpha}}{ \upalpha} \biggr) \acute{\mathrm{y}} \biggl( \frac{\xi ^{\upalpha}}{ \upalpha} \biggr) \,\frac{ {\mathrm {d}} \xi}{\xi ^{1-\upalpha}} \biggr)\, \frac{ {\mathrm {d}} \nu}{\nu ^{1- \upalpha}}. $$
(12)

Let \(( \frac{ \nu ^{\upalpha}}{ \upalpha} - \frac{\xi ^{\upalpha}}{ \upalpha} ) = \frac{\mathrm{u}^{\upalpha}}{\upalpha}\), then we get

$$ E_{\upalpha } \bigl[ ( \mathrm{y}*\acute{\mathrm{y}} ) \bigr]( \mathrm{s}) = \mathrm{s} \int _{0}^{ \infty} \biggl( \int _{0}^{ \infty} e^{ -\frac{1}{\mathrm{s}} ( \frac{ \mathrm{u}^{\upalpha}}{ \upalpha} + \frac{ \xi ^{\upalpha }}{ \upalpha \upalpha} )} \mathrm{y} \biggl( \frac{\mathrm{u}^{\upalpha}}{ \upalpha} \biggr)\, \frac{ {\mathrm {d}} \mathrm{u}}{\mathrm{u}^{1- \upalpha}} \biggr) \acute{ \mathrm{y}} \biggl( \frac{ \xi ^{\upalpha}}{ \upalpha} \biggr) \,\frac{ {\mathrm {d}} \xi}{\xi ^{1-\upalpha}}, $$
(13)

which can be written as

$$ E_{\upalpha } \bigl[ (\mathrm{y}*\acute{\mathrm{y}}) \bigr]( \mathrm{s}) = \frac{1}{\mathrm{s}} E_{\upalpha}[\mathrm{y}]( \mathrm{s}) E_{\upalpha}[\acute{\mathrm{y}}](\mathrm{s}). $$
(14)

 □

Finally, we can define the inverse \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) as follows.

Definition 3.7

For a piece-wise continuous on \([0,\infty )\) and Con-exponentially bounded \(\mathrm{y}(\nu )\) whose \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) is \(\mathrm{Y}(\mathrm{s})\), we call \(\mathrm{y}(\nu )\) the inverse \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) of \(\mathrm{Y}(\mathrm{s})\) and write \(\mathrm{y}(\nu ) = E_{\upalpha}^{-1} [\mathrm{Y}(\mathrm{s})]\). Symbolically

$$ \mathrm{y}(\nu ) =E_{\upalpha}^{-1} \bigl[\mathrm{Y}( \mathrm{s})\bigr]\quad \iff\quad \mathrm{Y}(\mathrm{s}) =E_{\upalpha }\bigl[\mathrm{y}( \nu )\bigr]. $$
(15)

The inverse \(\mathbb{C}_{\mathcal{D}}\mathrm{ET}\) possesses a linear property as indicated in the following result.

Theorem 3.8

Given two ET, \(\mathrm{Y}(\mathrm{s})\) and \(\acute{\mathrm{Y}}(\mathrm{s})\) then,

$$ E_{\upalpha}^{-1} \bigl[\lambda _{1} \mathrm{Y}( \mathrm{s}) +\lambda _{2} \acute{\mathrm{Y}}(\mathrm{s}) \bigr] = \lambda _{1} E_{\upalpha}^{-1} \bigl[ \mathrm{Y}( \mathrm{s})\bigr] + \lambda _{2} E_{\upalpha}^{-1} \bigl[ \acute{\mathrm{Y}}(\mathrm{s})\bigr],$$

for any constants \(\lambda _{1}, \lambda _{2} \in \mathbb{R}\).

Proof

Suppose that \(E_{\upalpha }[\mathrm{y}(\nu )] = \mathrm{Y}(\mathrm{s})\) and \(E_{\upalpha }[\acute{\mathrm{y}}(\nu )]=\acute{\mathrm{Y}}( \mathrm{s})\). Since

$$\begin{aligned} E_{\upalpha } \bigl[\lambda _{1} \mathrm{y}(\nu ) + \lambda _{2} \acute{\mathrm{y}}(\nu ) \bigr](\mathrm{s}) & = \lambda _{1} E_{ \upalpha }\bigl[\mathrm{y}(\nu )\bigr](\mathrm{s}) + \lambda _{2} E_{\upalpha }\bigl[ \acute{\mathrm{y}}(\nu )\bigr] ( \mathrm{s}) \\ & = \lambda _{1} \mathrm{Y}(\mathrm{s}) + \lambda _{2} \acute{\mathrm{Y}}(\mathrm{s}), \end{aligned}$$

we have \(E_{\upalpha}^{-1} [\lambda _{1} \mathrm{Y}(\mathrm{s}) + \lambda _{2} \acute{\mathrm{Y}}(\mathrm{s}) ] = \lambda _{1} E_{ \upalpha}^{-1} [\mathrm{Y}(\mathrm{s})] + \lambda _{2} E_{\upalpha}^{-1} [\acute{\mathrm{Y}}(\mathrm{s})]\). □

Remark 3.3

It is easy to show that the relationship between \(\mathbb{C}_{\mathcal{D}}L\mathbb{T}\) and \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) is

$$ E_{\upalpha }\bigl[\mathrm{y}(\nu )\bigr](\mathrm{s}) = \mathrm{s} L_{ \mathbb{C}}^{ \upalpha} \bigl[\mathrm{y}(\nu )\bigr] \biggl( \frac{1}{\mathrm{s}} \biggr), \quad \mathrm{s}>0, 0 < \upalpha \leq 1.$$

4 Conformable Elzaki transform \(\mathrm{HP}\mathbb{M}\)

By solving for \(L_{\mathbb{C}}^{ \upalpha} \mathrm{y}(u,\nu )\), Eq. (1) can be written as

$$ L_{\mathbb{C}}^{ \upalpha} \mathrm{y}(u,\nu ) = \mathcal{H}(u, \nu ) - \mathcal{N}_{1} \bigl( \mathrm{y}(u,\nu ) \bigr) - \mathcal{N}_{2} \bigl( \mathrm{y}(u,\nu ) \bigr). $$
(16)

By implementing the \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) on both sides of the above equation, we get

$$ E_{\upalpha } \bigl[ L_{\mathbb{C}}^{ \upalpha} \mathrm{y}(u,\nu ) \bigr] = E_{\upalpha } \bigl[ \mathcal{H} (u,\nu ) - \mathcal{N}_{1} \bigl( \mathrm{y}(u,\nu ) \bigr) - \mathcal{N}_{2} \bigl( \mathrm{y}(u,\nu ) \bigr) \bigr]. $$
(17)

Using Remark 2.1, we get

$$ \frac{1}{\mathrm{s}} E_{\upalpha } \bigl[\mathrm{y}(u,\nu ) \bigr]( \mathrm{s} ) - \mathrm{s} \mathrm{y}(u,0) = E_{\upalpha } \bigl[ \mathrm{y}(u,\nu ) - \mathcal{N}_{1} \bigl( \mathrm{y}(u, \nu ) \bigr) - \mathcal{N}_{2} \bigl( \mathrm{y}(y,\nu ) \bigr) \bigr]. $$
(18)

After substituting the initial condition, the Eq. (1) can be re-written as

$$\begin{aligned} E_{\upalpha }\bigl[\mathrm{y}(u,\nu )\bigr](\mathrm{s}) ={} & \mathrm{s}^{2} \mathrm{y}(u) + \mathrm{s} E_{\upalpha } \bigl[ \mathcal{H}(u,\nu ) \bigr] \\ & {} - \mathrm{s} E_{\upalpha } \bigl[ \mathcal{N}_{1} \bigl( \mathrm{y}(u,\nu ) \bigr) \bigr] - \mathrm{s} E_{\upalpha } \bigl[ \mathcal{N}_{2} \bigl( \mathrm{y}(u,\nu ) \bigr) \bigr]. \end{aligned}$$
(19)

Finally, by applying inverse \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\), we get

$$ \mathrm{y}(u,\nu ) = \mathrm{Y}(u,t) - E_{\upalpha}^{-1} \bigl[ \mathrm{s} E_{\upalpha } \bigl[ \mathcal{N}_{1} \bigl( \mathrm{y}(u, \nu ) \bigr) + \mathcal{N}_{2} \bigl( \mathrm{y}(u,\nu ) \bigr) \bigr] \bigr], $$
(20)

where \(\mathrm{Y}(u,\nu )\) represents the term that has emerged from the source term and \(\mathbb{I}\mathbbm{.}\mathbb{C}\). The \(\mathrm{HP}\mathbb{M}\) suggests the solution \((u,\nu )\) to be decomposed into the infinite series of components [29, 30],

$$ \mathrm{y}(u,\nu ) = \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{y}_{n} (u,\nu ), $$
(21)

and non-linear term \(\mathcal{N}_{1} ( \mathrm{y}(u,\nu ) )\) is decomposed into

$$ \mathcal{N}_{1} \bigl( \mathrm{y}(u,\nu ) \bigr) = \sum _{n=0}^{ \infty} \mathrm{q}^{n} \mathrm{A}_{n} (\mathrm{y}), $$
(22)

for some He’s polynomials \(\mathrm{A}_{n} (\mathrm{y})\) [31, 32] given by

$$ \mathrm{A}_{n} (\mathrm{y}_{0}, \mathrm{y}_{1}, \dots , \mathrm{y}_{n} ) = \frac{1}{n!} \frac{ \partial ^{n}}{ \partial \mathrm{q}^{n}} \Biggl[ \mathcal{N}_{1} \Biggl( \sum _{i=0}^{\infty} \mathrm{q}^{i} \mathrm{y}_{i} \Biggr) \Biggr], \quad n=0,1,2,\dots . $$
(23)

Using Eqs. (19) and (20) in Eq. (18), we get

$$\begin{aligned} \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{y}_{n} (u,\nu ) = {}& \mathrm{P}_{0} (u,\nu ) - \mathrm{q} \Biggl( E_{\upalpha}^{-1} \Biggl[ \mathrm{s} E_{\upalpha } \Biggl[ \mathcal{N}_{2} \Biggl( \sum _{n=0}^{ \infty} \mathrm{q}^{n} \mathrm{y}_{n} (u, \nu ) \Biggr) \\ & {} + \sum_{n=0}^{ \infty} \mathrm{q}^{n} \mathrm{A}_{n} ( \mathrm{y}) \Biggr] \Biggr] \Biggr), \end{aligned}$$
(24)

which is the coupled \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) and \(\mathrm{HP}\mathbb{M}\) via He’s polynomials. The approximation can be easily obtained by comparing all like powers of the coefficients q as follows

$$\begin{aligned} \begin{aligned} \mathrm{q}^{0} & :\quad \mathrm{y}_{0} (u,\nu ) = \mathrm{P}_{0}(u, \nu ), \\ \mathrm{q}^{1} & :\quad \mathrm{y}_{1}(u,\nu ) = - E^{-1}_{\upalpha } \bigl[ \mathrm{s} E_{\upalpha} \bigl[ \bigl[ \mathcal{N}_{2} \mathrm{y}_{0}( u,\nu )\bigr] + \bigl[ \mathrm{A}_{0}(\mathrm{s}) \bigr] \bigr] \bigr], \\ \mathrm{q}^{2} & : \quad \mathrm{y}_{2}(u,\nu ) = - E^{-1}_{\upalpha } \bigl[ \mathrm{s} E_{\upalpha} \bigl[ \bigl[ \mathcal{N}_{2} \bigl( \mathrm{y}_{1}(u,\nu ) \bigr) \bigr] + \bigl[ \mathrm{A}_{1} ( \mathrm{s}) \bigr] \bigr], \bigr] \\ \mathrm{q}^{3} & :\quad \mathrm{y}_{3} (u,\nu ) = - E^{-1}_{\upalpha } \bigl[ \mathrm{s} E_{\upalpha} \bigl[ \bigl[ \mathcal{N}_{2} \bigl( \mathrm{y}_{2}(u,\nu ) \bigr) \bigr] + \bigl[ \mathrm{A}_{2} ( \mathrm{s} ) \bigr] \bigr] \bigr], \\ & \quad \dots . \end{aligned} \end{aligned}$$
(25)

Then the solution is

$$ \mathrm{y}(u,\nu ) = \sum_{n=0}^{ \infty} \mathrm{y}_{n} (u,\nu ) = \mathrm{y}_{0} (u,\nu ) + \mathrm{y}_{1} (u,\nu ) + \mathrm{y}_{2} (u, \nu )+ \cdots . $$
(26)

Finally, to authenticate the obtained solution, we will establish results on the uniqueness and convergence of the solution. To prove the results, we will consider the Banach space \([0,\tau _{\circ}]\) of all functions continuous on \([0,\tau _{\circ}]\) with supremum norm. Furthermore, we will assume that \(\mathrm{y}(u,\nu ), \mathrm{y}_{n}(u,\nu ) \in [0, \tau _{\circ}]\).

Theorem 4.1

(Uniqueness theorem)

The solution obtained by \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\mathrm{HP}\mathbb{M}\) of \(\mathbb{FPDE}s\) (14) has a unique solution, whenever \(0<\gamma <1\).

Proof

The solution of Eq. (14) is of the form \(\mathrm{y}(u,\nu ) = \sum_{n=0}^{\infty}\mathrm{q}^{n} \mathrm{y}_{n}(u,\nu )\), where

$$ \mathrm{y}(u,\nu ) =\mathrm{y}(u,0) + E^{-1}_{\upalpha} \bigl[ \mathrm{s} E_{\upalpha } \bigl[ \mathcal{H}(u,\nu ) - \mathcal{N}_{1} \bigl(\mathrm{y}(u,\nu ) \bigr) - \mathcal{N}_{2} \bigl( \mathrm{y}(u, \nu ) \bigr) \bigr] \bigr].$$

Let \(\mathrm{y}(u,\nu )\) & \(\acute{\mathrm{y}}(u,\nu )\) be two distinct solutions of Eq. (14), then we have

$$\begin{aligned} \bigl\lvert \mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u,\nu ) \bigr\rvert ={}& \bigl\vert - E^{-1}_{ \upalpha} \bigl[ \mathrm{s} E_{\upalpha } \bigl[ \mathcal{N}_{1} \bigl( \mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u, \nu ) \bigr) \\ &{} + \mathcal{N}_{2} \bigl( \mathrm{y}(u,\nu ) - \acute{ \mathrm{y}}(u,\nu ) \bigr) \bigr] \bigr] \bigr\vert . \end{aligned}$$

Using Theorem 3.4, we get

$$\begin{aligned} \bigl\vert \mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u,\nu ) \bigr\vert \leq {}& \int _{0}^{\nu} \bigl( \bigl\vert \mathcal{N}_{1} \bigl( \mathrm{y}(u, \nu ) - \acute{\mathrm{y}}(u,\nu ) \bigr) \bigr\vert \\ & {} + \bigl\vert \mathcal{N}_{2} \bigl( \mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u,\nu ) \bigr) \bigr\vert \bigr) \biggl\vert \biggl( \frac{\nu ^{\upalpha}}{ \upalpha} - \frac{\xi ^{\upalpha}}{ \upalpha} \biggr) \biggr\vert \,\frac{ {\mathrm {d}} \xi}{\xi ^{1-\upalpha}}. \end{aligned}$$

We now assume that \(\mathcal{N}_{1}\) and \(\mathcal{N}_{2}\) satisfy the Lipschitz condition, so \(\mathcal{N}_{2}\) is a bounded operator with

$$ \bigl\vert \mathcal{N}_{2} \bigl( \mathrm{y}(u,\nu ) \bigr) - \mathcal{N}_{2} \bigl( \acute{\mathrm{y}}(u,\nu ) \bigr) \bigr\vert \leq \lambda _{1} \bigl\vert \mathrm{y}(u,\nu ) - \acute{ \mathrm{y}}(u, \nu ) \bigr\vert ,$$

for \(\lambda _{1}>0\), and \(\mathcal{N}_{1}\) is given by

$$ \bigl\vert \mathcal{N}_{1} \bigl( \mathrm{y}(u,\nu ) \bigr) - \mathcal{N}_{1} \bigl( \acute{\mathrm{y}}(u,\nu ) \bigr) \bigr\vert \leq \lambda _{2} \bigl\vert \mathrm{y}(u,\nu ) - \acute{ \mathrm{y}}(u, \nu ) \bigr\vert ,$$

for \(\lambda _{2}>0\). Then the above equation can be written as

$$\begin{aligned} \bigl\vert \mathrm{y}(u, \nu ) - \acute{\mathrm{y}}(u,\nu ) \bigr\vert \leq{}& \int _{0}^{\nu} \bigl( \lambda _{1} \bigl\vert \mathrm{y}(u, \nu ) - \acute{\mathrm{y}}(u,\nu ) \bigr\vert \\ & {} + \lambda _{2} |\mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u, \nu ) \bigr) \biggl\vert \biggl( \frac{\nu ^{\upalpha}}{\upalpha} - \frac{\xi ^{\upalpha}}{ \upalpha} \biggr) \biggr\vert \,\frac{ {\mathrm {d}} \xi }{\xi ^{1-\upalpha}}. \end{aligned}$$

Now, using mean value theorem of Con-integral calculus [33],

$$ \bigl\vert \mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u,\nu ) | \bigr\vert \leq ( \lambda _{1} + \lambda _{2}) \bigl\vert \mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u,\nu ) \bigr\vert \frac{\breve{M} \tau _{\circ}^{\upalpha}}{ \upalpha},$$

where

$$ \breve{M} = \max \biggl\{ \frac{\nu ^{\upalpha}}{ \upalpha} - \frac{\tau ^{\upalpha}}{ \upalpha} : \forall \nu \in [0,\tau _{0}] \biggr\} .$$

Hence

$$ \bigl\vert \mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u,\nu ) \bigr\vert \leq \bigl\vert \mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u,\nu ) \bigr\vert \gamma ,$$

where \(\gamma = ( \lambda _{1}+\lambda _{2} ) \frac{\breve{M}\tau _{\circ}^{\upalpha}}{\upalpha}\). So, \((1 - \gamma )| \mathrm{y}(u,\nu ) - \acute{\mathrm{y}}(u,\nu ) | \leq 0\), implies \(\mathrm{y}(u,\nu ) = \acute{\mathrm{y}}(u,\nu )\) whenever, \(0<\gamma <1\). □

Theorem 4.2

Assume that initial guess \(\mathrm{y}_{0}\) remains inside the ball \(\pmb{B}(\mathrm{y},r)\) of the solution \(\mathrm{y}(u,\nu )\). Then, the series solution \(\sum_{n=0}^{\infty} \mathrm{y}_{n}\) is convergent if \(\exists \epsilon \in (0,1)\) such that \(\lVert \mathrm{y}_{n+1} \rVert \leq \epsilon \lVert \mathrm{y}_{n} \rVert \).

Proof

We need to prove that partial sums \({s_{n}}= \sum_{n=0}^{n}\mathrm{y}_{n}\) is a Cauchy sequence in \((C[0,\tau _{\circ}], \lVert \cdot \rVert )\). As

$$\begin{aligned} \lVert s_{n+1} - s_{n} \rVert \leq \lVert \mathrm{y}_{n+1} \rVert & \leq \epsilon \lVert \mathrm{y}_{n} \rVert \leq \epsilon ^{2} \lVert \mathrm{y}_{n-1} \rVert \leq \cdots \leq \epsilon ^{n+1} \lVert \mathrm{y}_{o} \rVert , \end{aligned}$$

Hence

$$\begin{aligned} \lVert s_{n} - s_{m} \rVert &\leq \Biggl\lVert \sum _{i=m+1}^{n} \mathrm{y}_{i} \Biggr\rVert \leq \sum_{i = m+1}^{n} \lVert \mathrm{y}_{i} \rVert \leq \epsilon ^{m+1} \sum_{i=0}^{n-m-1} \epsilon ^{i} \lVert \mathrm{y}_{0} \rVert \\ & \leq \epsilon ^{m+1} \frac{1-\epsilon ^{m-n}}{ 1-\epsilon} \lVert \mathrm{y}_{0} \rVert , \quad \forall m,n \in \mathbb{N}, (n\geq m). \end{aligned}$$

Since \(\epsilon \in (0,1)\), hence

$$ \lVert s_{n}-s_{m} \rVert \leq \frac{\epsilon ^{m+1}}{1-\epsilon} \lVert \mathrm{y}_{0} \rVert ,$$

\(\mathrm{y}_{0}\) is also bounded; therefore, \(\lVert s_{n}-s_{m} \rVert \to 0\) as \(m,n \to \infty \). Hence \(s_{n}\) is a Cauchy sequence in \((C[0,\tau _{\circ}], \lVert \cdot \rVert )\), so \(\sum_{n=0}^{\infty} \mathrm{y}_{n}(u,\nu )\) is convergent. □

Remark 4.1

Note that th \(\frac{\epsilon ^{m+1}}{1-\epsilon} \lVert \mathrm{y}_{0} \rVert \) is the maximum truncation error of \(\mathrm{y}(u,\nu )\).

5 Applications of the proposed technique

In this section, we apply the \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\mathrm{HP}\mathbb{M}\) for solving \(\mathbb{N}\mathbbm{-}\mathbb{TFPDE}s\).

Example 5.1

Consider \(\mathbb{N}\mathbbm{-}\mathbb{TFPDE}s\) as follows

$$ \textstyle\begin{cases} \frac{\partial ^{\upalpha }\mathrm{y}}{\partial \nu ^{\upalpha}} + \mathrm{y}(u,\nu )\frac{\partial \mathrm{y}}{\partial u}=0,& \nu \geq 0, 0< \upalpha \leq 1, \\ \mathbb{I}\mathbbm{.}\mathbb{C}\mathbbm{.}:\quad \mathrm{y}(u,0)=-u. & \end{cases} $$
(27)

If \(\upalpha = 1\), then Eq. (25) becomes the classical \(\mathbb{N}\mathbbm{-}\mathbb{PDE}\) [20]. By taking \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) on both sides of the equation and from the properties of \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\), Eq. (25) reduces to

$$ E_{\upalpha }\bigl[\mathrm{y}(u,\nu )\bigr](\mathrm{s}) = \mathrm{y}(u,0) \mathrm{s}^{2} - \mathrm{s} E_{\upalpha } \biggl[\mathrm{y} \frac{\partial \mathrm{y}}{\partial u} \biggr]. $$
(28)

Using \(\mathbb{I}\mathbbm{.}\mathbb{C}\) and inverse \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\), we have

$$ \mathrm{y}(u,\nu ) = -u- E_{\upalpha}^{-1} \biggl[ \mathrm{s} E_{ \upalpha } \biggl[ \mathrm{y} \frac{\partial \mathrm{y}}{\partial u} \biggr] \biggr]. $$
(29)

After applying the \(\mathrm{HP}\mathbb{M}\), we have

$$ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{y}_{n} = -u - \mathrm{q} \Biggl( E_{\upalpha}^{-1} \Biggl[ \mathrm{s} E_{\upalpha } \Biggl[ \sum_{n=0}^{ \infty} \mathrm{q}^{n} \mathrm{A}_{n} (\mathrm{y}) \Biggr] \Biggr] \Biggr), $$
(30)

where

$$ \sum_{n=0}^{ \infty} \mathrm{q}^{n} \mathrm{A}_{n} (\mathrm{y}) = \mathrm{y}\frac{\partial \mathrm{y}}{\partial u}.$$

Here, \(\mathrm{A}_{n} (\mathrm{y})\) are He’s polynomials that represent the non-linear term. So, we have the first few components of He’s polynomials

$$\begin{aligned} \mathrm{A}_{0} (\mathrm{y}) & =\mathrm{y}_{0} \frac{\partial \mathrm{y}_{0}}{\partial u}, \\ \mathrm{A}_{1} (\mathrm{y}) & = 2 \mathrm{y}_{0} \frac{\partial \mathrm{y}_{1}}{ \partial u} +\mathrm{y}_{0} \frac{\partial ^{2} \mathrm{y}_{1}}{\partial u^{2}} + \mathrm{y}_{1} \frac{\partial ^{2} \mathrm{y}_{0}}{ \partial u^{2}}, \\ \mathrm{A}_{2} (\mathrm{y}) & =2 \mathrm{y}_{0} \frac{\partial \mathrm{y}_{1}}{ \partial u} + \biggl( \frac{\partial \mathrm{y}_{1}}{\partial u} \biggr)^{2} + \mathrm{y}_{0} \frac{\partial ^{2} \mathrm{y}_{2}}{ \partial u^{2}} + \mathrm{y}_{2} \frac{\partial ^{2} \mathrm{y}_{0}}{\partial u^{2}} + \mathrm{y}_{1} \frac{\partial ^{2} \mathrm{y}_{1}}{\partial u^{2}}, \end{aligned}$$

and so on. Comparing the coefficients of like power of q, we get

$$\begin{aligned} \begin{aligned} \mathrm{q}^{0} :\quad \mathrm{y}_{0}(u, \nu ) &= -u, \\ \mathrm{q}^{1} :\quad \mathrm{y}_{1}(u,\nu ) & = - E^{-1}_{\upalpha } \bigl[ \mathrm{s} E_{\upalpha} \bigl[ \mathrm{A}_{0}(\mathrm{y}) \bigr] \bigr] = -E^{-1}_{\upalpha } \biggl[ \mathrm{s} E_{\upalpha} \biggl[ \mathrm{y}_{0} \frac{\partial \mathrm{y}_{0}}{\partial u} \biggr] \biggr] = -u\frac{\nu ^{\upalpha}}{ \upalpha}, \\ \mathrm{q}^{2} :\quad \mathrm{y}_{2}( u,\nu ) & = - E^{-1}_{\upalpha } \bigl[ \mathrm{s} E_{\upalpha} \bigl[ \mathrm{A}_{1}( \mathrm{y}) \bigr] \bigr] \\ & = -E^{-1}_{\upalpha } \biggl[\mathrm{s} E_{\upalpha} \biggl[ \mathrm{y}_{0} \frac{\partial \mathrm{y}_{1}}{\partial u} + \mathrm{y}_{1} \frac{\partial \mathrm{y}_{0}}{\partial u} \biggr] \biggr] = -u \biggl(\frac{ \nu ^{\upalpha}}{ \upalpha} \biggr)^{2}, \\ \mathrm{q}^{3} : \quad \mathrm{y}_{3}(u,\nu ) & = - E^{-1}_{\upalpha } \bigl[ \mathrm{s} E_{\upalpha} \bigl[ \mathrm{A}_{2}(\mathrm{y}) \bigr] \bigr] \\ & =-E^{-1}_{\upalpha} \biggl[ \mathrm{s}E_{ \upalpha} \biggl[\mathrm{y}_{0} \frac{\partial \mathrm{y}_{2}}{\partial u}+\mathrm{y}_{1} \frac{\partial \mathrm{y}_{1}}{\partial u} + \mathrm{y}_{2} \frac{\partial \mathrm{y}_{0}}{\partial u} \biggr] \biggr] = -u \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{3}. \end{aligned} \end{aligned}$$
(31)

Similarly, the approximations may be obtained in the following way

$$\begin{aligned} \mathrm{q}^{4} :\quad \mathrm{y}_{4} (u,\nu ) & = -u \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{4}, \end{aligned}$$
(32)
$$\begin{aligned} \mathrm{q}^{5} : \quad \mathrm{y}_{5} (u, \nu ) & = -u \biggl( \frac{ \nu ^{\upalpha}}{\upalpha} \biggr)^{5}, \end{aligned}$$
(33)

and so on. Substituting Eqs. (31) and (32) in the following equation

$$ \mathrm{y}(u,\nu ) = \sum_{n=0}^{\infty} \mathrm{y}_{n} (u,\nu ) = \mathrm{y}_{0} (u,\nu ) + \mathrm{y}_{1} (u,\nu ) + \mathrm{y}_{2} (u, \nu ) + \mathrm{y}_{3} (u,\nu )+ \cdots , $$
(34)

we get

$$\begin{aligned} \mathrm{y}(u,\nu ) & = -u \biggl(1 + \frac{\nu ^{\upalpha}}{\upalpha} + \biggl( \frac{ \nu ^{\upalpha}}{ \upalpha} \biggr)^{2} + \biggl( \frac{ \nu ^{\upalpha}}{\upalpha} \biggr)^{3} + \biggl( \frac{ \nu ^{\upalpha}}{ \upalpha} \biggr)^{4} + \cdots \biggr) \\ & = \frac{u}{\frac{\nu ^{\upalpha}}{\upalpha}-1},\quad \forall \nu \in [ 0, \upalpha ^{\frac{1}{ \upalpha}} ). \end{aligned}$$
(35)

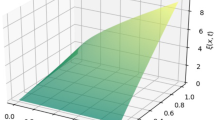
The numerical solution for various values of α, i.e., for \(\upalpha =0.5, 0.7\), is given in Fig. 1. For \(\upalpha =1\) as a special case, we have the solution, \(\mathrm{y}(u,\nu )= \frac{u}{\nu -1} \), which is the same solution as in [20].

Figure 1
figure 1

Numerical solution using \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\mathrm{HP}\mathbb{M}\) in Example 5.1 for \(\upalpha =0.5, 0.7\)

Full size image

Example 5.2

Consider \(\mathbb{N}\mathbbm{-}\mathbb{TFPDE}\) as follows

$$ \textstyle\begin{cases} \frac{\partial ^{\upalpha }\mathrm{y}(u,\nu )}{\partial \nu ^{\upalpha}} = ( \frac{\partial \mathrm{y}(u,\nu )}{\partial y} )^{2} + \mathrm{y}(u,\nu ) \frac{\partial ^{2} \mathrm{y}(u,\nu )}{\partial u^{2}},& \nu \geq 0, 0< \upalpha \leq 1, \\ \mathbb{I}\mathbbm{.}\mathbb{C}\mathbbm{.}:\quad \mathrm{y}(u,0)=u^{2}. \end{cases} $$
(36)

If \(\upalpha =1\), then for \(m=1\), Eq. (36) becomes the classical porous medium equation \(\mathbb{PDE}\) [24], given by

$$ \frac{\partial \mathrm{y}(u,\nu )}{\partial \nu} = \frac{\partial}{\partial u} \biggl(\mathrm{y}(u,\nu )^{m} \frac{\partial \mathrm{y}(u,\nu )}{\partial u} \biggr). $$

Taking \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) on both sides of the Eq. (36) and using properties of \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\), we have

$$ E_{\upalpha }\bigl[\mathrm{y}(u,\nu )\bigr](\mathrm{s}) = \mathrm{y}(u,0) \mathrm{s}^{2} + \mathrm{s} E_{\upalpha } \biggl[ \biggl( \frac{\partial \mathrm{y}}{ \partial u} \biggr)^{2} + \mathrm{y} \frac{\partial ^{2} \mathrm{y}}{\partial u^{2} } \biggr]. $$
(37)

Applying inverse \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) subject to the \(\mathbb{I}\mathbbm{.}\mathbb{C}\mathbbm{.}\), we get

$$ \mathrm{y}(u,\nu )=u^{2} + E_{\upalpha}^{-1} \biggl[ \mathrm{s} E_{ \upalpha } \biggl[ \biggl(\frac{\partial \mathrm{y}}{ \partial u} \biggr)^{2} + \mathrm{y} \frac{\partial ^{2} \mathrm{y}}{ \partial u^{2} } \biggr] \biggr]. $$
(38)

With the help of \(\mathrm{HP}\mathbb{M}\), the above equation can be written as

$$ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{y}_{n} = u^{2} + \mathrm{q} \Biggl( E_{\upalpha}^{-1} \Biggl[ \mathrm{y} E_{\upalpha } \Biggl[ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{A}_{n} ( \mathrm{y}) \Biggr] \Biggr] \Biggr), $$
(39)

where

$$ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{A}_{n} (\mathrm{y}) = \biggl(\frac{\partial \mathrm{y}}{ \partial u} \biggr)^{2} + \mathrm{y} \frac{\partial ^{2} \mathrm{y}}{\partial u^{2} }.$$

Here, \(\mathrm{A}_{n} (\mathrm{y})\) are He’s polynomials that represent the non-linear term. The first few terms of He’s polynomials are

$$\begin{aligned} \mathrm{A}_{0} (\mathrm{y}) & = \biggl( \frac{\partial \mathrm{y}_{0}}{\partial u} \biggr)^{2} + \mathrm{y}_{0} \frac{\partial ^{2} \mathrm{y}_{0}}{\partial u^{2} }, \\ \mathrm{A}_{1} (\mathrm{y}) & = 2 \frac{\partial \mathrm{y}_{0}}{\partial u} \frac{\partial \mathrm{y}_{1}}{\partial u} + \mathrm{y}_{0} \frac{\partial ^{2} \mathrm{y}_{1}}{\partial u^{2} } + \mathrm{y}_{1} \frac{\partial ^{2} \mathrm{y}_{0}}{\partial u^{2} }, \\ \mathrm{A}_{2} (\mathrm{y})& = 2 \frac{\partial \mathrm{y}_{0}}{\partial u} \frac{\partial \mathrm{y}_{2}}{\partial u}+ \biggl( \frac{\partial \mathrm{y}_{1}}{\partial u} \biggr)^{2} + \mathrm{y}_{0} \frac{\partial ^{2} \mathrm{y}_{2}}{\partial u^{2} } +u_{2} \frac{\partial ^{2} \mathrm{y}_{0}}{\partial u^{2} } + \mathrm{y}_{1} \frac{\partial ^{2} \mathrm{y}_{1}}{\partial u^{2} }, \end{aligned}$$

and so on. The like powers of the coefficient, q can be equated as

$$\begin{aligned} \begin{aligned} \mathrm{q}^{0} : \quad \mathrm{y}_{0}(u, \nu ) ={}& u^{2}, \\ \mathrm{q}^{1} : \quad \mathrm{y}_{1}( u,\nu ) ={}& E^{-1}_{\upalpha } \bigl[\mathrm{s} E_{\upalpha} \bigl[ \mathrm{A}_{0}(\mathrm{y}) \bigr] \bigr] \\ ={}& E^{-1}_{\upalpha } \biggl[\mathrm{s} E_{\upalpha} \biggl[ \biggl( \frac{\partial \mathrm{y}_{0}}{\partial u} \biggr)^{2} + \mathrm{y}_{0} \frac{\partial ^{2} \mathrm{y}_{0}}{\partial u^{2}} \biggr] \biggr] = 6 u^{2} \frac{\nu ^{\upalpha}}{\upalpha}, \\ \mathrm{q}^{2} :\quad \mathrm{y}_{2}( u,\nu ) ={}& E^{-1}_{\upalpha } \bigl[ \mathrm{s} E_{\upalpha} \bigl[ \mathrm{A}_{1}(\mathrm{y}) \bigr] \bigr] \\ ={}& E^{-1}_{\upalpha } \biggl[\mathrm{s} E_{\upalpha} \biggl[2 \frac{\partial \mathrm{w}_{0}}{\partial x} \frac{\partial \mathrm{w}_{1}}{\partial x} + \mathrm{w}_{0} \frac{ \partial ^{2} \mathrm{w}_{1}}{ \partial x^{2} } + \mathrm{w}_{1} \frac{\partial ^{2} \mathrm{w}_{0}}{\partial x^{2} } \biggr] \biggr] \\ ={}& 36 u^{2} \biggl(\frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{2}, \\ \mathrm{q}^{3} : \quad \mathrm{y}_{3}(u,\nu ) = {}& E^{-1}_{\upalpha } \bigl[ \mathrm{s} E_{\upalpha} \bigl[ \mathrm{A}_{2}(\mathrm{y}) \bigr] \bigr] \\ = {}& E^{-1}_{\upalpha } \biggl[ \mathrm{s} E_{\upalpha} \biggl[2 \frac{\partial \mathrm{w}_{0}}{ \partial x} \frac{\partial \mathrm{w}_{2}}{ \partial x} + \biggl( \frac{\partial \mathrm{w}_{1}}{\partial x} \biggr)^{2} + \mathrm{w}_{0} \frac{\partial ^{2} \mathrm{w}_{2}}{\partial x^{2} } \\ & {} +\mathrm{w}_{2} \frac{\partial ^{2} \mathrm{w}_{0}}{\partial x^{2} } + \mathrm{w}_{1} \frac{\partial ^{2} \mathrm{w}_{1}}{\partial x^{2} } \biggr] \biggr] \\ ={}&216 u^{2} \biggl(\frac{ \nu ^{\upalpha}}{\upalpha} \biggr)^{3}. \end{aligned} \end{aligned}$$
(40)

Similarly, the approximations may be obtained in the following way

$$\begin{aligned} \mathrm{q}^{4} :\quad \mathrm{y}_{4} (u,\nu ) & = 6^{4} u^{2} \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{4}, \end{aligned}$$
(41)
$$\begin{aligned} \mathrm{q}^{5} :\quad \mathrm{y}_{5} (u,\nu ) & = 6^{5} u^{2} \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{5}, \end{aligned}$$
(42)

and so on. Substituting Eqs. (40) and (41) in the following equation

$$ \mathrm{y}(u,\nu ) = \sum_{n=0}^{\infty} \mathrm{y}_{n} (u,\nu ) = \mathrm{y}_{0} (u,\nu )+ \mathrm{y}_{1} (u,\nu )+\mathrm{y}_{2} (u, \nu )+ \mathrm{y}_{3}(u,\nu )+\cdots , $$
(43)

we have

$$\begin{aligned} \mathrm{y}(u,\nu ) & = u^{2} \biggl(1 + \frac{6\nu ^{\upalpha}\upalpha}{ \upalpha} + \biggl( \frac{6\nu ^{\upalpha}}{ \upalpha} \biggr)^{2} + \biggl( \frac{6\nu ^{\upalpha}}{\upalpha} \biggr)^{3} + \biggl( \frac{6 \nu ^{\upalpha}}{ \upalpha} \biggr)^{4}+ \cdots \biggr) \\ & = \frac{u^{2}}{1- \frac{6\nu ^{\upalpha}}{\upalpha}}, \quad \forall \nu \in \biggl[0, \biggl( \frac{\upalpha}{6}\biggr)^{ \frac{1}{\upalpha}} \biggr). \end{aligned}$$
(44)

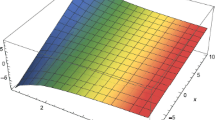
The numerical solution for different values of α, i.e., for \(\upalpha =0.5, 0.7\), is presented in Fig. 2. For \(\upalpha =1\), we have the classical solution subject to \(\mathbb{I}\mathbbm{.}\mathbb{C}\mathbbm{.}\), of the Eq. (36) as

$$ \mathrm{y}(u,\nu ) =\frac{u^{2}}{1-6\nu}, $$
(45)

which is the same solution as in [24].

Figure 2
figure 2

Numerical solution using \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\mathrm{HP}\mathbb{M}\) in Example 5.2 for \(\upalpha =0.5, 0.7\)

Full size image

Example 5.3

Consider the time-fractional non-dimensional Fisher equation

$$ \textstyle\begin{cases} \frac{\partial ^{\upalpha }\mathrm{y}(u,\nu )}{\partial \nu ^{\upalpha}} = \frac{\partial ^{2} \mathrm{y}(u,\nu ) }{ \partial u^{2}} + \mathrm{y}(u,\nu ) ( 1 -\mathrm{y}(u,\nu ) ),& \nu \geq 0, 0< \upalpha \leq 1 , \\ \mathbb{I}\mathbbm{.}\mathbb{C}\mathbbm{.}: \quad \mathrm{y}(u,0)=\lambda . \end{cases} $$
(46)

For \(\upalpha =1\), we have the classical non-dimensional Fisher equations [34] as follows

$$ \frac{\partial \mathrm{y}(u,\nu )}{\partial \nu} = \frac{\partial ^{2} \mathrm{y}(u,\nu ) }{\partial u^{2}} + \mathrm{y}(u, \nu ) \bigl( 1 - \mathrm{y}(u,\nu )\bigr). $$
(47)

Taking \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) on both sides of the Eq. (46) and using the properties of \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\), we have

$$ \biggl(\frac{1}{s}-1 \biggr)E_{\upalpha }\bigl[y(u,v) \bigr]=y(u,0)s+E_{\upalpha } \biggl[\frac{\partial ^{2} y}{\partial u^{2}}-y^{2} \biggr]. $$
(48)

By rearranging all the terms appropriately, the above equation becomes

$$ E_{\upalpha }\bigl[\mathrm{y}(u,\nu )\bigr] = \mathrm{y}(u,0) \biggl( \frac{\mathrm{s}^{2}}{1-\mathrm{s}} \biggr) + \biggl( \frac{\mathrm{s}}{1-\mathrm{s}} \biggr) E_{\upalpha } \biggl[ \frac{\partial ^{2} \mathrm{y}}{\partial u^{2}} - \mathrm{y} \biggr]. $$
(49)

Using \(\mathbb{I}\mathbbm{.}\mathbb{C}\mathbbm{.}\) and inverse \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\), we reduce Eq. (49) to

$$ \mathrm{y}(u,\nu ) =\lambda e^{\frac{\nu ^{\upalpha}}{\upalpha}} + E^{-1}_{ \upalpha } \biggl[ \biggl( \frac{\mathrm{s}}{1-\mathrm{s}} \biggr) E_{ \upalpha } \biggl[ \frac{\partial ^{2} \mathrm{y}}{ \partial u^{2}} - \mathrm{y}^{2} \biggr] \biggr]. $$
(50)

After successful application of the \(\mathrm{HP}\mathbb{M}\), we get

$$ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{y}_{n} = \lambda e^{ \frac{\nu ^{\upalpha}}{\upalpha}} + \mathrm{q} \Biggl(E_{\upalpha}^{-1} \Biggl[ \biggl(\frac{\mathrm{s}}{1-\mathrm{s}} \biggr) E_{\upalpha } \Biggl[ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{A}_{n} (\mathrm{y}) \Biggr] \Biggr] \Biggr),$$

where

$$ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{A}_{n} (\mathrm{y}) = \frac{\partial ^{2} \mathrm{y}}{\partial u^{2}} - \mathrm{y}^{2}.$$

Here, \(\mathrm{A}_{n} (\mathrm{y})\) are He’s polynomials that represent the non-linear terms, and the first three components of He’s polynomials are

$$\begin{aligned} \mathrm{A}_{0} (\mathrm{y}) & = \frac{\partial ^{2} \mathrm{y}_{0}}{\partial u^{2}}- \mathrm{y}_{0}^{2}, \\ \mathrm{A}_{1} (\mathrm{y}) & = \frac{\partial ^{2} \mathrm{y}_{1}}{\partial u^{2} }-2 \mathrm{y}_{0} \mathrm{y}_{1}, \\ \mathrm{A}_{2} (\mathrm{y}) & = \frac{\partial ^{2} \mathrm{y}_{2}}{\partial u^{2} }- \mathrm{y}^{2}_{1} - 2\mathrm{y}_{0} \mathrm{y}_{2} \end{aligned}$$

and so on. Comparing like powers of the coefficient q, we get

$$\begin{aligned} \begin{aligned} \mathrm{q}^{0} : \quad \mathrm{y}_{0}(u, \nu ) & = \lambda e^{ \frac{\nu ^{\upalpha}}{\upalpha}} , \\ \mathrm{q}^{1} : \quad \mathrm{y}_{1}( u,\nu ) & = E^{-1}_{\upalpha } \biggl[ \biggl(\frac{\mathrm{s}}{1-\mathrm{s}} \biggr) E_{\upalpha }\bigl[ \mathrm{A}_{0} (\mathrm{y})\bigr] \biggr] \\ & = E^{-1}_{\upalpha} \biggl[ \biggl( \frac{\mathrm{s}}{1-\mathrm{s}} \biggr) E_{\upalpha } \biggl[ \frac{\partial ^{2} \mathrm{y}_{0}}{ \partial u^{2}} - \mathrm{y}_{0}^{2} \biggr] \biggr] = -\lambda ^{2} e^{\frac{ \nu ^{\upalpha}}{\upalpha}} \bigl(e^{ \frac{\nu ^{\upalpha}}{ \upalpha}}-1 \bigr) , \\ \mathrm{q}^{2} : \quad \mathrm{y}_{2}(u,\nu ) & = E^{-1}_{\upalpha } \biggl[ \biggl(\frac{\mathrm{s}}{1-\mathrm{s}} \biggr) E_{\upalpha }\bigl[ \mathrm{A}_{1} (\mathrm{y})\bigr] \biggr] \\ & = E^{-1}_{\upalpha } \biggl[ \biggl( \frac{\mathrm{s}}{1-\mathrm{s}} \biggr) E_{\upalpha } \biggl[ \frac{\partial ^{2} \mathrm{y}_{1}}{ \partial u^{2} }-2 \mathrm{y}_{0} \mathrm{y}_{1} \biggr] \biggr] =\lambda ^{3} e^{ \frac{\nu ^{\upalpha}}{\upalpha}} \bigl(e^{ \frac{\nu ^{\upalpha}}{\upalpha}}-1 \bigr)^{2} , \\ \mathrm{q}^{3} : \quad \mathrm{y}_{3}(u,\nu ) & = E^{-1}_{\upalpha} \biggl[ \biggl(\frac{\mathrm{s}}{1-\mathrm{s}} \biggr) E_{\upalpha }\bigl[ \mathrm{A}_{2} (\mathrm{y})\bigr] \biggr] \\ & = E^{-1}_{\upalpha } \biggl[ \biggl(\frac{\mathrm{s}}{1-\mathrm{s}} \biggr) E_{\upalpha } \biggl[ \frac{\partial ^{2} \mathrm{y}_{2}}{ \partial u^{2} } - \mathrm{y}^{2}_{1} - 2 \mathrm{y}_{0} \mathrm{y}_{2} \biggr] \biggr] \\ & = - \lambda ^{4}e^{ \frac{\nu ^{\upalpha}}{ \upalpha}} \bigl( e^{ \frac{\nu ^{\upalpha}}{ \upalpha}}-1 \bigr)^{3}. \end{aligned} \end{aligned}$$
(51)

Similarly, the approximations may be obtained in the following way

$$\begin{aligned} \begin{aligned} \mathrm{q}^{4} :\quad \mathrm{y}_{4} (u,\nu ) & = \lambda ^{5}e^{ \frac{\nu ^{\upalpha}}{\upalpha}} \bigl(e^{ \frac{\nu ^{\upalpha}}{\upalpha}}-1 \bigr)^{4} , \\ \mathrm{q}^{5} :\quad \mathrm{y}_{5} (u,\nu ) & = - \lambda ^{6} e^{ \frac{ \nu ^{\upalpha}}{\upalpha}} \bigl(e^{ \frac{\nu ^{\upalpha}}{\upalpha}} - 1 \bigr)^{5}, \end{aligned} \end{aligned}$$
(52)

and so on. Using Eqs. (51) and (52) in the following equation

$$ \mathrm{y}(u,\nu )= \sum_{n=0}^{\infty} \mathrm{y}_{n} (u,\nu ) = \mathrm{y}_{0} (u,\nu ) + \mathrm{y}_{1} (u,\nu ) + \mathrm{y}_{2} (u, \nu ) + \mathrm{y}_{3} (u,\nu ) +\cdots , $$

we get

$$\begin{aligned} \mathrm{y}(u,\nu ) ={} &\lambda e^{\frac{\nu ^{\upalpha}}{ \upalpha}} \bigl( 1 - \lambda \bigl( e^{\frac{\nu ^{\upalpha}}{ \upalpha}} - 1 \bigr) + \lambda ^{2} \bigl(e^{\frac{\nu ^{\upalpha}}{ \upalpha}} - 1 \bigr)^{2} + \lambda ^{3} \bigl(e^{ \frac{\nu ^{\upalpha }\upalpha}{ \upalpha }} - 1 \bigr)^{3} \\ & {} + \lambda ^{4} \bigl(e^{ \frac{\nu ^{\upalpha}\upalpha}{ \upalpha}}-1 \bigr)^{4} + \cdots \bigr) \\ ={}& \frac{\lambda e^{ \frac{\nu ^{\upalpha}}{\upalpha}}}{ 1 + \lambda (e^{ \frac{\nu ^{\upalpha}}{ \upalpha}}-1 )}, \quad \forall \nu \geq 0, \end{aligned}$$
(53)

such that \(| \lambda (e^{\frac{\nu ^{\upalpha}}{\upalpha}}-1)| <1\). The numerical solution for different values of α and λ, i.e., for \(\upalpha =0.5, 0.7\) and \(\lambda =0.1, 0.5\), is given in Fig. 3. For \(\upalpha =1\) as a special case, we have the classical solution of the problem as follows:

$$ \mathrm{y}(u,\nu )= \frac{\lambda e^{\nu}}{1 +\lambda (e^{\nu}-1 )}{, }$$

which is the same solution in [34].

Figure 3
figure 3

Numerical solution using \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\mathrm{HP}\mathbb{M}\) in Example 5.3 for \(\upalpha =0.5, 0.7\) and \(\lambda =0.1, 0.5\)

Full size image

Example 5.4

Consider the time-fractional (2 + 1)-dimensional Burger equation

$$ \textstyle\begin{cases} \frac{\partial ^{\upalpha }\mathrm{y}(u,w,\nu )}{ \partial t^{\upalpha}}+w(x,y,t) \frac{\partial \mathrm{y}(u,w,\nu )}{ \partial u} & \\ \quad{} + \mathrm{y}(u,w,\nu ) \frac{\partial \mathrm{y}(u,w,\nu )}{ \partial w} - \epsilon ( \frac{\partial ^{2} \mathrm{y}(u,w,\nu )}{\partial u^{2} } + \frac{\partial ^{2} \mathrm{y}(u,w,\nu )}{\partial w^{2}} )=0,& \nu \geq 0, 0< \upalpha \leq 1, \\ \mathbb{I}\mathbbm{.}\mathbb{C}\mathbbm{.},\quad \mathrm{y}(u,w,0)=u+w. \end{cases} $$
(54)

If we put \(\upalpha =1\), we have the classical (2 + 1)-dimensional Burger equation [35]. Taking \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) on both sides of the Eq. (54) and using properties of \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\), we have

$$ E_{\upalpha }\bigl[\mathrm{y}(u,w,\nu )\bigr](\mathrm{s})=\mathrm{y}(u,w,0) \mathrm{s}^{2} -\mathrm{s} E_{\upalpha } \biggl[ \biggl( \mathrm{y} \frac{\partial \mathrm{y}}{\partial u}+ \mathrm{y} \frac{\partial \mathrm{y}}{\partial w} \biggr)- \epsilon \biggl( \frac{\partial ^{2} \mathrm{y}}{\partial u^{2} }+ \frac{\partial ^{2} \mathrm{y}}{\partial w^{2}} \biggr) \biggr] $$
(55)

Now, taking inverse \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\) subject to \(\mathbb{I}\mathbbm{.}\mathbb{C}\)., we get

$$ \mathrm{y}(u,w,\nu ) (\mathrm{s})=u+w - E^{-1}_{\upalpha } \biggl[ \mathrm{s} E_{\upalpha } \biggl[\mathrm{y} \frac{\partial \mathrm{y}}{\partial u} + \mathrm{y} \frac{\partial \mathrm{y}}{\partial w}-\epsilon \biggl( \frac{\partial ^{2} \mathrm{y}}{\partial u^{2} }+ \frac{\partial ^{2} \mathrm{y}}{\partial w^{2}} \biggr) \biggr] \biggr]. $$
(56)

Finally, applying HPM, we have

$$ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{y}_{n} = (u+w) - \mathrm{q} \Biggl(E_{\upalpha}^{-1} \Biggl[ \mathrm{s} E_{\upalpha } \Biggl[ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{A}_{n} ( \mathrm{y}) \Biggr] \Biggr] \Biggr), $$
(57)

where

$$ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{A}_{n} (\mathrm{y}) = \mathrm{y} \frac{\partial \mathrm{y}}{\partial u} + \mathrm{y} \frac{\partial \mathrm{y}}{\partial w}-\epsilon \biggl( \frac{\partial ^{2} \mathrm{y}}{\partial u^{2} } + \frac{\partial ^{2} \mathrm{y}}{\partial w^{2}} \biggr).$$

Here, \(\mathrm{A}_{n} (\mathrm{y})\) are He’s polynomials that represent the non-linear terms, and one can write the first few components of He’s polynomials as follows

$$\begin{aligned} \mathrm{A}_{0} (\mathrm{y})& =\mathrm{y}_{0} \frac{\partial \mathrm{y}_{0}}{\partial u}+\mathrm{y}_{0} \frac{\partial \mathrm{y}_{0}}{\partial w} - \epsilon \biggl( \frac{\partial ^{2} \mathrm{y}_{0}}{\partial u^{2}} + \frac{\partial ^{2} \mathrm{y}_{0}}{\partial w^{2} } \biggr), \\ \mathrm{A}_{1} (\mathrm{y})& =\mathrm{y}_{0} \frac{\partial \mathrm{y}_{1}}{\partial u} + \mathrm{y}_{1} \frac{\partial \mathrm{y}_{0}}{\partial u} + \mathrm{y}_{0} \frac{\partial \mathrm{y}_{1}}{\partial w} + \mathrm{y}_{1} \frac{\partial \mathrm{y}_{0}}{\partial w} \\ & \quad - \epsilon \biggl( \frac{\partial ^{2} \mathrm{y}_{0}}{\partial u^{2}} + \frac{\partial ^{2} \mathrm{y}_{0}}{\partial w^{2} } \biggr), \\ \mathrm{A}_{2} (\mathrm{y}) & = \mathrm{y}_{0} \frac{\partial \mathrm{y}_{2}}{\partial u} + \mathrm{y}_{1} \frac{\partial \mathrm{y}_{1}}{\partial u} + \mathrm{y}_{2} \frac{\partial \mathrm{y}_{0}}{\partial u} + \mathrm{y}_{0} \frac{\partial \mathrm{y}_{2}}{\partial w} \\ & \quad + \mathrm{y}_{1} \frac{\partial \mathrm{y}_{1}}{\partial w} + \mathrm{y}_{2} \frac{\partial \mathrm{y}_{0}}{\partial w} - \epsilon \biggl( \frac{ \partial ^{2} \mathrm{y}_{0}}{ \partial u^{2}} + \frac{\partial ^{2} \mathrm{y}_{0}}{\partial w^{2} } \biggr), \end{aligned}$$

and so on. By comparing the like coefficient of the power of q, we get

$$\begin{aligned} \mathrm{q}^{0} : \quad \mathrm{y}_{0}(u,w,t) & =u+w, \\ \mathrm{q}^{1} :\quad \mathrm{y}_{1}(u,w, \nu ) & = - E^{-1}_{ \upalpha } \bigl[ \mathrm{s} E_{\upalpha }\bigl[ \mathrm{A}_{0} ( \mathrm{y}) \bigr] \bigr] \\ & = - E^{-1}_{\upalpha } \biggl[ \mathrm{s} E_{\upalpha } \biggl[ \mathrm{y}_{0} \frac{\partial \mathrm{y}_{0}}{ \partial u} + \mathrm{y}_{0} \frac{ \partial \mathrm{y}_{0}}{\partial w} - \epsilon \biggl( \frac{\partial ^{2} \mathrm{y}_{0}}{\partial u^{2}} + \frac{\partial ^{2} \mathrm{y}_{0}}{\partial w^{2} } \biggr) \biggr] \biggr] \\ & = - 2 (u+w) \frac{\nu ^{\upalpha}}{\upalpha}, \\ \mathrm{q}^{2} : \quad \mathrm{y}_{2}(u,w, \nu ) & =- E^{-1}_{ \upalpha } \bigl[ \mathrm{s} E_{\upalpha }\bigl[ \mathrm{A}_{1} ( \mathrm{y})\bigr] \bigr] \\ & = - E^{-1}_{\upalpha } \biggl[ \mathrm{s} E_{\upalpha } \biggl[ \mathrm{y}_{0} \frac{\partial \mathrm{y}_{1}}{ \partial u} + \mathrm{y}_{1} \frac{ \partial \mathrm{y}_{0}}{\partial u} + \mathrm{y}_{0} \frac{\partial w_{1}}{ \partial w}+ \mathrm{y}_{1} \frac{\partial \mathrm{y}_{0}}{ \partial w} \\ &\quad - \epsilon \biggl( \frac{\partial ^{2} \mathrm{y}_{0}}{ \partial u^{2}} + \frac{\partial ^{2} \mathrm{y}_{0}}{ \partial w^{2} } \biggr) \biggr] \biggr] = 4(u+w) \biggl( \frac{\nu ^{\upalpha}}{ \upalpha} \biggr)^{3}, \\ \mathrm{q}^{3} :\quad \mathrm{y}_{3}(u,w, \nu ) & = - E^{-1}_{ \upalpha } \bigl[\mathrm{s} E_{\upalpha }\bigl[ \mathrm{A}_{2} ( \mathrm{y})\bigr] \bigr] \\ &= - E^{-1}_{\upalpha } \biggl[ \mathrm{s} E_{\upalpha } \biggl[ \mathrm{y}_{0} \frac{\partial \mathrm{y}_{2}}{\partial u} + \mathrm{y}_{1} \frac{\partial \mathrm{y}_{1}}{\partial u} + \mathrm{y}_{2} \frac{\partial \mathrm{y}_{0}}{\partial u} + \mathrm{y}_{0} \frac{\partial \mathrm{y}_{2}}{\partial w} \\ &\quad {}+ \mathrm{y}_{1} \frac{\partial \mathrm{y}_{1}}{ \partial w} + \mathrm{y}_{2} \frac{ \partial \mathrm{y}_{0}}{\partial w} - \epsilon \biggl( \frac{\partial ^{2} \mathrm{y}_{0}}{ \partial u^{2}} + \frac{\partial ^{2} \mathrm{y}_{0}}{ \partial w^{2} } \biggr) \biggr] \biggr] \\ & = -8(u+w) \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{3}, \end{aligned}$$

Similarly, the approximations may be obtained in the following way

$$\begin{aligned} \mathrm{q}^{4} :\quad \mathrm{y}_{4} (u,w,\nu ) & = 16 ( u+w) \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{4}, \\ \mathrm{q}^{5} : \quad \mathrm{y}_{5} (u,w,\nu ) & = -32(u +w) \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{5}, \end{aligned}$$

and so on. Substituting the above values in the following equation:

$$ \mathrm{y}(u,w,\nu ) = \mathrm{y}_{0} (u,w,\nu ) + \mathrm{y}_{1} (u,w, \nu ) + \mathrm{y}_{2} (u,w,\nu ) + \mathrm{y}_{3} (u,w,\nu )+ \cdots , $$
(58)

we get,

$$\begin{aligned} \mathrm{y}(u,w,\nu ) & = (u+w) \biggl(1-2 \frac{\nu ^{\upalpha}}{\upalpha}+2^{2} \biggl( \frac {\nu ^{\upalpha}}{\upalpha} \biggr)^{2} - 2^{3} \biggl( \frac {\nu ^{\upalpha}}{\upalpha} \biggr)^{3} + 2^{4} \biggl( \frac{\nu ^{\upalpha}}{ \upalpha} \biggr)^{4} + \cdots \biggr) \end{aligned}$$
(59)
$$\begin{aligned} & = \frac{u+w}{1-2 \frac{\nu ^{\upalpha}}{\upalpha}},\quad \forall \nu \in \biggl[ 0, \biggl( \frac{ \upalpha}{2} \biggr)^{ \frac{1}{\upalpha}} \biggr). \end{aligned}$$
(60)

The numerical solution for different values of α, i.e., for \(\upalpha =0.5, 0.7\), is presented in Fig. 4. For \(\upalpha =1\), we have the classical solution of the problem as follows

$$ \mathrm{y}(u,w,\nu )= \frac{u+w}{1-2\nu},$$

which is the same solution as given in [35].

Figure 4
figure 4

Numerical solution using \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\mathrm{HP}\mathbb{M}\) in Example 5.4 for \(\upalpha =0.5, 0.7\)

Full size image

Remark 5.1

The above example can easily be generalized to the case of time fractional (\(n+ 1\))-dimensional Burger’s equation.

$$\begin{aligned} \frac{ \partial ^{\upalpha }\mathrm{y}( u_{1},u_{2},\dots , u_{n}, \nu ) }{ \partial \nu ^{\upalpha}} & + \mathrm{y}(u_{1},u_{2}, \dots , u_{n} ,\nu ) \frac{\partial \mathrm{y}(u_{1},u_{2},\dots ,u_{n},\nu )}{ \partial u} \\ & \quad + \mathrm{y}(u_{1},u_{2},\dots , u_{n}, \nu ) \frac{ \partial \mathrm{y}(u_{1},u_{2},\dots , u_{n}, \nu )}{ \partial w} \\ & \quad {- \epsilon \biggl( \frac{\partial ^{2} \mathrm{y}(u_{1},u_{2},\dots , u_{n}, \nu )}{ \partial u^{2} }} \end{aligned}$$
(61)
$$\begin{aligned} & \quad {+ \frac{ \partial ^{2} \mathrm{y}(u_{1},u_{2},\dots , u_{n}, \nu )}{ \partial w^{2}} \biggr)} \\ & = 0,\quad \forall \nu \geq 0, 0< \upalpha \leq 1, \end{aligned}$$
(62)

with \(\mathbb{I}\mathbbm{.}\mathbb{C}\mathbbm{.}\), \(\mathrm{y}(u_{1},u_{2},\dots , u_{n}, 0)=u_{1} + u_{2}+ \cdots +u_{n}\). If \(\upalpha =1\), then Eq. (61) becomes the classical \((n+1)\)-dimensional Burger equation [35]. Repeating the similar procedure, we have

$$\begin{aligned} \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{y}_{n} (u_{1},u_{2}, \dots , u_{n}, \nu ) ={}& (u_{1} + u_{2}+ \cdots +u_{n} ) -\mathrm{q} \Biggl(E_{\upalpha}^{-1} \Biggl[\mathrm{s} E_{ \upalpha } \Biggl[ \sum_{n=0}^{\infty} \mathrm{q}^{n} \mathrm{A}_{n} ( \mathrm{y}) \Biggr] \Biggr] \Biggr), \end{aligned}$$

where

$$\begin{aligned} &\mathrm{A}_{0} (\mathrm{y}) =\sum_{i=1}^{n} \biggl( \mathrm{y}_{0} \frac{\partial \mathrm{y}_{0}}{\partial u_{i}} + \mathrm{y}_{0} \frac{\partial \mathrm{y}_{0}}{\partial u} \biggr) - \epsilon \sum_{i=1}^{n} \biggl( \frac{\partial ^{2} \mathrm{y}}{\partial u_{i}^{2}} \biggr), \\ & \mathrm{A}_{1} (\mathrm{y}) =\sum_{i=1}^{n} \biggl( \mathrm{y}_{0} \frac{\partial \mathrm{y}_{1}}{\partial u_{i}} + \mathrm{y}_{1} \frac{\partial \mathrm{y}_{0}}{\partial u_{i}} \biggr) -\epsilon \sum_{i=1}^{n} \biggl(\frac{\partial ^{2} \mathrm{y}}{\partial u_{i}^{2}} \biggr), \end{aligned}$$

and so on. Comparing the power of the coefficient q, we have

$$\begin{aligned} \begin{aligned} & \mathrm{q}^{0} :\quad \mathrm{y}_{0}(u_{1},u_{2}, \dots , u_{n}, \nu ) = \sum_{i=1}^{n} u_{i}, \\ & \mathrm{q}^{1} : \quad \mathrm{y}_{1}(u_{1},u_{2}, \dots , u_{n}, \nu ) = -n \frac{\nu ^{\upalpha}}{\upalpha} \sum _{i=1}^{n} u_{i}, \\ & \mathrm{q}^{2} : \quad \mathrm{y}_{2}(u_{1},u_{2}, \dots , u_{n}, \nu ) = n^{2} \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{2}\sum_{i=1}^{n} u_{i}, \\ & \mathrm{q}^{3} : \quad \mathrm{y}_{3}(u_{1},u_{2}, \dots , u_{n}, \nu ) = -n^{3} \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{3} \sum_{i=1}^{n} u_{i}, \end{aligned} \end{aligned}$$
(63)

and also

$$\begin{aligned} \begin{aligned} & \mathrm{q}^{4} : \quad \mathrm{y}_{4}(u_{1},u_{2}, \dots , u_{n}, \nu ) = n^{4} \biggl( \frac{\nu ^{\upalpha}}{\upalpha} \biggr)^{4}\sum_{i=1}^{n} u_{i}, \\ &\mathrm{q}^{5} : \quad \mathrm{y}_{5}(u_{1},u_{2}, \dots , u_{n}, \nu ) = -n^{5} \biggl( \frac{ \nu ^{\upalpha}}{\upalpha} \biggr)^{5}\sum_{i=1}^{n} u_{i}, \end{aligned} \end{aligned}$$
(64)

and so on. Therefore, substituting Eqs. (63) and (64) in the following equation

$$\begin{aligned} \mathrm{y}(u_{1},u_{2},\dots , u_{n}, \nu ) ={}&\mathrm{y}_{0} (u_{1},u_{2}, \dots , u_{n}, \nu ) + \mathrm{y}_{1} (u_{1},u_{2}, \dots , u_{n}, \nu ) \\ & {} +\mathrm{y}_{2} (u_{1},u_{2}, \dots , u_{n}, \nu ) + \mathrm{y}_{3} (u_{1},u_{2},\dots , u_{n}, \nu )+\cdots , \end{aligned}$$

we obtain

$$\begin{aligned} \mathrm{y}(u_{1},u_{2},\dots , u_{n}, \nu ) ={}& \sum_{i=1}^{n} u_{i} \biggl(1-n \frac {\nu ^{\upalpha}}{\upalpha} + n^{2} \biggl( \frac {\nu ^{\upalpha}}{\upalpha} \biggr)^{2} - n^{3} \biggl( \frac {\nu ^{\upalpha}}{\upalpha} \biggr)^{3} \\ & {} + n^{4} \biggl(\frac {\nu ^{\upalpha}}{\upalpha} \biggr)^{4} + \cdots \biggr) \\ ={}& \frac{1}{1-n \frac{ \nu ^{\upalpha}}{\upalpha}} \sum_{i=1}^{n} u_{i}, \quad \forall \nu \in \biggl[ 0, \frac{\upalpha}{n}^{ \frac{1}{\upalpha}} \biggr). \end{aligned}$$
(65)

For \(\upalpha =1\) as a special case, the classical solution can be found as follows:

$$ \mathrm{y}(u_{1},u_{2},\dots , u_{n}, \nu ) = \frac{1}{1 - n \nu} \sum_{i=1}^{n} u_{i}, $$
(66)

which is the same solution as in [35].

6 Conclusion

In this paper, we have presented \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\mathrm{HP}\mathbb{M}\) as a novel approach for solving \(\mathbb{N}\mathbbm{-}\mathbb{TFPDE}s\). We have also established the results on the uniqueness and convergence of the solution. The numerical results show that the suggested method is effective in finding exact and approximate solutions for \(\mathbb{N}\mathbbm{-}\mathbb{TFPDE}s\). The efficiency and approximation of the given technique have been verified through four different problems. Moreover, it is interesting to note that \(\mathbb{C}_{\mathcal{D}}\mathrm{E}\mathbb{T}\mathrm{HP}\mathbb{M}\) is able to significantly reduce the amount of computing work required compared to traditional approaches while retaining good numerical accuracy. The suggested technique has a distinct advantage over the decomposition method and can handle non-linear problems without using Adomian polynomials. Finally, this approach can be used to solve a variety of both linear and non-linear \(\mathbb{TFPDE}s\).