1 Introduction

It is vital to utilize mathematical models to investigate various economic processes in order to make appropriate decisions. The time gap between supply and demand explains economic volatility. The mismatch between supply and demand responses, as Leontief in [26] pointed out, might be an essential component in defining market equilibrium. The market dynamics of supply and demand have been increasingly modeled in this regard. Commodity-price volatility can, in fact, offer a planning challenge for many businesses. The cobweb theorem is the name given to this phenomena, Waugh in [29]. The cobweb models, in particular [1, 17], which represent the pricing dynamics on a market for a nonstorable meal that takes a unit of time to create. In economic dynamics, the cobweb model has been proposed as a benchmark model [13, 19, 22].

The global demand for fractional calculus (FC) appears to be increasing exponentially. In the modeling of applied mathematics, physics, image processing, and engineering, FC has drawn a lot of interest due to its influential qualities in communicating the complex dynamics of nonsentimental systems [4, 5]. The traditional cobweb model with static expectations is thus a very useful tool for studying price dynamics. If supply and demand are linear, though, one of three types of occurrences can be observed: convergence to steady-state balance, series of period two, and unbounded variations. The equilibrium between supply and demand may not always be available due to the influence of many factors such as political stability, economic conditions, and tax-rate variation.

In a fluctuating market, we perceive a variation in price, quantity, or other noise, which prevents us from making investment decisions or deciding how much to supply or how many items to produce from one period to the next. Muth [22] explored efficient markets and the theory of price fluctuations using the cobweb framework. Nonlinear cobweb dynamics were studied by Gaffney et al. [4, 5]. Furthermore, some work on cobweb models including time delays has been completed. Matsumoto et al. [27] and Gori et al. [20, 21] investigated the terminal behavior and Hopf bifurcation of the cobweb model with time delays.

The integer-order calculus is troublesome for various physical systems with fractional (noninteger) derivatives in their real dynamics. Fractional-order differential equations are employed to accurately represent these systems. In heat-transfer systems, for example [16], financial systems [30], and electromagnetic systems [18], the fractional-order calculus was used to model the data. In recent years, there has been a significant increase in the use of fractional-order equations in stability theory [7, 14, 25, 28, 30], and various papers have been published in this area.

Bohner and Hatipoğlu [8] studied cobweb models involving conformable fractional derivatives. They provided the solutions as well as the sufficient conditions for the stability of the equilibrium value. Moreover, two distinct forms of discrete fractional cobweb models are shown in [10]. In [9], they expanded their findings to time scales. Chen and coworkers in [12] explored two types of Caputo fractional derivative dynamic cobweb models. In order to provide adequate conditions for the equilibrium’s stability, the researchers provided analytical responses.

In this paper, we propose a dynamic cobweb model with a Caputo–Katugampola fractional derivative of order \(\alpha \in (0,1)\), \(\rho > 0\) for the classic model and with noise perturbation. Section 2 begins with a review of the essential features of the Mittag–Leffler function and the Caputo–Katugampola operator. Sections 3 and 4 define and obtain our key results for the situations of a Caputo–Katugampola fractional derivative in the supply and demand functions, as well as their perturbations. Section 5 contains several examples to illustrate the theoretical results. Finally, in Sect. 6, some conclusions are presented.

2 Preliminaries

In this section, we review some fundamentals of the fractional calculus. Moreover, we adopt the notations of the Caputo–Katugampola fractional derivative and integral from [3, 6, 23, 24].

Definition 1

(Katugampola fractional integral)

The Katugampola fractional integral of order \(0<\alpha <1\), \(\rho >0\) of a function \(u \in L^{1}([a,b]), 0< a< b\), is defined by

$$\begin{aligned} I_{a^{+}}^{\alpha ,\rho }u ( t ) = \frac{\rho ^{1-\alpha }}{\Gamma ( \alpha ) } \int _{a}^{t} \frac{s^{\rho -1}u ( s ) }{ ( t^{\rho }-s^{\rho } ) ^{1-\alpha }}\,ds, \end{aligned}$$

where Γ is the Gamma function.

Definition 2

(Katugampola fractional derivative)

The Katugampola fractional derivative of order \(0<\alpha <1\), \(\rho >0\) of a function u on \([a,b], 0< a< b\), is defined by

$$\begin{aligned} D_{a^{+}}^{\alpha ,\rho }u ( t ) = \frac{\rho ^{\alpha }}{\Gamma ( 1-\alpha ) } t^{1-\rho} \frac{d}{dt} \int _{a}^{t} \frac{s^{\rho -1}u ( s ) }{ ( t^{\rho }-s^{\rho } ) ^{\alpha }}\,ds. \end{aligned}$$

Definition 3

(Caputo–Katugampola fractional derivative)

The Caputo–Katugampola fractional derivative of order \(0<\alpha <1\), \(\rho >0\) of a function u on \([a,b], 0< a< b\), is defined by

$$\begin{aligned} {}^{C}D_{a^{+}}^{\alpha ,\rho }u ( t ) &=D_{a^{+}}^{\alpha , \rho } \bigl[u ( t )-u ( a )\bigr] \\ &=\frac{\rho ^{\alpha }}{\Gamma ( 1-\alpha ) } t^{1-\rho} \frac{d}{dt} \int _{a}^{t} \frac{s^{\rho -1}[u ( s )-u(a)] }{ ( t^{\rho }-s^{\rho } ) ^{\alpha }}\,ds. \end{aligned}$$

Lemma 1

If u is a constant, then the fractional derivative of u is \({}^{C}D_{a^{+}}^{\alpha ,\rho }u ( t ) =0\).

Definition 4

The Mittag–Leffler function with two parameters is defined as

$$\begin{aligned} E_{\alpha ,\beta}(z)= \sum_{k=0}^{+\infty} \frac{z^{k}}{\Gamma (k \alpha +\beta )}, \end{aligned}$$

where \(\alpha >0\), \(\beta >0\), \(z\in \mathbb{C}\).

When \(\beta =1\), one has \(E_{\alpha}(z)=E_{\alpha ,1}(z)\).

Lemma 2

([11])

Let h be a continuous function on J. Then, the solution of problem

$$\begin{aligned} \textstyle\begin{cases} {}^{C}D_{a^{+}}^{\alpha ,\rho }u ( t ) +\lambda u ( t ) =h ( t ) \quad t\in J\textit{, }0< \alpha < 1 \textit{, }a\textit{,}\rho >0\textit{,} \\ u ( a ) =u_{a}\textit{,}\end{cases}\displaystyle \end{aligned}$$
(1)

is given by

$$\begin{aligned} u ( t ) ={}&u_{a}E_{\alpha } \biggl( -\lambda \biggl( \frac{t^{\rho }-a^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \\ &{}+ \int _{a}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{ \alpha -1}E_{\alpha ,\alpha } \biggl( -\lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1}h ( s ) \,ds. \end{aligned}$$

Lemma 3

([15])

Let \(A\in \mathbb{R} ^{d\times d}\). Assume that the spectrum of A satisfies

$$\begin{aligned} \sigma ( A ) \subset \biggl\{ \lambda \in \mathbb{C} \backslash \{ 0 \} : \vert \arg \lambda \vert >\frac{\alpha \pi }{2} \biggr\} . \end{aligned}$$

Then, the following statements hold:

  1. (i)

    \(\lim_{t\rightarrow +\infty } \Vert E_{\alpha } ( At^{\alpha } ) \Vert _{2} =0\).

  2. (ii)

    \(\int _{0}^{+\infty }t^{ \alpha -1} \Vert E_{\alpha ,\alpha } ( At^{\alpha } ) \Vert _{2} \,dt<\infty \),

where \(\Vert \cdot \Vert _{2}\) is the 2-norm for a matrix.

3 Cobweb model with a Caputo–Katugampola fractional derivative in the demand function

The basic cobweb models with a Caputo–Katugampola fractional derivative in the demand function are studied in this section.

3.1 Basic Cobweb model

The basic cobweb model with a Caputo–Katugampola fractional derivative in the demand function is given in the following form

$$\begin{aligned} \begin{aligned} &D(t)= \gamma +\beta \bigl( p(t)+ {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t) \bigr), \\ &S(t)= \gamma _{1}+\beta _{1}p(t), \\ &D(t)=S(t), \end{aligned} \end{aligned}$$
(2)

where \(0<\alpha <1\), \(\rho >0\), γ, β, \(\gamma _{1}\), \(\beta _{1}\in \mathbb{R}\), \(\beta \neq 0\), \(\beta \neq \beta _{1}\).

Theorem 1

The unique solution of (2) is given by

$$\begin{aligned} p(t)=E_{\alpha } \biggl( \lambda \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \biggl[ p_{0}+\frac{r}{\lambda} \biggr]-\frac{r}{\lambda}, \end{aligned}$$
(3)

where \(\lambda =\frac{\beta _{1}-\beta}{\beta}\), \(r=\frac{\gamma _{1}-\gamma}{\beta}\) and \(p_{0}\in \mathbb{R}\).

Proof

It is clear from (2) that

$$\begin{aligned} \gamma +\beta \bigl( p(t)+ {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t) \bigr)= \gamma _{1}+\beta _{1}p(t), \end{aligned}$$

that is,

$$\begin{aligned} {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t)=\lambda p(t)+r. \end{aligned}$$

Let \(x(t)=p(t)+\frac{r}{\lambda}\). We have

$$\begin{aligned} {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }x(t) &={}^{C}D_{t_{0}^{+}}^{\alpha , \rho }p(t) \\ &=\lambda p(t)+r \\ &=\lambda \biggl(x(t)-\frac{r}{\lambda} \biggr)+r \\ &=\lambda x(t). \end{aligned}$$

Using Lemma 2, we obtain

$$\begin{aligned} x(t) &=E_{\alpha } \biggl( \lambda \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) x(t_{0}) \\ &=E_{\alpha } \biggl( \lambda \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \biggl[ p(t_{0})+\frac{r}{\lambda} \biggr]. \end{aligned}$$

Hence,

$$\begin{aligned} p(t)=E_{\alpha } \biggl( \lambda \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \biggl[ p_{0}+\frac{r}{\lambda} \biggr]- \frac{r}{\lambda}, \end{aligned}$$

where \(p_{0}=p(t_{0})\). □

Remark 1

\(p_{e}=\frac{\gamma _{1}-\gamma}{\beta -\beta _{1}}\) is the equilibrium value of the system (2).

Theorem 2

Suppose that \(\beta _{1}<\beta \). Then, the solution of (2) converges to the equilibrium value \(p_{e}\).

Proof

We have \(\beta _{1}< b\), then \(\lambda <0\). It follows from Lemma 3 that

$$\begin{aligned} \lim_{t\to +\infty} E_{\alpha } \biggl( \lambda \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr)=0. \end{aligned}$$

Therefore,

$$\begin{aligned} \lim_{t\to +\infty} p(t)=-\frac{r}{\lambda}= \frac{\gamma _{1}-\gamma}{\beta -\beta _{1}}. \end{aligned}$$

 □

3.2 Perturbed cobweb model

We consider the system

$$\begin{aligned} \begin{aligned} &D(t)= \gamma +\beta \bigl( p(t)+ {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t) \bigr), \\ &S(t)= \gamma _{1}+\beta _{1}p(t), \\ &D(t)=S(t)+h(t), \end{aligned} \end{aligned}$$
(4)

where h is a continuous function, \(0<\alpha <1\), \(\rho >0\), γ, β, \(\gamma _{1}\), \(\beta _{1}\in \mathbb{R}\), \(\beta \neq 0\), \(\beta \neq \beta _{1}\).

Theorem 3

The unique solution of (4) is given by

$$\begin{aligned} p(t)={}&E_{\alpha } \biggl( \lambda \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \biggl[ p_{0}+\frac{r}{\lambda} \biggr]- \frac{r}{\lambda}\\ &{}+ \int _{t_{0}}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{ \alpha ,\alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1} \frac{h ( s )}{\beta} \,ds, \end{aligned}$$

where \(\lambda = \frac{\beta _{1}-\beta}{\beta}\), \(r=\frac{\gamma _{1}-\gamma}{\beta}\) and \(p_{0}\in \mathbb{R}\).

Proof

It follows from (4) that

$$\begin{aligned} \gamma +\beta \bigl( p(t)+ {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t) \bigr)= \gamma _{1}+\beta _{1}p(t)+h(t), \end{aligned}$$

that is,

$$\begin{aligned} {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t)=\lambda p(t)+r+ \frac{h(t)}{\beta}. \end{aligned}$$

Let \(x(t)= p(t)+\frac{r}{\lambda}\). We have

$$\begin{aligned} {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }x(t) &={}^{C}D_{t_{0}^{+}}^{\alpha , \rho }p(t) \\ &=\lambda p(t)+r+\frac{h(t)}{\beta} \\ &=\lambda x(t)+\frac{h(t)}{\beta}. \end{aligned}$$

Using Lemma 2, we obtain

$$\begin{aligned} x(t) ={}&E_{\alpha } \biggl( \lambda \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) x(t_{0}) \\ &{}+ \int _{t_{0}}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{ \alpha -1}E_{\alpha ,\alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1} \frac{h ( s )}{\beta} \,ds. \end{aligned}$$

Hence,

$$\begin{aligned} p(t)={}&E_{\alpha } \biggl( \lambda \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \biggl[ p_{0}+\frac{r}{\lambda} \biggr]- \frac{r}{\lambda}\\ &{}+ \int _{t_{0}}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{ \alpha ,\alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1} \frac{h ( s )}{\beta} \,ds, \end{aligned}$$

where \(p_{0}=p(t_{0})\). □

For the convergence of solutions of systems (4) to \(p_{e}\), we consider the following assumption \((H_{1})\): The function \(h(t)\) satisfies:

$$\begin{aligned} \lim_{t\to +\infty} \int _{t_{0}}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{\alpha , \alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1}h ( s ) \,ds=0. \end{aligned}$$
(5)

Remark 2

If \(\lim_{t\to +\infty}h(t)=0\), then \((H_{1})\) holds.

Indeed, suppose that \(\lim_{t\to +\infty}h(t)=0\). Let \(T>t_{0}\).

For \(t\geq T\), we have

$$\begin{aligned} & \biggl\vert \int _{t_{0}}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{\alpha ,\alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1}h ( s ) \,ds \biggr\vert \\ &\quad\leq \int _{t_{0}}^{T} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{\alpha ,\alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1}h ( s ) \,ds \\ &\qquad{}+ \int _{T}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{ \alpha -1}E_{\alpha ,\alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1}h ( s ) \,ds \\ &\quad\leq \sup_{s\geq t_{0}} \bigl\vert h(s) \bigr\vert \int _{t_{0}}^{T} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{\alpha , \alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1} \,ds \\ &\qquad{}+\sup_{s\geq T} \bigl\vert h(s) \bigr\vert \int _{T}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{\alpha , \alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1} \,ds \\ &\quad\leq \sup_{s\geq t_{0}} \bigl\vert h(s) \bigr\vert \int _{ \frac{t^{\rho }-T^{\rho }}{\rho }}^{ \frac{t^{\rho }-t_{0}^{\rho }}{\rho }} u^{\alpha -1}E_{\alpha , \alpha } \bigl( \lambda u^{\alpha } \bigr) \,du +\sup_{s\geq T} \bigl\vert h(s) \bigr\vert \int _{0}^{+\infty}u^{\alpha -1}E_{\alpha ,\alpha } \bigl( \lambda u^{ \alpha } \bigr) \,du. \end{aligned}$$
(6)

This show that,

$$\begin{aligned} \lim_{t\to +\infty} \int _{t_{0}}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{\alpha , \alpha } \biggl( \lambda \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1}h ( s ) \,ds=0. \end{aligned}$$

Theorem 4

Suppose that \(\beta _{1}<\beta \) and \((H_{1})\) holds. Then, the solution of (2) converges to the value \(p_{e}\).

4 Cobweb model with a Caputo–Katugampola fractional derivative in the supply function

In this section, the basic cobweb model with a Caputo–Katugampola fractional derivative in the supply function is investigated.

4.1 Basic cobweb model

The basic cobweb model with a Caputo–Katugampola fractional derivative in the supply function is defined as:

$$\begin{aligned} \begin{aligned} &D(t)= \gamma +\beta p(t), \\ &S(t)= \gamma _{1}+\beta _{1} \bigl( p(t)+c {}^{C}D_{t_{0}^{+}}^{\alpha , \rho }p(t) \bigr), \\ &D(t)=S(t), \end{aligned} \end{aligned}$$
(7)

where \(0<\alpha <1\), \(\rho >0\), γ, β, \(\gamma _{1}\), \(\beta _{1}\), \(c \in \mathbb{R}\), \(\beta _{1}\neq 0, c\neq 0\), \(\beta \neq \beta _{1}\).

Theorem 5

The unique solution of (7) is given by

$$\begin{aligned} p(t)=E_{\alpha } \biggl( \widetilde{\lambda} \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \biggl[ p_{0}+ \frac{\widetilde{r}}{\widetilde{\lambda}} \biggr]- \frac{\widetilde{r}}{\widetilde{\lambda}}, \end{aligned}$$
(8)

where \(\widetilde{\lambda}=\frac{\beta -\beta _{1}}{\beta _{1} c}\), \(\widetilde{r}=\frac{\gamma -\gamma _{1}}{\beta _{1} c}\) and \(p_{0}\in \mathbb{R}\).

Proof

It follows from (7) that

$$\begin{aligned} \gamma _{1}+\beta _{1} \bigl( p(t)+c {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t) \bigr)=\gamma +\beta p(t), \end{aligned}$$

that is,

$$\begin{aligned} {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t)=\widetilde{\lambda} p(t)+ \widetilde{r}. \end{aligned}$$

In the same way as Theorem 1, we obtain

$$\begin{aligned} p(t)=E_{\alpha } \biggl( \widetilde{\lambda} \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \biggl[ p_{0}+\frac{\widetilde{r}}{\widetilde{\lambda}} \biggr]- \frac{\widetilde{r}}{\widetilde{\lambda}}, \end{aligned}$$

where \(p_{0}=p(t_{0})\). □

Remark 3

\(p_{e}=\frac{\gamma _{1}-\gamma}{\beta -\beta _{1}}\) is the equilibrium value of the system (7).

Theorem 6

Suppose that \(\beta -\beta _{1}<\beta _{1}c\). Then, the solution of (7) converges to the equilibrium value \(p_{e}\).

4.2 Perturbed cobweb model

We consider the system

$$\begin{aligned} \begin{aligned}& D(t)= \gamma +\beta p(t), \\ &S(t)= \gamma _{1}+\beta _{1} \bigl( p(t)+c {}^{C}D_{t_{0}^{+}}^{\alpha , \rho }p(t) \bigr), \\ &D(t)=S(t)+g(t), \end{aligned} \end{aligned}$$
(9)

where g is a continuous function, \(0<\alpha <1\), \(\rho >0\), γ, β, \(\gamma _{1}\), \(\beta _{1}\), \(c \in \mathbb{R}\), \(\beta _{1}\neq 0, c\neq 0\), \(\beta \neq \beta _{1}\).

Theorem 7

The unique solution of (9) is given by

$$\begin{aligned} p(t)={}&E_{\alpha } \biggl( \widetilde{\lambda} \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \biggl[ p_{0}+ \frac{\widetilde{r}}{\widetilde{\lambda}} \biggr]- \frac{\widetilde{r}}{\widetilde{\lambda}}\\ &{}+ \int _{t_{0}}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{\alpha , \alpha } \biggl( \widetilde{\lambda} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1} \frac{g ( s )}{\beta _{1} c} \,ds, \end{aligned}$$

where \(p_{0}\in \mathbb{R}\).

Proof

It follows from (9) that

$$\begin{aligned} \gamma _{1}+\beta _{1} \bigl( p(t)+c {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t) \bigr)+g(t)=\gamma +\beta p(t), \end{aligned}$$

that is,

$$\begin{aligned} {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t)=\widetilde{\lambda} p(t)+ \widetilde{r}-\frac{g(t)}{\beta _{1} c}. \end{aligned}$$

In the same way as Theorem 3, we obtain

$$\begin{aligned} p(t)={}&E_{\alpha } \biggl( \widetilde{\lambda} \biggl( \frac{t^{\rho}-t_{0}^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) \biggl[ p_{0}+ \frac{\widetilde{r}}{\widetilde{\lambda}} \biggr]- \frac{\widetilde{r}}{\widetilde{\lambda}}\\ &{}+ \int _{t_{0}}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{\alpha , \alpha } \biggl( \widetilde{\lambda} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1} \frac{g ( s )}{\beta _{1} c} \,ds, \end{aligned}$$

where \(p_{0}=p(t_{0})\). □

For the convergence of solutions of systems (4) to \(p_{e}\), we consider the following assumption \((H_{2})\): The function \(g(t)\) satisfies:

$$\begin{aligned} \lim_{t\to +\infty} \int _{t_{0}}^{t} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha -1}E_{\alpha , \alpha } \biggl( \widetilde{\lambda} \biggl( \frac{t^{\rho }-s^{\rho }}{\rho } \biggr) ^{\alpha } \biggr) s^{\rho -1}g ( s ) \,ds=0. \end{aligned}$$
(10)

Theorem 8

Suppose that \(\beta -\beta _{1}<\beta _{1} c\) and \((H_{2})\) holds. Then, the solution of (2) converges to the value \(p_{e}\).

5 Numerical results

In this section, we provide two numerical examples to demonstrate our theoretical findings.

Example 1

Consider the basic cobweb model with a Caputo–Katugampola fractional derivative in the demand function as follows:

$$\begin{aligned} \begin{aligned} &D(t)= \gamma +\beta \bigl( p(t)+ {}^{C}D_{t_{0}^{+}}^{\alpha ,\rho }p(t) \bigr), \\ &S(t)= \gamma _{1}+\beta _{1} p(t), \\ &D(t)=S(t), \end{aligned} \end{aligned}$$

with \(\gamma = -10, \beta = 6, \gamma _{1} = 5, \beta _{1} = 3\), and \(p_{0} = 10\). By choosing these parameters, one can deduce that

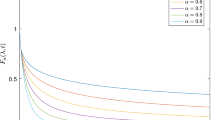
$$\begin{aligned} &\lambda = \frac{\beta _{1}-\beta}{\beta} = -0.5,\qquad r = \frac{\gamma _{1} - \gamma}{\gamma} = -1.5\quad \text{and}\quad p_{e} = \frac{\gamma _{1}-\gamma}{\beta -\beta _{1}} = 5,\\ &\beta _{1} < \beta . \end{aligned}$$

Moreover, we consider the perturbed model (4) with \(h(t) = 1/t\). Thus, all the assumptions in Theorems 2 and 4 are satisfied, hence, the solution \(p(t)\) of both models, basic and perturbed, should converge to the value \(p_{e} = 5\). By computing the equation (3) with different values of \(\alpha , \rho \), and the values of the given parameters, we can obtain the values, \(p_{m}\), for the basic model. Furthermore, we obtain the numerical solutions for the corresponding discrete models and compute the values of \(p_{a}\) and \(p_{a}^{*}\) for the basic and the perturbed model, respectively. Table 1 shows the values \(p_{m}, p_{a}\), and \(p_{a}^{*}\) with various values of \(\alpha , \rho \), and t. Figures 1 and 2 show the values of \(p(t)\) for the unperturbed and perturbed models at different values of ρ and \(\alpha =0.9\). It is obvious that by choosing a sufficiently large t, both models always convergent to the value \(p_{e} = 5\).

Figure 1
figure 1

The values of \(p(t)\) (left) and the approximate values of \(p(t)\) (right) for Example 1 at various values of ρ and \(\alpha = 0.9\)

Full size image
Figure 2
figure 2

The approximate values of \(p(t)\) for the perturbed basic cobweb model, Example 1, at various values of ρ and \(\alpha = 0.9\)

Full size image
Table 1 The values of \(p(t)\) for the unperturbed and perturbed model of Example 1
Full size table

Example 2

Consider the basic cobweb model with a Caputo–Katugampola fractional derivative in the supply function as follows:

$$\begin{aligned} \begin{aligned} &D(t)= \gamma +\beta p(t), \\ &S(t)= \gamma _{1}+\beta _{1} \bigl(p(t)+ c\cdot {}^{C}D_{t_{0}^{+}}^{ \alpha ,\rho }p(t) \bigr), \\ &D(t)=S(t), \end{aligned} \end{aligned}$$

with \(\gamma = 4, \beta = 6, \gamma _{1} = -20, \beta _{1} = 2, c=2\), and \(p_{0} = 10\). Taking these values leads to:

$$\begin{aligned} \widetilde{\lambda} = \frac{\beta -\beta _{1}}{\beta _{1}c} = -1.5, \qquad\widetilde{r} = \frac{\gamma _{1} - \gamma}{\beta _{1}c} = 6, \end{aligned}$$

and

$$\begin{aligned} p_{e} = \frac{\gamma _{1}-\gamma}{\beta -\beta _{1}} = 4,\qquad \beta - \beta _{1} < \beta _{1}c. \end{aligned}$$

Furthermore, in the perturbed model (9) we take \(g(t) = 1/t\). It is clear that all the assumptions in Theorems 5 and 7 are fulfilled. Consequently, the solution \(p(t)\) of the perturbed and unperturbed models should converge to the value \(p_{e} = 4\). To obtain the values, \(p_{m}\), of the unperturbed model, we have solved equation (8) at different values of \(\alpha , \rho \). In addition, the values \(p_{a}\) for the corresponding unperturbed discrete model are computed. For the perturbed model, we have computed the approximate solution of \(p(t)\) and then obtained the values \(p_{a}^{*}\). Table 2 displays the values of \(p_{m}, p_{a}\), and \(p_{a}^{*}\) with different values of \(\alpha , \rho \) and t. In Figs. 3 and 4, we display the values of \(p(t)\) for the unperturbed and perturbed models at different values of ρ and \(\alpha =0.7\). It is evident that when t becomes larger both models always convergent to the point \(p_{e} = 4\).

Figure 3
figure 3

The values of \(p(t)\) (left) and the approximate values of \(p(t)\) (right) for Example 2 at various values of ρ and \(\alpha = 0.7\)

Full size image
Figure 4
figure 4

The approximate values of \(p(t)\) for the perturbed basic cobweb model, Example 2, at various values of ρ and \(\alpha = 0.7\)

Full size image
Table 2 The values of \(p(t)\) for the unperturbed and perturbed model of Example 2
Full size table

Remark 4

The numerical results were obtained using a numerical scheme based on a decomposition formula for the Caputo–Katugampola derivative. This scheme was proposed by Almeida et al. and it is used to solve such kinds of problem numerically, for more details see [2]. Furthermore, the numerical values of the Mittag–Leffler functions can be computed by using the MATLAB code known as mlf, which is available on the MathWorks website.

6 Conclusion

In this paper, we studied continuous cobweb models with the Caputo–Katugampola derivative for supply and demand functions, as well as their perturbations. It is demonstrated that in both the perturbed and unperturbed cases, each solution converges to a single equilibrium. Additionally, some numerical results are included to confirm the theoretical results. The equilibrium forms are an essential component in economic sciences, for which mathematics strives to provide theoretical equations, and this is our future goal.