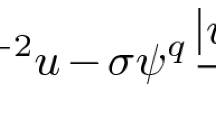Abstract
This paper deals with the existence of solutions for the noncooperative Schrödinger–Kirchhoff system involving the p-Laplacian operator and critical nonlinearities on the Heisenberg group. Under some suitable conditions, together with the limit index theory and the concentration–compactness principle, we obtain the existence and multiplicity of solutions for this system. To our best knowledge, the existence results for the noncooperative system with p-Laplacian and critical nonlinearities are new on the Heisenberg group.
Similar content being viewed by others
1 Introduction and main result
In this paper, we consider the existence of solutions for the noncooperative Schrödinger–Kirchhoff system involving the p-Laplacian operator and critical nonlinearity on the Heisenberg group:
where \(\Delta _{H,p}\) is the p-Laplacian with \(1< p< Q\) and \(p^{\ast}=Qp/(Q-p)\) is the critical Sobolev exponent on the Heisenberg group, \(F=F(\xi ,u,v)\), \(F_{u}=\frac{\partial F}{\partial u}\), \(F_{v}= \frac{\partial F}{\partial v}\), K and V are the Kirchhoff function and potential function, which satisfy the conditions given later. The operator \(\Delta _{H,p}\varphi \) is called p Kohn–Spencer Laplacian, which is defined as follows:
for all \(\varphi \in C^{2}(\mathbb{H}^{n})\).
Kirchhoff’s problem has a physical background, which is an extension of the model proposed by Kirchhoff [11] in 1883. Moreover, by considering the effect of string length changes during vibrations, Kirchhoff proposed Kirchhoff model with the following equation, which is an extension of D’Alembert wave equation:
where ρ, \(p_{0}\), λ, E, L are constants that represent some physical meanings, respectively. Later, more and more scholars carried out research on a Kirchhoff-type model. We also refer to [5, 8, 16, 18, 20, 24] for a wide list of contributions along with [1].
For our problems, first of all, we assume that the Kirchhoff function K: \(\mathbb{R}_{0}^{+}\rightarrow \mathbb{R}_{0}^{+}\), the potential function \(V(\xi )\), and the function \(F(\xi ,u,v)\) satisfy the following conditions:
- \((K_{1})\):
-
\(K\in C(\mathbb{R}_{0}^{+}\rightarrow \mathbb{R}_{0}^{+})\) satisfies \(\inf_{t\in \mathbb{R}_{0}^{+}} K(t)\geq k_{0}>0 \), where \(k_{0}\) is a positive constant.
- \((K_{2})\):
-
There exists \(\theta \in (1,{p^{\ast}}/{p})\) satisfying
$$ \theta \mathcal {K}(t) \geq K(t)t \quad \text{for all } t\geq 0,$$where \(\mathcal {K}(t)=\int _{0}^{t} K(\varsigma )\,d\varsigma \).
- \((V_{1})\):
-
\(V: \mathbb{H}^{n}\rightarrow \mathbb{R}^{+}\) is a continuous function, and there exists \(V_{0}>0\) such that \(\inf_{\xi \in \mathbb{H}^{n}}V(\xi )\geq V_{0}\).
- \((V_{2})\):
-
For every \(d > 0\) such that
$$ \operatorname{meas} \bigl( \bigl\{ \xi \in \mathbb{H}^{n}: V(\xi ) \leq d \bigr\} \bigr) < \infty ,$$where \(\operatorname{meas} (\cdot )\) denotes Lebesgue measure in \(\mathbb{H}^{n}\).
- \((F_{1})\):
-
\(F\in C(\mathbb{H}^{n}\times \mathbb{R}^{2},\mathbb{R}^{+})\), where \(\mathbb{R}^{+} = \{\xi \in \mathbb{R}|\xi \geq 0\}\); and there exist \(c_{0}, c_{1}>0\), \(p< q< p^{\ast}\) such that
$$ \bigl\vert F_{s}(r,s,t) \bigr\vert + \bigl\vert F_{t}(r,s,t) \bigr\vert \leq c_{0} \vert s \vert ^{\frac{p-1}{2}}+c_{1} \vert t \vert ^{ \frac{p-1}{2}}. $$ - \((F_{2})\):
-
\(sF_{s}(\xi ,s,t)\geq 0\), \(tF_{t}(\xi ,s,t)\geq 0\), and there exists \(\tau \in (\theta p,p^{\ast})\) such that
$$ 0< \tau F(\xi ,s,t) \leq sF_{s}(\xi ,s,t)+tF_{t}(\xi ,s,t)$$for any \((\xi ,s,t)\in (\mathbb{H}^{n}\times \mathbb{R}^{2},\mathbb{R}^{+})\).
- \((F_{3})\):
-
F is even: \(F(\xi ,s,t)=F(\xi ,-s,-t)\) for all \((\xi ,s,t)\in \mathbb{H}^{n}\times \mathbb{R}^{2}\).
Note that condition \((V_{2})\) is weaker than the coercivity assumption \(V(x)\rightarrow \infty \) as \(|\xi |\rightarrow \infty \), which was first proposed by Bartsch and Wang in [2] to overcome the lack of compactness.
Now, we give some notations on the Heisenberg group. Let \(\mathbb{H}^{n}\) be the Heisenberg Lie group of topological dimension \(2n+1\), that is, the Lie group which has \(\mathbb{R}^{2n+2}\) as a background manifold, endowed with the non-Abelian group law
with
The inverse is given by \(\xi ^{-1}=-\xi \) so that \((\xi \circ \xi ')^{-1} = (\xi ')^{-1}\circ {\xi}^{-1}\).
The anisotropic dilation structure on the Heisenberg group leads to the Korányi norm, which is defined by
Therefore, the Koranyi norm is homogeneous of degree 1 with respect to the dilations \(\delta _{R}, R>0\), that is,
For \(s>0\), a natural group of dilation on \(\mathbb{H}^{n}\) is defined by \(\delta _{s}(\xi )=(sx,sy,s^{2}t)\). Hence, \(\delta _{s}(\xi _{0}\circ \xi ) = \delta _{s}(\xi _{0})\circ \delta _{s}( \xi )\). For all \(\xi =(x,y,t)\in \mathbb{H}^{n}\), it is easy to verify that the Jacobian determinant of dilatations \(\delta _{s}: \mathbb{H}^{n}\to \mathbb{H}^{n}\) is constant and equal to \(\mathbb{R}^{2n+2}\). That is the reason why the natural number \(Q=2n+2\) is called homogeneous dimension of \(\mathbb{H}^{n}\) and critical exponents \(Q^{*}:= \frac{NQ}{N-Q}\).
The horizontal gradient of a \(C^{1}\) function u: \(\mathbb{H}^{n}\rightarrow R\) is defined by
It is obvious that \(D_{H}u\in \operatorname{span}\{X_{j},Y_{j}\}_{j=1}^{n}\). At the same time, for any horizontal vector field function \(X=X(\xi )\), \(X=\{x^{j}X_{j}+\widetilde{x}^{j}Y_{j}\}_{j=1}^{n}\) of class \(C^{1}(\mathbb{H}^{n}, \mathbb{R}^{2n})\), we define the horizontal divergence of X by
Also, if \(u\in C^{2}(\mathbb{H}^{n})\), then the Kohn–Spencer Laplacian in \(\mathbb{H}^{n}\) is either equivalent to the horizontal Laplacian or the sub-Laplacian of u is
where
The Lie algebra of left-invariant vector fields is generated by the following vector fields:
The left-invariant distance \(d_{H}\) on \(\mathbb{H}^{n}\) is accordingly defined by
For a complete treatment on the Heisenberg group functional setting, we refer to [7, 10, 14, 23].
The inspiration for our study to problem (1.1) is the application of the Heisenberg group. Recently, the reason why many scholars are interested in the Heisenberg group is its important applications in quantum mechanics, partial differential equations, and other fields. We try to put the same theorem applicable to a Euclidean space on the Heisenberg group, and many scholars are studying this kind of problem.
Next, we will focus on some latest progress of study related to our problem. In [4], the authors obtained the existence of solutions for the sub-elliptic equation involving small, nontrivial perturbations in the whole space \(\mathbb{H}^{n}\)
where V is a continuous potential and f has exponential growth. After that, using a minimization argument and the Ekeland variational principle, Lam and Lu [13] considered that in the absence of perturbation \((\varepsilon =0)\), and they obtained the existence and multiplicity of solutions of problem (1.3). Subsequently, by variational methods, Pucci et al. [25, 26] dealt with the existence of nontrivial solutions for \((p, Q)\) equations and \((p, Q)\) system in the Heisenberg group \(\mathbb{H}^{n}\) by considering the case without the potential function.
On the other hand, in the Euclidean space, Li [15] considered the strongly indefinite functional involving p-Laplacian elliptic system with the help of limit index theory:
More precisely, they obtained an unbounded sequence of solutions with appropriate conditions for F. There are many works in the literature on this subject that are very connected to this problem. Let us refer to some of them for further reference [9, 15, 17, 19, 21, 22, 27].
Inspired by the above references, our main aim in this paper is to consider the existence and multiplicity of solutions for problem (1.1) involving p-Laplacian operator and critical nonlinearity on the Heisenberg group. Undoubtedly, the lack of compactness makes us encounter serious difficulties. It is worth noting the argument developed in [9], where one of the emphases is to verify the proof the \((PS)_{c}\) condition. In this paper, we use the concentration–compactness principle and the concentration–compactness principle at infinity on the classical Sobolev spaces in the Heisenberg group to prove that the \((PS)_{c}\) condition holds. To the best of our knowledge, this paper is the first to deal with noncooperative Schrödinger–Kirchhoff systems with p-Laplacian and critical nonlinearity on the Heisenberg group. Furthermore, although some properties are similar between Kohn Laplacian \(\Delta _{H}\) and the classical Laplacian Δ, the similarities may be deceitful; see, e.g., [7].
Now, we are ready to state our main results.
Theorem 1.1
Assume that V satisfies \((V_{1})\) and \((V_{2})\), K satisfies \((K_{1})\)–\((K_{2})\), and F satisfies \((F_{1})\)–\((F_{3})\), then problem (1.1) possesses infinitely solutions.
This paper is organized as follows. In Sect. 2, we present some necessary preliminary knowledge on the Heisenberg group and collect some properties about the space \(HW^{1,p}\). In Sect. 3, we recall the limit index theory due to Li [15]. In Sect. 4, we use the concentration–compactness principle to prove \((PS)_{c}\) conditions. Section 5 is devoted to the proofs of Theorem 1.1.
2 Preliminaries
In this section, we give some useful facts about classical Sobolev spaces on the Heisenberg group and provide some technical lemmas.
Let \(1\leq p< Q\) be a real number. Denote by \(HW^{1,p}(\mathbb{H}^{n})\) the horizontal Sobolev space consisting of the functions \(u\in L^{p}(\mathbb{H}^{n})\) such that \(D_{H}u\in L^{p}\) exists in the sense of distributions and \(|D_{H}u|_{H}\in L^{p}(\mathbb{H}^{n})\), equipped with the natural norm
For brevity, we use the notation \(\|\cdot \|_{p}=\|\cdot \|_{L^{p}}\) to denote the usual \(L^{p}\)-norm.
Let \(HW^{1,p}_{V}(\mathbb{H}^{n})\) represent the completion of \(C_{c}^{\infty}(\mathbb{H}^{n})\) with the norm
Due to \((V_{1})\), we can obtain \(L^{p}(\mathbb{H}^{n},V)=(L^{p}(\mathbb{H}^{n},V),\|\cdot \|_{p,V})\) is a uniformly convex Banach space.
According to Folland and Stein [6], the elliptical Sobolev embedding theorem and C-R Yamabe problem are often closely linked together. It is valid in the more general case of the Carnot group, but we state it in the establishment of the Heisenberg group.
The continuous embedding of \(HW^{1,Q}(\mathbb{H}^{n})\hookrightarrow L^{s}(\mathbb{H}^{n})\) for all \(s\geq Q\) by [4]. That is, there exists a positive constant C such that
From [28] that \(C_{p^{\ast}}\) is achieved in the Folland–Stein space \(S^{1,p}(H^{n})\). We define the optimal Sobolev constant \(C_{p^{\ast}}\) of the Folland–Stein inequality as follows:
Let \(Y=HW_{V}^{1,p}(\mathbb{H}^{n})\times HW_{V}^{1,p}(\mathbb{H}^{n})\), equipped with the norm
for all \((u,v)\in Y\).
We will use the embedding theorem below to prove the existence of weak solutions to problem (1.1).
The energy functional corresponding to problem (1.1) is defined as follows:
Under the assumption, it is obvious that the energy \(\mathcal {J}: Y\rightarrow \mathbb{R}\) connected with problem (1.1) is well defined and \(\mathcal {J}\in C^{1}(Y\rightarrow \mathbb{R})\),
for all \((u,v)\in Y\) and \((\varphi ,\phi )\in Y\). Therefore, the critical points of function \(\mathcal {J}\) are weak solutions of problem (1.1).
Next, we recall the concentration–compactness principle of the p Laplacian on the Heisenberg group.
Definition 2.1
Let \(\mathcal {M}(\mathbb{H})\) show the finite nonnegative Radon measures space in \(\mathbb{H}^{n}\). For any \(\mu \in \mathcal {M}(\mathbb{H}^{n})\), \(\mu (\mathbb{H}^{n})=\|\mu \|\) holds. We say that \(\mu _{n}\stackrel{\ast}{\rightharpoonup} \mu \) in \(\mathcal {M}(\mathbb{H}^{n})\) if \((\mu _{n},\eta )\rightarrow (\mu ,\eta )\) holds for all \(\eta \in C_{0}(\mathbb{H}^{n})\) as \(n\rightarrow \infty \).
Proposition 2.1
Let \(\sigma \in (-\infty ,\mathcal {H}_{p})\) and let \((u_{k})_{k}\) be a sequence in \(S^{1,p}(\mathbb{H}^{n})\) such that \(u_{k}\rightharpoonup u\) in \(S^{1,p}(\mathbb{H}^{n})\), and \(|u_{k}|^{p^{\ast}}\,d\xi \stackrel{\ast}{\rightharpoonup}\nu \), \(|D_{H}u_{k}|_{H}^{p}\,d\xi \stackrel{\ast}{\rightharpoonup}\mu \), \(|u_{k}|^{p}\psi ^{p}\frac{d\xi}{r(\xi )^{p}} \stackrel{\ast}{\rightharpoonup}\omega \) in \(\mathcal {M}(\mathbb{H}^{n})\) for some appropriate \(u\in S^{1,p}(\mathbb{H}^{n})\) and finite nonnegative Radon measure μ, ν, ω on \(\mathbb{H}^{n}\). Then there exists an at most countable set J, a family of points \(\{\xi _{k}\}_{j\in J}\subset \mathbb{H}^{n}\), two families of nonnegative numbers \(\{\mu _{k}\}_{j\in J}\), and \(\{\nu _{k}\}_{j\in J}\), and there are nonnegative numbers \(\nu _{0}\), \(\mu _{0}\), \(\omega _{0}\) such that
where \(C_{p^{\ast}}=I_{0}\) and \(I_{\sigma} =\inf_{u\in S^{1,p}(\mathbb{H}^{n}),u \neq 0} \frac{\|D_{H}u\|_{p}^{p}-\sigma \|u\|_{H_{p}}^{p}}{\|u\|_{p^{\ast}}^{p}}\), while \(\delta _{0}\), \(\delta _{\xi _{j}}\) are the Dirac functions at the points O and \(\xi _{j}\) of \(\mathbb{H}^{n}\), respectively.
Proposition 2.2
Let \((u_{k})_{k}\) be a sequence in \(S^{1,p}(\mathbb{H}^{n})\) as in Proposition 2.1and define
and
Then
where μ, ν, ω are the measures introduced in Proposition 2.1. Moreover, the following inequality holds if \(\sigma =0\):
Remark 2.1
Weak (resp. strong) convergence is denoted by ⇀ (resp., →). \(G_{1}=O(Q)\) is the group of orthogonal linear transformations in \(\mathbb{H}^{n}\). \(E=HW^{1,p}(\mathbb{H}^{n})\), \(E_{G_{1}}=HW_{O(Q)}^{1,p} :=\{u\in HW^{1,p}(\mathbb{H}^{n}): gu(\xi )=u(g^{-1} \xi )=u(\xi ), g\in O(Q)\}\). \(G_{2}=Z_{2}\), \(Y=E\times E\), \(X=Y_{G_{1}}=E_{G_{1}}\times E_{G_{1}}\), c denotes a positive constant.
3 Limit index theory
In this section, we review the limit index theory by Li [15] and give the following definitions.
Definition 3.1
The action of a topological group G on a normed space Z is a continuous map
such that
The action is isometric if
and in this case Z is called the G-space.
The set of invariant points is defined by
A set \(A\subset Z\) is invariant if \(gA=A\) for every \(g\in G\). A function \(\varphi : Z\rightarrow R\) is invariant \(\varphi \circ g=\varphi \) for every \(g\in G\), \(z\in Z\). A map \(f: Z\rightarrow Z\) is equivariant if \(g\circ f=f\circ g\) for every \(g\in G\).
Assume that Z is a G-Banach space, that is, there is a G isometric action on Z. Let
be a family of all G-invariant closed subsets of Z, and let
be a class of all G-equivariant mappings of Z. Finally, we call the set
the G-orbit of u.
Definition 3.2
([15])
An index for \((G, \sum , \Gamma )\) is a mapping \(i:=\sum \rightarrow \mathcal {Z}_{+}\cup \{+\infty \}\) (where \(\mathcal {Z}_{+}\) is the set of all nonnegative integers) such that, for all \(A, B\in \Sigma \), \(h\in \Gamma \), the following conditions are satisfied:
-
(1)
\(i(A)=0 \Leftrightarrow A=\emptyset \);
-
(2)
(Monotonicity) \(A\subset B\Rightarrow i(A)\leq i(B)\);
-
(3)
(Subadditivity) \(i(A\cup B)\leq i(A)+i(B)\);
-
(4)
(Supervariance) \(i(A)\leq i(\overline{h(A)})\), \(\forall h\in \Gamma \);
-
(5)
(Continuity) If A is compact and \(A\cap \operatorname{Fix}(G)=\emptyset \), then \(i(A)<+\infty \) and there is a G-invariant neighborhood N of A such that \(i(\overline{N})=i(A)\);
-
(6)
(Normalization) If \(\xi \notin \operatorname{Fix}(G)\), then \(i(O(\xi ))=1\).
Definition 3.3
([3])
An index theory is said to satisfy the d-dimensional property if there is a positive integer d such that
for all dk-dimensional subspaces \(V^{dk}\in \Sigma \) such that \(V^{dk} \cap \operatorname{Fix}(G)=\{0\}\), where \(S_{1}\) is the unit sphere in Z.
Suppose that U and V are G-invariant closed subspaces of Z such that
where V is infinite dimensional and
where \(V_{j}\) is a \(dn_{j}\)-dimensional G-invariant subspace of V, \(j = 1, 2,\ldots \) , and \(V_{1}\subset V_{1}\subset \cdots \subset V_{1} \subset \cdots \) . Let
and \(\forall A\in \sum \), let
Definition 3.4
([15])
Let i be an index theory satisfying the d-dimensional property. A limit index with respect to \((Z_{j})\) introduced by i is a mapping
given by
Proposition 3.1
([15])
Let \(A, B\in \sum \), then \(i^{\infty}\) satisfies:
-
(1)
\(A=\emptyset \Rightarrow i^{\infty}=-\infty \);
-
(2)
(Monotonicity) \(A\subset B\Rightarrow i^{\infty}(A)\leq i^{ \infty}(B)\);
-
(3)
(Subadditivity) \(i^{\infty}(A\cup B)\leq i^{\infty}(A)+i^{\infty}(B)\);
-
(4)
If \(V\cap \operatorname{Fix}\{G\}=0\), then \(i^{\infty}(S_{\varrho}\cap V)=0\), where \(S_{\varrho}=\{z\in Z:\|z\|=\varrho \}\);
-
(5)
If \(Y_{0}\) and \(\widetilde{Y_{0}}\) are G-invariant closed subspaces of V such that \(V=Y_{0}\oplus \widetilde{Y_{0}}\), \(\widetilde{Y_{0}}\subset V_{j_{0}} \) for some \(j_{0}\) and \(\dim(Y_{0})=dm\), then \(i^{\infty}(S_{\varrho}\cap Y_{0})\geq -m\).
Definition 3.5
([29])
A functional \(\mathcal {J}\in C^{1}(Z,R)\) is said to satisfy the condition \((PS)_{c}^{\ast}\) if any sequence \(\{u_{n_{k}}\}, u_{n_{k}}\in Z_{u_{n_{k}}}\) such that
possesses a convergent subsequence, where \(Z_{u_{n_{k}}}\) is the \(n_{k}\)-dimensional subspace of Z, \(\mathcal {J}_{n_{k}}=\mathcal {J}|_{Z_{u_{n_{k}}}}\).
Theorem 3.1
([15])
Assume that
- \((B_{1})\):
-
\(\mathcal {J}\in C^{1}(Z,R)\) is G-invariant;
- \((B_{2})\):
-
There are G-invariant closed subspaces U and V such that V is infinite dimensional and \(Z=U\oplus V\);
- \((B_{3})\):
-
There is a sequence of G-invariant finite dimensional subspaces
$$ V_{1}\subset V_{2} \subset \cdots \subset V_{j} \subset \cdots , \qquad \dim(V_{j})=dn_{j},$$such that \(V=\overline{\bigcup_{j=1}^{\infty }V_{j}}\);
- \((B_{4})\):
-
There is an index theory i on Z satisfying the d-dimensional property;
- \((B_{5})\):
-
There are G-invariant subspaces \(Y_{0}\), \(\widetilde{Y_{0}}\), \(Y_{1}\) of V such that \(V=Y_{0}\oplus \widetilde{Y_{0}}, Y_{1}\), \(\widetilde{Y_{0}}\subset V_{j_{0}}\) for some \(j_{0}\) and \(\dim(\widetilde{Y_{0}})=dm< dk=\dim(Y_{1})\);
- \((B_{6})\):
-
There are α, β and \(\alpha <\beta \) such that f satisfies \((PS)_{c}^{\ast}\), \(\forall c\in [\alpha ,\beta ]\);
- \((B_{7})\):
-
$$ \textstyle\begin{cases} (\mathrm{a}) & \textit{either}\quad \operatorname{Fix}(G)\subset U\oplus Y_{1} \quad \textit{or} \quad \operatorname{Fix}(G) \cap V=\{0\}, \\ (\mathrm{b}) & \textit{there is} \quad \varrho >0 \quad \textit{such that}\quad \forall u\in Y_{0}\cap S_{\varrho}, \quad f(z)\geq \alpha , \\ (\mathrm{c}) & \forall z\in U\oplus Y_{1},\quad f(z)\leq \beta , \end{cases} $$
if \(i^{\infty}\) is the limit index corresponding to i, then the numbers
are critical values of f, and \(\alpha \leq c_{-k+1}\leq \cdots \leq c_{-m}\leq \beta \). Moreover, if \(c=c_{l}=\cdots =c_{l+r}\), \(r\geq 0\), then \(i(\mathbb{K}_{c})\geq r+1\), where \(\mathbb{K}_{c}=\{z\in Z: df(z)=0,f(z)=c\}\).
4 Verification of the \((PS)_{c}\) condition
In this section, with the help of the concentration–compactness principle in the classical Sobolev space on the Heisenberg group stated above, we show a careful analysis of the behavior of minimizing sequences, which is able to recover compactness below some critical threshold.
It is obvious that \({\mathcal {J}}\in C^{1}\). Moreover, the weak solution of problem (1.1) is consistent with the critical point of \({\mathcal {J}}\). According to \((H_{4})\) and \((H_{6})\), we can obtain that \({\mathcal {J}}\) is \(O(Q)\)-invariant. Combining with the principle of symmetric criticality due to Krawcewicz and Marzantowicz [12], we get that \((u,v)\) is a critical point of \({\mathcal {J}}\) if and only if \((u,v)\) is a critical point of \(\widetilde{\mathcal {J}}={\mathcal {J}}|_{X=E_{G_{1}}\times E_{G_{1}}}\). So, we are going to focus on verifying the existence of a sequence of critical points of \({\mathcal {J}}\) on X. At the same time, let E be a real Banach space and \(\widetilde{\mathcal {J}}: E\rightarrow \mathbb{R}\) be a function of class \(C^{1}\).
Lemma 4.1
Suppose that condition V satisfies \((V_{1})\) and \((V_{2})\), K satisfies \((K_{1})\)–\((K_{2})\), F satisfies \((F_{1})\)–\((F_{3})\). Let \(\{(u_{n_{k}}, v_{n_{k}})\}\) be a sequence such that \(\{(u_{n_{k}}, v_{n_{k}})\}\in X_{n_{k}}\).
where \(\mathcal {J}_{n_{k}}=\mathcal {J}|_{X_{n_{k}}}\), then \(\{(u_{n_{k}},v_{n_{k}})\}\) contains a subsequence converging strongly in X.
Proof
To this aim, we need two steps as follows.
Step 1. We show that \(\{(u_{n_{k}},v_{n_{k}})\}\) is bounded in X.
By conditions \((M_{1})\) and \((F_{2})\), we obtain that
Since \(p>1\), from (4.1), we obtain that \(\|u_{n_{k}}\|\) is bounded.
On the other hand, using condition \((F_{2})\), we have
This shows that \(\{v_{n_{k}}\}\) is bounded in E. Therefore, \(\|u_{n_{k}}\|_{p}+\|v_{n_{k}}\|_{p}\) is bounded in X.
Step 2. We prove that \(\{(u_{n_{k}},v_{n_{k}})\}\) contains a subsequence converging strongly in X.
Note that \(\{u_{n_{k}}\}\) is bounded in \(E_{G_{1}}\). Therefore, up to a sequence, \(u_{n_{k}}\rightharpoonup u_{0}\) weakly in \(E_{G_{1}}\) and \(u_{n_{k}}(\xi )\rightarrow u_{0}(\xi )\), a.e. in \(\mathbb{H}^{n}\).
(I). We claim that \(u_{n_{k}}(\xi )\rightarrow u_{0}(\xi )\) strongly in \(E_{G_{1}}\). It follows from conditions \((K_{1})\) and \((F_{2})\) that
This fact implies that
(II). In the following we will prove that there exists \(v\in E_{G_{1}}\) such that
Since \(\{v_{n_{k}}\}\) is also bounded in E, we suppose that there exist \(v_{0}\) and a subsequence, still denoted by \(\{v_{n_{k}}\}\subset E\), such that
From Proposition 2.1, we obtain that
Then
where J is at most countable, \(\{\nu _{j}\}_{j}\subset \mathbb{H}^{n}\), \(\delta _{O}\), \(\delta _{x_{j}}\) are the Dirac functions at the points O and \(\xi _{j}\) of \(\mathbb{H}^{n}\), respectively.
Concentration at infinity of the sequence \({v_{n_{k}} }\) is described by the following quantities:
Now, we will prove that the following three claims hold.
Claim 1.
In fact, fix \(\phi \in C_{c}^{\infty}(\mathbb{H}^{n})\) such that \(0\leq \phi \leq 1\), \(\phi (O)=1\) and supp \(\phi =\overline{B_{1}}\). Take \(\varepsilon >0\) and put \(\phi _{\varepsilon}(\xi )=\phi (\delta _{1 / \varepsilon}(\xi ))\), \(\xi \in \mathbb{H}^{n}\).
Then we get that \(\{v_{n_{k}}\phi _{\varepsilon}\}\) is bounded in E.
Hence, we obtain that
that is,
In the following, we estimate each term in (4.5).
In fact, arguing as before, we have
Now, by the compactness result (see Proposition 2.1), we know that
Therefore, from (4.6) and (4.7), we deduce that
Also, we can get that
and
Hence, from (4.5) and the aforementioned arguments, we obtain
Combining with (4.4), we can deduce
Claim 2. Analyzing the concentration at ∞.
Choosing a appropriate cut-off function \(\Psi \in C_{c}^{\infty}(\mathbb{H}^{n})\) such that \(0\leq \Psi \leq 1\), \(\Psi = 0\) in \(B_{1}\) and \(\Psi =1\) in \(B_{2}^{c}\). We take \(R>0\) and choose \(\Psi _{R}(\xi )=\Psi (\delta _{1/R(\xi )})\), \(\xi \in \mathbb{H}^{n}\), then \(\{v_{n_{k}}\Psi _{R}\}\) is bounded in E and
that is,
In the following, we estimate each term in (4.13).
In fact, in the first integral of the right-hand side of (4.13), using the compactness result (see Proposition 2.2), we have
For the second integral of the right-hand side of (4.13), it follows that
Hence, we get
We also can have
and
Note that \(v_{n_{k}}\rightharpoonup v\) weakly in E, then \(\int _{\mathbb{H}^{n}}F_{v}(\xi ,u,v)(v_{n_{k}}-v)\Psi _{R} \,d\xi \rightarrow 0\). As
by condition \((F_{1})\), for any \(\varepsilon >0\), there exists \(R_{1}>0\) such that, when \(R>R_{1}\),
Note that \(\int _{\mathbb{H}^{n}}F_{v}(\xi ,u,v)v\Psi _{R}\,d\xi \rightarrow 0\) as \(R\rightarrow \infty \). Thus, we can deduce that
Due to Proposition 2.2, we deduce that
Claim 3. (ii) and (iv) cannot occur.
By contradiction, we assume that for some \(j\in J\), then by condition \((F_{2})\), we have
This is impossible. Consequently, \(\nu _{\infty}=0\). Similarly, we can prove that (ii) cannot hold for each j. Hence
Moreover, the Brézis–Lieb lemma implies that
Now, we define an operator as follows:
for any \(v, \varpi \in E\). The Hölder inequality gives
Hence, for each \(v\in E\), the linear functional \(\mathcal {L}(v)\) is continuous on E. Hence, the weak convergence of \(v_{n_{k}}\) in E gives that
Clearly, \(\langle \mathcal {J}(v_{n_{k}}),v_{n_{k}}-v_{0}\rangle \rightarrow 0\) as \(n\rightarrow \infty \). Hence, by (4.21), one has
By famous Simon inequalities,
for all \(s,t \in H^{n}\), where \(C_{p}^{\prime }\) and \(C_{p}^{\prime \prime }\) are positive constants depending only on p.
If \(p>2\), then if follows from (4.23) that
as \(n\rightarrow \infty \). Hence, \(v_{n_{k}}\rightarrow v_{0}\) in E.
It remains to deal with the case \(1< p<2\). In order to reach this aim, from (4.23) we get
as \(n\rightarrow \infty \). Consequently, \(v_{n_{k}}\rightarrow v_{0}\) in E.
Therefore, we can deduce that \(v_{n_{k}}\rightarrow v_{0}\) in E as \(n\rightarrow \infty \). The proof of convergence of \(\{u_{n_{k}}\}\) is similar, so we omit it.
Consequently, we obtain that \(\{(u_{n_{k}},v_{n_{k}})\}\) contains a sequence converging strongly in X. □
5 Proof of Theorem 1.1
Proof
Now we will prove the condition of Theorem 3.1. Set
where m and k are to be determined. It is obvious that \(Y_{0}\), \(Y_{1}\) are G-invariant and \(\operatorname{codim} {_{V}}Y_{0}=m\), \(\operatorname{dim} Y_{1}=k\). Clearly, \((B_{1})\), \((B_{2})\), \((B_{4})\) in Theorem 3.1 are satisfied. Set \(V_{j}=E_{G_{1}}^{(j)}=\) \(\operatorname{span} \{e_{1},e_{2},\ldots , e_{j}\}\), then \((B_{3})\) is also satisfied. By \(\operatorname{dim} \widetilde{Y_{0}}=1< k=\operatorname{dim}Y_{1}\), \((B_{5})\) holds. In the following, we prove the condition \((B_{7})\). Since \(\operatorname{Fix}(G)\cap V=0\), (a) of \((B_{7})\) are satisfied. It remains to verify (b), (c) of \((B_{7})\).
(i) If \((0,v)\in Y_{0}\cap S_{\varrho m}\) (where \(\varrho _{m}\) is to be determined), then by \((F_{1})\) and \((F_{2})\),
since \(p< q< p^{\ast}\), there exists \(\varrho >0\) such that \(\mathcal {J}(0,v)\geq \alpha \) for every \(\|v\|=\varrho \), that is, (b) of \((B_{7})\) holds.
(ii) From \((H_{1})\), we have
Therefore, we choose α such that
For each \((u,v)\in U\oplus Y_{1}\), we get
Since all norms are equivalent on the finite dimensional space \(Y_{1}\), we can choose \(k>m\) and \(\beta _{k}>\alpha _{m}\) such that
hence, we have \((c)\) in \((B_{7})\). Using Lemma 4.1, for any \([\alpha _{m}, \beta _{k}]\), \(\mathcal {J}(u,v)\) satisfies the condition of \((PS)_{c}^{\ast}\), then \((B_{6})\) in Theorem 3.1 is satisfied. Therefore, according to Theorem 3.1,
are critical values of \(\mathcal {J}\). Letting \(m\rightarrow \infty \), we can get an unbounded sequence of critical values \(c_{j}\). And since the functional \(\mathcal {J}\) is even, we have two critical points \(\pm u_{j}\) of \(\mathcal {J}\) corresponding to \(c_{j}\). □
Availability of data and materials
Not applicable.
References
Alves, C.O., Corrês, F.J.S.A., Ma, T.F.: Positive solutions for a quasilinear elliptic equation of Kirchhoff type. Comput. Math. Appl. 49, 85–93 (2005)
Bartsch, T., Wang, Z.Q.: Existence and multiplicity results for some superlinear elliptic problems on \(\mathbb{R}^{n}\). Commun. Partial Differ. Equ. 20, 1725–1741 (1995)
Benci, V.: On critical point theory for indefinite functionals in presence of symmetries. Trans. Am. Math. Soc. 274, 533–572 (1982)
Cohn, W.S., Lam, N., Lu, G., Yang, Y.: The Moser–Trudinger inequality in unbounded domains of Heisenberg group and sub-elliptic equations. Nonlinear Anal. 75, 4483–4495 (2012)
Figueiredo, G.M., Severo, U.B.: Ground state solution for a Kirchhoff problem with exponential critical growth. Milan J. Math. 84, 23–39 (2016)
Folland, G.B., Stein, E.M.: Estimates for the ∂̄b complex and analysis on the Heisenberg group. Commun. Pure Appl. Math. 27, 429–522 (1974)
Garofalo, N., Lanconelli, E.: Frequency functions on the Heisenberg group, the uncertainty principle and unique continuation. Ann. Inst. Fourier 40, 313–356 (1990)
He, X., Zou, W.: Infinitely many positive solutions of Kirchhoff type problems. Nonlinear Anal. 70, 1407–1414 (2009)
Huang, D.W., Li, Y.Q.: Multiplicity of solutions for a noncooperative p-Laplacian elliptic system in \(\mathbb{R}^{N}\). J. Differ. Equ. 215, 206–223 (2005)
Ivanov, S.P., Vassilev, D.N.: Extremals for the Sobolev Inequality and the Quaternionic Contact Yamabe Problem. World Scientific, Hackensack (2011)
Kirchhoff, G.: Mechanik. Teubner, Leipzig (1883)
Krawcewicz, W., Marzantowicz, W.: Some remarks on the Lusternik–Schnirelman method for non-differentiable functionals invariant with respect to a finite group action. Rocky Mt. J. Math. 20, 1041–1049 (1990)
Lam, N., Lu, G.: Sharp Moser–Trudinger inequality on the Heisenberg group at the critical case and applications. Adv. Math. 231, 3259–3287 (2012)
Leonardi, G.P., Masnou, S.: On the isoperimetric problem in the Heisenberg group \(\mathbb{H}^{n}\). Ann. Mat. Pura Appl. 184, 533–553 (2005)
Li, Y.Q.: A limit index theory and its application. Nonlinear Anal. TMA 25, 1371–1389 (1995)
Liang, S., Pucci, P., Zhang, B.: Multiple solutions for critical Choquard–Kirchhoff type equations. Adv. Nonlinear Anal. 10, 400–419 (2021)
Liang, S., Shi, S.: Multiplicity of solutions for the noncooperative \(p(x)\)-Laplacian operator elliptic system involving the critical growth. J. Dyn. Control Syst. 18, 379–396 (2012)
Liang, S., Shi, S.: Soliton solutions to Kirchhoff type problems involving the critical growth in \(\mathbb{R}^{N}\). Nonlinear Anal. 81, 31–41 (2013)
Liang, S., Zhang, J.: Multiple solutions for noncooperative \(p(x)\)-Laplacian equations in \(\mathbb{R}^{N}\) involving the critical exponent. J. Math. Anal. Appl. 403, 344–356 (2013)
Liang, S., Zhang, J.: Existence of solutions for Kirchhoff type problems with critical nonlinearity in \(\mathbb{R}^{3}\). Nonlinear Anal., Real World Appl. 17, 126–136 (2014)
Liang, S.H., Bisci, G.M., Zhang, B.L.: Multiple solutions for a noncooperative Kirchhoff-type system involving the fractional p-Laplacian and critical exponents. Math. Nachr. 291, 1533–1546 (2018)
Liang, S.H., Zhang, J.H.: Multiplicity of solutions for the noncooperative Schrödinger–Kirchhoff system involving the fractional p-Laplacian in \(\mathbb{R}^{N}\). Z. Angew. Math. Phys. 68, 63 (2017)
Loiudice, A.: Improved Sobolev inequalities on the Heisenberg group. Nonlinear Anal. 62, 953–962 (2005)
Perera, K., Zhang, Z.: Nontrivial solutions of Kirchhoff-type problems via the Yang index. J. Differ. Equ. 221, 246–255 (2006)
Pucci, P., Temperini, L.: \((p, Q)\) systems with critical exponential nonlinearities in the Heisenberg group. Open Math. 18, 1423–1439 (2020)
Pucci, P., Temperini, L.: Existence for singular critical exponential \((p, Q)\) equations in the Heisenberg group. Adv. Calc. Var. (2021). https://doi.org/10.1515/acv-2020-0028
Pucci, P., Xiang, M.Q., Zhang, B.L.: Multiple solutions for nonhomogeneous Schrödinger–Kirchhoff type equations involving the fractional p-Laplacian in \(\mathbb{R}^{N}\). Calc. Var. Partial Differ. Equ. 54, 2785–2806 (2015)
Vassilev, D.: Existence of solutions and regularity near the characteristic boundary for sub-Laplacian equations on Carnot groups. Pac. J. Math. 227, 361–397 (2006)
Willem, M.: Minimax Theorems. Progress in Nonlinear Differential Equations and Their Applications, vol. 24. Birkhäser, Boston (1996)
Funding
X. Sun was supported by the Graduate Scientific Research Project of Changchun Normal University (SGSRPCNU [2022], Grant No. 056). Y. Song was supported by the National Natural Science Foundation of China (Grant No. 12001061), the Research Foundation of Department of Education of Jilin Province (Grant No. JJKH20220822KJ), and the Natural Science Foundation of Jilin Province (Grant No. YDZJ202201ZYTS582).
Author information
Authors and Affiliations
Contributions
X. Sun and Sh. Bai wrote the main manuscript text. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, X., Bai, S. & Song, Y. On the noncooperative Schrödinger–Kirchhoff system involving the critical nonlinearities on the Heisenberg group. Bound Value Probl 2022, 75 (2022). https://doi.org/10.1186/s13661-022-01657-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-022-01657-3