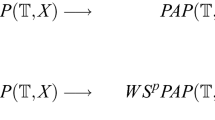Local pseudo almost automorphic functions with applications to semilinear dynamic equations on changing-periodic time scales

Abstract

In this paper, based on the concepts of changing-periodic time scales, we introduce a notion of local pseudo almost automorphic functions on an arbitrary time scale with a bounded graininess function μ. Then, some properties of local pseudo almost automorphic functions are investigated. As applications, by adopting the concept of a Π-semigroup on time scales, we obtain some new sufficient conditions for the existence of local pseudo almost automorphic mild solutions for a class of semilinear dynamic equations on arbitrary time scales.

1 Introduction

Almost periodic and almost automorphic functions are widely studied and applied in the literature, and there have been several natural and powerful generalizations of classical almost automorphic functions (see [1,2,3,4]). In [5,6,7], the authors introduced the concept of pseudo almost automorphic functions, which generalizes both the classical concept of almost automorphy and that of pseudo almost periodicity. Moreover, they proved that the space of pseudo almost automorphic functions is complete, which solves a key fundamental problem on this issue and it paves the way for further study and applications of pseudo almost automorphic functions. For other contributions concerning pseudo almost automorphy, we refer the reader to [8, 9] and the references therein related to applications (see [10,11,12,13,14,15,16,17]). In [18], N’Guérékata and Pankov introduced another generalization of almost automorphic functions, i.e., Stepanov-like almost automorphic functions. This notion was, subsequently, used to study the existence of weak Stepanov-like almost automorphic solutions to some parabolic evolution equations. In addition, Diagana and N’Guérékata studied the existence and uniqueness of almost automorphic solutions to some evolution equations on Banach spaces with Stepanov-like almost automorphic coefficients; we refer the reader to [19, 20] and the references therein for more contributions concerning Stepanov-like almost automorphy.

Almost periodicity and almost automorphy of functions were extended to time scales and were studied with the development of the time scale theory initiated by Hilger in 1988 (see [21,22,23,24]). Various types of time variables can be unified and applied to dynamic equations to obtain many results for almost periodic and almost automorphic solutions (see [25,26,27]). For example, one can obtain difference equations by taking a regular discrete type of time variable like $\mathbb{T}=h\mathbb{Z}$, $h>0$, or differential equations by taking a continuous type of time variable like $\mathbb{T}=\mathbb{R}$. Time scales $h\mathbb{Z}$ and $\mathbb{R}$ have some very nice properties so that the dynamic change of functions established on them can be described well because of the closedness for the translation of time variables. Periodic time scales have a nice closedness for the translation of time variables (see [28]). For example, consider the following periodic time scale:

$$ \mathbb{T}=\bigcup_{k=-\infty }^{+\infty } \bigl[k(a+b),k(a+b)+a \bigr], \quad a,b\in \mathbb{R}, k\in \mathbb{Z}. $$

(1.1)

We can take its periodicity set $\varPi _{0}=\{n(a+b), n\in \mathbb{Z}\}$ as the translations number set for time scale (1.1). Under the translation of any number from $\varPi _{0}$, the time scale $\mathbb{T}$ will coincide with itself, and in this case, we say $\mathbb{T}$ is with “complete closedness”. Further, the time scale $\mathbb{T}$ also includes the classical time scales since if $a=1$, $b=0$, then $\mathbb{T}=\mathbb{R}$; if $a=0$, $b=h$, $h>0$, then $\mathbb{T}=h \mathbb{Z}$. A time scale with such a type of “complete closedness” assists in conquering the difficulties of defining and studying functions on time scales.

In 2014, Wang and Agarwal introduced the concept of almost periodic time scales to describe that a time scale is with “almost complete closedness” (see [29, 30]). For example, consider the following time scale:

Let $a>1$ and consider the following almost periodic time scale:

$$ \mathbb{P}_{a,|\sin \sqrt{3}t+\sin \sqrt{7}t|}=\bigcup_{m=1}^{ \infty }[p_{m},a+p_{m}], $$

where

$$\begin{aligned} p_{m} =&(m-1)a+\sum_{k=1}^{m-1} \bigl\vert \sin \sqrt{3} \bigl(ka+ \vert \sin \sqrt{3}a+\sin \sqrt{7}a \vert \\ &{}+ \bigl\vert \sin \sqrt{3} \bigl(2a+ \vert \sin \sqrt{3}a+\sin \sqrt{7}a \vert \bigr) \\ &{}+\sin \sqrt{7} \bigl(2a+ \vert \sin \sqrt{3} a+\sin \sqrt{7}a \vert \bigr) \bigr\vert \\ &{}+\cdots + \bigl|\sin \sqrt{3} \bigl((k-1)a+ \vert \sin \sqrt{3}a+\sin \sqrt{7}a \vert \bigr) \\ &\underbrace{{}+\sin \sqrt{7} \bigl((k-1)a+ \vert \sin \sqrt{3}a+\sin \sqrt{7}a \vert \bigr) \bigr|}_{k\text{ terms}} \bigr) \\ &{}+\sin \sqrt{7} \bigl(ka+ \vert \sin \sqrt{3} a+\sin \sqrt{7}a \vert \\ &{}+ \bigl\vert \sin \sqrt{3} \bigl(2a+ \vert \sin \sqrt{3} a+\sin \sqrt{7}a \vert \bigr) \\ &{}+\sin \sqrt{7} \bigl(2a+ \vert \sin \sqrt{3}a+\sin \sqrt{7}a \vert \bigr) \bigr\vert \\ &{}+\cdots + \bigl|\sin \sqrt{3} \bigl((k-1)a+ \vert \sin \sqrt{3}a+\sin \sqrt{7}a \vert \bigr) \\ &\underbrace{{}+\sin \sqrt{7} \bigl((k-1)a+ \vert \sin \sqrt{3} a+\sin \sqrt{7}a \vert \bigr) \bigr|}_{k\text{ terms}} \bigr) \bigr\vert . \end{aligned}$$

(1.2)

Then we have

$$ \sigma (t)= \textstyle\begin{cases} t,& \text{if }\in \bigcup_{m=1}^{\infty }[p_{m},a+p_{m}), \\ t+ \vert \sin \sqrt{3} t+\sin \sqrt{7}t \vert , &\text{if }t\in \bigcup_{m=1} ^{\infty }\{a+p_{m}\} \end{cases} $$

and

$$ \mu (t)= \textstyle\begin{cases} 0,& \text{if }t\in \bigcup_{m=1}^{\infty }[p_{m},a+p_{m}), \\ \vert \sin \sqrt{3}t+\sin \sqrt{7}t \vert ,& \text{if }t\in \bigcup_{m=1}^{ \infty }\{a+p_{m}\}. \end{cases} $$

This type of time scales can describe the “double almost periodicity” of an object with almost periodic dynamic behavior in the real world. We can take its almost periodicity set $\varPi _{\varepsilon }=E\{\varepsilon ,\mathbb{T}\}$ as the translations number set for time scale (1.2). Under the translation of any number from $\varPi _{\varepsilon }$, the time scale $\mathbb{T}$ will almost coincide with itself when $\varepsilon >0$ is sufficiently small, and in this case, we say $\mathbb{T}$ is with “almost complete closedness”. This type of time scales is more general and comprehensive than periodic time scales.

Therefore, “complete closedness” and “almost complete closedness” of time scales under translations are significant and pivotal when introducing and studying functions on time scales. To solve the closedness of an arbitrary time scale, in 2015, a completely new concept called “changing-periodic time scales” was proposed in [31], which provides an effective method to decompose an arbitrary time scale with the bounded graininess function μ into an accountable union of periodic time scales, that is, there exist accountable periodic sub-timescales with “complete closedness” so that they can cover an arbitrary time scale with the bounded graininess function μ. This new idea may be difficult to be understood if we adopt the concept of periodic time scales introduced by Kaufmann and Raffoul (see [28]) because all the periodic sub-timescales with “complete closedness” in [31] are with “translation direction” which was not considered in [28]. For example, consider

$$ \mathbb{T}=\bigcup_{k=0}^{+\infty } \bigl[k(a+b),k(a+b)+a \bigr],\quad a,b\in \mathbb{R}^{+}, k\in \mathbb{Z}. $$

(1.3)

A time scale of the type (1.3) should be regarded as a periodic time scale in [31]. However, according to the concept of periodic time scales from [28], (1.3) is not a periodic time scale. In fact, for any $t\in \mathbb{T}$, we have $t+(a+b) \in \mathbb{T}$, but there exists $t_{0}=0\in \mathbb{T}$ such that $t_{0}-(a+b)=-(a+b)\notin \mathbb{T}$. Nevertheless, (1.3) has nice closedness in translation for time variables if the time scale is only translated towards the positive direction, because for any $t\in \mathbb{T}$, we have $t+(a+b)\in \mathbb{T}$. In 2016, Wang, Agarwal, and O’Regan attached time scales under translations with “translation direction” and introduced several new concepts of periodic time scales to improve the results from [31, 32] (see [33, 34]), Moreover, Agarwal and O’Regan provided some key notes and comments on changing-periodic time scales (see [35]). Based on these fundamental works, we find a feasible and plausible way to solve the closedness under translations for arbitrary time scales with bounded graininess function μ, which paves the way for introducing some new well-defined functions on periodic sub-timescales with “complete closedness”. Therefore, it is possible to investigate almost periodicity and almost automorphy of solutions for dynamic equations on an arbitrary time scale based on these basic works.

Motivated by the above, we first propose the concept of local almost automorphic functions and investigate their relative properties. Then we introduce the concept of a local pseudo almost automorphic function and deduce some important relative properties on time scales. Finally, as applications, using the concept of a Π-semigroup that was introduced in 2016 for time scales (see [36]), we obtain some new sufficient conditions for the existence of local pseudo almost automorphic solutions for a class of semilinear dynamic equations on time scales.

The organization of this paper is as follows. In Sect. 2, we introduce some notations and definitions and state some preliminary results needed in the later sections. In Sect. 3, we propose the concepts of local almost automorphic functions on time scales in a Banach space. Based on these, the concept of local pseudo almost automorphic function is also introduced and some basic properties are investigated. In Sect. 4, as applications of our results, by using the concept of a Π-semigroup that was introduced in 2016 for time scales, we establish the existence of the local pseudo almost automorphic solutions for a class of semilinear dynamic equations on arbitrary time scales.

2 Local semigroup on changing-periodic time scales

Based on the knowledge of changing-periodic time scales in the literature [31, 35], we will present some basic properties of semigroups induced by changing-periodic time scales.

Definition 2.1

([31, 33])

Let $\mathbb{T}$ be an infinite time scale. We say $\mathbb{T}$ is a changing-periodic or a piecewise-periodic time scale if the following conditions are fulfilled:

• (a) $\mathbb{T}= (\bigcup_{i=1}^{\infty } \mathbb{T}_{i} )\cup \mathbb{T}_{r}$ and $\{\mathbb{T}_{i}\} _{i\in \mathbb{Z}^{+}}$ is a well-connected timescale sequence, where $\mathbb{T}_{r}=\bigcup_{i=1}^{k}[\alpha _{i},\beta _{i}]$ and k is some finite number, and $[\alpha _{i},\beta _{i}]$ are closed intervals for $i=1,2,\ldots ,k$ or $\mathbb{T}_{r}=\emptyset$;

• (b) $S_{i}$ is a nonempty subset of $\mathbb{R}$ with $0\notin S_{i}$ for each $i\in \mathbb{Z}^{+}$ and $\varPi = ( \bigcup_{i=1}^{\infty }S_{i} )\cup R_{0}$, where $R_{0}=\{0\}$ or $R_{0}=\emptyset$;

• (c) for all $t\in \mathbb{T}_{i}$ and all $\omega \in S_{i}$, we have $t+\omega \in \mathbb{T}_{i}$, i.e., $\mathbb{T}_{i}$ is an ω-periodic time scale;

• (d) for $i\neq j$, for all $t\in \mathbb{T}_{i}\setminus \{t _{ij}^{k}\}$ and all $\omega \in S_{j}$, we have $t+\omega \notin \mathbb{T}$, where $\{t_{ij}^{k}\}$ is the connected points set of the timescale sequence $\{\mathbb{T}_{i}\}_{i\in \mathbb{Z}^{+}}$;

• (e) $R_{0}=\{0\}$ if and only if $\mathbb{T}_{r}$ is a zero-periodic time scale and $R_{0}=\emptyset$ if and only if $\mathbb{T}_{r}=\emptyset$;

and the set Π is called a changing-periods set of $\mathbb{T}$, $\mathbb{T}_{i}$ is called the periodic sub-timescale of $\mathbb{T}$, and $S_{i}$ is called the periods subset of $\mathbb{T}$ or the periods set of $\mathbb{T}_{i}$, $\mathbb{T}_{r}$ is called the remain timescale of $\mathbb{T}$ and $R_{0}$ the remain periods set of $\mathbb{T}$.

Theorem 2.1

([31, 33])

If $\mathbb{T}$ is an infinite time scale and the graininess function $\mu :\mathbb{T}\rightarrow \mathbb{R}^{+}$ is bounded, then $\mathbb{T}$ is a changing-periodic time scale.

Theorem 2.2

(Decomposition theorem of time scales, [31, 33])

Let $\mathbb{T}$ be an infinite time scale and the graininess function $\mu :\mathbb{T}\rightarrow \mathbb{R}^{+}$ be bounded, then $\mathbb{T}$ is a changing-periodic time scale, i.e., there exists a countable periodic decomposition such that $\mathbb{T}= ( \bigcup_{i=1}^{\infty }\mathbb{T}_{i} )\cup \mathbb{T} _{r}$ and $\mathbb{T}_{i}$ is an ω-periodic sub-timescale, $\omega \in S_{i}$, $i\in \mathbb{Z}^{+}$, where $\mathbb{T}_{i}$, $S _{i}$, $\mathbb{T}_{r}$ satisfy the conditions in Definition 2.1.

Definition 2.2

Let $\mathbb{T}$ be a changing-periodic time scale, i.e., there exists an index function $\tau _{t}$ for all $t\in \mathbb{T}$ such that $t+\tau _{t}\in \mathbb{T}$. The set $S_{\tau _{t}}:=\{\tau :t+\tau \in \mathbb{T}_{\tau _{t}},\forall t\in \mathbb{T}_{\tau _{t}}\}$ is called the invariant translation number set of the sub-timescale $\mathbb{T}_{\tau _{t}}$.

Definition 2.3

If $S_{\tau _{t}}^{+}:=S_{\tau _{t}}\cap [0,+\infty )\notin \{\{0 \},\emptyset \}$, then we say $S_{\tau _{t}}^{+}$ is a positive-direction semigroup induced by the changing-periodic time scale $\mathbb{T}$; if $S_{\tau _{t}}^{-}:=S_{\tau _{t}}\cap (-\infty ,0] \notin \{\{0\},\emptyset \}$, then we say $S_{\tau _{t}} ^{-}$ is a negative-direction semigroup induced by $\mathbb{T}$.

Example 2.1

Let a changing-periodic time scale be the following:

$$ \mathbb{T}= \biggl\{ 2k,\frac{2}{11}k+1:k\in \mathbb{Z} \biggr\} \cup \Biggl\{ \bigcup_{i=-\infty }^{+\infty } \biggl[ \frac{2}{3}i,\frac{2}{3}i+1 \biggr] \Biggr\} . $$

The time scale can be easily decomposed into the sub-timescales as follows:

$$ \mathbb{T}_{1}=\{2k:k\in \mathbb{Z}\},\qquad \mathbb{T}_{2}= \biggl\{ \frac{2}{11}k+1:k\in \mathbb{Z} \biggr\} , \qquad \mathbb{T}_{3}= \bigcup_{i=-\infty }^{+\infty } \biggl[ \frac{2}{3}i, \frac{2}{3}i+1 \biggr]. $$

Obviously, $\mathbb{T}=\mathbb{T}_{1}\cup \mathbb{T}_{2}\cup \mathbb{T}_{3}$, and hence there exists an index function $\tau _{t}$ as follows:

$$ \tau _{t}= \textstyle\begin{cases} 1, & t\in \mathbb{T}_{1}, \\ 2, & t\in \mathbb{T}_{2}, \\ 3, & t\in \mathbb{T}_{3}. \end{cases} $$

According to Theorem 1.2 (decomposition theorem of time scales) from [34], we have

$$ S_{\tau _{t}}= \textstyle\begin{cases} S_{1}=\{\tau : t+\tau \in \mathbb{T}_{1}, \forall t\in \mathbb{T} _{1}\}=\{2n:n\in \mathbb{Z}\}, \\ S_{2}=\{\tau : t+\tau \in \mathbb{T}_{2}, \forall t\in \mathbb{T} _{2}\}=\{\frac{2}{11}n:n\in \mathbb{Z}\}, \\ S_{3}=\{\tau : t+\tau \in \mathbb{T}_{3}, \forall t\in \mathbb{T} _{3}\}=\{\frac{2}{3}n:n\in \mathbb{Z}\}. \end{cases} $$

Hence, the positive-direction semigroup induced by $\mathbb{T}$ is

$$ S_{\tau _{t}}^{+}= \textstyle\begin{cases} S_{1}^{+}=\{\tau \in \mathbb{Z}^{+}: t+\tau \in \mathbb{T}_{1}, \forall t\in \mathbb{T}_{1}\}=\{2n:n\in \mathbb{Z}^{+}\}, \\ S_{2}^{+}=\{\tau \in \mathbb{Z}^{+}: t+\tau \in \mathbb{T}_{2}, \forall t\in \mathbb{T}_{2}\}=\{\frac{2}{11}n:n\in \mathbb{Z}^{+}\}, \\ S_{3}^{+}=\{\tau \in \mathbb{Z}^{+}: t+\tau \in \mathbb{T}_{3}, \forall t\in \mathbb{T}_{3}\}=\{\frac{2}{3}n:n\in \mathbb{Z}^{+}\}. \end{cases} $$

Moreover, the negative-direction semigroup induced by $\mathbb{T}$ is

$$ S_{\tau _{t}}^{-}= \textstyle\begin{cases} S_{1}^{-}=\{\tau \in \mathbb{Z}^{-}: t+\tau \in \mathbb{T}_{1}, \forall t\in \mathbb{T}_{1}\}=\{2n:n\in \mathbb{Z}^{-}\}, \\ S_{2}^{-}=\{\tau \in \mathbb{Z}^{-}: t+\tau \in \mathbb{T}_{2}, \forall t\in \mathbb{T}_{2}\}=\{\frac{2}{11}n:n\in \mathbb{Z}^{-}\}, \\ S_{3}^{-}=\{\tau \in \mathbb{Z}^{-}: t+\tau \in \mathbb{T}_{3}, \forall t\in \mathbb{T}_{3}\}=\{\frac{2}{3}n:n\in \mathbb{Z}^{-}\}. \end{cases} $$

Example 2.2

Some changing-periodic time scales may only possess one-way semigroups. Let

$$ \mathbb{T}= \Biggl\{ \bigcup_{k=1}^{\infty } \biggl[\frac{1}{3}k, \frac{1}{3}k+\frac{3}{4} \biggr] \Biggr\} \cup \Biggl\{ \bigcup_{k=1} ^{\infty } \biggl[-\frac{2}{13}k,-\frac{2}{13}k- \frac{1}{7} \biggr] \Biggr\} . $$

The time scale can be easily decomposed into the sub-timescales as follows:

$$ \mathbb{T}_{1}=\bigcup_{k=1}^{\infty } \biggl[\frac{1}{3}k,\frac{1}{3}k+ \frac{3}{4} \biggr],\qquad \mathbb{T}_{2}=\bigcup_{k=1}^{\infty } \biggl[-\frac{2}{13}k,- \frac{2}{13}k-\frac{1}{7} \biggr]. $$

Obviously, $\mathbb{T}=\mathbb{T}_{1}\cup \mathbb{T}_{2}$, and hence there exists an index function $\tau _{t}$ as follows:

$$ \tau _{t}= \textstyle\begin{cases} 1, & t\in \mathbb{T}_{1}, \\ 2, & t\in \mathbb{T}_{2}. \end{cases} $$

According to Theorem 1.2 (decomposition theorem of time scales) from [34], we have

$$\begin{aligned}& S_{\tau _{t}}^{+}= S_{1}^{+}= \bigl\{ \tau \in \mathbb{Z}^{+}: t+\tau \in \mathbb{T}_{1}, \forall t\in \mathbb{T}_{1} \bigr\} = \biggl\{ \frac{1}{3}n:n \in \mathbb{Z}^{+} \biggr\} , \\& S_{\tau _{t}}^{-}=S_{2}^{-}= \bigl\{ \tau \in \mathbb{Z}^{-}: t+\tau \in \mathbb{T}_{2}, \forall t\in \mathbb{T}_{2} \bigr\} = \biggl\{ \frac{2}{13}n:n \in \mathbb{Z}^{-} \biggr\} . \end{aligned}$$

Note that for $\mathbb{T}_{1}$, $S_{1}^{-}=\{0\}$; for $\mathbb{T} _{2}$, $S_{2}^{+}=\{0\}$. Hence, there exist only one-way semigroups for this changing-periodic time scale.

By using the basic knowledge of Π-semigroup introduced in the literature [36], we can introduce the concept of local Π-semigroup attached with translation direction on changing-periodic time scales.

Definition 2.4

Let $\mathbb{T}$ be a changing-periodic time scale, and $\{T_{\tau } \}$ be a family of bounded linear operators on a Banach space $\mathbb{X}$. If for all $\tau _{1},\tau _{2}\in S_{\tau _{t}}^{+}$ (or $S_{\tau _{t}}^{-}$) the following holds:

$$ T_{\tau _{1}+\tau _{2}}=T_{\tau _{1}}T_{\tau _{2}}, $$

(2.1)

then $\{T_{\tau }:\tau \in S_{\tau _{t}}^{+}\}$ (or $\{T_{\tau }: \tau \in S_{\tau _{t}}^{-}\}$) is called a local one-parameter operator semigroup; if (2.1) holds for all $\tau \in S_{\tau _{t}}$, we call $\{T_{\tau }:\tau \in S_{\tau _{t}}\}$ a local one-parameter operator group.

Definition 2.5

Let $\mathbb{T}$ be a periodic time scale, and $\{T_{\tau }:\tau \in S_{\tau _{t}}^{+}\}$ (or $\{T_{\tau }:\tau \in S_{\tau _{t}}^{-}\}$) be an operator group on a Banach space $\mathbb{X}$, i.e.,

$$ T_{\tau _{1}}T_{\tau _{2}}=T_{\tau _{1}+\tau _{2}},\quad \tau _{1}, \tau _{2}\in S_{\tau _{t}}^{+} \ \bigl(\text{or } \tau _{1},\tau _{2}\in S_{\tau _{t}} ^{-} \bigr),\qquad T_{0}=I. $$

If, for every $\tau _{0}\geq 0$ (or $\tau \leq 0$) and any $\varepsilon >0$, there is a neighborhood U of $\tau _{0}$ (i.e., $U=(\tau _{0}- \delta ,\tau _{0}+\delta )\cap S_{\tau _{t}}^{+}$ (or $U=(\tau _{0}- \delta ,\tau _{0}+\delta )\cap S_{\tau _{t}}^{-}$) for some $\delta >0$) such that

$$ \Vert T_{\tau }x-T_{\tau _{0}}x \Vert < \varepsilon \quad \text{for all }\tau \in U, $$

then we call $\{T_{\tau }:\tau \in S_{\tau _{t}}^{+}\}$ (or $\{T_{ \tau }:\tau \in S_{\tau _{t}}^{-}\}$) the local strong-continuous operator semigroup or the local Π-semigroup.

Definition 2.6

If $S_{\tau _{t}}^{+}\notin \{\{0\},\emptyset \}$, then we say the Π-semigroup $\{T_{\tau _{t}}:\tau _{t}\in S_{\tau _{t}}^{+} \}$ is a positive-direction local Π-semigroup on the changing-periodic time scale $\mathbb{T}$; if $S_{\tau _{t}}^{-}\notin \{\{0\},\emptyset \}$, then we say the Π-semigroup $\{T_{\tau _{t}}:\tau _{t}\in S_{\tau _{t}}^{-}\}$ is a negative-direction local Π-semigroup on $\mathbb{T}$.

Remark 2.1

Note that local Π-semigroups on changing-periodic time scales are operator semigroups on the sub-timescale $\mathbb{T}_{\tau _{t}}$, so the semigroups induced by time scales and Π-semigroups on time scales are completely different concepts through comparing Definitions 2.3 and 2.6.

Remark 2.2

In fact, the Π-semigroup for time scales proposed in [36] is more general than the $C_{0}$-semigroup on time scales proposed in [37] since the condition $\forall t_{1},t_{2} \in \mathbb{T}$, $t_{1}\pm t_{2}\in \mathbb{T}$ is not required for the Π-semigroup, i.e., the condition that $\mathbb{T}$ is closed for addition and subtraction can be removed. Since changing-periodic time scales can be decomposed into countable sub-timescales with the properties of CCTS, all the properties of the Π-semigroup on CCTS can be naturally extended to its sub-timescales when the decomposition of theorem of time scales is applied.

3 Local pseudo almost automorphic functions on sub-CCTS

In this section, we introduce the new concept of local pseudo almost automorphic functions on changing-periodic time scales and obtain some basic properties.

Definition 3.1

Each sub-timescale of a changing-periodic time scale is called the complete-closed sub-timescale, short for sub-CCTS.

Definition 3.2

Let $\mathbb{X}$ be a Banach space and $\mathbb{T}$ be a changing-periodic time scale.

• (i) Let $f:\mathbb{T}\rightarrow \mathbb{X}$ be a bounded continuous function. We say that f is local-almost automorphic if, for every adaption factor sequence $\{s_{n}^{\tau }\}_{n=1}^{\infty } \subset S_{\tau _{t}}$, we can extract a subsequence $\{\tau _{n}^{ \tau }\}_{n=1}^{\infty }$ such that

  $$ g(t)=\lim_{n\rightarrow \infty }f \bigl(t+\tau _{n}^{\tau } \bigr) $$

  (3.1)

  is well defined for each $t\in \mathbb{T}$ and

  $$ f(t)=\lim_{n\rightarrow \infty }g \bigl(t+\tau _{n}^{\tau } \bigr) $$

  (3.2)

  is well defined for each $t\in \mathbb{T}$. We shall denote by $LAA(\mathbb{T},\mathbb{X})$ the set of all such functions.

• (ii) A continuous function $f:\mathbb{T}\times B\rightarrow \mathbb{X}$ is said to be local-almost automorphic if $f(t,x)$ is local-almost automorphic in $t\in \mathbb{T}$ uniformly for all $x\in B$, where B is any bounded subset of $\mathbb{X}$ or $B=\mathbb{X}$. We shall denote by $LAA(\mathbb{T}\times \mathbb{X}, \mathbb{X})$ the set of all such functions.

Definition 3.2 also has the following equivalent form.

Definition 3.3

Let $\mathbb{X}$ be a Banach space, $\mathbb{T}$ be a changing-periodic time scale, and $f:\mathbb{T}\rightarrow \mathbb{X}$ be a bounded continuous function. We say that f is local-almost automorphic if, for every adaption factor sequence $\{s_{n}^{\tau }\}_{n=1}^{\infty } \subset S_{\tau _{t}}$, we can extract a subsequence $\{\tau _{n}^{ \tau }\}_{n=1}^{\infty }$ ($\tau _{i}^{\tau }\neq \tau _{j}^{\tau }$ for $i\neq j$) such that

$$ f(t)=\lim_{m\rightarrow \infty }\lim_{n\rightarrow \infty }f \bigl(t+\tau _{n}^{\tau }+\tau _{m}^{\tau } \bigr) $$

is well defined for each $t\in \mathbb{T}$.

Definition 3.4

If $S_{\tau _{t}}^{+}\notin \{\{0\},\emptyset \}$, then we say f is positive-direction local-almost automorphic; if $S_{\tau _{t}}^{-}\notin \{\{0\},\emptyset \}$, then we say f is negative-direction local-almost automorphic; if $S_{\tau _{t}}^{\pm } \notin \{\{0\},\emptyset \}$, then we say f is bi-direction local-almost automorphic.

Definition 3.5

Let $f,g\in C(\mathbb{T}\times D,\mathbb{E}^{n})$ be uniformly local-almost automorphic and $\mathbb{T}$ be a changing-periodic time scale. We say f and g are synchronously local-almost automorphic if f, g are almost automorphic on the same periodic sub-timescales of the changing-periodic time scale $\mathbb{T}$.

Remark 3.1

Throughout this section, we always assume that all the functions on the same changing-periodic time scale are synchronously local-almost automorphic, i.e., all the functions satisfy Definition 3.5.

Definition 3.6

• (i) The set of bounded continuous functions with local vanishing mean value is defined as

  $$\begin{aligned} LAA_{0}(\mathbb{T},\mathbb{X}) =& \biggl\{ \phi \in BC_{\mathrm{rd}}(\mathbb{T}, \mathbb{X}):\lim_{T\rightarrow \infty } \frac{1}{T} \int _{t_{0}} ^{t_{0}+T} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s=0, \\ &\text{where }t_{0}\in \mathbb{T}, T\in S_{\tau _{t_{0}}} \biggr\} . \end{aligned}$$

• (ii) Similarly, we define $LAA_{0}(\mathbb{T}\times \mathbb{X},\mathbb{X})$ to be the collection of all functions $f\in BC_{\mathrm{rd}}(\mathbb{T}\times \mathbb{X},\mathbb{X})$ satisfying

  $$ \lim_{T\rightarrow \infty }\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert f(s,x) \bigr\Vert \Delta _{\tau _{s}} s=0,\quad \text{where }t_{0}\in \mathbb{T}, T \in S_{\tau _{t_{0}}}, $$

uniformly for x in any bounded subset of $\mathbb{X}$.

Remark 3.2

In Definition 3.6, for any $t_{0}\in \mathbb{T}$, if $S_{ \tau _{t_{0}}}^{\pm }\notin \{\{0\},\emptyset \}$, i.e., $S_{\tau _{t_{0}}}^{+}=S_{\tau _{t_{0}}}\cap [0,+\infty )\notin \{\{0\},\emptyset \}$ and $S_{\tau _{t_{0}}}^{-}=S_{\tau _{t _{0}}}\cap (-\infty ,0]\notin \{\{0\},\emptyset \}$, then $\mathbb{T}_{\tau _{t_{0}}}$ is a bi-direction periodic sub-timescale. Hence, we obtain

$$ \lim_{T\rightarrow +\infty }\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s=0,\qquad \lim_{T\rightarrow +\infty } \frac{1}{-T} \int _{t_{0}}^{t_{0}-T} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s=0, $$

so,

$$ \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s=0, \qquad \lim_{T\rightarrow +\infty } \frac{1}{2T} \int _{t_{0}-T}^{t_{0}} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s=0. $$

Thus we obtain

$$\begin{aligned}& \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{t_{0}-T}^{t _{0}+T} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s \\& \quad = \lim_{T\rightarrow +\infty }\frac{1}{2T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s+\lim_{T\rightarrow +\infty } \frac{1}{2T} \int _{t_{0}-T}^{t_{0}} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s=0. \end{aligned}$$

Therefore, if $\mathbb{T}_{\tau _{t_{0}}}$ is a bi-direction periodic sub-timescale, then the space $LAA_{0}$ is as follows:

$$\begin{aligned} LAA_{0}(\mathbb{T},\mathbb{X}) =& \biggl\{ \phi \in BC_{\mathrm{rd}}(\mathbb{T}, \mathbb{X}):\lim_{T\rightarrow \infty } \frac{1}{2T} \int _{t_{0}-T} ^{t_{0}+T} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s=0, \\ &\text{where } t_{0}\in \mathbb{T} , T\in S_{\tau _{t_{0}}} \biggr\} . \end{aligned}$$

Now, we introduce the set $LPAA(\mathbb{T},\mathbb{X})$ and $LPAA(\mathbb{T}\times \mathbb{X},\mathbb{X})$ of local pseudo almost automorphic functions:

$$\begin{aligned}& LPAA(\mathbb{T},\mathbb{X})= \bigl\{ f=g+\phi \in BC_{\mathrm{rd}}(\mathbb{T}, \mathbb{X}):g\in LAA(\mathbb{T},\mathbb{X}) \text{ and } \phi \in LAA_{0}(\mathbb{T},\mathbb{X}) \bigr\} ; \\& \begin{aligned} LPAA(\mathbb{T}\times \mathbb{X},\mathbb{X}) &= \bigl\{ f=g+\phi \in BC _{\mathrm{rd}}(\mathbb{T}\times \mathbb{X},\mathbb{X}): g\in LAA( \mathbb{T} \times \mathbb{X},\mathbb{X}) \\ &\quad \text{and } \phi \in LAA_{0}(\mathbb{T}\times \mathbb{X}, \mathbb{X}) \bigr\} . \end{aligned} \end{aligned}$$

From the definition of $LPAA(\mathbb{T},\mathbb{X})$, one can easily show the following theorem.

Theorem 3.1

For any $t\in \mathbb{T}$, let $\varOmega \subset \mathbb{T}_{\tau _{t}}$, $f=g+\phi$ be a local pseudo almost automorphic function. Then we have

$$ \bigl\{ g(t):t\in \varOmega \bigr\} \subset \overline{ \bigl\{ f(t):t \in \varOmega \bigr\} }. $$

(3.3)

Proof

We claim that $LAA_{0}(\mathbb{T},\mathbb{X})$ is a closed sub-space. In fact, for any $\{\phi _{m}\}\subset LAA_{0}(\mathbb{T},\mathbb{X})$ and $\phi _{m}\rightarrow \phi$, $m\rightarrow +\infty$, we obtain

$$\begin{aligned} \lim_{T\rightarrow \infty }\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}}s \leq &\lim_{T\rightarrow \infty } \frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi _{m}(s)-\phi (s) \bigr\Vert \Delta _{\tau _{s}}s \\ &{}+\lim_{T\rightarrow \infty }\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi _{m}(s) \bigr\Vert \Delta _{\tau _{s}}s=0, \end{aligned}$$

which implies that $LAA_{0}(\mathbb{T},\mathbb{X})$ is a closed sub-space. Hence, $LAA_{0}(\mathbb{T},\mathbb{X})$ is a Banach space.

Therefore, we have $LPAA(\mathbb{T},\mathbb{X})=LAA(\mathbb{T}, \mathbb{X})\oplus LAA_{0}(\mathbb{T},\mathbb{X})$, which implies that (3.3) holds. This completes the proof. □

Corollary 3.1

The decomposition of a local pseudo almost automorphic function is unique.

Proof

Suppose that $f\in LPAA(\mathbb{T},\mathbb{X})$ has two decompositions, that is, $f=g_{1}+\phi _{1}=g_{2}+\phi _{2}$, where $g_{1},g_{2}\in LAA( \mathbb{T},\mathbb{X})$ and $\phi _{1},\phi _{2}\in LAA_{0}(\mathbb{T}, \mathbb{X})$. Then $(g_{1}-g_{2})+(\phi _{1}-\phi _{2})=f-f=0$. Using Theorem 3.1, we know $(g_{1}-g_{2})(t)=0$ for each $t\in \varOmega$. Thus, $g_{1}=g_{2}$. Therefore, $\phi _{1}=\phi _{2}$. Hence, the decomposition of f is unique. This completes the proof. □

In the following, using the knowledge of Δ-measurability on time scales, we can obtain the following lemma.

Lemma 3.1

Let $f\in BC_{\mathrm{rd}}(\mathbb{T},\mathbb{X})$. Then $f\in LAA_{0}( \mathbb{T},\mathbb{X})$ if and only if, for any $\varepsilon >0$,

$$ \lim_{T\rightarrow \infty }\frac{1}{T}\mu _{\Delta _{\tau _{t_{0}}}} \bigl(M_{T,\varepsilon }(f) \bigr)=0 $$

and

$$ M_{T,\varepsilon }(f):= \bigl\{ t\in [t_{0},t_{0}+T)_{\mathbb{T}_{ \tau _{t_{0}}}}: \bigl\Vert f(t) \bigr\Vert \geq \varepsilon , t_{0}\in \mathbb{T}, T \in S_{\tau _{t_{0}}} \bigr\} , $$

where $\mu _{\Delta _{\tau _{t_{0}}}}(\cdot )$ denotes the Δ-measurability on the periodic sub-timescale $\mathbb{T}_{ \tau _{t_{0}}}$ of the time scale $\mathbb{T}$.

Proof

Without loss of generality, we assume that, for $t_{0}\in \mathbb{T}$, $S_{\tau _{t_{0}}}^{+}\notin \{\{0\},\emptyset \}$, i.e., $\mathbb{T}_{\tau _{t_{0}}}$ is a positive-direction periodic sub-timescale.

• (i) Necessity. By contradiction suppose that there exists $\varepsilon _{0}>0$ such that

  $$ \lim_{T\rightarrow \infty }\frac{1}{T}\mu _{\Delta _{\tau _{t_{0}}}} \bigl(M_{T,\varepsilon _{0}}(f) \bigr)\neq 0. $$

  Then there exists $\delta >0$ such that, for every $n\in \mathbb{N}$, $T_{n}\in S_{\tau _{t_{0}}}$,

  $$ {\frac{1}{T_{n}}}\mu _{\Delta _{\tau _{t_{0}}}} \bigl(M_{T_{n},\varepsilon _{0}}(f) \bigr) \geq \delta $$

  for some $T_{n}>n$. Thus we have

  $$\begin{aligned}& \frac{1}{T_{n}} \int _{t_{0}}^{t_{0}+T_{n}} \bigl\Vert f(s) \bigr\Vert \Delta _{\tau _{s}} s \\& \quad = \frac{1}{T_{n}} \int _{M_{T_{n},\varepsilon _{0}}(f)} \bigl\Vert f(s) \bigr\Vert \Delta _{\tau _{s}} s+\frac{1}{T_{n}} \int _{[t_{0},t_{0}+T_{n})_{\mathbb{T}_{\tau _{t}}}\setminus M_{T_{n}, \varepsilon _{0}}(f)} \bigl\Vert f(s) \bigr\Vert \Delta _{\tau _{s}} s \\& \quad \geq \frac{1}{T_{n}} \int _{M_{T_{n},\varepsilon _{0}}(f)} \bigl\Vert f(s) \bigr\Vert \Delta _{\tau _{s}} s\geq \frac{\varepsilon _{0}}{T_{n}} \int _{M_{T_{n},\varepsilon _{0}}(f)}\Delta _{\tau _{s}} s\geq \varepsilon _{0}\delta . \end{aligned}$$

  This contradicts the assumption.

• (ii) Sufficiency. From the statement of Lemma 3.1 it is clear that $\|f\|\leq M$, M is some constant. For any $\varepsilon >0$, there exists $T_{0}>0$ such that, for $T>T_{0}$,

  $$ \frac{1}{T}\mu _{\Delta _{\tau _{t_{0}}}} \bigl(M_{T,\varepsilon }(f) \bigr)< \frac{\varepsilon }{M+1}. $$

  Then

  $$\begin{aligned}& \frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert f(s) \bigr\Vert \Delta _{\tau _{s}} s \\& \quad = \frac{1}{T} \biggl( \int _{M_{T,\varepsilon }(f)} \Vert f(s) \Vert \Delta _{\tau _{s}} s+ \int _{[t_{0},t_{0}+T)_{\mathbb{T}_{\tau _{t}}}\setminus M_{T,\varepsilon }(f)} \bigl\Vert f(s) \bigr\Vert \Delta _{\tau _{s}} s \biggr) \\& \quad \leq \frac{M}{T}\mu _{\Delta _{\tau _{t_{0}}}} \bigl(M_{T,\varepsilon }(f) \bigr)+ \frac{1}{T} \bigl(T-\mu _{\Delta _{\tau _{t_{0}}}} \bigl(M_{T,\varepsilon }(f) \bigr) \bigr)\cdot \frac{1}{M+1} \\& \quad \leq \frac{M\varepsilon }{M+1}+\frac{1}{M+1}. \end{aligned}$$

  Hence,

  $$ \lim_{T\rightarrow \infty } \int _{t_{0}}^{t_{0}+T} \bigl\Vert f(s) \bigr\Vert \Delta _{\tau _{s}} s=0. $$

  That is, $f\in LAA_{0}(\mathbb{T},\mathbb{X})$.

A similar argument can be supplied for the case $S_{\tau _{t_{0}}}^{-} \notin \{\{0\},\emptyset \}$, i.e., $\mathbb{T}_{\tau _{t _{0}}}$ is a negative-direction periodic sub-timescale, and the case $S_{\tau _{t_{0}}}^{\pm }\notin \{\{0\},\emptyset \}$, i.e., $\mathbb{T}_{\tau _{t_{0}}}$ is a bi-direction periodic sub-timescale, and one can easily obtain the same result (we omit the details). This completes the proof. □

Theorem 3.2

Let $f=g+\phi \in LPAA(\mathbb{T}\times \mathbb{X},\mathbb{X})$ with $g\in LAA(\mathbb{T}\times \mathbb{X},\mathbb{X})$, $\phi \in LAA_{0}( \mathbb{T}\times \mathbb{X},\mathbb{X})$. Assume:

• (i) $g(t,x)$ is uniformly continuous on any bounded subset uniformly for $t\in \mathbb{T}$.

• (ii) There exists a nonnegative function $\varrho ^{*}\in L ^{p}(\mathbb{T}_{\tau _{t}})$ ($1\leq p\leq \infty$) such that

  $$ \bigl\Vert f(t,x)-f(t,y) \bigr\Vert \leq \varrho ^{*}(t) \Vert x-y \Vert $$

  for all $x,y\in \mathbb{X}$ and $t\in \mathbb{T}_{\tau _{t}}$.

If $x\in LPAA(\mathbb{T},\mathbb{X})$, then $f (\cdot ,x(\cdot ) )\in LPAA(\mathbb{T},\mathbb{X})$, where

$$ L^{p}(\mathbb{T}_{\tau _{t_{0}}}):= \biggl\{ \varrho ^{*}:\mathbb{T}_{\tau _{t}}\rightarrow \mathbb{\mathbb{R}}: \int _{\mathbb{T}_{\tau _{t}}} \bigl[ \varrho ^{*}(s) \bigr]^{p}\Delta _{\tau _{s}} s< \infty \biggr\} $$

and

$$ \bigl\Vert \varrho ^{*} \bigr\Vert _{L^{p}(\mathbb{T}_{\tau _{t}})}= \biggl( \int _{\mathbb{T}_{\tau _{t}}} \bigl[\varrho ^{*}(s) \bigr]^{p}\Delta _{\tau _{s}} s \biggr)^{\frac{1}{p}}. $$

Proof

Without loss of generality, we assume that, for $t\in \mathbb{T}$, $S_{\tau _{t}}^{+}\notin \{\{0\},\emptyset \}$, i.e., $\mathbb{T}_{\tau _{t}}$ is a positive-direction periodic sub-timescale.

Since $f\in LPAA(\mathbb{T}\times \mathbb{X},\mathbb{X})$ and $x\in LPAA(\mathbb{T},\mathbb{X})$, we have by definition that $f=g+\phi$ and $x=\alpha +\beta$, where $g\in LAA(\mathbb{T}\times \mathbb{X},\mathbb{X})$, $\phi \in LAA_{0}(\mathbb{T}\times \mathbb{X}, \mathbb{X})$, $\alpha \in LAA(\mathbb{T},\mathbb{X})$, $\beta \in LAA _{0}(\mathbb{T},\mathbb{X})$. Thus the function f can be decomposed as

$$ f \bigl(t,x(t) \bigr)=g \bigl(t,\alpha (t) \bigr)+f \bigl(t,x(t) \bigr)-f \bigl(t, \alpha (t) \bigr)+\phi \bigl(t,\alpha (t) \bigr). $$

Let

$$ G(t)=g \bigl(t,\alpha (t) \bigr); \qquad \varPhi (t)=f \bigl(t,x(t) \bigr)-f \bigl(t, \alpha (t) \bigr)+\phi \bigl(t,\alpha (t) \bigr). $$

From $g(t,x)\in LAA(\mathbb{T}\times \mathbb{X},\mathbb{X})$, then for every sequence of real numbers $\{s_{n}^{\tau }\}_{n=1}^{\infty } \subset S_{\tau _{t}}$, we can extract a subsequence $\{\tau _{n}^{ \tau }\}_{n=1}^{\infty }$ such that

$$ g^{*}(t,x)=\lim_{n\rightarrow \infty }g \bigl(t+\tau _{n}^{\tau },x \bigr) $$

is well defined for each $t\in \mathbb{T}$ and

$$ g(t,x)=\lim_{n\rightarrow \infty }g^{*} \bigl(t+\tau _{n}^{\tau },x \bigr) $$

is well defined for each $t\in \mathbb{T}$. In view of assumption (i) and $\alpha \in LAA(\mathbb{T},\mathbb{X})$, one can extract $\{\tau _{n}^{\prime }\}_{n=1}^{\infty }\subset \{\tau _{n}^{\tau }\}_{n=1} ^{\infty }$ such that

$$ \lim_{n\rightarrow \infty }g \bigl(t+\tau _{n}^{\prime }, \alpha \bigl(t+\tau _{n}^{\prime } \bigr) \bigr)=\lim _{n\rightarrow \infty }g \bigl(t+\tau _{n}^{\prime }, \alpha ^{*}(t) \bigr)=g^{*} \bigl(t,\alpha ^{*}(t) \bigr) $$

and

$$ \lim_{n\rightarrow \infty }g^{*} \bigl(t+\tau _{n}^{\prime },\alpha ^{*} \bigl(t+ \tau _{n}^{\prime } \bigr) \bigr)=\lim_{n\rightarrow \infty }g^{*} \bigl(t+\tau _{n}^{\prime },\alpha (t) \bigr)=g \bigl(t, \alpha (t) \bigr). $$

Hence, $G(t)\in LAA(\mathbb{T},\mathbb{X})$. To show that $f ( \cdot ,x(\cdot ) )\in LPAA(\mathbb{T},\mathbb{X})$, it is sufficient to prove that $\varPhi (t)\in LAA_{0}(\mathbb{T},\mathbb{X})$.

First, we prove that $f (t,x(t) )-f (t,\alpha (t) )\in LAA _{0}(\mathbb{T},\mathbb{X})$. Clearly, $f (t,x(t) )-f (t, \alpha (t) )$ is bounded and rd-continuous. We can assume $\|f (t,x(t) )-f (t,\alpha (t) ) \|\leq M$, $\forall t\in \mathbb{T}_{\tau _{t}}$.

Since $x(t)$, $\alpha (t)$ are bounded, we can choose a bounded subset $B_{\tau _{t}}\subset \mathbb{T}_{\tau _{t}}$ such that $x(\mathbb{T} _{\tau _{t}}), \alpha (\mathbb{T}_{\tau _{t}})\subset B_{\tau _{t}}$, where $x(\mathbb{T}_{\tau _{t}})$, $\alpha (\mathbb{T}_{\tau _{t}})$ denote the value field of x, α under $\mathbb{T}_{\tau _{t}}$. Under assumption (ii), for given $\varepsilon >0$, $\|x-y\|\leq \varepsilon$ implies that

$$ \bigl\Vert f(t,x)-f(t,y) \bigr\Vert < \varepsilon \varrho ^{*}(t) \quad \text{for all } t \in \mathbb{T}_{\tau _{t}}. $$

Since $\beta (t)\in LAA_{0}(\mathbb{T},\mathbb{X})$, Lemma 3.1 yields that

$$ \lim_{T\rightarrow \infty }\frac{1}{T}\mu _{\Delta _{\tau _{t}}} \bigl(M_{T,\varepsilon } \bigl(\beta (t) \bigr) \bigr)=0. $$

Thus, for any $t_{0}\in \mathbb{T}_{\tau _{t}}$, $T\in S_{\tau _{t_{0}}}$, we obtain

$$\begin{aligned}& \frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert f \bigl(t,x(t) \bigr)-f \bigl(t, \alpha (t) \bigr) \bigr\Vert \Delta _{\tau _{t}} t \\& \quad = \frac{1}{T} \int _{M_{T,\varepsilon }(\beta (t))} \bigl\Vert f \bigl(t,x(t) \bigr)-f \bigl(t, \alpha (t) \bigr) \bigr\Vert \Delta _{\tau _{t}} t \\& \qquad {} +\frac{1}{T} \int _{[t_{0},t_{0}+T)_{\mathbb{T}_{\tau _{t}}}\setminus M_{T,\varepsilon }(\beta (t))} \bigl\Vert f \bigl(t,x(t) \bigr)-f \bigl(t, \alpha (t) \bigr) \bigr\Vert \Delta _{\tau _{t}} t \\& \quad \leq \frac{M}{T}\mu _{\Delta _{\tau _{t}}} \bigl(M_{T,\varepsilon } \bigl( \beta (t) \bigr) \bigr)+\frac{\varepsilon }{T} \int _{t_{0}}^{t_{0}+T}\varrho ^{*}(t)\Delta _{\tau _{t}} t. \end{aligned}$$

Case 1.:

If $p=1$, we obtain that

$$ \frac{\varepsilon }{T} \int _{t_{0}}^{t_{0}+T}\varrho ^{*}(t) \Delta _{\tau _{t}} t\leq \frac{\varepsilon }{T} \int _{\mathbb{T}_{\tau _{t}}}\varrho ^{*}(t)\Delta _{\tau _{t}} t\leq \frac{ \varepsilon \Vert \varrho ^{*} \Vert _{L^{p}(\mathbb{T}_{\tau _{t}})}}{T}. $$

Case 2.:

If $p=\infty$, we obtain that

$$ \frac{\varepsilon }{T} \int _{t_{0}}^{t_{0}+T}\varrho ^{*}(t) \Delta _{\tau _{t}} t\leq \varepsilon \bigl\Vert \varrho ^{*} \bigr\Vert _{L^{\infty }( \mathbb{T}_{\tau _{t}})}. $$

Case 3.:

If $1< p<\infty$, then

$$ \frac{\varepsilon }{T} \int _{t_{0}}^{t_{0}+T}\varrho ^{*}(t) \Delta _{\tau _{t}} t\leq \frac{\varepsilon }{T} \biggl( \int _{t_{0}}^{t _{0}+T} \bigl[\varrho ^{*}(t) \bigr]^{p}\Delta _{\tau _{t}} t \biggr)^{\frac{1}{p}} \biggl( \int _{t_{0}}^{t_{0}+T}\Delta _{\tau _{t}} t \biggr)^{\frac{1}{q}} \leq \frac{\varepsilon \Vert \varrho ^{*} \Vert _{L^{p}(\mathbb{T}_{\tau _{t}})}}{T ^{1-\frac{1}{q}}}, $$

where $q=p(p-1)^{-1}$. Hence, we obtain

$$ \lim_{T\rightarrow \infty }\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert f \bigl(t,x(t) \bigr)-f \bigl(t,\alpha (t) \bigr) \bigr\Vert \Delta _{\tau _{t}} t=0. $$

Next, we show that $\phi (t,\alpha (t) )\in LAA_{0}(\mathbb{T}, \mathbb{X})$. Let $\varepsilon >0$. Since $g(t,x)$ is uniformly continuous in any bounded subset uniformly for $t\in \mathbb{T}$, there exists $\delta >0$ such that $\|g(t,x)-g(t,y)\|\leq \varepsilon$ for all $x, y\in B_{\tau _{t}}$ with $\|x-y\|\leq \delta$. Let $\delta _{0}=\min \{\varepsilon ,\delta \}$. Then

$$ \bigl\Vert \phi (t,x)-\phi (r,x) \bigr\Vert \leq \bigl\Vert f(t,x)-f(t,y) \bigr\Vert + \bigl\Vert g(t,x)-g(t,y) \bigr\Vert \leq \varepsilon \bigl( \varrho ^{*}(t)+1 \bigr) $$

for all $x, y\in B_{\tau _{t}}$ with $\|x-y\|\leq \delta _{0}$.

Set $I=\alpha ([t_{0},t_{0}+T)_{\mathbb{T}_{\tau _{t}}})$, where $T\in S_{\tau _{t}}$. Then I is compact in $\mathbb{R}$ since the image of a compact set under a continuous mapping is compact. Therefore, one can find a finite number of open balls $O_{k}$ ($k=1,2,\ldots ,m$) with center $x_{k}\in I$ and radius $\delta _{0}$ small enough such that $I\subset \bigcup_{k=1}^{m}O_{k}$ and

$$ \bigl\Vert \phi \bigl(t,\alpha (t) \bigr)-\phi (t,x_{k}) \bigr\Vert \leq \varepsilon \bigl(\varrho ^{*}(t)+1 \bigr),\quad \alpha (t) \in O_{k}, t\in [t_{0},t_{0}+T)_{ \mathbb{T}_{\tau _{t}}}. $$

Suppose $\|\phi (t,x_{p})\|=\max_{1\leq k\leq m}\{\|\phi (t,x _{k})\|\}$, where p is an index number among $\{1,2,\ldots , m\}$. The set $B_{\tau _{t}}^{k}=\{t\in [t_{0},t_{0}+T)_{\mathbb{T}_{\tau _{t}}}: \alpha (t)\in O_{k}\}$ is open in $[t_{0},t_{0}+T)_{\mathbb{T}_{\tau _{t}}}=\bigcup_{k=1}^{m}B_{\tau _{t}}^{k}$. Let

$$ E_{\tau _{t}}^{1}=B_{\tau _{t}}^{1},\qquad E_{\tau _{t}}^{k}=B_{\tau _{t}}^{k}\bigm\backslash \bigcup_{j=1}^{k-1}B _{\tau _{t}}^{j}\quad (2\leq k\leq m). $$

Then $E_{\tau _{t}}^{i}\cap E_{\tau _{t}}^{j}=\emptyset$ when $i\neq j$, $1\leq i$, $j\leq m$. Observe

$$\begin{aligned}& \frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi \bigl(t,\alpha (t) \bigr) \bigr\Vert \Delta _{\tau _{t}} t \\& \quad = \frac{1}{T} \int _{\bigcup _{k=1}^{m}B_{\tau _{t}}^{k}} \bigl\Vert \phi \bigl(t,\alpha (t) \bigr) \bigr\Vert \Delta _{\tau _{t}} t \\& \quad \leq \frac{1}{T}\sum_{k=1}^{m} \int _{B_{\tau _{t}}^{k}} \bigl( \bigl\Vert \phi \bigl(t,\alpha (t) \bigr)-\phi (t,x_{k}) \bigr\Vert + \bigl\Vert \phi (t,x _{k}) \bigr\Vert \bigr)\Delta _{\tau _{t}} t \\& \quad \leq \frac{1}{T}\sum_{k=1}^{m} \int _{B_{\tau _{t}}^{k}}\varepsilon \bigl(\varrho ^{*}(t)+1 \bigr)\Delta _{\tau _{t}} t+\frac{1}{T}\sum _{k=1}^{m} \int _{B_{\tau _{t}}^{k}} \bigl\Vert \phi (t,x_{k}) \bigr\Vert \Delta _{\tau _{t}} t \\& \quad \leq \varepsilon +\frac{\varepsilon }{T} \int _{t_{0}}^{t_{0}+T} \varrho ^{*}(t) \Delta _{\tau _{t}} t+\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi (t,x_{p}) \bigr\Vert \Delta _{\tau _{t}} t. \end{aligned}$$

Using the same discussion as above, we obtain

$$ \lim_{T\rightarrow \infty }\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi \bigl(t,\alpha (t) \bigr) \bigr\Vert \Delta _{\tau _{t}} t=0. $$

That is, $\phi (t,\alpha (t) )\in LAA_{0}(\mathbb{T}, \mathbb{X})$. Hence, $G(t)\in LAA(\mathbb{T},\mathbb{X})$ and $\varPhi (t)\in LAA_{0}(\mathbb{T},\mathbb{X})$. This means that $f (\cdot ,x(\cdot ) )\in LPAA(\mathbb{T},\mathbb{X})$.

A similar argument can be supplied for the case $S_{\tau _{t}}^{-} \notin \{\{0\},\emptyset \}$, i.e., $\mathbb{T}_{\tau _{t}}$ is a negative-direction periodic sub-timescale, and the case $S_{\tau _{t}}^{\pm }\notin \{\{0\},\emptyset \}$, i.e., $\mathbb{T}_{\tau _{t}}$ is a bi-direction periodic sub-timescale, and one can easily obtain the same result (we omit the details). This completes the proof. □

4 Applications to semilinear dynamic equations

In this section, we discuss local almost automorphic mild solutions for dynamic equations on changing-periodic time scales. We use our recent new concept of a Π-semigroup (for more details on a Π-semigroup, see [36]).

Consider the following differential equation:

$$ x^{\Delta }(t)=Ax(t)+f \bigl(t,x(t) \bigr),\quad t\in \mathbb{T}, $$

(4.1)

where A is the infinitesimal generator of a Π-semigroup for the periodic sub-timescale $\mathbb{T}_{\tau _{t}}$, $x:\mathbb{T}_{\tau _{t}}\rightarrow \mathbb{X}$, $f:\mathbb{T}_{\tau _{t}}\times \mathbb{X}\rightarrow \mathbb{X}$.

Definition 4.1

A local mild solution to (4.1) is a continuous function $x(t):\mathbb{T}_{\tau _{t}}\rightarrow \mathbb{X}$ satisfying

$$ x(t)=\mathscr{T}^{\tau }_{t,t_{0}}x(t_{0})+ \int _{t_{0}}^{t} \mathscr{T}^{\tau }_{t,s}f \bigl(s,x(s) \bigr)\Delta _{\tau _{s}} s $$

for all $t\geq t_{0}$ and all $t_{0}\in \mathbb{T}_{\tau _{t}}$, where $\mathscr{T}^{\tau }_{t,t_{0}}$ is the moving-operator on $\mathbb{T} _{\tau _{t}}$.

Remark 4.1

Note that from Definition 3.20 in the literature [36], one can obtain $\mathscr{T}^{\tau }_{t,t_{0}}=e^{\tau }_{A}(t,t_{0})$, where $e^{\tau }_{A}(t,t_{0})$ is the exponential function generated by A on $\mathbb{T}_{\tau _{t}}$.

Now, we investigate the existence and uniqueness of a pseudo almost automorphic solution to (4.1). We need the following assumptions:

($\mathrm{H}_{1}$):

Let A be the infinitesimal generator of a Π-semigroup $\{T_{\tau }:\tau \in S_{\tau _{t}}\}$. The moving-operator family $\{\mathscr{T}^{\tau }_{t,t_{0}}:t,t_{0} \in \mathbb{T}_{\tau _{t}},t\geq t_{0} \}$ is exponentially stable, that is, there exist $K>0$, $\omega >0$ such that

$$ \bigl\Vert \mathscr{T}^{\tau }_{t,t_{0}} \bigr\Vert \leq Ke^{\tau }_{\ominus \omega }(t,t _{0})\quad \text{for all }t \in \mathbb{T}_{\tau _{t}}. $$

($\mathrm{H}_{2}$):

$f:\mathbb{R}\times \mathbb{X}\rightarrow \mathbb{X}$ is local pseudo almost automorphic.

($\mathrm{H}_{3}$):

There exists a nonnegative function $\varrho _{0} \in L^{p}(\mathbb{T}_{\tau _{t}},\mathbb{R}^{+})$ ($p=1,2$) such that

$$ \bigl\Vert f(t,x)-f(t,y) \bigr\Vert \leq \varrho _{0}(t) \Vert x-y \Vert $$

for all $x,y\in \mathbb{X}$ and $t\in \mathbb{T}_{\tau _{t}}$.

Lemma 4.1

Let $v\in LAA(\mathbb{T},\mathbb{X})$. If $S_{\tau _{t}}^{-}\notin \{\{0\},\emptyset \}$ and $u:\mathbb{T}_{\tau _{t}} \rightarrow \mathbb{X}$ is the function defined by

$$ u(t)= \int _{-\infty }^{t}\mathscr{T}^{\tau }_{t,s}v(s) \Delta _{\tau _{s}} s,\quad t\geq s, $$

then $u(\cdot )\in LAA(\mathbb{T},\mathbb{X})$. If $S_{\tau _{t}}^{+} \notin \{\{0\},\emptyset \}$ and $u:\mathbb{T}_{\tau _{t}} \rightarrow \mathbb{X}$ is the function defined by

$$ u(t)= \int _{t}^{+\infty }\mathscr{T}^{\tau }_{t,s}v(s) \Delta _{\tau _{s}} s, \quad t\geq s, $$

then $u(\cdot )\in LAA(\mathbb{T},\mathbb{X})$.

Proof

Obviously, $u(t)$ is a continuous functions on $\mathbb{T}_{\tau _{t}}$. Let $\{s_{n}^{\tau }\}_{n=1}^{\infty }\subset S_{\tau _{t}}^{-}$ be an arbitrary sequence of real numbers. Since v is local almost automorphic, there exists a subsequence $\{\tau _{n}^{\tau }\}_{n=1} ^{\infty }\subset \{s_{n}^{\tau }\}_{n=1}^{\infty }$ such that $h(t):=\lim_{n\rightarrow \infty }v(t+\tau _{n}^{\tau })$ is well defined for each $t\in \mathbb{T}$.

Now, we consider

$$\begin{aligned} u \bigl(t+\tau _{n}^{\tau } \bigr) =& \int _{-\infty }^{t+\tau _{n}^{\tau }} \mathscr{T}^{\tau }_{t+\tau _{n}^{\tau },s}v(s) \Delta _{\tau _{s}} s= \int _{-\infty }^{t}\mathscr{T}^{\tau }_{t,s}v \bigl(s+\tau _{n}^{\tau } \bigr) \Delta _{\tau _{s}} s \\ =& \int _{-\infty }^{t}\mathscr{T}^{\tau }_{t,s}v_{n}(s) \Delta _{\tau _{s}} s, \end{aligned}$$

where $v_{n}(s)=v(s+\tau _{n}^{\tau })$, $n=1,2,\ldots$ . We have

$$\begin{aligned} \bigl\Vert u \bigl(t+\tau _{n}^{\tau } \bigr) \bigr\Vert \leq & \int _{-\infty }^{t} \bigl\Vert \mathscr{T}^{ \tau }_{t,s}v_{n}(s) \bigr\Vert \Delta _{\tau _{s}} s\leq \int _{-\infty }^{t}Ke ^{\tau }_{\ominus \omega }(t,s) \bigl\Vert v_{n}(s) \bigr\Vert \Delta _{\tau _{s}} s \\ \leq &K \Vert v \Vert _{LAA(\mathbb{T},\mathbb{X})} \int _{-\infty }^{t}e^{ \tau }_{\ominus \omega }(t,s) \Delta _{\tau _{s}} s \\ \leq &\frac{K}{1+\underline{\mu }\omega } \Vert v \Vert _{LAA(\mathbb{T}, \mathbb{X})} \int _{-\infty }^{t}e^{\tau }_{\ominus \omega } \bigl(t, \sigma (s) \bigr)\Delta _{\tau _{s}} s \\ \leq &-\frac{K(1+\omega \underline{\mu })}{\omega (1+\underline{ \mu }\omega )} \bigl(e^{\tau }_{\ominus \omega }(t,-\infty )-e^{\tau } _{\ominus \omega }(t,t) \bigr) \Vert v \Vert _{LAA(\mathbb{T},\mathbb{X})} \\ =&\frac{K}{\omega } \Vert v \Vert _{LAA(\mathbb{T},\mathbb{X})}, \end{aligned}$$

where $\underline{\mu }=\inf_{s\in \mathbb{T}_{\tau _{t}}}\mu _{\tau }(s)$ and $\|v\|_{LAA(\mathbb{T},\mathbb{X})}:= \sup_{s\in \mathbb{T}_{\tau _{t}}}\|v(s)\|$.

By the continuity of the moving-operator $\{\mathscr{T}^{\tau }_{t}:t,t _{0}\in \mathbb{T}_{\tau _{t}},t\geq t_{0}\}$ it follows that

$$ \mathscr{T}^{\tau }_{t,s}v_{n}(s)\rightarrow \mathscr{T}^{\tau }_{t,s}h(s), \quad \text{as }n\rightarrow \infty, $$

for each $s\in \mathbb{T}_{\tau _{t}}$ fixed and any $t\geq s$, and we get

$$ \lim_{n\rightarrow \infty }u \bigl(t+\tau _{n}^{\tau } \bigr)= \int _{-\infty }^{t}\mathscr{T}^{\tau }_{t,s}h(s) \Delta _{\tau _{s}} s $$

by the Lebesgue dominated convergence theorem. Furthermore, if $S_{\tau _{t}}^{+}\notin \{\{0\},\emptyset \}$, i.e., $\mathbb{T}_{\tau _{t}}$ is a positive-direction periodic sub-timescale, analogously to the above proof, we can also obtain

$$ \lim_{n\rightarrow \infty }u \bigl(t+\tau _{n}^{\tau } \bigr)= \int _{t}^{+ \infty }\mathscr{T}^{\tau }_{t,s}h(s) \Delta _{\tau _{s}} s. $$

This shows that $u(t)$ is a local almost automorphic function. The proof is complete. □

Lemma 4.2

Let $f=g+\phi \in LPAA(\mathbb{T},\mathbb{X})$ and $\{ \mathscr{T}^{\tau }_{t,t_{0}}:t,t_{0}\in \mathbb{T}_{\tau _{t}},t \geq t_{0} \}$ be exponentially stable. If $S_{\tau _{t}}^{-} \notin \{\{0\},\emptyset \}$, then $F(t):=\int _{-\infty } ^{t}\mathscr{T}_{t,s}f(s)\Delta s\in LPAA(\mathbb{T},\mathbb{X})$. If $S_{\tau _{t}}^{+}\notin \{\{0\},\emptyset \}$, then $F(t):=\int _{t}^{+\infty }\mathscr{T}_{t,s}f(s)\Delta s\in LPAA( \mathbb{T},\mathbb{X})$.

Proof

Let $F(t)=G(t)+\varPhi (t)$, where

$$ G(t):= \int _{-\infty }^{t}\mathscr{T}^{\tau }_{t,s}g(s) \Delta _{\tau _{s}} s \quad \text{and}\quad \varPhi (t):= \int _{-\infty }^{t}\mathscr{T}^{\tau }_{t,s} \phi (s) \Delta _{\tau _{s}} s. $$

Then, by Lemma 4.1, $G(t)\in LAA(\mathbb{T},\mathbb{X})$. Now we show that $\varPhi (t)\in LAA_{0}(\mathbb{T},\mathbb{X})$.

In fact, for $S_{\tau _{t}}^{-}\notin \{\{0\},\emptyset \}$, i.e., $\mathbb{T}_{\tau _{t}}$ is a negative-direction periodic sub-timescale, we obtain

$$ \frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \varPhi (s) \bigr\Vert \Delta _{\tau _{s}} s= \frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl\Vert \int _{-\infty }^{s} \mathscr{T}^{\tau }_{s,\theta } \phi (\theta )\Delta _{\tau _{\theta }} \theta \biggr\Vert \Delta _{\tau _{s}} s\leq I_{1}+I_{2}, $$

where

$$ I_{1}:=\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl\Vert \int _{-\infty }^{t _{0}+T}\mathscr{T}^{\tau }_{s,\theta } \phi (\theta ) \Delta _{\tau _{\theta }}\theta \biggr\Vert \Delta _{\tau _{s}} s $$

and

$$ I_{2}:=\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl\Vert \int _{t_{0}+T}^{s} \mathscr{T}^{\tau }_{s,\theta } \phi (\theta )\Delta _{\tau _{\theta }} \theta \biggr\Vert \Delta _{\tau _{s}} s. $$

One can obtain

$$\begin{aligned} I_{1} :=&\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl\Vert \int _{-\infty }^{t _{0}+T}\mathscr{T}^{\tau }_{s,\theta } \phi (\theta ) \Delta _{\tau _{\theta }}\theta \biggr\Vert \Delta _{\tau _{s}} s \\ \leq &\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl( \int _{-\infty }^{t_{0}+T} \bigl\Vert \mathscr{T}^{\tau }_{s,\theta } \bigr\Vert \bigl\Vert \phi ( \theta ) \bigr\Vert \Delta _{\tau _{\theta }}\theta \biggr)\Delta _{\tau _{s}} s \\ \leq &\frac{K}{T} \int _{t_{0}}^{t_{0}+T} \biggl( \int _{-\infty }^{t_{0}+T}e ^{\tau }_{\ominus \omega }(s, \theta ) \bigl\Vert \phi (\theta ) \bigr\Vert \Delta _{\tau _{\theta }}\theta \biggr)\Delta _{\tau _{s}} s \\ \leq &-\frac{K(1+\underline{\mu }\omega )}{T\omega (1+\underline{ \mu }\omega )} \Vert \phi \Vert _{LAA_{0}(\mathbb{T},\mathbb{X})} \int _{t_{0}} ^{t_{0}+T} \bigl(e^{\tau }_{\ominus \omega }(s,- \infty )-e^{\tau }_{ \ominus \omega }(s,t_{0}+T) \bigr)\Delta _{\tau _{s}} s \\ \leq &\frac{K(1+\bar{\mu }\omega )}{T\omega } \Vert \phi \Vert _{LAA_{0}( \mathbb{T},\mathbb{X})} \int _{t_{0}}^{t_{0}+T}e^{\tau }_{\omega } \bigl(t_{0}+T,\sigma (s) \bigr)\Delta _{\tau _{s}}s \\ \leq &\frac{K(1+\bar{\mu }\omega )}{T\omega } \Vert \phi \Vert _{LAA_{0}( \mathbb{T},\mathbb{X})} \bigl(e^{\tau }_{\omega }(t_{0}+T,t_{0})-e^{ \tau }_{\omega }(t_{0}+T,t_{0}+T) \bigr) \\ \leq &\frac{K(1+\bar{\mu }\omega )}{T\omega } \Vert \phi \Vert _{LAA_{0}( \mathbb{T},\mathbb{X})} \bigl(e^{\tau }_{\omega }(t_{0}+T,t_{0})-1 \bigr). \end{aligned}$$

Since $\|\phi \|_{LAA_{0}(\mathbb{T},\mathbb{X})}:=\sup_{s\in \mathbb{T}_{\tau _{t}}}\|\phi (s)\|<\infty$, let $T\rightarrow -\infty$, then $\lim_{T\rightarrow -\infty }I _{1}=0$. Also

$$\begin{aligned} I_{2} :=&\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl\Vert \int _{t_{0}+T}^{s} \mathscr{T}^{\tau }_{s,\theta } \phi (\theta )\Delta _{\tau _{\theta }} \theta \biggr\Vert \Delta _{\tau _{s}} s \\ \leq &\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl( \int _{t_{0}+T}^{s} \bigl\Vert \mathscr{T}^{\tau }_{s,\theta } \bigr\Vert \bigl\Vert \phi ( \theta ) \bigr\Vert \Delta _{\tau _{\theta }}\theta \biggr)\Delta _{\tau _{s}} s \\ \leq &\frac{K}{T} \int _{t_{0}}^{t_{0}+T} \biggl( \int _{t_{0}+T}^{s}e^{ \tau }_{\ominus \omega }(s, \theta )\Delta _{\tau _{\theta }}\theta \biggr) \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s \\ \leq &-\frac{K(1+\underline{\mu }\omega )}{T\omega (1+\underline{ \mu }\omega )} \int _{t_{0}}^{t_{0}+T} \bigl(e^{\tau }_{\ominus \omega }(s,t _{0}+T)-e^{\tau }_{\ominus \omega }(s,s) \bigr) \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s \\ \leq &\frac{K(1+\omega \bar{\mu })}{T\omega } \bigl(e_{\omega }^{ \tau }(t_{0}+T,t_{0})-e^{\tau }_{\omega }(t_{0}+T,t_{0}+T) \bigr)+\frac{K}{T \omega } \int _{t_{0}}^{t_{0}+T} \bigl\Vert \phi (s) \bigr\Vert \Delta _{\tau _{s}} s. \end{aligned}$$

Since $\phi \in LAA_{0}(\mathbb{T},\mathbb{X})$, then $\lim_{T\rightarrow -\infty }\frac{1}{T}\int _{t_{0}}^{t_{0}+T}\| \phi (s)\|\Delta _{\tau _{s}} s=0$. Hence $\lim_{T\rightarrow -\infty }I_{2}=0$.

For $S_{\tau _{t}}^{+}\notin \{\{0\},\emptyset \}$, i.e., $\mathbb{T}_{\tau _{t}}$ is a positive-direction periodic sub-timescale, we obtain

$$ \frac{1}{T} \int _{t_{0}}^{t_{0}+T} \bigl\Vert \varPhi (s) \bigr\Vert \Delta _{\tau _{s}} s= \frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl\Vert \int _{s}^{+\infty } \mathscr{T}^{\tau }_{s,\theta } \phi (\theta )\Delta _{\tau _{\theta }} \theta \biggr\Vert \Delta _{\tau _{s}} s\leq I_{1}+I_{2}, $$

where

$$ I_{1}:=\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl\Vert \int _{t_{0}}^{+\infty }\mathscr{T}^{\tau }_{s,\theta } \phi (\theta )\Delta _{\tau _{\theta }} \theta \biggr\Vert \Delta _{\tau _{s}} s $$

and

$$ I_{2}:=\frac{1}{T} \int _{t_{0}}^{t_{0}+T} \biggl\Vert \int _{t_{0}}^{s} \mathscr{T}^{\tau }_{s,\theta } \phi (\theta )\Delta _{\tau _{\theta }} \theta \biggr\Vert \Delta _{\tau _{s}} s. $$

Similar to the above discussion for the case $S_{\tau _{t}}^{-}\notin \{\{0\},\emptyset \}$, we also obtain $\lim_{T\rightarrow +\infty }I_{1}=0$ and $\lim_{T\rightarrow +\infty }I_{2}=0$. Therefore, we obtain the desired result. This completes the proof. □

Through Lemma 4.2, we can obtain the following theorem to guarantee the existence of a unique local pseudo almost automorphic mild solution for (4.1).

Theorem 4.1

Under assumptions ($\mathrm{H}_{1}$)–($\mathrm{H}_{3}$), if $S_{\tau _{t}}^{-}\neq \{0\}$ or $S_{\tau _{t}}^{+}\notin \{\{0\},\emptyset \}$, then (4.1) has a unique local pseudo almost automorphic mild solution.

Proof

For the case $S_{\tau _{t}}^{-}\notin \{\{0\},\emptyset \}$, we consider the nonlinear operator $\mathscr{F}_{\tau }$ given by

$$ (\mathscr{F}_{\tau }x) (t)= \int _{-\infty }^{t}\mathscr{T}^{\tau }_{t,s}f \bigl(s,x(s) \bigr)\Delta _{\tau _{s}} s. $$

By Lemma 4.2, we see $\mathscr{F}_{\tau }$ maps $LPAA(\mathbb{T}, \mathbb{X})$ into $LPAA(\mathbb{T},\mathbb{X})$.

Case 1: $\varrho _{0}\in L^{1}(\mathbb{T}_{\tau _{t}})$. Let $x,y\in LPAA(\mathbb{T},\mathbb{X})$ and observe

$$\begin{aligned} \Vert \mathscr{F}_{\tau }x-\mathscr{F}_{\tau }y \Vert \leq &\sup_{t\in \mathbb{T}_{\tau _{t}}} \int _{-\infty }^{t} \bigl\Vert \mathscr{T}^{\tau }_{t,s} \bigl[f \bigl(s,x(s) \bigr)-f \bigl(s,y(s) \bigr) \bigr] \bigr\Vert \Delta _{\tau _{s}} s \\ \leq &\sup_{t\in \mathbb{T}_{\tau _{t}}} \int _{-\infty }^{t} \bigl\Vert \mathscr{T}^{\tau }_{t,s} \bigr\Vert \varrho _{0}(s) \bigl\Vert x(s)-y(s) \bigr\Vert \Delta _{\tau _{s}} s \\ \leq &K \Vert x-y \Vert _{\mathbb{X}} \int _{-\infty }^{t}e^{\tau }_{\ominus \omega }(t,s) \varrho _{0}(s)\Delta _{\tau _{s}} s \\ \leq & K \Vert x-y \Vert \int _{-\infty }^{t}\varrho _{0}(s)\Delta _{\tau _{s}} s, \end{aligned}$$

and

$$\begin{aligned} \bigl\Vert \mathscr{F}_{\tau }^{2}x-\mathscr{F}_{\tau }^{2}y \bigr\Vert \leq &K \int _{-\infty }^{t}\varrho _{0}(s) \bigl\Vert \mathscr{F}_{\tau }x(s)- \mathscr{F}_{\tau }y(s) \bigr\Vert \Delta _{\tau _{s}} s \\ \leq &K^{2} \Vert x-y \Vert \int _{-\infty }^{t}\varrho _{0}(s) \int _{-\infty } ^{s}\varrho _{0}(\theta )\Delta _{\tau _{\theta }}\theta \Delta _{\tau _{s}} s \\ \leq &\frac{K^{2}}{2} \Vert x-y \Vert \biggl( \int _{-\infty }^{t}\varrho _{0}(s) \Delta _{\tau _{s}} s \biggr)^{2}. \end{aligned}$$

Induction on n in the same way gives

$$ \bigl\Vert \mathscr{F}_{\tau }^{n}x-\mathscr{F}_{\tau }^{n}y \bigr\Vert \leq \frac{K^{n}}{n!} \Vert x-y \Vert \biggl( \int _{-\infty }^{t}\varrho _{0}(s) \Delta _{\tau _{s}} s \biggr)^{n}. $$

Therefore,

$$ \bigl\Vert \mathscr{F}_{\tau }^{n}x-\mathscr{F}_{\tau }^{n}y \bigr\Vert \leq \frac{(K \Vert \varrho _{0} \Vert _{L^{1}(\mathbb{T}_{\tau _{t}})})^{n}}{n!} \Vert x-y \Vert . $$

For sufficiently large n, ${ \frac{(K\|\varrho _{0}\|_{L^{1}(\mathbb{T}_{\tau _{t}})})^{n}}{n!}}<1$. From the Banach contraction mapping theorem, the mapping $\mathscr{F} _{\tau }$ has a unique fixed point $x\in LPAA(\mathbb{T},\mathbb{X})$, and this fixed point satisfies the integral equation

$$ x(t)= \int _{-\infty }^{t}\mathscr{T}^{\tau }_{t,s}f \bigl(s,x(s) \bigr) \Delta _{\tau _{s}} s\quad \text{for all }t\in \mathbb{T}_{\tau _{t}}. $$

Case 2: $\varrho _{0}\in L^{2}(\mathbb{T}_{\tau _{t}})$. First, put

$$ \lambda (t)= \int _{-\infty }^{t}\varrho _{0}^{2}(s) \Delta _{\tau _{s}} s. $$

Since $0<\lambda (t)<\int _{-\infty }^{+\infty }\varrho _{0}^{2}(t) \Delta _{\tau _{t}} t<+\infty$, $\lambda (t)$ is bounded. We let $\lambda _{0}=\sup_{s\in \mathbb{T}_{\tau _{t}}}\lambda (s)$. Then we define an equivalent norm over $LPAA(\mathbb{T},\mathbb{X})$ as follows:

$$ \Vert f \Vert _{c,t_{0}}=e^{\tau }_{\ominus \lambda _{0}}(t_{0},c) \Vert f \Vert , $$

where $c,t_{0}\in \mathbb{T}_{\tau _{t}}$, $c\geq t_{0}$ are fixed positive numbers. We have

$$\begin{aligned}& \Vert \mathscr{F}_{\tau }x-\mathscr{F}_{\tau }y \Vert \\& \quad \leq \sup_{t\in \mathbb{T}_{\tau _{t}}} \int _{-\infty }^{t} \bigl\Vert \mathscr{T}^{\tau }_{t,s} \bigl[f \bigl(s,x(s) \bigr)-f \bigl(s,y(s) \bigr) \bigr] \bigr\Vert \Delta _{\tau _{s}} s \\& \quad \leq \sup_{t\in \mathbb{T}_{\tau _{t}}} \int _{-\infty }^{t} \varrho _{0}(s) \bigl\Vert \mathscr{T}^{\tau }_{t,s} \bigr\Vert \bigl\Vert x(s)-y(s) \bigr\Vert \Delta _{\tau _{s}} s \\& \quad \leq K \int _{-\infty }^{t}e^{\tau }_{\ominus \omega }(t,s) \varrho (s)e ^{\tau }_{\lambda _{0}}(t_{0},c)\Delta _{\tau _{s}} s \Vert x-y \Vert _{c,t_{0}} \\& \quad \leq K \biggl( \int _{-\infty }^{t} \bigl[e^{\tau }_{\lambda _{0}}(t_{0},c) \bigr]^{2}\varrho _{0}^{2}(s)\Delta _{\tau _{s}} s \biggr)^{\frac{1}{2}} \biggl( \int _{-\infty }^{t} \bigl[e^{\tau }_{\ominus \omega }(t,s) \bigr]^{2} \Delta _{\tau _{s}} s \biggr)^{\frac{1}{2}} \Vert x-y \Vert _{c,t_{0}}. \end{aligned}$$

Therefore, one has

$$\begin{aligned} \int _{-\infty }^{t} \bigl[e^{\tau }_{\ominus \omega }(t,s) \bigr]^{2} \Delta _{\tau _{s}} s \leq & \int _{-\infty }^{t}e^{\tau }_{\ominus \omega }(t,s) \Delta _{\tau _{s}} s \\ \leq &\frac{1}{1+\underline{\mu }\omega } \int _{-\infty }^{t}e^{ \tau }_{\ominus \omega } \bigl(t,\sigma (s) \bigr)\Delta _{\tau _{s}} s \\ \leq &-\frac{1}{\omega } \bigl(e^{\tau }_{\ominus \omega }(t,-\infty )-e ^{\tau }_{\ominus \omega }(t,t) \bigr) \leq \frac{1}{\omega }. \end{aligned}$$

Furthermore,

$$ \int _{-\infty }^{t} \bigl[e^{\tau }_{\lambda _{0}}(t_{0},c) \bigr]^{2} \varrho _{0}^{2}(s)\Delta _{\tau _{s}} s\leq \int _{-\infty }^{t}e^{ \tau }_{\ominus \lambda _{0}}(c,t_{0}) \varrho _{0}^{2}(s)\Delta _{\tau _{s}} s\leq \lambda _{0}e^{\tau }_{\ominus \lambda _{0}}(c,t_{0}). $$

As a result, we obtain

$$ \Vert \mathscr{F}_{\tau }x-\mathscr{F}_{\tau }y \Vert _{c,t_{0}}\leq K \biggl(\frac{1}{ \omega } \biggr)^{\frac{1}{2}} \lambda _{0}^{\frac{1}{2}} \bigl(e^{\tau } _{\ominus \lambda _{0}}(c,t_{0}) \bigr)^{\frac{1}{2}} \Vert x-y \Vert _{c,t_{0}}:= \xi \Vert x-y \Vert _{c,t_{0}}, $$

where $\xi =K ({ \frac{1}{\omega }} )^{\frac{1}{2}}\lambda _{0}^{\frac{1}{2}} (e ^{\tau }_{\ominus \lambda _{0}}(c,t_{0}) )^{\frac{1}{2}}$. Hence, it is easy to observe that one can take sufficiently large $c>t_{0}$ such that $\xi <1$. Thus $\mathscr{F}_{\tau }$ is a contractive mapping. We get a fixed point $x\in LPAA(\mathbb{T},\mathbb{X})$ by the Banach fixed point theorem.

For the case $S_{\tau _{t}}^{+}\notin \{\{0\},\emptyset \}$, we consider the nonlinear operator $\mathscr{F}_{\tau }$ given by

$$ (\mathscr{F}_{\tau }x) (t)= \int _{t}^{+\infty }\mathscr{T}^{\tau }_{t,s}f \bigl(s,x(s) \bigr)\Delta _{\tau _{s}} s. $$

By Lemma 4.2, we see $\mathscr{F}_{\tau }$ maps $LPAA(\mathbb{T}, \mathbb{X})$ into $LPAA(\mathbb{T},\mathbb{X})$. A similar argument can be supplied for the case $S_{\tau _{t_{0}}}^{+}\notin \{\{0\}, \emptyset \}$, so we omit it here. This completes the proof. □

Example 4.1

Let $x_{1}^{\Delta }=-x_{2}$ and $x_{2}^{\Delta }=x_{1}$, then one can easily calculate that $x_{1}=\cos _{1}(t,t_{0})$ and $x_{2}=\sin _{1}(t,t _{0})$. Consider two time scales as follows:

$$\begin{aligned} \mathbb{T}_{1} =& \bigl\{ 4k,(4k+2)\pi :k\in \mathbb{Z}^{+} \bigr\} \cup \Biggl(\bigcup_{k=1}^{+\infty } \bigl[(4k-1)\pi ,4k\pi \bigr] \Biggr) \\ &{}\cup \mathbb{P}_{a,|\sin \sqrt{3}t+\sin \sqrt{7}t|} \end{aligned}$$

and

$$\begin{aligned} \mathbb{T}_{2}=\bigcup_{k=0}^{+\infty }[5k,5k+4] \cup \mathbb{T} _{H_{n}}, \quad \text{where }\mathbb{T}_{H_{n}}= \{H_{n}:n\in \mathbb{N} _{0}\} \end{aligned}$$

and $H_{n}$ is harmonic numbers.

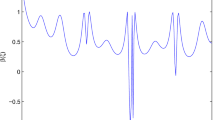
Since $\mathbb{T}_{1}$, $\mathbb{T}_{2}$ are changing-periodic time scales, according to the decomposition theorem of time scales, one can obtain the periodic sub-timescale which is included in $\mathbb{T}_{1}$ as $\{4k,(4k+2)\pi :k\in \mathbb{Z}^{+}\}\cup (\bigcup_{k=1}^{+\infty }[(4k-1) \pi ,4k\pi ])$ and the periodic sub-timescale of $\mathbb{T}_{2}$ as $\bigcup_{k=0}^{+\infty }[5k,5k+4]$. By Theorem 4.1, there are local almost automorphic solutions on these periodic sub-timescales, see Figs. 1–6.

Figure 1

The local almost automorphic solution $x_{1}$ on the sub-periodic time scales $\{4k,(4k+2)\pi :k\in \mathbb{Z}^{+}\}\cup (\bigcup_{k=1}^{+\infty }[(4k-1)\pi ,4k\pi ])$

Figure 2

The local almost automorphic solution $x_{1}$ on the sub-periodic time scale $\bigcup_{k=0}^{+\infty }[5k,5k+4]$

Figure 3

The local almost automorphic solution $x_{2}$ on the sub-periodic time scales $\{4k,(4k+2)\pi :k\in \mathbb{Z}^{+}\}\cup (\bigcup_{k=1}^{+\infty }[(4k-1)\pi ,4k\pi ])$

Figure 4

The local almost automorphic solution $x_{2}$ on the sub-periodic time scale $\bigcup_{k=0}^{+\infty }[5k,5k+4]$

Figure 5

The local almost automorphic solutions $x_{1}$, $x_{2}$ on the sub-periodic time scales $\{4k,(4k+2)\pi :k\in \mathbb{Z}^{+}\}\cup (\bigcup_{k=1}^{+\infty }[(4k-1)\pi ,4k\pi ])$

Figure 6

The local almost automorphic solutions $x_{1}$, $x_{2}$ on the sub-periodic time scales $\bigcup_{k=0}^{+\infty }[5k,5k+4]$

5 Conclusion

In this section, we introduce the concept of local almost automorphic functions on changing-periodic time scales and obtain some new results on local almost automorphic solutions for a class of semilinear dynamic equations by using the Π-semigroup for time scales. Based on changing-periodic time scales, we are able to study almost automorphic problems on an arbitrary time scale. Before we could only discuss almost automorphic problems on the time scales with “complete closedness”. For example, in the past, it was impossible to study almost automorphic problems on the following time scale:

$$ \mathbb{P}_{a,e^{-t}}=\bigcup_{m=1}^{\infty }[p_{m},a+p_{m}], \quad a>1 , t>a , t\in \mathbb{T}, $$

where

$$\begin{aligned} p_{m} =&(m-1)a+\sum_{k=1}^{m-1} \exp \bigl\{ - \bigl[ka+\exp (-a)+\exp \bigl(- \bigl(2a+\exp (-a) \bigr) \bigr)+ \cdots \\ &\underbrace{{}+\exp \bigl(- \bigl((k-1)a+\exp (-a) \bigr) \bigr) \bigr]} _{k\text{ terms}} \bigr\} . \end{aligned}$$

Then we have

$$ \sigma (t)= \textstyle\begin{cases} t,& \text{if }t\in \bigcup_{m=1}^{\infty }[p_{m},a+p_{m}), \\ t+e^{-t},& \text{if }t\in \bigcup_{m=1}^{\infty }\{a+p_{m}\} \end{cases} $$

and

$$ \mu (t)= \textstyle\begin{cases} 0,& \text{if }t\in \bigcup_{m=1}^{\infty }[p_{m},a+p_{m}), \\ e^{-t}, & \text{if }t\in \bigcup_{m=1}^{\infty }\{a+p_{m}\}. \end{cases} $$

However, by using the knowledge of changing-periodic time scales, through the decomposition theorem of time scales, we are able to study almost automorphic problems on such a type of time scale. For example, from Theorem 4.1, we see that (4.1) has a unique local almost automorphic solution on the time scale $\mathbb{P}_{a,e^{-t}}$. Moreover, we can consider periodic or almost periodic problems for dynamic equations on an arbitrary time scale through this effective tool in the future.