1 Introduction

Each field of life depends on fluids such as water, milk, juices, blood, glycerin, grease, paints, oils, polymer solutions, etc. and their direct or indirect motions. For most of these fluids, a linear stress-strain relationship does not exist [1] and the classical Navier–Stokes equation cannot describe their behavior. There are lots of fluid models in literature depending upon their response under different circumstances. Among them, the model that has received more attention is the rate type fluid model. The first rate type model, which is viscoelastic and still utilized generally, was given by Maxwell [2]. Although Maxwell developed this model for air, not for polymeric liquids, his methodology can be summed up to provide a plethora of models. Rajagopal and Srinivasa [3] developed a comprehensive thermodynamic framework by using the concept of Maxwell’s work, which provides a base for making a class of rate type viscoelastic fluids. In the presence of transverse magnetic field, Nayak [4] studied both the heat and mass flow rate of viscous fluid through a medium which is porous considering both heat source and sink. Shateyi [5] used a numerical approach to study the MHD flow of a Maxwell fluid past a stretching plate in the presence of chemical reaction. Shah et al. [6] analyzed the unsteady flow of a magnetohydrodynamic (MHD) second grade fluid over a stretching sheet by using similarity transformations.

Many types of fluid motions, in different geometries, have important applications in chemical industry, bioengineering, mechanical engineering, plasma physics, geophysics, etc. The movement of fluids in circular cylinders has a lot of applications in biological analysis, food industry, petroleum industry, and oil exploitation [7,8,9]. A variety of Newtonian fluid motions was studied by Bathchelor [10] in circular pipes, but Ting [11] was the first author who found exact solutions about the movement of non-Newtonian fluids. Srivastava [12] was the first who studied the motions of Maxwell fluids through a circular cylinder and obtained analytical solutions. Other exact solutions for motions of Maxwell fluids in cylindrical domains have been obtained by Rahaman and Ramkisson [13], Fetecau and Corina Fetecau [14], Vieru et al. [15], Jamil and Fetecau [16], Jamil et al. [17], Zeb et al. [18], and Corina Fetecau et al. [19]. Recently, Nehad et al. [20] provided the first general solutions for rotational motions of rate type fluids between circular cylinders.

However, in all the above discussed articles, the effects of long-term memory as one of viscoelastic properties of non-Newtonian fluids have been ignored. As far as we know, the memory formalism can be represented using fractional derivatives [21], and the fractional models have gained an increasing interest in many fields including viscoelasticity. The first authors who used fractional derivatives in viscoelasticity were Bagley and Torvik [22], while Caputo and Mainardi [23, 24] got a very good agreement with experimental data using fractional calculus. Recently, the applicability of fractional calculus in fluid mechanics has been continuously increasing because differential equations can describe some important physical phenomena’ more accurately with fractional derivatives instead of ordinary derivatives. Makris et al. [25] utilized exploratory information in order to calibrate a fractional derivative Maxwell model. All the more precisely, they found an estimation of the partial parameter for the relating material properties to be in superb concurrence with test results.

Based on the above-mentioned remarks, in the last decade many researchers used the fractional derivatives as a remarkable tool to analyze the properties of viscoelastic fluids [26,27,28,29,30,31,32,33,34]. However, in all these works the motion of the fluid is generated by a cylinder that is rotating around its axis with a given velocity or applies to the fluid a shear stress that is given by a partial differential equation. Consequently, in the existing literature, there is no exact solution about the motions of fractional rate type fluid developed by an infinite cylinder that applies a constant, accelerated, or oscillating shear stress to the fluid. Such solutions for ordinary rate type fluids were recently obtained by Fetecau et al. [35] and Rauf et al. [36] for constant and oscillating stress, respectively, which is on the boundary, while the solutions from [28] and [37] do not examine the constant shear on the boundary as the researchers claimed there. On the other hand, as it was shown by Renardy [38, 39], the boundary conditions on tangential stresses are very significant and a well-posed boundary problem can be generated in this way.

Our objective in this note is to determine closed form solutions of rotational motion of fractional Maxwell fluid in an infinite circular pipe that applies a couple to the fluid which is time dependent. To do that, contrary to the usual rule from the literature, we use the constitutive equation for the tangential stress, which is the result of elimination of velocity field between the constitutive equations and relevant motion of fluid. The solutions for the current flow model that have been achieved fulfill all imposed initial and boundary conditions. Solutions for Newtonian and ordinary Maxwell fluids having similar motion are also obtained as limiting cases. Finally, the effect of fractional parameter and relaxation time on the velocity and shear stress fields as well as some comparisons with ordinary Maxwell and Newtonian fluids are graphically underlined and discussed.

2 Governing equations

Let us consider an incompressible fractional Maxwell fluid at rest in an infinite circular cylinder of radius R. After time \(t = 0\) the cylinder is set in rotational motion about its axis by a time-dependent torque per unit length \(2\pi R g t\) [40], where g is a constant. Because of shear, the fluid is steadily moved and its velocity is

$$\begin{aligned} \mathbf{v}=\mathbf{v}(r,t)=w(r,t)\mathbf{e}_{\theta } \end{aligned}$$
(1)

in a suitable cylindrical coordinate system r, θ, and z. Here, \(\mathbf{e}_{\theta }\) is the unit vector in the θ direction. For such a movement the imperative of incompressibility is fulfilled.

In addition, we assume that the extra-stress S corresponding to such a motion is also a function of r and t. The fluid being at rest up to the moment \(t = 0\) results in

$$\begin{aligned} \mathbf{v}(r,0)=\mathbf{0}, \qquad \mathbf{S}(r,0) = \mathbf{0}. \end{aligned}$$
(2)

In view of Eqs. (1) and (2), the constitutive equation of Maxwell fluids implies \(S_{rr} = S_{rz} = S_{\theta z} = S_{zz} = 0\) and the appropriate partial differential equation [26]

$$\begin{aligned} \biggl(1+\lambda \frac{\partial }{\partial t} \biggr)\tau {(r,t)} = \mu \biggl( \frac{\partial }{\partial t}- \frac{1}{r} \biggr){w(r,t)}, \end{aligned}$$
(3)

where \(\tau (r,t) = S_{r\theta } (r,t)\) is the non-trivial shear stress, μ is the dynamic viscosity, and λ is the relaxation time. Without body forces, the balance of linear momentum becomes

$$\begin{aligned} \rho \frac{\partial {w(r,t)}}{\partial {t}}= \biggl(\frac{\partial }{ \partial t}+ \frac{2}{r} \biggr){\tau {(r,t)}}. \end{aligned}$$
(4)

The significant conditions (initial and boundary) are

$$\begin{aligned}& \tau {(r,t)}|_{t=0}={\frac{\partial \tau {(r,t)}}{\partial t}}\bigg|_{t=0} =0, \qquad w(r,0)=0, \quad r\in [0,R], \end{aligned}$$
(5)
$$\begin{aligned}& \tau {(r,t)}|_{r=R} = gt \quad \text{for } t>0. \end{aligned}$$
(6)

As we have to solve a motion problem with shear stress on the boundary, we follow [41] and eradicate the velocity field between Eqs. (3) and (4). The control equation for shear stress is

$$\begin{aligned} \biggl(1+\lambda \frac{\partial }{\partial t} \biggr)\frac{\partial {\tau {(r,t)}}}{\partial {t}} =\nu \biggl( \frac{\partial ^{2}}{\partial r^{2}}+{\frac{1}{r}} {\frac{\partial }{\partial {r}}}-\frac{4}{r^{2}} \biggr) \tau {(r,t)}. \end{aligned}$$
(7)

To make the governing equation corresponding to the fractional model, namely

$$\begin{aligned} \bigl(1+\lambda ^{\eta }D^{\eta }_{t} \bigr) \frac{\partial \tau {(r,t)}}{\partial t} =\nu \biggl(\frac{\partial ^{2}}{\partial r^{2}}+ \frac{1}{r} \frac{\partial }{\partial r}-\frac{4}{r^{2}} \biggr)\tau {(r,t)}, \end{aligned}$$
(8)

we replaced the inner time derivative with fractional differential operator [42] from Eq. (7)

$$\begin{aligned} D^{\eta }_{t} g(t)= \textstyle\begin{cases} \frac{1}{\varGamma (1-\eta )} \frac{d}{dt}\int _{0}^{t} \frac{g(\tau )}{(t- \tau )^{\eta }} \,d\tau ,& 0\leq \eta < 1; \\ \frac{d}{dt}g(t),& \eta =1, \end{cases}\displaystyle \end{aligned}$$
(9)

where \(\varGamma (\cdot )\) is the gamma function. In the following, Laplace and finite Hankel transforms are used to solve the fractional partial differential Eq. (8) with the help of initial and boundary conditions (5) and (6). At once the shear stress is determined, the velocity field is obtained using Eq. (4).

3 Solution of the flow problem

3.1 Calculation of the stress field

By applying Laplace transformation on Eqs. (6) and (8), we get

$$\begin{aligned}& \bigl(s+\lambda ^{\eta }s^{\eta +1} \bigr) \overline{\tau } (r,s) = \nu \biggl(\frac{\partial ^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}- \frac{4}{r^{2}} \biggr)\overline{\tau } (r,s), \end{aligned}$$
(10)
$$\begin{aligned}& \overline{\tau }(r,s)= \frac{g}{s^{2}}. \end{aligned}$$
(11)

In the above relations, Laplace transform of \(\tau (r,t)\) is \(\overline{\tau }(r,s)\) and s is the Laplace transform parameter. Finite Hankel transform and its inverse are [43]

$$\begin{aligned}& \varPsi _{{H}}(r_{{n}})= \int _{0}^{R}r \varPsi (r)J_{2}(rr_{{n}})\,dr , \end{aligned}$$
(12)
$$\begin{aligned}& \varPsi (r)=\frac{2}{R^{2}}\sum_{n=1}^{\infty } \frac{J_{2}(rr_{{n}})}{[J ^{\prime }_{2}(Rr_{{n}})]^{2}} \varPsi _{{H}}(r_{{n}}). \end{aligned}$$
(13)

In the above relations, \(J^{\prime }_{2}(Rr_{{n}})=J_{1}(Rr_{{n}})\) [43], \(J_{2}(\cdot)\) represents the second order Bessel function of the first kind, and \(r_{{n}}\) are the positive roots of \(J_{2}(Rr_{{n}})=0\). Multiplying Eq. (10) with \(rJ_{2}(rr_{{n}})\) and then integrating from 0 to R and using the identity [35]

$$\begin{aligned}& \int _{0}^{R} \biggl(\frac{\partial ^{2}{\overline{\tau }}(r,s)}{\partial r^{2}}+ \frac{1}{r} \frac{\partial {\overline{\tau }}(r,s) }{\partial r}-\frac{4{\overline{ \tau }}(r,s)}{r^{2}} \biggr)rJ_{2}(rr_{{n}})\,dr \\& \quad =-Rr_{{n}}J^{\prime }_{2}(Rr_{{n}})\overline{ \tau }_{(}R,s)-r_{{n}} ^{2}\overline{\tau }_{{H}}(r_{{n}},s), \end{aligned}$$
(14)

we obtain

$$\begin{aligned} \overline{\tau }_{{H}}(r_{{n}},s)=\frac{-gR\nu r_{{n}}J_{1}(Rr _{{n}})}{s^{2}[s+\lambda ^{\eta }s^{\eta +1}+\nu r_{{n}}^{2}]}, \end{aligned}$$
(15)

or in an equivalent form

$$\begin{aligned} \overline{\tau }_{{H}}(r_{{n}},s)=\frac{-gRJ_{1}(Rr_{{n}})}{r _{{n}}s^{2}}+ \frac{gRJ_{1}(Rr_{{n}})(1+\lambda ^{\eta }s^{\eta })}{r _{{n}}s[s+\lambda ^{\eta }s^{\eta +1}+\nu r_{{n}}^{2}]}. \end{aligned}$$
(16)

By using the identity

$$\begin{aligned} \frac{1}{(s+\lambda ^{\eta }s^{\eta +1}+\nu r_{n}^{2})}=\frac{1}{ \lambda ^{\eta }}\sum_{\ell =0}^{\infty } \biggl(\frac{-\nu r_{n}^{2}}{ \lambda ^{\eta }} \biggr)^{\ell } \frac{s^{-\ell -1}}{(s^{\eta }+ \lambda ^{-\eta })^{\ell +1}}, \end{aligned}$$
(17)

in Eq. (16), we get

$$\begin{aligned}& \overline{\tau }_{{H}}(r_{{n}},s) \\& \quad = \frac{-gRJ_{1}(Rr_{{n}})}{r_{{n}}s^{2}}+\frac{gR}{\lambda ^{ \eta }r_{{n}}}J_{1}(Rr_{{n}})\sum _{\ell =0}^{\infty } \biggl(\frac{- \nu r_{n}^{2}}{\lambda ^{\eta }} \biggr)^{\ell } \biggl[\frac{s^{- \ell -2}+\lambda ^{\eta }s^{\eta -\ell -2}}{(s^{\eta }+\lambda ^{- \eta })^{\ell +1}} \biggr]. \end{aligned}$$
(18)

Applying the inverse Hankel transform and bearing in mind the identity

$$\begin{aligned} r^{2}=-2R\sum_{n=1}^{\infty } \frac{J_{2}(rr_{{n}})}{r_{{n}}J _{1}(Rr_{{n}})}, \end{aligned}$$
(19)

we get

$$\begin{aligned} \overline{\tau }(r,s)=\frac{gr^{2}}{R^{2} s^{2}}+\frac{2g}{\lambda ^{\eta }R}\sum _{n=1}^{\infty }\frac{J_{2}(rr_{{n}})}{r_{{n}}J _{1}(Rr_{{n}})}\sum _{\ell =0}^{\infty } \biggl(\frac{-\nu r_{n}^{2}}{ \lambda ^{\eta }} \biggr)^{\ell } \biggl[\frac{s^{-\ell -2}+\lambda ^{ \eta }s^{\eta -\ell -2}}{(s^{\eta }+\lambda ^{-\eta })^{\ell +1}} \biggr]. \end{aligned}$$
(20)

To obtain the final expression for stress field, we apply the inverse Laplace transform to Eq. (20) and use the definition of generalized \(G_{\ell , \jmath , \zeta }(\sigma , t)\) function [44]

$$\begin{aligned} &G_{\ell , \jmath , \zeta }(\sigma ,t) \\ &\quad = L^{-1} \biggl\{ \frac{s^{ \jmath }}{(s^{\ell }-\sigma )^{\zeta }} \biggr\} \\ &\quad =\sum_{i=0}^{\infty }\frac{\sigma ^{i} \varGamma (\zeta +i)}{\varGamma ( \zeta )\varGamma (i+1)} \frac{t^{(\zeta +i)\ell -\jmath -1}}{\varGamma [( \zeta +i)\ell -\jmath ]} ;\quad \operatorname{Re}(\ell \zeta -\jmath )>0, \operatorname{Re}(s)>0, \biggl\vert \frac{\sigma }{s^{\ell }} \biggr\vert < 1. \end{aligned}$$
(21)

The obtained solution

$$\begin{aligned} \tau (r,t)&= gt \biggl(\frac{r}{R} \biggr)^{2}+ \frac{2g}{\lambda ^{\eta }R} \sum_{n=1}^{\infty } \frac{J_{2}(rr_{{n}})}{r_{{n}}J_{1}(Rr_{{n}})}\sum_{\ell =0}^{\infty } \biggl( \frac{-\nu r_{n}^{2}}{ \lambda ^{\eta }} \biggr)^{\ell } \\ &\quad {}\times\bigl[G_{\eta , -\ell -2,\ell +1} \bigl({-\lambda ^{-\eta }},t \bigr)+ \lambda ^{\eta }G_{\eta , \eta -\ell -2,\ell +1} \bigl({-\lambda ^{- \eta }},t \bigr) \bigr] \end{aligned}$$
(22)

clearly satisfies the boundary condition (6). Direct computation also proves that both initial conditions are satisfied. In order to prove the second initial condition, Eq. (22) has to be again taken into consideration.

3.2 Calculation of the velocity field

For velocity field we substitute Eq. (22) in Eq. (4), we get

$$\begin{aligned} \frac{\partial w(r,t)}{\partial t}&=\frac{4grt}{\rho R^{2}}+\frac{2g}{ \lambda ^{\eta }R\rho }\sum _{n=1}^{\infty }\frac{J_{1}(rr_{{n}})}{J _{1}(Rr_{{n}})}\sum _{\ell =0}^{\infty } \biggl(\frac{-\nu r_{n}^{2}}{ \lambda ^{\eta }} \biggr)^{\ell } \\ &\quad {}\times\bigl[G_{\eta , -\ell -2,\ell +1} \bigl({-\lambda ^{-\eta }},t \bigr)+ \lambda ^{\eta }G_{\eta , \eta -\ell -2,\ell +1} \bigl({-\lambda ^{- \eta }},t \bigr) \bigr]. \end{aligned}$$
(23)

Integrating with respect to t, using Eq. (2) and the relation

$$\begin{aligned} \int G_{\ell , \jmath , \zeta }(\sigma , t)\,dt= G_{\ell , \jmath -1, \zeta }(\sigma , t)+c, \end{aligned}$$
(24)

where c is the constant of integration, we get

$$\begin{aligned} w(r,t)&=\frac{2gr}{\rho } \biggl(\frac{t}{R} \biggr)^{2}+ \frac{2g}{ \lambda ^{\eta }R\rho }\sum_{n=1}^{\infty } \frac{J_{1}(rr_{{n}})}{J _{1}(Rr_{{n}})}\sum_{\ell =0}^{\infty } \biggl( \frac{-\nu r_{n}^{2}}{ \lambda ^{\eta }} \biggr)^{\ell } \\ &\quad {}\times\bigl[G_{\eta , -\ell -3,\ell +1} \bigl({-\lambda ^{-\eta }},t \bigr)+ \lambda ^{\eta }G_{\eta , \eta -\ell -3,\ell +1} \bigl({-\lambda ^{- \eta }},t \bigr) \bigr]. \end{aligned}$$
(25)

If we substitute \(t=0\) in Eqs. (22) and (25), then both equations reduce to Eqs. (5) and (2), respectively. Boundary condition Eq. (6) can be obtained by taking \(r=R\) in Eq. (22). This implies that our general solution satisfies all imposed conditions.

4 Limiting cases

4.1 Ordinary Maxwell fluid

By taking \(\eta \rightarrow 1\) in Eqs. (22) and (25), we get

$$\begin{aligned}& \begin{aligned}[b] {\tau }_{\mathrm{OMF}}(r,t)&= gt \biggl(\frac{r}{R} \biggr)^{2}+ \frac{2g}{\lambda R}\sum_{n=1}^{\infty } \frac{J_{2}(rr_{{n}})}{r _{{n}}J_{1}(Rr_{{n}})}\sum_{\ell =0}^{\infty } \biggl( \frac{- \nu r_{n}^{2}}{\lambda } \biggr)^{\ell } \\ &\quad {}\times\bigl[G_{1, -\ell -2,\ell +1} \bigl({-\lambda ^{-1}},t \bigr)+\lambda G_{1, -\ell -1,\ell +1} \bigl({-\lambda ^{-1}},t \bigr) \bigr], \end{aligned} \end{aligned}$$
(26)
$$\begin{aligned}& \begin{aligned}[b] {w}_{\mathrm{OMF}}(r,t)&=\frac{2gr}{\rho } \biggl(\frac{t}{R} \biggr)^{2}+\frac{2g}{ \lambda R\rho }\sum_{n=1}^{\infty } \frac{J_{1}(rr_{{n}})}{J_{1}(Rr _{{n}})}\sum_{\ell =0}^{\infty } \biggl( \frac{-\nu r_{n}^{2}}{ \lambda } \biggr)^{\ell } \\ &\quad {}\times\bigl[G_{1, -\ell -3,\ell +1} \bigl({-\lambda ^{-1}},t \bigr)+\lambda G_{1, -\ell -2,\ell +1} \bigl({-\lambda ^{-1}},t \bigr) \bigr], \end{aligned} \end{aligned}$$
(27)

which are the solutions corresponding to the ordinary Maxwell fluid performing the same motion.

4.2 Newtonian fluid

Now letting \(\lambda \rightarrow 0\) in Eqs. (26) and (27) and using the relation

$$\begin{aligned} \frac{1}{{\lambda }^{c}}G_{m, n, c}\bigl({-\lambda ^{-1}},t\bigr)= \frac{t^{-n-1}}{ \varGamma (-n)}, \quad n< 0, \text{ when } \lambda \rightarrow 0, \end{aligned}$$

we recover the solutions

$$\begin{aligned}& {\tau }_{\mathrm{NF}}(r,t)= gt \biggl(\frac{r}{R} \biggr)^{2}+ \frac{2g}{\nu R} \sum_{n=1}^{\infty } \frac{J_{2}(rr_{{n}})}{r_{n}^{3} J_{1}(Rr_{{n}})} \bigl(1-e^{-\nu r_{n}^{2} t} \bigr), \end{aligned}$$
(28)
$$\begin{aligned}& {w}_{\mathrm{NF}}(r,t)=\frac{2gr}{\rho } \biggl(\frac{t}{R} \biggr)^{2}-\frac{2g}{ \mu \nu R}\sum_{n=1}^{\infty } \frac{J_{1}(rr_{{n}})}{ r_{n}^{4}J _{1}(Rr_{{n}})} \bigl(1-\nu r_{n}^{2} t-e^{-\nu r_{n}^{2} t} \bigr), \end{aligned}$$
(29)

corresponding to Newtonian fluids. Indeed, Eq. (29) is identical to Eq. (24) obtained by Fetecau et al. [45].

5 Numerical results and conclusions

In this note, the flow of a fractional Maxwell fluid through an infinite circular cylinder that applies a time-dependent torque per unit length to the fluid is analytically studied using the integral transform technique. To do that, contrary to the usual line from the literature, the governing equation for the non-trivial shear stress is used and the first exact solutions for such motions of rate type fluids are obtained. These solutions, which are presented in series form in terms of some generalized functions, satisfy all imposed initial and boundary conditions and are easily reduced to similar solutions for Newtonian and ordinary Maxwell fluids. It is worth pointing out the fact that our limiting solution (28) for the shear stress corresponding to a Newtonian fluid is identical to that obtained in [45, Eq. (24)], while the adequate velocity field (29) corrects a similar result from the same reference.

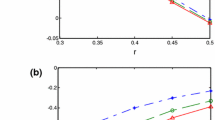
In order to bring to light some relevant physical aspects of the present results, the profiles of the velocity field \(w(r,t)\) and the shear stress \(\tau (r,t)\), given by Eqs. (25) and (22), have been displayed against r for different values of the relaxation time λ, the fractional parameter η, time t, and kinematic viscosity ν. The variations of the two physical entities at different times are presented in Fig. 1. As it was to be expected, both the velocity and the shear stress are increasing functions of t on the whole flow domain. They smoothly increase from the zero value at the middle of the channel up to the maximum values on the boundary. Moreover, as it clearly results from Fig. 1(a), the boundary condition (6) is satisfied. Figure 2 indicates that both stress and velocity fields are decreasing functions of the relaxation time λ. The effect of fractional parameter η can be observed in Fig. 3, it is noted that both velocity field and shear stress on the fluid decrease by increasing the value of η. The behavior of shear stress and velocity field against kinematic viscosity ν can be seen in Fig. 4. It is clear that as fluid becomes more viscous, stress increases but the velocity decreases as expected. Figure 5(a) and 5(b) represent the comparison between the three models: fractional Maxwell, ordinary Maxwell, and Newtonian. Newtonian fluid is more sensitive than other fluids. The effect of stress on Newtonian fluid is significant as compared to fractional or ordinary Maxwell fluid. Due to quick response, the velocity field of Newtonian fluid is also greater than that of other fluid models. In graphical illustration we observe the following aspects.

  • It is observed that with the passage of time velocity field and shear stress both increase for the above fractional fluid flow model.

  • It is noted that both shear stress and velocity field are decreasing functions of relaxation time λ and fractional parameter η.

  • As expected, velocity of the fluid decreases as fluid becomes more thick but tangential stress increases.

  • It can be seen from graphs that, for every physical parameter, shear stress and velocity field decrease smoothly from maximum (near the circular cylinder) to zero (at the center or axis of cylinder).

  • The effect of stress on Newtonian fluid is higher as compared to that on the fractional and ordinary Maxwell fluids. Due to quick response, the value of velocity field is greater than that of other fluid models.

  • From general solution, we recover the solution for shear stress for Newtonian fluid [45, Eq. (24)].

  • In all figures we use SI units, and roots are approximated by \({r_{n}} = \frac{{(4n-1)\pi } }{{({4R})}}\).

Figure 1
figure 1

Profiles of the shear stress \(\tau (r,t)\) and the velocity \(w(r,t)\) given by Eqs. (22) and (25), respectively, for \(R=1\), \(g=2\), \(\nu =0.001\), \(\eta =0.001\), \(\lambda =10\), \(\rho =800 \), and different values of t

Full size image
Figure 2
figure 2

Profiles of the shear stress \(\tau (r,t)\) and the velocity \(w(r,t)\) given by Eqs. (22) and (25), respectively, for \(R=1\), \(g=2\), \(\eta =0.45\), \(\nu =0.2\), \(t=7\), \(\rho =800 \), and different values of λ

Full size image
Figure 3
figure 3

Profiles of the shear stress \(\tau (r,t)\) and the velocity \(w(r,t)\) given by Eqs. (22) and (25), respectively, for \(R=1\), \(g=2\), \(\nu =0.134\), \(t=1\), \(\lambda =0.2\), \(\rho =800 \), and different values of η

Full size image
Figure 4
figure 4

Profiles of the shear stress \(\tau (r,t)\) and the velocity \(w(r,t)\) given by Eqs. (22) and (25), respectively, for \(R=1\), \(g=2\), \(\eta =0.1\), \(\lambda =0.9\), \(t=4\), \(\rho =800\), and different values of ν

Full size image
Figure 5
figure 5

Comparison of stress fields \(\tau (r)\), velocity fields \(w(r)\) for fractional Maxwell, ordinary Maxwell, and Newtonian fluid for \(R=1\), \(\nu =0.29\), \(\rho =800\), \(g=2\), \(\lambda =0.1\), \(t=0.3\), \(\eta =0.14\)

Full size image