Abstract
The present study deals with the head-on collision process between capillary–gravity solitary waves in a finite channel. The present mathematical modeling is based on Nwogu’s Boussinesq model. This model is suitable for both shallow and deep water waves. We have considered the surface tension effects. To examine the asymptotic behavior, we employed the Poincaré–Lighthill–Kuo method. The resulting series solutions are given up to third-order approximation. The physical features are discussed for wave speed, head-on collision profile, maximum run-up, distortion profile, the velocity at the bottom, and phase shift profile, etc. A comparison is also given as a particular case in our study. According to the results, it is noticed that the free parameter and the surface tension tend to decline the solitary-wave profile significantly. However, the maximum run-up amplitude was affected in great measure due to the surface tension and the free parameter.
Similar content being viewed by others
1 Introduction
The Korteweg–de Vries (KdV) equation [1] is used to represent the asymptotic behavior of weakly nonlinear two-dimensional unidirectional solitary waves in shallow water. Gardner et al. [2] have shown the exact solution for the solitary waves with the help of the inverse scattering transform (IST) scheme. One noticed that when the solitary waves come closer, they collide, interchange their position and energies, and obtain their real shapes after the separation process. During the whole process of collision, the solitary waves have extraordinary stable properties. The unique effect in this entire process of collision is the phase shifts. It is also believed that the solitary waves with striking colliding properties can only be kept in a conservative system.
To investigate the head-on collision between solitary waves, one must use the asymptotic expansion to examine the original governing equations. Although the IST method is helpful to determine the collision process, the IST method is only beneficial if the solitary waves are traveling in the same direction (or overtaking collision [2, 3]). Therefore, various authors examined the head-on collision process with asymptotic methods. For instance, Su and Mirie [4] determined the head-on collision between solitary waves using the Poincaré–Lighthill–Kuo (PLK) scheme. Afterward, Dai [5] examined a similar process in a two-layer fluid with surface tension effects with the upper and lower wall flat and rigid. Mirie and Su [6, 7] also considered the different forms of asymptotic expansion for the two-layer fluid model and explained a generalized and modified form of the KdV equations. Later, Zhu and Dai [8, 9] also determined the two-layer fluid model with different asymptotic expansion and surface tension effects and explained a generalized and modified form of KdV equations. Bhatti and Lu [10] investigated the head-on collision between solitary waves in the presence of a thin elastic plate floating on the surface of incompressible water. Later, Bhatti and Lu [11] considered the behavior of an electric current on the head-on collision between solitary waves in the presence of an elastic plate. Recently, Bhatti and Lu [12] discussed the head-on collision between hydroelastic solitary waves in a finite channel having an elastic plate floating on the surface of the fluid. They considered the two-layer fluid model and used the PLK method to obtain the perturbation solutions.
In the present study, we have used Nwogu’s Boussinesq model [13] to determine the head-on collision between capillary–gravity solitary waves. The advantage of this model is that it can be used to examine in a broader range, so that it is suitable for shallow water waves and for deep water waves [14, 15]. Zhang et al. [16] presented a comparative study of various Boussinesq models. Chen et al. [17] examined the head-on collision between solitary waves for a uniformly constant depth (\(h\equiv 1\)). They also used the PLK method to admeasure the asymptotic solutions for the governing equations.
The final issue of the present study is to determine the head-on collision between capillary–gravity waves using a singular perturbation approach. Therefore, we have used the PLK scheme to explore the head-on collision process between water waves traveling in the opposite direction. This method gives the possibility to examine different physical features during the process of head-on collision, as compared with other analytical and numerical methods [18–26]. The mathematical outcomes in terms of series solutions are described by up to third-order approximations. A comparison with the previously published results is also given to validate the current findings. All the graphical results are plotted for the leading parameters and described in detail.
2 Mathematical modeling
Consider two solitary waves propagating in the transverse direction in a finite channel. The channel is filled with an inviscid and incompressible fluid with irrotational flow. A Cartesian coordinate \((x,z_{d})\) system is ideal for the physical modeling. The x-axis lies in the horizontal direction and the \(z_{d}\)-axis is located in the vertical direction i.e. \(z_{d}=0\) located at the undisturbed free surface whereas \(z_{d}=-h(x)\) is located at the bottom of the channel. Nwogu’s Boussinesq model describes this by [13]
where g is the gravitational acceleration, \(P_{a}\) the atmospheric pressure, u represents the velocity vector at an arbitrary depth \(z_{d}\), and ρ is the density of the fluid.
We assume a finite channel with one-dimensional flow having constant water depth h. Nwogu’s Boussinesq model for capillary–gravity waves is as follows \(\mathbf{u} = ( u(x,t),0,0) \):
where
and d is the free parameter corresponding to the depth level.
Nwogu’s Boussinesq model [13] proposed that if the velocity \((z_{d}= -0.531h)\) at the depth is considered, then the associated dispersion relation can be improved over that defined by the theory of classical potential flow. Therefore, Nwogu shows that the free parameter d is an essential parameter for the pivotal mathematical modeling and is beneficial to explain different problems. For example, when \(d=0\), the results for the classical Boussinesq equation can be obtained from Eqs. (3) and (4). Furthermore, when \(d=-1/2\) or \(d=-1/3\), we obtain two new mathematical models corresponding to the velocity field u which represents the bottom and depth-mean velocities, respectively. The depth-mean system is almost similar to a system at a water depth with \(d=-1/3\). The present findings can be reduced to the previously published data [17] by taking \(T \rightarrow 0\), \(h \equiv 1\).
3 Proposed methodology
In the subsequent section, we will employ the PLK method. Introducing the coordinate transformation in the wave frame as
where the dimensionless parameter ε\((0< \varepsilon \ll 1 )\) describes the order of the magnitude of the wave amplitude, \(\tilde{\xi }_{0}\) and \(\tilde{\eta }_{0}\) are the right- and left-going phase variables, \(k_{r}\) and \(k_{l}\) are the wave numbers of order unity representing the right- and left-going wave, \(C_{l}\) and \(C_{r}\) represent the wave speeds of left- and right-going solitary waves. The phase function transformation with a combination of wave frame coordinates reads
Here θ and φ represents the phase functions which will be determined during the perturbation solutions. The main reason of these functions is to make asymptotic approximations, which allows one to determine the phase changes during the collision process. According to the theory of Ursell’s relationship, we considered the scaling of horizontal wavelength \(\varepsilon ^{1/2}\) in Eq. (6).
The phase speed \(c(k)\) reads
where
By taking \(T =0\) in Eq. (8), the phase speed is similar to that obtained by Nwogu [13]. Introduce a column vector v defined as
The following series expansions can be described with the help of the PLK method:
where \(\bar{c}=c(k_{l})\), a and b represent the amplitude factors, and the variables having subscripts will be determined during the perturbation analysis.
4 Analysis of the perturbation
Applying the asymptotic expansion Eqs. (11) to (15), we will get a set of partial differential equations with the coefficients \(\varepsilon ^{\frac{3}{2} }, \varepsilon ^{\frac{5}{2} }, \varepsilon ^{\frac{7}{2} }, \ldots \) , which can be determined in the following form.
4.1 Coefficients of \(\varepsilon ^{3/2}\)
The equations for \(\mathbf{v}_{1}\) take the following form:
where
To analyze the solutions at the first-order approximation, we used a matrix system in this order and the subsequent orders. Zhu and Dai [8] applied this procedure for the two-layer fluid model to determine the head-on collision process.
The right and left characteristic vectors of n read
and, for \(\tilde{\mathbf{n}}\), it reads
Introducing the left and right characteristic vectors in the above equations helps to examine the solutions in the subsequent orders. Left characteristics vectors are beneficial to solving the coupled equations at higher order, whereas right characteristic vectors will be helpful to considering the solutions at each order of approximations. The formulated equations are nonlinear and it is not possible to write the exact solutions. Therefore, the left and right characteristic vectors will be helpful to examine the solutions. Dai et al. [27] used a similar methodology to analyze the head-on collision through a compressible Mooney–Rivlin elastic rod. Dai [5] applied the aforementioned technique to admeasure the two-layer fluid problem with free surface.
We found the solution of Eq. (16) as
where \(f(\tilde{\xi })\) and \(g(\tilde{\eta })\) are the arbitrary functions, which will be examined in the upcoming order.
4.2 Coefficients of \(\varepsilon ^{5/2}\)
The equations for \(\mathbf{v}_{2}\) take the following form:
where \(\mathbf{e}_{j}\) and \(\tilde{\mathbf{e}}_{j} \) (\(j=1,\dots , 4\)) are given in Appendix 1. The solution of Eq. (21) in generalized form reads
where \(x_{1}(\tilde{\xi },\tilde{\eta })\) and \(y_{1}(\tilde{\xi }, \tilde{\eta })\) are the functions to be examined. Applying Eq. (22) in Eq. (21), and multiplying it by l, we obtain
where \(\mathbf{l} \tilde{\mathbf{n}}\mathbf{r}\), \(\mathbf{l} \mathbf{e}_{j}\) and \(\mathbf{l} \tilde{\mathbf{e}}_{j} \) (\(j=1,\ldots,4\)) denotes the inner products, i.e. \(\mathbf{l} \cdot \tilde{\mathbf{n}} \cdot \mathbf{r}\), \(\mathbf{l}\cdot \mathbf{e}_{n} \) and \(\mathbf{l}\cdot \tilde{\mathbf{e}}_{n} \), respectively.
Equation (23) can be further divided into three groups: secular terms, local terms, and non-local terms.
4.2.1 Secular terms
Secular terms are those terms, when we integrate with respect to η̃, that become unbounded in time/space, because these terms do not depend on η̃. Therefore, these terms will show a secular attitude. These terms in this order are found as
Let
then Eq. (24) takes the following form:
The solution of the third-order KdV is found as
where
Similarly
4.2.2 Non-local terms
In this group, we found two terms that do not describe the secular behavior but we can examine the phase-shift profile with the help of these terms.
The non-local terms at this order are
It follows that
where
Similarly, we have
4.2.3 Local terms
The local terms at this order take the following form:
After integrating and some simplification has been performed, the solution of the above can be written as
where
Similarly
Here \(f_{1}(\tilde{\xi })\) and \(g_{1}(\tilde{\eta })\) are the unknown functions which can be determined in the upcoming order.
4.3 Coefficients of \(\varepsilon ^{7/2}\)
The equations for \(\mathbf{v}_{3}\) take the following form:
where n and \(\tilde{\mathbf{n}}\) are given while \(\mathbf{f}_{j}\) and \(\tilde{\mathbf{f}}_{j} \) (\(j=1,\dots , 8\)) are given in Appendix 1.
Let us consider the generalization in the following form:
where \(x_{2}(\tilde{\xi },\tilde{\eta })\) and \(y_{2}(\tilde{\xi }, \tilde{\eta })\) are the functions to be determined. A similar procedure at this order has been used for the solutions as mentioned in the previous Sect. 4.2.
4.3.1 Secular terms
The secular terms at this order read
After some simplification, the above equation is reduced to the following form:
where \(k_{14}\), \(k_{15}\) and \(k_{16}\) are given in Appendix 2.
After integrating the above equation we obtain
From the above equation, we notice that the first term on the right-hand side of the above equation shows a secular behavior, which reveals that it becomes unbounded when \(\tilde{\xi } \rightarrow \pm \infty \) and the resulting solutions will no more be asymptotic. This term must vanish. Let
The solution of Eq. (44) reads
where \(k_{17}\) and \(k_{18}\) are given in Appendix 2.
The homogeneous solution in Eq. (46) has been ignored because in the higher-order approximation it is noticed that the homogeneous solution only produces a uniform phase shift in the wave motion, which reveals a simple phase shift as given above. Therefore, we ignored this term.
Similarly, we have
The results for Eqs. (37) and (39) have been completed.
4.3.2 Non-local terms
The non-local terms occur in the following form:
The above equation reduces to
where
Similarly
where
From the above equations, it is noticed that the terms show a simple phase in contrast with the first-order phase shift distribution. However, only one term \(\tilde{\theta }_{1,0}\) or \((\tilde{\varphi } _{1,0} )\) depends on ξ̃ or (η̃) as \(\tilde{\eta } \rightarrow +\infty \) or (\(\tilde{\xi } \rightarrow - \infty \)) as given in Eqs. (51) and (54). Therefore, the functions \(\theta _{1}\) and \(\varphi _{1}\) move into the argument of the independent variable ξ̃ and η̃ of the given functions f and g. As a result, it will create distortion in the wave profile, and the wave will tilt back in the direction of propagation as plotted in Fig. 11.
4.3.3 Local terms
The following are the local terms that appear at this order:
After some simplification and performing the integration, we get
where \(k_{19}\), \(k_{20}\) and \(k_{21}\) are given in Appendix B. Similarly
Here \(f_{2}(\tilde{\xi })\) and \(g_{2}(\tilde{\eta })\) are the unknown functions which can easily be obtained in the next order. We finish our analysis here and the solutions of \(f_{2}(\tilde{\xi })\) and \(g_{2}(\tilde{\eta })\) are not presented.
5 Summary of the results
The analytical series solutions obtained in the previous section are combined and described below.
The wave elevation at the free surface can be written using Eqs. (20) and (22), and we obtain
where \(x_{1} (\tilde{\xi }, \tilde{\eta })\) and \(y_{1}(\tilde{\xi }, \tilde{\eta })\) are given in Eqs. (37) and (39).
The distortion profile can be evaluated via Eq. (59). The terms which are the products of \(f(\tilde{\xi }) \times g(\tilde{\eta })\) must disappear. The distortion profile at the free surface can be obtained by taking \(g(\tilde{\eta })=0\), we have
The maximum run-up at the time of collision at the free surface can be achieved by considering \(f=g=1\) in Eq. (59). We get
At the bottom of the channel the velocity distribution can be obtained from Eqs. (20) and (22), and we have
The asymptotic solutions for the wave speeds can be obtained by means of Eqs. (25) and (45), then we have
The phase shifts at the time of collision process read
where \((\theta _{j}, \varphi _{j} )\)\((j=1,2)\) are mentioned in Eqs. (33), (35), (50), and (53), respectively.
6 Discussion
This section belongs to the graphical outcomes for all the leading parameters included in the present formulation. Computational software, Mathematica (10.3v), has been used to determine the solutions and graphical results. Particularly, we have computed the head-on collision profile, phase shift distribution, maximum run-up amplitude, wave speed, and distortion profile during the interaction between the solitary waves. We have used the following values of the governing parameters for the graphical purpose: \(g=9.8\) m s−2, \(\rho =10^{3}\) kg m−3, \(h = 1\) and \(T =0.075\) N m−1.
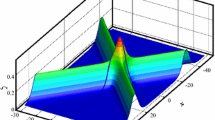
Figures 1 to 3 show the variation of surface tension τ, the free parameter d, and the depth h for the head-on collision profile. We can see from Fig. 1 that the wave profile tends to diminish for higher values of surface tension parameter τ. In Fig. 2, we noticed that the wave profile also tends to reduce due to the enhancement in the free parameter d. Furthermore, at \(d=0\), the present results turn into the classical Boussinesq equation. However, for \(d=-1/3\) in Eqs. (3) and (4) we get another set of differential equations and the relevant fields \(u(x,t)\) represents the bottom and depth-mean velocities, respectively. From Fig. 3, it is observed that the wave profile significantly rises for higher values of h. Figure 4 shows the comparison of the head-on collision profile as a special case of our study. The present results are similar to the previously published results when \(\tau =0\), \(h=1\). In this figure, we noticed that the present results excellently matched with the previously published results.
Comparison of Head-on collision between two solitary waves. Solid line [17] \(\tau =0\), \(h=1\), dot-dashed line: \(\tau =0.4\), \(h=1\), dot-dot-dashed line: \(\tau =0.4\), \(h=2\)
Figures 5 and 6 show the variation maximum run-up with wave amplitude for different values of free parameter d and the surface tension parameter h. It is noticed from Fig. 5 that the inclusion of the free parameter enhances the maximum run-up amplitude as compared with the classical Boussinesq equation, but as the value of the free parameter increases, the maximum run-up amplitudes tend to decline. Figure 6 shows that an enhancement in the surface tension parameter tends to produce a significant resistance for the maximum run-up amplitude, and as a result, it declines.
Figures 7 and 8 are plotted for the phase shift profile to see the behavior of the surface tension τ and the free parameter d. It can be viewed from this figure that the free parameter remarkably boosts the phase shift profile. Further, we can see that when the free parameter \(d=0\), the magnitude of the phase shift profile is small, whereas the inclusion of the free parameter enhances the phase shift profile. In Fig. 8, a similar trend has been noticed against the surface tension parameter. In this figure, we can also see that in the absence of the surface tension parameter, \(\tau =0\), the magnitude of the phase shift profile is small. In contrast, the inclusion of the surface tension parameter boosts the phase shift profile.
Figures 9 and 10 are plotted for the wave speed profile to examine the inclusion of the surface tension parameter τ and free parameter d. It appears from Fig. 9 that an enhancement in the free parameter d enhances the wave speed in a significant manner. Furthermore, we can see that when the free parameter \(d=0\), the wave speed faces a significant resistance, whereas the presence of the free parameter enhances the wave speed. From Fig. 10, it is observed that the wave speed uniformly increases due to the increment of the surface tension parameter and keeps increasing in the whole domain.
Figure 11 is drawn to see the distortion profile during the collision process. It can be viewed from this figure that, before and after the collision between both solitary waves, the wave profile is symmetric, but after the collision process, a minor tilting occurs. As a result, the wave profile tilts backward in the direction of propagation.
7 Conclusions
This article deals with the head-on collision between capillary–gravity solitary waves in shallow water. The bottom of the channel is considered to be flat. The impact of the surface tension is also taken into account. To examine the asymptotic behavior, we have employed the PLK scheme for the coupled nonlinear equations. The solutions up to the third approximation are presented in detail. In particular, we have presented an expression for the velocity at the bottom of the channel, phase shift profile, wave speed, and wave elevation. A comparison is also presented with previously published data to validate the current findings. The main findings are summarized below:
- (i)
It is noticed that the free parameter and the surface tension tend to decline the solitary-wave profile significantly.
- (ii)
The maximum run-up amplitude is affected greatly due to the surface tension and free parameter.
- (iii)
Phase shift becomes an increasing function due to the strong influence of the surface tension and free parameter.
- (iv)
It is noticed that only minor tilting appears after the collision process; however, the wave profile remains symmetric before the collision process.
- (v)
A comparison shows that the present results perfectly matched with previously published findings.
The present results provide an excellent benchmark for further study on Nwogu’s Boussinesq model with multi-layer fluid. Furthermore, the present modeling has neglected the porosity effects, and this will be taken into account soon.
References
Korteweg, D.J., De Vries, G.: On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 39(240), 422–443 (1895)
Gardner, C.S., Greene, J.M., Kruskal, M.D., Miura, R.M.: Method for solving the Korteweg-de Vries equation. Phys. Rev. Lett. 19(19), 1095–1097 (1967)
Novikov, S., Manakov, S., Pitaevskii, L., Zakharov, V.: Theory of Solitons: The Inverse Scattering Method. Springer, Berlin (1984)
Su, C.H., Mirie, R.M.: On head-on collisions between two solitary waves. J. Fluid Mech. 98(3), 509–525 (1980)
Dai, S.Q.: The interaction of two pairs of solitary waves in a two-fluid system. Sci. Sin., Ser. A 27(5), 507–520 (1984)
Mirie, R.M., Su, C.H.: Internal solitary waves and their head-on collision. II. Phys. Fluids 29(1), 31–37 (1986)
Mirie, R.M., Su, C.H.: Internal solitary waves and their head-on collision. Part 1. J. Fluid Mech. 147, 213–231 (1984)
Zhu, Y., Dai, S.: On head-on collison between two gKdV solitary waves in a stratified fluid. Acta Mech. Sin. 7(4), 300–308 (1991)
Zhu, Y.: Head-on collision between two mKdV solitary waves in a two-layer fluid system. Appl. Math. Mech. 13(5), 407–417 (1992)
Bhatti, M.M., Lu, D.Q.: Head-on collision between two hydroelastic solitary waves in shallow water. Qual. Theory Dyn. Syst. 17(1), 103–122 (2018)
Bhatti, M.M., Lu, D.Q.: Analytical study of the head-on collision process between hydroelastic solitary waves in the presence of a uniform current. Symmetry 11(3), 333 (2019)
Bhatti, M.M., Lu, D.Q.: Hydroelastic solitary wave during the head-on collision process in a stratified fluid. J. Mech. Eng. Sci. 233(17), 6135–6148 (2019)
Nwogu, O.: Alternative form of Boussinesq equations for nearshore wave propagation. J. Waterw. Port Coast. Ocean Eng. 119(6), 618–638 (1993)
Wei, G., Kirby, J.T.: Time-dependent numerical code for extended Boussinesq equations. J. Waterw. Port Coast. Ocean Eng. 121(5), 251–261 (1995)
Wei, G., Kirby, J.T., Grilli, S.T., Subramanya, R.: A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves. J. Fluid Mech. 294, 71–92 (1995)
Zhang, J.E., Chen, C., Li, Y.: On Boussinesq models of constant depth. Phys. Fluids 16(5), 1287–1296 (2004)
Chen, C.L., Huang, S.J., Zhang, J.E.: On head-on collisions between two solitary waves of Nwogu’s Boussinesq model. J. Phys. Soc. Jpn. 77(1), 014003 (2008)
Fenton, J.D., Rienecker, M.M.: A Fourier method for solving nonlinear water-wave problems: application to solitary-wave interactions. J. Fluid Mech. 118, 411–443 (1982)
Cırstea, F.-C.Ş., Rădulescu, V.D.: Existence and uniqueness of positive solutions to a semilinear elliptic problem in rn. J. Math. Anal. Appl. 229(2), 417–425 (1999)
Craciun, E.-M., Soós, E.: Anti-plane states in an anisotropic elastic body containing an elliptical hole. Math. Mech. Solids 11(5), 459–466 (2006)
Marsavina, L., Nurse, A.D., Braescu, L., Craciun, E.M.: Stress singularity of symmetric free-edge joints with elasto-plastic behaviour. Comput. Mater. Sci. 52(1), 282–286 (2012)
Marin, M., Nicaise, S.: Existence and stability results for thermoelastic dipolar bodies with double porosity. Contin. Mech. Thermodyn. 28(6), 1645–1657 (2016)
Marin, M., Baleanu, D., Vlase, S.: Effect of microtemperatures for micropolar thermoelastic bodies. Struct. Eng. Mech. 61(3), 381–387 (2017)
Marin, M., Craciun, E.: Uniqueness results for a boundary value problem in dipolar thermoelasticity to model composite materials. Composites Part B. Engineering 126, 27–37 (2017)
Khan, A.A., Bukhari, S.R., Marin, M., Ellahi, R.: Effects of chemical reaction on third-grade mhd fluid flow under the influence of heat and mass transfer with variable reactive index. Heat Transfer Research 50(11) (2019)
Alamri, S.Z., Khan, A.A., Azeez, M., Ellahi, R.: Effects of mass transfer on mhd second grade fluid towards stretching cylinder: a novel perspective of Cattaneo–Christov heat flux model. Phys. Lett. A 383(2–3), 276–281 (2019)
Dai, H.H., Dai, S.Q., Huo, Y.: Head-on collision between two solitary waves in a compressible Mooney–Rivlin elastic rod. Wave Motion 32(2), 93–111 (2000)
Acknowledgements
The authors would like to thank the reviewers for their help to improve the quality of the article.
Availability of data and materials
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
Funding
There is no funding.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with the same responsibility. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
where \(k_{m}\) (\(m=2,4, \dots , 13\)) are defined in Appendix 2.
Appendix 2
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marin, M., Bhatti, M.M. Head-on collision between capillary–gravity solitary waves. Bound Value Probl 2020, 12 (2020). https://doi.org/10.1186/s13661-019-01321-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13661-019-01321-3