1 Introduction

The Richards equation (RE) presents the movement of water in unsaturated soils [1]. It is usually a nonlinear parabolic partial differential equation for one-dimensional horizontal infiltration problem, which can be expressed as [2, 3]

$$ \frac{\partial\theta}{\partial t} = \frac{\partial}{\partial x} \biggl( D ( \theta )\frac{\partial\theta}{\partial x} \biggr), $$
(1)

where θ is the volumetric water content of unsaturated porous media, x and t are the space and time coordinates, and \(D(\theta)\) is the hydraulic diffusivity. We consider the analytical solution in a finite domain \(0\leq x \leq L\), which owns the Dirichlet boundary conditions

$$ \theta|_{x = 0} = \theta_{L},\qquad\theta|_{x = L} = \theta_{0}, $$
(2)

where \(\theta_{L}\) (\(\neq\theta_{0}\)) and \(\theta_{0}\) are constant moisture contents in wetting front analysis, and the initial condition is

$$ \theta|_{t = 0} = \theta_{0}. $$
(3)

In these years, Heaslet and Alksne technique [4], perturbation technique [5], traveling wave method [6], and series method [7–10] are used to obtain an analytical solution of RE with semi-infinite boundaries. Fourier transformation, separation of variables [11, 12], and other approaches [13–19] are applied for some linear or linearized RE with finite boundaries (2). Nevertheless, there are few approximate analytical solutions of equations (1)-(3) that can illustrate the long-time behavior for water infiltration in constant moisture content boundary conditions of equation (2), especially when the hydraulic diffusivity is an arbitrary function of θ. Our goal is deriving an approximate analytical solution of equations (1)-(3).

Motivated by the methods and approaches mentioned, we focus on analyzing the water infiltration varying from a transient state to steady one and try to approximate the changes of water profile. By a series expansion technique we construct an approximate solution about space variable x and water profile to approximate the water content distribution for arbitrary diffusivity in RE. In addition, we analyze the relationship of time variable t and θ in a definite space coordinate.

2 Wetting front analysis

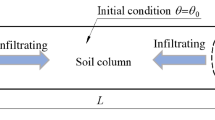
The RE for horizontal infiltration with initial and boundary conditions equations (2)-(3) in this paper is divided into two parts: water infiltration in semiinfinite layer and in finite layer by boundary analysis [20, 21]. Before the wetting front arrives at the boundary point \(x=L\), it is considered as a semiinfinite boundary problem, which is well approximated by the Boltzmann solution [4], shifted front solution [5], and series solution [9]. The profiles of infiltration in semiinfinite layer are shown by dotted lines in Figure 1, and the front position of the finite boundary problem is shown by solid and thick solid lines in Figure 1. The thick solid line shows a steady flow for water infiltration and presents a steady state that is irrelevant to time variable t. The steady flow can be described by the ordinary differential equation

$$ \frac{\mathrm{d}}{\mathrm{d}x} \biggl( D ( \theta )\frac{\mathrm{d}\theta}{\mathrm{d}x} \biggr) = 0 $$
(4)

with Dirichlet boundary conditions

$$ \theta|_{x = 0} = \theta_{L},\qquad\theta|_{x = L} = \theta_{0}. $$
(5)

The analytical solution of equation (4) with (5) can be solved as

$$ x = \frac{L}{\int_{\theta_{0}}^{\theta_{L}} D\,\mathrm{d}\theta} \biggl( \int_{\theta_{0}}^{\theta_{L}} D\,\mathrm{d}\theta- \int_{\theta_{0}}^{\theta} D\,\mathrm{d}\theta \biggr). $$
(6)
Figure 1
figure 1

Horizontal infiltration in a finite layer. Dotted lines show the wetting front position in semiinfinite boundary problem, and solid and thick solid lines show it in finite boundary one.

Full size image

The solid lines in Figure 1 show the process of water infiltration varying from a transient flow to steady one. In this section, we construct an approximate analytical solution to simulate the infiltrate process.

Introducing the Boltzmann variable \(\phi=x/t^{1/2}\), we can transform equation (1) as

$$ - \frac{1}{2}\phi\frac{\mathrm{d}\theta_{r}}{\mathrm{d}\phi} = \frac{\mathrm{d}}{\mathrm{d}\phi} \biggl( D ( \theta_{r} + \theta_{0} )\frac{\mathrm{d}\theta_{r}}{\mathrm{d}\phi} \biggr), $$
(7)

where \(\theta_{r}=\theta-\theta_{0}\). Integrating equation (7), we obtain

$$ \int_{0}^{\theta_{r}} \phi\,\mathrm{d}\theta_{r} = - 2D ( \theta_{r} + \theta_{0} )\frac{\mathrm{d}\theta_{r}}{\mathrm{d}\phi} + C, $$
(8)

where

$$ C = 2D ( \theta_{r} + \theta_{0} )\frac{\mathrm{d}\theta_{r}}{\mathrm{d}\phi} \bigg|_{\theta_{r} = 0} . $$
(9)

By the mean value theorem equation (8) can be written as

$$ \phi ( \eta\theta_{r} ) = - 2\frac{D ( \theta_{r} + \theta_{0} )}{\theta_{r}}\frac{\mathrm{d}\theta_{r}}{\mathrm {d}\phi} + \frac{C}{\theta_{r}}, $$
(10)

where \(\eta\in(0,1)\). Substituting \(\theta _{\beta}=\eta\theta_{r} \) and \(\theta _{r}=\theta_{\beta}+a \) into equation (10), we obtain

$$ \phi ( \theta_{\beta} ) = - 2\frac{D ( \theta_{\beta} + a + \theta_{0} )}{\theta_{\beta}} \frac{\mathrm{d}\theta_{\beta}}{ \mathrm{d}\phi} + \frac{C}{\theta_{\beta} + a}, $$
(11)

where a is a constant. Integrating equation (11), we obtain

$$ \int_{0}^{\phi} \biggl[ \phi \bigl( \eta ( \theta_{\beta} + a ) + \theta_{0} \bigr) - \frac{C}{\theta_{\beta} + a} \biggr]\,\mathrm{d}\phi= 2 \int_{\theta_{\beta}}^{\theta_{L} - \theta_{0} - a} \frac{D ( \theta_{\beta} + a + \theta_{0} )}{\theta_{\beta}} \,\mathrm{d} \theta_{\beta}, $$
(12)

which yields

$$ \biggl[ \phi \bigl( \eta ( \theta_{\zeta} + a ) + \theta_{0} \bigr) - \frac{C}{\theta_{\zeta} + a} \biggr]\phi= 2 \int_{\theta_{\beta}}^{\theta_{L} - \theta_{0} - a} \frac{D ( \theta_{\beta} + a + \theta_{0} )}{\theta_{\beta}} \,\mathrm{d} \theta_{\beta}, $$
(13)

where \(\theta_{\zeta}=\theta _{\beta}+\zeta(\theta_{L}-\theta _{0}-a-\theta_{\beta})\) and \(\zeta\in(0,1)\). Equation (13) shows the relationship between the Boltzmann variable ϕ and the integration function ξ,

$$ \xi= \int_{\theta_{\beta}}^{\theta_{L} - \theta_{0} - a} \frac{D ( \theta_{\beta} + a + \theta_{0} )}{\theta_{\beta}} \,\mathrm{d} \theta_{\beta}. $$
(14)

Influenced by a series expansion technique [9], we show the analytical solution of the Boltzmann variable as a series

$$ \phi ( \xi ) \approx\sum_{i = 1}^{n} U_{i}\xi^{i}, $$
(15)

where \(U _{i} \) (\(i=1,2,3,\ldots,n\)) are calculation parameters. Based on zero and \(\theta_{\beta}\), we apply the integer-order derivatives theorem [22] to equation (8):

$$ \frac{\mathrm{d}^{ ( k )}}{\mathrm{d}\theta_{\beta}^{ ( k )}} \biggl( \int_{0}^{\theta_{\beta}} \phi\,\mathrm{d}\theta_{\beta} + 2D\frac{\mathrm{d}\theta_{\beta}}{\mathrm{d}\phi} \biggr)\bigg|_{\theta_{\beta} = \theta_{L} - \theta_{0} - a} = 2\frac{\mathrm{d}^{ ( k )}}{\mathrm{d}\theta_{\beta}^{ ( k )}} \biggl[ D \frac{\mathrm{d}\theta_{\beta}}{\mathrm{d}\phi} \bigg|_{\theta_{\beta} = 0} \biggr]\bigg|_{\theta_{\beta} = \theta_{L} - \theta_{0} - a} , $$
(16)

where \(k=0,1,2,3,\ldots,n-1\). The parameters \(U _{i} \) can be obtained by substituting equation (15) into equation (16) and solving nonlinear algebraic equations. When \(a=0\), equation (15) with (16) is the series solution for semiinfinite problem [9]. Considering this, we construct an approximate relationship between space variable x and water content \(\theta_{\beta} \) in both semiinfinite and finite boundaries as

$$ x \approx \left \{ \textstyle\begin{array}{l@{\quad}l} \sqrt{t} \phi, &a = 0, t \le t_{L}, \\ \frac{L}{\phi|_{\theta_{\beta} = 0} }\phi,& 0 > a \ge a_{L}, t > t_{L}, \end{array}\displaystyle \right . $$
(17)

where \(a _{L} \) can be solved by comparing equation (17) and Taylor expansion of equation (6) based on ξ, \(t _{L} \) is the time of the wetting front that arrives at the finite boundary point \(x=L \) and can be calculated by substituting \(x=L \) into equation (17):

$$ t_{L} \approx L^{2} \Big/ \Biggl( \sum _{i = 1}^{n} U_{i} \biggl( \int_{0}^{\theta_{L} - \theta_{0}} \frac{D}{\widetilde{\theta_{\beta}}} \,\mathrm{d} \widetilde{\theta_{\beta}} \biggr)^{i} \Biggr)^{2}. $$
(18)

In equation (17), the approximations of water profiles for horizontal infiltration are shown as the calculation parameter a varies. When \(t>t _{L}\), we substitute \(\theta_{r}=\theta-\theta_{0}\), \(\theta_{r}=\theta_{\beta}+a\), and equation (17) into equation (1):

$$ \frac{\partial\theta}{\partial t} = \frac{\phi|_{\theta_{\beta} = 0} }{L} \biggl( \frac{\partial\phi}{\partial\theta_{\beta}} \biggr)^{ - 1} + \frac{\partial}{\partial\theta_{\beta}} \biggl( D\frac{\phi|_{\theta_{\beta} = 0} }{L} \biggl( \frac{\partial \phi}{\partial\theta_{\beta}} \biggr)^{ - 1} \biggr). $$
(19)

Substituting equations (14) and (15) into (17), \(\theta _{\beta} \) can be shown as a function of a in a definite space point \(x=x _{d} \in(0,L)\):

$$ x_{d} \approx\frac{L\sum_{i = 1}^{n} U_{i} ( \int_{\theta_{\beta}}^{\theta_{L} - \theta_{0} - a} \frac{D}{\widetilde{\theta_{\beta}}} \,\mathrm{d}\widetilde{\theta_{\beta}} )^{i}}{\sum_{i = 1}^{n} U_{i} ( \int_{0}^{\theta_{L} - \theta_{0} - a} \frac{D}{\widetilde{\theta_{\beta}}} \,\mathrm{d}\widetilde{\theta_{\beta}} )^{i}}, $$
(20)

and \(\theta=\theta_{0}+\theta _{\beta}+a\). We take a as

$$ a = a_{j}\quad (j=0,1,2,3,\ldots), $$
(21)

where \(a _{j} \in[a _{L},0)\) is a given constant. Then the corresponding \(\theta_{j} \) can be obtained from equation (20). Substituting \(a=a _{j} \) and \(\theta_{j}=\theta_{\beta j}+\theta _{0}+a _{j} \) into equation (19), we can calculate the value of \(\partial \theta/ \partial t \) at \(x=x _{d}\). We apply a polynomial series to approximate the changes

$$ \frac{\partial\theta}{\partial t} \approx\sum_{k = 0}^{n_{1}} V_{k}\theta^{k}, $$
(22)

where \(k=0,1,2,3,\ldots,n _{1}\), and \(V _{k} \) can be calculated by the least-squares method. Then the time variable t can be solved:

$$ t = \int_{\theta_{\beta0}}^{\theta} \frac{1}{\sum_{k = 0}^{n_{1}} V_{k}\theta^{k}} \,\mathrm{d}\theta- t_{L}, $$
(23)

where \(\theta_{\beta 0}\) is the water content as the wetting front arriving at the boundary point \(x=L \) and can be solved from

$$ \frac{x_{d}}{\sqrt{t_{L}}} \approx\sum_{i = 1}^{n} U_{i} \biggl( \int_{\theta_{\beta0}}^{\theta_{L} - \theta_{0}} \frac{D}{\widetilde{\theta_{\beta}}} \,\mathrm{d} \widetilde{\theta_{\beta}} \biggr)^{i}. $$
(24)

3 Numerical simulation

In this section, two examples are shown to confirm the accuracy of the present method.

Example 1

(Power-law model)

We take the power law diffusivity from Hall’s mortar [23, 24] model as \(D(\theta)=247.1\theta^{4}\). The initial and boundary values are taken as \(\theta_{0}=0.5\) and \(\theta_{L}=1\), respectively, and L in equation (2) is 13 mm. Before the wetting front arrives at the point \(x=13\mbox{ mm}\), it can be treated as a semiinfinite problem. Applying equation (17) at \(a=0\), we have

$$ \phi\approx\sum_{i = 1}^{n} U_{i} \biggl( \int_{\theta_{r}}^{0.5} \frac{247.1 ( \theta_{r} + 0.5 )^{4}}{\theta_{r}}\,\mathrm{d} \theta_{r} \biggr)^{i}, $$
(25)

where \(U _{i} \) are calculated as n varies from 1 to 5.

  • \(n=1\): \(U _{1}=0.1445249313\).

  • \(n=2\): \(U _{1}=0.1667699993\), \(U _{2}=-3.374544704\times10^{-4}\).

  • \(n=3\): \(U _{1}=0.1571011460\), \(U _{2}=-3.178898137\times10^{-4}\), \(U _{3}=8.78800083\times10^{-7}\).

  • \(n=4\): \(U _{1}=0.1620248146\), \(U _{2}=-3.278527209\times10^{-4}\), \(U _{3}=9.921998925\times10^{-7}\), \(U_{4}=-3.797520062\times10^{-9}\).

  • \(n=5\): \(U _{1}=0.1589918636\), \(U _{2}=-3.217156285\times10^{-4}\), \(U _{3}=9.214216339\times10^{-7}\), \(U_{4}=-3.620798276\times10^{-9}\), \(U_{5}=1.360893606\times10^{-11}\).

Compared with the finite element method (FEM), we depict approximations of orders 1-5 of ϕ in Figure 2 and present relative errors of the 5th-order solution in Table 1.

Figure 2
figure 2

Results of ϕ obtained from the FEM and approximations of orders 1-5.

Full size image
Table 1 Results of θ obtained from the FEM and fifth-order approximation
Full size table

We obtain that the present approximations are more close to the FEM as order increases from 1 to 5 in Figure 2, and the maximum relative error is 1.353% in 20.1946 mm/min1/2 in Table 1. According to the fith-order approximation above and equation (18), we obtain that \(t _{L}=0.1276\mbox{ min}\) when the wetting front arrives at the boundary point \(x=13\mbox{ mm}\). Applying equations (19)-(24), \(x _{d}=9\mbox{ mm}\) is taken as a definite space value in \(a _{j} \) and \(\theta_{j} \) calculation, and the sixth-order approximation of \(\partial\theta/ \partial t \) is presented as

$$ \begin{aligned}[b] \frac{\partial\theta}{\partial t} \approx{} &{-} 13 \mbox{,}667.969585\theta^{6} + 56\mbox{,}224.381941 \theta^{5} - 96\mbox{,}658.819517\theta ^{4} + 88 \mbox{,}993.549536\theta^{3} \\ &- 46\mbox{,}337.629110\theta^{2} + 12\mbox{,}947.589875\theta- 1 \mbox{,}515.864672. \end{aligned} $$
(26)

When \(t \geq t _{L}\), the fifth-order approximation between the space variable x and water content θ is

$$\begin{aligned}[b] x \approx{}&\frac{13}{\sum_{i = 1}^{5} U_{i} ( \int_{0}^{0.5 - a} \frac{247.1 ( \theta_{\beta} + a + 0.5 )^{4}}{\theta_{\beta}} \,\mathrm{d}\theta_{\beta} )^{i}}\\ &\times \sum_{i = 1}^{5} U_{i} \biggl( \int_{\theta- a - 0.5}^{0.5 - a} \frac{247.1 ( \theta_{\beta} + a + 0.5 )^{4}}{\theta_{\beta}} \,\mathrm{d} \theta_{\beta} \biggr)^{i},\end{aligned} $$
(27)

where \(U _{i} \) can be obtained by solving equation (16) for different a. As t increases, we calculate the approximations for \(a=0\), \(a=-0.001\), \(a=-0.005\), \(a=-0.025\), \(a=-0.1\), and \(a=-0.2\), and the corresponding time by solving equation (26). The corresponding water profiles are shown in Figure 3, which presents the process of water infiltration varying from transient state to steady one. The thick solid line in Figure 3 is derived by equation (6) and shows the steady solution in front analysis. The solid lines and dotted ones are obtained by the FEM and present method, respectively, and show the changes of water profiles as time goes by. Compared with the FEM, the relative errors between solid lines and dotted ones are shown in Figure 4.

Figure 3
figure 3

The changes of water profile for power law model. Dotted lines show the present approximations, and solid lines show the results by the FEM.

Full size image
Figure 4
figure 4

Relative errors of present solutions and the FEM.

Full size image

We observe that the present approximation is agreed with numerical solution, and the maximum relative error of present solution is less than −3% in Figure 4. In addition, we solve equation (26) and derive the relationship between the time variable t and water content θ, which shows that the present solution approximates well with the FEM as time increases in Figure 5, and the maximum relative error is less than 2% in Table 2.

Figure 5
figure 5

Relationship between t and θ in \(\pmb{{x_{d}=9\mbox{ mm}}}\) .

Full size image
Table 2 The results of θ obtained from the present method and the FEM in \(\pmb{x_{{d}}=9\mbox{ mm}}\)
Full size table

Example 2

(van Genuchten model)

The hydraulic diffusivity defined by the van Genuchten model [25, 26] is

$$ D ( \theta ) = K_{s}k_{r}\frac{\partial H}{\partial \theta}, $$
(28)

where \(K _{s} \) is the saturated hydraulic conductivity, H is the water head, and \(k _{r} \) is the intrinsic permeability [26]

$$\begin{gathered} H = \frac{1}{\alpha} \biggl[ \biggl( \frac{\theta- \theta_{R}}{\theta _{S} - \theta_{R}} \biggr)^{ - 1 / m} - 1 \biggr]^{1 / n},\\ k_{r} = \biggl( \frac{\theta- \theta_{R}}{\theta_{S} - \theta_{R}} \biggr)^{1 / 2} \biggl[ 1 - \biggl( 1 - \biggl( \frac{\theta- \theta_{R}}{\theta_{S} - \theta_{R}} \biggr)^{1 / m} \biggr)^{m} \biggr]^{2},\end{gathered} $$
(29)

where \(\theta_{R} \) is the residual volumetric water content, \(\theta_{S} \) is the saturated volumetric water content, α is a parameter related to the mean pore-size, n is a parameter related to the uniformity of the pore-size distribution, and \(m =1-1/n\). We take the parameters of Glendale clay loam [27] as \(\theta_{R}=0.106\), \(\theta_{S}=0.469\), \(\alpha=1.04\mbox{ m}^{-1}\), \(m=0.283\), and \(K _{s}=1.52\times10^{-6} \mbox{ m}\cdot\mbox{s}^{-1}\). The length of L is taken as \(2\times10^{-3} \mbox{ m}\), and the initial and boundary values in equations (2)-(3) are \(\theta_{0}=0.25\) and \(\theta _{L}=0.4\).

According to (28)-(29), the diffusivity in (1) is

$$ D ( \theta_{r} + 0.25 ) = \frac{c_{1} [ 1 - ( 1 - ( c_{2} ( \theta_{r} + 0.25 ) - c_{3} )^{c_{4}} )^{0.283} ]^{2}}{ [ ( c_{2} ( \theta_{r} + 0.25 ) - c_{3} )^{ - c_{4}} - 1 ]^{c_{5}} ( c_{2} ( \theta_{r} + 0.25 ) - c_{3} )^{c_{6}}}, $$
(30)

where \(\theta_{r}=\theta-0.25\). Substituting the parameters of Glendale clay loam [27] into equations (28) and (29), we obtain that \(c _{1}=0.1020084959\times10^{-4}\), \(c _{2}=2.754820937\), \(c _{3}=0.2920110193\), \(c _{4}=3.533568905\), \(c _{5}=0.282999998\), in \(c _{6}=4.033568905\) in equation (30). Similarly, we derive ϕ at \(a=0\) before the wetting front travels through the boundary point \(x=2\times10^{-3} \mbox{ m}\):

$$ \phi\approx\sum_{i = 1}^{n} U_{i} \biggl( \int_{\theta_{r}}^{0.15} \frac{D ( \theta_{r} + 0.25 )}{\theta_{r}}\,\mathrm{d} \theta_{r} \biggr)^{i}, $$
(31)

where first- and second-order approximations of \(U _{i} \) are

  • \(n=1\): \(U _{1}=3\mbox{,}266.070514\).

  • \(n=2\): \(U _{1}=3\mbox{,}600.557734\), \(U _{2}=-2.796118274\times10^{9}\).

Compared with the FEM, first- and second-order approximate solutions of ϕ are presented in Figure 6, and the relative errors are shown in Table 3.

Figure 6
figure 6

Results of ϕ obtained from the FEM and approximations of orders 1-2.

Full size image
Table 3 Results of θ obtained from the FEM and second-order approximation
Full size table

We observe that the present approximations are closer to the FEM as order varies from 1 to 2 in Figure 6, and the maximal value of the relative error is −2.097% in 0.8397 mm/min1/2 for second-order approximation in Table 3.

From the second-order approximation above and equation (18) we obtain \(t _{L}=3.582\mbox{ s}\) when the wetting front arrives at the boundary point \(x=2\times10^{-3} \mbox{ m}\). Similarly, \(x _{d}=1.5\times10^{-3} \mbox{ m}\) is taken as a definite space value in \(a _{j} \) and \(\theta_{j} \) calculation, and the sixth-order approximation of \(\partial\theta/ \partial t \) is presented as

$$ \begin{aligned}[b] \frac{\partial\theta}{\partial t} \approx{}& 5\mbox{,}672 \mbox{,}855.52832\theta^{6} - 10\mbox{,}187\mbox{,}681.423 \theta^{5} + 7\mbox{,}615\mbox{,}774.92597\theta^{4} \\ & - 3 \mbox{,}033\mbox{,}314.6831\theta^{3}+ 678\mbox{,}883.519123\theta^{2} - 80\mbox{,}948.6314005\theta\\&+ 4 \mbox{,}017.3694807. \end{aligned} $$
(32)

Then the second-order approximation between the space variable x and water content θ is

$$ x \approx\frac{0.002}{\sum_{i = 1}^{2} U_{i} ( \int_{0}^{0.15 - a} \frac{D ( \theta_{\beta} + a + 0.25 )}{\theta_{\beta}} \,\mathrm{d}\theta_{\beta} )^{i}} \sum_{i = 1}^{2} U_{i} \biggl( \int_{\theta- a - 0.25}^{0.15 - a} \frac{D ( \theta_{\beta} + a + 0.25 )}{\theta_{\beta}} \,\mathrm{d} \theta_{\beta} \biggr)^{i}, $$
(33)

where \(U _{i} \) can be calculated by solving equation (16) as a varies. As t increases, we calculate the approximations for \(a=0\), \(a=-0.0003\), \(a=-0.005\), and \(a=-0.03\) and the corresponding time by solving equation (32). The corresponding water profiles are shown in Figure 7, where the thick solid line shows the steady solution in equation (6). The dotted lines show the present approximations, and solid lines show the results by the FEM as time increases. Compared with the FEM, the relative errors are shown in Figure 8.

Figure 7
figure 7

The changes of water profile for the van Genuchten model. Dotted lines show the present approximations, and solid lines show the results by the FEM.

Full size image
Figure 8
figure 8

Relative errors of present approximations and the FEM.

Full size image

The present approximation agrees with numerical solution, and the maximum relative error of present solution is less than −3% in Figure 8. In addition, we solve equation (32) and derive the relationship between time variable t and water content θ, which is shown in Figure 9, and the relative errors are presented in Table 4.

Figure 9
figure 9

Relationship between t and θ in \(\pmb{{x_{{d}}=1.5\mbox{ mm}}}\) .

Full size image
Table 4 The results of θ obtained from the present method and the FEM in \(\pmb{x_{{d}}=1.5\mbox{ mm}}\)
Full size table

The present solution shown by dotted line approximates well with the FEM shown by solid lines in time simulation in Figure 9, and the maximum relative error is −2.0534% in Table 4.

4 Conclusion

In this paper, we analyzed the changes of wetting front position and derived an approximate analytical solution of RE with finite boundaries (2). The solid lines in Figure 1 can be approximated by the solution equation (17), which is a series solution. According to equation (17), the series solution in fact is an approximation for semiinfinite boundary with different initial values, which means that the process of water infiltration varying from transient flow to steady one in Figure 1 can be simulated by the solution of semiinfinite problem with a variable initial value. The presented examples for the power law and van Genuchten model demonstrate the accuracy of the present solution by comparing the present results with the results obtained by the FEM.