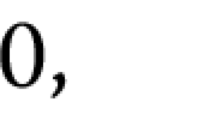The equation
$$ \textstyle\begin{cases} - ( {a + b\int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } ) \Delta u + u = \lambda \vert u \vert ^{{p - 2}}u + \vert u \vert ^{4}u\quad{\text{in }}{\mathbb {R}^{3}}, \\ u > 0, \quad\quad u \in{H^{1}}({\mathbb{R}^{3}}), \end{cases} $$
(3.1)
is the limiting equation of (1.1). In view of [23], we have the following.
Proposition 3.1
Equation (3.1) has a positive ground-state solution
\(\tilde{u} \in{H^{1}}({\mathbb{R}^{3}})\)
with
\(c < \frac{1}{ 4}ab{S^{3}} + \frac{1}{ {24}}{b^{3}}{S^{6}} + \frac{1}{ {24}}{({b^{2}}{S^{4}} + 4aS)^{\frac{3}{2}}} \), where
c
is the least energy level of (3.1).
Equation (1.1) can be rewritten as
$$ \textstyle\begin{cases} - ( {a + b\int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } ) \Delta u + V(\varepsilon x)u = \lambda W(\varepsilon x) \vert u \vert ^{{p - 2}}u + \vert u \vert ^{4}u\quad{\text{in }}{\mathbb{R}^{3}}, \\ u > 0, \quad\quad u \in{H^{1}}({\mathbb{R}^{3}}),\end{cases} $$
(3.2)
and the corresponding energy functional is
$$\begin{aligned} {I_{\varepsilon}}(u) &= \frac{a}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} + \frac{b}{ 4}{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } \biggr)^{2}} \\ &\quad{} - \frac{\lambda}{ p} \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl({u^{+} } \bigr)}^{p}}} - \frac{1}{ 6} \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} , \quad u \in{H^{1}} \bigl({\mathbb {R}^{3}} \bigr) . \end{aligned} $$
Since V is bounded and \(\tau: = \min_{{\mathbb {R}^{3}}} V > 0\),
$${ \Vert u \Vert _{\varepsilon}}: = { \biggl( { \int _{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2} + V( \varepsilon x){u^{2}}} } \biggr)^{\frac{1}{2}}} $$
is an equivalent norm in \({H^{1}}({\mathbb{R}^{3}})\).
By Proposition 3.1, for any \({x_{0}} \in{\mathbb{R}^{3}}\), let \({w_{\mu}}\) be a positive ground-state solution to the equation
$$\textstyle\begin{cases} - ( {a + b\int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } ) \Delta u + V({x_{0}})u = \mu [ {\lambda W({x_{0}}) \vert u \vert ^{{p - 2}}u + \vert u \vert ^{4}u} ] \quad{\text{in }}{\mathbb{R}^{3}}, \\ u > 0, \quad\quad u \in{H^{1}}({\mathbb{R}^{3}}), \quad\quad 0 < \mu \le1,\end{cases} $$
with the energy functional
$$\begin{aligned} {I_{V({x_{0}}),W({x_{0}}),\mu}}(u) &= \frac{a}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V({x_{0}}){u^{2}}} + \frac{b}{ 4}{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } \biggr)^{2}} \\ &\quad{} - \frac{1}{ p}\mu\lambda \int_{{\mathbb{R}^{3}}} {W({x_{0}}){{ \bigl({u^{+} } \bigr)}^{p}}} - \frac{1}{ 6}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} , \quad u \in{H^{1}} \bigl({\mathbb {R}^{3}} \bigr), 0 < \mu \le1. \end{aligned} $$
Denote the mountain-pass level of \({I_{V({x_{0}}),W({x_{0}}),\mu}}\) by \({c_{V({x_{0}}),W({x_{0}}),\mu}}\). From [23], we see that
$$\begin{aligned} {c_{V({x_{0}}),W({x_{0}}),\mu}}&: = \inf_{\gamma \in {\Gamma_{V({x_{0}}),W({x_{0}}),\mu}}} \max_{t \in [0,1]} {I_{V({x_{0}}),W({x_{0}}),\mu}} \bigl(\gamma(t) \bigr) \\ &= \inf_{u \in{H^{1}}({\mathbb {R}^{3}})\backslash\{ 0\} } \max_{t > 0} {I_{V({x_{0}}),W({x_{0}}),\mu}}({u_{t}}) = \inf_{u \in {\mathcal{M}_{V({x_{0}}),W({x_{0}}),\mu}}} {I_{V({x_{0}}),W({x_{0}}),\mu }}(u) > 0, \end{aligned} $$
where
$$\begin{aligned}& {\Gamma_{V({x_{0}}),W({x_{0}}),\mu}}: = \bigl\{ {\gamma \in C \bigl([0,1],{H^{1}} \bigl({\mathbb{R}^{3}} \bigr) \bigr):\gamma(0) = 0,{I_{V({x_{0}}),W({x_{0}}),\mu}} \bigl(\gamma(1) \bigr) < 0} \bigr\} , \\& {\mathcal{M}_{V({x_{0}}),W({x_{0}}),\mu}}: = \bigl\{ {u \in {H^{1}} \bigl({ \mathbb{R}^{3}} \bigr)\backslash\{ 0\} :{G_{V({x_{0}}),W({x_{0}}),\mu }}(u) = 0} \bigr\} \end{aligned}$$
and
$$\begin{aligned} {G_{V({x_{0}}),W({x_{0}}),\mu}}(u) &= 2a \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + 4 \int_{{\mathbb{R}^{3}}} {V({x_{0}}){u^{2}}} + 2b{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } \biggr)^{2}} \\ &\quad{} - \mu \biggl[ {\frac{{p + 6}}{ p}\lambda \int_{{\mathbb{R}^{3}}} {W({x_{0}}){{ \bigl({u^{+} } \bigr)}^{p}}} + 2 \int _{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} } \biggr]. \end{aligned} $$
We have the following lemma.
Lemma 3.2
For any
\(\{ {\mu_{n}}\}\)
with
\({\mu_{n}} \to{1^{-} }\), up to a subsequence, \(\exists\{ {y_{n}}\} \subset{\mathbb{R}^{3}}\)
such that
\(\{ {w_{{\mu_{n}}}}(x + {y_{n}})\} \)
is convergent in
\({H^{1}}({\mathbb{R}^{3}})\).
Proof
Since
$$\begin{aligned} {c_{V({x_{0}}),W({x_{0}}),\frac{1}{2}}}& \ge{c_{V({x_{0}}),W({x_{0}}),{\mu_{n}}}} \\ &= {I_{V({x_{0}}),W({x_{0}}),{\mu _{n}}}}({w_{{\mu_{n}}}}) - \frac{1}{ {p + 6}}{G_{V({x_{0}}),W({x_{0}}),{\mu_{n}}}}({w_{{\mu_{n}}}}) \\ &= \frac{{p + 2}}{ {2(p + 6)}}a \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla{w_{{\mu _{n}}}}} \vert }^{2}}} + \frac{{p - 2}}{ {2(p + 6)}} \int_{{\mathbb{R}^{3}}} {V({x_{0}})w_{{\mu_{n}}}^{2}} \\ &\quad{} + \frac {{p - 2}}{ {4(p + 6)}}b{ \biggl( { \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla {w_{{\mu_{n}}}}} \vert }^{2}}} } \biggr)^{2}} + \frac{{6 - p}}{ {6(p + 6)}}{ \mu_{n}} \int_{{\mathbb{R}^{3}}} {w_{{\mu_{n}}}^{6}} , \end{aligned}$$
\(\{ {w_{{\mu_{n}}}}\} \) is bounded in \({H^{1}}({\mathbb{R}^{3}})\).
By the vanishing theorem, \(\exists\{ {y_{n}}\} \subset{\mathbb{R}^{3}}\) and set \({{\tilde{w}}_{{\mu_{n}}}}(x): = {w_{{\mu_{n}}}}(x + {y_{n}})\), we may assume that \(\exists\tilde{w} \in{H^{1}}({\mathbb{R}^{3}})\backslash \{ 0\} \) such that
$$\textstyle\begin{cases} {{\tilde{w}}_{{\mu_{n}}}} \rightharpoonup\tilde{w}\quad{\text{in }}{H^{1}}({\mathbb{R}^{3}}), \\ {{\tilde{w}}_{{\mu_{n}}}} \to\tilde{w}\quad{\text{in }}L_{\mathrm{loc}} ^{s}({\mathbb{R}^{3}}) {\text{ for all }}1 \le s < 6, \\ {{\tilde{w}}_{{\mu_{n}}}} \to\tilde{w}\quad {\text{a.e. in }}{\mathbb{R}^{3}}.\end{cases} $$
Moreover, w̃ satisfies
$$- \bigl(a + b{A^{2}} \bigr)\Delta\tilde{w} + V({x_{0}}) \tilde{w} = \lambda W({x_{0}}){ \bigl({{\tilde{w}}^{+} } \bigr)^{p - 1}} + { \bigl({{\tilde{w}}^{+} } \bigr)^{5}}, $$
where \({A^{2}} = \lim_{n \to\infty} \int_{{\mathbb {R}^{3}}} {{{ \vert {\nabla{{\tilde{w}}_{{\mu_{n}}}}} \vert }^{2}}} \) and \(\int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla\tilde{w}} \vert }^{2}}} \le{A^{2}}\).
Next, we claim that
$$ \lim_{n \to\infty} {c_{V({x_{0}}),W({x_{0}}),{\mu _{n}}}} = {c_{V({x_{0}}),W({x_{0}}),1}} . $$
(3.3)
Indeed, \(\exists{t_{n}} > 0\) such that \({({w_{1}})_{{t_{n}}}} \in{\mathcal {M}_{V({x_{0}}),W({x_{0}}),{\mu_{n}}}}\), then \(\frac {{d{I_{V({x_{0}}),W({x_{0}}),{\mu_{n}}}}({{({w_{1}})}_{t}})}}{ {dt}}| _{t = {t_{n}}} = 0\) shows that \(\{ {t_{n}}\} \) is bounded. Hence, we have
$$\begin{aligned} {c_{V({x_{0}}),W({x_{0}}),1}} &\le{c_{V({x_{0}}),W({x_{0}}),{\mu_{n}}}} \le {I_{V({x_{0}}),W({x_{0}}),{\mu_{n}}}} \bigl({({w_{1}})_{{t_{n}}}} \bigr) \\ &= {I_{V({x_{0}}),W({x_{0}}),1}} \bigl({({w_{1}})_{{t_{n}}}} \bigr) + \frac{1}{ p}(1 - {\mu_{n}})\lambda \int_{{\mathbb{R}^{3}}} {W({x_{0}}) ({w_{1}})_{{t_{n}}}^{p}} + \frac{1}{ 6}(1 - {\mu_{n}}) \int_{{\mathbb{R}^{3}}} {({w_{1}})_{{t_{n}}}^{6}} \\ &\le{I_{V({x_{0}}),W({x_{0}}),1}}({w_{1}}) + o(1) = {c_{V({x_{0}}),W({x_{0}}),1}} + o(1), \end{aligned} $$
(3.3) holds.
Since \(\lim_{n \to\infty} \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla{{\tilde{w}}_{{\mu_{n}}}}} \vert }^{2}}} \ge \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla\tilde{w}} \vert }^{2}}} \), we check that \({G_{V({x_{0}}),W({x_{0}}),1}}(\tilde{w}) \le0\), then by (3.3), we get \({{\tilde{w}}_{{\mu_{n}}}} \to\tilde{w}\) in \({H^{1}}({\mathbb{R}^{3}})\). □
By Lemma 3.2, \(\tilde{w}_{{\mu_{n}}}^{6}\), \(\tilde{w}_{{\mu_{n}}}^{p}\), \(\tilde{w}_{{\mu_{n}}}^{2}\) are uniformly integrable near ∞. Since \(\{ {\mu_{n}}\} \) is arbitrary, then \(\exists{\delta_{0}} > 0\) small but fixed, \(\{ {y_{\mu}}\} \subset{\mathbb{R}^{3}}\) for all \(\mu \in[1 - {\delta_{0}},1]\),
$$ \tilde{w}_{\mu}^{6},\tilde{w}_{\mu}^{p}, \tilde{w}_{\mu}^{2}{\text{ are uniformly integrable near }} \infty, $$
(3.4)
where \({{\tilde{w}}_{\mu}}(x): = {w_{\mu}}(x + {y_{\mu}})\).
Next, we will show that \(\exists\bar{C} > 0\) which is independent of \(\mu \in[1 - {\delta_{0}},1]\) such that
$$ \int_{{\mathbb{R}^{3}}} {w_{\mu}^{p}} + \int_{{\mathbb{R}^{3}}} {w_{\mu}^{6}} \ge\bar{C}. $$
(3.5)
Indeed, assuming the contrary, \(\exists\{ {\mu_{j}}\} \subset[1 - {\delta_{0}},1]\) with \({\mu_{j}} \to{1^{-} }\) such that
$$\int_{{\mathbb{R}^{3}}} {w_{{\mu_{j}}}^{p}} + \int_{{\mathbb{R}^{3}}} {w_{{\mu_{j}}}^{6}} \to0\quad {\text{as }}j \to\infty. $$
In view of the definition of \({w_{{\mu_{j}}}}\),
$$a \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla{w_{{\mu_{j}}}}} \vert }^{2}}} + \int_{{\mathbb{R}^{3}}} {V({x_{0}})w_{{\mu_{j}}}^{2}} + b{ \biggl( { \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla{w_{{\mu _{j}}}}} \vert }^{2}}} } \biggr)^{2}} = \lambda{\mu_{j}} \int _{{\mathbb{R}^{3}}} {W({x_{0}})w_{{\mu_{j}}}^{p}} + {\mu_{j}} \int_{{\mathbb {R}^{3}}} {w_{{\mu_{j}}}^{6}} , $$
then \({ \Vert {{w_{{\mu_{j}}}}} \Vert _{{H^{1}}({\mathbb {R}^{3}})}} \to0\) as \(j \to\infty\), which contradicts \({c_{V({x_{0}}),W({x_{0}}),1}} > 0\) by (3.3).
Consider the following functional:
$$\begin{aligned} {I_{\varepsilon,\mu}}(u)& = \frac{a}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} + \frac{b}{ 4}{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } \biggr)^{2}} \\ &\quad{} - \mu \biggl[ {\frac{\lambda}{ p} \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl({u^{+} } \bigr)}^{p}}} + \frac{1}{ 6} \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} } \biggr],\quad u \in {H^{1}} \bigl({\mathbb{R}^{3}} \bigr), \mu \in[1 - { \delta_{0}},1]. \end{aligned} $$
Denote
$$A(u):= \frac{a}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} + \frac{b}{ 4}{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } \biggr)^{2}} $$
and
$$B(u): = \biggl[ {\frac{\lambda}{ p} \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl({u^{+} } \bigr)}^{p}}} + \frac{1}{ 6} \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} } \biggr], $$
we will show that \(A(u)\) and \(B(u)\) satisfy the conditions of Proposition 2.2 for \(\varepsilon > 0\) small.
For any \(u \in{H^{1}}({\mathbb{R}^{3}})\),
$$\frac{\lambda}{ p} \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl({u^{+} } \bigr)}^{p}}} + \frac{1}{ 6} \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} \ge0 $$
and
$$\frac{a}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} + \frac{b}{ 4}{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } \biggr)^{2}} \to + \infty\quad {\text{as }} { \Vert u \Vert _{{H^{1}}({\mathbb{R}^{3}})}} \to\infty. $$
Set \({W_{\varepsilon,\mu,t}}(x): = t\eta ( {\sqrt{\varepsilon}\frac{x}{ {{t^{2}}}} - \frac{{{x_{0}}}}{ {\sqrt{\varepsilon}{t^{2}}}}} ){{\tilde{w}}_{\mu}} ( {\frac{x}{ {{t^{2}}}} - \frac{{{x_{0}}}}{ {\varepsilon{t^{2}}}}} )\), where η is a smooth cut-off function with \(0 \le\eta \le1\), \(\eta = 1\) on \({B_{1}}(0)\), \(\eta = 0\) on \({\mathbb{R}^{3}}\backslash{B_{2}}(0)\), \(\vert \nabla\eta \vert \le C\).
Since \({\delta_{0}} > 0\) is small, we may assume that \(1 - {\delta_{0}} > \frac{1}{ 2}\), then \({I_{\varepsilon,\mu}}(u) \le{I_{{{ \Vert V \Vert }_{{L^{\infty}}}},\inf W,\frac{1}{2}}}(u)\) and
$$\begin{aligned}& {I_{{{ \Vert V \Vert }_{{L^{\infty}}}},\inf W,\frac{1}{2}}}({W_{\varepsilon,\mu,t}}) \\& \quad = \frac{a}{ 2} \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla{W_{\varepsilon,\mu ,t}}} \vert }^{2}}} + \frac{1}{ 2}{ \Vert V \Vert _{{L^{\infty}}}} \int_{{\mathbb{R}^{3}}} {W_{\varepsilon,\mu,t}^{2}} + \frac{b}{ 4}{ \biggl( { \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla {W_{\varepsilon,\mu,t}}} \vert }^{2}}} } \biggr)^{2}} \\& \quad\quad{} - \frac{\lambda}{ {2p}}\inf W \int_{{\mathbb{R}^{3}}} {W_{\varepsilon,\mu,t}^{p}} - \frac{1}{ {12}} \int_{{\mathbb{R}^{3}}} {W_{\varepsilon,\mu,t}^{6}} \\& \quad \mathop{=} ^{x' = \frac{x}{t^{2}} - \frac{{{x_{0}}}}{{\varepsilon{t^{2}}}}} \frac{a}{ 2}{t^{4}} \int_{{\mathbb{R}^{3}}} {{{ \bigl\vert {\nabla\eta \bigl( {\sqrt{\varepsilon}x'} \bigr)\sqrt{\varepsilon}{{\tilde{w}}_{\mu}} \bigl(x' \bigr) + \eta \bigl( {\sqrt{\varepsilon}x'} \bigr)\nabla{{\tilde{w}}_{\mu}} \bigl(x' \bigr)} \bigr\vert }^{2}}} \\& \quad\quad{} + \frac{1}{ 2}{ \Vert V \Vert _{{L^{\infty}}}} {t^{8}} \int_{{\mathbb {R}^{3}}} {{\eta^{2}} \bigl( {\sqrt{\varepsilon}x'} \bigr)\tilde{w}_{\mu}^{2} \bigl(x' \bigr)} \\& \quad\quad{} + \frac{b}{ 4}{t^{8}} { \biggl( { \int_{{\mathbb{R}^{3}}} {{{ \bigl\vert {\nabla\eta \bigl( {\sqrt{\varepsilon}x'} \bigr)\sqrt{\varepsilon}{{\tilde{w}}_{\mu}} \bigl(x' \bigr) + \eta \bigl( {\sqrt{\varepsilon}x'} \bigr)\nabla {{\tilde{w}}_{\mu}} \bigl(x' \bigr)} \bigr\vert }^{2}}} } \biggr)^{2}} \\& \quad\quad{}- \frac{\lambda}{ {2p}} \inf _{{\mathbb{R}^{3}}} W{t^{p + 6}} \int _{{\mathbb{R}^{3}}} {{\eta^{p}} \bigl( {\sqrt{\varepsilon}x'} \bigr)\tilde{w}_{\mu}^{p} \bigl(x' \bigr)} \\& \quad\quad{} - \frac{1}{ {12}}{t^{12}} \int_{{\mathbb{R}^{3}}} {{\eta^{6}} \bigl( {\sqrt {\varepsilon}x'} \bigr)\tilde{w}_{\mu}^{6} \bigl(x' \bigr)} \\& \quad \le C{t^{4}} \biggl( { \int_{{\mathbb{R}^{3}}} {\tilde{w}_{\mu}^{2}} + \int _{{\mathbb{R}^{3}}} {{{ \vert {\nabla{{\tilde{w}}_{\mu}}} \vert }^{2}}} } \biggr) + C{t^{8}} \biggl( {{{ \biggl( { \int_{{\mathbb {R}^{3}}} {\tilde{w}_{\mu}^{2}} } \biggr)}^{2}} + {{ \biggl( { \int_{{\mathbb {R}^{3}}} {{{ \vert {\nabla{{\tilde{w}}_{\mu}}} \vert }^{2}}} } \biggr)}^{2}}} \biggr) + C{t^{8}} \int_{{\mathbb{R}^{3}}} {\tilde{w}_{\mu}^{2}} \\& \quad\quad{} - \frac{\lambda}{ {2p}}\inf_{{\mathbb{R}^{3}}} W{t^{p + 6}} \int_{{B_{1/\sqrt {\varepsilon}}}(0)} {\tilde{w}_{\mu}^{p}} - \frac{1}{ {12}}{t^{12}} \int_{{B_{1/\sqrt{\varepsilon}}}(0)} {\tilde{w}_{\mu}^{6}} \to - \infty \end{aligned}$$
as \(t \to + \infty\) uniformly for all \(\varepsilon > 0\) small and \(\mu \in[1 - {\delta_{0}},1]\), where we have used (3.4) and (3.5). Taking \({t_{0}} > 0\) large, we get
$${I_{\varepsilon,\mu}}({W_{\varepsilon,\mu,{t_{0}}}}) \le{I_{{{ \Vert V \Vert }_{{L^{\infty}}}},\inf W,\frac{1}{2}}}({W_{\varepsilon,\mu,{t_{0}}}}) < - 2 $$
for all \(\mu \in[1 - {\delta_{0}},1]\), \(\varepsilon > 0\) small.
Using the Sobolev embedding theorem, we have
$$\begin{aligned} {I_{\varepsilon,\mu}}(u) &\ge\frac{a}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{\tau}{ 2} \int_{{\mathbb{R}^{3}}} {{u^{2}}} - \frac{\kappa}{ p}\lambda \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{p}}} - \frac{1}{ 6} \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} \\ &\ge C \Vert u \Vert _{{H^{1}}({\mathbb{R}^{3}})}^{2} - C\lambda \Vert u \Vert _{{H^{1}}({\mathbb{R}^{3}})}^{p} - C \Vert u \Vert _{{H^{1}}({\mathbb{R}^{3}})}^{6} > 0 \end{aligned} $$
for all \(u \in{H^{1}}({\mathbb{R}^{3}})\) with \({ \Vert u \Vert _{{H^{1}}({\mathbb{R}^{3}})}}\) small since \(p > 2\).
Hence, we can define
$${c_{\varepsilon,\mu}}: = \inf_{\gamma \in{\Gamma _{\mu}} } \max_{t \in[0,1]} {I_{\varepsilon,\mu }} \bigl(\gamma(t) \bigr) > \max \bigl\{ {I_{\varepsilon,\mu}}(0),{I_{\varepsilon ,\mu}}({W_{\varepsilon,\mu,{t_{0}}}}) \bigr\} $$
for all \(\mu \in[1 - {\delta_{0}},1]\), \(\varepsilon > 0\) small, where
$${\Gamma_{\mu}}: = \bigl\{ {\gamma \in C \bigl([0,1],{H^{1}} \bigl({\mathbb {R}^{3}} \bigr) \bigr):\gamma(0) = 0,\gamma(1) = {W_{\varepsilon,\mu,{t_{0}}}}} \bigr\} . $$
Lemma 3.3
For any
\({x_{0}} \in{\mathbb{R}^{3}}\), \(\lim_{\varepsilon \to0} {c_{\varepsilon,\mu}} \le {c_{V({x_{0}}),W({x_{0}}),\mu}}\)
uniformly for all
\(\mu \in[1 - {\delta_{0}},1]\).
Proof
Define \({W_{\varepsilon,\mu,0}}: = \lim_{t \to0} {W_{\varepsilon,\mu,t}}\) in \({{H^{1}}({\mathbb{R}^{3}})}\) sense, then \({W_{\varepsilon,\mu,0}} = 0\). Thus, setting \({\gamma_{\mu}}(s): = {W_{\varepsilon,\mu,s{t_{0}}}}\) (\(0 \le s \le1\)), we have \({\gamma_{\mu}} \in{\Gamma_{\mu}}\), then
$${c_{\varepsilon,\mu}} \le\max_{s \in[0,1]} {I_{\varepsilon,\mu}} \bigl({ \gamma_{\mu}}(s) \bigr) = \max_{t \in[0,{t_{0}}]} {I_{\varepsilon,\mu}}({W_{\varepsilon,\mu,t}}) $$
and we just need to verify that
$$ \lim_{\varepsilon \to0} \max_{t \in[0,{t_{0}}]} {I_{\varepsilon,\mu}}({W_{\varepsilon,\mu,t}}) \le {c_{V({x_{0}}),W({x_{0}}),\mu}} $$
(3.6)
uniformly for \(\mu \in[1 - {\delta_{0}},1]\).
Indeed,
$$\begin{aligned}& \max_{t \in[0,{t_{0}}]} {I_{\varepsilon,\mu }}({W_{\varepsilon,\mu,t}}) \\& \quad \mathop{=} ^{x' = \frac{x}{t^{2}} - \frac{{{x_{0}}}}{{\varepsilon{t^{2}}}}} \max_{t \in[0,{t_{0}}]} \frac{a}{ 2}{t^{4}} \int_{{\mathbb{R}^{3}}} {{{ \bigl\vert {\nabla\eta \bigl( {\sqrt{\varepsilon}x'} \bigr)\sqrt{\varepsilon}{{\tilde{w}}_{\mu}} \bigl(x' \bigr) + \eta \bigl( {\sqrt{\varepsilon}x'} \bigr)\nabla{{\tilde{w}}_{\mu}} \bigl(x' \bigr)} \bigr\vert }^{2}}} \\& \quad\quad{} + \frac{1}{ 2}{t^{8}} \int_{{\mathbb{R}^{3}}} {V \bigl(\varepsilon{t^{2}}x' + {x_{0}} \bigr){\eta ^{2}} \bigl( {\sqrt{\varepsilon}x'} \bigr)\tilde{w}_{\mu}^{2} \bigl(x' \bigr)} \\& \quad\quad{} + \frac{b}{ 4}{t^{8}} { \biggl( { \int_{{\mathbb{R}^{3}}} {{{ \bigl\vert {\nabla\eta \bigl( {\sqrt{\varepsilon}x'} \bigr)\sqrt{\varepsilon}{{\tilde{w}}_{\mu}} \bigl(x' \bigr) + \eta \bigl( {\sqrt{\varepsilon}x'} \bigr)\nabla {{\tilde{w}}_{\mu}} \bigl(x' \bigr)} \bigr\vert }^{2}}} } \biggr)^{2}} \\& \quad\quad{} - \frac{\lambda}{ p}\mu{t^{p + 6}} \int_{{\mathbb{R}^{3}}} {W \bigl(\varepsilon{t^{2}}x' + {x_{0}} \bigr){\eta^{p}} \bigl( {\sqrt{\varepsilon}x'} \bigr)\tilde{w}_{\mu}^{p} \bigl(x' \bigr)} - \frac{1}{ 6}\mu{t^{12}} \int_{{\mathbb{R}^{3}}} {{\eta^{6}} \bigl( {\sqrt {\varepsilon}x'} \bigr)\tilde{w}_{\mu}^{6} \bigl(x' \bigr)} \\& \quad \le o(1) + \max_{t \in[0,{t_{0}}]} \frac{a}{ 2}{t^{4}} \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla{{\tilde{w}}_{\mu}}} \vert }^{2}}} + \frac{1}{ 2}{t^{8}} \int_{{\mathbb{R}^{3}}} {V({x_{0}})\tilde{w}_{\mu}^{2}} + \frac{b}{ 4}{t^{8}} { \biggl( { \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla {{\tilde{w}}_{\mu}}} \vert }^{2}}} } \biggr)^{2}} \\& \quad\quad{} - \frac{\lambda}{ p}\mu{t^{p + 6}} \int_{{\mathbb{R}^{3}}} {W({x_{0}})\tilde{w}_{\mu}^{p}} - \frac{1}{ 6}\mu{t^{12}} \int_{{\mathbb{R}^{3}}} {\tilde{w}_{\mu}^{6}} \\& \quad \le o(1) + \sup_{t \in[0, + \infty)} {I_{V({x_{0}}),W({x_{0}}),\mu}} \bigl({({{\tilde{w}}_{\mu}})_{t}} \bigr) \\& \quad = o(1) + {c_{V({x_{0}}),W({x_{0}}),\mu}}, \end{aligned}$$
where we have used (3.4). Notice that \(o(1) \to0\) as \(\varepsilon \to0\) uniformly for \(\mu \in[1 - {\delta_{0}},1]\), then (3.6) holds, the lemma is proved. □
Suppose that \((P_{1})\)-(i) holds, assume that \({x_{v}} \in\mathcal{V}\) such that
$$W({x_{v}}): = \max_{x \in\mathcal{V}} W(x). $$
By \((P_{2})\)-(i), \(\tau < {\tau_{\infty}}\) and \(W({x_{v}}) \ge{\kappa _{\infty}}\), then \({c_{\tau,W({x_{v}}),\mu}} < {c_{{\tau_{\infty}},{\kappa_{\infty,\mu}}}}\), and combining with Lemma 3.3, we have
$$ {c_{\varepsilon,\mu}} < {c_{{\tau_{\infty}},{\kappa_{\infty,\mu}}}} $$
(3.7)
for all \(\mu \in[1 - {\delta_{0}},1]\) and \(\varepsilon > 0\) small. Similarly, if \((P_{2})\)-(ii) holds, (3.7) is still true for all \(\mu \in[1 - {\delta_{0}},1]\) and \(\varepsilon > 0\) small.
Lemma 3.4
Suppose that
\((P_{1})\), \((P_{2})\), \((P_{3})\)
hold and
\(p \in(3,4]\). Fix
\(\varepsilon > 0\), for every
\(\mu \in[1 - {\delta_{0}},1]\), let
\(\{ {u_{n}}\} \subset{H^{1}}({\mathbb{R}^{3}})\)
be a bounded
\({({\textit {PS}})_{c}}\)
sequence for
\({I_{\varepsilon,\mu}}\)
with
\(0 < c < \frac{1}{ 4}ab\frac{{{S^{3}}}}{ \mu} + \frac{1}{ {24}}{b^{3}}\frac{{{S^{6}}}}{ {{\mu^{2}}}} + \frac{1}{ {24}}{ ( {{b^{2}}\frac{{{S^{4}}}}{ {{\mu^{4/3}}}} + 4a\frac{S}{ {{\mu^{1/3}}}}} )^{\frac{3}{2}}}\), then there exists a
\(u \in{H^{1}}({\mathbb{R}^{3}})\), a number
\(k \in\mathbb{N} \cup\{ 0\} \), k
functions
\({w_{1}},\ldots,{w_{k}}\)
of
\({H^{1}}({\mathbb{R}^{3}})\)
and
k
sequences of points
\(\{y_{n}^{j}\} \subset {\mathbb{R}^{3}}\), \(1 \le j \le k\)
and
\(A \in\mathbb{R}\), such that
-
(i)
\({u_{n}} \rightharpoonup u\)
in
\({H^{1}}({\mathbb{R}^{3}})\)
with
\({{J'}_{\varepsilon,\mu}}(u) = 0\)
and
\(\int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} \to{A^{2}}\)
as
\(n \to\infty\);
-
(ii)
\(\vert y_{n}^{j} \vert \to + \infty\), \(\vert y_{n}^{i} - y_{n}^{j} \vert \to + \infty\)
as
\(n \to\infty\)
if
\(i \ne j\);
-
(iii)
\({w_{j}} \ne0\)
and
\({{J'}_{{\tau_{\infty}},{\kappa_{\infty,\mu }}}}({w_{j}}) = 0\);
-
(iv)
\({ \Vert {{u_{n}} - u - \sum_{j = 1}^{k} {w_{j}}( \cdot - y_{n}^{j})} \Vert _{{H^{1}}({\mathbb{R}^{3}})}} \to0\)
as
\(n \to\infty\);
-
(v)
\({I_{\varepsilon,\mu}}({u_{n}}) + \frac{b}{ 4}{A^{4}} = {J_{\varepsilon,\mu}}(u) + \sum_{j = 1}^{k} {{J_{{\tau_{\infty}},{\kappa_{\infty,\mu}}}}({w_{j}})} + o(1)\);
-
(vi)
\({A^{2}} = \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \sum_{j = 1}^{k} {\int_{{\mathbb{R}^{3}}} { \vert \nabla{w_{j}} \vert ^{2}} } \),
where
$$\begin{aligned} {J_{\varepsilon,\mu}}(u) &= \frac{{a + b{A^{2}}}}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} \\ &\quad{} - \frac{\mu}{ p}\lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl({u^{+} } \bigr)}^{p}}} - \frac{1}{ 6}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} ,\quad u \in{H^{1}} \bigl({\mathbb {R}^{3}} \bigr), \end{aligned} $$
and
$$\begin{aligned} {J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}(u) &= \frac{{a + b{A^{2}}}}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{1}{ 2}{\tau_{\infty}} \int_{{\mathbb{R}^{3}}} {{u^{2}}} \\ &\quad{} - \frac{\mu}{ p}\lambda{\kappa_{\infty}} \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{p}}} - \frac{1}{ 6}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} , \quad u \in{H^{1}} \bigl({\mathbb {R}^{3}} \bigr). \end{aligned} $$
Proof
Since \(\{ {u_{n}}\} \) is bounded in \({H^{1}}({\mathbb{R}^{3}})\), then \(\exists u \in{H^{1}}({\mathbb{R}^{3}})\) and \(A \in\mathbb{R}\), up to a subsequence, such that as \(n \to\infty\),
$${u_{n}} \rightharpoonup u\quad{\text{in }} {H^{1}} \bigl({ \mathbb{R}^{3}} \bigr),\quad\quad \int _{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} \to {A^{2}}\quad {\text{and}}\quad \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} \le{A^{2}}. $$
\({{I'}_{\varepsilon,\mu}}({u_{n}}) \to0\) implies that
$$\begin{gathered} \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} {\nabla u \cdot\nabla\varphi} + \int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u\varphi} - \mu\lambda \int _{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl({u^{+} } \bigr)}^{p - 1}}\varphi} - \mu \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{5}}\varphi} = 0, \\ \quad \forall \varphi \in{H^{1}} \bigl({\mathbb{R}^{3}} \bigr), \end{gathered} $$
i.e.
\({{J'}_{\varepsilon,\mu}}(u) = 0\).
Since
$$\begin{aligned}& {J_{\varepsilon,\mu}}({u_{n}}) \\& \quad = \frac{{a + b{A^{2}}}}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u_{n}^{2}} - \frac{\mu}{ p}\lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl(u_{n}^{+} \bigr)}^{p}}} - \frac{1}{ 6}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n}^{+} \bigr)}^{6}}} \\& \quad = \frac{a}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u_{n}^{2}} + \frac{b}{ 4}{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} } \biggr)^{2}} - \frac{\mu}{ p}\lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl(u_{n}^{+} \bigr)}^{p}}} \\& \quad\quad{} - \frac{1}{ 6}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n}^{+} \bigr)}^{6}}} + \frac{b}{ 4}{A^{4}} + o(1) \\& \quad = {I_{\varepsilon,\mu}}({u_{n}}) + \frac{b}{ 4}{A^{4}} + o(1) \end{aligned}$$
and
$$\begin{aligned}& \bigl\langle {{{J'}_{\varepsilon,\mu}}({u_{n}}), \varphi} \bigr\rangle \\& \quad = \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} {\nabla{u_{n}} \cdot\nabla \varphi} + \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u_{n}}\varphi} - \mu \lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl(u_{n}^{+} \bigr)}^{p - 1}}\varphi} - \mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n}^{+} \bigr)}^{5}} \varphi} \\& \quad = \bigl\langle {{{I'}_{\varepsilon,\mu}}({u_{n}}),\varphi} \bigr\rangle + o(1) \int_{{\mathbb{R}^{3}}} {\nabla{u_{n}} \cdot\nabla \varphi} \\& \quad = \bigl\langle {{{I'}_{\varepsilon,\mu}}({u_{n}}),\varphi} \bigr\rangle + o(1){ \Vert \varphi \Vert _{{H^{1}}({\mathbb {R}^{3}})}}, \end{aligned}$$
we conclude that as \(n \to\infty\),
$$ {J_{\varepsilon,\mu}}({u_{n}}) \to c + \frac{b}{ 4}{A^{4}} $$
(3.8)
and
$$ {{J'}_{\varepsilon,\mu}}({u_{n}}) \to0\quad { \text{in }} { \bigl( {{H^{1}} \bigl({\mathbb{R}^{3}} \bigr)} \bigr)^{ - 1}}. $$
(3.9)
Step 1: Set \({u_{n,1}} = {u_{n}} - u\), by the Brezis-Lieb theorem ([24], Theorem 1),
$$\begin{aligned}& \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} = \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} - \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + o(1), \end{aligned}$$
(3.10)
$$\begin{aligned}& \int_{{\mathbb{R}^{3}}} {u_{n,1}^{2}} = \int_{{\mathbb{R}^{3}}} {u_{n}^{2}} - \int_{{\mathbb{R}^{3}}} {{u^{2}}} + o(1), \\& \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{p}}} = \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n}^{+} \bigr)}^{p}}} - \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{p}}} + o(1), \\& \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{6}}} = \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n}^{+} \bigr)}^{6}}} - \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} + o(1), \end{aligned}$$
(3.11)
$$\begin{aligned}& {J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({u_{n,1}}) = {J_{\varepsilon,\mu}}({u_{n}}) - {J_{\varepsilon,\mu}}(u) + o(1), \end{aligned}$$
(3.12)
$$\begin{aligned}& {{J'}_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({u_{n,1}}) \to0 \quad { \text{in }} { \bigl( {{H^{1}} \bigl({\mathbb{R}^{3}} \bigr)} \bigr)^{ - 1}}. \end{aligned}$$
(3.13)
Next, we claim that one of the following conclusions holds for \({u_{n,1}}\):
-
(1)
\({u_{n,1}} \to0\) in \({{H^{1}}({\mathbb{R}^{3}})}\) or
-
(2)
\(\exists r,\beta > 0\) and a sequence \(\{ y_{n}^{1}\} \subset {\mathbb{R}^{3}}\) such that
$$\int_{{B_{r}}(y_{n}^{1})} {u_{n,1}^{2}} \ge\beta > 0. $$
Indeed, suppose that (2) does not hold, then by the vanishing theorem due to Lion ([25], Lemma 1.1), we have
$$ {u_{n,1}} \to0\quad{\text{in }} {L^{s}} \bigl({ \mathbb{R}^{3}} \bigr) {\text{ for }}s \in(2,6), $$
(3.14)
and combining with \(\langle{{{J'}_{{\tau_{\infty}},{\kappa _{\infty}},\mu}}({u_{n,1}}),{u_{n,1}}} \rangle = o(1)\), we get
$$ \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} + {\tau_{\infty}} \int_{{\mathbb{R}^{3}}} {u_{n,1}^{2}} - \mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{6}}} = o(1). $$
(3.15)
Now, we have the following equalities:
$$\textstyle\begin{cases} {J_{\varepsilon,\mu}}(u) = \frac{{a + b{A^{2}}}}{2}\int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{1}{2}\int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} - \frac{\mu}{p}\lambda\int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{({u^{+} })}^{p}}} - \frac{1}{6}\mu\int_{{\mathbb{R}^{3}}} {{{({u^{+} })}^{6}}} ,\\ 0 = (a + b{A^{2}})\int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} - \mu \lambda\int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{({u^{+} })}^{p}}} - \mu \int_{{\mathbb{R}^{3}}} {{{({u^{+} })}^{6}}} ,\\ 0 = \frac{{a + b{A^{2}}}}{2}\int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{3}{2}\int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} + \frac{1}{2}\int_{{\mathbb{R}^{3}}} {(DV(\varepsilon x),\varepsilon x){u^{2}}} \\ \hphantom{0 =}{}- \frac{3}{p}\mu\lambda\int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{({u^{+} })}^{p}}} - \frac{1}{p}\mu\lambda\int_{{\mathbb{R}^{3}}} {(DW(\varepsilon x),\varepsilon x){{({u^{+} })}^{p}}} - \frac{1}{2}\mu\int_{{\mathbb{R}^{3}}} {{{({u^{+} })}^{6}}} .\end{cases} $$
The first one comes from the definition of \({J_{\varepsilon,\mu}}\). The second one follows by \(\langle{{{J'}_{\varepsilon,\mu }}(u),u} \rangle = 0\). The third one is the Pohozaev identity applying to \({{J'}_{\varepsilon,\mu}}(u) = 0\). From these equalities and \((P_{3})\), we have
$$\begin{aligned}& {J_{\varepsilon,\mu}}(u) - \frac{b}{ 4}{A^{2}} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} \\& \quad = {J_{\varepsilon,\mu}}(u) - \frac{b}{ 4}{A^{2}} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} \\& \quad\quad{} - \frac{1}{ q+6} \biggl[ {2 \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + 4 \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} + \int_{{\mathbb{R}^{3}}} { \bigl(DV(\varepsilon x),\varepsilon x \bigr){u^{2}}} } \\& \quad\quad{} - \frac{{p + 6}}{ p}\mu\lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl({u^{+} } \bigr)}^{p}}} - \frac{2}{ p}\mu\lambda \int_{{\mathbb{R}^{3}}} { \bigl(DW(\varepsilon x),\varepsilon x \bigr){{ \bigl({u^{+} } \bigr)}^{p}}} - 2\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} \biggr] \\& \quad = \frac{{2(q + 2)a + (q - 2)b{A^{2}}}}{ {4(q + 6)}} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{{6 - q}}{ {6(q + 6)}}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} \\& \quad\quad{} + \frac{{q - 2}}{ {2(q + 6)}} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} - \frac{1}{ {(q + 6)}} \int_{{\mathbb{R}^{3}}} { \bigl(DV(\varepsilon x),\varepsilon x \bigr){u^{2}}} \\& \quad\quad{} + \frac{1}{ p}\frac{{p - q}}{ {q + 6}}\mu\lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl({u^{+} } \bigr)}^{p}}} + \frac{1}{ p}\frac{2}{ {q + 6}}\mu\lambda \int_{{\mathbb{R}^{3}}} { \bigl(DW(\varepsilon x),\varepsilon x \bigr){{ \bigl({u^{+} } \bigr)}^{p}}} \ge0. \end{aligned}$$
(3.16)
In view of (3.8), (3.10), (3.11), (3.12), (3.14) and (3.16), we have
$$\begin{aligned} c &= {J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({u_{n,1}}) + {J_{\varepsilon,\mu}}(u) - \frac{b}{ 4}{A^{4}} + o(1) \\ &\ge{J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({u_{n,1}}) + \frac{b}{ 4}{A^{2}} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} - \frac{b}{ 4}{A^{4}} + o(1) \\ &= \frac{{a + b{A^{2}}}}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} + \frac{1}{ 2}{\tau_{\infty}} \int_{{\mathbb{R}^{3}}} {u_{n,1}^{2}} - \frac{1}{ p}\mu\lambda{\kappa_{\infty}} \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{p}}} - \frac{1}{ 6}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{6}}} \\ &\quad{} + \frac{b}{ 4}{A^{2}} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} - \frac{b}{ 4}{A^{4}} + o(1) \\ & = \frac{a}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} + \frac{1}{ 2}{\tau_{\infty}} \int_{{\mathbb{R}^{3}}} {u_{n,1}^{2}} + \frac{b}{ 4}{A^{2}} \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} - \frac{1}{ 6}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{6}}} + o(1). \end{aligned}$$
(3.17)
Using the definition of S, we get
$$ \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} \ge S{ \biggl( { \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{6}}} } \biggr)^{\frac{1}{3}}}. $$
(3.18)
In view of (3.15), we assume that
$$\begin{aligned}& a \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} + {\tau_{\infty}} \int_{{\mathbb{R}^{3}}} {u_{n,1}^{2}} \to{l_{1}}, \end{aligned}$$
(3.19)
$$\begin{aligned}& b{A^{2}} \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} \to{l_{2}}, \end{aligned}$$
(3.20)
$$\begin{aligned}& \mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{6}}} \to{l_{1}} + {l_{2}}. \end{aligned}$$
(3.21)
Equations (3.10), (3.17), (3.18), (3.19), (3.20) and (3.21) yield
$$\begin{aligned}& \begin{aligned}[b] {l_{1}} &= \lim _{n \to\infty} a \int_{{\mathbb {R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} + {\tau_{\infty}} \int_{{\mathbb{R}^{3}}} {u_{n,1}^{2}} \ge\lim _{n \to \infty} a \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} \\ &\ge\lim_{n \to\infty} aS{ \biggl( { \int_{{\mathbb {R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{6}}} } \biggr)^{\frac{1}{3}}} = aS{ \biggl( {\frac{{{l_{1}} + {l_{2}}}}{ \mu}} \biggr)^{\frac{1}{3}}}, \end{aligned} \end{aligned}$$
(3.22)
$$\begin{aligned}& \begin{aligned}[b] {l_{2}} &= \lim _{n \to\infty} b{A^{2}} \int_{{\mathbb {R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} = \lim_{n \to\infty} b \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} + \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} } \biggr) \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} \\ &\ge\lim_{n \to\infty} b{ \biggl( { \int_{{\mathbb {R}^{3}}} { \vert \nabla{u_{n,1}} \vert ^{2}} } \biggr)^{2}} \ge\lim_{n \to\infty} b{S^{2}} { \biggl( { \int _{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,1}^{+} \bigr)}^{6}}} } \biggr)^{\frac{2}{3}}} \ge b{S^{2}} { \biggl( {\frac{{{l_{1}} + {l_{2}}}}{ \mu}} \biggr)^{\frac{2}{3}}} , \end{aligned} \end{aligned}$$
(3.23)
and
$$ c \ge\frac{1}{ 2}{l_{1}} + \frac{1}{ 4}{l_{2}} - \frac{1}{ 6}({l_{1}} + {l_{2}}) = \frac{1}{ 3}{l_{1}} + \frac{1}{ {12}}{l_{2}}. $$
(3.24)
Combining (3.22) and (3.23), we have
$${l_{1}} + {l_{2}} \ge aS{ \biggl( {\frac{{{l_{1}} + {l_{2}}}}{ \mu}} \biggr)^{\frac{1}{3}}} + b{S^{2}} { \biggl( {\frac{{{l_{1}} + {l_{2}}}}{ \mu}} \biggr)^{\frac{2}{3}}}. $$
If \({l_{1}} + {l_{2}} \ne0\), we get
$${({l_{1}} + {l_{2}})^{\frac{1}{3}}} \ge\frac{1}{ 2} \biggl[ {b{{ \biggl( {\frac{S}{ {{\mu^{1/3}}}}} \biggr)}^{2}} + \sqrt{ \frac{{{b^{2}}{S^{4}}}}{ {{\mu^{4/3}}}} + \frac{{4aS}}{ {{\mu^{1/3}}}}} } \biggr], $$
then
$$\begin{aligned} c &\ge\frac{1}{ 3}{l_{1}} + \frac{1}{ {12}}{l_{2}} \ge\frac{1}{ 3}\frac{{aS}}{ {{\mu^{1/3}}}}{( {{l_{1}} + {l_{2}}} )^{\frac{1}{3}}} + \frac{1}{ {12}} \frac{{b{S^{2}}}}{ {{\mu^{2/3}}}}{( {{l_{1}} + {l_{2}}} )^{\frac{2}{3}}} \\ &\ge\frac{1}{ 4}ab\frac{{{S^{3}}}}{ \mu} + \frac{1}{ {24}}{b^{3}} \frac{{{S^{6}}}}{ {{\mu^{2}}}} + \frac{1}{ {24}}{ \biggl({b^{2}} \frac{{{S^{4}}}}{ {{\mu^{4/3}}}} + 4a\frac{S}{ {{\mu^{1/3}}}} \biggr)^{\frac{3}{2}}}, \end{aligned} $$
a contradiction. Hence \({l_{1}} + {l_{2}} = 0\), i.e.
$${u_{n,1}} \to0\quad{\text{in }} {H^{1}} \bigl({ \mathbb{R}^{3}} \bigr) {\text{ as }}n \to \infty, $$
(1) holds.
If (1) holds, the proof is completed for \(k=0\). If (2) holds, denote \({w_{n,1}}(x) = {u_{n,1}}(x + y_{n}^{1})\), then
$$\int_{{B_{r}}(0)} {w_{n,1}^{2}} \ge\beta > 0. $$
Up to a subsequence, \({w_{n,1}} \rightharpoonup{w_{1}}\) in \({H^{1}}({\mathbb{R}^{3}})\) with \({w_{1}} \ne0\) and \({{J'}_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({w_{1}}) = 0\). Moreover, \({u_{n,1}} \rightharpoonup0\) in \({H^{1}}({\mathbb{R}^{3}})\) implies that \(\{ y_{n}^{1}\} \) is unbounded.
Step 2: Set \({u_{n,2}}(x) = {u_{n}}(x) - u(x) - {w_{1}}(x - y_{n}^{1})\), we can similarly check that
$$\begin{aligned}& \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n,2}} \vert ^{2}} = \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} - \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} - \int _{{\mathbb{R}^{3}}} { \vert \nabla{w_{1}} \vert ^{2}} + o(1), \\& \int_{{\mathbb{R}^{3}}} {u_{n,2}^{2}} = \int_{{\mathbb{R}^{3}}} {u_{n}^{2}} - \int_{{\mathbb{R}^{3}}} {{u^{2}}} - \int_{{\mathbb{R}^{3}}} {w_{1}^{2}} + o(1), \\& \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,2}^{+} \bigr)}^{p}}} = \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n}^{+} \bigr)}^{p}}} - \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{p}}} - \int _{{\mathbb{R}^{3}}} {{{ \bigl(w_{1}^{+} \bigr)}^{p}}} + o(1), \\& \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n,2}^{+} \bigr)}^{6}}} = \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{n}^{+} \bigr)}^{6}}} - \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} - \int _{{\mathbb{R}^{3}}} {{{ \bigl(w_{1}^{+} \bigr)}^{6}}} + o(1), \\& {J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({u_{n,2}}) = {J_{\varepsilon,\mu}}({u_{n}}) - {J_{\varepsilon,\mu}}(u) - {J_{{\tau _{\infty}},{\kappa_{\infty}},\mu}}({w_{1}}) + o(1), \\& {{J'}_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({u_{n,2}}) \to0 \quad {\text{in }} { \bigl( {{H^{1}} \bigl({\mathbb{R}^{3}} \bigr)} \bigr)^{ - 1}}. \end{aligned}$$
Similar to Step 1, if (1) holds for \({u_{n,2}}\), then
$$\begin{aligned}& { \Vert {{u_{n,2}}} \Vert _{{H^{1}}({\mathbb{R}^{3}})}} = { \bigl\Vert {{u_{n}} - u - {w_{1}} \bigl(x - y_{n}^{1} \bigr)} \bigr\Vert _{{H^{1}}({\mathbb{R}^{3}})}} \to0\quad {\text{as }}n \to\infty, \\& c + \frac{b}{ 4}{A^{4}} + o(1) = {J_{\varepsilon,\mu}}({u_{n}}) = {J_{\varepsilon,\mu }}(u) + {J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({w_{1}}) + o(1) \end{aligned}$$
and
$$\begin{aligned} A^{2} + o(1) &= \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} = \int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{n,2}} \vert ^{2}} + \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \int_{{\mathbb{R}^{3}}} { \vert \nabla {w_{1}} \vert ^{2}} + o(1) \\ &= \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \int _{{\mathbb{R}^{3}}} { \vert \nabla{w_{1}} \vert ^{2}} + o(1), \end{aligned} $$
the lemma holds for \(k=1\).
If (2) holds for \({{u_{n,2}}}\), i.e.
\(\exists r',\beta' > 0\) and a sequence \(\{ y_{n}^{2}\} \subset{\mathbb{R}^{3}}\) such that
$$\int_{{B_{r'}}(y_{n}^{2})} {u_{n,2}^{2}} \ge \beta' > 0, $$
then
$$\int_{{B_{r'}}(y_{n}^{2} - y_{n}^{1})} {u_{n,2}^{2} \bigl(x + y_{n}^{1} \bigr)} \ge\beta' > 0. $$
\({u_{n,2}}(x + y_{n}^{1}) \rightharpoonup0\) in \({{H^{1}}({\mathbb{R}^{3}})}\) implies that \(\vert y_{n}^{2} - y_{n}^{1} \vert \to + \infty\).
Since \(\{ y_{n}^{1}\} \) is unbounded and \({w_{1}} \in{H^{1}}({\mathbb {R}^{3}})\), we can easily check that
$${w_{1}} \bigl(x - y_{n}^{1} \bigr) \rightharpoonup0\quad{\text{in }} {H^{1}} \bigl({\mathbb{R}^{3}} \bigr), $$
then
$${u_{n,2}}(x): = {u_{n}}(x) - u(x) - {w_{1}} \bigl(x - y_{n}^{1} \bigr) \rightharpoonup 0\quad{\text{in }} {H^{1}} \bigl({\mathbb{R}^{3}} \bigr) {\text{ as }}n \to \infty, $$
which implies that \(\{ y_{n}^{2}\} \) must be unbounded. Denote \({w_{n,2}}(x) = {u_{n,2}}(x + y_{n}^{2})\), then
$$\int_{{B_{r'}}(0)} {w_{n,2}^{2}} \ge \beta' > 0, $$
up to a subsequence, \({w_{n,2}} \rightharpoonup{w_{2}}\) in \({H^{1}}({\mathbb{R}^{3}})\) with \({w_{2}} \ne0\) and \({{J'}_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({w_{2}}) = 0\) and next proceed by iteration. Since \({w_{k}}\) is a nontrivial critical point of \({J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}\), \({J_{{\tau_{\infty}},{\kappa_{\infty}},\mu }}({w_{k}}) \ge{{c'}_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}\), where \({{c'}_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}\) is the mountain-pass value of the functional \({J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}\). Hence the iteration must stop at some finite index k. The proof is completed. □
Proof of Theorem 2.1(A)-\((a_{1})\)
We divide the proof into three steps.
Step 1: Since \({I_{\varepsilon,\mu}}\) possesses the geometry of Proposition 2.2 for \(\varepsilon > 0\) small with \(\mu \in[1 - {\delta_{0}},1]\), then by Proposition 2.2, for \(\varepsilon > 0\) small but fixed, for almost every \(\mu \in[1 - {\delta_{0}},1]\), there exists a bounded \({({\text{PS}})_{{c_{\varepsilon,\mu}}}}\) sequence \(\{ {u_{n}}\} \) for \({I_{\varepsilon,\mu}}\). Using the same argument as in the proof of Lemma 3.5 of [23], we can check that
$${c_{{\tau_{\infty}},{\kappa_{\infty}},\mu}} < \frac{1}{ 4}ab\frac{{{S^{3}}}}{ \mu} + \frac{1}{ {24}}{b^{3}}\frac{{{S^{6}}}}{ {{\mu^{2}}}} + \frac{1}{ {24}}{ \biggl( {{b^{2}}\frac{{{S^{4}}}}{ {{\mu^{4/3}}}} + 4a\frac{S}{ {{\mu^{1/3}}}}} \biggr)^{\frac{3}{2}}}, \quad \mu \in[1 - {\delta_{0}},1], $$
for \(\lambda > 0\) large. Combining with (3.7), we have
$${c_{\varepsilon,\mu}} < \frac{1}{ 4}ab\frac{{{S^{3}}}}{ \mu} + \frac{1}{ {24}}{b^{3}}\frac{{{S^{6}}}}{ {{\mu^{2}}}} + \frac{1}{ {24}}{ \biggl( {{b^{2}}\frac{{{S^{4}}}}{ {{\mu^{4/3}}}} + 4a\frac{S}{ {{\mu^{1/3}}}}} \biggr)^{\frac{3}{2}}}, \quad \mu \in[1 - {\delta_{0}},1], $$
for \(\lambda > 0\) large, \(\varepsilon > 0\) small.
In view of Lemma 3.4, there exist a \({u_{\varepsilon,\mu}} \in{H^{1}}({\mathbb{R}^{3}})\), a number \(k \in\mathbb{N} \cup\{ 0\} \), k functions \({w_{1}},\ldots,{w_{k}}\) of \({H^{1}}({\mathbb{R}^{3}})\) and k sequences of points \(\{y_{n}^{j}\} \subset{\mathbb{R}^{3}}\), \(1 \le j \le k\) and \({A_{\varepsilon,\mu}} \in\mathbb{R}\), such that
-
(i)
\({u_{n}} \rightharpoonup{u_{\varepsilon,\mu}}\) in \({H^{1}}({\mathbb{R}^{3}})\) with \({{J'}_{\varepsilon,\mu }}({u_{\varepsilon,\mu}}) = 0\) and \(\int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} \to A_{\varepsilon,\mu}^{2}\) as \(n \to\infty\);
-
(ii)
\(\vert y_{n}^{j} \vert \to + \infty\), \(\vert y_{n}^{i} - y_{n}^{j} \vert \to + \infty\) as \(n \to\infty\) if \(i \ne j\);
-
(iii)
\({w_{j}} \ne0\) and \({{J'}_{{\tau_{\infty}},{\kappa_{\infty,\mu }}}}({w_{j}}) = 0\);
-
(iv)
\({ \Vert {{u_{n}} - {u_{\varepsilon,\mu}} - {w_{j}}( \cdot - y_{n}^{j})} \Vert _{{H^{1}}({\mathbb{R}^{3}})}} \to0\) as \(n \to \infty\);
-
(v)
\({I_{\varepsilon,\mu}}({u_{n}}) + \frac{b}{ 4}A_{\varepsilon,\mu}^{4} = {J_{\varepsilon,\mu}}({u_{\varepsilon ,\mu}}) + \sum_{j = 1}^{k} {{J_{{\tau_{\infty}},{\kappa _{\infty,\mu}}}}({w_{j}})} + o(1)\);
-
(vi)
\(A_{\varepsilon,\mu}^{2} = \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{\varepsilon,\mu}} \vert ^{2}} + \sum_{j = 1}^{k} {\int_{{\mathbb{R}^{3}}} { \vert \nabla{w_{j}} \vert ^{2}} } \).
By (3.16), we have
$$ {J_{\varepsilon,\mu}}({u_{\varepsilon,\mu}}) \ge\frac{b}{ 4}A_{\varepsilon,\mu}^{2} \int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{\varepsilon,\mu}} \vert ^{2}} . $$
(3.25)
Applying Pohozaev’s identity to \({{J'}_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({w_{j}}) = 0\), we have
$${{\tilde{P}}_{\varepsilon,\mu}}({w_{j}}) = \frac{{a + bA_{\varepsilon ,\mu}^{2}}}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla{w_{j}} \vert ^{2}} + \frac{3}{ 2}{\tau_{\infty}} \int_{{\mathbb{R}^{3}}} {w_{j}^{2}} - \frac{3}{ p} \mu\lambda{\kappa_{\infty}} \int_{{\mathbb{R}^{3}}} {{{ \bigl(w_{j}^{+} \bigr)}^{p}}} - \frac{1}{ 2}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(w_{j}^{+} \bigr)}^{6}}} = 0, $$
then
$$\begin{aligned} 0 &= \bigl\langle {{{J'}_{{\tau_{\infty}},{\kappa_{\infty}},\mu }}({w_{j}}),{w_{j}}} \bigr\rangle + 2{{\tilde{P}}_{\varepsilon,\mu }}({w_{j}}) \\ &= 2 \bigl(a + bA_{\varepsilon,\mu}^{2} \bigr) \int_{{\mathbb{R}^{3}}} { \vert \nabla{w_{j}} \vert ^{2}} + 4{\tau_{\infty}} \int_{{\mathbb {R}^{3}}} {w_{j}^{2}} - \frac{{p + 6}}{ p} \mu\lambda{\kappa_{\infty}} \int_{{\mathbb{R}^{3}}} {{{ \bigl(w_{j}^{+} \bigr)}^{p}}} - 2\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(w_{j}^{+} \bigr)}^{6}}} \\ &\ge{G_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({w_{j}}). \end{aligned}$$
(3.26)
Hence, there exists \({t_{j}} \in(0,1]\) such that \({({w_{j}})_{{t_{j}}}}: = {t_{j}}{w_{j}}(t_{j}^{ - 2}x) \in{\mathcal{M}_{{\tau_{\infty}},{\kappa _{\infty}},\mu}}\), we get
$$\begin{aligned}& {J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({w_{j}}) - \frac{b}{ 4}A_{\varepsilon,\mu}^{2} \int_{{\mathbb{R}^{3}}} { \vert \nabla {w_{j}} \vert ^{2}} \\& \quad = {J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({w_{j}}) - \frac{b}{ 4}A_{\varepsilon,\mu}^{2} \int_{{\mathbb{R}^{3}}} { \vert \nabla {w_{j}} \vert ^{2}} - \frac{1}{ 8} \bigl( { \bigl\langle {{{J'}_{{\tau_{\infty}},{\kappa_{\infty}},\mu }}({w_{j}}),{w_{j}}} \bigr\rangle + 2{{\tilde{P}}_{\varepsilon,\mu }}({w_{j}})} \bigr) \\& \quad = \frac{a}{ 4} \int_{{\mathbb{R}^{3}}} { \vert \nabla{w_{j}} \vert ^{2}} + \frac{1}{ {12}}{\tau_{\infty}} \int_{{\mathbb{R}^{3}}} {w_{j}^{2}} + \frac{{p - 3}}{ {6p}} \mu\lambda{\kappa_{\infty}} \int_{{\mathbb{R}^{3}}} {{{ \bigl(w_{j}^{+} \bigr)}^{p}}} + \frac{1}{ {12}}\mu \int_{{\mathbb{R}^{3}}} {{{ \bigl(w_{j}^{+} \bigr)}^{6}}} \\& \quad \ge\frac{a}{ 4}t_{j}^{3} \int_{{\mathbb{R}^{3}}} { \vert \nabla{w_{j}} \vert ^{2}} + \frac{1}{ {12}}{\tau_{\infty}}t_{j}^{5} \int_{{\mathbb{R}^{3}}} {w_{j}^{2}} + \frac{{p - 3}}{ {6p}} \mu\lambda{\kappa_{\infty}}t_{j}^{p + 3} \int_{{\mathbb{R}^{3}}} {{{ \bigl(w_{j}^{+} \bigr)}^{p}}} + \frac{1}{ {12}}\mu t_{j}^{9} \int_{{\mathbb{R}^{3}}} {{{ \bigl(w_{j}^{+} \bigr)}^{6}}} \\& \quad = {I_{{\tau_{\infty}},{\kappa_{\infty}},\mu}} \bigl( {{{({w_{j}})}_{{t_{j}}}}} \bigr) - \frac{1}{ 6}{G_{{\tau_{\infty}},{\kappa_{\infty}},\mu}} \bigl( {{{({w_{j}})}_{{t_{j}}}}} \bigr) \ge{c_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}, \end{aligned}$$
(3.27)
and combining with (3.25), we have
$$\begin{aligned} {c_{\varepsilon,\mu}} + \frac{b}{ 4}A_{\varepsilon,\mu}^{4} &= {J_{\varepsilon,\mu}}({u_{\varepsilon ,\mu}}) + \sum_{j = 1}^{k} {{J_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}({w_{j}})} \\ &\ge\frac{b}{ 4}A_{\varepsilon,\mu}^{2} \int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{\varepsilon,\mu}} \vert ^{2}} + k{c_{{\tau_{\infty}},{\kappa_{\infty}},\mu}} + \frac{b}{ 4}A_{\varepsilon,\mu}^{2} \sum_{j = 1}^{k} { \int_{{\mathbb {R}^{3}}} { \vert \nabla{w_{j}} \vert ^{2}} } \\ &= \frac{b}{ 4}A_{\varepsilon,\mu}^{4} + k{c_{{\tau_{\infty}},{\kappa_{\infty}},\mu }}. \end{aligned} $$
If \(k \ge1\), we get \({c_{\varepsilon,\mu}} \ge{c_{{\tau_{\infty}},{\kappa_{\infty}},\mu}}\) for \(\varepsilon > 0\) small, which contradicts (3.7). Hence \(k = 0\), then \({u_{n}} \to {u_{\varepsilon,\mu}}\) in \({H^{1}}({\mathbb{R}^{3}})\) for \(\varepsilon > 0\) small and almost every \(\mu \in[1 - {\delta_{0}},1]\), i.e. for \(\varepsilon > 0\) small and almost every \(\mu \in[1 - {\delta_{0}},1]\), \({{I'}_{\varepsilon,\mu}}({u_{\varepsilon,\mu}}) = 0\) and \({I_{\varepsilon,\mu}}({u_{\varepsilon,\mu}}) = {c_{\varepsilon,\mu}}\).
Step 2: Fix \(\varepsilon > 0\) small, choose a sequence \(\{ {\mu_{n}}\} \subset[1 - {\delta_{0}},1]\) satisfying \({\mu_{n}} \to1\), we get a sequence of nontrivial critical points \(\{ {u_{\varepsilon,{\mu _{n}}}}\} \) of \({I_{\varepsilon,{\mu_{n}}}}\) with \({I_{\varepsilon,{\mu _{n}}}}({u_{\varepsilon,{\mu_{n}}}}) = {c_{\varepsilon,{\mu_{n}}}}\). We have the following equalities:
$$\textstyle\begin{cases} \frac{a}{2}\int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{\varepsilon,{\mu _{n}}}} \vert ^{2}} + \frac{1}{2}\int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u_{\varepsilon,{\mu _{n}}}^{2}} + \frac{b}{4}{ ( {\int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{\varepsilon,{\mu_{n}}}} \vert ^{2}} } )^{2}} \\ \quad{} - {\mu_{n}}\frac{\lambda}{p}\int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{(u_{\varepsilon,{\mu _{n}}}^{+} )}^{p}}} - {\mu_{n}}\frac{1}{6}\int_{{\mathbb{R}^{3}}} {{{(u_{\varepsilon,{\mu_{n}}}^{+} )}^{6}}} = {c_{\varepsilon,{\mu_{n}}}}, \\ a\int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{\varepsilon,{\mu _{n}}}} \vert ^{2}} + \int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u_{\varepsilon,{\mu_{n}}}^{2}} + b{ ( {\int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{\varepsilon,{\mu_{n}}}} \vert ^{2}} } )^{2}} \\ \quad{} - {\mu_{n}}\lambda\int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{(u_{\varepsilon,{\mu_{n}}}^{+} )}^{p}}} - {\mu_{n}}\int_{{\mathbb {R}^{3}}} {{{(u_{\varepsilon,{\mu_{n}}}^{+} )}^{6}}} = 0, \\ \frac{a}{2}\int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{\varepsilon,{\mu _{n}}}} \vert ^{2}} + \frac{3}{2}\int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u_{\varepsilon,{\mu _{n}}}^{2}} + \frac{1}{2}\int_{{\mathbb{R}^{3}}} {(DV(\varepsilon x),\varepsilon x)u_{\varepsilon,{\mu_{n}}}^{2}} \\ \quad {}+ \frac{b}{2}{ ( {\int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{\varepsilon,{\mu_{n}}}} \vert ^{2}} } )^{2}} - \frac{3}{p}{\mu_{n}}\lambda\int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{(u_{\varepsilon,{\mu_{n}}}^{+} )}^{p}}} \\ \quad{} - \frac{1}{p}{\mu_{n}}\lambda\int_{{\mathbb{R}^{3}}} {(DW(\varepsilon x),\varepsilon x){{(u_{\varepsilon,{\mu_{n}}}^{+} )}^{p}}} - \frac{1}{2}{\mu_{n}}\int_{{\mathbb{R}^{3}}} {{{(u_{\varepsilon,{\mu_{n}}}^{+} )}^{6}}} = 0.\end{cases} $$
The first one comes from the definition of \({c_{\varepsilon,{\mu _{n}}}}\). The second one follows by \(\langle{{I'}_{\varepsilon ,{\mu_{n}}}}({u_{\varepsilon,{\mu_{n}}}}), {u_{\varepsilon,{\mu_{n}}}} \rangle = 0\). The third one is the Pohozaev identity applying to \({{I'}_{\varepsilon,{\mu_{n}}}}({u_{\varepsilon,{\mu_{n}}}}) = 0\), then we get
$$\begin{aligned}& \frac{{q + 2}}{ {2(q + 6)}}a \int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{\varepsilon,{\mu_{n}}}} \vert ^{2}} + \frac{{q - 2}}{ {4(q + 6)}}b{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{\varepsilon,{\mu_{n}}}} \vert ^{2}} } \biggr)^{2}} + \frac{{6 - q}}{ {6(q + 6)}}{ \mu_{n}} \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{\varepsilon,{\mu _{n}}}^{+} \bigr)}^{6}}} \\& \quad\quad{} + \frac{{q - 2}}{ {2(q + 6)}} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u_{\varepsilon ,{\mu_{n}}}^{2}} - \frac{1}{ {(q + 6)}} \int_{{\mathbb{R}^{3}}} { \bigl(DV(\varepsilon x),\varepsilon x \bigr)u_{\varepsilon,{\mu_{n}}}^{2}} \\& \quad\quad{} + \frac{1}{ p}\frac{{p - q}}{ {q + 6}}{\mu_{n}}\lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl(u_{\varepsilon,{\mu_{n}}}^{+} \bigr)}^{p}}} + \frac{1}{ p}\frac{2}{ {q + 6}}{\mu_{n}} \lambda \int_{{\mathbb{R}^{3}}} { \bigl(DW(\varepsilon x),\varepsilon x \bigr){{ \bigl(u_{\varepsilon,{\mu_{n}}}^{+} \bigr)}^{p}}} \\& \quad = {c_{\varepsilon,{\mu_{n}}}} \le{c_{\varepsilon,1 - {\delta_{0}}}} \end{aligned}$$
(3.28)
and
$$\begin{aligned} & \biggl( {\frac{1}{ 2} - \frac{1}{ p}} \biggr)a \int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{\varepsilon,{\mu_{n}}}} \vert ^{2}} + \biggl( {\frac{1}{ 2} - \frac{1}{ p}} \biggr) \int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u_{\varepsilon ,{\mu_{n}}}^{2}} + \biggl( {\frac{1}{ 4} - \frac{1}{ p}} \biggr)b{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{\varepsilon,{\mu_{n}}}} \vert ^{2}} } \biggr)^{2}} \\ &\quad{} + \biggl( {\frac{1}{ p} - \frac{1}{ 6}} \biggr){\mu_{n}} \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{\varepsilon,{\mu _{n}}}^{+} \bigr)}^{6}}} = {c_{\varepsilon,{\mu_{n}}}} \le{c_{\varepsilon,1 - {\delta_{0}}}}. \end{aligned}$$
(3.29)
By (3.28) and \((P_{3})\), \(\int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{\varepsilon,{\mu_{n}}}} \vert ^{2}} \) must be bounded, then by (3.29), \(a\int_{{\mathbb{R}^{3}}} { \vert \nabla {u_{\varepsilon,{\mu_{n}}}} \vert ^{2}} + \int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u_{\varepsilon,{\mu_{n}}}^{2}} \) is bounded, i.e.
\(\{ {u_{\varepsilon,{\mu_{n}}}}\} \) is bounded in \({H^{1}}({\mathbb{R}^{3}})\). Hence, we get
$$\begin{gathered} \lim_{n \to\infty} {I_{\varepsilon ,1}}({u_{\varepsilon,{\mu_{n}}}}) \\ \quad = \lim_{n \to\infty} \biggl( {{I_{\varepsilon ,{\mu_{n}}}}({u_{\varepsilon,{\mu_{n}}}}) + \frac{1}{ p}({\mu_{n}} - 1)\lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl(u_{\varepsilon,{\mu_{n}}}^{+} \bigr)}^{p}}} + \frac{1}{ 6}({\mu_{n}} - 1) \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{\varepsilon,{\mu_{n}}}^{+} \bigr)}^{6}}} } \biggr) \\ \quad = \lim_{n \to\infty} {c_{\varepsilon,{\mu_{n}}}} = {c_{\varepsilon,1}} \end{gathered} $$
and
$$\begin{aligned}& \bigl\vert { \bigl\langle {{{I'}_{\varepsilon,1}}({u_{\varepsilon ,{\mu_{n}}}}), \varphi} \bigr\rangle } \bigr\vert \\& \quad = \biggl\vert { \bigl\langle {{{I'}_{\varepsilon,{\mu _{n}}}}({u_{\varepsilon,{\mu_{n}}}}), \varphi} \bigr\rangle + \frac{1}{ p}({\mu_{n}} - 1)\lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl(u_{\varepsilon,{\mu_{n}}}^{+} \bigr)}^{p - 1}}\varphi} + \frac{1}{ 6}({\mu_{n}} - 1) \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{\varepsilon,{\mu_{n}}}^{+} \bigr)}^{5}} \varphi} } \biggr\vert \\& \quad \le C(1 - {\mu_{n}})\lambda{ \biggl( { \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{\varepsilon,{\mu_{n}}}^{+} \bigr)}^{p}}} } \biggr)^{\frac{{p - 1}}{p}}} { \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \varphi \vert ^{p}} } \biggr)^{\frac{1}{p}}} \\& \quad\quad{} + (1 - {\mu_{n}}){ \biggl( { \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{\varepsilon,{\mu_{n}}}^{+} \bigr)}^{6}}} } \biggr)^{\frac{5}{6}}} { \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \varphi \vert ^{6}} } \biggr)^{\frac{1}{6}}} \\& \quad = o(1){ \Vert \varphi \Vert _{{H^{1}}({\mathbb{R}^{3}})}}, \quad \forall\varphi \in{H^{1}} \bigl({\mathbb{R}^{3}} \bigr), \end{aligned}$$
i.e.
\(\{ {u_{\varepsilon,{\mu_{n}}}}\} \) is, in fact, a bounded \({({\text{PS}})_{{c_{\varepsilon,1}}}}\) sequence for \({I_{\varepsilon}} = {I_{\varepsilon,1}}\). Using the same argument in Step 1 with \(\mu = 1\), we can easily check that \(\exists {u_{\varepsilon,1}} \in{H^{1}}({\mathbb{R}^{3}})\) such that \({u_{\varepsilon,{\mu_{n}}}} \to{u_{\varepsilon,1}}\) in \({H^{1}}({\mathbb{R}^{3}})\) and \({{I'}_{\varepsilon}}({u_{\varepsilon,1}}) = 0\), \({I_{\varepsilon}}({u_{\varepsilon,1}}) = {c_{\varepsilon,1}}\).
Step 3: Next, we prove the existence of a ground-state solution for (3.2). Set
$${m_{\varepsilon}}: = \inf \bigl\{ {I_{\varepsilon}}(u)| {{{I'}_{\varepsilon}}(u) = 0} , u \in{H^{1}} \bigl({ \mathbb{R}^{3}} \bigr)\backslash\{ 0\} \bigr\} . $$
By (3.28) and \((P_{3})\), we see that \(0 \le{m_{\varepsilon}} \le {I_{\varepsilon}}({u_{\varepsilon,1}}) = {c_{\varepsilon,1}} < + \infty\). Let \(\{ {u_{n}}\} \) be a sequence of nontrivial critical points of \({I_{\varepsilon}}\) such that \({I_{\varepsilon}}({u_{n}}) \to {m_{\varepsilon}}\). By the same argument as in Step 2, we see that \(\{ {u_{n}}\} \) is a bounded \({({\text{PS}})_{{m_{\varepsilon}}}}\) sequence of \({I_{\varepsilon}}\). Similar to the argument in Step 1, we see that \(\exists{w_{\varepsilon}} \in{H^{1}}({\mathbb {R}^{3}})\) such that
$$ {u_{n}} \to{w_{\varepsilon}} \quad{\text{in }} {H^{1}} \bigl({\mathbb{R}^{3}} \bigr). $$
(3.30)
Next, we will show that \({m_{\varepsilon}} > 0\). Since
$$\begin{aligned} 0 &= \bigl\langle {{{I'}_{\varepsilon}}({u_{n}}),{u_{n}}} \bigr\rangle \\ &= a \int_{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} + \int_{{\mathbb{R}^{3}}} {V(\varepsilon x)u_{n}^{2}} + b{ \biggl( { \int _{{\mathbb{R}^{3}}} { \vert \nabla{u_{n}} \vert ^{2}} } \biggr)^{2}} - \lambda \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl(u_{n}^{+} \bigr)}^{p}}} - \int_{{\mathbb{R}^{3}}} {{{ \bigl(u_{\varepsilon,{\mu_{n}}}^{+} \bigr)}^{6}}} \\ &\ge C \Vert {{u_{n}}} \Vert _{{H^{1}}({\mathbb{R}^{3}})}^{2} - C \lambda \Vert {{u_{n}}} \Vert _{{H^{1}}({\mathbb{R}^{3}})}^{p} - C \Vert {{u_{n}}} \Vert _{{H^{1}}({\mathbb{R}^{3}})}^{6}, \end{aligned} $$
which implies that \({ \Vert {{u_{n}}} \Vert _{{H^{1}}({\mathbb {R}^{3}})}} \ge{C^{*} } > 0\), then by (3.30), \({ \Vert {{w_{\varepsilon}}} \Vert _{{H^{1}}({\mathbb{R}^{3}})}} \ge{C^{*} } > 0\), i.e.
\({w_{\varepsilon}} \ne0\). Similar to (3.28), we deduce that \({m_{\varepsilon}} > 0\). Hence \({I_{\varepsilon}}({w_{\varepsilon}}) = {m_{\varepsilon}} > 0\), \({{I'}_{\varepsilon}}({w_{\varepsilon}}) = 0\). By the standard elliptic estimate and the strong maximum principle, we see that \({w_{\varepsilon}} > 0\). Set \({u_{\varepsilon}}(x) = {w_{\varepsilon}}( x/ {\varepsilon} )\), \({u_{\varepsilon}}\) is in fact a positive ground-state solution of (1.1). □
Next, we will prove the concentration result of Theorem 2.1 by using a similar method related to Proposition 2.2 in [1].
Proof of Theorem 2.1(A)-\((a_{2})\)
For any \({\varepsilon_{j}} \to0\), similar to (3.28), (3.29), we can easily check that \({w_{{\varepsilon_{j}}}}\) is bounded in \({H^{1}}({\mathbb{R}^{3}})\).
By the vanishing theorem, we have \(\exists\{ y_{{\varepsilon_{j}}}^{1}\} \subset{\mathbb{R}^{3}}\), \(R,\beta > 0\) such that
$$\int_{{B_{R}}(y_{{\varepsilon_{j}}}^{1})} {w_{{\varepsilon_{j}}}^{2}} \ge \beta > 0. $$
Set \({v_{{\varepsilon_{j}}}}(x) = {w_{{\varepsilon_{j}}}}(x + y_{{\varepsilon_{j}}}^{1})\), then \({v_{{\varepsilon_{j}}}}\) satisfies
$$ - \biggl( {a + b \int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla {v_{{\varepsilon_{j}}}}} \vert }^{2}}} } \biggr)\Delta {v_{{\varepsilon_{j}}}} + V \bigl({ \varepsilon_{j}}x + {\varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr){v_{{\varepsilon_{j}}}} = \lambda W \bigl({\varepsilon_{j}}x + { \varepsilon_{j}}y_{{\varepsilon _{j}}}^{1} \bigr)v_{{\varepsilon_{j}}}^{p - 1} + v_{{\varepsilon_{j}}}^{5}, $$
(3.31)
and, up to a subsequence, \(\exists{v_{1}} \in{H^{1}}({\mathbb {R}^{3}})\backslash\{ 0\} \), such that
$$ \textstyle\begin{cases} {v_{{\varepsilon_{j}}}} \rightharpoonup{v_{1}}\quad{\text{in }}{H^{1}}({\mathbb{R}^{3}}), \\ {v_{{\varepsilon_{j}}}} \to{v_{1}}\quad{\text{in }}L_{\mathrm{loc}}^{s}({\mathbb{R}^{3}}), 1 \le s < 6, \\ {v_{{\varepsilon_{j}}}} \to{v_{1}}\quad {\text{a.e.}}\end{cases} $$
(3.32)
Denote \({A^{2}}: = \lim_{j \to\infty} \int _{{\mathbb{R}^{3}}} {{{ \vert {\nabla{v_{{\varepsilon_{j}}}}} \vert }^{2}}} \), and it is trivial that
$$\int_{{\mathbb{R}^{3}}} {{{ \vert {\nabla{v_{1}}} \vert }^{2}}} \le{A^{2}}. $$
Since V and W are bounded with \(\tau > 0\) and \(\inf_{{\mathbb{R}^{3}}} W > 0\), then, up to a subsequence, as \(j \to\infty\),
$$V \bigl({\varepsilon_{j}}y_{{\varepsilon_{j}}}^{1} \bigr) \to V \bigl({x^{1}} \bigr) > 0,\quad\quad W \bigl({\varepsilon_{j}}y_{{\varepsilon_{j}}}^{1} \bigr) \to W \bigl({x^{1}} \bigr) > 0, $$
where
$${\varepsilon_{j}}y_{{\varepsilon_{j}}}^{1} \to{x^{1}} \quad {\text{as }}j \to \infty \ \bigl({x^{1}} {\text{ might be }} \infty \bigr). $$
In view of the uniformly continuous of V and W in \({\mathbb {R}^{3}}\), we can easily check that
$$V \bigl({\varepsilon_{j}}x + {\varepsilon_{j}}y_{{\varepsilon_{j}}}^{1} \bigr) \to V \bigl({x^{1}} \bigr) > 0,\quad\quad W \bigl({\varepsilon_{j}}x + {\varepsilon_{j}}y_{{\varepsilon _{j}}}^{1} \bigr) \to W \bigl({x^{1}} \bigr) > 0\quad {\text{as }}j \to\infty $$
uniformly on any compact set. Consequently, we have
$$\bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} {\nabla{v_{1}} \cdot\nabla\varphi } + V \bigl({x^{1}} \bigr) \int_{{\mathbb{R}^{3}}} {{v_{1}}\varphi} = \lambda W \bigl({x^{1}} \bigr) \int_{{\mathbb{R}^{3}}} {v_{1}^{p - 1}\varphi} + \int_{{\mathbb {R}^{3}}} {v_{1}^{5}\varphi} , \quad \forall \varphi \in C_{c}^{\infty}\bigl({\mathbb{R}^{3}} \bigr), $$
then \({{v_{1}}}\) solves
$$ - \bigl(a + b{A^{2}} \bigr)\Delta u + V \bigl({x^{1}} \bigr)u = \lambda W \bigl({x^{1}} \bigr){u^{p - 1}} + {u^{5}} $$
(3.33)
with the energy functional \({J_{V({x^{1}}),W({x^{1}})}}\), where the functional is defined as
$$ \begin{aligned}[b] &{J_{{a_{0}},{b_{0}}}}(u) = \frac{{a + b{A^{2}}}}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{{{a_{0}}}}{ 2} \int_{{\mathbb{R}^{3}}} {{u^{2}}} - \frac{{{b_{0}}}}{ p}\lambda \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{p}}} - \frac{1}{ 6} \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} , \\ &\quad u \in{H^{1}} \bigl({\mathbb{R}^{3}} \bigr), \end{aligned} $$
(3.34)
\({a_{0}},{b_{0}}\) are positive constants.
Set
$$\begin{gathered} {J_{\varepsilon}}(u): = \frac{{a + b{A^{2}}}}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla u \vert ^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V(\varepsilon x){u^{2}}} - \frac{\lambda}{ p} \int_{{\mathbb{R}^{3}}} {W(\varepsilon x){{ \bigl({u^{+} } \bigr)}^{p}}} - \frac{1}{ 6} \int_{{\mathbb{R}^{3}}} {{{ \bigl({u^{+} } \bigr)}^{6}}} , \\ \quad u \in{H^{1}} \bigl({\mathbb{R}^{3}} \bigr). \end{gathered} $$
Similar to (3.8), (3.9), we have
$${J_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}}}}) = {I_{{\varepsilon _{j}}}}({w_{{\varepsilon_{j}}}}) + \frac{b}{ 4}{A^{4}} + o(1) $$
and
$${{J'}_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}}}}) \to0\quad{\text{in }} { \bigl( {{H^{1}} \bigl({\mathbb{R}^{3}} \bigr)} \bigr)^{ - 1}} {\text{ as }}j \to \infty. $$
Now, we consider \({w_{{\varepsilon_{j}},1}}(x) = {w_{{\varepsilon _{j}}}}(x) - {v_{1}}(x - y_{{\varepsilon_{j}}}^{1}){\chi_{{\varepsilon _{j}}}}(x - y_{{\varepsilon_{j}}}^{1})\), where \({\chi_{\varepsilon}}(x) = \chi ( {\sqrt{\varepsilon}x} )\) for \(\varepsilon > 0\) small and \(\chi(x)\) is a smooth cut-off function with \(0 \le\chi(x) \le1\), \(\chi(x) = 1\) on \({B_{1}}(0)\), \(\chi(x) = 0\) on \({\mathbb {R}^{3}}\backslash{B_{2}}(0)\) and \(\vert \nabla\chi \vert \le C\) for some constant \(C > 0\). It is easy to verify that \({w_{{\varepsilon_{j}},1}}(x)\) is bounded in \({{H^{1}}({\mathbb{R}^{3}})}\). Furthermore, for any \(\varphi \in{H^{1}}({\mathbb{R}^{3}})\) with \({ \Vert \varphi \Vert _{{H^{1}}({\mathbb{R}^{3}})}} \le1\), we have
$$\begin{aligned} \bigl\langle {{{J'}_{{\varepsilon_{j}}}}({w_{{\varepsilon _{j}},1}}), \varphi} \bigr\rangle &= \bigl\langle {{{J'}_{{\varepsilon _{j}}}}({w_{{\varepsilon_{j}}}}), \varphi} \bigr\rangle - \bigl\langle {{{J'}_{{\varepsilon_{j}}}} \bigl({v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){\chi _{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr) \bigr), \varphi} \bigr\rangle \\ &\quad{} + \lambda \int_{{\mathbb{R}^{3}}} {W({\varepsilon_{j}}x) \bigl( {w_{{\varepsilon_{j}}}^{p - 1}\varphi - {{ \bigl(w_{{\varepsilon_{j}},1}^{+} \bigr)}^{p - 1}}\varphi - {{ \bigl( {{v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){\chi _{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr)} \bigr)}^{p - 1}}\varphi} \bigr)} \\ &\quad{} + \int_{{\mathbb{R}^{3}}} { \bigl( {w_{{\varepsilon_{j}}}^{5}\varphi - {{ \bigl(w_{{\varepsilon_{j}},1}^{+} \bigr)}^{5}}\varphi - {{ \bigl( {{v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){ \chi_{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr)} \bigr)}^{5}}\varphi} \bigr)} \\ &= o(1) + (I) + (\mathit{II}) + (\mathit{III}). \end{aligned}$$
(3.35)
First, we see
$$\begin{aligned} (I) &= - \bigl\langle {{{J'}_{{\varepsilon_{j}}}} \bigl({v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){ \chi_{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr) \bigr), \varphi} \bigr\rangle \\ &= - \bigl\langle {{{J'}_{{\varepsilon_{j}}}} \bigl({v_{1}} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr){\chi_{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr) \bigr),\varphi } \bigr\rangle + \bigl\langle {{{J'}_{V({x^{1}}),W({x^{1}})}}({v_{1}}),{ \chi_{{\varepsilon_{j}}}} \varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} \bigr\rangle \\ &= - \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} {\nabla({v_{1}} {\chi _{{\varepsilon_{j}}}}) \cdot\nabla\varphi \bigl(x + y_{{\varepsilon _{j}}}^{1} \bigr)} + \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} {\nabla{v_{1}} \cdot \nabla \bigl({ \chi_{{\varepsilon_{j}}}}\varphi \bigl(x + y_{{\varepsilon _{j}}}^{1} \bigr) \bigr)} \\ &\quad{} - \int_{{\mathbb{R}^{3}}} {V \bigl({\varepsilon_{j}}x + {\varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr){v_{1}} { \chi_{{\varepsilon_{j}}}}\varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} + \int_{{\mathbb{R}^{3}}} {V \bigl({x^{1}} \bigr){v_{1}} { \chi _{{\varepsilon_{j}}}}\varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} \\ &\quad {}+ \lambda \int_{{\mathbb{R}^{3}}} {W \bigl({\varepsilon_{j}}x + {\varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr){{({v_{1}} { \chi_{{\varepsilon_{j}}}})}^{p - 1}}\varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} - \lambda \int_{{\mathbb {R}^{3}}} {W \bigl({x^{1}} \bigr)v_{1}^{p - 1}{ \chi_{{\varepsilon_{j}}}}\varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} \\ &\quad{} + \int_{{\mathbb{R}^{3}}} {{{({v_{1}} {\chi_{{\varepsilon _{j}}}})}^{5}} \varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} - \int_{{\mathbb {R}^{3}}} {v_{1}^{5}{\chi_{{\varepsilon_{j}}}} \varphi \bigl(x + y_{{\varepsilon _{j}}}^{1} \bigr)} = o(1), \end{aligned}$$
(3.36)
where we have used (3.33).
Next, we study \((\mathit{II})\),
$$ \begin{aligned}[b] (\mathit{II}) &= \lambda \int_{{\mathbb{R}^{3}}} {W({\varepsilon_{j}}x) \bigl( {w_{{\varepsilon_{j}}}^{p - 1}\varphi - {{ \bigl(w_{{\varepsilon_{j}},1}^{+} \bigr)}^{p - 1}}\varphi - {{ \bigl( {{v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){\chi _{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr)} \bigr)}^{p - 1}}\varphi} \bigr)} \\ &= \lambda \int_{{\mathbb{R}^{3}}} {W \bigl({\varepsilon_{j}}x + {\varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr) \bigl( {v_{{\varepsilon_{j}}}^{p - 1} - {{ \bigl(w_{{\varepsilon_{j}},1}^{+} \bigr)}^{p - 1}} \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr) - {{({v_{1}} { \chi_{{\varepsilon_{j}}}})}^{p - 1}}} \bigr)} \varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr). \end{aligned} $$
(3.37)
For any given \(\delta > 0\) small, we can choose a bounded domain \(\Lambda \subset{\mathbb{R}^{3}}\) such that
$$\int_{{\mathbb{R}^{3}}\backslash\Lambda} { \vert \nabla {v_{1}} \vert ^{2} + v_{1}^{2} + v_{1}^{p} + v_{1}^{6}} \le\delta. $$
Hence,
$$\begin{aligned}& \biggl\vert { \int_{{\mathbb{R}^{3}}\backslash\Lambda} {W \bigl({\varepsilon_{j}}x + { \varepsilon_{j}}y_{{\varepsilon _{j}}}^{1} \bigr){{ \bigl({v_{1}}(x){\chi_{{\varepsilon_{j}}}}(x) \bigr)}^{p - 1}}} \varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} \biggr\vert \\& \quad \le C \int_{{\mathbb{R}^{3}}\backslash\Lambda} {v_{1}^{p - 1}(x) \bigl\vert \varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr) \bigr\vert } \\& \quad \le C{ \biggl( { \int_{{\mathbb{R}^{3}}\backslash\Lambda} {v_{1}^{p}} } \biggr)^{\frac{{p - 1}}{p}}} { \biggl( { \int_{{\mathbb{R}^{3}}\backslash\Lambda} { \bigl\vert \varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr) \bigr\vert ^{p}} } \biggr)^{\frac{1}{p}}} \\& \quad \le C \Vert \varphi \Vert _{{H^{1}}({\mathbb {R}^{3}})}{\delta^{\frac{{p - 1}}{p}}} \le C{ \delta^{\frac{{p - 1}}{p}}} \end{aligned}$$
(3.38)
and
$$\begin{aligned}& \biggl\vert { \int_{{\mathbb{R}^{3}}\backslash\Lambda} {W \bigl({\varepsilon_{j}}x + { \varepsilon_{j}}y_{{\varepsilon_{j}}}^{1} \bigr) \bigl( {v_{{\varepsilon_{j}}}^{p - 1}(x) - {{ \bigl(w_{{\varepsilon_{j}},1}^{+} \bigr)}^{p - 1}} \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} \bigr) \varphi \bigl(x + y_{{\varepsilon _{j}}}^{1} \bigr)}} \biggr\vert \\& \quad = \biggl\vert { \int_{{\mathbb{R}^{3}}\backslash\Lambda} {W \bigl({\varepsilon_{j}}x + { \varepsilon_{j}}y_{{\varepsilon_{j}}}^{1} \bigr) \bigl( {v_{{\varepsilon_{j}}}^{p - 1}(x) - {{ \bigl( {{v_{{\varepsilon_{j}}}}(x) - {v_{1}}(x){\chi_{{\varepsilon_{j}}}}(x)} \bigr)}^{ + (p - 1)}}} \bigr) \varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} } \biggr\vert \\& \quad \le C \int_{{\mathbb{R}^{3}}\backslash\Lambda} {{v_{1}} \bigl(v_{1}^{p - 2} + v_{{\varepsilon_{j}}}^{p - 2} \bigr) \bigl\vert \varphi \bigl(x + y_{{\varepsilon _{j}}}^{1} \bigr) \bigr\vert } \\& \quad \le C{ \biggl( { \int_{{\mathbb{R}^{3}}\backslash\Lambda} {v_{1}^{p}} } \biggr)^{\frac{{p - 1}}{p}}} { \biggl( { \int_{{\mathbb{R}^{3}}\backslash\Lambda} { \bigl\vert \varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr) \bigr\vert ^{p}} } \biggr)^{\frac{1}{p}}} \\& \quad\quad{} + C{ \biggl( { \int_{{\mathbb{R}^{3}}\backslash\Lambda} {v_{1}^{p}} } \biggr)^{\frac{1}{p}}} { \biggl( { \int_{{\mathbb{R}^{3}}\backslash\Lambda} {v_{{\varepsilon_{j}}}^{p}} } \biggr)^{\frac{{p - 2}}{p}}} { \biggl( { \int_{{\mathbb{R}^{3}}\backslash\Lambda} { \bigl\vert \varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr) \bigr\vert ^{p}} } \biggr)^{\frac{1}{p}}} \\& \quad \le C{ \Vert \varphi \Vert _{{H^{1}}({\mathbb {R}^{3}})}} { \biggl( { \int_{{\mathbb{R}^{3}}\backslash\Lambda} {v_{1}^{p}} } \biggr)^{\frac{{p - 1}}{p}}} + C{ \Vert \varphi \Vert _{{H^{1}}({\mathbb {R}^{3}})}} { \biggl( { \int_{{\mathbb{R}^{3}}\backslash\Lambda} {v_{1}^{p}} } \biggr)^{\frac{1}{p}}} \\& \quad \le C \bigl( {{\delta^{\frac{{p - 1}}{p}}} + {\delta^{\frac{1}{p}}}} \bigr). \end{aligned}$$
(3.39)
In view of (3.32), \({v_{{\varepsilon_{j}}}} \to{v_{1}} {\text{ in }}{L^{p}}(\Lambda)\). Since \(\Lambda \subset{B_{1/\sqrt{{\varepsilon _{j}}} }}(0)\) for \({{\varepsilon_{j}}}\) small, we have
$$\begin{aligned}& \biggl\vert { \int_{\Lambda}{W \bigl({\varepsilon_{j}}x + { \varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr) \bigl( {v_{{\varepsilon_{j}}}^{p - 1} - {{ \bigl(w_{{\varepsilon_{j}},1}^{+} \bigr)}^{p - 1}} \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr) - {{({v_{1}} { \chi_{{\varepsilon_{j}}}})}^{p - 1}}} \bigr)\varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} } \biggr\vert \\& \quad = \biggl\vert { \int_{\Lambda}{W \bigl({\varepsilon_{j}}x + { \varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr) \bigl( {v_{{\varepsilon_{j}}}^{p - 1} - {{({v_{{\varepsilon_{j}}}} - {v_{1}})}^{ + (p - 1)}} - v_{1}^{p - 1}} \bigr)\varphi \bigl(x + y_{{\varepsilon_{j}}}^{1} \bigr)} } \biggr\vert \\& \quad \le C{ \biggl( { \int_{\Lambda}{ \vert {v_{{\varepsilon_{j}}}} - {v_{1}} \vert ^{p}} } \biggr)^{\frac{{p - 1}}{p}}} { \biggl( { \int_{\Lambda}{ \bigl\vert \varphi \bigl(x + y_{{\varepsilon _{j}}}^{1} \bigr) \bigr\vert ^{p}} } \biggr)^{\frac{1}{p}}} \\& \quad\quad{} + C{ \biggl( { \int_{\Lambda}{ \bigl\vert v_{{\varepsilon_{j}}}^{p - 1} - v_{1}^{p - 1} \bigr\vert ^{{\frac{p}{{p - 1}}}}} } \biggr)^{\frac{{p - 1}}{p}}} { \biggl( { \int_{\Lambda}{ \bigl\vert \varphi \bigl(x + y_{{\varepsilon _{j}}}^{1} \bigr) \bigr\vert ^{p}} } \biggr)^{\frac{1}{p}}} \\& \quad \le C{ \Vert \varphi \Vert _{{H^{1}}({\mathbb {R}^{3}})}} { \biggl( { \int_{\Lambda}{ \vert {v_{{\varepsilon_{j}}}} - {v_{1}} \vert ^{p}} } \biggr)^{\frac{{p - 1}}{p}}} + C{ \Vert \varphi \Vert _{{H^{1}}({\mathbb {R}^{3}})}} { \biggl( { \int_{\Lambda}{ \bigl\vert v_{{\varepsilon_{j}}}^{p - 1} - v_{1}^{p - 1} \bigr\vert ^{{\frac{p}{{p - 1}}}}} } \biggr)^{\frac{{p - 1}}{p}}} \\& \quad = o(1). \end{aligned}$$
(3.40)
Therefore, (3.37)-(3.40) lead to \((\mathit{II}) = o(1)\). Before studying \((\mathit{III})\), we first claim that
$$ {v_{{\varepsilon_{j}}}} \to{v_{1}} \quad{\text{in }} L_{\mathrm{loc}}^{6} \bigl({\mathbb{R}^{3}} \bigr). $$
(3.41)
Indeed, in view of (3.32), we may assume that
$$\vert \nabla{v_{{\varepsilon_{j}}}} \vert ^{2} \rightharpoonup \vert \nabla{v_{1}} \vert ^{2} + \mu\quad {\text{and}}\quad v_{{\varepsilon_{j}}}^{6} \rightharpoonup v_{1}^{6} + \nu, $$
where μ and ν are two bounded nonnegative measures on \({\mathbb{R}^{3}}\). By the concentration compactness principle II (Lemma 1.1 of [26]), we obtain an at most countable index set Γ, sequence \(\{ {x_{i}}\} \subset{\mathbb{R}^{3}}\) and \(\{ {{\mu_{i}}} \},\{ {{\nu_{i}}} \} \subset( {0,\infty} )\) such that
$$ \mu \ge\sum_{i \in\Gamma} {{ \mu_{i}}} { \delta _{{x_{i}}}},\quad\quad \nu= \sum _{i \in\Gamma} {{ \nu_{i}}} {\delta _{{x_{i}}}} \quad { \text{and}}\quad S{( {{ \nu_{i}}} )^{\frac{1}{3}}} \le{\mu _{i}}. $$
(3.42)
It suffices to show that, for any bounded domain Ω, \({\{ {x_{i}}\} _{i \in\Gamma}} \cap\Omega = \emptyset\). Suppose, by contradiction, that \({x_{i}} \in\Omega\) for some \(i \in\Gamma\). Define, for \(\rho > 0\), the function \({\psi_{\rho}}( x ): = \psi( {\frac{{x - {x_{i}}}}{ \rho}} )\) where ψ is a smooth cut-off function such that \(\psi = 1\) on \({B_{1}}( 0 )\), \(\psi = 0\) on \({\mathbb{R}^{3}}\backslash {B_{2}}(0)\), \(0 \le\psi \le1\) and \(\vert {\nabla\psi} \vert \le C\). We suppose that ρ is chosen in such a way that the support of \({\psi_{\rho}}\) is contained in Ω. By (3.31), we see
$$ \begin{aligned}[b] & a \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{{\varepsilon _{j}}}} \vert ^{2}{\psi_{\rho}}} + a \int_{{\mathbb{R}^{3}}} {(\nabla{v_{{\varepsilon_{j}}}} \cdot\nabla{ \psi_{\rho}}){v_{{\varepsilon_{j}}}}} + \int_{{\mathbb{R}^{3}}} {V \bigl({\varepsilon _{j}}x + { \varepsilon_{j}}y_{{\varepsilon_{j}}}^{1} \bigr)v_{{\varepsilon _{j}}}^{2}{ \psi_{\rho}}} \\ &\quad\quad{} + b \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{{\varepsilon _{j}}}} \vert ^{2}} \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{{\varepsilon_{j}}}} \vert ^{2}{\psi_{\rho}}} } \biggr) + b \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{{\varepsilon _{j}}}} \vert ^{2}} \int_{{\mathbb{R}^{3}}} {(\nabla {v_{{\varepsilon_{j}}}} \cdot\nabla{ \psi_{\rho}}){v_{{\varepsilon _{j}}}}} \\ &\quad = \lambda \int_{{\mathbb{R}^{3}}} {W \bigl({\varepsilon_{j}}x + {\varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr)v_{{\varepsilon_{j}}}^{p}{ \psi_{\rho}}} + \int _{{\mathbb{R}^{3}}} {v_{{\varepsilon_{j}}}^{6}{ \psi_{\rho}}} . \end{aligned} $$
(3.43)
Since
$$\begin{aligned}& \mathop{\overline{\lim} } _{j \to\infty} \biggl\vert { \int _{{\mathbb{R}^{3}}} {(\nabla{v_{{\varepsilon_{j}}}} \cdot\nabla{\psi _{\rho}}){v_{{\varepsilon_{j}}}} } } \biggr\vert \le\mathop{\overline { \lim} } _{j \to\infty} { \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{{\varepsilon_{j}}}} \vert ^{2}} } \biggr)^{\frac{1}{2}}} \cdot{ \biggl( { \int_{{\mathbb{R}^{3}}} {v_{{\varepsilon _{j}}}^{2} \vert \nabla{ \psi_{\rho}} \vert ^{2}} } \biggr)^{\frac{1}{2}}} \\& \hphantom{ \mathop{\overline{\lim} } _{j \to\infty} \biggl\vert { \int _{{\mathbb{R}^{3}}} {(\nabla{v_{{\varepsilon_{j}}}} \cdot\nabla{\psi _{\rho}}){v_{{\varepsilon_{j}}}} } } \biggr\vert }\le C{ \biggl( { \int_{{\mathbb{R}^{3}}} {v_{1}^{2} \vert \nabla{\psi _{\rho}} \vert ^{2}} } \biggr)^{\frac{1}{2}}} \le C{ \biggl( { \int_{{B_{2\rho}}({x_{i}})} {v_{1}^{6}} } \biggr)^{\frac{1}{6}}} { \biggl( { \int_{{B_{2\rho}}({x_{i}})} { \vert \nabla{\psi _{\rho}} \vert ^{3}} } \biggr)^{\frac{1}{3}}} \\& \hphantom{ \mathop{\overline{\lim} } _{j \to\infty} \biggl\vert { \int _{{\mathbb{R}^{3}}} {(\nabla{v_{{\varepsilon_{j}}}} \cdot\nabla{\psi _{\rho}}){v_{{\varepsilon_{j}}}} } } \biggr\vert }\le C{ \biggl( { \int_{{B_{2\rho}}({x_{i}})} {v_{1}^{6}} } \biggr)^{\frac{1}{6}}} \to0\quad {\text{as }}\rho \to0, \end{aligned}$$
(3.44)
$$\begin{aligned}& \mathop{\overline{\lim} } _{j \to\infty} a \int_{{\mathbb {R}^{3}}} { \vert \nabla{v_{{\varepsilon_{j}}}} \vert ^{2}{\psi_{\rho}}} \ge a \int_{{\mathbb{R}^{3}}} { \vert \nabla {v_{1}} \vert ^{2}{\psi_{\rho}}} + a{\mu_{i}} \to a{ \mu_{i}} \quad {\text{as }}\rho \to0, \end{aligned}$$
(3.45)
$$\begin{aligned}& \begin{aligned}[b] & \mathop{\overline{\lim} } _{j \to\infty} b \int_{{\mathbb {R}^{3}}} { \vert \nabla{v_{{\varepsilon_{j}}}} \vert ^{2}} \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{{\varepsilon _{j}}}} \vert ^{2}{\psi_{\rho}}} } \biggr) \\ &\quad{} \ge\mathop{\overline{\lim} } _{j \to\infty} b{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{{\varepsilon _{j}}}} \vert ^{2}{\psi_{\rho}}} } \biggr)^{2}} \\ &\quad{} \ge b{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{1}} \vert ^{2}{\psi_{\rho}}} + {\mu_{i}}} \biggr)^{2}} \to b\mu_{i}^{2}\quad {\text{as }}\rho \to0, \end{aligned} \end{aligned}$$
(3.46)
$$\begin{aligned}& \begin{aligned}[b] & \mathop{\overline{\lim} } _{j \to\infty} \lambda \int _{{\mathbb{R}^{3}}} {W \bigl({\varepsilon_{j}}x + { \varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr)v_{{\varepsilon_{j}}}^{p}{ \psi_{\rho}}} \\ &\quad = \lambda \int_{{\mathbb{R}^{3}}} {W \bigl({x^{1}} \bigr)v_{1}^{p}{ \psi_{\rho}}} \to 0\quad {\text{as }}\rho \to0, \end{aligned} \end{aligned}$$
(3.47)
and
$$ \mathop{\overline{\lim} } _{j \to\infty} \int_{{\mathbb {R}^{3}}} {v_{{\varepsilon_{j}}}^{6}{ \psi_{\rho}}} = \int_{{\mathbb{R}^{3}}} {v_{1}^{p}{\psi_{\rho}}} + {\nu_{i}} \to{\nu_{i}} \quad {\text{as }}\rho \to0, $$
(3.48)
we obtain from (3.43)
$$a{\mu_{i}} + b\mu_{i}^{2} \le{ \nu_{i}}. $$
Combining with (3.42), we have
$${( {{\nu_{i}}} )^{1/3}} \ge\frac{{b{S^{2}} + \sqrt{{b^{2}}{S^{4}} + 4aS} }}{ {2}}. $$
On the other hand,
$$\begin{aligned} {m_{{\varepsilon_{j}}}} & = {I_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}}}}) - \frac{1}{ {q + 6}} \bigl[ { \bigl\langle {{{I'}_{{\varepsilon _{j}}}}({w_{{\varepsilon_{j}}}}),{w_{{\varepsilon_{j}}}}} \bigr\rangle + 2{P_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}}}})} \bigr] \\ &= \frac{{q + 2}}{ {2(q + 6)}}a \int_{{\mathbb{R}^{3}}} { \vert \nabla {w_{{\varepsilon_{j}}}} \vert ^{2}} + \frac{{q - 2}}{ {4(q + 6)}}b{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla {w_{{\varepsilon_{j}}}} \vert ^{2}} } \biggr)^{2}} + \frac{{6 - q}}{ {6(q + 6)}} \int_{{\mathbb{R}^{3}}} {w_{{\varepsilon_{j}}}^{6}} \\ &\quad{} + \frac{1}{ {2(q + 6)}} \biggl[ { \int_{{\mathbb{R}^{3}}} { \bigl((q - 2)V({\varepsilon _{j}}x) - 2 \bigl(\nabla V({\varepsilon_{j}}x),{\varepsilon _{j}}x \bigr) \bigr)w_{{\varepsilon_{j}}}^{2}} } \biggr] \\ &\quad{} + \frac{\lambda}{ {p(q + 6)}} \biggl[ { \int_{{\mathbb{R}^{3}}} { \bigl((p - q)W({\varepsilon _{j}}x) + 2 \bigl(\nabla W({\varepsilon_{j}}x),{\varepsilon _{j}}x \bigr) \bigr)w_{{\varepsilon_{j}}}^{p}} } \biggr] \\ & \ge\frac{{q + 2}}{ {2(q + 6)}}a \int_{{\mathbb{R}^{3}}} { \vert \nabla {w_{{\varepsilon_{j}}}} \vert ^{2}} + \frac{{q - 2}}{ {4(q + 6)}}b{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla {w_{{\varepsilon_{j}}}} \vert ^{2}} } \biggr)^{2}} + \frac{{6 - q}}{ {6(q + 6)}} \int_{{\mathbb{R}^{3}}} {w_{{\varepsilon_{j}}}^{6}} \\ &= \frac{{q + 2}}{ {2(q + 6)}}a \int_{{\mathbb{R}^{3}}} { \vert \nabla {v_{{\varepsilon_{j}}}} \vert ^{2}} + \frac{{q - 2}}{ {4(q + 6)}}b{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla {v_{{\varepsilon_{j}}}} \vert ^{2}} } \biggr)^{2}} + \frac{{6 - q}}{ {6(q + 6)}} \int_{{\mathbb{R}^{3}}} {v_{{\varepsilon_{j}}}^{6}} \\ &\ge\frac{{q + 2}}{ {2(q + 6)}}a{\mu_{i}} + \frac{{q - 2}}{ {4(q + 6)}}b \mu_{i}^{2} + \frac{{6 - q}}{ {6(q + 6)}}{\nu_{i}} + o(1), \end{aligned}$$
(3.49)
where we have used \((P_{3})\) and notice that
$$\begin{aligned} {P_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}}}})&: = \frac{a}{ 2} \int_{{\mathbb{R}^{3}}} { \vert \nabla{w_{{\varepsilon _{j}}}} \vert ^{2}} + \frac{3}{ 2} \int_{{\mathbb{R}^{3}}} {V({\varepsilon_{j}}x)w_{{\varepsilon_{j}}}^{2}} + \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} { \bigl(DV({\varepsilon_{j}}x),{ \varepsilon _{j}}x \bigr)w_{{\varepsilon_{j}}}^{2}} \\ &\quad{} + \frac{b}{ 2}{ \biggl( { \int_{{\mathbb{R}^{3}}} { \vert \nabla {w_{{\varepsilon_{j}}}} \vert ^{2}} } \biggr)^{2}} - \frac{3}{ p}\lambda \int_{{\mathbb{R}^{3}}} {W({\varepsilon_{j}}x)w_{{\varepsilon _{j}}}^{p}} \\ &\quad{} - \frac{1}{ p}\lambda \int_{{\mathbb{R}^{3}}} { \bigl(DW({\varepsilon_{j}}x),{ \varepsilon _{j}}x \bigr)w_{{\varepsilon_{j}}}^{p}} - \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {w_{{\varepsilon_{j}}}^{6}} \\ & = 0 \end{aligned}$$
is the Pohozaev identity applying to \({{I'}_{{\varepsilon _{j}}}}({w_{{\varepsilon_{j}}}}) = 0\).
Since \({m_{{\varepsilon_{j}}}} \le{c_{{\varepsilon_{j}},1}} \le {c_{V({x_{0}}),W({x_{0}}),1}} + o(1) < \frac{1}{ 4}ab{S^{3}} + \frac{1}{ {24}}{b^{3}}{S^{6}} + \frac{1}{ {24}}{ ( {{b^{2}}{S^{4}} + 4aS} )^{\frac{3}{2}}}\) for any \({x_{0}} \in{\mathbb{R}^{3}}\) and \({\varepsilon_{j}} > 0\) small, then, up to a subsequence, we may assume that, as \(j \to\infty\),
$${m_{{\varepsilon_{j}}}} \to\overline{c} < \frac{1}{ 4}ab{S^{3}} + \frac{1}{ {24}}{b^{3}} {S^{6}} + \frac{1}{ {24}}{ \bigl( {{b^{2}} {S^{4}} + 4aS} \bigr)^{\frac{3}{2}}}. $$
By (3.49),
$$\begin{aligned} \bar{c} &\ge\frac{{q + 2}}{ {2(q + 6)}}a{\mu_{i}} + \frac{{q - 2}}{ {4(q + 6)}}b\mu_{i}^{2} + \frac{{6 - q}}{ {6(q + 6)}}{ \nu_{i}} \\ &\ge\frac{{q + 2}}{ {2(q + 6)}}aS{({\nu_{i}})^{1/3}} + \frac{{q - 2}}{ {4(q + 6)}}b{S^{2}} {({\nu_{i}})^{2/3}} + \frac{{6 - q}}{ {6(q + 6)}}{\nu_{i}} \\ &\ge\frac{{q + 2}}{ {2(q + 6)}}aS\frac{{b{S^{2}} + \sqrt{{b^{2}}{S^{4}} + 4aS} }}{ 2} + \frac{{q - 2}}{ {4(q + 6)}}b{S^{2}} { \biggl( {\frac{{b{S^{2}} + \sqrt{{b^{2}}{S^{4}} + 4aS} }}{ 2}} \biggr)^{2}} \\ &\quad{} + \frac{{6 - q}}{ {6(q + 6)}}{ \biggl( {\frac{{b{S^{2}} + \sqrt{{b^{2}}{S^{4}} + 4aS} }}{ 2}} \biggr)^{3}} \\ &= \frac{1}{ 4}ab{S^{3}} + \frac{1}{ {24}}{b^{3}} {S^{6}} + \frac{1}{ {24}}{ \bigl( {{b^{2}} {S^{4}} + 4aS} \bigr)^{\frac{3}{2}}}. \end{aligned}$$
This leads to a contradiction, hence (3.41) holds.
Similar to the proof of \((\mathit{II})\), we can easily check that \((\mathit{III}) = o(1)\). By (3.35), we have
$${{J'}_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}},1}}) \to0\quad{\text{in }} { \bigl( {{H^{1}} \bigl({\mathbb{R}^{3}} \bigr)} \bigr)^{ - 1}} {\text{ as }}j \to \infty. $$
We also claim that
$$ {J_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}},1}}) \to\overline{c} + \frac{b}{ 4}{A^{4}} - {J_{V({x^{1}}),W({x^{1}})}}({v_{1}})\quad { \text{as }}j \to\infty. $$
(3.50)
Indeed,
$$\begin{aligned}& {J_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}},1}}) = {J_{{\varepsilon _{j}}}}({w_{{\varepsilon_{j}}}}) - {J_{{\varepsilon_{j}}}} \bigl({v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){ \chi_{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr) \bigr) \\ & \hphantom{{J_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}},1}})}\quad{} - \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} {\nabla \bigl({v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){\chi_{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr) \bigr) \cdot\nabla{w_{{\varepsilon_{j}},1}}} \\ & \hphantom{{J_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}},1}})}\quad{} - \int_{{\mathbb{R}^{3}}} {V({\varepsilon_{j}}x){v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){\chi_{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr){w_{{\varepsilon_{j}},1}}(x)} \\ & \hphantom{{J_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}},1}})}\quad{} + \frac{\lambda}{ p} \int_{{\mathbb{R}^{3}}} {W({\varepsilon_{j}}x) \bigl( {w_{{\varepsilon_{j}}}^{p} - {{ \bigl(w_{{\varepsilon_{j}},1}^{+} \bigr)}^{p}} - v_{1}^{p} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr)\chi_{{\varepsilon_{j}}}^{p} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr)} \bigr)} \\ & \hphantom{{J_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}},1}})}\quad{} + \frac{1}{ 6} \int_{{\mathbb{R}^{3}}} { \bigl( {w_{{\varepsilon_{j}}}^{6} - {{ \bigl(w_{{\varepsilon_{j}},1}^{+} \bigr)}^{6}} - v_{1}^{6} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr)\chi_{{\varepsilon_{j}}}^{6} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr)} \bigr)} \\ & \hphantom{{J_{{\varepsilon_{j}}}}({w_{{\varepsilon_{j}},1}})}= \overline{c} + \frac{b}{ 4}{A^{4}} + o(1) + (\mathit{IV}) + (V) + (\mathit{VI}) + (\mathit{VII}) + (\mathit{VIII}), \\ & (\mathit{IV}) = - {J_{{\varepsilon_{j}}}} \bigl({v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){\chi _{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr) \bigr) \\ & \hphantom{(\mathit{IV})} = - \frac{{a + b{A^{2}}}}{ 2} \int_{{\mathbb{R}^{3}}} { \bigl\vert \nabla({v_{1}} {\chi _{{\varepsilon_{j}}}}) \bigr\vert ^{2}} - \frac{1}{ 2} \int_{{\mathbb{R}^{3}}} {V \bigl({\varepsilon_{j}}x + {\varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr){{({v_{1}} { \chi_{{\varepsilon_{j}}}})}^{2}}} \\& \hphantom{(\mathit{IV})} \quad{} + \frac{\lambda}{ p} \int_{{\mathbb{R}^{3}}} {W \bigl({\varepsilon_{j}}x + {\varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr){{({v_{1}} { \chi_{{\varepsilon_{j}}}})}^{p}}} + \frac{1}{ 6} \int_{{\mathbb{R}^{3}}} {{{({v_{1}} {\chi_{{\varepsilon_{j}}}})}^{6}}} \\& \hphantom{(\mathit{IV})} = - {J_{V({x^{1}}),W({x^{1}})}}({v_{1}}) + o(1), \\& (V) = - \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} {\nabla \bigl({v_{1}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr){\chi_{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr) \bigr) \cdot\nabla{w_{{\varepsilon_{j}},1}}} \\& \hphantom{(V)}= - \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} {\nabla({v_{1}} {\chi _{{\varepsilon_{j}}}}) \cdot\nabla({v_{{\varepsilon_{j}}}} - {v_{1}} {\chi _{{\varepsilon_{j}}}})} \\& \hphantom{(V)}= \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} { \bigl\vert \nabla({v_{1}} {\chi _{{\varepsilon_{j}}}}) \bigr\vert ^{2}} - \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb {R}^{3}}} {\nabla({v_{1}} {\chi_{{\varepsilon_{j}}}}) \nabla {v_{{\varepsilon_{j}}}}} \\& \hphantom{(V)}= \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{1}} \vert ^{2}\chi_{{\varepsilon_{j}}}^{2}} - \bigl(a + b{A^{2}} \bigr) \int_{{\mathbb {R}^{3}}} {\nabla{v_{1}}\nabla{v_{{\varepsilon_{j}}}} { \chi_{{\varepsilon _{j}}}}} + o(1) = o(1), \end{aligned}$$
where we have used (3.32).
Similar to \((V)\), \((\mathit{II})\), \((\mathit{III})\), we can easily check that \((\mathit{VI})=o(1)\), \((\mathit{VII})=o(1)\) and \((\mathit{VIII})=o(1)\), then (3.50) holds.
Next, we repeat the above procedure for \({w_{{\varepsilon_{j}},1}}\) and so on. It is easy to see that \({J_{V({x^{i}}),W({x^{i}})}}({v_{i}})\) obtained in this process is always larger than the mountain-pass value of \({J_{\tau,\kappa}}\), therefore, the process will stop at finite k. Similar to the proof of Lemma 3.4, we see that, for \({\varepsilon_{j}} \to0\), there is a sequence of j, a nonnegative integer k and k sequences \(\{ y_{{\varepsilon_{j}}}^{i}\} \), \(1 \le i \le k\), such that, as \(j \to\infty\),
$$\begin{aligned}& { \Biggl\Vert {{w_{{\varepsilon_{j}}}}(x) - \sum _{i = 1}^{k} {{v_{i}} \bigl(x - y_{{\varepsilon_{j}}}^{i} \bigr){ \chi_{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon_{j}}}^{i} \bigr)} } \Biggr\Vert _{{H^{1}}({\mathbb{R}^{3}})}} \to0, \end{aligned}$$
(3.51)
$$\begin{aligned}& \bar{c} + \frac{b}{ 4}{A^{4}} = \sum _{i = 1}^{k} {J_{V({x^{i}}),W({x^{i}})}}({v_{i}})\quad { \text{and}}\quad {A^{2}} = \sum_{i = 1}^{k} { \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{i}} \vert ^{2}} } , \end{aligned}$$
(3.52)
where \({{v_{i}}}\) is a nontrivial critical point of \({{J_{V({x^{i}}),W({x^{i}})}}}\).
Using the same argument as in (3.27), we get
$${J_{V({x^{i}}),W({x^{i}})}}({v_{i}}) \ge{c_{V({x^{i}}),W({x^{i}}),1}} + \frac{b}{ 4}{A^{2}} \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{i}} \vert ^{2}} , $$
then in view of (3.52), we have
$$\begin{aligned} \overline{c} + \frac{b}{ 4}{A^{4}} &= \sum_{i = 1}^{k} {{J_{V({x^{i}}),W({x^{i}})}}({v_{i}})} \\ &\ge\sum_{i = 1}^{k} {{c_{V({x^{i}}),W({x^{i}}),1}}} + \frac{b}{ 4}{A^{2}}\sum_{i = 1}^{k} { \int_{{\mathbb{R}^{3}}} { \vert \nabla{v_{i}} \vert ^{2}} } \\ &= \sum_{i = 1}^{k} {{c_{V({x^{i}}),W({x^{i}}),1}}} + \frac{b}{ 4}{A^{4}}, \end{aligned} $$
i.e.
$$\overline{c} \ge\sum_{i = 1}^{k} {{c_{V({x^{i}}),W({x^{i}}),1}}} . $$
In view of Lemma 3.3 and (3.7), \(\overline{c} \le {c_{V({x^{1}}),W({x^{1}}),1}}\), then we conclude that \(k=1\), i.e.
$$\overline{c} = {c_{V({x^{1}}),W({x^{1}}),1}}. $$
By (3.51), we have
$${ \bigl\Vert {{w_{{\varepsilon_{j}}}}(x) - {v_{1}} \bigl(x - y_{{\varepsilon _{j}}}^{1} \bigr){\chi_{{\varepsilon_{j}}}} \bigl(x - y_{{\varepsilon_{j}}}^{1} \bigr)} \bigr\Vert _{{H^{1}}({\mathbb{R}^{3}})}} \to0, $$
then by the Sobolev inequality, we get
$${ \Vert {{v_{{\varepsilon_{j}}}} - {v_{1}}} \Vert _{{L^{6}}({\mathbb{R}^{3}})}} \le{ \Vert {{v_{{\varepsilon_{j}}}} - {v_{1}} {\chi_{{\varepsilon_{j}}}}} \Vert _{{L^{6}}({\mathbb {R}^{3}})}} + { \Vert {{v_{1}} {\chi_{{\varepsilon_{j}}}} - {v_{1}}} \Vert _{{L^{6}}({\mathbb{R}^{3}})}} \to0\quad {\text{as }}j \to\infty. $$
Hence, \(v_{{\varepsilon_{j}}}^{6}\) is uniformly integrable near ∞, the Brezis-Kato type argument and the maximum principle yield
$$ \lim_{ \vert x \vert \to\infty} {v_{{\varepsilon_{j}}}}(x) = 0 \quad {\text{uniformly for }}j. $$
(3.53)
Next, we assume that \((P_{2})\)-(i) holds.
We claim that \(\{ {\varepsilon_{j}}y_{{\varepsilon_{j}}}^{1}\} \) is bounded. Assuming to the contrary that \(\vert {\varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \vert \to\infty\), then \(V({x^{1}}) = {\tau_{\infty}} > \tau\) and \(W({x^{1}}) = {\kappa_{\infty}} \le W({x_{v}})\), hence \({c_{V({x^{1}}),W({x^{1}}),1}} = {c_{{\tau_{\infty}},{\kappa_{\infty}},1}} > {c_{\tau,W({x_{v}}),1}}\). But, from Lemma 3.3, we have
$$ {c_{V({x^{1}}),W({x^{1}}),1}} = \overline{c} = \lim_{j \to\infty} {m_{{\varepsilon_{j}}}} \le\lim_{j \to \infty} {c_{{\varepsilon_{j}},1}} \le{c_{V({x_{v}}),W({x_{v}}),1}} = {c_{\tau,W({x_{v}}),1}}, $$
(3.54)
a contradiction.
We will show that \({x^{1}} \in{\mathcal{A}_{v}}\). In fact, if \({x^{1}} \in \mathcal{V}\), by (3.54), we have
$${c_{\tau,W({x^{1}}),1}} \le{c_{V({x^{1}}),W({x^{1}}),1}} \le{c_{\tau,W({x_{v}}),1}}, $$
which implies that \(W({x^{1}}) \ge W({x_{v}})\). By the definition of \(W({x_{v}})\), \(W({x^{1}}) \le\max_{x \in\mathcal{V}} W(x) = W({x_{v}})\), then \(W({x^{1}}) = W({x_{v}})\).
If \({x^{1}} \notin\mathcal{V}\), then \(V({x^{1}}) > \tau\). Assuming to the contrary that \(W({x^{1}}) \le W({x_{v}})\), then \({c_{V({x^{1}}),W({x^{1}}),1}} > {c_{\tau,W({x_{v}}),1}}\), which contradicts (3.54).
Let \({P_{{\varepsilon_{j}}}}\) a maximum point of \({v_{{\varepsilon _{j}}}}\), since \(\Delta{v_{{\varepsilon_{j}}}}({P_{{\varepsilon_{j}}}}) \le0\), (3.31) implies that
$$V \bigl({\varepsilon_{j}} {P_{{\varepsilon_{j}}}} + {\varepsilon _{j}}y_{{\varepsilon_{j}}}^{1} \bigr){v_{{\varepsilon_{j}}}}({P_{{\varepsilon _{j}}}}) \le\lambda W \bigl({\varepsilon_{j}} {P_{{\varepsilon_{j}}}} + { \varepsilon_{j}}y_{{\varepsilon_{j}}}^{1} \bigr)v_{{\varepsilon_{j}}}^{p - 1}({P_{{\varepsilon_{j}}}}) + v_{{\varepsilon_{j}}}^{5}({P_{{\varepsilon_{j}}}}) $$
which gives \({v_{{\varepsilon_{j}}}}({P_{{\varepsilon_{j}}}}) \ge C > 0\). By (3.53), \({P_{{\varepsilon_{j}}}}\) must be bounded. Denote \({x_{{\varepsilon_{j}}}} = {\varepsilon_{j}}{P_{{\varepsilon_{j}}}} + {\varepsilon_{j}}y_{{\varepsilon_{j}}}^{1}\), it is clear that \({x_{{\varepsilon_{j}}}}\) is a maximum point of \({u_{{\varepsilon _{j}}}}\), then \({x_{{\varepsilon_{j}}}} \to{\mathcal{A}_{v}}\). Since \(\{ {{\varepsilon_{j}}}\}\) is arbitrary, Theorem 2.1(A)-\((a_{2})\) is proved. □
To complete the proof of Theorem 2.1(A), we only need to prove the exponential decay result. Since the proof is standard (see [20], for example), we omit the details for simplicity. Note that all the conclusions of Theorem 2.1(B) can be similarly proved to Theorem 2.1(A). Thus, this completes the proof of Theorem 2.1.