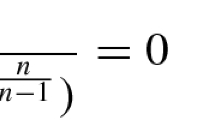1 Introduction

Consider the class of degenerate singular quasilinear elliptic equations in \(\mathbb {R}^{N}\)

$$ -\operatorname{div} \bigl[A(x,\nabla u) \nabla u \bigr] = g(x,u) \quad \forall x\in \mathbb {R}^{N}, $$
(1)

where A is a nonnegative unbounded function that vanishes at some points of \(\mathbb {R}^{N}\). More specifically, we consider variants of this class of equations of the type

$$ -\operatorname{div} \biggl[\frac{ \vert \nabla u \vert ^{p-2}\nabla u}{ \vert x \vert ^{ap}} \biggr]+ \lambda \frac{ \vert u \vert ^{p-2} u}{ \vert x \vert ^{(a+1)p}} = \alpha\frac{ \vert u \vert ^{q-2} u }{ \vert x \vert ^{bq}}+ \beta K(x) \frac{ \vert u \vert ^{r-2}u}{ \vert x \vert ^{dr}} + f(x), $$
(2)

where \(x\in \mathbb {R}^{N}\), \(1< p \leq N-1\), \(q=q(a,b):=\frac{Np}{N-p(a+1-b)}\), \(\alpha, \beta\) and λ are parameters, \(0< a<\frac{N-p}{p}\), \(a\leq b\leq a+1\), \(d,r\in \mathbb {R}\), \(K\in L^{\frac{q}{q-r}}_{r(d-b)} (\mathbb {R}^{N})\) and f is a function that belongs to the dual space of

$$L^{a}_{b}\bigl(\mathbb {R}^{N}\bigr) = \biggl\{ u: \mathbb {R}^{N} \rightarrow \mathbb {R}; \int_{\mathbb {R}^{N}} \vert x \vert ^{-bq} \vert u \vert ^{q} < \infty \biggr\} . $$

Equations of this type arise in existence problems of stationary anisotropic solutions for the Schrödinger equation [2], in theory of non-Newtonian fluids [3], in problems of flow through porous media [4], in study of pseudoplastic fluids [5], in dynamic models for galaxies with cylindrical symmetry [6], and several other models. Variants of problem (2) in the radial setting were initially treated by Clément, de Figueiredo and Mitidieri [7] who proved, for example, the Brézis and Nirenberg [8] result for this radial operator. In recent years, several researchers have studied variants of problem (2) in the radial setting; see references [9–12].

Schindler [13] studied variants of this class of equations on unbounded cylinders. Under certain conditions on the function f, he showed that the problem

$$ \textstyle\begin{cases} -\Delta_{p} u + \vert u \vert ^{p-2} u = f(u) & \mbox{in } \Omega,\\ u=0 & \mbox{on } \partial\Omega, \end{cases} $$
(3)

has a weak solution in \(W_{0}^{1,p}(\Omega)\), where Ω is an unbounded cylindrical domain, \(\Omega\subset \mathbb {R}^{N}\), \(N\geq3\) and \(2\leq p< N\). The lack of compactness of the Sobolev embedding makes standard variational techniques more delicate. To solve this lack of compactness, the author introduces a modified concentration-compactness principle for which a version of the mountain pass lemma [14] may be applied.

Afterwards, Hashimoto, Ishiwata and Ôtani [15] studied the following problem involving the p-Laplacian operator:

$$ \textstyle\begin{cases} -\Delta_{p} u = \vert u \vert ^{q-2} u & \mbox{in } \Omega,\\ u = 0 & \mbox{on } \partial\Omega, \end{cases} $$
(4)

in infinite tube-shaped domains \(\Omega :=\Omega_{d} \times \mathbb {R}^{N-d}\), where \(\Omega_{d}\) are d-dimensional annulus domains with \(N\geq3\). Using the concentration-compactness principle at infinity for partially symmetric functions and the variational method due to Ishiwata and Ôtani [16], they proved the existence of at least one positive solution u to problem (4) belonging to \(W_{0}^{1,p}(\Omega)\cap L^{\infty}(\Omega)\), for \(2\leq d\leq N-1\) and \(p< q< p_{d}^{\dagger}\), where

$$p_{d}^{\dagger} :=\textstyle\begin{cases} \frac{(N-d+1)p}{N-d+1-p}, & \mbox{for } p< N-d+1; \\ \infty, & \mbox{for } p\geq N-d+1. \end{cases} $$

More recently, Clapp and Szulkin [17] studied the supercritical case for the following problem involving the Laplacian operator:

$$ \textstyle\begin{cases} -\Delta u = \vert u \vert ^{p-2}u & \mbox{in } \Omega, \\ u = 0 & \mbox{on } \partial\Omega, \end{cases} $$
(5)

in an unbounded cylindrical domain

$$\Omega :=\bigl\{ x=(y,z) \in \mathbb {R}^{m+1}\times \mathbb {R}^{N-m-1} ; 0< a< \vert y \vert < b < \infty \bigr\} , $$

where \(1\leq m < N-2\). The authors showed that if \(2< p<2_{N,m}^{*}:=\frac{2(N-m)}{(N-m)-2}\), then problem (5) has infinite invariant solutions and one of these solutions is positive. Note that \(2_{N,m}^{*}\) is the critical Sobolev exponent in dimension \(N-m\), which is greater than the usual critical Sobolev exponent \(2^{*}=\frac{2N}{N-2}\). This existence result has been proved using the index theory (see [18], Theorem II.5.7), and the argument used to prove the positivity of the solution was the maximum principle.

Motivated by the recent results in [17], in this work we study the effect of the topology of the domain on existence and multiplicity results in the supercritical case of the following problem:

$$ \textstyle\begin{cases} -\operatorname{div} (\frac{ \vert \nabla u \vert ^{p-2} \nabla u}{ \vert y \vert ^{ap}} ) = \frac { \vert u \vert ^{q-2} u}{ \vert y \vert ^{bq}} + f(x) & \mbox{in } \Omega, \\ u = 0 & \mbox{on } \partial\Omega, \end{cases} $$
(6)

in an unbounded cylindrical domain

$$\Omega :=\bigl\{ (y,z)\in \mathbb {R}^{m+1}\times \mathbb {R}^{N-m-1} ; 0< A< \vert y \vert < B < \infty \bigr\} , $$

where \(p>1\), \(1\leq m< N-p\), \(q=q(a,b):=\frac{Np}{N-p (a+1-b)}\), \(a- \frac{m}{N-m} < b < a+1\), \(a < \frac{ (m+1)-p}{p}\) and \(A,B\in \mathbb {R}_{+}\).

In this present work, as the domain is unbounded, the lack of compactness of the Sobolev embedding \(W_{0}^{1,p}(\Omega)\hookrightarrow L^{q}(\Omega)\) (\(p\leq q < p^{*}:=\frac{pN}{N-p} \)) makes standard variational techniques more delicate.

Generally speaking, some geometrical and topological properties of the domain can help us to show existence results for elliptic problems; for example, the symmetry of the domain can be used to improve the Sobolev embedding. However, since we consider unbounded domains, the lack of compactness of the Sobolev embedding does not follow immediately from the standard variational techniques. This is one of the main difficulties we have to deal with in this work.

First we consider problem (6) in the case where \(f\equiv0\), and we get the following existence result. Note that in its statement, \(p_{N,m}^{*}\) is the critical Sobolev exponent in dimension \(N-m\), which is greater than the usual critical Sobolev exponent \(p^{*}=\frac{pN}{N-p}\).

Theorem 1

If \(1\leq m < N-p\), \(f\equiv0\) and \(p< q< p^{*}_{N,m}\), then problem (6) has at least one invariant solution.

A natural question is to check what happens to the previous problem under the presence of certain perturbations. For this purpose, we shall consider the perturbed problem by a function f belonging to the dual space of \(W_{0}^{1,p}(\Omega)\), denoted by \(W_{0}^{-1,p}(\Omega)\), and we get the following existence and multiplicity result.

Theorem 2

If \(1\leq m < N-p\) and \(p< q< p^{*}_{N,m}\), then there is a constant \(\overline{\varepsilon} >0\) such that for any \(f\in W_{0}^{-1,p}(\Omega)\) with \(0< \Vert f \Vert _{-1} < \overline{\varepsilon}\), problem (6) has at least two invariant solutions.

To prove these results, we study an auxiliary problem and show that its solutions are axially symmetric and belong to the space \(W_{0}^{1,p}(S)\subset W_{0}^{1,p}(\Omega)\), where \(S:=(A,B)\times \mathbb {R}^{N-m-1}\). As usual, this is done by defining an energy functional \(I \colon W_{0}^{1,p}(S) \to \mathbb {R}\) and by showing the existence of critical points for I in the space \(W_{0}^{1,p}(S)\). These critical points are the weak solutions of the auxiliary problem and, by our setting, they also solve problem (6).

Since S is an unbounded domain, the difficulty to prove Theorems 1 and 2 lies in the fact that \(W_{0}^{1,p}(S)\) cannot be compactly embedded into \(L^{q}(S)\) for any \(q\in(p, p_{N,m}^{*})\). In order to solve the lack of compactness, we construct a subspace of invariant functions \(W_{0,G}^{1,p}(S)\subset W_{0}^{1,p}(S)\) with compact embedding \(W_{0,G}^{1,p}(S)\hookrightarrow L^{q}(S)\) for \(q\in (p,p_{N,m}^{*})\) (see [19, 20]).

Using the principle of symmetric criticality [21], we can look for critical points of I restricted on \(W_{0,G}^{1,p}(S)\). In this way we obtain a weak solution in \(W_{0,G}^{1,p}(S)\) for our problem using the mountain pass theorem of Ambrosetti and Rabinowitz [22]. Finally, to show the existence of a second solution, we use Ekeland’s variational principle [23].

Since \(q\in(p,p_{N,m}^{*})\) and \(p_{N,m}^{*}>p^{*}\), in problem (6) we consider not only the subcritical and critical cases but also the supercritical one.

Note that the p-Laplacian operator \(\Delta_{p} u= \operatorname{div} ( \vert \nabla u \vert ^{p-2} \nabla u )\) is a special case of the operator \(\operatorname{div} (\frac{ \vert \nabla u \vert ^{p-2} \nabla u}{ \vert y \vert ^{ap}} )\); therefore, Theorems 1 and 2 improve the results of Hashimoto, Ishiwata and Ôtani [15].

This work is organized as follows. In Section 2 we introduce some notation and state some well-known results, such as the principle of symmetric criticality and the mountain pass theorem. In Section 3 we introduce the auxiliary problem, whose solutions are also solutions to problem (6). To ensure the existence of solutions to the auxiliary problem, we use the results of the previous section as well as Ekeland’s variational principle.

2 Preliminaries

In this section, we give some results which are used in the proofs of our main theorems. First, we denote by \(O(N)\) the group of linear isometries of \(\mathbb {R}^{N}\). Recall that if G is a closed subgroup of \(O(N)\), then an open subset Ω of \(\mathbb {R}^{N}\) is G-invariant if \(g\Omega=\Omega\) for every \(g\in G\). Furthermore, a function \(u: \Omega\rightarrow \mathbb {R}\) is called G-invariant if \(u(gx)=u(x)\) for all \(g\in G\), \(x \in\Omega\).

Definition 1

The action of a topological group G on a normed space X is continuous maps \(G\times X\longrightarrow X: [ g,u ]\rightarrow gu\) such that \(1\cdot u= u\), \((g_{1} g_{2}) u=g_{1}(g_{2} u)\) and \(u\mapsto gu\) is linear. The action is isometric if \(\Vert gu \Vert = \Vert u \Vert \). The space of invariant points is defined by

$$\operatorname{Fix}(G):=\{u\in X; gu=u, \forall g\in G \}. $$

A function \(\varphi: X\longrightarrow \mathbb {R}\) is invariant if \(\varphi\circ g = \varphi\) for every \(g\in G\).

Now we can state a result by Palais [21].

Lemma 1

Principle of symmetric criticality

Assume that the action of the topological group G on the Banach space X is isometric. If \(\varphi\in C^{1}(X,\mathbb {R})\) is invariant and if u is a critical point of φ on \(\operatorname{Fix}(G)\), then u is a critical point of φ.

A frequently used compactness criterion is the Palais-Smale condition (PS condition, in short).

Definition 2

Palais-Smale condition

If X is a Banach space and \(\Phi\in\mathcal{C}^{1}(X,\mathbb {R})\), then the functional Φ satisfies the Palais-Smale condition if any sequence \(\{u_{n} \}\subset X\) for which

$$\bigl\vert \Phi(u_{n}) \bigr\vert \leq \mbox{constant},\quad \mbox{and}\quad \Phi'(u_{n})\rightarrow0\quad \mbox{in } X' $$

possesses a convergent subsequence.

We finish this section with the statement of the well-known result by Ambrosetti and Rabinowitz [22].

Lemma 2

Ambrosetti-Rabinowitz mountain pass theorem

If X is a Banach space, \(\Phi\in\mathcal{C}^{1}( X,\mathbb {R})\) satisfies the PS condition, \(\Phi(0)=0\) and

  1. (i)

    there are constants \(\rho,\alpha>0\) such that \(\Phi \vert_{\partial B_{\rho}}>\alpha\),

  2. (ii)

    there is \(e\in X\setminus\overline{B_{\rho}}\) such that \(\Phi(e)<0\),

then Φ possesses a critical value \(\overline{c}\geq\alpha\), with

$$\overline{c}:=\inf_{g\in\Gamma}\max_{u\in g ( [0,1 ] )} \Phi(u), $$

where \(\Gamma= \{g\in \mathcal{C}( [0,1 ] ,X); g(0)=0 \textit{ and } g(1)=e \}\).

3 Proof of the main results

In our arguments, the proof of Theorem 2 contains the existence result which is stated as in Theorem 1. Therefore, for the sake of brevity, we will deal only with problem (6) in the case where f is not necessarily identical to zero.

An axially symmetric function \(u(y,z)=v( \vert y \vert ,z)\) solves problem (6) if, and only if, \(v:=v(r,z)\) (with \(r= \vert y \vert \)) solves

$$ \textstyle\begin{cases} -\operatorname{div} (r^{m-ap} \vert \nabla v \vert ^{p-2}\nabla v )= r^{m-bq} \vert v \vert ^{q-2}v + r^{m} f & \mbox{in } S, \\ v= 0 & \mbox{on } \partial S, \end{cases} $$
(7)

where \(S:=(A,B)\times \mathbb {R}^{N-m-1}\) and \(\partial S:= \{ A,B \} \times \mathbb {R}^{N-m-1}\).

We denote by \(W_{0}^{1,p}(S)\) the subspace of axially symmetric functions of \(W_{0}^{1,p}(\Omega)\) with the norm defined by \(\Vert v \Vert = ( \int_{S} \vert \nabla v \vert ^{p} \,dx )^{\frac{1}{p}}\). This norm \(\Vert \cdot \Vert \) is equivalent to the standard norm on \(W_{0}^{1,p}(S)\) (see [24], pp.158-159).

If \(G:=O(N-m-1)\) is the group of isometries of \(\mathbb {R}^{N-m-1}\), then

$$\operatorname{Fix}(G)=W_{0,G}^{1,p}(S)= \bigl\{ v\in W_{0}^{1,p}(S) : v(r,gz)=v(r,z), \forall g\in G \bigr\} $$

and

$$L^{q}(S)^{G}= \bigl\{ v\in L^{q}(S) : v(r,gz)=v(r,z), \forall g \in G \bigr\} $$

are the subspaces of invariant functions.

Since \(A< r< B\), then the norms on \(W_{0,G}^{1,p}(S)\) and \(L^{q}(S)^{G}\) given by

$$ \Vert v \Vert _{m,a,p}:=\biggl( \int_{S} r^{m-ap} \vert \nabla v \vert ^{p}\, dx \biggr)^{\frac{1}{p}}\quad \mbox{and}\quad \vert v \vert _{m,b,q}:=\biggl( \int_{S} r^{m-bq} \vert v \vert ^{q} \,dx \biggr)^{\frac{1}{q}} $$
(8)

are equivalent to the standard norms on \(W_{0}^{1,p}(S)\) and \(L^{q}(S)\), respectively.

Denote \(X:=W_{0}^{1,p}(S)\) and \(E:=W_{0,G}^{1,p}(S)\). Let \(I\colon X\to \mathbb {R}\) be the energy functional associated to problem (7) and defined by

$$I(v)= \frac{1}{p} \int_{S} r^{m-ap} \vert \nabla v \vert ^{p} - \frac{1}{q} \int_{S} r^{m-bq} \vert v \vert ^{q} - \int_{S} r^{m} f v, $$

where

$$I'(v) (\varphi)= \int_{S} r^{m-ap} \vert \nabla v \vert ^{p-2}\nabla v\nabla\varphi- \int_{S} r^{m-bq} \vert v \vert ^{q-2}v \varphi - \int_{S} r^{m}f\varphi \quad \forall \varphi\in X . $$

Applying the principle of symmetric criticality (Lemma 1), we can look for critical points of the functional I constrained to E, which are weak solutions to problem (7).

Using Maz’ja’s inequality for the parameters in problem (7), for \(N-m>p\geq1\), \(q:=\frac{Np}{N-p (a+1-b)}\), \(a- \frac{m}{N-m} \leq b\leq a+1\) and \(a < \frac{(m+1)-p}{p}\), we get the existence of a positive constant C such that

$$\biggl( \int_{S} r^{m-bq} \vert v \vert ^{q}\, dx \biggr)^{\frac{1}{q}} \leq C \biggl( \int_{S} r^{m-ap} \vert \nabla v \vert ^{p}\, dx \biggr)^{\frac{1}{p}} $$

for every \(v\in X\). Therefore, the functional I is well defined for these parameters and the functions in the intervals and spaces previously mentioned.

In [19, 20], we have an important result of compactness which ensures that the embedding \(W_{0,G}^{1,p}(S)\hookrightarrow L^{q}(S)\) is compact for \(1\leq m < N-p\) and \(q\in(p,p_{N,m}^{*})\), where \(p_{N,m}^{*}:=\frac{p(N-m)}{N-m-p}\). So, \(W_{0,G}^{1,p}(S)\) can be compactly embedded into \(L^{q}(S)^{G}\) for the norms defined in (8).

Note that when \(b=a+1\) and \(b= a- \frac{m}{N-m}\), we have \(q=p\) and \(q=p_{N,m}^{*}\), respectively. Hence, we will consider \(a- \frac{m}{N-m} < b < a+1\), so that the compactness result and Maz’ja’s inequality are both satisfied.

The following lemma shows that the functional I verifies the geometry conditions of the mountain pass theorem.

Lemma 3

Let \(I\vert_{E}\) be the energy functional associated to problem (7); then

  1. (i)

    there are \(\overline{\varepsilon},\rho, \alpha>0\) such that \(I \vert_{\partial B_{\rho}}\geq\alpha\), since \(0< \Vert f \Vert _{E^{-1}}<\overline{\varepsilon}\);

  2. (ii)

    there is \(e\in E\setminus\overline{B_{\rho}}\) such that \(I(e)<0\).

Proof

(i) For any \(\varepsilon>0\), we deduce that

$$ \begin{aligned} \biggl\vert \int_{S} r^{m}f v \biggr\vert &\leq C_{1} \biggl\vert \int_{S} f v \biggr\vert \leq \bigl(\varepsilon^{\frac{1}{p}} \Vert v \Vert _{m,a,p} \bigr)\cdot \biggl(\frac{C_{1}}{\varepsilon ^{\frac{1}{p}}} \Vert f \Vert _{E^{-1}} \biggr) \\ &\leq \frac{\varepsilon}{p} \Vert v \Vert _{m,a,p}^{p} + \frac{C_{2}}{p' \varepsilon^{\frac{p'}{p}}} \Vert f \Vert _{E^{-1}}^{p'} \end{aligned} $$

for all \(v\in E\), where \(\frac{1}{p} + \frac{1}{p'}=1\). Therefore,

$$ \begin{aligned}[b] I(v)&= \frac{1}{p} \Vert v \Vert _{m,a,p}^{p} -\frac {1}{q} \vert v \vert _{m,b,q}^{q} - \int_{S} r^{m}f v \\ &\geq \frac{1}{p} \Vert v \Vert _{m,a,p}^{p} - \frac {1}{qS_{q}^{q}} \Vert v \Vert _{m,a,p}^{q}- \frac{\varepsilon}{p} \Vert v \Vert _{m,a,p}^{p} - \frac{C_{2}}{p' \varepsilon^{\frac{p'}{p}}} \Vert f \Vert _{E^{-1}}^{p'} \\ &= \biggl(\frac{1-\varepsilon}{p}-\frac{1}{qS_{q}^{q}} \Vert v \Vert _{m,a,p}^{q-p} \biggr) \Vert v \Vert _{m,a,p}^{p} - \frac{C_{2}}{p' \varepsilon^{\frac{p'}{p}}} \Vert f \Vert _{E^{-1}}^{p'}, \end{aligned} $$
(9)

where \(S_{q}\) is the best constant in the embedding \(W_{0,G}^{1,p}(S)\hookrightarrow L^{q}(S)^{G}\).

By fixing \(\varepsilon\in(0,1)\), we can find \(\rho>0\), with \(\Vert v \Vert _{m,a,p}=\rho\), \(\overline{\varepsilon}>0\) and \(\alpha >0\), such that the conclusion of the lemma holds true. For example, we can take

$$\rho= \bigl(MqS_{q}^{q} \bigr)^{\frac{1}{q-p}}, \qquad \overline{ \varepsilon}= \frac{C_{2}^{\frac{-1}{p'}} p^{\prime\frac{1}{p'}} \varepsilon^{\frac{1}{p}}}{2} M^{\frac{q}{p'(q-p)}} \bigl( qS_{q}^{q} \bigr)^{\frac{p}{p'(q-p)}},\qquad \alpha=\frac{1}{2} M^{\frac{q}{q-p}} \bigl(qS_{q}^{q} \bigr)^{\frac{p}{q-p}}, $$

where \(M=\frac{1}{2} (\frac{1-\varepsilon}{p} )>0\).

(ii) Let \(v\in E\) such that \(\Vert v \Vert _{a,m,p}=1\). Then, for any \(t>1\), we have

$$I(tv)=\frac{1}{p} t^{p} -\frac{1}{q} \vert v \vert _{m,b,q}^{q} t^{q} - t \int_{S} r^{m}fv. $$

Since \(q>p>1\), then we have \(\lim_{t\to\infty} I(tv)= -\infty\). So, there is \(e\in E\setminus\overline{B_{\rho}}\) such that \(I(e)<0\). □

Lemma 4

The functional I satisfies the Palais-Smale condition in E.

Proof

Let \(\{v_{n} \}\) be a Palais-Smale sequence for the functional I in E, i.e.,

  1. 1.

    \(\vert I(v_{n}) \vert \leq M\) for some \(M>0\) and

  2. 2.

    \(I'(v_{n})\to0\) in \(E^{-1}\), where \(E^{-1}\) is the dual space of E.

First we will show that \(\{v_{n} \}\) is bounded in E. Assume by contradiction that

$$ \Vert v_{n} \Vert _{m,a,p}\to\infty \quad \mbox{as } n\to\infty. $$
(10)

Given \(\varepsilon>0\), by items 1 and 2 we deduce that

$$ \biggl\vert I(v_{n})-\frac{1}{q} I'(v_{n})v_{n} \biggr\vert \leq M + \frac{\varepsilon}{q} \Vert v_{n} \Vert _{m,a,p} $$
(11)

for \(n\in\mathbb{N}\) large enough.

Moreover, we also have

$$ \biggl\vert I(v_{n})-\frac{1}{q} I'(v_{n}) (v_{n}) \biggr\vert \geq \biggl( \frac{1}{p} -\frac{1}{q} \biggr) \Vert v_{n} \Vert _{m,a,p}^{p}- C_{1} \biggl(1-\frac{1}{q} \biggr) \Vert f \Vert _{E^{-1}} \Vert v_{n} \Vert _{m,a,p} $$
(12)

for all \(n\in\mathbb{N}\).

Hence, for n large enough, we have

$$\biggl(\frac{1}{p}-\frac{1}{q} \biggr) \Vert v_{n} \Vert _{m,a,p}^{p} \leq M + \biggl(\frac{\varepsilon}{q} + C_{1} \biggl(1-\frac {1}{q} \biggr) \Vert f \Vert _{E^{-1}} \biggr) \Vert v_{n} \Vert _{m,a,p}. $$

Letting \(n\to\infty\) in the previous inequality, we obtain a contradiction since \(1< p< q\). This implies that \(\{v_{n} \}\) is bounded in E.

Now we will prove that \(\{v_{n} \}\) is a Cauchy sequence in E. In [25] it is proved that the inequality

$$ \vert \xi-\eta \vert ^{p} \leq \textstyle\begin{cases} ( \vert \xi \vert ^{p-2} \xi- \vert \eta \vert ^{p-2}\eta ) (\xi-\eta ), & \mbox{if } p\geq2; \\ ( \vert \xi \vert ^{p-2} \xi- \vert \eta \vert ^{p-2}\eta ) (\xi-\eta )^{\frac{p}{2}} ( \vert \xi \vert ^{p} + \vert \eta \vert ^{p} )^{\frac{2-p}{2}}, & \mbox{if } 1< p< 2, \end{cases} $$
(13)

holds for all \(\xi, \eta\in \mathbb {R}^{N}\). Hence,

$$ \begin{aligned} \int_{S} r^{m-ap} \vert \nabla v_{i}- \nabla v_{j} \vert ^{p} &\leq \int_{S} r^{m-ap} \bigl( \vert \nabla v_{i} \vert ^{p-2}\nabla v_{i} - \vert \nabla v_{j} \vert ^{p-2}\nabla v_{j} \bigr) (\nabla v_{i}-\nabla v_{j} ) \\ &\leq \bigl\vert I'(v_{i}) (v_{i}-v_{j}) \bigr\vert + \bigl\vert I'(v_{j}) (v_{i}-v_{j}) \bigr\vert \\ &\quad {} + \biggl\vert \int_{S} r^{m-bq} \bigl( \vert v_{i} \vert ^{q-2}v_{i} - \vert v_{j} \vert ^{q-2}v_{j} \bigr) (v_{i}-v_{j} ) \biggr\vert \\ &:=I_{1} + I_{2}+ I_{3}. \end{aligned} $$

Since \(\{v_{n} \}\) is a Palais-Smale sequence, it follows that \(I_{1}=o ( \Vert v_{n} \Vert _{m,a,p} )\) and \(I_{2}=o ( \Vert v_{n} \Vert _{m,a,p} )\).

Using Hölder’s inequality, we have

$$ \begin{aligned} \biggl\vert \int_{S} r^{m-bq} \bigl( \vert v_{i} \vert ^{q-2}v_{i} - \vert v_{j} \vert ^{q-2}v_{j} \bigr) (v_{i}-v_{j} ) \biggr\vert &\leq \int_{S} r^{m-bq} \bigl( \vert v_{i} \vert ^{q-1} + \vert v_{j} \vert ^{q-1} \bigr) \vert v_{i}-v_{j} \vert \\ &= \int_{S} \bigl(r^{\frac{m-bq}{q}} \vert v_{i} \vert \bigr)^{q-1} r^{\frac{m-bq}{q}} \vert v_{i}-v_{j} \vert \\ &\quad {} + \int_{S} \bigl(r^{\frac{m-bq}{q}} \vert v_{j} \vert \bigr)^{q-1} r^{\frac{m-bq}{q}} \vert v_{i}-v_{j} \vert \\ &\leq \bigl( \vert v_{i} \vert _{m,b,q}^{q-1} + \vert v_{j} \vert _{m,b,q}^{q-1} \bigr) \vert v_{i}- v_{j} \vert _{m,b,q}. \end{aligned} $$

It follows from the previous inequality and from the compact embedding \(W_{0,G}^{1,p}(S)\hookrightarrow L^{q}(S)^{G}\) that \(I_{3}= o ( \Vert v_{n} \Vert _{a,m,p} )\). Therefore, \(\{v_{n} \}\) is a Cauchy sequence and the functional I satisfies the Palais-Smale condition. □

Lemma 5

The functional I is weakly lower semicontinuous in E, i.e., if \(\{v_{n} \}\) converges weakly to v in E, then \(I(v)\leq\liminf I(v_{n})\).

Proof

Let a sequence \(\{v_{n} \}\subset E\) be weakly convergent to v in E. Since the norm \(\Vert \cdot \Vert _{m,a,p}\) is weakly lower semicontinuous in E, it follows that

$$ \frac{1}{p} \int_{S} r^{m-ap} \vert \nabla v \vert ^{p} \leq \liminf_{n\to\infty} \biggl(\frac{1}{p} \int_{S} r^{m-ap} \vert \nabla v_{n} \vert ^{p} \biggr). $$
(14)

We can conclude from the compact embedding \(W_{0,G}^{1,p}(S)\hookrightarrow L^{q}(S)^{G}\) that \(\{v_{n} \}\) converges strongly to v in \(L^{q}(S)^{G}\). Therefore,

$$ \lim_{n\to\infty}\frac{1}{q} \int_{S} r^{m-bq} \vert v_{n} \vert ^{q} = \frac{1}{q} \int_{S} r^{m-bq} \vert v \vert ^{p}. $$
(15)

By hypothesis, the sequence \(\{v_{n} \}\) converges weakly to v in E and \(f\in W_{0}^{-1,p}(\Omega)\subset E^{-1}\); hence,

$$ \lim_{n\to\infty} \int_{S} r^{m} fv_{n} = \int_{S} r^{m} f v. $$
(16)

Finally, combining (14), (15) and (16), we deduce that

$$ \begin{gathered} \liminf_{n\to\infty} I(v_{n}) \\ \quad = \liminf_{n\to\infty} \biggl[ \frac{1}{p} \int_{S} r^{m-ap} \vert \nabla v_{n} \vert ^{p} - \biggl( \lim_{n\to\infty}\frac{1}{q} \int_{S} r^{m-bq} \vert \nabla v_{n} \vert ^{q} + \lim_{n\to\infty} \int_{S} r^{m} fv_{n} \biggr) \biggr] \\ \quad \geq I(v); \end{gathered} $$

therefore, the functional I is weakly lower semicontinuous in E. □

Proof of Theorem 2

By Lemmas 3 and 4, all the assumptions of the mountain pass theorem in [22] are satisfied. Hence, we deduce the existence of \(v_{1}^{*} \in W_{0,G}^{1,p}(S)\) which is a weak solution to problem (7) and \(I(v_{1}^{*})=\overline{c}>0\).

Now, we will prove that there is a second weak solution \(v_{2}^{*} \in W_{0,G}^{1,p}(S)\) such that \(v_{1}^{*}\neq v_{2}^{*}\). For \(\rho>0\) given as in Lemma 3, we define the number \(\underline{c}\) by

$$\underline{c}:=\inf_{ \{v\in E: \Vert v \Vert _{m,a,p}\leq\rho \}} I(v). $$

It is clear that \(\underline{c}\leq I(0)=0\). If \(\underline{c}=I(0)\), then 0 is a minimum value for I; hence,

$$0= I'(0) (\varphi) = - \int_{S} r^{m} f \varphi, \quad \forall\varphi\in E, $$

which contradicts the fact that \(f\neq0\). Therefore, \(\underline{c}< I(0)=0\).

Denote by \(\overline{B}_{\rho}\) the closed ball of radius ρ centered at the origin in E, i.e.,

$$\overline{B}_{\rho}= \bigl\{ v\in E : \Vert v \Vert _{m,a,p} \leq\rho \bigr\} . $$

It follows that the set \(\overline{B}_{\rho}\) is a complete metric space with respect to distance defined by \(d(u,v):=\Vert u-v \Vert _{m,a,p}\) for all \(u, v\in\overline{B}_{\rho}\).

By Lemma 5, the functional I is weakly lower semicontinuous and bounded from below by relation (9).

Let ε such that \(0<\varepsilon< \inf_{\partial B_{\rho}} I - \inf_{B_{\rho}} I\). Using Ekeland’s variational principle [23] for the functional \(I: \overline{B}_{\rho}\rightarrow \mathbb {R}\), there is a function \(v_{\varepsilon}\in\overline{B}_{\rho}\) such that

$$I(v_{\varepsilon})< \inf_{\overline{B}_{\rho}} I + \varepsilon, I(v_{\varepsilon}) < I(v) + \varepsilon \Vert v-v_{\varepsilon} \Vert _{m,a,p},\quad v\neq v_{\varepsilon}. $$

Since

$$I(v_{\varepsilon})\leq \inf_{\overline{B}_{\rho}} I + \varepsilon\leq \inf _{B_{\rho}} I + \varepsilon< \inf_{\partial B_{\rho}} I, $$

it follows that \(v_{\epsilon}\in B_{\rho}\).

We now define the functional \(K: \overline{B_{\rho}}\rightarrow \mathbb {R}\) by \(K(v)=I(v) + \varepsilon \Vert v-v_{\varepsilon} \Vert _{m,a,p}\). It is immediate that \(v_{\varepsilon}\) is a minimum point of K, and so

$$ \frac{K(v_{\varepsilon}+ t\varphi) - K(v_{\varepsilon})}{t} \geq0 $$
(17)

for \(t>0\) small enough and \(\varphi\in B_{\rho}\). From inequality (17) we deduce that

$$ \frac{I(v_{\varepsilon}+ t\varphi) - I(v_{\varepsilon})}{t} + \varepsilon \Vert \varphi \Vert _{m,a,p} \geq0. $$
(18)

It follows from (18) by letting \(t\to0^{+}\) that \(I'(v_{\varepsilon})\varphi+\varepsilon \Vert \varphi \Vert _{m,a,p} \geq 0\). Note that −φ also belongs to \(B_{\rho}\). So, replacing φ by −φ, we have

$$I'(v_{\varepsilon}) (-\varphi) + \varepsilon \Vert {-}\varphi \Vert _{m,a,p} \geq0 $$

or simply \(I'(v_{\varepsilon})(\varphi)\leq\varepsilon \Vert \varphi \Vert _{m,a,p}\). In this way, we can deduce that \(\Vert I'(v_{\epsilon}) \Vert _{E^{-1}} \leq\varepsilon\).

Therefore, from the previous information we can conclude that there is a sequence \(\{v_{k} \}\subset B_{\rho}\) such that

$$I(v_{k})\to\underline{c} \quad \mbox{and}\quad I'(v_{k}) \to0 \quad \mbox{in } E^{-1} \mbox{ as } k\to\infty. $$

Using Lemma 4 we can show that up to a subsequence, \(\{v_{k} \}\) converges strongly to some \(v_{2}^{*}\in E\). Thus, \(v_{2}^{*}\) is a weak solution of (7) and \(v_{2}^{*}\) is a non-trivial solution since \(I(v_{2}^{*})=\underline{c}<0\). Finally, since \(I(v_{1}^{*})=\overline{c}>0>\underline{c}=I(v_{2}^{*})\), then \(v_{2}^{*}\neq v_{1}^{*}\). □