1 Introduction

Fractional calculus is an important theoretical branch of mathematical theories [1], which has been widely applied in various fields such as the complex physical, mechanical, biological, and engineering fields. For example, fractional calculus has been applied to model the nonlinear oscillations of earthquake [2], fluid-dynamic traffic [3], continuum and statistical mechanics [4], signal processing [5], control theory [6] and dynamics of interfaces between nanoparticles and subtracts [7]. In these practical applications, fractional calculus has a certain geometric and physical meaning. Due to its historical dependence and globally related characteristics, fractional differentiation can be approximately represented and vigorously developed in the anomalous diffusion. In view of the fact that fractional calculus has great practical significance, it is very important to study fractional differential equations. In general, the exact solutions of many fractional partial differential equations cannot be obtained, so scholars are committed to obtaining their numerical solutions to reflect the exact solutions. In recent years, the theory of fractional calculus has been greatly developed, and lots of articles about fractional calculus have been published. Numerical algorithms for different types of fractional differential equations have been presented. These algorithms include the Chebyshev and Legendre polynomials method [8, 9], the wavelet method [10, 11], the piecewise constant orthogonal functions method [12], the differential transform method [13], the collocation method [14], the Adomian decomposition method [15], and so on. In [16], the authors proposed a compact exponential scheme for the time fractional convection-diffusion reaction equation with variable coefficients. In [11], the authors acquired the numerical solution of fractional Poisson equations using a two-dimensional Legendre wavelet. In [17], Maleknejad and Mahdiani proposed to solve nonlinear mixed Volterra-Fredholm integral equations with two-dimensional block pulse functions using a direct method. Reference [18] gave the numerical methods for solving two-dimensional nonlinear integral equations of fractional order by using a two-dimensional block pulse operational matrix. In this study, we applied two-dimensional block pulse functions to obtain the numerical solutions of fractional Poisson type equations with Dirichlet and Neumann boundary conditions.

The current paper is organized as follows. In Section 2, the model with respect to Poisson type equations is given. In Section 3, some basic definitions and mathematical preliminaries of fractional calculus are introduced. Section 4 introduces the definitions and properties of two-dimensional block pulse functions. In Section 5, we discussed the error analysis of our approach. Section 6 introduces the method for solving fractional Poisson type equations. In Section 7, the proposed approach is tested through several numerical examples. Finally, a conclusion is given in Section 8.

2 Illustration of the proposed model

In the following, we introduce the propagation of an elastic wave for a one-dimensional rod model under the action of impact load.

The rod fixed at left and the right is exerted on a tensile impact load P, the length of it is L, as is shown in Figure 1. The basic equation of this problem with boundary condition is given as

$$ \left \{ \textstyle\begin{array}{l} \frac{\partial^{2}u}{\partial x^{2}} - \frac{1}{c^{2}}\frac{\partial^{2}u}{\partial t^{2}} = 0 \quad ( 0 < x < L ), \\ u ( x,0 ) = \dot{u}(x,L) = 0,\qquad u(0,t) = 0,\qquad\sigma ( L,t ) = P, \end{array}\displaystyle \right . $$
(1)

where \(c = \sqrt{E / p}\), is the wave velocity. The displacement analytical solution of the rod is

$$ \begin{aligned}[b] u(x,t) ={}& \frac{c}{E}\biggl\{ \biggl[H \biggl( t + \frac{x - L}{c} \biggr) - H \biggl( t - \frac{x + L}{c} \biggr)\biggr]\\ & - \biggl[H \biggl( t + \frac{x - 3L}{c} \biggr) - H \biggl( t - \frac{x + 3L}{c} \biggr)\biggr] \\ &+ \biggl[H \biggl( t + \frac{x - 5L}{c} \biggr) - H \biggl( t - \frac{x + 5L}{c} \biggr)\biggr] - \cdots \biggr\} , \end{aligned} $$
(2)

where \(H(x)\) is a Heaviside step function:

$$ H(x) = \left \{ \textstyle\begin{array}{l@{\quad}l} 1,& x > 0, \\ 0,& x < 0. \end{array}\displaystyle \right . $$
(3)
Figure 1
figure 1

One-dimensional bar model under the impact load.

Full size image

Based on the above model, we propose the following fractional Poisson equations model:

$$ \frac{\partial^{\nu} u}{\partial x^{\nu}} ( x,t ) + \frac{\partial^{\gamma} u}{\partial t^{\gamma}} ( x,t ) = g ( x,t ) \quad( 0 \le x \le L,0 \le t \le \tau ), $$
(4)

with Dirichlet boundary conditions

$$ \left \{ \textstyle\begin{array}{l} u ( x,0 ) = f_{0} ( x ),\qquad u ( 0,t ) = g_{0} ( t ); \\ u ( x,\tau ) = f_{1} ( x ), \qquad u ( L,t ) = g_{1} ( t ). \end{array}\displaystyle \right . $$
(5)

The Neumann boundary conditions are

$$ \left \{ \textstyle\begin{array}{l} u ( x,0 ) = f_{0} ( x ),\qquad u ( 0,t ) = g_{0} ( t ); \\ \frac{\partial u}{\partial t}\vert _{(x,\tau )} = f_{1} ( x ),\qquad \frac{\partial u}{\partial x}\vert _{(L,t)} = g_{1} ( t ). \end{array}\displaystyle \right . $$
(6)

3 Preliminaries and notations

In this section, we gave some necessary definitions and preliminaries of the fractional calculus theory which will be used in the article [1].

Definition 1

The Riemann-Liouville fractional integral operator \(I^{\nu}\) of order ν is given by

$$ \bigl( I^{\nu} f \bigr) ( t ) = \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{1}{\Gamma ( \nu )}\int_{ 0}^{ t} ( t - \tau )^{\nu - 1} f ( \tau )\, \mathrm{d}\tau, & \nu > 0; \\ f ( t ),& \nu = 0. \end{array}\displaystyle \right . $$
(7)

Definition 2

The Caputo definition of fractional differential operator is given by

$$ {}_{c}D^{\nu} f ( t ) = \left \{ \textstyle\begin{array}{l@{\quad}l} \frac{1}{\Gamma ( m - \nu )}\int_{0}^{t} \frac{f^{ ( m )} ( \tau )}{ ( t - \tau )^{\nu - m + 1}}\, \mathrm{d}\tau, & 0< m - 1 \le \nu < m; \\ \frac{\mathrm{d}^{m}f ( t )}{\mathrm{d}t^{m}}, & \nu = m\in N^{+}. \end{array}\displaystyle \right . $$
(8)

For the Caputo derivative, we have

$$ {}_{c}D^{\nu} t^{\gamma} = \left \{ \textstyle\begin{array}{l@{\quad}l} 0,& \mbox{for } \gamma \in N_{0} \mbox{ and } \gamma < \lceil \nu \rceil; \\ \frac{\Gamma ( \gamma + 1 )}{\Gamma ( \gamma + 1 - \nu )}t^{\gamma - \nu}, &\mbox{for } \gamma \in N_{0} \mbox{ and } \gamma \ge \lceil \nu \rceil \mbox{ or } \gamma \notin N_{0}\mbox{ and } \gamma > \lfloor \nu \rfloor. \end{array}\displaystyle \right . $$
(9)

4 Two-dimensional block pulse functions

One-dimensional block pulse functions have been widely used for differential and integral equations. More details for block pulse functions of the one-dimensional case are given in [19]. These conclusions can be extended to the two-dimensional block pulse functions.

4.1 Definitions and properties

2D-BPFs are defined as

$$ \phi_{i_{1},i_{2}} ( x,t ) = \left \{ \textstyle\begin{array}{l@{\quad}l} 0,& ( i_{1} - 1 )h_{1} \le x < i_{1}h_{1} \mbox{ and } ( i_{2} - 1 )h_{2} \le x < i_{2}h_{2}, \\ 1, &\mbox{otherwise}, \end{array}\displaystyle \right . $$
(10)

where \(i_{1} = 1,2, \ldots,m_{1}\) and \(i_{2} = 1,2, \ldots, m_{2}\) with positive integer values for \(m_{1}\), \(m_{2}\) and \({h_{1} = \frac{T_{1}}{m_{1}}}\), \(h_{2} = \frac{T_{2}}{m_{2}}\), \(T_{1},T_{2} \in N^{ +}\).

They have the following properties:

  1. 1.

    Disjointness:

    $$ \phi_{i_{1},i_{2}} ( x,t )\phi_{j_{1},j_{2}} ( x,t ) = \left \{ \textstyle\begin{array}{l@{\quad}l} \phi_{i_{1},i_{2}} ( x,t ), &i_{1} = j_{1} \mbox{ and } i_{2} = j_{2}, \\ 0,& \mbox{otherwise}. \end{array}\displaystyle \right . $$
    (11)
  2. 2.

    Orthogonality:

    $$ \int_{0}^{T_{1}} \int_{0}^{T_{2}} \phi_{i_{1},i_{2}} ( x,t ) \phi_{j_{1,}j_{2}} ( x,t )\,\mathrm{d}t\,\mathrm{d}x = \left \{ \textstyle\begin{array}{l@{\quad}l} h_{1}h_{2},& i_{1} = i_{2} \mbox{ and } j_{1} = j_{2}, \\ 0, &\mbox{otherwise}. \end{array}\displaystyle \right . $$
    (12)

    In the region of \(x \in [ 0,T_{1} )\) and \(t \in [ 0,T_{2} )\), where \(i_{1},j_{1} = 1,2, \ldots,m_{1}\) and \(i_{2},j_{2} = 1,2, \ldots,m_{2}\).

  3. 3.

    Completeness: For every \(u \in L^{2} ( [ 0,T_{1} ) \times [ 0,T_{2} ) )\) when \(m_{1}\) and \(m_{2}\) approach infinity, Parseval’s identity holds:

    $$ \int_{0}^{T_{1}} \int_{0}^{T_{2}} u^{2} ( x,t )\,\mathrm{d}t\, \mathrm{d}x = \sum_{i_{1} = 1}^{\infty} \sum _{i_{2} = 1}^{\infty} u_{i_{1},i_{2}}^{2} \bigl\Vert \phi_{i_{1},i_{2}} ( x,t ) \bigr\Vert ^{2}, $$
    (13)

    where

    $$u_{i_{1},i_{2}} = \frac{1}{h_{1}h_{2}} \int_{0}^{T_{1}} \int_{0}^{T_{2}} u ( x,t )\phi_{i_{1},i_{2}} ( x,t )\, \mathrm{d}t\,\mathrm{d}x. $$

4.2 BPFs expansions

A function \(u ( x,t ) \in L^{2} ( [ 0,T_{1} ) \times [ 0,T_{2} ) )\) can be expressed as

$$ u ( x,t ) \cong \sum_{i_{1} = 1}^{m_{1}} \sum _{i_{2} = 1}^{m_{2}} u_{i_{1},i_{2}} \phi_{i_{1},i_{2}} ( x,t ) = V^{T}\Phi ( x,t ), $$
(14)

where

$$ \begin{aligned} &V = [ u_{11}, \ldots,u_{1,m_{2}}, \ldots, u_{m_{1},1}, \ldots,u_{m_{1},m_{2}} ]^{T}, \\ &\Phi ( x,t ) = \bigl[ \phi_{1,1} ( x,t ), \ldots,\phi_{1,m_{2}} ( x,t ), \ldots, \phi_{m_{1},1} ( x,t ), \ldots, \phi_{m_{1},m_{2}} ( x,t ) \bigr]^{T}. \end{aligned} $$
(15)

The block pulse coefficients \(u_{i_{1},i_{2}}\) are obtained by

$$ u_{i_{1},i_{2}} = \frac{1}{h_{1}h_{2}} \int_{ ( i_{1} - 1 )h_{1}}^{i_{1}h_{1}} \int_{ ( i_{2} - 1 )h_{2}}^{i_{2}h_{2}} u ( x,t )\,\mathrm{d}t\,\mathrm{d}x. $$
(16)

Since each of the two-dimensional block pulse functions takes only one value in its sub-region, the 2D-BPFs can be expanded by the two 1D-BPFs:

$$ \phi_{i_{1},i_{2}} ( x,t ) = \phi_{i_{1}} ( x )\phi_{i_{2}} ( t ), $$
(17)

where \(\phi_{i_{1}} ( x )\) and \(\phi_{i_{2}} ( t )\) are the 1D-BPFs related to the variables x and t, respectively. Then we have

$$ u ( x,t ) \cong \Phi^{T} ( x )U\Phi ( t ), $$
(18)

where

$$ \begin{aligned} &U = \left [ \textstyle\begin{array}{@{}cccc@{}} u_{1,1} & u_{1,2} & \cdots & u_{1,m_{1}} \\ u_{2,1} & u_{2,2} & \cdots & u_{2,m_{1}} \\ \vdots & \vdots & \ddots & \vdots \\ u_{m_{1},1} & u_{m_{1},2} & \cdots & u_{m_{1},m_{2}} \end{array}\displaystyle \right ], \\ &\Phi ( x ) = \bigl[ \phi_{1} ( x ),\phi_{2} ( x ), \ldots, \phi_{m_{1}} ( x ) \bigr]^{T},\qquad\Phi ( t ) = \bigl[ \phi_{1} ( t ),\phi_{2} ( t ), \ldots,\phi_{m_{2}} ( t ) \bigr]^{T}. \end{aligned} $$
(19)

4.3 Operational matrix

In this part, we may simply introduce the operational matrix of fractional integration of block pulse functions; more details can be found in [20].

Let \(m_{1} = m_{2} = m\) and \(T_{1} = T_{2} = T\). If \(I^{\alpha}\) is the fractional integration operator of the block pulse functions, we can get

$$ I^{\alpha} \Phi ( x ) \cong F_{\alpha} \Phi ( x ), $$
(20)

where

$$ F_{\alpha} = \biggl( \frac{T}{m} \biggr)^{\alpha} \frac{1}{\Gamma ( \alpha + 2 )} \left [ \textstyle\begin{array}{@{}ccccc@{}} 1 & \xi_{1} & \xi_{2} & \cdots & \xi_{m - 1} \\ 0 & 1 & \xi_{1} & \cdots & \xi_{m - 2} \\ 0 & 0 & 1 & \cdots & \xi_{m - 3} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{array}\displaystyle \right ] $$

and

$$\xi_{k} = ( k + 1 )^{\alpha + 1} - 2k^{\alpha + 1} + ( k - 1 )^{\alpha + 1}. $$

\(F_{\alpha}\) is called the block pulse operational matrix of fractional integration.

Let \(D_{\alpha}\) is the block pulse operational matrix for the fractional differentiation. According to the property of fractional calculus, \(D_{\alpha} F_{\alpha} = I\), we can easily obtain the matrix \(D_{\alpha}\) by inverting the \(F_{\alpha}\) matrix.

5 Error analysis

The error can be achieved when a function \(u ( x,t )\) is represented by 2D-BPFs over the region \(D = [ 0,T ) \times [ 0,T )\). Let \(m_{1} = m_{2} = m\), so \(h_{1} = h_{2} = \frac{T}{m}\).

We can define the error between \(u ( x,t )\) and its 2D-BPFs approximation, \(u_{m} ( x,t )\), over the sub-region \(D_{i_{1},i_{2}}\) as follows:

$$ e_{i_{1},i_{2}} ( x,t ) = u_{i_{1},i_{2}}\phi_{i_{1},i_{2}} ( x,t ) - u ( x,t ) = u_{i_{1},i_{2}} - u ( x,t ), \quad( x,t ) \in D_{i_{1},i_{2}}, $$
(21)

where

$$D_{i_{1},i_{2}} = \biggl\{ ( x,t )\biggm\vert \frac{i_{1} - 1}{m} \le x < \frac{i_{1}}{m},\frac{i_{2} - 1}{m} \le t < \frac{i_{2}}{m} \biggr\} . $$

Using the mean value theorem

$$ \Vert e_{i_{1},i_{2}} \Vert ^{2} \le \frac{2}{m^{4}}M^{2}, $$
(22)

where \(\Vert u' ( x,t ) \Vert \le M\). Then the error function \(e ( x,t )\) is defined as follows:

$$ e ( x,t ) = u_{m} ( x,t ) - u ( x,t ). $$
(23)

By using equation (22), we have

$$ \bigl\Vert e ( x,t ) \bigr\Vert ^{2} \le \frac{2}{m^{2}}M^{2}, $$
(24)

hence \(\Vert e ( x,t ) \Vert = O ( \frac{1}{m} )\).

From equation (24), the conclusion is drawn that the method in this paper is convergent when it is used to solve the numerical solutions of fractional partial differential equations. For more details see [21].

6 Description of the proposed method

In the section, we will use the two-dimensional block pulse function to obtain the numerical solutions of equation (4) with Dirichlet and Neumann boundary conditions. We suppose \(m_{1} = m_{2} = m\). Then we have

$$\begin{aligned}& \frac{\partial^{v}u}{\partial x^{v}} \cong \frac{\partial^{v} ( \Phi^{T} ( x )U\Phi ( t ) )}{\partial x^{v}} = \biggl[ \frac{\partial^{v}\Phi ( x )}{\partial x^{v}} \biggr]U\Phi ( t ) = \Phi^{T} ( x )\mathbf{D}_{v}^{T}U \Phi ( t ), \end{aligned}$$
(25)
$$\begin{aligned}& \frac{\partial^{\gamma} u}{\partial t^{\gamma}} \cong \frac{\partial^{\gamma} ( \Phi^{T} ( x )U\Phi ( t ) )}{\partial t^{\gamma}} = \Phi^{T} ( x )U\frac{\partial^{\gamma} ( \Phi ( t ) )}{\partial t^{\gamma}} = \Phi^{T} ( x )U \mathbf{D}_{\gamma} \Phi ( t ). \end{aligned}$$
(26)

Using equation (18), the function \(g ( x,t )\) of equation (4) can be expressed as

$$ g ( x,t ) \cong \Phi^{T} ( x )G\Phi ( t ), $$
(27)

where \(G = ( g_{ij} )_{m \times m}\). Substituting equations (25)-(27) into equation (4), we have

$$ \Phi^{T} ( x )\mathbf{D}_{v}^{T}U\Phi ( t ) + \Phi^{T} ( x )U\mathbf{D}_{\gamma} \Phi ( t ) = \Phi^{T} ( x )G\Phi ( t ), $$
(28)

and dispersing equation (28) by the points \(( x_{i},t_{j} )\) (\(i,j = 1,2, \ldots,m \)), we obtain

$$ \mathbf{D}_{v}^{T}U + U\mathbf{D}_{\gamma} = G, $$
(29)

which is a Sylvester equation.

  1. (i)

    Dirichlet boundary conditions: For equation (4) with boundary conditions of equation (5), we have

    $$ \begin{aligned} &\Phi^{T} ( x ) U\Phi ( 0 ) \approx \Phi^{T} ( x ) C_{1},\qquad \Phi^{T} ( 0 ) U\Phi ( t ) \approx C_{3}^{T}\Phi ( t ), \\ &\Phi^{T} ( x ) U\Phi ( \tau ) \approx \Phi^{T} ( x ) C_{2}, \qquad\Phi^{T} ( L ) U\Phi ( t ) \approx C_{4}^{T}\Phi ( t ). \end{aligned} $$
    (30)

    The entries of vector \(\Phi^{T} ( x )\) and \(\Phi ( t )\) are independent, so from equation (30) we can obtain

    $$ \begin{aligned} &\Lambda_{1} = U\Phi ( 0 ) - C_{1} \approx 0,\qquad \Lambda_{3} = \Phi^{T} ( 0 ) U - C_{3}^{T} \approx 0, \\ &\Lambda_{2} = U\Phi ( \tau ) - C_{2} \approx 0,\qquad \Lambda_{4} = \Phi^{T} ( L ) U - C_{4}^{T} \approx 0, \end{aligned} $$
    (31)
  2. (ii)

    Neumann boundary conditions: Similar to equation (31), we can obtain

    $$ \begin{aligned} &\Lambda_{1} = U\Phi ( 0 ) - C_{1} \approx 0,\quad\quad \Lambda_{3} = \Phi^{T} ( 0 ) U - C_{3}^{T} \approx 0, \\ &\Lambda_{2} = U\mathbf{D}_{1}\Phi ( \tau ) - C_{2} \approx 0,\qquad \Lambda_{4} = \Phi^{T} ( L )\mathbf{D}_{1}^{T} U - C_{4}^{T} \approx 0, \end{aligned} $$
    (32)

    equation (29) together with equation (31) or equation (32) gives a system of linear equations, we apply the least-square-method to solve the system, then the unknown function can be found.

7 Numerical experiments

In this section, we applied several numerical examples to test our proposed method, and compared the obtained numerical results with those obtained by the Legendre and the CAS wavelet methods.

Example 1

Consider the following Laplace equation:

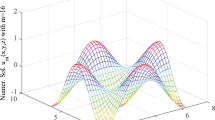
$$ \frac{\partial^{v}u ( x,t )}{\partial x^{v}} + \frac{\partial^{\gamma} u ( x,t )}{\partial t^{\gamma}} = 0, $$
(33)

with Dirichlet boundary conditions \(u(x,0) = 0\), \(u(0,t) = 0\), \(u(x,1) = \sinh (x)\sin (1)\), \(u(1,t) = \sinh (1)\sin(t)\). The exact solution of this problem for \(v = \gamma = 2\) is \(u(x,t) = \sinh (x)\sin (t)\). The graph of the exact solution is shown in Figure 2. The graphs of numerical solutions for \(m = 8,16,32\) are shown in Figures 3, 4, 5.

Figure 2
figure 2

Exact solution for Example 1 .

Full size image
Figure 3
figure 3

Numerical solution of \(\pmb{m=8}\) for Example 1 .

Full size image
Figure 4
figure 4

Numerical solution of \(\pmb{m=16}\) for Example 1 .

Full size image
Figure 5
figure 5

Numerical solution of \(\pmb{m=32}\) for Example 1 .

Full size image

Example 2

Consider the following fractional Poisson equation:

$$ \frac{\partial^{4 / 3}u}{\partial x^{4 / 3}} + \frac{\partial^{3 / 2}u}{\partial t^{3 / 2}} = 3x^{2 / 3}t ( t - 2 ) \big/\Gamma \biggl( \frac{2}{3} \biggr) + 4\sqrt{t} x ( x - 2 )/\sqrt{\pi}, $$
(34)

with homogeneous boundary conditions \(u ( x,0 ) = u ( x,2 ) = u ( 0,t ) = u ( 2,t ) = 0\). The analytical solution of this problem is \(u ( x,t ) = xt(x - 2)(t - 2)\). The graph of exact solution is shown in Figure 6. The graphs of numerical solutions for \(m = 16,32,64\) in some nodes \(( x,t ) \in [ 0,2 ] \times [ 0,2 ]\) are shown in Figures 7, 8, 9. From Examples 1 and Examples 2, it can be concluded that the numerical solutions approximate the exact solutions well as m grows.

Figure 6
figure 6

Exact solution for Example 2 .

Full size image
Figure 7
figure 7

Numerical solution of \(\pmb{m=16}\) for Example 2 .

Full size image
Figure 8
figure 8

Numerical solution of \(\pmb{m=32}\) for Example 2 .

Full size image
Figure 9
figure 9

Numerical solution of \(\pmb{m=64}\) for Example 2 .

Full size image

Example 3

Consider the following Poisson equation:

$$ \frac{\partial^{\nu} u ( x,t )}{\partial x^{\nu}} + \frac{\partial^{\gamma} u ( x,t )}{\partial t^{\gamma}} = x \bigl(6 + x^{2} \bigr)e^{ - t}, $$
(35)

with the Neuman boundary condition \(u ( x,0 ) = x^{3}\), \(u(0,t) = 0\), \(\frac{\partial u ( x,1 )}{\partial t} = - x^{3}e^{ - 1}\), \(\frac{\partial u ( 1,t )}{\partial x} = 3e^{ - t}\). The analytical solution of this problem for \(\nu = \gamma = 2\) is \(u ( x,t ) = x^{3}e^{ - t}\). Numerical results for some values of v, γ and m are listed in Table 1. The contrastive graphs for our method, the Legendre and the CAS wavelet methods for \(m = 16,32,64\) are shown in Figures 10, 11, 12. Table 1 shows that the numerical solutions are close to the analytical solution with m increasing and the fractional order of v, γ approaches 2. From Figures 10, 11, 12, it can be seen that our approach has a great advantage over CAS wavelet method. Moreover, when \(m = 64\), our method can achieve the same satisfactory results as the Legendre wavelet method.

Figure 10
figure 10

When \(\pmb{m=16}\) , the numerical solutions obtained by our method and those obtained by the Legendre and CAS wavelet methods at \(\pmb{t=0.3, 0.6, 0.95}\) ; see (a), (b), and (c).

Full size image
Figure 11
figure 11

When \(\pmb{m=32}\) , the numerical solutions obtained by our method and those obtained by the Legendre and CAS wavelet methods at \(\pmb{t=0.3, 0.6, 0.95}\) ; see (a), (b), and (c).

Full size image
Figure 12
figure 12

When \(\pmb{m=64}\) , the numerical solutions obtained by our method and those obtained by the Legendre and CAS wavelet methods at \(\pmb{t=0.3, 0.6, 0.95}\) ; see (a), (b), and (c).

Full size image
Table 1 Numerical results of some values of v , γ and m for Examples 3
Full size table

Example 4

Consider equation (35) with Neumann boundary conditions \(u(x,0) = 0\), \(u(0,t) = 0\), \(\frac{\partial u(x,2)}{\partial t} = 4x^{2}\), \(\frac{\partial u(2,t)}{\partial x} = 4t^{2}\). The analytical solution of this problem for \(v = \gamma = \frac{3}{2}\) is \(u(x,t) = x^{2}t^{2}\). Numerical results obtained by our method for \(m = 16,32,64,128\) in some nodes \(( x,t ) \in [ 0,2 ] \times [ 0,2 ]\) are listed in Table 2. In the processor of Inter(R) Core(TM) i3-4150 CPU @ 3.50 Hz, RAM 4.00 GB and 32 bit Windows operating system, we use MATLAB R2010b to obtain the computing results and computing time for our method and the Legendre wavelet method. The contrastive graph of computing time is shown in Figure 13 (unit: second). Figure 13 shows that our method consumed less computing time than the Legendre wavelet method. This example aims to illustrate that our method has the advantages of easy theoretical construction and being less time consuming.

Figure 13
figure 13

The computing time consumed by our method and that consumed by the Legendre wavelet method.

Full size image
Table 2 Numerical results of different m for Examples 4
Full size table

8 Conclusion

In the present analysis, we have applied two-dimensional block pulse functions to approximate the solutions of Poisson type equations with two kinds of boundary conditions. Using this method, the system of fractional partial differential equations has been reduced to solving a system of algebraic equations. The accuracy of the solutions of the original problems will be improved using suitable \(m_{1}\) and \(m_{2}\). The block pulse functions are orthogonal piecewise continuous functions which prompts flexibility for applications. Compared with other numerical methods, our proposed method has the great advantages of easy theoretical construction and being less time consuming. Additionally, the illustrated examples analyze and justify the ability and the reliability of the proposed method.