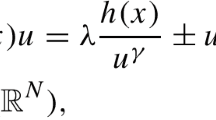Existence of a ground state solution for a class of singular elliptic problem in $\mathbb{R}^{N}$

Abstract

In this paper, we prove the existence of a ground state solution for a quasi-linear singular elliptic equation in $\mathbb{R}^{N}$ with exponential growth by using the mountain-pass theorem and the Vitali convergence theorem.

1 Introduction and main results

Let $\Omega\subset\mathbb{R}^{N}$ be a bounded smooth domain; there are many results on the following problem:

$$ \textstyle\begin{cases} -\operatorname{div}(\vert \triangledown u\vert ^{p-2}\triangledown u) =f(x, u), \quad x \in \Omega, \\ u\in W^{1, p}_{0}(\Omega), \end{cases} $$

(1.1)

when $p=2$, $\vert f(x, u)\vert \leq c(\vert u\vert +\vert u\vert ^{q-1})$, $1< q\leq 2^{*}=\frac{2N}{N-2}$, $N\geq3$, for the corresponding results one may refer to Brézis [1], Brézis and Nirenberg [2], Bartsch and Willem [3] and Capozzi, Fortunato and Palmieri [4]. Garcia and Alonso [5] generalized Brézis, Nirenberg’s existence and nonexistence results to p-Laplace equation. Moreover, let us consider the following semilinear Schrödinger equation:

$$ \textstyle\begin{cases} -\triangle u+V(x)u =f(x, u), \quad x \in \mathbb{R}^{N}, \\ u\in H_{0}^{1}(\mathbb{R}^{N}), \end{cases} $$

(1.2)

where $\vert f(x, u)\vert \leq c(\vert u\vert +\vert u\vert ^{q-1})$, $1< q\leq 2^{*}=\frac{2N}{N-2}$. Problem (1.2) is considered in many papers such as by Kryszewski and Szulkin [6], Alama and Li [7], Ding and Ni [8] and Jeanjean [9]. The Sobolev embedding theorems and critical point theory, in particular the mountain-pass theorem would play an important role in studying problems (1.1) and (1.2) since both of them have a variational structure. When $p = N$ and $f(x, u)$ behaves like $e^{\alpha \vert u\vert ^{\frac{N}{N-1}}}$ as $\vert u\vert \rightarrow\infty$, problem (1.1) was studied by Adimurthi [10], Adimurthi and Yadava [11], Ruf et al. [12, 13], do Ó [14], Panda [15], and the references therein, all these results are based on the Trudinger-Moser inequality [16–18] and critical point theory.

Let us consider the problem

$$ -\operatorname{div}\bigl(\vert \triangledown u\vert ^{N-2}\triangledown u\bigr)+V(x)\vert u\vert ^{N-2}u = \frac{f(x, u)}{\vert x\vert ^{\eta}},\quad x\in \mathbb{R}^{N} , $$

(1.3)

where $N\geq 2$, $0 \leq \eta < N$, $V : \mathbb{R}^{N}\rightarrow \mathbb{R}$ is a continuous function, $f (x, s)$ is continuous in $\mathbb{R}^{N}\times \mathbb{R}$ and behaves like $e^{\alpha \vert s\vert ^{\frac{N}{N-1}}}$ as $\vert s\vert \rightarrow\infty$. The problems of this type are important in many fields of sciences, notably the fields of electromagnetism, astronomy, and fluid dynamics, because they can be used to accurately describe the behavior of electric, gravitational, and fluid potentials. Many works focus on the subcritical and critical growth of the nonlinearity which allows us to treat the problem using general critical point theory. Problem (1.3) can be compared with (1.2) in this way: the Sobolev embedding theorem can be applied to (1.2), while the Trudinger-Moser type embedding theorem can be applied to (1.3). When $\eta = 0$, problem (1.3) was studied by Cao [19] in the case $N = 2$, by Panda [20], do Ó [21] and Alves and Figueiredo [22] in the general dimensional case. When $0 < \eta<N$, problem (1.3) is closely related to a singular Trudinger-Moser type inequality [23], Theorem 1.1 or [24], Theorem 3.

For the problem

$$ -\operatorname{div}\bigl(\vert \triangledown u\vert ^{N-2}\triangledown u\bigr)+V(x)\vert u\vert ^{N-2}u = \frac{f(x, u)}{\vert x\vert ^{\eta}}+\varepsilon h(x),\quad x\in \mathbb{R}^{N}, $$

(1.4)

when $\eta=0$, the multiplicity of the solutions of the problem (1.4) is proved by do Ó, Medeiros and Severo [25] using Ekeland variational principle and the mountain-pass theorem. When $\eta>0$, the existence of a nontrival weak solution of the problem (1.4) is proved by Adimurthi and Yang [23], furthermore, they get a weak solution of negative energy when ε is small enough, however, the difference of these two solutions has not been proved in Adimurthi and Yang [23]. In Yang [26], the author derives similar results for the bi-Laplacian operator in dimension four and Yang [27] constructs the existence and multiplicity of a weak solution for the N-Laplacian elliptic equation. Lam and Lu [28] considered the existence and multiplicity of a nontrivial weak solution for non-uniformly N-Laplacian elliptic equation.

For the problem

$$ \textstyle\begin{cases} -\triangle u =Q(x)f(u), \quad x \in \mathbb{R}^{N}, \\ u\in D^{1, 2}(\mathbb{R}^{N}), \end{cases} $$

(1.5)

where $N\geq 3$, f is continuous with subcritical growth and $Q \in L^{\infty}(\mathbb{R}^{N} )\cap L^{r} (\mathbb{R}^{N} )$, for some $r \geq 1$, is positive almost everywhere in $\mathbb{R}^{N}$, the existence of a ground state solution of problem (1.5) is proved by Alves, Montenegro and Souto [29]. Motivated by [29], Abreu [30] considered the problem

$$ \textstyle\begin{cases} -\triangle u =Q(x)\frac{f(u)}{\vert x\vert ^{\eta}}, \quad x \in \mathbb{R}^{2}, \\ u\in H_{0}^{1}(\mathbb{R}^{2}), \end{cases} $$

(1.6)

where $0 \leq \eta <\frac{1}{2}$, $f(s)$ is continuous and behaves like $e^{\alpha \vert s\vert ^{2}}$ when $\vert s\vert \rightarrow \infty$, $Q \in L^{\infty}(\mathbb{R}^{N} )\cap L^{r} (\mathbb{R}^{N} )$, for some $r \geq 1$, is positive almost everywhere in $\mathbb{R}^{N}$, Abreu [30] showed the existence of a ground state solution of problem (1.6) in $H_{0}^{1}(\mathbb{R}^{2})$.

In this paper, we consider the problem

$$ \textstyle\begin{cases} -\operatorname{div}(\vert \triangledown u\vert ^{N-2}\triangledown u)+V(x)\vert u\vert ^{N-2}u =Q(x)\frac{f(u)}{\vert x\vert ^{\eta}}, \quad x \in \mathbb{R}^{N}, \\ u\in W^{1, N}(\mathbb{R}^{N}), \end{cases}\displaystyle \hspace{90pt}(P_{\eta}) $$

where $N\geq2$, $0\leq\eta< N$, $V : \mathbb{R}^{N} \rightarrow \mathbb{R}$ is a continuous function satisfying the following hypothesis:

$(V_{0})$ :

$V(x) \geq V_{0 }> 0$.

Suppose $Q : \mathbb{R}^{N} \rightarrow\mathbb{ R}\cup\{-\infty, +\infty\}$ satisfying:

$(Q_{1})$ :

$Q>0$ is positive almost everywhere in $\mathbb{R}^{N}$.

$(Q_{2})$ :

$Q\in L^{\infty}(\mathbb{R}^{N})$.

Furthermore, we assume that $f : \mathbb{R} \rightarrow \mathbb{R}$ is a continuous function satisfying:

$(f_{0})$ :

$f (t) = o(\vert t\vert ^{N-1} )$ as $t \rightarrow 0$, i.e. $\lim_{t\rightarrow0}\frac{f(t)}{\vert t\vert ^{N-1}}=0$.

$(f_{1})$ :

$f(t)$ has exponential subcritical growth at +∞, i.e. for all $\alpha > 0$, we have

$$\lim_{\vert t\vert \rightarrow +\infty}\frac{f(t)}{e^{\alpha \vert t\vert ^{\frac{N}{N-1}}}}= 0. $$

$(f_{2})$ :

There exists $\theta>N$ such that

$$0 < \theta F(t) \leq tf(t),\quad \forall t\in \mathbb{R}\backslash\{0\}, $$

where $F(t)=\int_{0}^{t}f(s)\,ds$, this is the well-known Ambrosetti-Rabinowitz condition.

Define a function space

$$E=\biggl\{ u \in W^{1, N}\bigl(\mathbb{R}^{N}\bigr)\Bigm| \int_{\mathbb{R}^{N}}V(x)\vert u\vert ^{N}\,dx< \infty\biggr\} , $$

which is equipped with the norm

$$\Vert u\Vert = \biggl( \int_{\mathbb{R}^{N}}\vert \triangledown u\vert ^{N}+V(x)\vert u \vert ^{N}\,dx \biggr)^{\frac{1}{N}}, $$

then the assumption $V(x)\geq V_{0}>0$ implies E is a reflexive Banach space. For $0\leq \eta< N$, we define a singular eigenvalue by

$$\lambda_{\eta}=\inf_{u\in E\backslash\{0\}}\frac{\Vert u \Vert ^{N}}{\int_{\mathbb{R}^{N}}\vert Q(x)\vert \frac{\vert u\vert ^{N}}{\vert x\vert ^{\eta}}\,dx}. $$

If $\eta = 0$, obviously we have $\lambda_{0} > 0$. If $0 <\eta <N$, the continuous embedding of $E\hookrightarrow L^{q}(\mathbb{R}^{N})$ ($q \geq N$) and the Hölder inequality imply

$$\begin{aligned} & \int_{\mathbb{R}^{N}}\bigl\vert Q(x)\bigr\vert \frac{\vert u\vert ^{N}}{\vert x\vert ^{\eta}}\,dx \\ &\quad \leq \Vert Q\Vert _{L^{\infty}(\mathbb{R}^{N})} \int_{\{\vert x\vert >1\}}\vert u\vert ^{N}\,dx +\Vert Q\Vert _{L^{\infty}(\mathbb{R}^{N})} \biggl( \int_{\{\vert x\vert \leq1\}}\vert u\vert ^{Nt}\,dx \biggr)^{\frac{1}{t}} \biggl( \int_{\{\vert x\vert \leq1\}}\frac{1}{\vert x\vert ^{\eta t'}}\,dx \biggr)^{\frac{1}{t'}} \\ &\quad \leq C \int_{\mathbb{R}^{N}}\bigl(\vert u\vert ^{N}+\vert \triangledown u \vert ^{N}\bigr)\,dx, \end{aligned}$$

where $1/t + 1/t' = 1$, $0 < \eta t'< N$, and thus $\lambda_{\eta} > 0$ since $V\geq V_{0}>0$.

For all $q \geq N$, the embedding

$$E\hookrightarrow W^{1, N}\bigl(\mathbb{R}^{N}\bigr) \hookrightarrow L^{q}\bigl(\mathbb{R}^{N}\bigr) $$

is continuous. Furthermore, we see that the embedding $E\hookrightarrow L^{q}(\mathbb{R}^{N})$ ($q\geq N$) is compact (see [23]) if V satisfies the following hypothesis:

$(V_{1})$ :

$\frac{1}{V}\in L^{1}(\mathbb{R}^{N})$.

Definition 1

We say that $u\in E$ is a weak solution of problem $(P_{\eta} )$ if

$$\int_{\mathbb{R}^{N}}\bigl(\vert \triangledown u\vert ^{N-2} \triangledown u \triangledown \phi +V(x)\vert u\vert ^{N-2}u\phi \bigr)\,dx- \int_{\mathbb{R}^{N}}Q(x)\frac{f(u)}{\vert x\vert ^{\eta}}\phi \,dx=0,\quad \forall \phi \in E. $$

Define $I:E\rightarrow \mathbb{R}$ by

$$ I(u)=\frac{1}{N}\Vert u\Vert - \int_{\mathbb{R}^{N}}Q(x)\frac{F(u)}{\vert x\vert ^{\eta}}\,dx,\quad u\in E. $$

(1.7)

From condition $(f_{1})$, it follows that there exist positive constants α and $C_{1}$ such that

$$\int_{\mathbb{R}^{N}}\biggl\vert Q(x)\frac{F(u)}{\vert x\vert ^{\eta}}\biggr\vert \,dx \leq C_{1}\Vert Q\Vert _{L^{\infty}(\mathbb{R}^{N})} \int_{\mathbb{R}^{N}}\frac{(e^{\alpha \vert u\vert ^{\frac{N}{N-1}}}-S_{N-2}(\alpha, u))}{\vert x\vert ^{\eta}}\,dx,\quad \forall u\in E, $$

where $S_{N-2}(\alpha, u)=\sum_{k=0}^{N-2}\frac{\alpha^{k}\vert u\vert ^{kN/(N-1)}}{k!}$, thus, I is well defined thanks to the Trudinger-Moser inequality and $I\in C^{1}(E, \mathbb{R})$. A straightforward calculation shows that

$$\bigl\langle I'(u), \phi\bigr\rangle = \int_{\mathbb{R}^{N}}\vert \triangledown u\vert ^{N-2} \triangledown u \triangledown \phi \,dx+ \int_{\mathbb{R}^{N}}V(x)\vert u\vert ^{N-2}u\phi \,dx- \int_{\mathbb{R}^{N}}Q(x)\frac{f(u)}{\vert x\vert ^{\eta}}\phi \,dx, $$

for all $u, \phi\in E$, hence, a critical point of (1.7) is a weak solution of $(P_{\eta})$.

Definition 2

[31]

A solution u of problem $(P_{\eta})$ is said to be ground state if

$$I(u)=\inf\bigl\{ I(\omega):\omega \in W^{1, N}\bigl(\mathbb{R}^{N} \bigr)\backslash\{0\},I'(\omega)\omega=0 \bigr\} , $$

where $I :E \rightarrow \mathbb{R}$ is the functional associated to $(P_{\eta})$.

In this paper, we prove the existence of a ground state solution about problem $(P_{\eta})$ under weak conditions.

Theorem 1.1

Suppose $V(x) \geq V_{0 }> 0$ in $\mathbb{R}^{N}(N\geq2)$, $(V_{1})$, $(f_{0})$-$(f_{2})$, η and σ are two numbers which satisfy

$$ 0\leq\eta< \frac{N-1}{N},\qquad \sigma>\frac{N-\eta}{N-1-N\eta}. $$

(1.8)

Let the function Q satisfy $(Q_{1})$-$(Q_{2})$ and

$(Q_{3})$ :

$Q\in L^{r}(\mathbb{R}^{N})$, for some $r > \frac{N^{2}\sigma}{\sigma(N-1-2\eta)+\eta-N}$,

then $(P_{\eta})$ has a nontrivial solution. Furthermore, if the function f also satisfies

$(f_{4})$ :

$s \mapsto \frac{f(s)}{s^{N-1}}$ is increasing for $s>0$

then this solution is a ground state.

This paper is organized as follows: in Section 2, we introduce some preliminary results. In Section 3, we demonstrate Theorem 1.1.

2 Preliminaries

Lemma 2.1

Let θ be the number given by the condition $(f_{2})$ and $\{u_{n}\}$ be a sequence satisfying

$$\limsup_{n\rightarrow\infty} \Vert u_{n}\Vert ^{\frac{N}{N-1}} \leq \biggl(\frac{N\theta}{\theta-N} \biggr)^{\frac{1}{N-1}}c^{\frac{1}{N-1}}, $$

for some $c > 0$. Then there exist constants $\alpha > 0$, $t > 1$, $C > 0$, independent of n, such that

$$\int_{\mathbb{R}^{N}} \biggl(\frac{e^{\alpha \vert u_{n}\vert ^{\frac{N}{N-1}}}-S_{N-2}(\alpha, u_{n})}{\vert x\vert ^{\eta}} \biggr)^{t}\,dx \leq C, $$

for n large enough.

Proof

Let

$$ \alpha=\frac{\alpha_{N}}{\sigma} \biggl(1-\frac{\eta}{N} \biggr) \biggl(\frac{\theta-N}{N\theta} \biggr)\frac{1}{c}, $$

(2.1)

where $\alpha_{N}=N\omega_{N-1}^{1/(N-1)}$ and $\omega_{N-1}$ is the measure of the unit sphere in $\mathbb{R}^{N}$.

Since $0\leq\eta< N$, we have $\alpha>0$. Moreover, let

$$m:=\frac{1}{N} \biggl(N-1+\sigma\cdot\frac{N}{N-\eta} \biggr) \biggl( \frac{N\theta}{\theta-N} \biggr)^{\frac{1}{N-1}} c^{\frac{1}{N-1}}, $$

then by (1.8)

$$\biggl(\frac{N\theta}{\theta-N} \biggr)^{\frac{1}{N-1}}c^{\frac{1}{N-1}}< m, $$

hence, passing to a subsequence, there exists $n_{0}\in \mathbb{N}$ such that

$$\Vert u_{n}\Vert ^{\frac{N}{N-1}}< m,\quad \forall n\geq n_{0}. $$

From (1.8), we also have

$$\frac{N^{2}}{2N-1}< \frac{N^{2}\sigma}{N-\eta+N\sigma+N\sigma \eta}. $$

Let t satisfy

$$ \frac{N^{2}}{2N-1}< t< \frac{N^{2}\sigma}{N-\eta+N\sigma+N\sigma \eta}. $$

(2.2)

For such t, we have

$$\frac{N^{2}}{2N-1}< t< \biggl(1-\frac{\eta t}{N} \biggr)\frac{N^{2}\sigma}{N-\eta+N\sigma}. $$

Let $\beta\in \mathbb{R}$ such that

$$t< \beta< \biggl(1-\frac{\eta t}{N} \biggr)\frac{N^{2}\sigma}{N-\eta+N\sigma}= \biggl(1- \frac{\eta t}{N} \biggr)\frac{\alpha_{N}}{\alpha m}. $$

Notice $\frac{m}{\Vert u_{n}\Vert ^{\frac{N}{N-1}}}> 1$, using Lemma 2.1 in Yang [27], we have

$$\int_{\mathbb{R}^{N}}\frac{ (e^{\alpha \vert u_{n}\vert ^{\frac{N}{N-1}}}-S_{N-2}(\alpha, u_{n}) )^{t}}{\vert x\vert ^{\eta t}}\,dx\leq C \int_{\mathbb{R}^{N}}\frac{e^{\beta\alpha m(\frac{\vert u_{n}\vert }{\Vert u_{n}\Vert })^{\frac{N}{N-1}}}-S_{N-2}(\beta\alpha m, \frac{\vert u_{n}\vert }{\Vert u_{n}\Vert })}{\vert x\vert ^{\eta t}}\,dx, $$

for each $n\geq n_{0}$. By the choice of β, we have

$$\beta\alpha m< \biggl(1-\frac{\eta t}{N} \biggr)\alpha_{N}. $$

Then we conclude the proof by using the Trudinger-Moser inequality [23, 24]. □

Lemma 2.2

Suppose $\{u_{n}\}$ is bounded in E and the assumptions of $(Q_{1})$-$(Q_{3})$ and $(f_{0})$-$(f_{1})$ are satisfied. If

$$Q(x)\frac{\vert f(u_{n}(x))u_{n}(x)\vert }{\vert x\vert ^{\eta}}\rightarrow Q(x)\frac{\vert f(u(x))u(x)\vert }{\vert x\vert ^{\eta}}\quad \textit{a.e. in } \mathbb{R}^{N}, $$

then

$$ \int_{\mathbb{R}^{N}}Q(x)\frac{f(u_{n})u_{n}}{\vert x\vert ^{\eta}}\,dx\rightarrow \int_{\mathbb{R}^{N}}Q(x)\frac{f(u)u}{\vert x\vert ^{\eta}}\,dx. $$

(2.3)

Proof

From $(f_{0})$ and $(f_{1})$, for all $\varepsilon>0$ and α, there exist positive constants δ, K, C, such that

$$\bigl\vert f(s)s\bigr\vert \leq \varepsilon \vert s\vert ^{N}+ \varepsilon C\vert s\vert ^{N+1}\bigl[e^{\alpha s^{\frac{N}{N-1}}}-S_{N-2}( \alpha, s)\bigr]+\max_{\delta\leq \vert s\vert \leq K}\bigl\vert f(s)s\bigr\vert ,\quad \forall s\in \mathbb{R}. $$

For $R > 0$, then

$$\begin{aligned} & \int_{B_{R}(0)}Q(x)\frac{\vert f(u_{n})u_{n}\vert }{\vert x\vert ^{\eta}}\,dx \\ &\quad \leq \varepsilon \Vert Q\Vert _{L^{\infty}(\mathbb{R}^{N})} \int_{\mathbb{R}^{N}}\frac{\vert u_{n}\vert ^{N}}{\vert x\vert ^{\eta}}\,dx+ \varepsilon C\Vert Q\Vert _{L^{\infty}(\mathbb{R}^{N})} \int_{\mathbb{R}^{N}}\vert u_{n}\vert \frac{(e^{\alpha u_{n}^{\frac{N}{N-1}}}-S_{N-2}(\alpha, u_{n}))}{\vert x\vert ^{\eta}}\,dx \\ &\qquad {}+\max_{\delta\leq \vert s\vert \leq K}\bigl\vert f(s)s\bigr\vert \bigl\vert {B_{R}(0)}\bigr\vert . \end{aligned}$$

Here, $\vert {B_{R}(0)}\vert$ denotes the volume of the ball ${B_{R}(0)}$. We can consider $\alpha>0$ given by (2.1) and Lemma 2.1 implies that there exists $t > 1$ such that, up to a subsequence,

$$\frac{e^{\alpha u_{n}^{\frac{N}{N-1}}}-S_{N-2}(\alpha, u_{n})}{\vert x\vert ^{\eta}} \in L^{t}\bigl(\mathbb{R}^{N}\bigr), \quad \forall n\in\mathbb{ N} , $$

and there exists $C > 0$ such that

$$\int_{\mathbb{R}^{N}} \biggl(\frac{e^{\alpha \vert u_{n}\vert ^{\frac{N}{N-1}}}-S_{N-2}(\alpha, u_{n})}{\vert x\vert ^{\eta}} \biggr)^{t}\,dx \leq C,\quad \forall n\in \mathbb{N} . $$

By applying Hölder’s inequality with exponents t and its conjugate $t'$ and using a continuous embedding, we see that there exist positive constants $C_{1}$ and $C_{2}$ such that

$$ \int_{B_{R}(0)}Q(x)\frac{\vert f(u_{n})u_{n}\vert }{\vert x\vert ^{\eta}}\,dx\leq\varepsilon C_{1}+\varepsilon C_{2}+\max_{\delta\leq \vert s\vert \leq K}\bigl\vert f(s)s\bigr\vert \bigl\vert {B_{R}(0)}\bigr\vert . $$

(2.4)

On the other hand, for all $\varepsilon> 0$ and all $\alpha> 0$, there exists $C = C(\varepsilon, \alpha) > 0$ such that

$$\bigl\vert f(s)s\bigr\vert \leq \varepsilon \vert s\vert ^{N}+C\vert s\vert ^{N+1}\bigl(e^{\alpha s^{\frac{N}{N-1}}}-S_{N-2}( \alpha, s)\bigr),\quad \forall s\in \mathbb{R}. $$

Then we have

$$\begin{aligned} & \int_{\mathbb{R}^{N}\backslash B_{R}(0)}Q(x)\frac{\vert f(u_{n})u_{n}\vert }{\vert x\vert ^{\eta}}\,dx \\ &\quad \leq\varepsilon \Vert Q\Vert _{L^{\infty}(\mathbb{R}^{N})} \int_{\mathbb{R}^{N}\backslash B_{R}(0)}\frac{\vert u_{n}\vert ^{N}}{\vert x\vert ^{\eta}}\,dx \\ &\qquad {}+C \int_{\mathbb{R}^{N}\backslash B_{R}(0)}Q(x)\vert u_{n}\vert ^{N+1} \frac{(e^{\alpha u_{n}^{\frac{N}{N-1}}}-S_{N-2}(\alpha, u_{n}))}{\vert x\vert ^{\eta}}\,dx. \end{aligned}$$

By considering $\alpha > 0$ given by (2.1) and applying the Holder inequality with exponents r given by $(Q_{3})$, t given by (2.2), and $N^{2}$ such that

$$\frac{1}{r}+\frac{1}{t}+\frac{1}{N^{2}}=1, $$

from the Hölder inequality and there being a continuous embedding, there exist positive constants $C_{3}$ and $C_{4}$ such that

$$\int_{\mathbb{R}^{N}\backslash B_{R}(0)}Q(x)\frac{\vert f(u_{n})u_{n}\vert }{\vert x\vert ^{\eta}}\,dx\leq\varepsilon C_{3}+C_{4} \biggl( \int_{\mathbb{R}^{N}\backslash B_{R}(0)}Q(x)^{r}\,dx \biggr)^{\frac{1}{r}}. $$

Using $(Q_{3})$, we have

$$\int_{\mathbb{R}^{N}\backslash B_{R}(0)}Q(x)^{r}\,dx\rightarrow 0\quad \mbox{as } R \rightarrow +\infty. $$

Thus, for $R > 0$ large enough,

$$ \int_{\mathbb{R}^{N}\backslash B_{R}(0)}Q(x)\frac{\vert f(u_{n})u_{n}\vert }{\vert x\vert ^{\eta}}\,dx\leq\varepsilon C_{3}+\varepsilon C_{4}. $$

(2.5)

From (2.4) and (2.5), the sequence

$$\biggl\{ Q(x)\frac{\vert f(u_{n})u_{n}\vert }{\vert x\vert ^{\eta}}\biggr\} $$

is equi-integrable. If

$$Q(x)\frac{\vert f(u_{n}(x))u_{n}(x)\vert }{\vert x\vert ^{\eta}}\rightarrow Q(x)\frac{\vert f(u(x))u(x)\vert }{\vert x\vert ^{\eta}} \quad \mbox{a.e. in } \mathbb{R}^{N}, $$

Vitali’s theorem implies (2.3). □

Firstly one proves that functional I has the geometry of the mountain-pass theorem, more exactly, we have the following lemma.

Lemma 2.3

[23]

If $V(x) \geq V_{0 }> 0$ in $\mathbb{R}^{N}$, $(V_{1})$, $(f_{0})$-$(f_{2})$ are satisfied, then the functional I verifies the following properties:

• (i) There exist $r, \rho > 0$, such that when $\Vert u\Vert =r$,

  $$I(u)\geq \rho. $$

• (ii) There exists $e\in B_{r}^{c}(0)$ with $I(e)<0$.

By Lemma 2.3, using a version of the mountain-pass theorem without the Palais-Smale condition (see [31]), we obtain the existence of a sequence $\{u_{n}\}$ in E satisfying

$$ I(u_{n})\rightarrow c\quad \mbox{and} \quad I'(u_{n})\rightarrow 0\quad \mbox{in }X', $$

(2.6)

where $c=\inf_{\gamma\in \Gamma}\max_{t\in[0, 1]}I(\gamma(t))>0$, $\Gamma=\{\gamma \in C([0, 1], X): \gamma(0) = 0, I(\gamma(1)) < 0\}$.

Lemma 2.4

[23]

Suppose $V(x) \geq V_{0 }> 0$ in $\mathbb{R}^{N}$, $(V_{1})$, $(f_{0})$-$(f_{2})$ are satisfied, let $\{u_{n}\}$ be an arbitrary Palais-Smale sequence, then $\{u_{n}\}$ is bounded and there exists a subsequence of $\{u_{n}\}$ (still denoted by $\{u_{n}\}$), $u\in E$ such that

$$ \textstyle\begin{cases} Q(x)\frac{f(u_{n})}{\vert x\vert ^{\eta}}\rightarrow Q(x)\frac{f(u)}{\vert x\vert ^{\eta}}\quad \textit{strongly in } L^{1}_{\mathrm{loc}}(\mathbb{R}^{N}), \\ \triangledown u_{n}\rightarrow \triangledown u\quad \textit{almost everywhere in }\mathbb{R}^{N},\\ \vert \triangledown u_{n}\vert ^{N-2}\triangledown u_{n}\rightharpoonup \vert \triangledown u\vert ^{N-2}\triangledown u\quad \textit{weakly in } (L^{N/(N-1)}(\mathbb{R}^{N}))^{N} . \end{cases} $$

Furthermore, u is a weak solution of $(P_{\eta})$.

3 Proof of the theorem

Proof of Theorem 1.1

By Lemma 2.3 and Lemma 2.4, we see that the Palais-Smale sequence $\{u_{n}\}$ at the mountain pass level c is bounded in E and its weak limit u is a critical point of the functional I.

We will show that u is nonzero. Since $\{u_{n}\}$ is a Palais-Smale sequence, Lemma 2.2 implies that

$$\lim_{n\rightarrow\infty} \Vert u_{n}\Vert ^{N}=\lim _{n\rightarrow\infty} \int_{\mathbb{R}^{N}}Q(x)\frac{f(u_{n})u_{n}}{\vert x\vert ^{\eta}}\,dx= \int_{\mathbb{R}^{N}}Q(x)\frac{f(u)u}{\vert x\vert ^{\eta}}\,dx. $$

Recalling that u is a critical point of I, we conclude that

$$\lim_{n\rightarrow\infty} \Vert u_{n}\Vert ^{N}= \int_{\mathbb{R}^{N}}Q(x)\frac{f(u)u}{\vert x\vert ^{\eta}}\,dx=\Vert u\Vert ^{N}. $$

If $u\equiv0$, then

$$\lim_{n\rightarrow\infty} \Vert u_{n}\Vert ^{N}=0. $$

Since $I\in C^{1}(E, \mathbb{R})$, we have

$$I(u_{n})\rightarrow 0, $$

and it is a contradiction because $I(u_{n})\rightarrow c$ and $c > 0$. This way, we conclude that u is nonzero.

Now, we will show that u is a ground state. Setting

$$m=\inf_{u\in \Lambda}I(u),\quad \Lambda:=\bigl\{ u\in E\backslash\{0 \}:I'(u)u=0\bigr\} . $$

Since $\{u_{n}\}$ is a Palais-Smale sequence, we see that

$$\begin{aligned} 2c&=\liminf_{n\rightarrow\infty}2I(u_{n})=\liminf _{n\rightarrow\infty}\bigl(2I(u_{n})-I'(u_{n})u_{n} \bigr) \\ &=\liminf_{n\rightarrow\infty} \int_{\mathbb{R}^{N}}Q(x)\frac{(f(u_{n})u_{n}-2F(u_{n}))}{\vert x\vert ^{\eta}}\,dx. \end{aligned}$$

By Fatou’s lemma,

$$2c\geq \int_{\mathbb{R}^{N}}Q(x)\frac{(f(u)u-2F(u))}{\vert x\vert ^{\eta}}\,dx. $$

If u is a critical point of I, we have

$$2I(u)=\bigl(2I(u)-I'(u)u\bigr)= \int_{\mathbb{R}^{N}}Q(x)\frac{(f(u)u-2F(u))}{\vert x\vert ^{\eta}}\,dx. $$

Hence, we can conclude that $I(u) \leq c$, thus $m\leq c$. On the other hand, as in the proof of Theorem 3.1 in [32], let $u\in \Lambda$ and define $h:(0, +\infty)\rightarrow \mathbb{R}$ by $h(t)=I(tu)$. We see that h is differentiable and

$$h'(t)=I'(tu)u=t^{N-1}\Vert u\Vert ^{N}- \int_{\mathbb{R}^{N}}Q(x)\frac{f(tu)u}{\vert x\vert ^{\eta}}\,dx,\quad \forall t>0. $$

Since $I'(u)u=0$, we get

$$h'(t)=I'(tu)u-t^{N-1}I'(u)u, $$

so

$$h'(t)=t^{N-1} \int_{\mathbb{R}^{N}}\frac{Q(x)}{\vert x\vert ^{\eta}} \biggl(\frac{f(u)}{u^{N-1}}-\frac{f(tu)}{(tu)^{N-1}} \biggr)u^{N}\,dx,\quad \forall t>0. $$

Using the condition $(f_{4})$, we conclude that $h'(t)>0$ for $0< t<1$ and $h'(t)<0$ for $t>1$, since $h'(1)=0$, thus,

$$I(u)=\max_{t\geq0}I(tu). $$

Now, define $\gamma:[0, 1]\rightarrow E$, $\gamma(t)=tt_{0}u$, where $t_{0}$ is a real number which satisfies $I(t_{0}u)<0$, we have $\gamma\in \Gamma$, and therefore

$$c\leq\max_{t\in[0, 1]}I\bigl(\gamma(t)\bigr)\leq\max _{t\geq0}I(tu)=I(u), $$

$u\in \Lambda$ is arbitrary, $c\leq m$, thus $I(u)=c=m$. This ends the proof of Theorem 1.1. □