1 Introduction

In this paper we consider the following inverse heat conduction problem with only boundary value:

$$\begin{aligned}& u_{t}=u_{xx},\quad 0< x< 1, 0< t< 2\pi, \\& u(0,t)=f(t),\quad 0\le t\le2\pi, \\& u_{x}(0,t)=g(t), \quad 0\le t\le2\pi, \end{aligned}$$
(1.1)

where f and g are given. This problem is ill posed [1]. We want to recover the temperature distribution \(u(x,\cdot)\) for \(0< x\leq1\) from the boundary data f and g.

The inverse heat conduction problem (IHCP) arises from many physical and engineering disciplines. It is well known that the problem is severely ill posed in the Hadamard sense that the solution (if it exists) does not depend continuously on the given data, i.e., a small measurement error in the given data can cause an enormous error in the solution [2–4]. To overcome such difficulties, some regularization techniques are required [5]. The IHCP has been considered by many authors using different methods. These methods include the wavelet and wavelet-Galerkin method [6–9], the Tikhonov method [10], the mollification method [11–13], the fundamental solution method [14], the Fourier method [15], and so on.

To the best of the knowledge of the authors, the results available in the literature are mainly devoted to the IHCP with known initial-boundary value. However, in practical real-life problems we cannot know the initial condition because the heat process has already started before we estimate the problem. A few works are developed for the IHCP without initial value [1, 16]. Ginsberg [17] used a cutoff method for an IHCP with only boundary value and gave a Hölder type error estimate. Recently, Liu and Wei [18] used a quasi-reversibility regularization method for solving an IHCP without initial data. Yang and Fu [19] applied a simplified Tikhonov regularization method for determining the heat source. In this paper, we will use a modified Tikhonov regularization method to deal with the IHCP without initial value (1.1) and obtain an order optimal error estimate between the approximate solution and the exact solution.

The paper is organized as follows. In Section 2, we give the formulation of the solution for problem (1.1) and present some preliminary results. In Section 3, we prove the conditional stability for the IHCP (1.1) by using the Hölder inequality. Section 4 proposes a modified Tikhonov regularization method. An order optimal error estimate for the approximate solution is obtained with a suitable choice of regularization parameter. To verify the efficiency and accuracy of the proposed method for problem (1.1), we give two numerical examples in Section 5. A brief conclusion is given in Section 6.

2 Mathematical formulation and preliminaries

Throughout this paper, we use the following formulation and lemmas. For the IHCP (1.1), we want to determine the temperature distribution \(u(x,\cdot)\) for \(0< x\leq1\) from the Cauchy data f and g. Since the Cauchy data f and g are measured, there will be measurement errors, and we would actually have measured Cauchy data \(f^{\delta}, g^{\delta}\in L^{2}[0, 2\pi]\), for which

$$ \bigl\Vert f-f^{\delta}\bigr\Vert \le\delta,\qquad \bigl\Vert g-g^{\delta}\bigr\Vert \leq\delta, $$
(2.1)

where the constant \(\delta>0\) represents a bound on the measurement error, \(\|\cdot\|\) and \((\cdot,\cdot)\) denote the norm and inner product on \(L^{2}[0,2\pi]\), respectively.

In the following, we split the IHCP (1.1) into two independent IHCPs:

$$\begin{aligned}& v_{t}=v_{xx},\quad 0< x< 1, 0< t< 2\pi, \\& v(0,t)=f(t),\quad 0\le t\le2\pi, \\& v_{x}(0,t)=0,\quad 0\le t\le2\pi, \end{aligned}$$
(2.2)

and

$$\begin{aligned}& w_{t}=w_{xx},\quad 0< x< 1, 0< t< 2\pi, \\& w(0,t)=0,\quad 0\le t\le2\pi, \\& w_{x}(0,t)=g(t), \quad 0\le t\le2\pi. \end{aligned}$$
(2.3)

Let \(v(x,t)\) and \(w(x,t)\) be the solution of problems (2.2) and (2.3), respectively. Then \(u=v+w\) is the solution of problem (1.1). Therefore, we only need solve problems (2.2) and (2.3), respectively.

By the method of separation of variables, the exact solutions of problems (2.2) and (2.3) are given by

$$ v(x, t)=\sum^{+\infty}_{n=-\infty} \bigl(f(t),e^{int} \bigr)e^{int}\cosh (\sqrt{in}x) $$
(2.4)

and

$$ w(x, t)=\sum^{+\infty}_{n=-\infty} \frac{1}{\sqrt{in}} \bigl(g(t),e^{int} \bigr)e^{int}\sinh( \sqrt{in}x). $$
(2.5)

Then the exact solution of problem (1.1) is given by

$$ u(x, t)=\sum^{+\infty}_{n=-\infty} \biggl[ \bigl(f(t),e^{int}\bigr)e^{int}\cosh(\sqrt{in}x)+ \frac{(g(t),e^{int})}{\sqrt{in}}e^{int}\sinh(\sqrt{in}x) \biggr]. $$
(2.6)

We assume also that there exists an a priori condition for problem (1.1):

$$ \max \bigl\{ \bigl\Vert v(1,\cdot)\bigr\Vert _{p}, \bigl\Vert w(1,\cdot)\bigr\Vert _{p} \bigr\} \le E,\quad p\ge0, $$
(2.7)

where \(\|v(1,\cdot)\|_{p}= \|\sum^{+\infty}_{n=-\infty}(1+n^{2})^{p/2} (v(1,\cdot), e^{in(\cdot)}) e^{in(\cdot)} \|\).

In order to give an error estimate for the regularized solution, we need the following lemma whose proof is similar to that of Lemma 3.2 in [20].

Lemma 2.1

Let \(0< x\leq1\), \(0<2\alpha<1/e^{\sqrt[4]{3}} \). We have the following inequalities:

$$\begin{aligned}& \sup_{s\geq0}\frac{e^{xs}}{1+\alpha^{2}e^{2s}}\leq \alpha^{-x}, \end{aligned}$$
(2.8)
$$\begin{aligned}& \sup_{s\geq0}\frac{e^{(1+x)s}(1+s^{4})^{-\frac{p}{2}}}{1+ {\alpha}^{2}e^{2s}}\le\alpha^{-(1+x)} \bigl(- \ln(2\alpha) \bigr)^{-\frac{2p}{2p+1}}. \end{aligned}$$
(2.9)

We need also the following results.

Lemma 2.2

Let \(0< x\leq 1\), then there holds [18]:

$$\begin{aligned}& \lim_{n\rightarrow o}\frac{\sinh(\sqrt{in}x)}{\sqrt{in}}=x, \qquad \biggl\vert \frac{\sinh(\sqrt{in}x)}{\sqrt{in}}\biggr\vert \leq\sqrt{2}xe^{\sqrt{\frac{|n|}{2}}x},\quad n\in \mathbb{Z}, \end{aligned}$$
(2.10)
$$\begin{aligned}& \bigl\vert \cosh(\sqrt{in}x)\bigr\vert \leq e^{\sqrt{\frac{|n|}{2}}x}, \qquad \bigl\vert \sinh(\sqrt{in}x)\bigr\vert \leq e^{\sqrt{\frac{|n|}{2}}x}, \quad n\in \mathbb{Z}, \end{aligned}$$
(2.11)
$$\begin{aligned}& \bigl\vert \cosh(\sqrt{in})\bigr\vert \geq c e^{\sqrt{\frac{|n|}{2}}},\qquad \bigl\vert \sinh(\sqrt{in})\bigr\vert \geq c e^{\sqrt{\frac{|n|}{2}}}, \quad |n|\in \mathbb{N}^{+}, \end{aligned}$$
(2.12)

where \(c=(1-e^{-\sqrt{2}})/2\).

3 Conditional stability

In this section, we will provide the conditional stabilities for problems (2.2), (2.3), and (1.1), respectively.

Theorem 3.1

Let the a priori bound (2.7) hold and \(v(x, t)\) be the solution of problem (2.2) given by (2.4) with the exact data \(f(t)\), then for a fixed \(x\in(0,1)\) the following estimate holds:

$$ \bigl\Vert v(x,\cdot)\bigr\Vert \le c^{-x}E^{x} \Vert f\Vert ^{1-x}. $$
(3.1)

Proof

By the Hölder inequality and (2.4), we have

$$\begin{aligned} \bigl\Vert v(x,\cdot)\bigr\Vert ^{2}&=\Biggl\Vert \sum ^{+\infty}_{n=-\infty} \cosh(\sqrt{in}x) \bigl(f,e^{in(\cdot)} \bigr)e^{in(\cdot)} \Biggr\Vert ^{2}=\sum ^{+\infty}_{n=-\infty}\bigl\vert \cosh(\sqrt{in}x)\bigr\vert ^{2}\vert f_{n}\vert ^{2} \\ &= \sum^{+\infty}_{n=-\infty} \bigl(\bigl\vert \cosh( \sqrt{in}x)\bigr\vert ^{2}\vert f_{n}\vert ^{2x} \bigr)\vert f_{n}\vert ^{2(1-x)} \\ &\le \Biggl[\sum^{+\infty}_{n=-\infty} \bigl(\bigl\vert \cosh(\sqrt {in}x)\bigr\vert ^{2}\vert f_{n} \vert ^{2x} \bigr)^{\frac{1}{x}} \Biggr]^{x} \Biggl[\sum ^{+\infty}_{n=-\infty} \bigl(\vert f_{n} \vert ^{2(1-x)} \bigr)^{\frac {1}{1-x}} \Biggr]^{1-x} \\ &= \Biggl[\sum^{+\infty}_{n=-\infty}\bigl\vert \cosh( \sqrt{in}x)\bigr\vert ^{\frac {2}{x}}\vert f_{n}\vert ^{2} \Biggr]^{x} \Biggl[\sum^{+\infty}_{n=-\infty} \vert f_{n}\vert ^{2} \Biggr]^{1-x} \\ &= \Biggl[\sum^{+\infty}_{n=-\infty}\bigl\vert \cosh( \sqrt{in}x)\bigr\vert ^{\frac{2}{x}}\bigl\vert \cosh (\sqrt{in})\bigr\vert ^{-2}\bigl\vert \bigl(v(1, \cdot), e^{in(\cdot)}\bigr)\bigr\vert ^{2} \Biggr]^{x} \Vert f\Vert ^{2(1-x)} \\ &\le \Biggl[\sum^{+\infty}_{n=-\infty}\bigl\vert \cosh(\sqrt{in}x)\bigr\vert ^{\frac {2}{x}}\bigl\vert \cosh(\sqrt{in})\bigr\vert ^{-2}\bigl(1+n^{2}\bigr)^{p}\bigl\vert \bigl(v(1, \cdot), e^{in(\cdot )}\bigr)\bigr\vert ^{2} \Biggr]^{x} \Vert f\Vert ^{2(1-x)} \\ &\le\max_{n\in\mathbb{Z}} \bigl[\bigl\vert \cosh(\sqrt{in}x)\bigr\vert ^{2}\bigl\vert \cosh(\sqrt {in})\bigr\vert ^{-2x} \bigr]\bigl\Vert v(1, \cdot)\bigr\Vert _{p}^{2x} \Vert f \Vert ^{2(1-x)}. \end{aligned}$$

Using (2.11) and (2.12), we have

$$ \bigl\vert \cosh(\sqrt{in}x)\bigr\vert ^{2}\bigl\vert \cosh( \sqrt{in})\bigr\vert ^{-2x}\le \bigl(e^{\sqrt{\vert n\vert /2}x} \bigr)^{2}\bigl(ce^{\sqrt{\vert n\vert /2}}\bigr)^{-2x}=c^{-2x}, \quad \vert n\vert \in\mathbb{N}^{+}, $$

then we get

$$ \max_{n\in\mathbb{Z}} \bigl[\bigl\vert \cosh(\sqrt{in}x)\bigr\vert ^{2}\bigl\vert \cosh(\sqrt {in})\bigr\vert ^{-2x} \bigr]= \max_{n\in\mathbb{Z}} \biggl\{ 1,\max_{n\in\mathbb {N}^{+}} \frac{\vert \cosh(\sqrt{in}x)\vert ^{2}}{\vert \cosh(\sqrt{in})\vert ^{2x}} \biggr\} \le c^{-2x}. $$

Combining with the a priori bound (2.7), we obtain

$$ \bigl\Vert v(x,\cdot)\bigr\Vert ^{2}\le c^{-2x}E^{2x} \Vert f\Vert ^{2(1-x)}. $$

The proof is completed. □

Remark 3.2

If \(v_{1}(x, t)\) and \(v_{2}(x, t)\) are the solutions of problem (2.2) with the exact data \(f_{1}(t)\) and \(f_{2}(t)\), respectively, then for a fixed \(x\in(0,1)\) we have

$$ \bigl\Vert v_{1}(x,\cdot)-v_{2}(x,\cdot) \bigr\Vert \le c^{-x}E^{x}\bigl\Vert f_{1}( \cdot)-f_{2}(\cdot)\bigr\Vert ^{1-x}. $$
(3.2)

Similarly, we have the following results.

Theorem 3.3

Suppose that \(w(x, t)\) is the solution of problem (2.3) given by (2.5) with the exact data \(g(t)\) and the a priori bound (2.7) is valid, then for a fixed \(x\in(0,1)\) the following estimate holds:

$$ \bigl\Vert w(x,\cdot)\bigr\Vert \le c^{-x}( \sqrt{2}x)^{1-x}E^{x}\Vert g\Vert ^{1-x}. $$
(3.3)

Proof

Using the Hölder inequality and (2.5), we have

$$\begin{aligned} \bigl\Vert w(x,\cdot)\bigr\Vert ^{2}&=\Biggl\Vert \sum ^{+\infty}_{n=-\infty} \frac{\sinh(\sqrt{in}x)}{\sqrt{in}}\bigl(g,e^{in(\cdot)} \bigr)e^{in(\cdot)} \Biggr\Vert ^{2}=\sum ^{+\infty}_{n=-\infty}\biggl\vert \frac{\sinh(\sqrt {in}x)}{\sqrt{in}}\biggr\vert ^{2}\vert g_{n}\vert ^{2} \\ &= \sum^{+\infty}_{n=-\infty} \bigl(\bigl\vert \bigl( \sinh(\sqrt{in}x)\bigr)/\sqrt {in}\bigr\vert ^{2}\vert g_{n}\vert ^{2x} \bigr)\vert g_{n}\vert ^{2(1-x)} \\ &\le \Biggl[\sum^{+\infty}_{n=-\infty} \bigl(\bigl\vert \bigl(\sinh(\sqrt{in}x)\bigr)/\sqrt {in}\bigr\vert ^{2} \vert g_{n}\vert ^{2x} \bigr)^{\frac{1}{x}} \Biggr]^{x} \Biggl[\sum^{+\infty}_{n=-\infty} \vert g_{n}\vert ^{2} \Biggr]^{1-x} \\ &= \Biggl[\sum^{+\infty}_{n=-\infty}\biggl\vert \frac{\sinh(\sqrt{in}x)}{\sqrt {in}}\biggr\vert ^{\frac{2}{x}}\biggl\vert \frac{\sinh(\sqrt{in})}{\sqrt{in}} \biggr\vert ^{-2}\bigl\vert \bigl(w(1, \cdot), e^{in(\cdot)}\bigr) \bigr\vert ^{2} \Biggr]^{x} \Vert g\Vert ^{2(1-x)} \\ &\le \Biggl[\sum^{+\infty}_{n=-\infty}\biggl\vert \frac{\sinh(\sqrt {in}x)}{\sqrt{in}}\biggr\vert ^{\frac{2}{x}}\biggl\vert \frac{\sinh(\sqrt{in})}{\sqrt {in}} \biggr\vert ^{-2}\bigl(1+n^{2}\bigr)^{p}\bigl\vert \bigl(w(1, \cdot), e^{in(\cdot)}\bigr)\bigr\vert ^{2} \Biggr]^{x} \Vert g\Vert ^{2(1-x)} \\ &\le\max_{n\in\mathbb{Z}} \biggl[\biggl\vert \frac{\sinh(\sqrt{in}x)}{\sqrt {in}}\biggr\vert ^{2}\biggl\vert \frac{\sinh(\sqrt{in})}{\sqrt{in}} \biggr\vert ^{-2x} \biggr]\bigl\Vert w(1, \cdot)\bigr\Vert _{p}^{2x} \Vert g\Vert ^{2(1-x)}. \end{aligned}$$

From (2.10)-(2.12), we get

$$\begin{aligned} \biggl\vert \frac{\sinh(\sqrt{in}x)}{\sqrt{in}}\biggr\vert ^{2}\biggl\vert \frac{\sinh (\sqrt{in})}{\sqrt{in}}\biggr\vert ^{-2x} &=\biggl\vert \frac{\sinh(\sqrt{in}x)}{\sqrt{in}} \biggr\vert ^{2(1-x)}\biggl\vert \frac {\sinh(\sqrt{in}x)}{\sinh(\sqrt{in})}\biggr\vert ^{2x} \\ &\le \bigl(\sqrt{2}xe^{\sqrt{|n|/2}x} \bigr)^{2(1-x)} \biggl( \frac{e^{\sqrt {|n|/2}x}}{c e^{\sqrt{|n|/2}}} \biggr)^{2x} \\ &=c^{-2x} (\sqrt{2}x )^{2(1-x)},\quad |n|\in\mathbb{N}^{+}, \end{aligned}$$

so

$$\begin{aligned} \max_{n\in\mathbb{Z}} \biggl[\biggl\vert \frac{\sinh(\sqrt{in}x)}{\sqrt {in}}\biggr\vert ^{2}\biggl\vert \frac{\sinh(\sqrt{in})}{\sqrt{in}} \biggr\vert ^{-2x} \biggr] &=\max_{n\in\mathbb{Z}} \biggl\{ x^{2},\max_{n\in\mathbb{N}^{+}} \frac{|(\sinh (\sqrt{in}x))/\sqrt{in}|^{2}}{|(\sinh(\sqrt{in}))/\sqrt{in}|^{2x}} \biggr\} \\ &\le c^{-2x} (\sqrt{2}x )^{2(1-x)}. \end{aligned}$$

Combining with (2.7), we obtain

$$ \bigl\Vert w(x,\cdot)\bigr\Vert ^{2}\le c^{-2x} ( \sqrt{2}x )^{2(1-x)}E^{2x}\Vert g\Vert ^{2(1-x)}. $$

Estimate (3.3) is proved. □

Remark 3.4

If \(w_{1}(x, t)\) and \(w_{2}(x, t)\) are the solutions of problem (2.3) with the exact data \(g_{1}(t)\) and \(g_{2}(t)\), respectively, then for a fixed \(x\in(0,1)\) we have

$$ \bigl\Vert w_{1}(x,\cdot)-w_{2}(x,\cdot) \bigr\Vert \le c^{-x} (\sqrt{2}x )^{(1-x)}E^{x}\bigl\Vert g_{1}(\cdot)-g_{2}(\cdot)\bigr\Vert ^{1-x}. $$
(3.4)

From Theorems 3.1 and 3.3, we then obtain the following theorem.

Theorem 3.5

Let the a priori bound (2.7) hold and \(u(x, t)\) be the solution of problem (1.1) given by (2.6) with the exact data \(f(t)\) and \(g(t)\), then for a fixed \(x\in(0,1)\) we have the following estimate:

$$ \bigl\Vert u(x,\cdot)\bigr\Vert \le c^{-x}E^{x} \Vert f\Vert ^{1-x}+c^{-x}(\sqrt{2}x)^{1-x}E^{x} \Vert g\Vert ^{1-x}. $$
(3.5)

Remark 3.6

If \(u_{1}(x, t)\) and \(u_{2}(x, t)\) are the solutions of problem (1.1) with the exact data pairs \([f_{1}(t), g_{1}(t)]\) and \([f_{2}(t), g_{2}(t)]\), respectively, then for a fixed \(x\in(0,1)\) we get

$$ \bigl\Vert u_{1}(x,\cdot)-u_{2}(x,\cdot) \bigr\Vert \le c^{-x}E^{x}\bigl\Vert f_{1}( \cdot)-f_{2}(\cdot)\bigr\Vert ^{1-x}+ c^{-x} ( \sqrt{2}x )^{(1-x)}E^{x}\bigl\Vert g_{1}( \cdot)-g_{2}(\cdot)\bigr\Vert ^{1-x}. $$
(3.6)

4 Regularization and error estimates

Since Cauchy problems (2.2) and (2.3) are all severely ill posed, we should apply a regularization method to solve them.

4.1 Regularization and error estimate for problem (2.2)

For problem (2.2), we define an operator \(K:v(x,\cdot)\rightarrow f(\cdot)\), then problem (2.2) can be rewritten as the following operator equation:

$$ Kv(x,t)=f(t),\quad 0< x\leq1. $$
(4.1)

Combining with equation (2.4), we have

$$ Kv(x,t)=\sum^{+\infty}_{n=-\infty} \bigl(v(x, t), e^{int}\bigr) \bigl(\cosh(\sqrt {in}x)\bigr)^{-1}e^{int}. $$
(4.2)

Consequently, K is an operator with eigenvalues

$$ k_{n}=\bigl(\cosh(\sqrt{in}x)\bigr)^{-1}. $$
(4.3)

For disturbed data \(f^{\delta}(t)\), we use the Tikhonov regularization method, which seeks a function \(v^{\delta}_{\alpha}(x,\cdot)\) from minimizing quadratic functional

$$ J_{\alpha}\bigl(v^{\delta}\bigr):={\bigl\Vert Kv^{\delta}-f^{\delta}\bigr\Vert }^{2}+{ \alpha}^{2}{\bigl\Vert v^{\delta}\bigr\Vert }^{2}. $$
(4.4)

According to Theorem 2.11 of [21], this Tikhonov functional \(J_{\alpha}\) has a unique minimum \(v^{\delta}_{\alpha}(x,\cdot)\) which is the unique solution of the normal equation

$$ K^{\ast}Kv^{\delta}_{\alpha}+ \alpha^{2} v^{\delta}_{\alpha}=K^{\ast}f^{\delta}, \quad \alpha>0, $$
(4.5)

here \(K^{\ast}\) is the adjoint of K. Using the properties of the inner product, we obtain the eigenvalues of operator \(K^{\ast}\):

$$ \overline{k}_{n}=\overline{\bigl(\cosh(\sqrt{in}x) \bigr)^{-1}}, $$
(4.6)

where the symbol \(\overline{h(\cdot)}\) denotes the complex conjugate of the function \(h(\cdot)\). Combining (4.2), (4.3), (4.6) with (4.5), we get

$$ \sum^{+\infty}_{n=-\infty}\bigl(\overline{k}_{n}k_{n}+ \alpha^{2}\bigr) \bigl(v^{\delta}_{\alpha}(x, t), e^{int}\bigr) e^{int}=\sum^{+\infty}_{n=-\infty} \overline{k}_{n} \bigl(f^{\delta}(t), e^{int}\bigr) e^{int}. $$

This yields

$$\begin{aligned} v^{\delta}_{\alpha}(x, t)&=\sum ^{+\infty}_{n=-\infty}\bigl(v^{\delta}_{\alpha}(x, t), e^{int}\bigr) e^{int} =\sum^{+\infty}_{n=-\infty} \frac{\overline{k}_{n}}{|k_{n}|^{2}+\alpha^{2}} \bigl(f^{\delta}(t),e^{int}\bigr) e^{int} \\ &=\sum^{+\infty}_{n=-\infty}\frac{\cosh(\sqrt{in}x)}{1+\alpha^{2}|\cosh (\sqrt{in}x)|^{2}} \bigl(f^{\delta}(t),e^{int}\bigr) e^{int}. \end{aligned}$$
(4.7)

We call \(v^{\delta}_{\alpha}(x,t)\) given by (4.7) the Tikhonov approximate solution of problem (2.2). In order to derive the error estimate between the regularized solution and the exact solution, we replace the original filter \(\frac{1}{1+\alpha^{2}|\cosh(\sqrt{in}x)|^{2}}\) with another filter \(\frac{1}{1+\alpha^{2}|\cosh(\sqrt{in})|^{2}}\). Thus, the modified regularized solution of problem (2.2) becomes

$$ v^{\delta,\ast}_{\alpha}(x, t):=\sum ^{+\infty}_{n=-\infty}\frac{\cosh (\sqrt{in}x)}{1+\alpha^{2}|\cosh(\sqrt{in})|^{2}} \bigl(f^{\delta}(t),e^{int} \bigr) e^{int}. $$
(4.8)

We then have an error estimate for the modified Tikhonov approximate solution of problem (2.2).

Theorem 4.1

Let \(v(x,t)\) given by (2.4) and \(v^{\delta,\ast}_{\alpha}(x,t)\) given by (4.8) be the exact solution and modified Tikhonov regularization solution of problem (2.2), respectively. Suppose that the noisy data \(f^{\delta}(t)\) satisfies (2.1) and the a priori condition (2.7) is valid. If \(0<2\alpha<1/e^{\sqrt[4]{3}} \) and we select the regularization parameter α as

$$ \alpha=(\delta/E) \bigl(\ln(E/\delta) \bigr)^{\frac{2p}{2p+1}}, $$
(4.9)

then for a fixed \(x\in(0,1]\), we have the following stability estimate:

$$ \bigl\Vert v(x,\cdot)-v^{\delta,\ast}_{\alpha}(x,\cdot) \bigr\Vert \le c^{-x}E^{x}\delta^{1-x} \biggl(\ln \frac{E}{\delta} \biggr)^{\frac{-2p}{2p+1}x} \bigl[1+c^{-1}+o(1) \bigr], \quad \delta\to0 $$
(4.10)

Proof

By using the triangle inequality, with (2.4) and (4.8), we have

$$\begin{aligned} \bigl\Vert v(x,\cdot)-v^{\delta,\ast}_{\alpha}(x,\cdot)\bigr\Vert =& \Biggl\Vert \sum^{+\infty}_{n=-\infty}k_{n}^{-1} \biggl[\bigl(f, e^{in(\cdot)}\bigr)- \frac{(f^{\delta}, e^{in(\cdot)})}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}}\biggr] e^{in(\cdot)} \Biggr\Vert \\ \le&\Biggl\Vert \sum^{+\infty}_{n=-\infty} \frac{k_{n}^{-1} \alpha^{2}|\cosh(\sqrt{in})|^{2}}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}} \bigl(f, e^{in(\cdot)}\bigr) e^{in(\cdot)}\Biggr\Vert \\ &{}+\Biggl\Vert \sum^{+\infty}_{n=-\infty} \frac{k_{n}^{-1}}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}} \bigl(f-f^{\delta}, e^{in(\cdot)}\bigr) e^{in(\cdot)} \Biggr\Vert \\ \le&\alpha^{2}\sup_{n\in\mathbb{Z}}\frac{|\cosh(\sqrt{in}x)\overline{\cosh (\sqrt{in})}|(1+n^{2})^{-\frac{p}{2}}}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}} \\ &{}\times\Biggl\Vert \sum^{+\infty}_{n=-\infty }\bigl(1+|n|^{2} \bigr)^{\frac{p}{2}} \bigl(v(1,\cdot), e^{in(\cdot)}\bigr) e^{in(\cdot)} \Biggr\Vert \\ &{}+\sup_{n\in\mathbb{Z}}\frac{|\cosh(\sqrt{in}x)|}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}}\Biggl\Vert \sum ^{+\infty}_{n=-\infty} \bigl(f-f^{\delta}, e^{in(\cdot)} \bigr) e^{in(\cdot)}\Biggr\Vert \\ =&\alpha^{2}\sup_{n\in\mathbb{Z}}A(n) \bigl\Vert v(1,\cdot) \bigr\Vert _{p} +\sup_{n\in\mathbb{Z}}B(n)\bigl\Vert f-f^{\delta}\bigr\Vert , \end{aligned}$$

where

$$ A(n)=\frac{|\cosh(\sqrt{in}x)\overline{\cosh(\sqrt{in})}|(1+n^{2})^{-\frac{p}{2}}}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}},\qquad B(n)=\frac{|\cosh(\sqrt{in}x)|}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}}. $$

Let \(s=\sqrt{|n|/2}\). Using the inequalities (2.11)-(2.12) and (2.8), we can get

$$ B(n)=\frac{|\cosh(\sqrt{in}x)|}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}}\leq\frac{e^{\sqrt{|n|/2}x}}{ 1+(c\alpha)^{2}e^{\sqrt{2|n|}}}=\frac{e^{xs}}{ 1+(c\alpha)^{2}e^{2s}}\leq(c \alpha)^{-x},\quad |n|\in\mathbb{N}^{+}. $$

Thus, we have

$$\begin{aligned} \sup_{n\in\mathbb{Z}}B(n)&=\max\biggl\{ \frac{1}{1+\alpha^{2}}, \sup_{|n|\in \mathbb{N}^{+}}\frac{|\cosh(\sqrt{in}x)|}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}}\biggr\} \\ &=\max \biggl\{ \frac{1}{1+\alpha^{2}}, (c\alpha)^{-x} \biggr\} =(c \alpha)^{-x}. \end{aligned}$$
(4.11)

Analogously, we can estimate \(\sup_{n\in\mathbb{Z}}A(n)\). From the inequalities (2.11)-(2.12) and (2.9), we get

$$\begin{aligned} A(n)&=\frac{|\cosh(\sqrt{in}x)\overline{\cosh(\sqrt {in})}|(1+n^{2})^{-\frac{p}{2}}}{ 1+\alpha^{2}|\cosh(\sqrt{in})|^{2}}\leq\frac{e^{\sqrt {|n|/2}(x+1)}(1+n^{2})^{-\frac{p}{2}}}{ 1+(c\alpha)^{2}e^{\sqrt{2|n|}}} \\ &\leq\frac{e^{(x+1)s}(1+s^{4})^{-\frac{p}{2}}}{ 1+(c\alpha)^{2}e^{2s}}\leq(c\alpha)^{-(x+1)}\biggl(\ln\frac{1}{2\alpha } \biggr)^{-\frac{2p}{2p+1}}, \quad |n|\in\mathbb{N}^{+}. \end{aligned}$$

Then we have

$$ \sup_{n\in\mathbb{Z}}A(n)= \max \biggl\{ \frac{1}{1+\alpha^{2}}, (c\alpha)^{-(x+1)}\biggl(\ln\frac{1}{2\alpha }\biggr)^{-\frac{2p}{2p+1}} \biggr\} =(c\alpha)^{-(x+1)}\biggl(\ln\frac{1}{2\alpha }\biggr)^{-\frac{2p}{2p+1}}. $$
(4.12)

Combining with (4.11)-(4.12), conditions (2.7), (2.1) and the choice of α given by (4.9), we obtain

$$\begin{aligned} \bigl\Vert v(x,\cdot)-v^{\delta,\ast}_{\alpha}(x,\cdot)\bigr\Vert \le& c^{-(x+1)} \alpha^{1-x}\biggl(\ln\frac{1}{2\alpha} \biggr)^{-\frac{2p}{2p+1}} E +(c\alpha)^{-x} \delta \\ \le& c^{-(x+1)}E \biggl(\frac{\delta}{E} \biggl(\ln\frac{E}{\delta} \biggr)^{\frac{2p}{2p+1}} \biggr)^{1-x} \biggl(\ln \biggl(\frac{E}{2\delta} \biggl(\ln\frac{E}{\delta} \biggr)^{-\frac {2p}{2p+1}} \biggr) \biggr)^{-\frac{2p}{2p+1}} \\ &{}+ \biggl(\frac{c\delta}{E} \biggl(\ln\frac{E}{\delta} \biggr)^{\frac {2p}{2p+1}} \biggr)^{-x} \delta \\ =&c^{-x}E^{x}\delta^{1-x} \biggl(\ln \frac{E}{\delta} \biggr)^{\frac{-2p}{2p+1}x} \biggl[c^{-1} \biggl( \frac{\ln\frac{E}{\delta }}{\ln\frac{E}{2\delta}-\frac{2p}{2p+1}\ln (\ln\frac{E}{\delta } )} \biggr)^{\frac{2p}{2p+1}}+1 \biggr]. \end{aligned}$$

Note that \(\frac{\ln(E/\delta)}{ \ln\frac{E}{2\delta}-\frac{2p}{2p+1}\ln (\ln\frac{E}{\delta} )}\to1\) for \(\delta\to0\). The proof is completed. □

4.2 Regularization and error estimate for problem (2.3)

For problem (2.3), the Tikhonov method involves minimizing the quadratic functional:

$$ {\bigl\Vert Tw^{\delta}-g^{\delta}\bigr\Vert }^{2}+{\alpha}^{2}{\bigl\Vert w^{\delta}\bigr\Vert }^{2}, $$
(4.13)

where \(T:w(x,\cdot)\rightarrow g(\cdot)\) is a forward operator. We know that the above Tikhonov functional has a unique minimum \(w^{\delta}_{\alpha}(x,\cdot)\) which is the unique solution of the normal equation

$$ T^{\ast}Tw^{\delta}_{\alpha}+ \alpha^{2} w^{\delta}_{\alpha}=T^{\ast}g^{\delta}, \quad \alpha>0. $$
(4.14)

We can obtain the Tikhonov regularized solution of problem (2.3):

$$ w^{\delta}_{\alpha}(x, t) =\sum ^{+\infty}_{n=-\infty}\frac{t_{n}^{-1}}{1+\alpha^{2}|\frac{\sinh(\sqrt {in}x)}{\sqrt{in}}|^{2}} \bigl(g^{\delta}(t),e^{int} \bigr) e^{int}, $$
(4.15)

where \(t_{n}=\frac{\sqrt{in}}{\sinh(\sqrt{in}x)}\) is the eigenvalues of operator T. Similarly, we use the filter \(\frac{1}{1+\alpha^{2} |\sinh(\sqrt{in})|^{2}}\) to replace the original filter \(\frac{1}{1+\alpha^{2}|\frac{\sinh(\sqrt{in}x)}{\sqrt{in}}|^{2}}\). Therefore, we get the modified regularized solution of problem (2.3):

$$ w^{\delta,\ast}_{\alpha}(x, t) =\sum ^{+\infty}_{n=-\infty}\frac{t_{n}^{-1}}{1+\alpha^{2}|\sinh(\sqrt {in})|^{2}} \bigl(g^{\delta}(t),e^{int} \bigr) e^{int}. $$
(4.16)

Theorem 4.2

Suppose that \(w(x,t)\) is the exact solution given by (2.5), and \(w^{\delta,\ast}_{\alpha}(x,t)\) given by (4.16) is the modified Tikhonov regularization solution of problem (2.3). Let the noisy data \(g^{\delta}(t)\) satisfy (2.1) and the a priori condition (2.7) be valid. If \(0<2\alpha<1/e^{\sqrt[4]{3}} \) and the regularization parameter is given by (4.9). Then for a fixed \(x\in(0,1]\), we have

$$ \bigl\Vert w(x,\cdot)-w^{\delta,\ast}_{\alpha}(x,\cdot) \bigr\Vert \le c^{-x}E^{x}\delta^{1-x} \biggl(\ln \frac{E}{\delta} \biggr)^{\frac{-2p}{2p+1}x} \bigl[\sqrt{2}x+c^{-1}+o(1) \bigr], \quad \delta\to0. $$
(4.17)

Proof

By using the triangle inequality, with (2.5) and (4.16), we have

$$\begin{aligned} \bigl\Vert w(x,\cdot)-w^{\delta,\ast}_{\alpha}(x,\cdot)\bigr\Vert =& \Biggl\Vert \sum^{+\infty}_{n=-\infty}t_{n}^{-1} \biggl[\bigl(g, e^{in(\cdot)}\bigr)- \frac{(g^{\delta}, e^{in(\cdot)})}{ 1+\alpha^{2}|\sinh(\sqrt{in})|^{2}}\biggr] e^{in(\cdot)} \Biggr\Vert \\ \le&\alpha^{2}\sup_{n\in\mathbb{Z}}\frac{|\sinh(\sqrt{in}x)\overline{\sinh (\sqrt{in})}|(1+n^{2})^{-\frac{p}{2}}}{ 1+\alpha^{2}|\sinh(\sqrt{in})|^{2}} \\ &{}\times \Biggl\Vert \sum^{+\infty}_{n=-\infty }\bigl(1+|n|^{2} \bigr)^{\frac{p}{2}} \bigl(w(1,\cdot), e^{in(\cdot)}\bigr) e^{in(\cdot)} \Biggr\Vert \\ &{}+\sup_{n\in\mathbb{Z}}\frac{|(\sinh(\sqrt{in}x))/\sqrt{in}|}{ 1+\alpha^{2}|\sinh(\sqrt{in})|^{2}} \Biggl\Vert \sum ^{+\infty}_{n=-\infty} \bigl(g-g^{\delta}, e^{in(\cdot)} \bigr) e^{in(\cdot)}\Biggr\Vert \\ =:&\alpha^{2}\sup_{n\in\mathbb{Z}}C(n) \bigl\Vert w(1,\cdot) \bigr\Vert _{p} +\sup_{n\in\mathbb{Z}}D(n)\bigl\Vert f-f^{\delta}\bigr\Vert . \end{aligned}$$

Using the methods dealing with \(\sup_{n\in\mathbb{Z}}A(n)\) and \(\sup_{n\in\mathbb{Z}}B(n)\), with (2.10)-(2.12), (2.8), and (2.9), we obtain

$$ \sup_{n\in\mathbb{Z}}C(n)\leq(c\alpha)^{-(x+1)} \biggl(\ln\frac{1}{2\alpha }\biggr)^{-\frac{2p}{2p+1}},\qquad \sup _{n\in\mathbb{Z}}D(n)\leq\sqrt{2}x(c\alpha)^{-x}. $$
(4.18)

Combining with (4.18), conditions (2.7), (2.1), and the choice of α given by (4.9), we get

$$\begin{aligned} \bigl\Vert w(x,\cdot)-w^{\delta,\ast}_{\alpha}(x,\cdot)\bigr\Vert & \le c^{-(x+1)} \alpha^{1-x}\biggl(\ln\frac{1}{2\alpha} \biggr)^{-\frac{2p}{2p+1}} E +\sqrt{2}x(c\alpha)^{-x} \delta \\ &\le c^{-x}E^{x}\delta^{1-x} \biggl(\ln \frac{E}{\delta} \biggr)^{\frac{-2p}{2p+1}x} \biggl[c^{-1} \biggl( \frac{\ln\frac{E}{\delta }}{\ln\frac{E}{2\delta}-\frac{2p}{2p+1}\ln (\ln\frac{E}{\delta } )} \biggr)^{\frac{2p}{2p+1}}+\sqrt{2}x \biggr]. \end{aligned}$$

Note that \(\frac{\ln(E/\delta)}{ \ln\frac{E}{2\delta}-\frac{2p}{2p+1}\ln (\ln\frac{E}{\delta} )}\to1\) for \(\delta\to0\). The theorem is proved. □

We give the regularized solution for problem (1.1):

$$ u^{\delta}_{\alpha}(x, t) =\sum ^{+\infty}_{n=-\infty} \biggl[\frac{(\cosh(\sqrt{in}x))(f^{\delta }(t),e^{int})}{1+\alpha^{2}|\cosh(\sqrt{in}x)|^{2}} + \frac{\frac{\sinh(\sqrt{in}x)}{\sqrt{in}} (g^{\delta }(t),e^{int})}{1+\alpha^{2}|\frac{\sinh(\sqrt{in}x)}{\sqrt{in}}|^{2}} \biggr] e^{int}. $$
(4.19)

Similarly, the modified Tikhonov regularized solution is

$$ u^{\delta,\ast}_{\alpha}(x, t) =\sum ^{+\infty}_{n=-\infty} \biggl[\frac{(\cosh(\sqrt{in}x))(f^{\delta }(t),e^{int})}{1+\alpha^{2}|\cosh(\sqrt{in})|^{2}} + \frac{\frac{\sinh(\sqrt{in}x)}{\sqrt{in}} (g^{\delta }(t),e^{int})}{1+\alpha^{2}|\sinh(\sqrt{in})|^{2}} \biggr] e^{int}. $$
(4.20)

Analogously, we have the error estimate for problem (1.1).

Theorem 4.3

Let \(u(x,t)\) be the exact solution given by (2.6), and \(u^{\delta,\ast}_{\alpha}(x,t)\) given by (4.20) be the modified Tikhonov regularization solution of problem (1.1). Suppose that the noisy data \(f^{\delta}(t)\) and \(g^{\delta}(t)\) satisfy (2.1) and the a priori condition (2.7) is valid. If \(0<2\alpha<1/e^{\sqrt[4]{3}} \) and the regularization parameter is chosen as (4.9), then for fixed \(x\in(0,1]\), we obtain

$$ \bigl\Vert u(x,\cdot)-u^{\delta,\ast}_{\alpha}(x,\cdot) \bigr\Vert \le c^{-x}E^{x}\delta^{1-x} \biggl(\ln \frac{E}{\delta} \biggr)^{\frac{-2p}{2p+1}x} \bigl[\sqrt{2}x+1+2c^{-1}+o(1) \bigr],\quad \delta \to0. $$
(4.21)

Remark 4.4

  1. (i)

    If we choose \(p=0\), estimate (4.21) becomes

    $$ \bigl\Vert u(x,\cdot)-u^{\delta,\ast}_{\alpha}(x,\cdot) \bigr\Vert \le \bigl((\sqrt{2}x+1)c^{-x}+2c^{-(x+1)} \bigr)E^{x} \delta^{1-x}, $$
    (4.22)

    it is a Hölder type stability estimate.

  2. (ii)

    If we choose \(p>0\), estimate (4.21) is a logarithmic-Hölder type error estimate, especially at \(x=1\), it is a logarithmic type convergence estimate.

5 Numerical experiments

In this section, we present two numerical examples to illustrate the effectiveness of the suggested regularization method. The grid numbers on the space and time intervals are taken to be \(M=101\), \(J=301\), refer to [18]. The noisy Cauchy data are generated by

$$ f^{\delta}(t_{j})=f(t_{j}) \bigl(1+\varepsilon\cdot \operatorname{rand}(j)\bigr),\qquad g^{\delta }(t_{j})=g(t_{j}) \bigl(1+\varepsilon\cdot \operatorname{rand}(j)\bigr), $$

where \(t_{j}\) is a set of discrete times on interval \([0,2\pi]\), \(f(t_{j})\) and \(g(t_{j})\) are the exact Cauchy data, \(\operatorname{rand}(t_{j})\) is a random number uniformly distributed on \([-1,1]\), and the magnitude ε indicates the relative noise level. In the tests, the noise level δ is computed according to

$$ \delta=\max \bigl\{ \bigl\Vert f-f^{\delta}\bigr\Vert ,\bigl\Vert g-g^{\delta}\bigr\Vert \bigr\} . $$

In order to present the performance of the modified Tikhonov method, we define the relative root mean square error at fixed x as

$$ e(u)=\frac{\sqrt{\sum_{j=1}^{J}(u(\cdot,t_{j})-u_{\alpha}^{\delta,*}(\cdot ,t_{j}))^{2}}}{\sqrt{\sum_{j=1}^{J}u^{2}(\cdot,t_{j})}}. $$
(5.1)

Example 1

The exact solution of problem (1.1) with \(f(t)=1-\cos t\) and \(g(t)=0\) is given by

$$ u(x,t)=1-\frac{1}{2}\biggl(e^{\frac{x}{\sqrt{2}}}\cos\biggl( \frac{x}{\sqrt {2}}+t\biggr)+e^{-\frac{x}{\sqrt{2}}}\cos\biggl(\frac{x}{\sqrt{2}}-t\biggr) \biggr). $$

As the regularized solution in (4.20) is an infinite series, we compute it from \(n=-50\) to \(n=50\) in both examples. If we take \(p=0\), the a priori bound can be calculated as \(E=3.1543\) according to (2.7), and the regularization parameter \(\alpha=0.0054, 0.0277\) from (4.9) for \(\varepsilon=0.01, 0.05\), respectively.

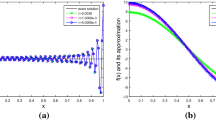
Figure 1 compares the stability of the regularized solution computed by the classic Tikhonov method and the modified Tikhonov method at fixed point \(x=0.4\) with \(\varepsilon=0.01\). The relative root mean square errors for them are \(e(u)=0.0060\) and \(e(u)=0.0059\), respectively. For these two methods, there is almost no difference in the numerical results. However, in theoretical analysis, it is much easier to obtain the explicit error estimate for the modified Tikhonov method than to do it for the classic Tikhonov method.

Figure 1
figure 1

The Tikhonov regularized solution and the modified Tikhonov regularized solution at fixed point \(\pmb{x=0.4}\) with \(\pmb{\varepsilon =0.01}\) .

Full size image

Figure 2 gives the comparison of the exact solution and its approximations with different noise. Since the exact solution \(u(x,t)\) is a periodic function with variable t, the approximate solution converges to the exact solution everywhere. We see that the approximations are acceptable for both interior and boundary temperature, and the numerical results are stable with the increase of noisy levels.

Figure 2
figure 2

Comparison of the exact solution with the modified Tikhonov regularized solution. (a) \(x=0.2\), (b) \(x=0.4\), (c) \(x=0.9\), (d) \(x=1\).

Full size image

Table 1 shows the relative root mean square errors for different x with \(\varepsilon=0.01\) and \(\varepsilon=0.05\), respectively. From this table, it is easy to see that the smaller the x the better the computed approximation. This is consistent with the theoretical result (4.21).

Table 1 The relative root mean square errors with \(\pmb{\varepsilon=0.01}\) and \(\pmb{\varepsilon=0.05}\) for Example 1
Full size table

In the next example, we will show the case in which the exact solution is not given.

Example 2

The solution itself satisfies the following equations:

$$\begin{aligned}& u_{t}=u_{xx},\quad 0< x< 1, 0< t< 2\pi, \\& u(0,t)=0,\quad 0\le t\le2\pi, \\& u(1,t)=H(t), \quad 0\le t\le2\pi, \end{aligned}$$
(5.2)

where \(H(t)\) is the Heaviside function. We use the method of the fundamental solution [14] to solve the forward problem and obtain \(g(t)=u_{x}(0,t)\). The boundary data \(g(t)\) is disturbed by a random error, and the modified Tikhonov method is used to stabilize this inverse heat conduction problem.

For this example, we can calculate by Matlab that \(E=2.5238\), and the regularization parameter \(\alpha=0.0059, 0.0165\) for \(\varepsilon=0.01, 0.03\), respectively.

In Figure 3, we see that the regularized solution is drastically oscillatory at \(t=2\pi\), while the numerical result is acceptable for other points. The reason for this phenomenon is that the solution \(u(x,t)\) is not periodic to variable t, and thus the Fourier series (2.6) does not converge at the endpoint.

Figure 3
figure 3

Comparison of the exact solution with the modified Tikhonov regularized solution. (a) \(x=0.2\), (b) \(x=0.4\).

Full size image

6 Conclusion

In this paper, the inverse heat conduction problem with only boundary value in a bounded domain has been investigated. The conditional stability is given. We propose a modified Tikhonov regularization method for obtaining a regularized solution. Based on an a priori assumption for the exact solution, the order optimal error estimate is obtained with a suitable choice of regularization parameter. Numerical examples show that our proposed method is effective and stable.